Figure 1.
The proposed Stair-Climbing Mobility System (SCMS) is characterized by the fact that it can climb up and down stairs of different sizes and maintain a stable equilibrium on the stair at all times without assistance. It is also characterized by the fact that it can estimate the size of the stair using laser distance sensors and generate safe and comfortable trajectories for the central platform when carrying a user.
Figure 1.
The proposed Stair-Climbing Mobility System (SCMS) is characterized by the fact that it can climb up and down stairs of different sizes and maintain a stable equilibrium on the stair at all times without assistance. It is also characterized by the fact that it can estimate the size of the stair using laser distance sensors and generate safe and comfortable trajectories for the central platform when carrying a user.
Figure 2.
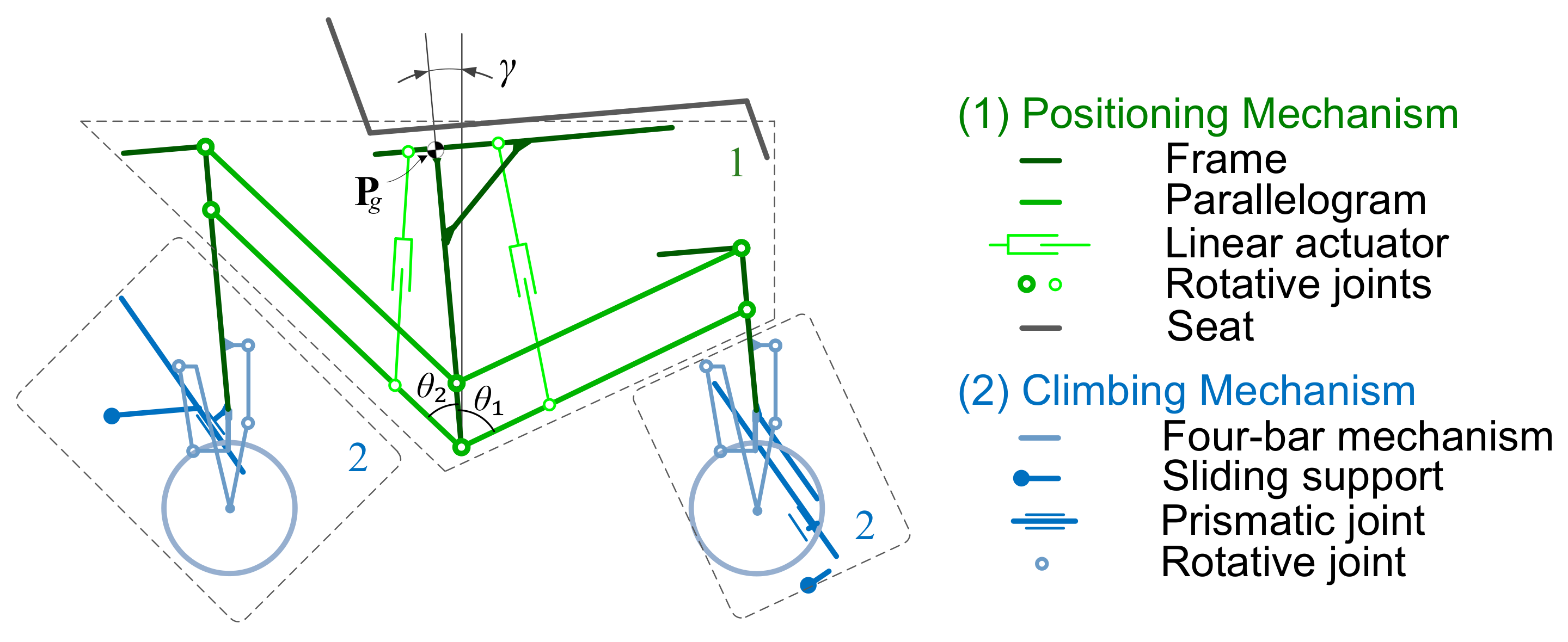
Kinematic scheme of the SCMS: (1) positioning mechanism, which is responsible for ensuring the posture of the entire vehicle; (2) climbing mechanism, which is responsible for surpassing the obstacle.
Figure 2.
Kinematic scheme of the SCMS: (1) positioning mechanism, which is responsible for ensuring the posture of the entire vehicle; (2) climbing mechanism, which is responsible for surpassing the obstacle.
Figure 3.
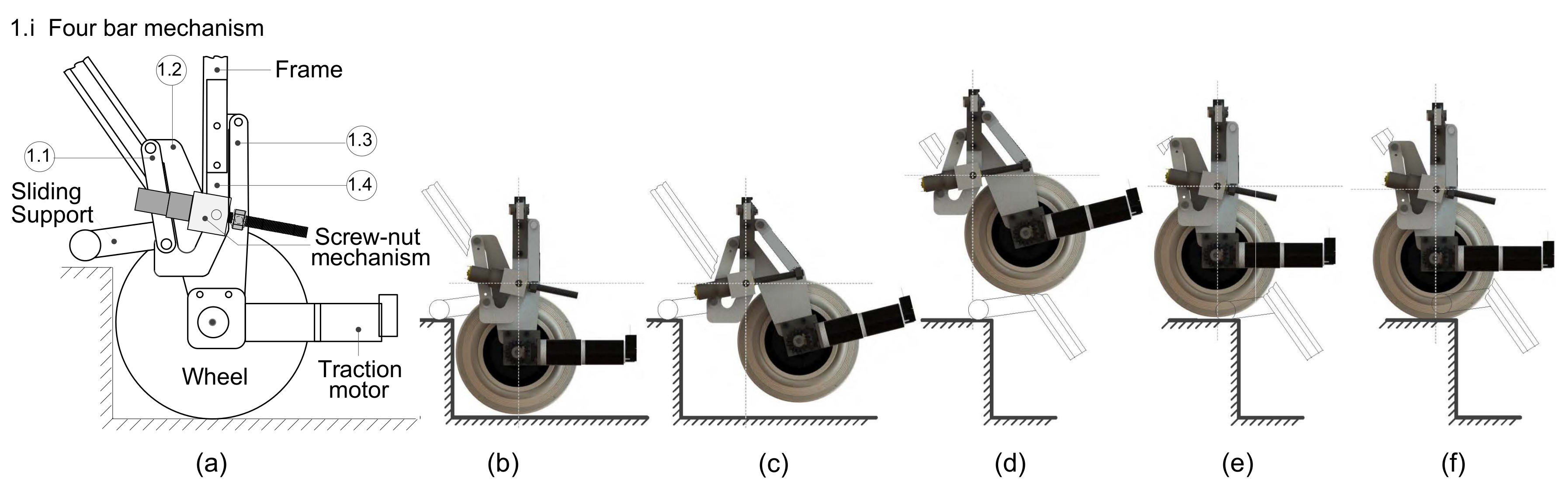
Actuating sequence of the rear climbing mechanism. . In (a) the wheel makes contact with the ground. In (b) the sliding support slides and makes contact with the step tread and the wheel is off the ground. In (c) the screw-nut mechanism is again actuated and the sliding support continues to slide. In (d) the sliding support is completely deployed. In (e) the screw-nut mechanism is actuated and the wheel moves backwards to its initial point. In (f) the wheel again makes contact with the ground and the sliding support is retracted.
Figure 3.
Actuating sequence of the rear climbing mechanism. . In (a) the wheel makes contact with the ground. In (b) the sliding support slides and makes contact with the step tread and the wheel is off the ground. In (c) the screw-nut mechanism is again actuated and the sliding support continues to slide. In (d) the sliding support is completely deployed. In (e) the screw-nut mechanism is actuated and the wheel moves backwards to its initial point. In (f) the wheel again makes contact with the ground and the sliding support is retracted.
Figure 4.
Possible configurations of the SCMS.
Figure 4.
Possible configurations of the SCMS.
Figure 5.
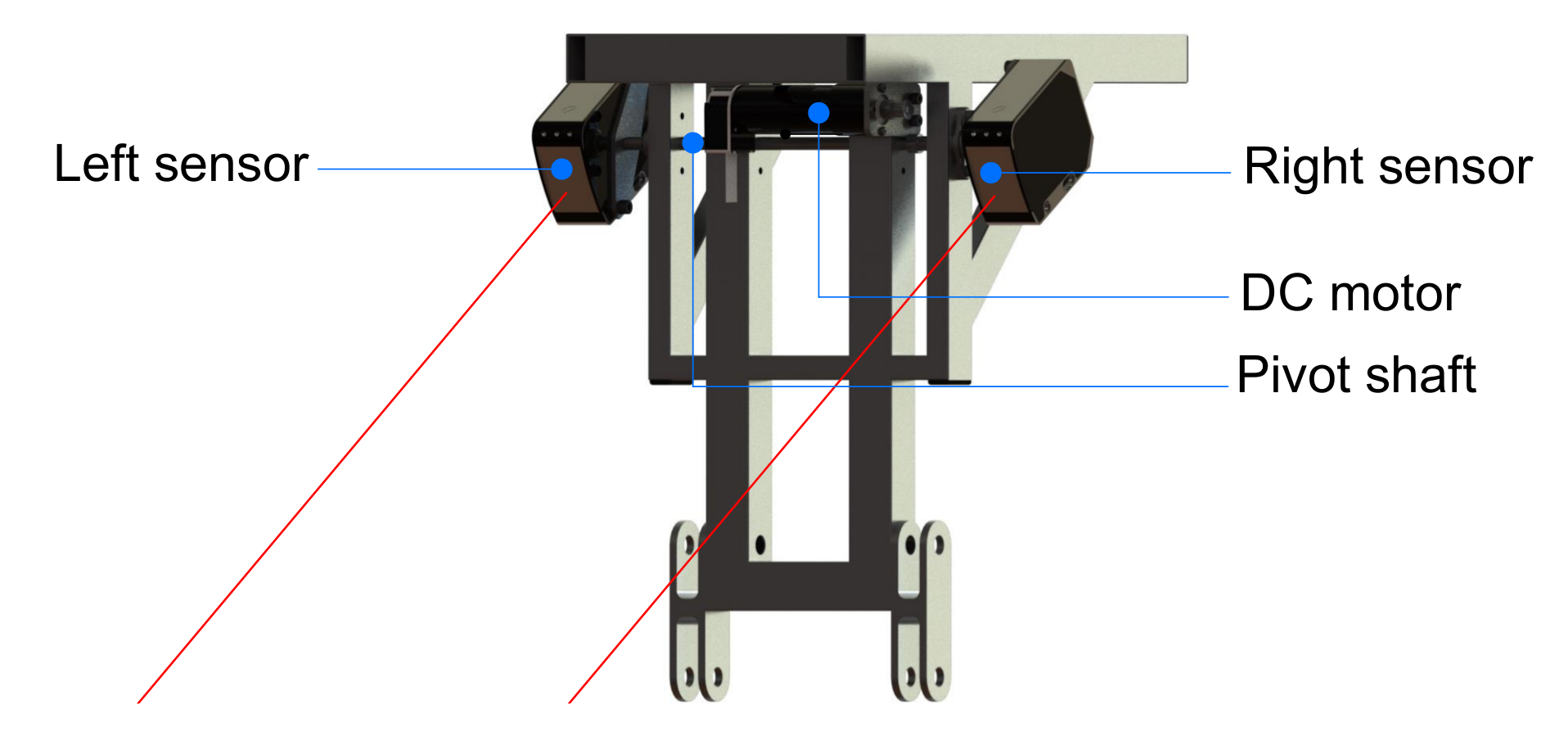
Scanning system positioned on the SCMS frame.
Figure 5.
Scanning system positioned on the SCMS frame.
Figure 6.
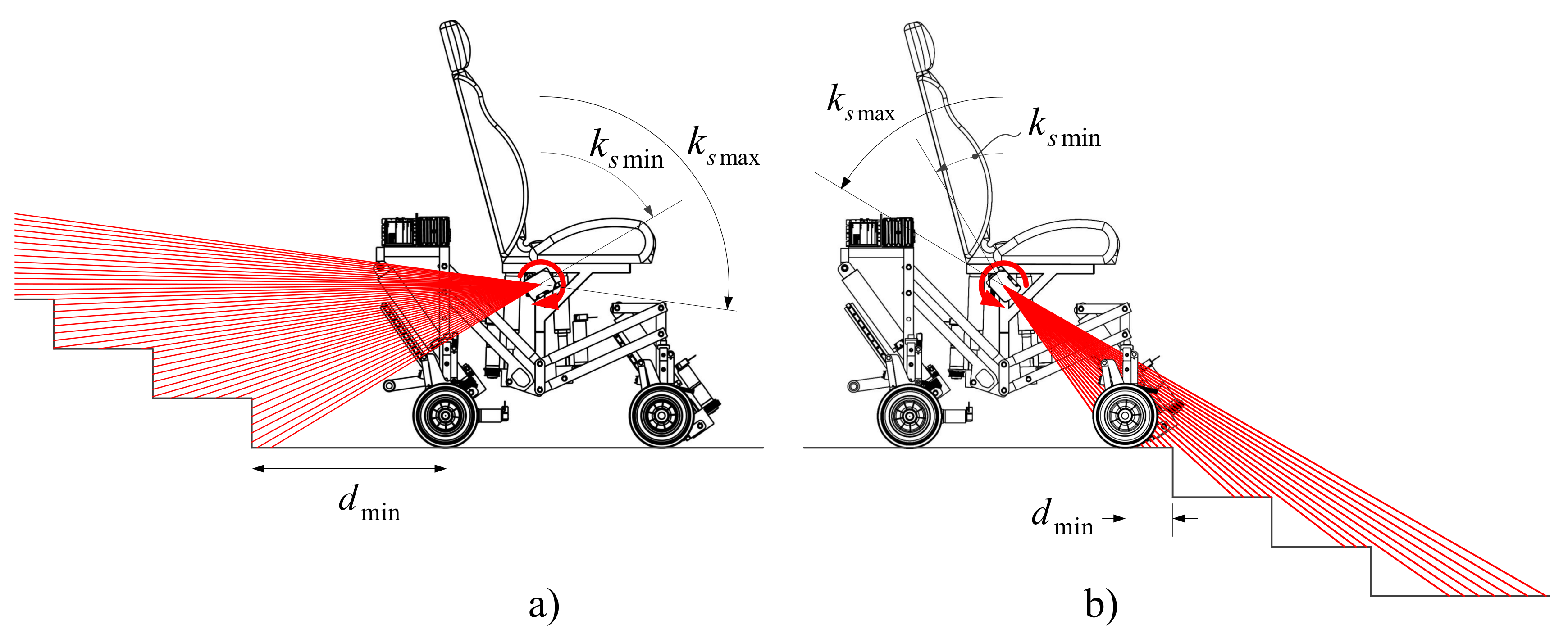
Side view of scanning on the staircase surface; (a) before climbing up and (b) before climbing down.
Figure 6.
Side view of scanning on the staircase surface; (a) before climbing up and (b) before climbing down.
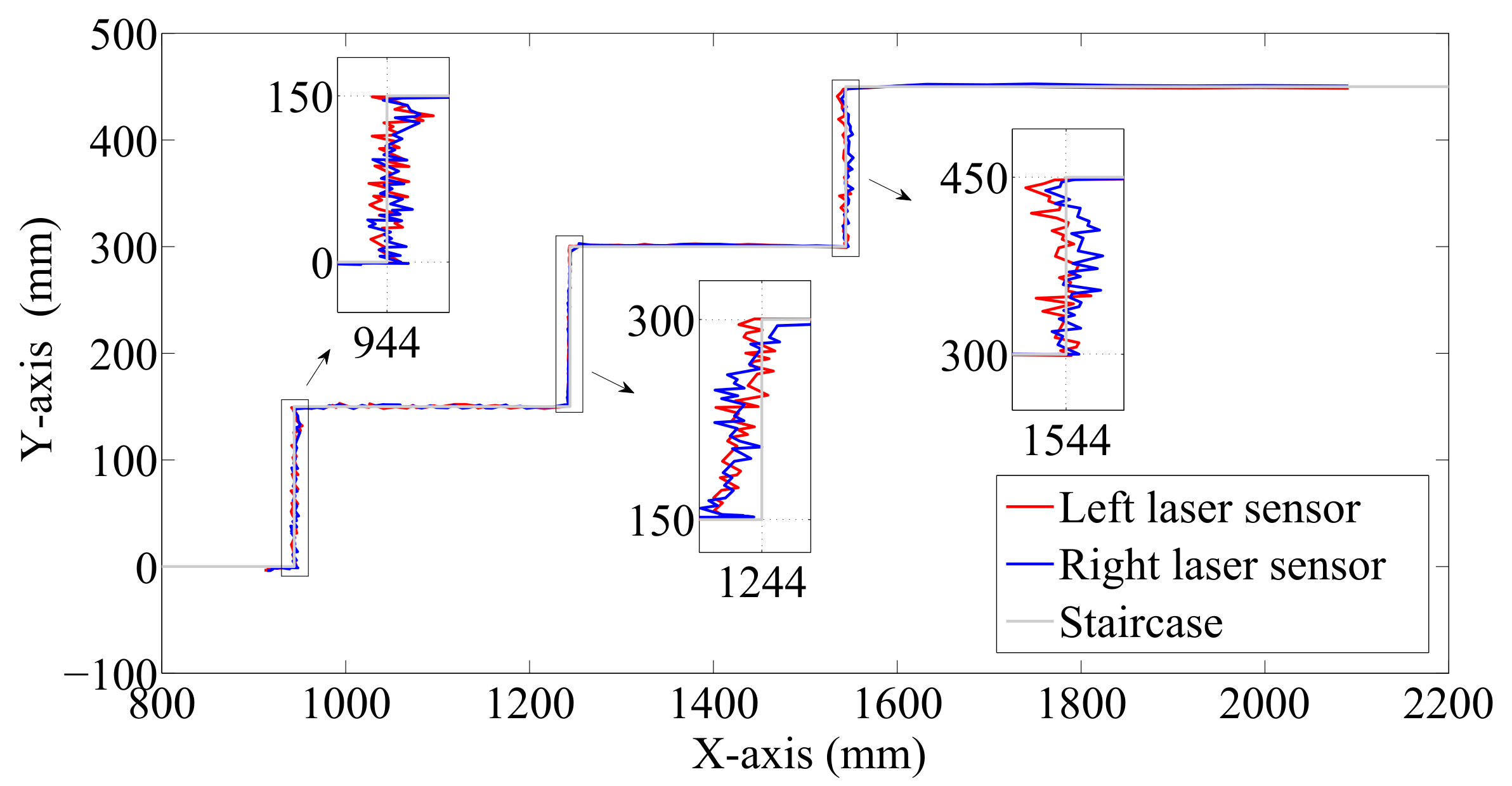
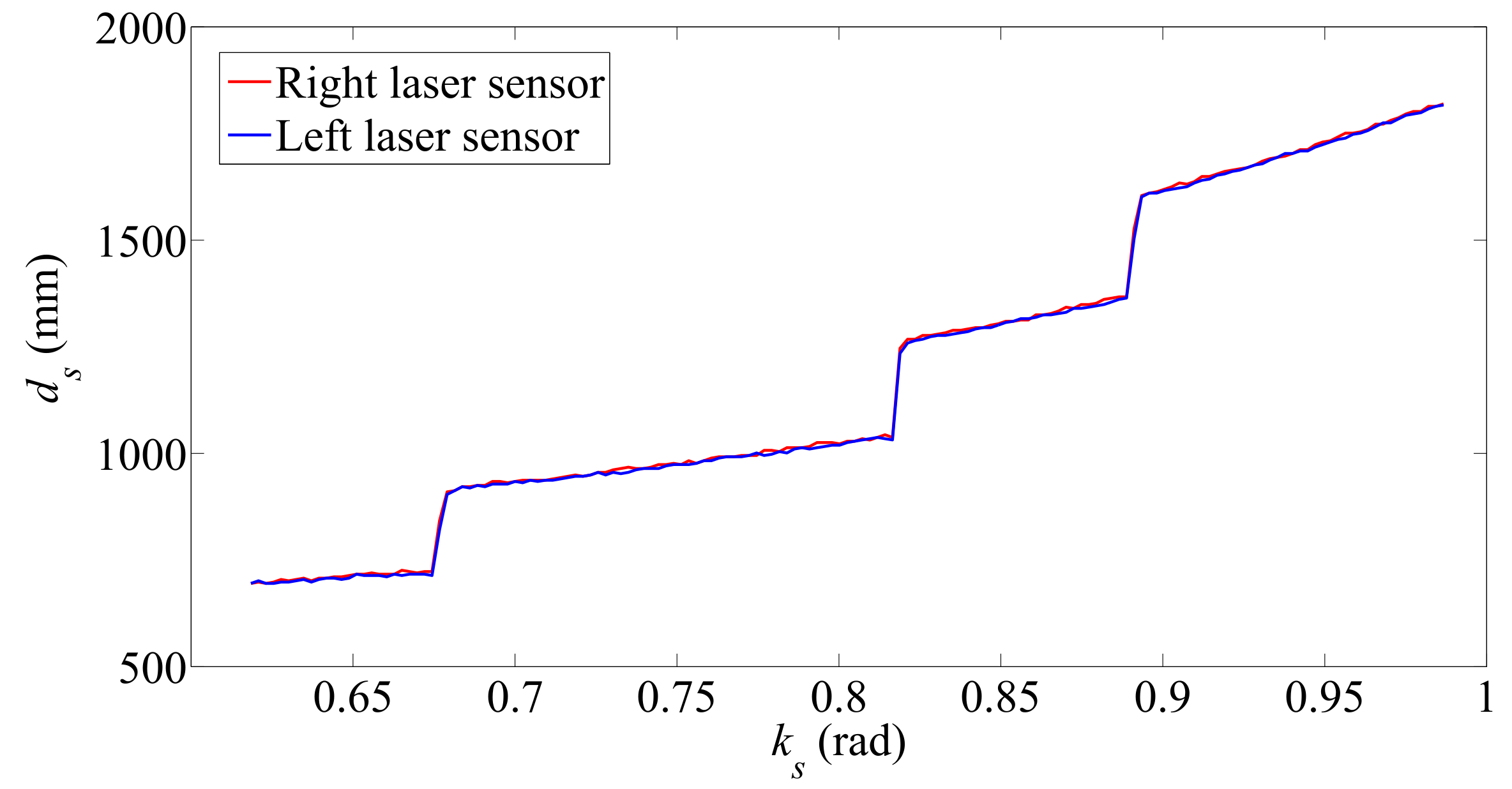
Figure 7.
Distance measured during the scanning on the staircase surface before climbing up.
Figure 7.
Distance measured during the scanning on the staircase surface before climbing up.
Figure 8.
Estimated shape and size of the staircase.
Figure 8.
Estimated shape and size of the staircase.
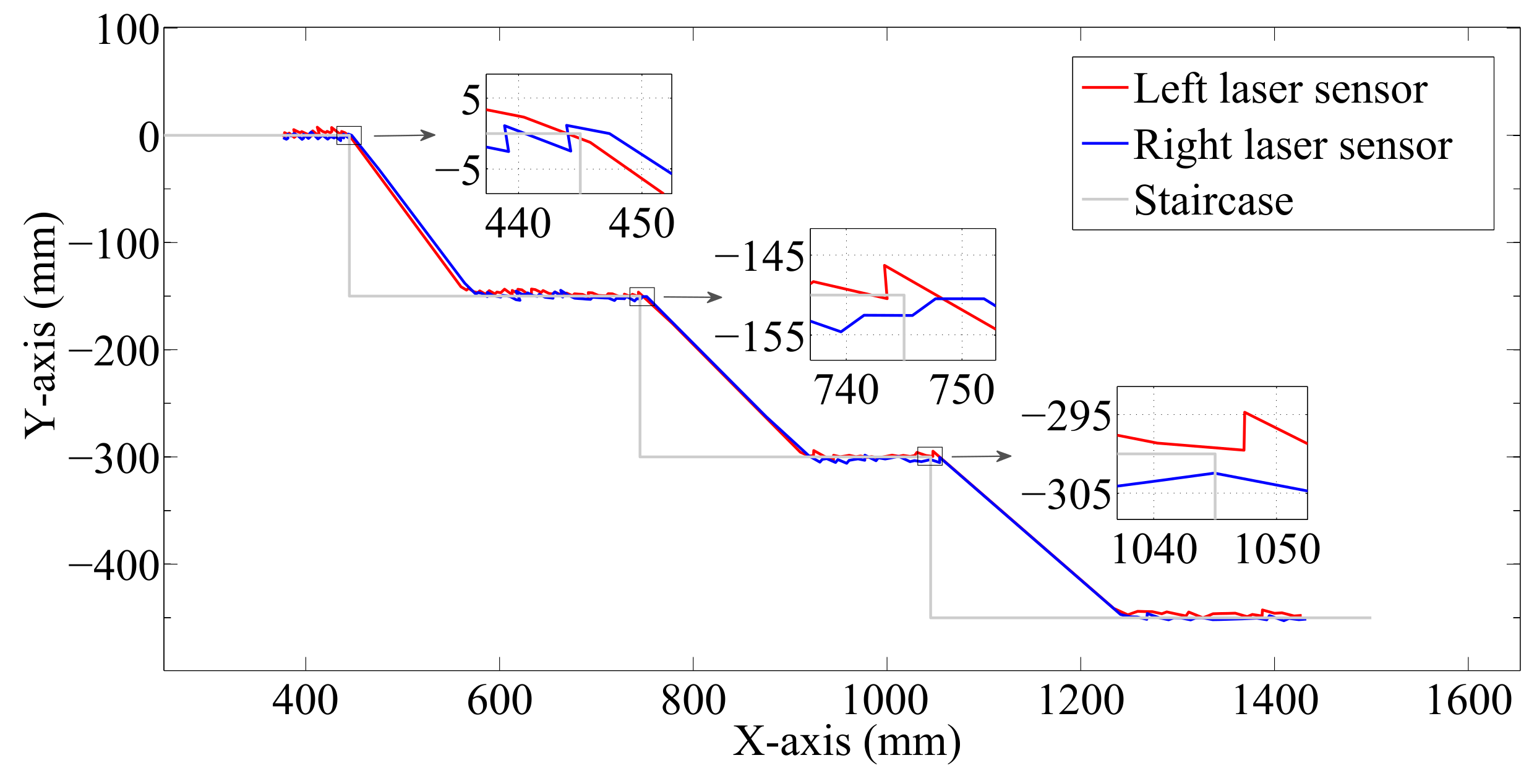
Figure 9.
Distance measured during the scanning on the staircase surface before climbing down.
Figure 9.
Distance measured during the scanning on the staircase surface before climbing down.
Figure 10.
Estimated shape and size of the staircase.
Figure 10.
Estimated shape and size of the staircase.
Figure 11.
General kinematic scheme for the different configurations of the SCMS.
Figure 11.
General kinematic scheme for the different configurations of the SCMS.
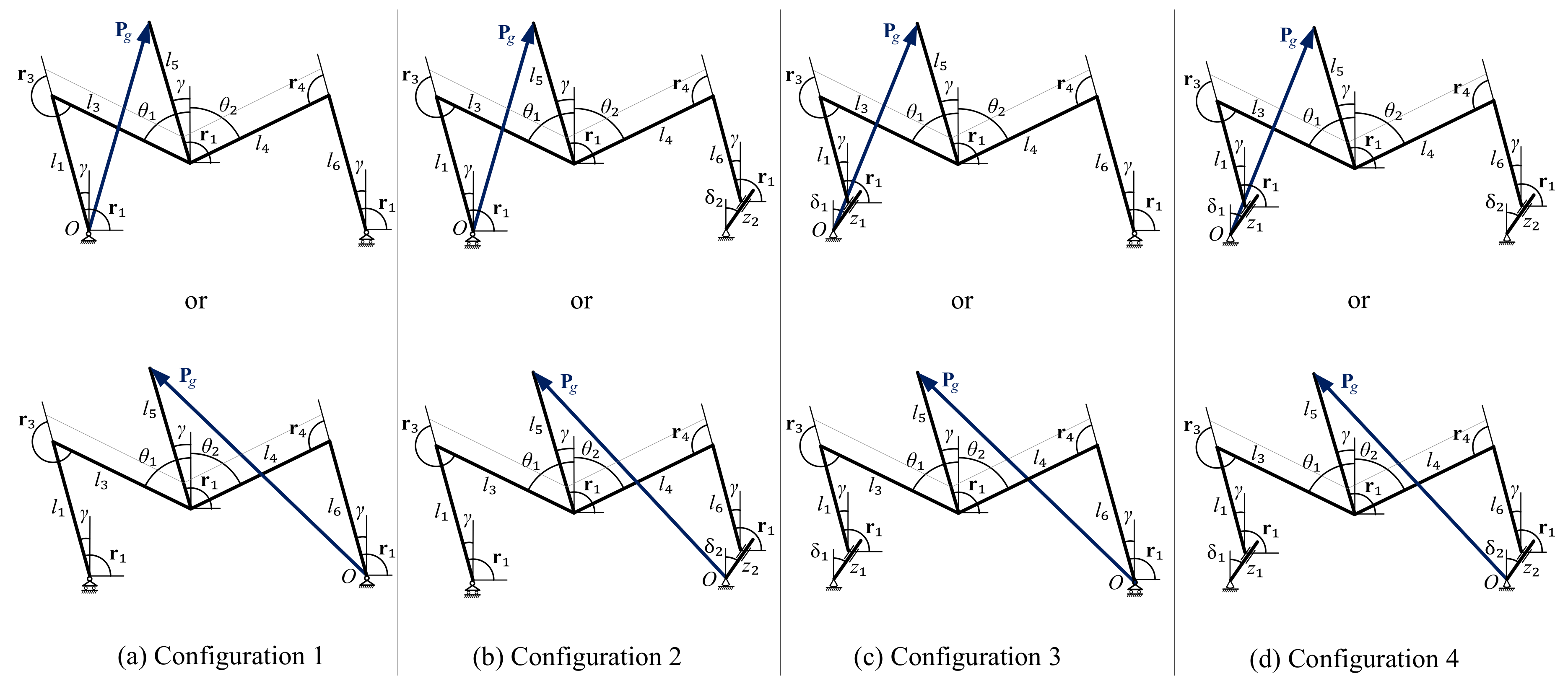
Figure 12.
Definition of the generalized coordinate variables for each of the configurations of the SCMS.
Figure 12.
Definition of the generalized coordinate variables for each of the configurations of the SCMS.
Figure 13.
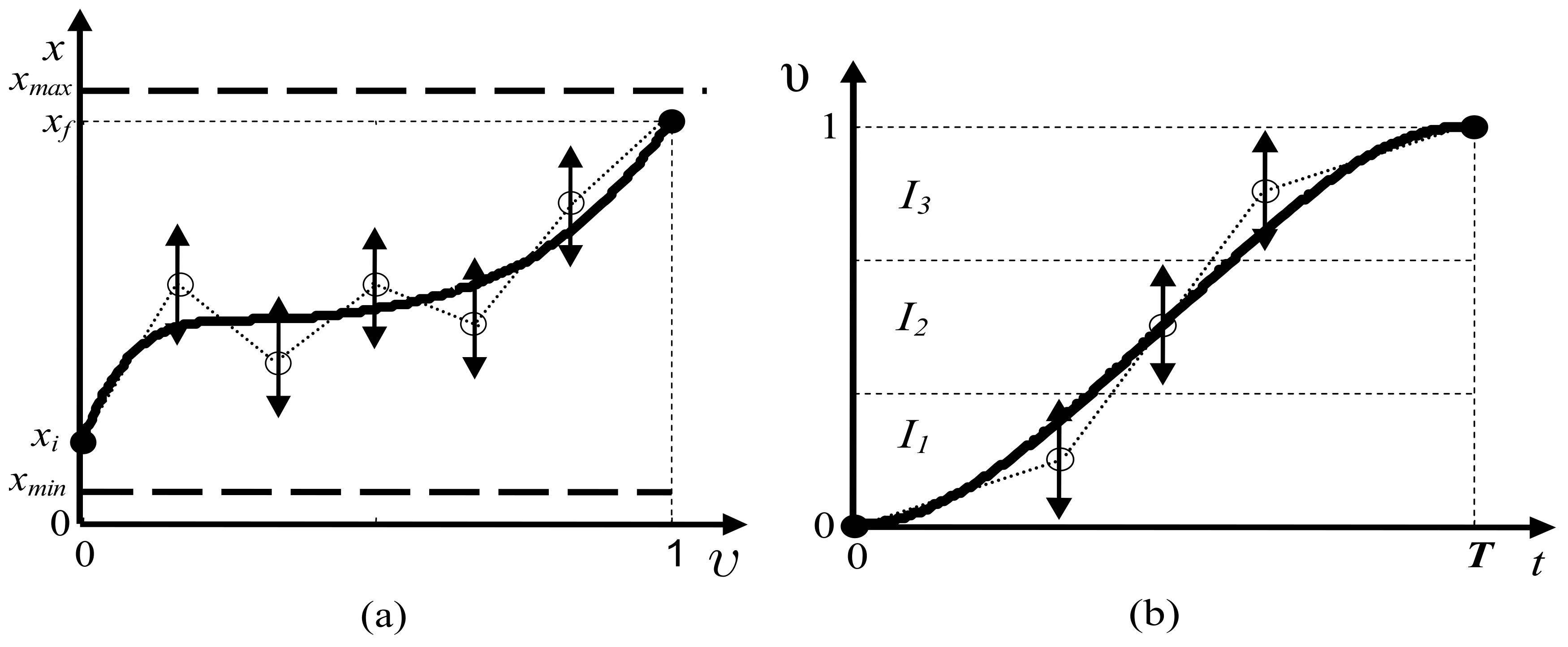
Path and motion profiles. (a) A path component profile and (b) the motion profile.
Figure 13.
Path and motion profiles. (a) A path component profile and (b) the motion profile.
Figure 14.
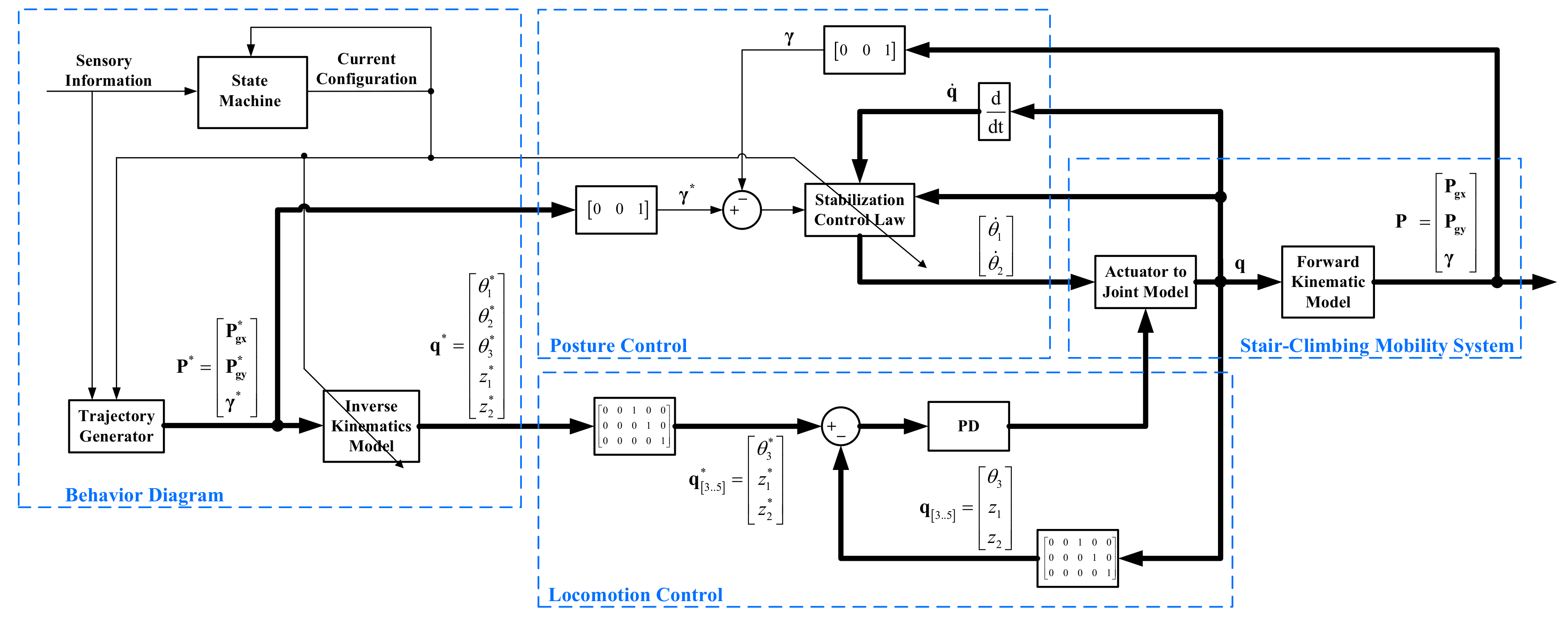
Control scheme of the proposed SCMS.
Figure 14.
Control scheme of the proposed SCMS.
Figure 15.
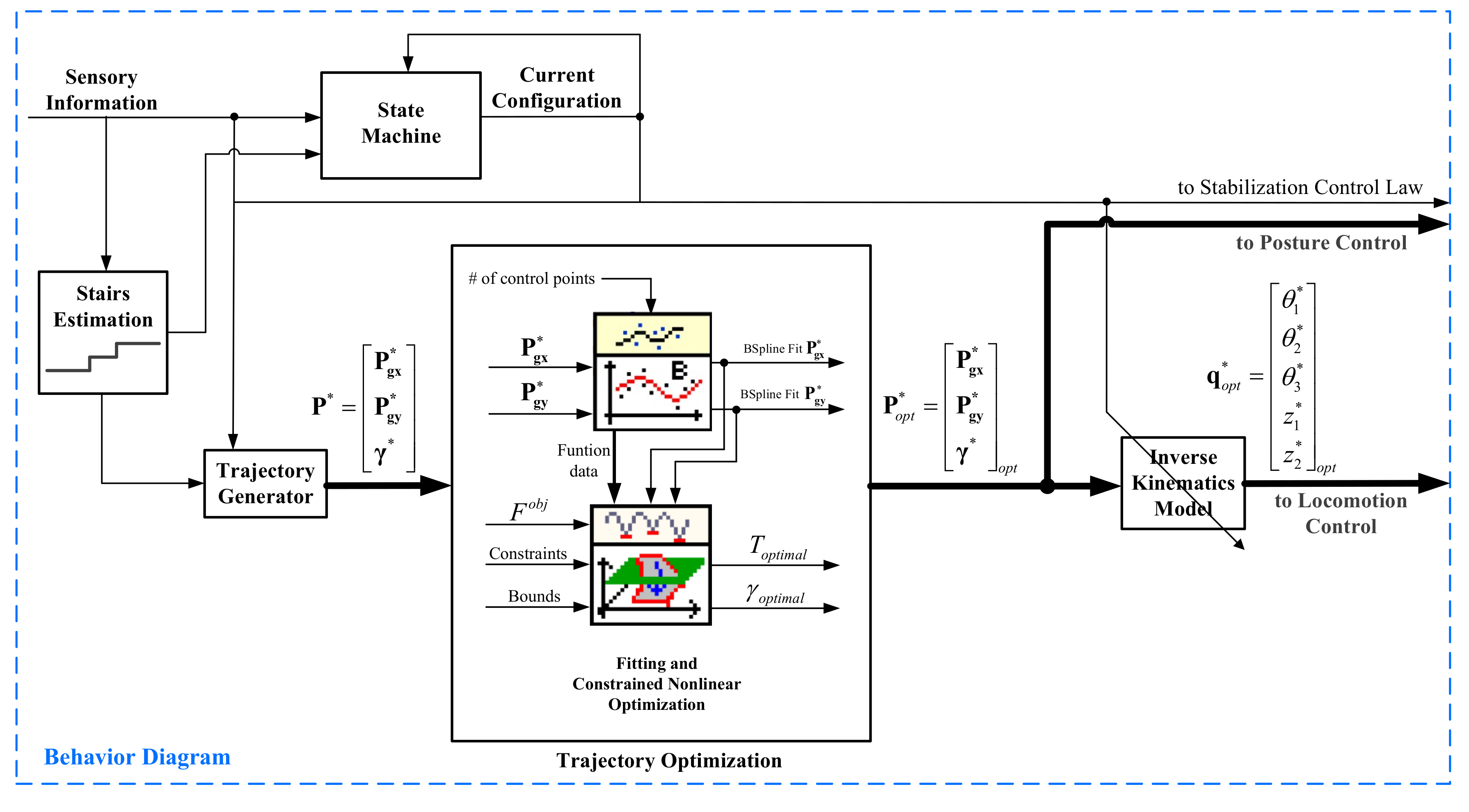
Scheme of the optimal trajectory generator based on constrained nonlinear optimization.
Figure 15.
Scheme of the optimal trajectory generator based on constrained nonlinear optimization.
Figure 16.
Position profiles of the center of mass of the SCMS used in the (a) first and (b) second experiments.
Figure 16.
Position profiles of the center of mass of the SCMS used in the (a) first and (b) second experiments.
Figure 17.
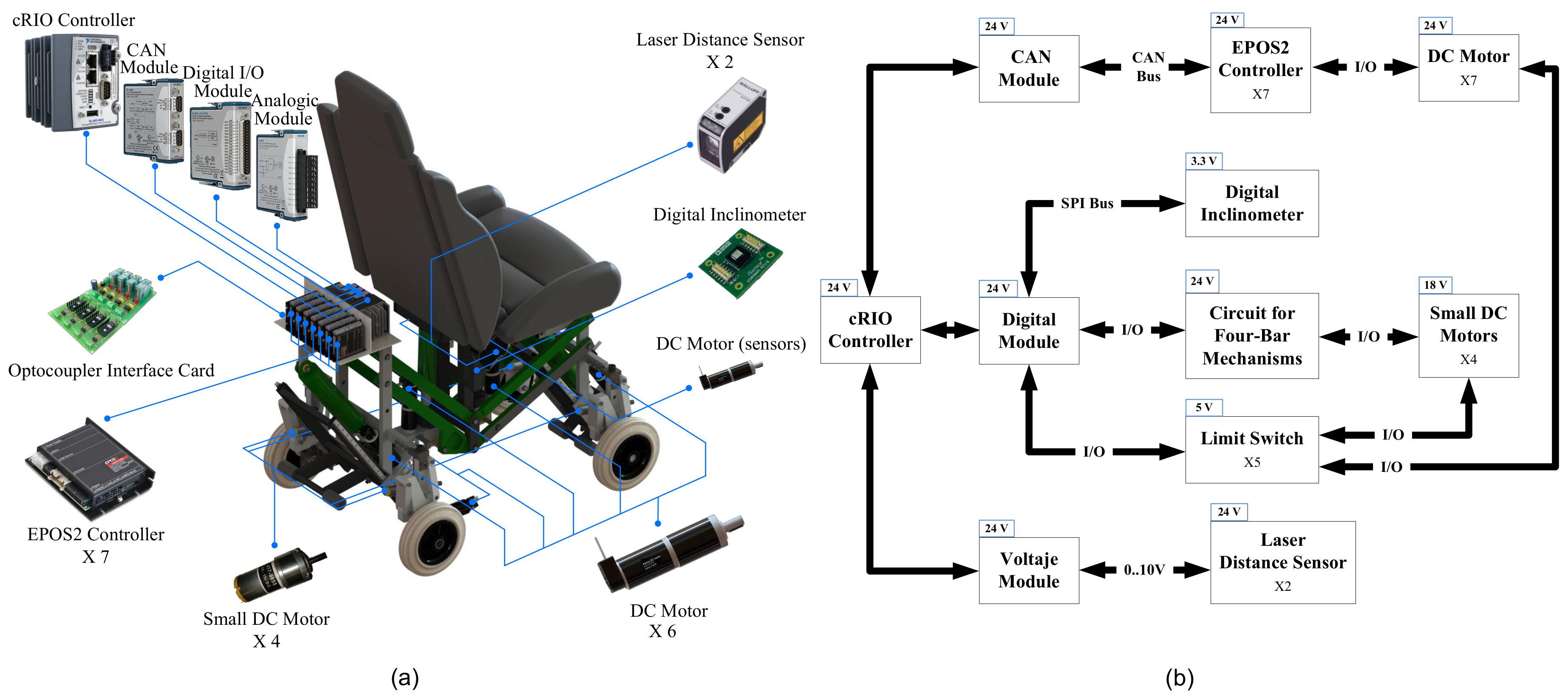
(a) Physical and (b) functional perspective of the hardware control system.
Figure 17.
(a) Physical and (b) functional perspective of the hardware control system.
Figure 18.
The two main Virtual Instruments (VIs) used to solve the optimization problem; (a) the B-Spline Fit VI and (b) the Constrained Nonlinear Optimization VI.
Figure 18.
The two main Virtual Instruments (VIs) used to solve the optimization problem; (a) the B-Spline Fit VI and (b) the Constrained Nonlinear Optimization VI.
Figure 19.
Sequence of climbing process when it surpasses a three-step staircase. All possible configurations of the SCMS are included; Configuration 1 in (
a,
c,
e,
i,
l); Configuration 2 in (
b,
d,
f); Configuration 3 in (
h,
j,
k); and Configuration 4 in (
g). See the video referenced in the
Supplementary Materials.
Figure 19.
Sequence of climbing process when it surpasses a three-step staircase. All possible configurations of the SCMS are included; Configuration 1 in (
a,
c,
e,
i,
l); Configuration 2 in (
b,
d,
f); Configuration 3 in (
h,
j,
k); and Configuration 4 in (
g). See the video referenced in the
Supplementary Materials.
Figure 20.
Sequence of descent process when it surpasses a three-step staircase. All possible configurations of the SCMS are included; Configuration 1 in (
a,
c,
e,
i,
l); Configuration 2 in (
h,
j,
k); Configuration 3 in (
b,
d,
f); and Configuration 4 in (
g). See the video referenced in the
Supplementary Materials.
Figure 20.
Sequence of descent process when it surpasses a three-step staircase. All possible configurations of the SCMS are included; Configuration 1 in (
a,
c,
e,
i,
l); Configuration 2 in (
h,
j,
k); Configuration 3 in (
b,
d,
f); and Configuration 4 in (
g). See the video referenced in the
Supplementary Materials.
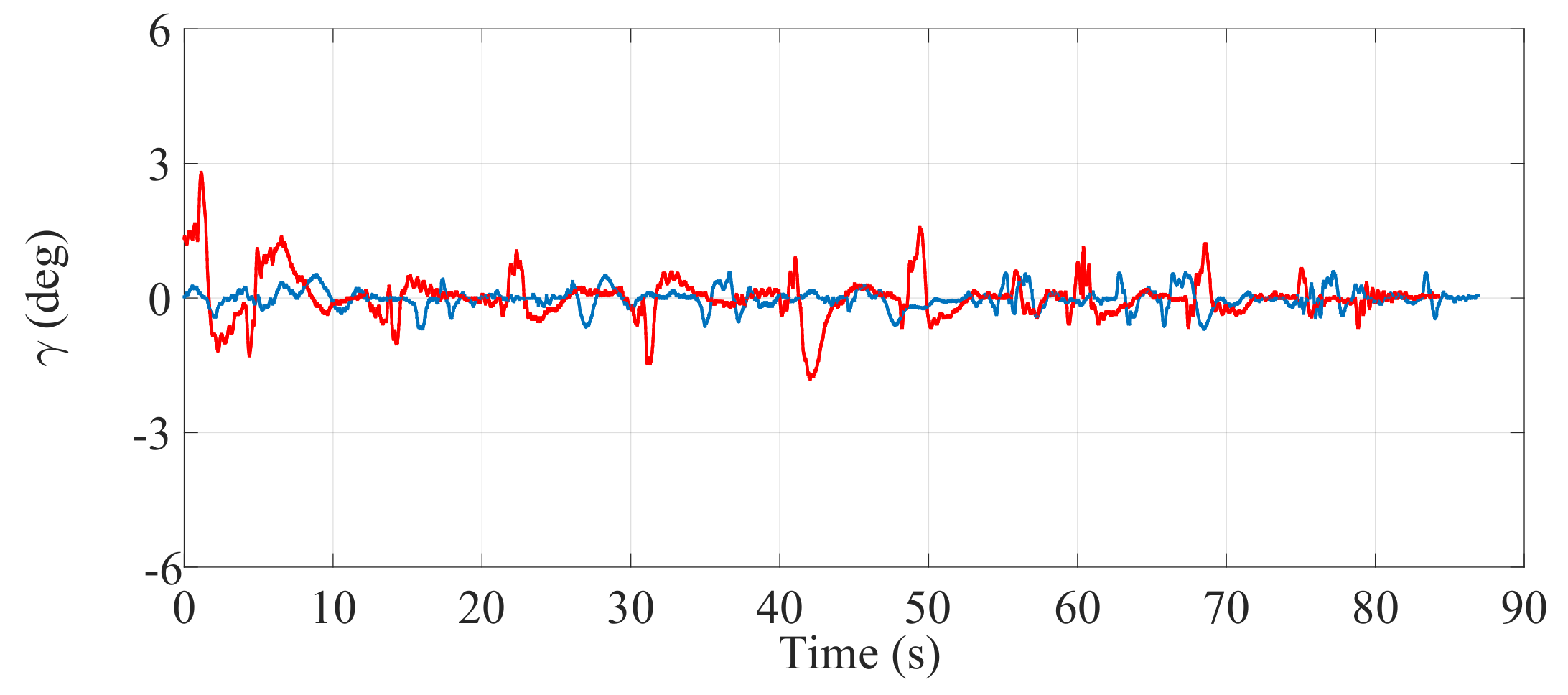
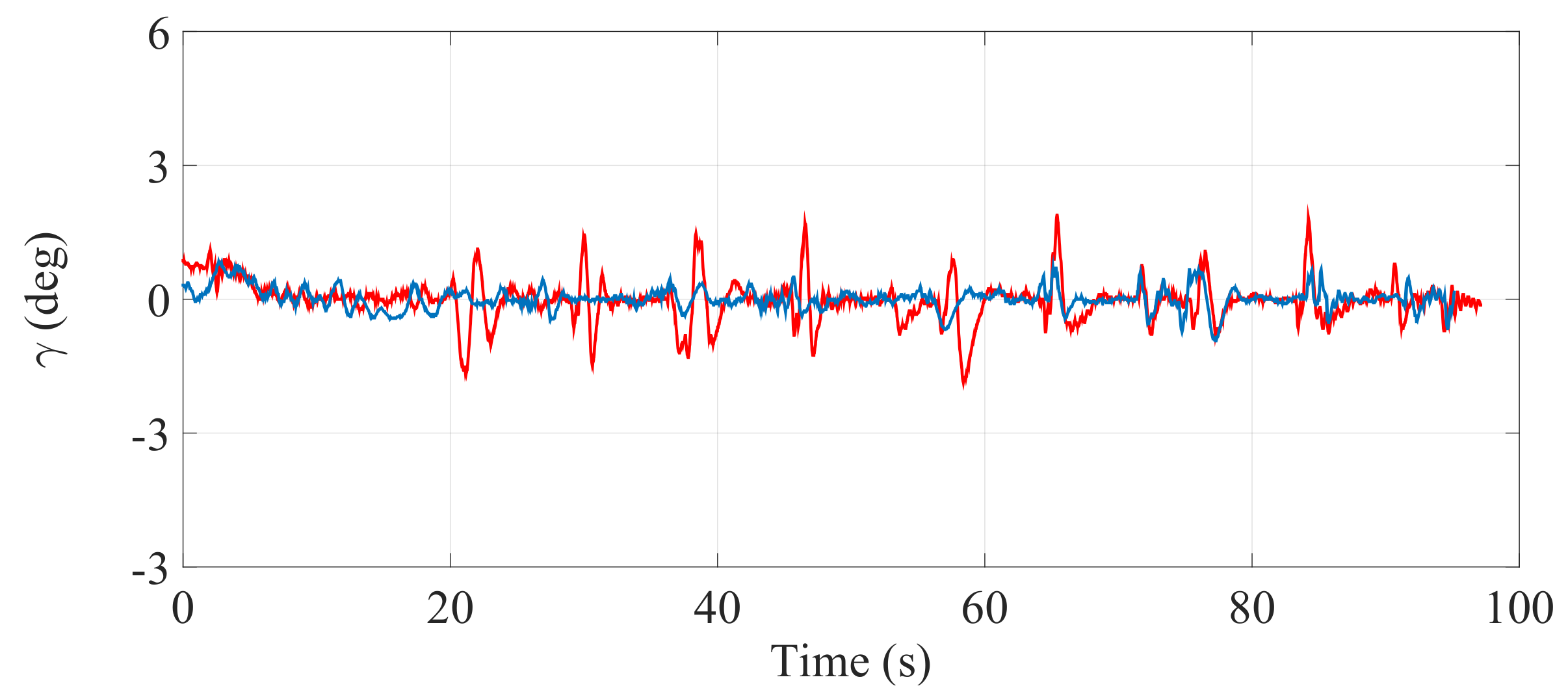
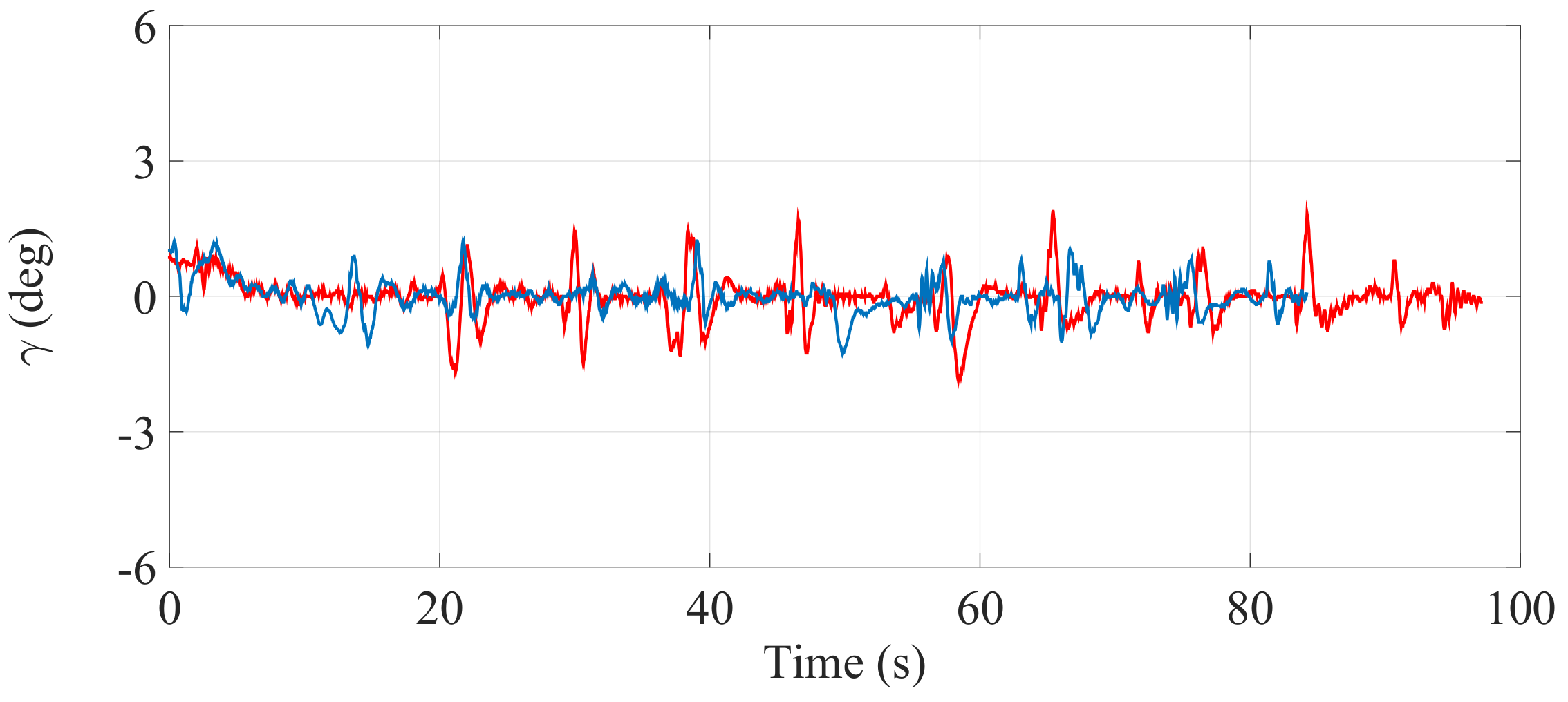
Figure 21.
Inclination of the SCMS frame () when the optimization is carried out with a equal to zero (—) and when the optimization is not considered (—).
Figure 21.
Inclination of the SCMS frame () when the optimization is carried out with a equal to zero (—) and when the optimization is not considered (—).
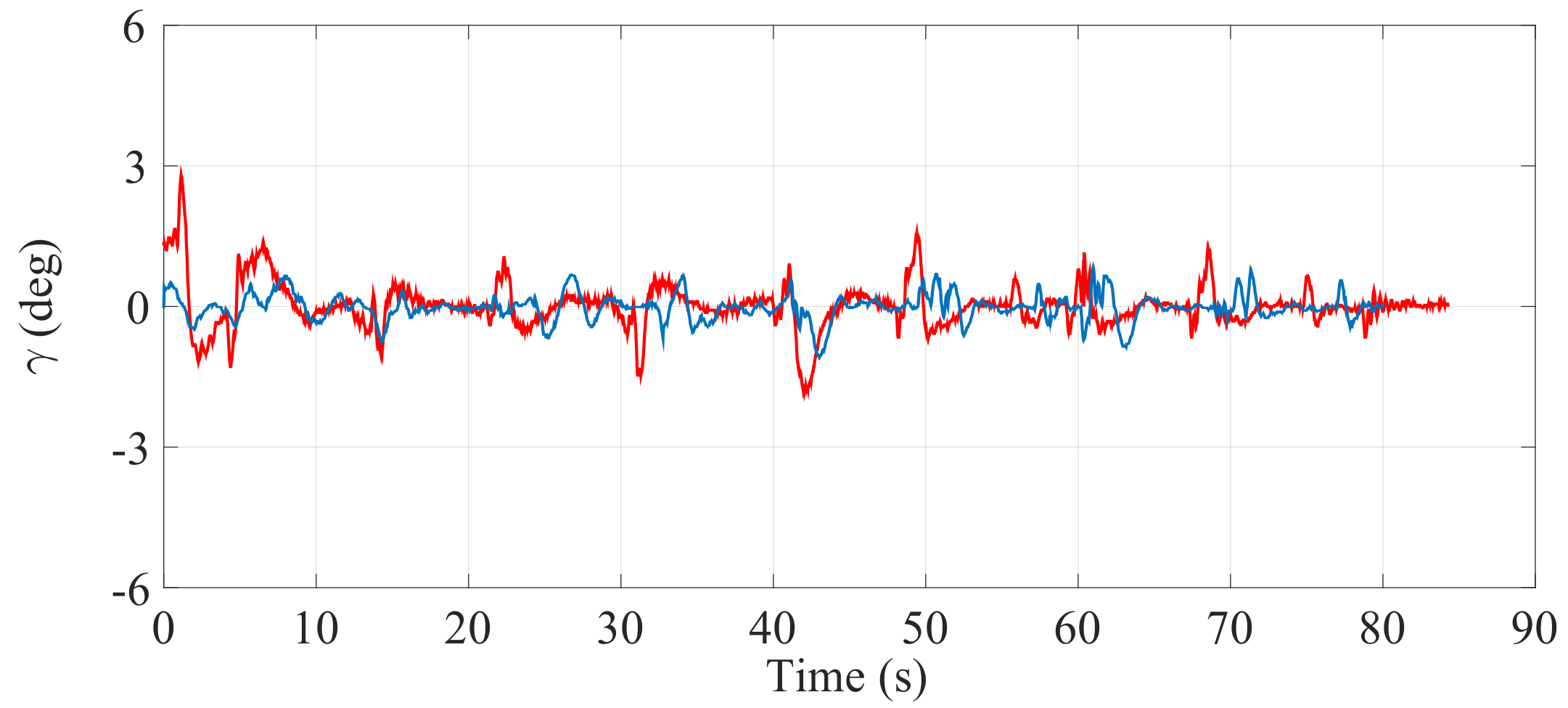
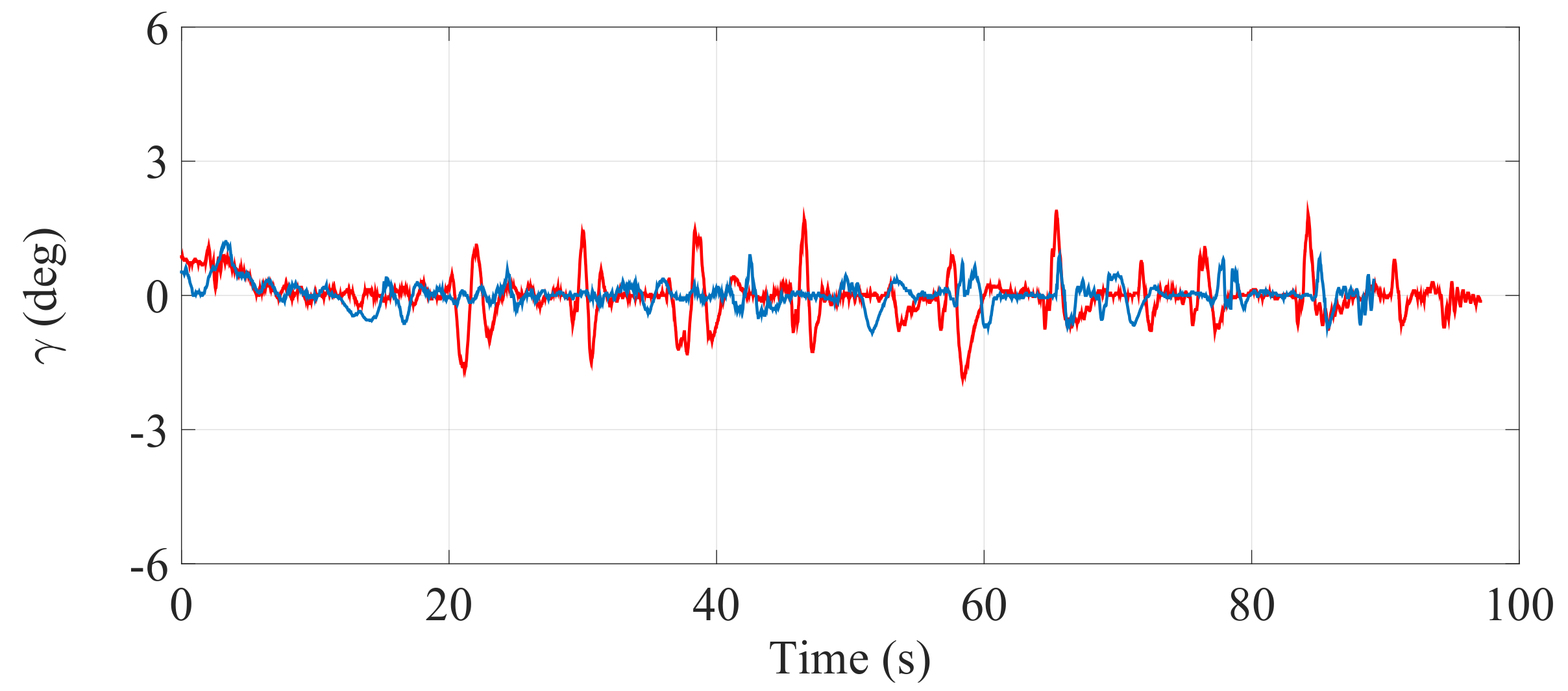
Figure 22.
Inclination of the SCMS frame () when the optimization is carried out with a equal to 0.5 (—) and when the optimization is not considered (—).
Figure 22.
Inclination of the SCMS frame () when the optimization is carried out with a equal to 0.5 (—) and when the optimization is not considered (—).
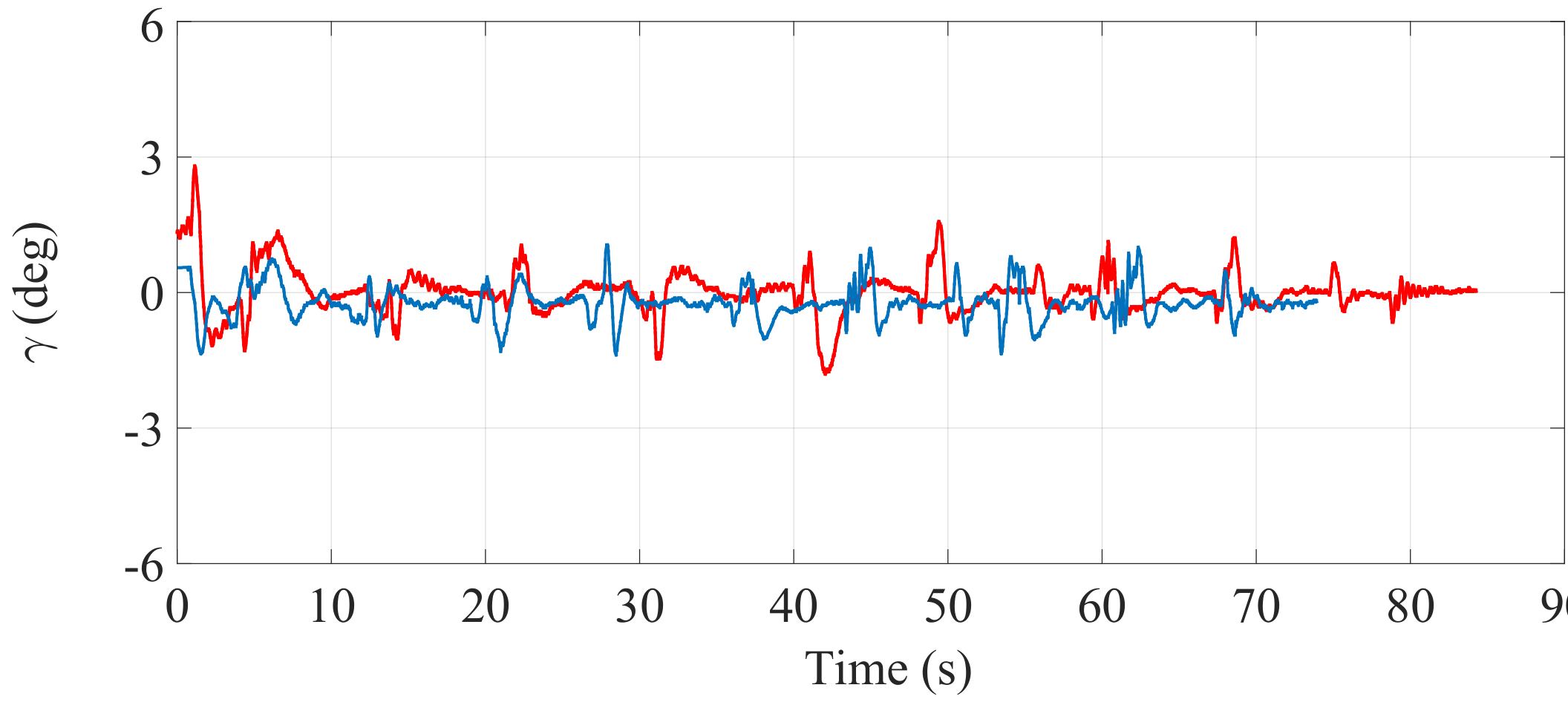
Figure 23.
Inclination of the SCMS frame () when the optimization is carried out with a equal to one (—) and when the optimization is not considered (—).
Figure 23.
Inclination of the SCMS frame () when the optimization is carried out with a equal to one (—) and when the optimization is not considered (—).
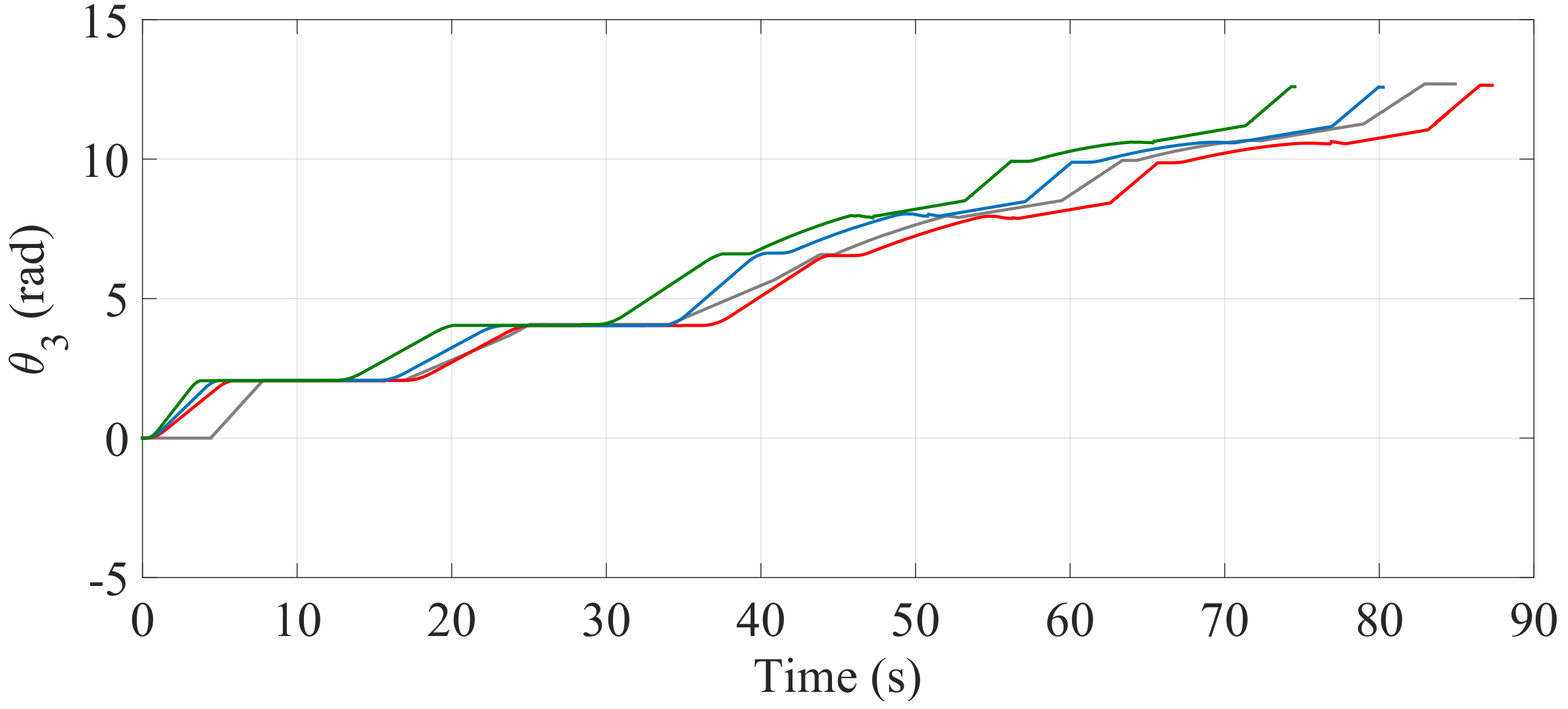
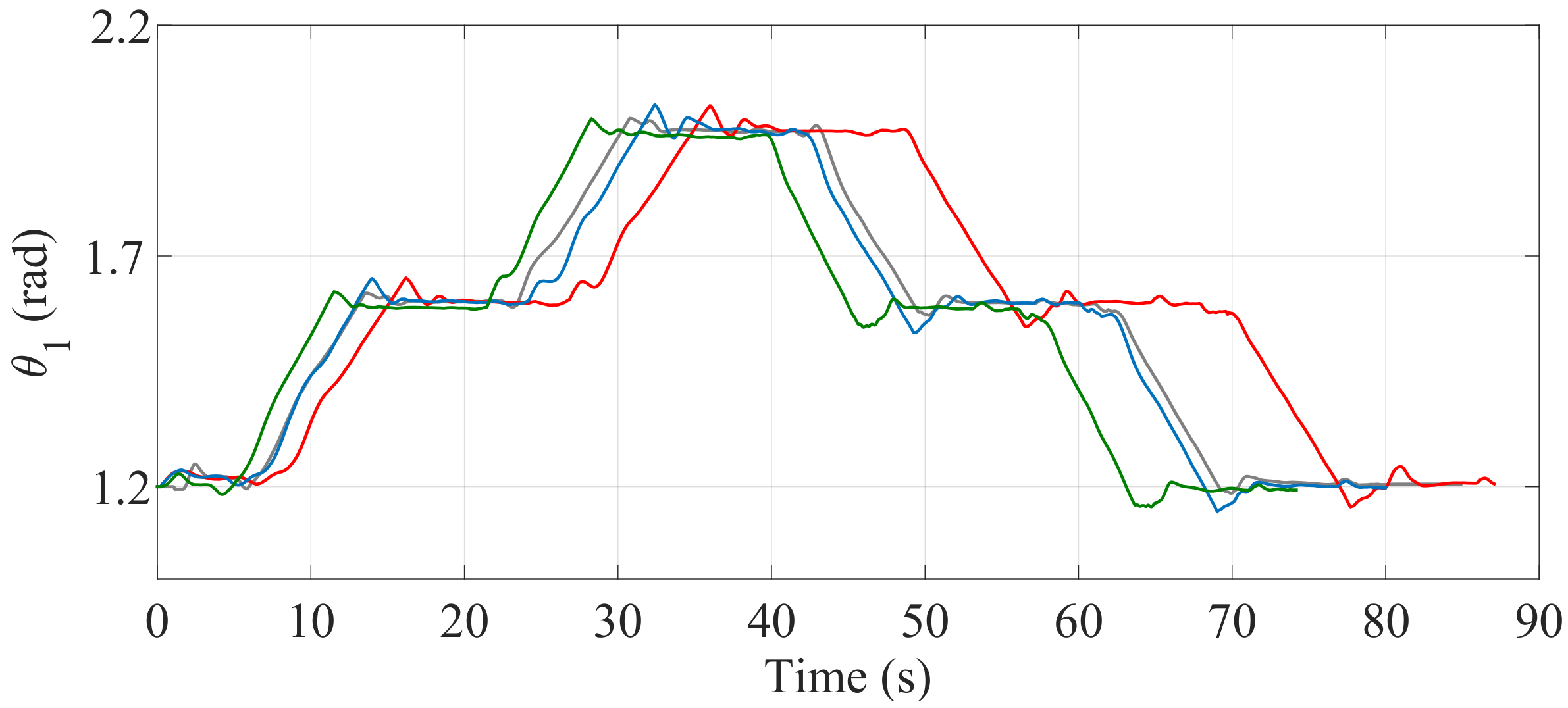
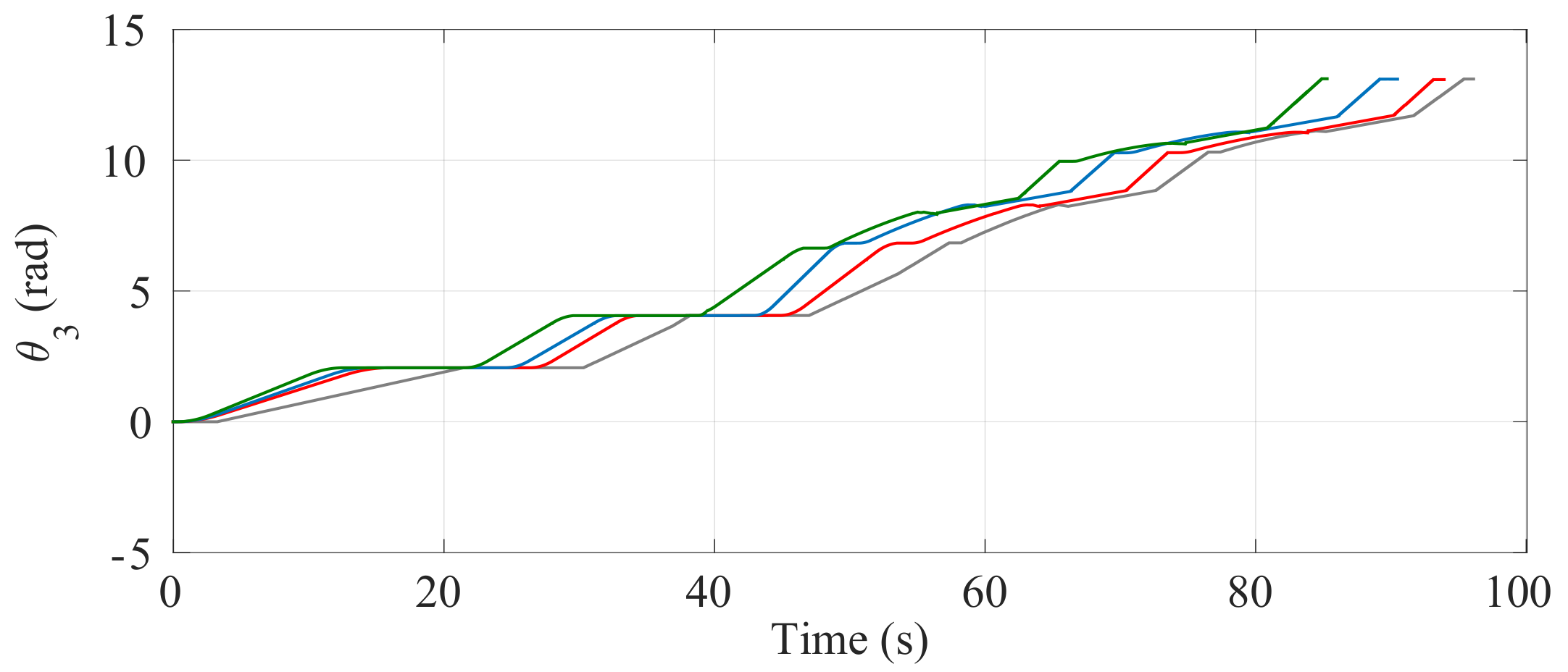
Figure 24.
Behavior of the angular position of the driving wheels () when the optimization is carried out with (—), (—) and (—) and when the optimization is not considered (—).
Figure 24.
Behavior of the angular position of the driving wheels () when the optimization is carried out with (—), (—) and (—) and when the optimization is not considered (—).
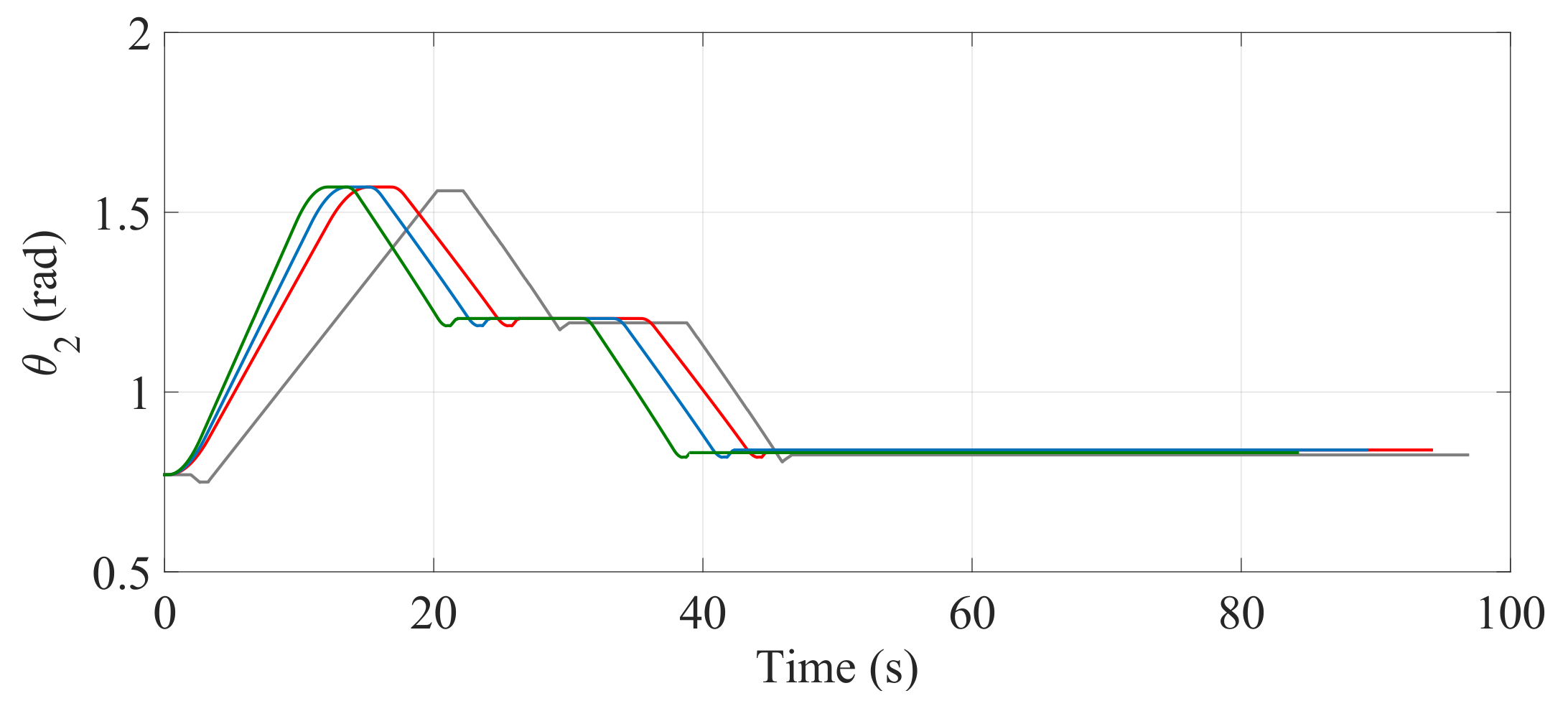
Figure 25.
Behavior of when the optimization is carried out with (—), (—) and (—) and when the optimization is not considered (—).
Figure 25.
Behavior of when the optimization is carried out with (—), (—) and (—) and when the optimization is not considered (—).
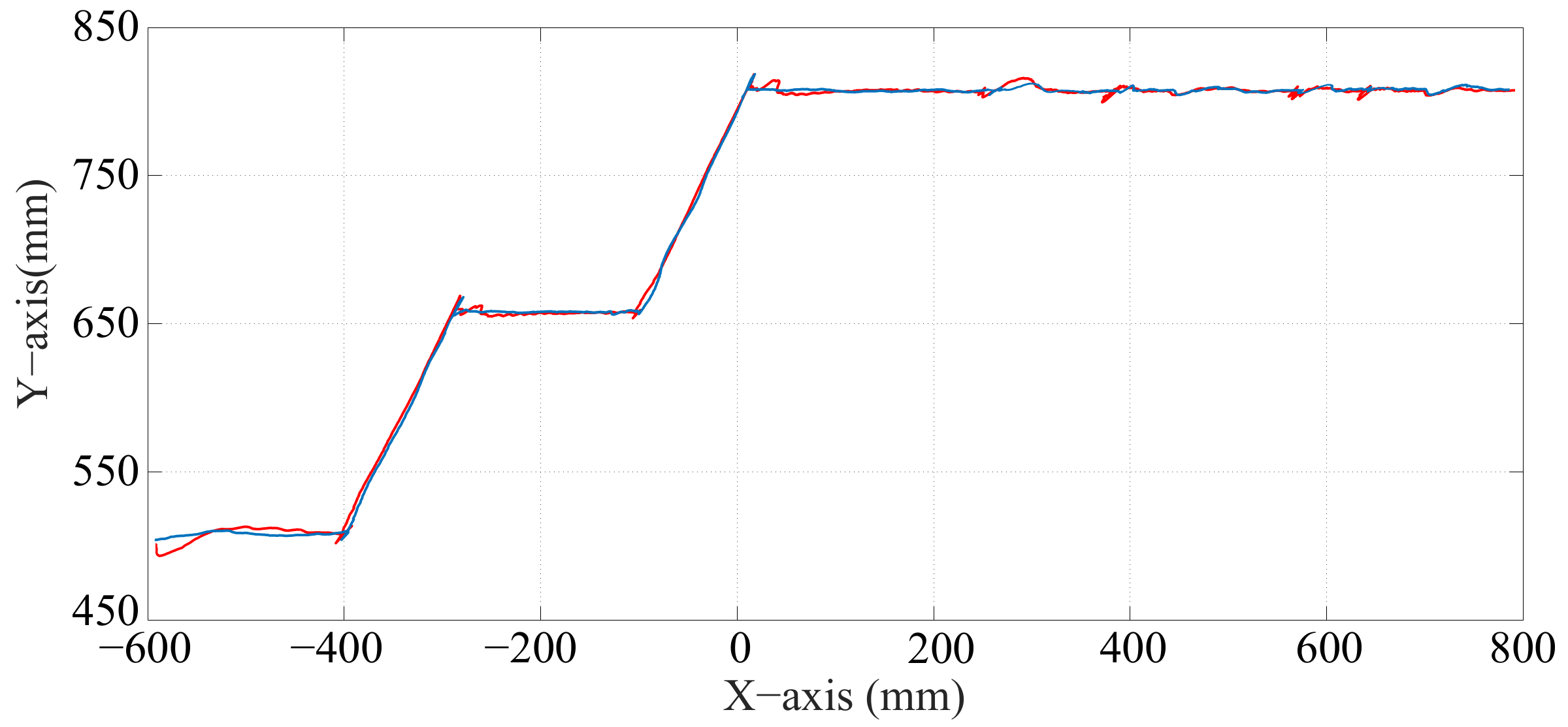
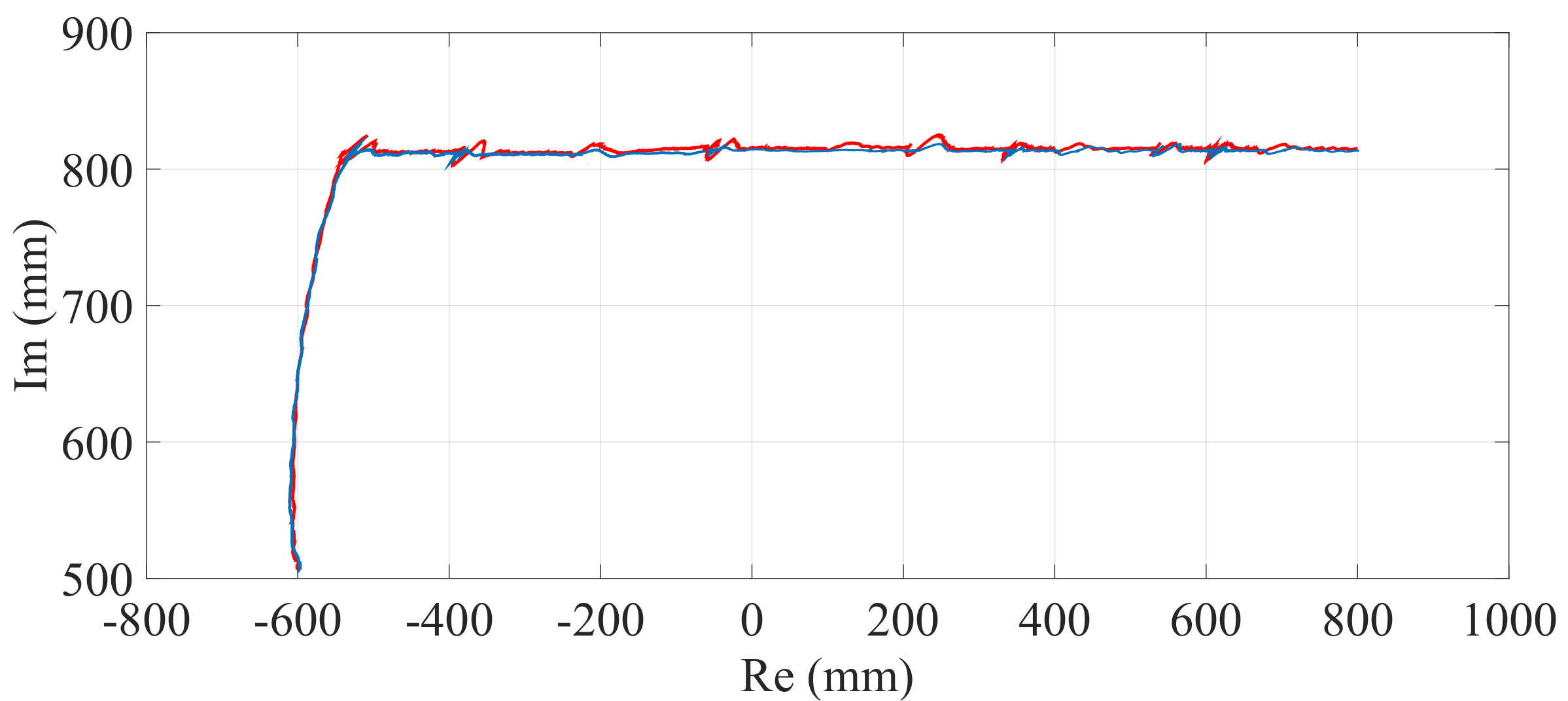
Figure 26.
Path of the center of mass () when the optimization is carried out with equal to zero (—) and when the optimization is not considered (—).
Figure 26.
Path of the center of mass () when the optimization is carried out with equal to zero (—) and when the optimization is not considered (—).
Figure 27.
Inclination of the SCMS frame () when the optimization is carried out with a equal to zero (—) and when the optimization is not considered (—).
Figure 27.
Inclination of the SCMS frame () when the optimization is carried out with a equal to zero (—) and when the optimization is not considered (—).
Figure 28.
Inclination of the SCMS frame () when the optimization is carried out with a equal to 0.5 (—) and when the optimization is not considered (—).
Figure 28.
Inclination of the SCMS frame () when the optimization is carried out with a equal to 0.5 (—) and when the optimization is not considered (—).
Figure 29.
Inclination of the SCMS frame () when the optimization is carried out with a equal to one (—) and when the optimization is not considered (—).
Figure 29.
Inclination of the SCMS frame () when the optimization is carried out with a equal to one (—) and when the optimization is not considered (—).
Figure 30.
Behavior of the angular position of the driving wheels () when the path is optimized with (—), (—) and (—) and when the optimization is not considered (—).
Figure 30.
Behavior of the angular position of the driving wheels () when the path is optimized with (—), (—) and (—) and when the optimization is not considered (—).
Figure 31.
Behavior of the angular position () when the path is optimized with (—), (—) and (—) and when the optimization is not considered (—).
Figure 31.
Behavior of the angular position () when the path is optimized with (—), (—) and (—) and when the optimization is not considered (—).
Figure 32.
Behavior of the angular position () when the path is optimized with (—), (—) and (—) and when the optimization is not considered (—).
Figure 32.
Behavior of the angular position () when the path is optimized with (—), (—) and (—) and when the optimization is not considered (—).
Figure 33.
Path of the center of mass () when the optimization is carried out with equal to zero (—) and when the optimization is not considered (—).
Figure 33.
Path of the center of mass () when the optimization is carried out with equal to zero (—) and when the optimization is not considered (—).
Table 1.
Initial expressions that define the current position of the SCMS.
Table 1.
Initial expressions that define the current position of the SCMS.
| Configurations | Expressions | |
|---|
| 1 (see Figure 11a) | | (1) |
| | | (2) |
| 2 (see Figure 11b) | | (3) |
| | Equation (2) | |
| 3 (see Figure 11c) | Equation (1) | |
| | | (4) |
| 4 (see Figure 11d) | Equation (3) | |
| | Equation (4) | |
Table 2.
Terms of differential equations of the implicit Jacobian for the four configurations (where and ).
Table 2.
Terms of differential equations of the implicit Jacobian for the four configurations (where and ).
| k | | | | g() |
|---|
| 1 | | | | |
| 2 | | | | |
| 3 | | | | |
| 4 | | | | |
| | | | | |
Table 3.
Specifications of the SCMS.
Table 3.
Specifications of the SCMS.
| Variable | Value |
|---|
| User’s weight | 70 kg |
| Vehicle weight | 60 kg |
| Height steps | 150 mm |
| Wide steps | 300 mm |
| Sampling time | 15 mm |
Table 4.
Dimensions of the SCMS’s links.
Table 4.
Dimensions of the SCMS’s links.
| Variable | Value |
|---|
| 270 mm |
| 410 mm |
| 420 mm |
| 323 mm |
| 390 mm |
| 35 deg |
| 100 mm |
Table 5.
Specifications of the motors and actuators.
Table 5.
Specifications of the motors and actuators.
| Variable and Value |
|---|
|
|
| /s |
| /s |
| rad |
| rad |
| rad |
| rad |
| rad/s |
| rad/s |
| rad/s |
| rad/s |
| mm |
| mm/s |
| mm/s |
Table 6.
Results obtained.
Table 6.
Results obtained.
| Climbing Time (s) | Comfort (Std) | Algorithm Execution Time (s) |
|---|
| 0 | 86 | 0.0019 | 2.6 |
| 0.5 | 80 | 0.0032 | 3.1 |
| 1 | 74 | 0.0047 | 4.0 |
| No optimization | 85 | 0.0053 | |
Table 7.
Results obtained.
Table 7.
Results obtained.
| Climbing Time (s) | Comfort (Std) | Algorithm Execution Time (s) |
|---|
| 0 | 95.2 | 0.0021 | 1.1 |
| 0.5 | 90.0 | 0.0033 | 1.9 |
| 1 | 84.3 | 0.0042 | 3.6 |
| No optimization | 97.3 | 0.0062 | |