A Generalized Polynomial Chaos-Based Approach to Analyze the Impacts of Process Deviations on MEMS Beams
Abstract
:1. Introduction
2. Methodology and Algorithm
3. Problem Presentations and Analysis
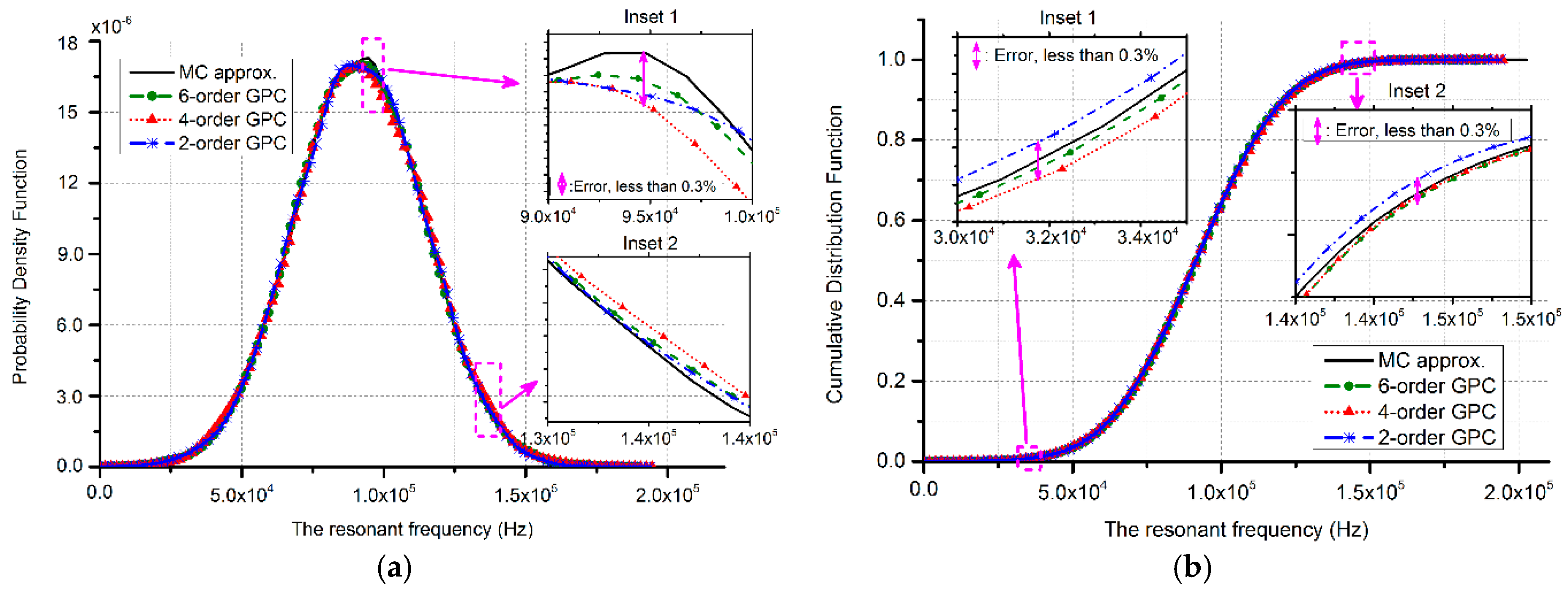
3.1. The Doubly-Clamped Beam
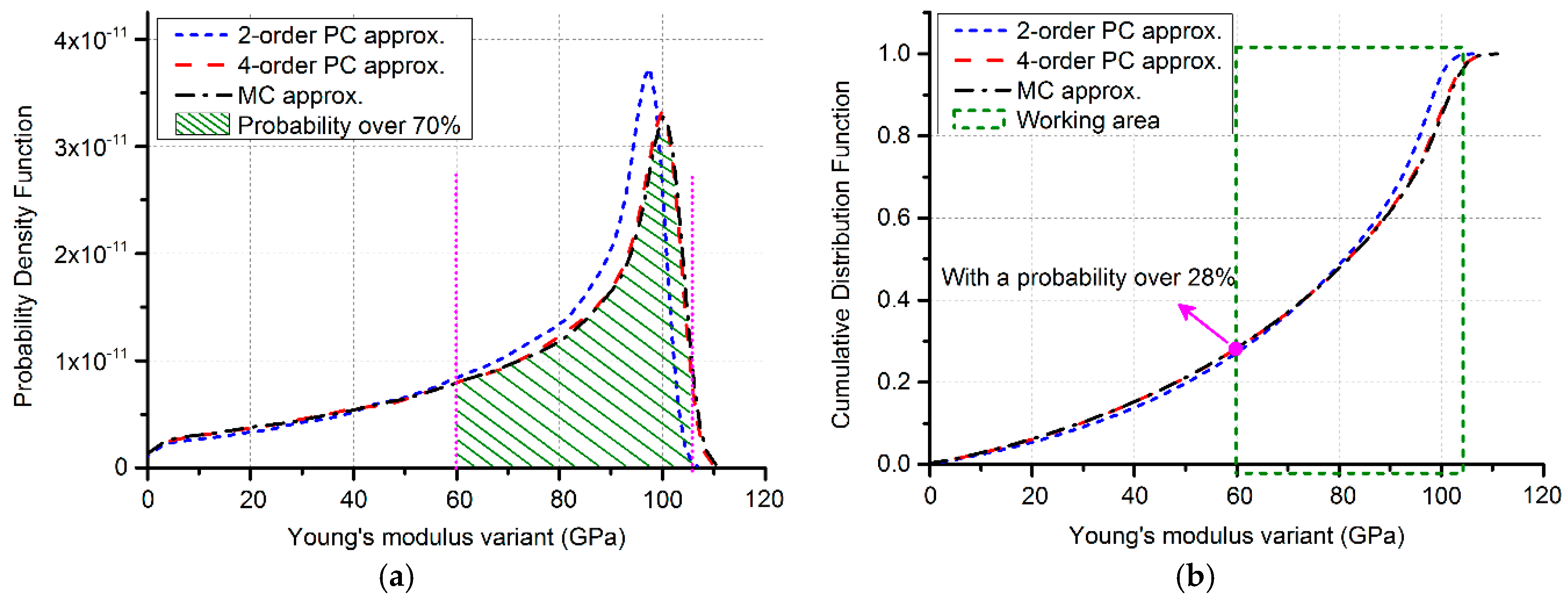
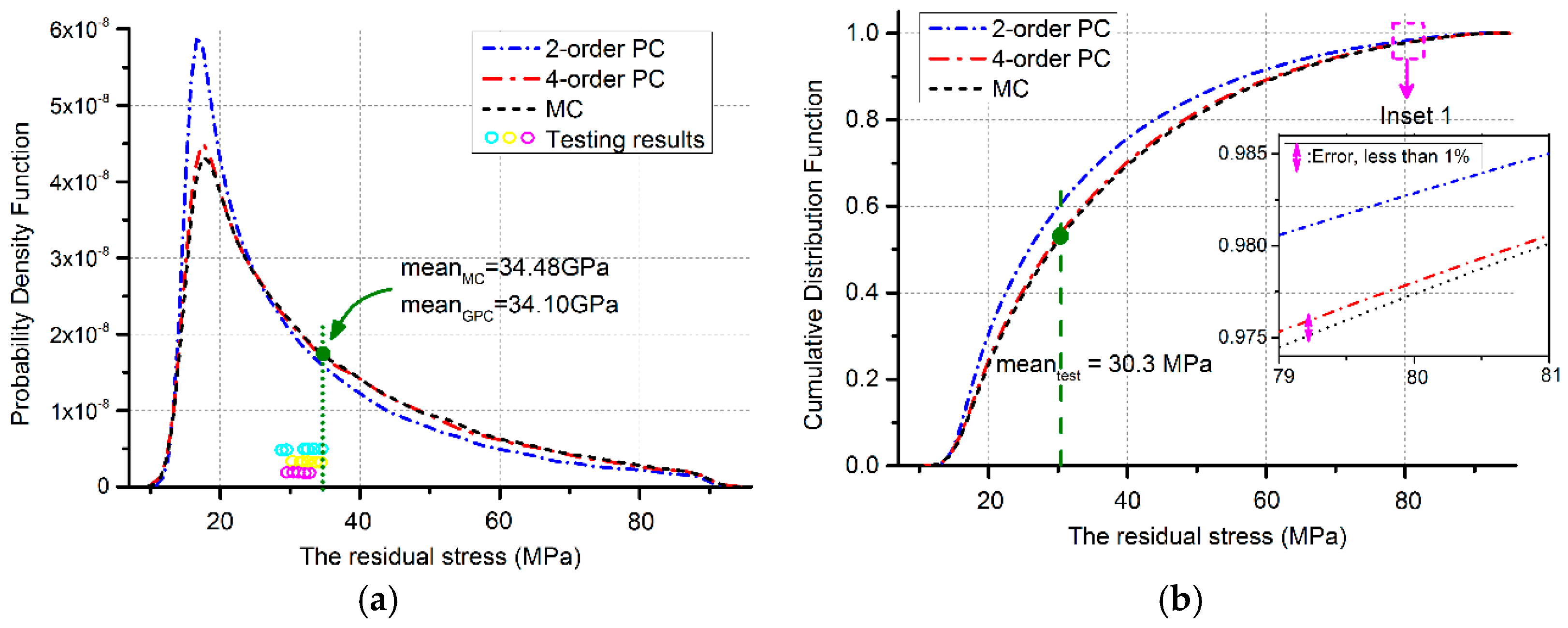
3.2. GaAs MMIC-Based MEMS Beams
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Senturia, S.D.; Azuru, N.; White, J. Simulating the behavior of MEMS devices: Computational methods and needs. IEEE Comput. Sci. Eng. 1997, 4, 30–43. [Google Scholar] [CrossRef]
- Gang, L.; Aluru, N.R. Efficient mixed-domain analysis of electrostatic MEMS. IEEE Trans. Comput. Aid. Des. 2003, 22, 1228–1242. [Google Scholar] [CrossRef]
- De, S.K.; Aluru, N.R. Full-lagrangian schemes for dynamic analysis of electrostatic MEMS. J. Microelectromech. Syst. 2004, 13, 737–758. [Google Scholar] [CrossRef]
- Sudipto, K.D.; Aluru, N.R. Coupling of hierarchical fluid models with electrostatic and mechanical models for the dynamic analysis of MEMS. J. Micromech. Microeng. 2006, 16, 1705. [Google Scholar]
- Liu, M.; Maute, K.; Frangopol, D.M. Multi-objective design optimization of electrostatically actuated microbeam resonators with and without parameter uncertainty. Reliab. Eng. Ssyt. Safe. 2007, 92, 1333–1343. [Google Scholar] [CrossRef]
- O’Hagan, A. Probabilistic uncertainty specification: Overview, elaboration techniques and their application to a mechanistic model of carbon flux. Environ. Modell. Softw. 2012, 36, 35–48. [Google Scholar] [CrossRef]
- Jenný, B.; Anthony, O. Learning about physical parameters: the importance of model discrepancy. Inverse. Probl. 2014, 30, 114007. [Google Scholar]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: New Jersey, NJ, USA, 2010. [Google Scholar]
- Mulloni, V.; Giacomozzi, F.; Margesin, B. Controlling stress and stress gradient during the release process in gold suspended micro-structures. Sensor. Actuat. A-Phys. 2010, 162, 93–99. [Google Scholar] [CrossRef]
- Zhiqiang, C.; Tian, W.C.; Zhang, X.T.; Wang, Y.K. Effect of deposition parameters on surface roughness and consequent electromagnetic performance of capacitive RF MEMS switches: A review. J. Micromech. Microeng. 2017, 27, 113003. [Google Scholar]
- Persano, A.; Quanranta, F.; Capoccia, G.; Proietti, E.; Lucibello, A.; Marcelli, R.; Bagolini, A.; Iannacci, J; Taurina, A; Siciliana, P. Influence of design and fabrication on RF performance of capacitive RF MEMS switches. Microsyst. Technol. 2016, 22, 1741–1746. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization—Part I: One-material structures. Comput. Method. Appl. Mech. Eng. 2001, 190, 6577–6604. [Google Scholar] [CrossRef]
- Mandy, A.P.; Hosein, Z.; Ole, S. Experimental validation of topology optimization for RF MEMS capacitive switch design. J. Microelectromech. Syst. 2013, 22, 1296–1309. [Google Scholar]
- Allen, M. Reliability-based analysis and design optimization of electrostatically actuated MEMS. Comput. Struct. 2004, 82, 1007–1020. [Google Scholar] [CrossRef]
- Han, J.S.; Kwak, B.M. Robust optimal design of a vibratory microgyroscope considering fabrication errors. J. Micromech. Microeng. 2001, 11, 662. [Google Scholar] [CrossRef]
- Kong, J.S. A methodology for analyzing the variability in the performance of a MEMS actuator made from a novel ceramic. Sens. Actuat. A-Phys. 2004, 116, 336–344. [Google Scholar] [CrossRef]
- Rong, L.; Paden, B.; Turner, K. MEMS resonators that are robust to process-induced feature width variations. J. Microelectromech. Syst. 2002, 11, 505–511. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. TECHNOMETRICS 1979, 21, 239–245. [Google Scholar]
- Kuo, F.; Schwab, C.; Sloan, I. Quasi-Monte Carlo finite element methods for a class of elliptic partial differential equations with random coefficients. SIAM J. Numer. Anal. 2012, 50, 3351–3374. [Google Scholar] [CrossRef]
- Wittwer, J.W.; Baker, M.S.; Howell, L.L. Robust design and model validation of nonlinear compliant micromechanisms. J. Microelectromech. Syst. 2006, 15, 33–41. [Google Scholar] [CrossRef]
- Klerber, M.; Hien, T.D. The Stochastic Finite Element Method: Basic Perturbation Technique and Computer Implementation, 1st ed.; Wiley: Chichester, UK, 1992. [Google Scholar]
- Liu, W.K.; Belytschko, T.; Mani, A. Probabilistic finite elements for nonlinear structural dynamics. Comput. Method. Appl. Mech. Eng. 1986, 56, 61–81. [Google Scholar] [CrossRef]
- Liu, W.K.; Belytschko, T.; Mani, A. Random field finite elements. Int. J. Numer. Meth. Eng. 1986, 23, 1831–1845. [Google Scholar] [CrossRef]
- Yamazaki, F. Neumann expansion for stochastic finite element analysis. J. Eng. Mech. 1988, 114, 1335–1354. [Google Scholar] [CrossRef]
- Zhang, D. Stochastic Methods for Flow in Porous Media: Coping with Uncertainties, 1st ed.; Academic Press: Millbrae, CA, USA, 2001. [Google Scholar]
- Gao, L.; Zhou, Z.-F.; Huang, Q.-A. Modeling of the effect of process variations on a micromachined doubly-clamped beam. Micromachines 2017, 8, 81. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G. The wiener—Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach, 1st ed.; Springer: Berlin, Germany, 2003. [Google Scholar]
- Schuëller, G.I. A state-of-the-art report on computational stochastic mechanics. Probabilist. Eng. Mech. 1997, 12, 197–321. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos. Comput. Method. Appl. Mech. Eng. 2002, 191, 4927–4948. [Google Scholar] [CrossRef]
- Knio, O.M.; Najm, H.N.; Ghanem, R.G. A stochastic projection method for fluid flow: I. basic formulation. J. Comput. Phys. 2001, 173, 481–511. [Google Scholar]
- Ghanem, R. Higher-order sensitivity of heat conduction problems to random data using the spectral stochastic finite element method. J. Heat Trans.-T ASME 1999, 121, 290–299. [Google Scholar] [CrossRef]
- Kosina, H.; Nedjalkov, M.; Selberherr, S. Theory of the Monte Carlo method for semiconductor device simulation. IEEE T. Electron. Dev. 2000, 47, 1898–1908. [Google Scholar] [CrossRef]
- Liu, C. Foundations of MEMS, 2nd ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Timoshenke, S. Vibration Problems in Engineering, 2 Reprint ed.; Wolfenden Press: Garberville, CA, USA, 2007. [Google Scholar]
- Yang, G.; Liao, X.; Zhang, Z. Young’s modulus and residual stress of MEMS gold beams based on the GaAs MMIC process. J. Micromech. Microeng. 2013, 23, 045002. [Google Scholar] [CrossRef]



| Parameters | Design Values Deviations |
|---|---|
| Beam length () | 170 1 |
| Beam thickness () | 2 0.5 |
| Material density () | 19.2 |
| Effective Young’s modulus () |
| GPC | MC | ||||
|---|---|---|---|---|---|
| 2-Order | 4-Order | 100 Runs | 1000 Runs | 100,000 Runs | |
| Mean value (GPa) | 31.55 | 34.10 | 31.27 | 33.66 | 34.48 |
| Error | 8.50% | 1.10% | 9.31% | 2.38% | -- |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Zhou, Z.-F.; Huang, Q.-A. A Generalized Polynomial Chaos-Based Approach to Analyze the Impacts of Process Deviations on MEMS Beams. Sensors 2017, 17, 2561. https://doi.org/10.3390/s17112561
Gao L, Zhou Z-F, Huang Q-A. A Generalized Polynomial Chaos-Based Approach to Analyze the Impacts of Process Deviations on MEMS Beams. Sensors. 2017; 17(11):2561. https://doi.org/10.3390/s17112561
Chicago/Turabian StyleGao, Lili, Zai-Fa Zhou, and Qing-An Huang. 2017. "A Generalized Polynomial Chaos-Based Approach to Analyze the Impacts of Process Deviations on MEMS Beams" Sensors 17, no. 11: 2561. https://doi.org/10.3390/s17112561
APA StyleGao, L., Zhou, Z.-F., & Huang, Q.-A. (2017). A Generalized Polynomial Chaos-Based Approach to Analyze the Impacts of Process Deviations on MEMS Beams. Sensors, 17(11), 2561. https://doi.org/10.3390/s17112561







