Dimension-Factorized Range Migration Algorithm for Regularly Distributed Array Imaging
Abstract
:1. Introduction
2. Proposed Method
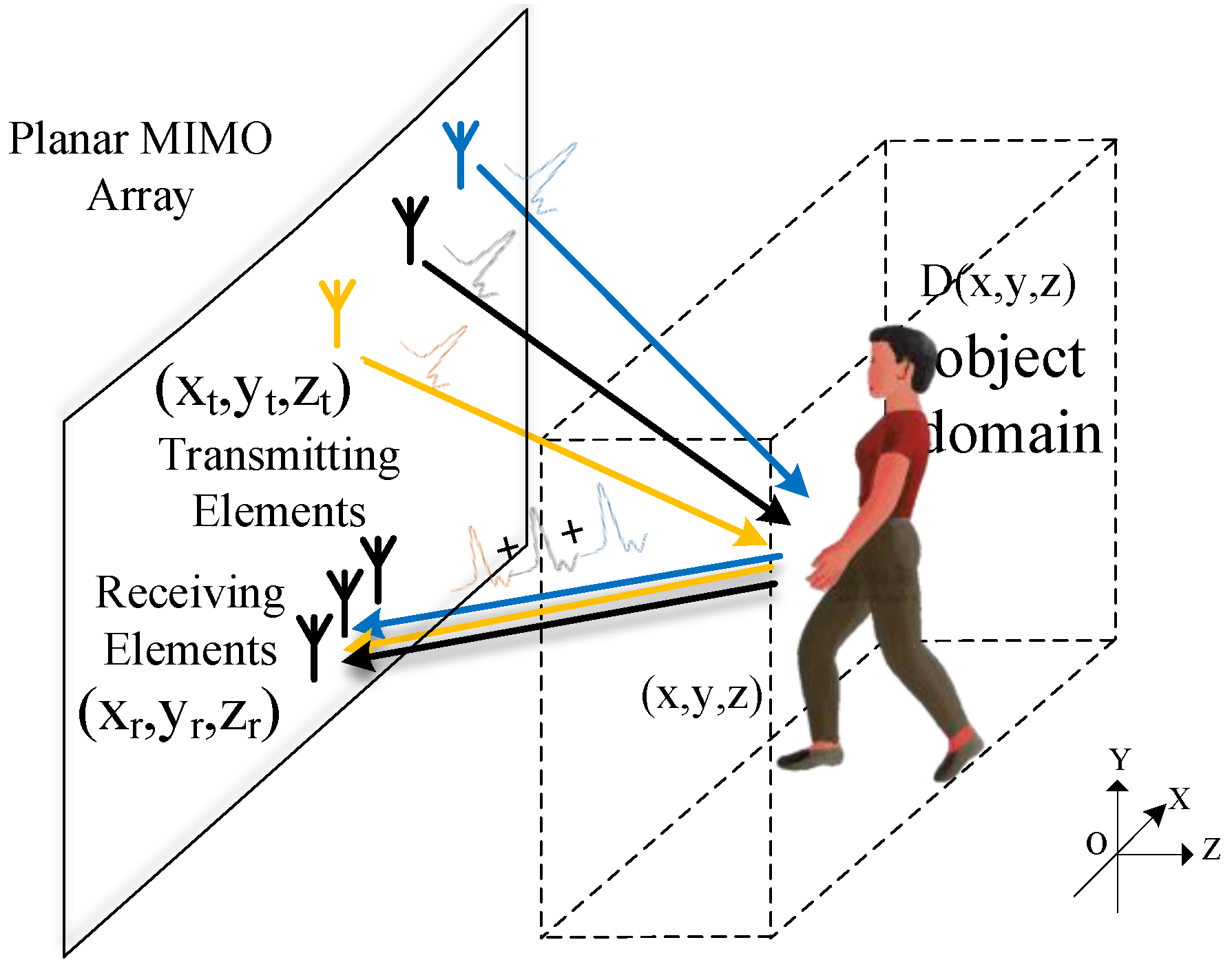
2.1. MIMO Range Migration Algorithm
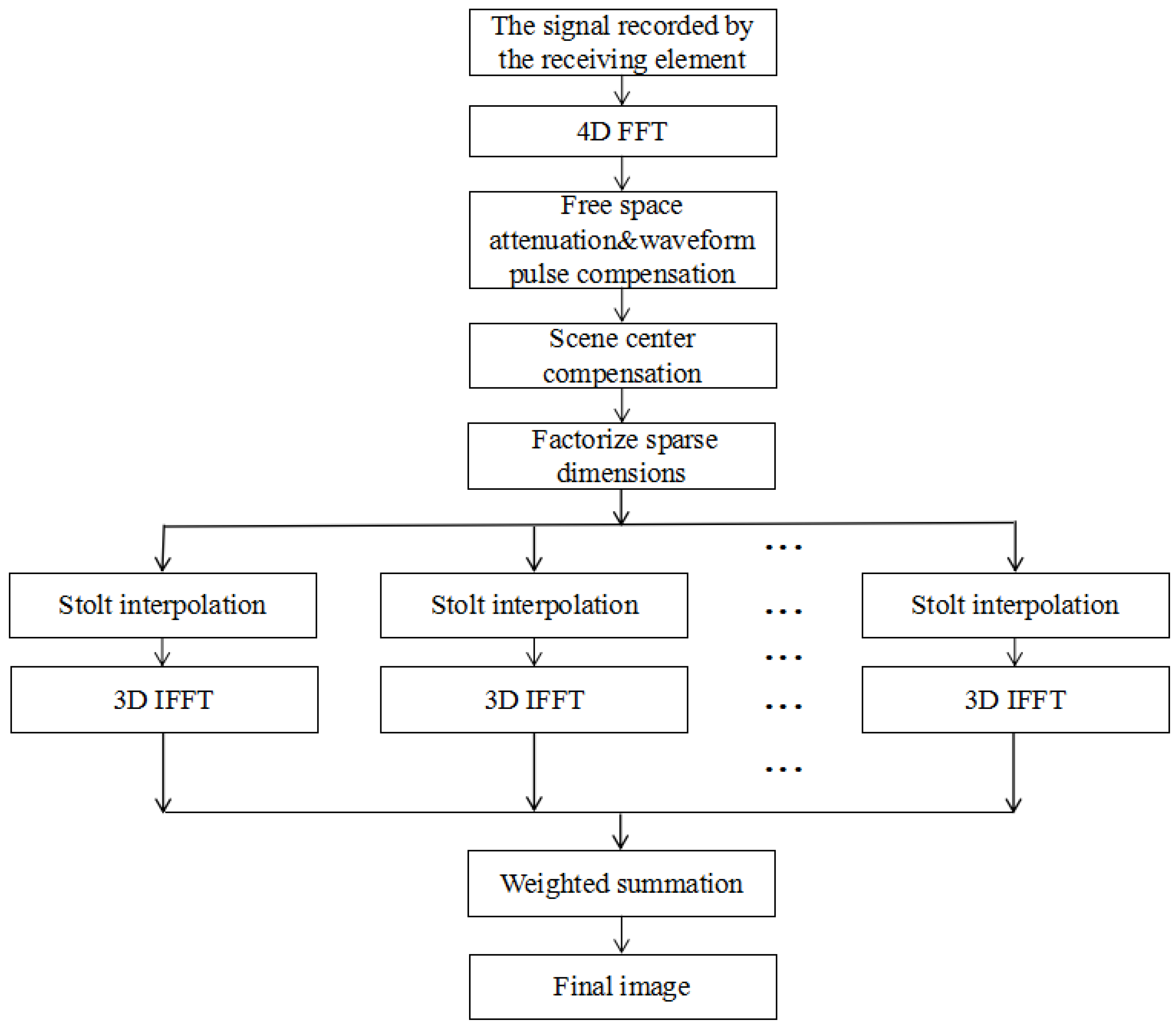
2.2. Dimension-Factorized Range Migration Algorithm
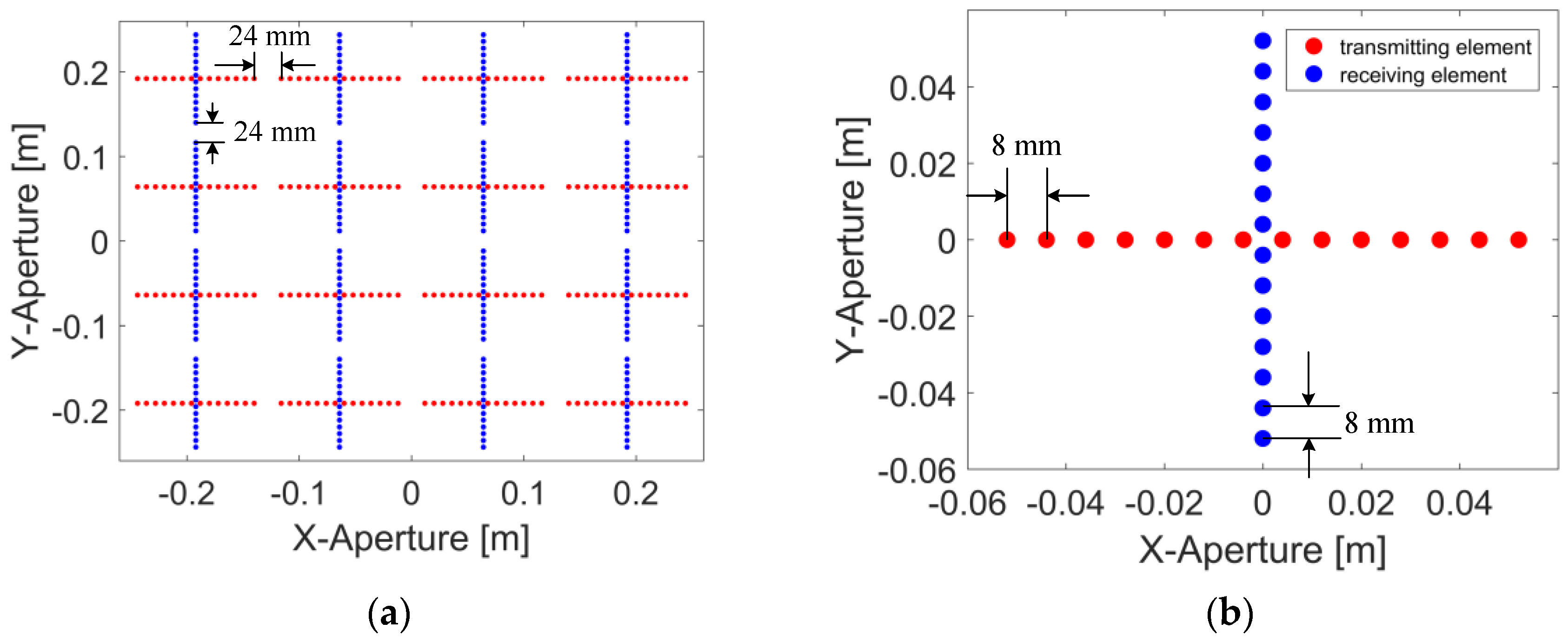
3. Simulation Results and Computation Load Estimation
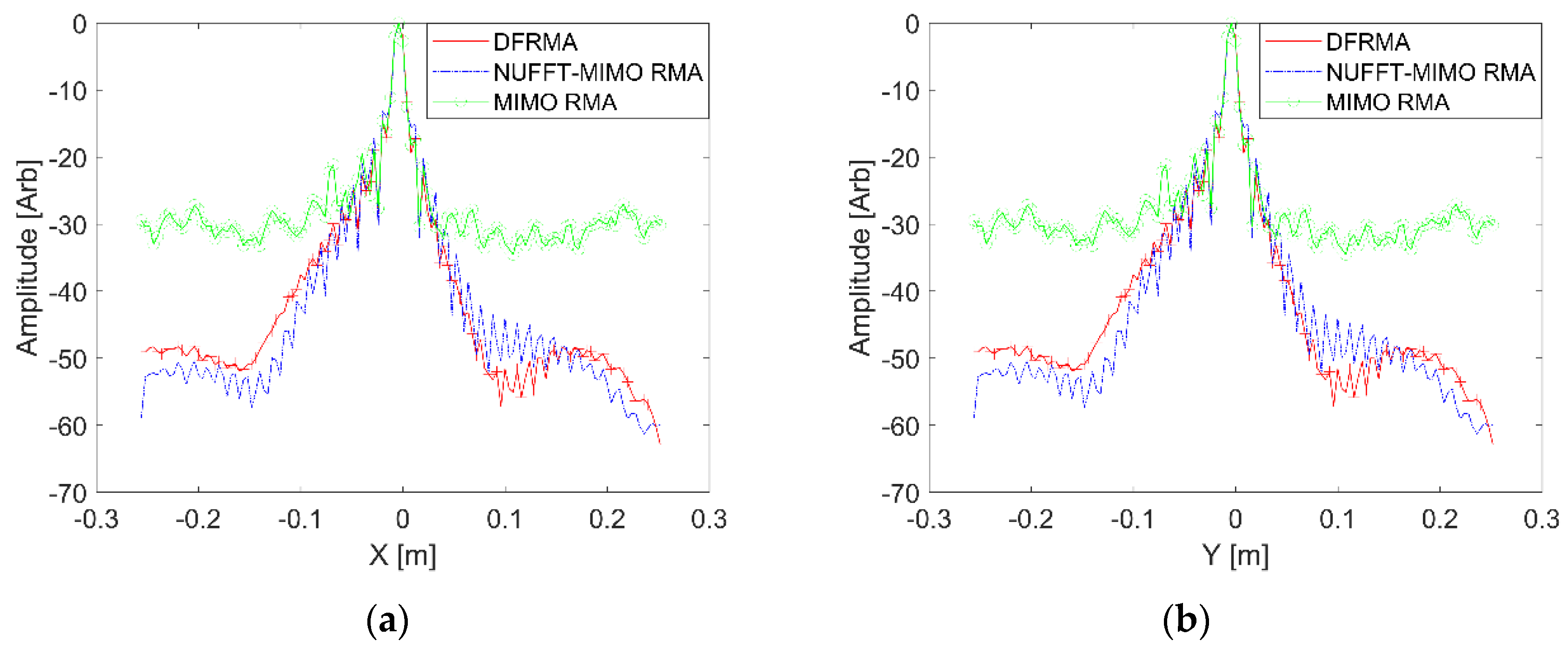
3.1. Point Spread Function
3.2. Numerical Simulation
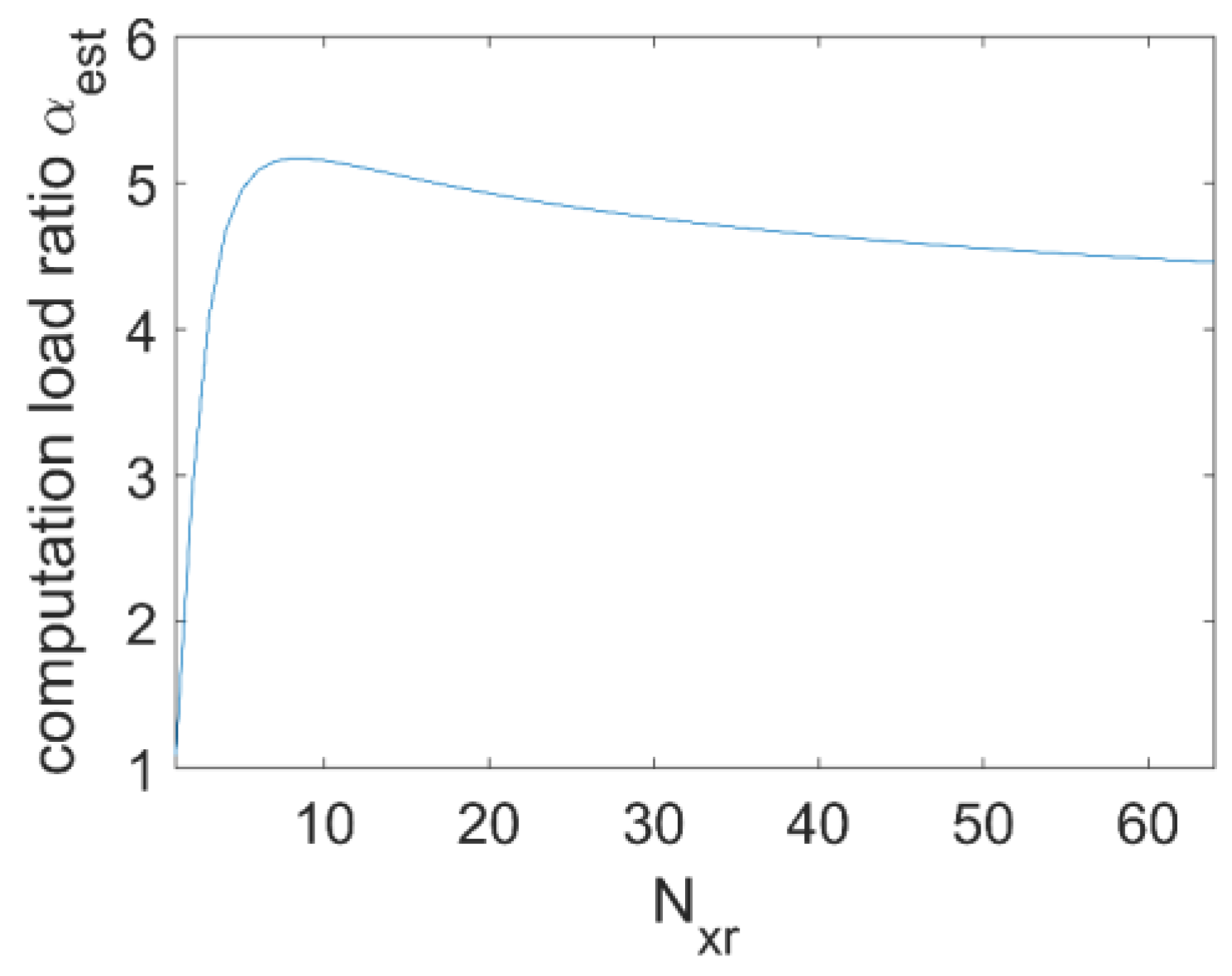
3.3. Computation Load Estimation
4. Conclusions
- In terms of precision, DF-RMA outperforms conventional MIMO RMA significantly. According to a comparison of PSFs, DF-RMA achieves strong background level suppression. In the numerical simulation of a contiguous target without added noise, the quality of the image is better than conventional MIMO RMA, and the precision is as high as NUFFT-based MIMO RMA. As for anti-noise performance, DF-RMA is at least 10 dB stronger than conventional MIMO RMA, judged by SNR;
- In terms of efficiency, DF-RMA is 5 times slower than conventional MIMO RMA at most (and can be nearly as fast as conventional MIMO RMA in cases of high sparsity), but more than 10 times faster than NUFFT-based MIMO RMA. Equally significantly, the structure of the algorithm is naturally adaptable to parallel computation, and it remains effective in a range of applications, especially those involving sparse arrays.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ahmed, S.S.; Genghammer, A.; Schiessl, A.; Schmidt, L.-P. Fully electronic E-band personnel imager of 2 m2 aperture based on a multistatic architecture. IEEE Trans. Microw. Theory Tech. 2013, 61, 651–657. [Google Scholar] [CrossRef]
- Gao, X.; Li, C.; Gu, S.; Fang, G. Study of a new millimeter-wave imaging scheme suitable for fast personal screening. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 787–790. [Google Scholar]
- Tan, W.; Hong, W.; Wang, Y.; Wu, Y. A novel spherical-wave three-dimensional imaging algorithm for microwave cylindrical scanning geometries. Prog. Electromagn. Res. 2011, 111, 43–70. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A.G. Three-dimensional near-field mimo array imaging using range migration techniques. IEEE Trans. Image Process 2012, 21, 3026–3033. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Yarovoy, A.; Aubry, P.; Zhuge, X. Experimental Verification of 2d uwb Mimo Antenna Array for Near-Field Imaging Radar. In Proceedings of the Microwave Conference, EuMC 2009, Rome, Italy, 29 September–1 October 2009; pp. 97–100. [Google Scholar]
- Yang, S.-H.; Kiang, J.-F. Optimization of sparse linear arrays using harmony search algorithms. IEEE Trans. Antennas Propag. 2015, 63, 4732–4738. [Google Scholar] [CrossRef]
- Tan, K.; Wu, S.; Wang, Y.; Ye, S.; Chen, J.; Fang, G. A novel two-dimensional sparse mimo array topology for uwb short-range imaging. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 702–705. [Google Scholar] [CrossRef]
- Liu, J.; Jia, Y.; Kong, L.; Yang, X.; Liu, Q.H. Mimo through-wall radar 3-d imaging of a human body in different postures. J.Electromag. Waves Appl. 2016, 30, 849–859. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A. Near-field ultra-wideband imaging with two-dimensional sparse mimo array. In Proceedings of the Fourth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–4. [Google Scholar]
- Ahmed, S.S.A. Electronic Microwave Imaging with Planar Multistatic Arrays; Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU): Erlangen, Germany, 2013. [Google Scholar]
- Zhuge, X.; Yarovoy, A.G. Study on two-dimensional sparse mimo uwb arrays for high resolution near-field imaging. IEEE Trans. Antennas Propag. 2012, 60, 4173–4182. [Google Scholar] [CrossRef]
- Steinberg, B.D. Principles of Aperture and Array System Design: Including Random and Adaptive arrays; Wiley-Interscience: New York, NY, USA, 1976. [Google Scholar]
- Zhuge, X.; Yarovoy, A.G.; Savelyev, T.; Ligthart, L. Modified kirchhoff migration for uwb mimo array-based radar imaging. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2692–2703. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, G.; Jin, T.; Lu, B.; Zhou, Z. Grating lobe mitigation based on extended coherence factor in sparse MIMO UWB array. In Proceedings of the 12th International Conference on Signal Processing (ICSP), Hangzhou, China, 19–23 October 2014; pp. 2098–2101. [Google Scholar]
- Camacho, J.; Parrilla, M.; Fritsch, C. Grating-lobes reduction by application of phase coherence factors. In Proceedings of the Ultrasonics Symposium, San Diego, CA, USA, 11–14 Ocotober 2010; pp. 341–344. [Google Scholar]
- Martinez-Graullera, O.; Romero-Laorden, D.; Ibanez, A.; Ullate, L.G. A new beamformer based on phase dispersion to improve 2D sparse array response. In Proceedings of the IEEE 7th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hoboken, NJ, USA, 17–20 June 2012; pp. 437–440. [Google Scholar]
- Yegulalp, A.F. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the The Record of the 1999 IEEE Radar Conference, New York, NY, USA, 20–22 April 1999; pp. 60–65. [Google Scholar]
- Ulander, L.M.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I. Fast time-domain algorithms for UWB bistatic sar processing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1982–1994. [Google Scholar] [CrossRef]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I. Phase error calculation for fast time-domain bistatic sar algorithms. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 631–639. [Google Scholar] [CrossRef]
- Moll, J.; Schops, P.; Krozer, V. Towards three-dimensional millimeter-wave radar with the bistatic fast-factorized back-projection algorithm: Potential and limitations. IEEE Trans. Terahertz Sci. Technol. 2012, 2, 432–440. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. Mimo Radar Signal Processing; Wiley-IEEE Press: New York, NY, USA, 2008; pp. 235–270. [Google Scholar]
- Guo, Q.; Zhang, X.; Chang, T.; Cui, H.-L.; Tian, X. Three-dimensional bistatic array imaging using range migration algorithm. Electron. Lett. 2017, 53, 193–194. [Google Scholar] [CrossRef]
- Greengard, L.; Lee, J.Y. Accelerating the nonuniform fast fourier transform. Siam Rev. 2006, 46, 443–454. [Google Scholar] [CrossRef]
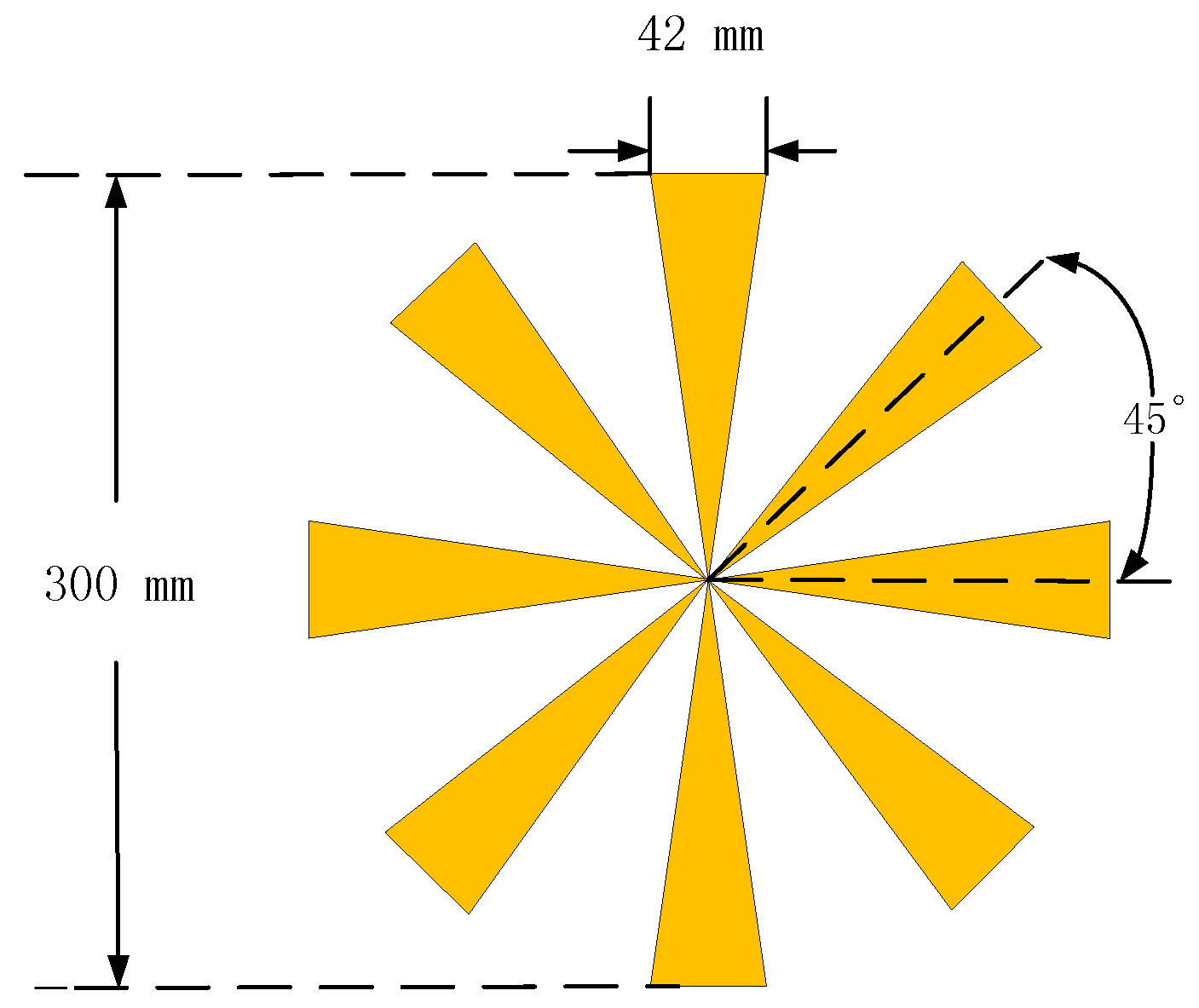
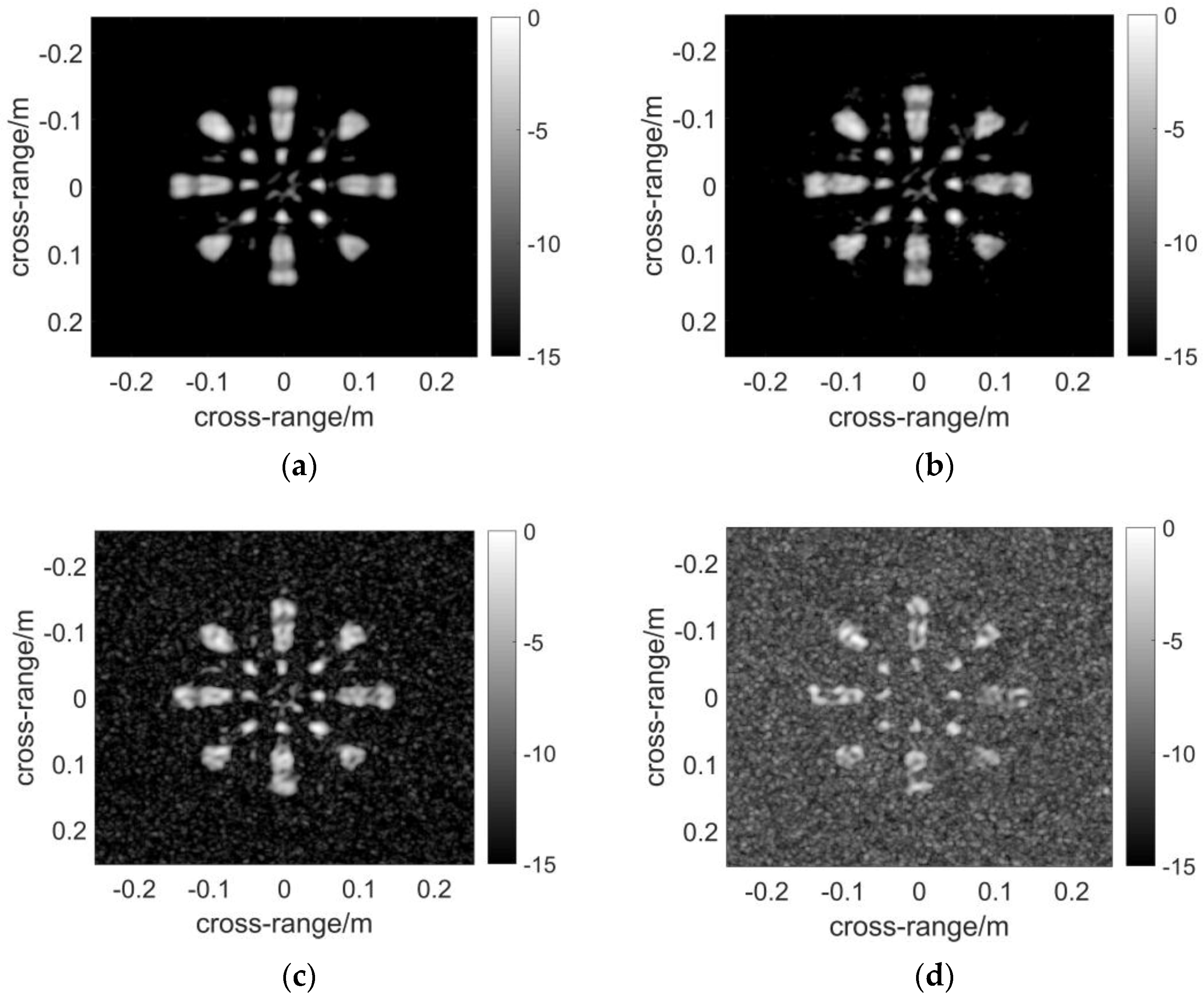

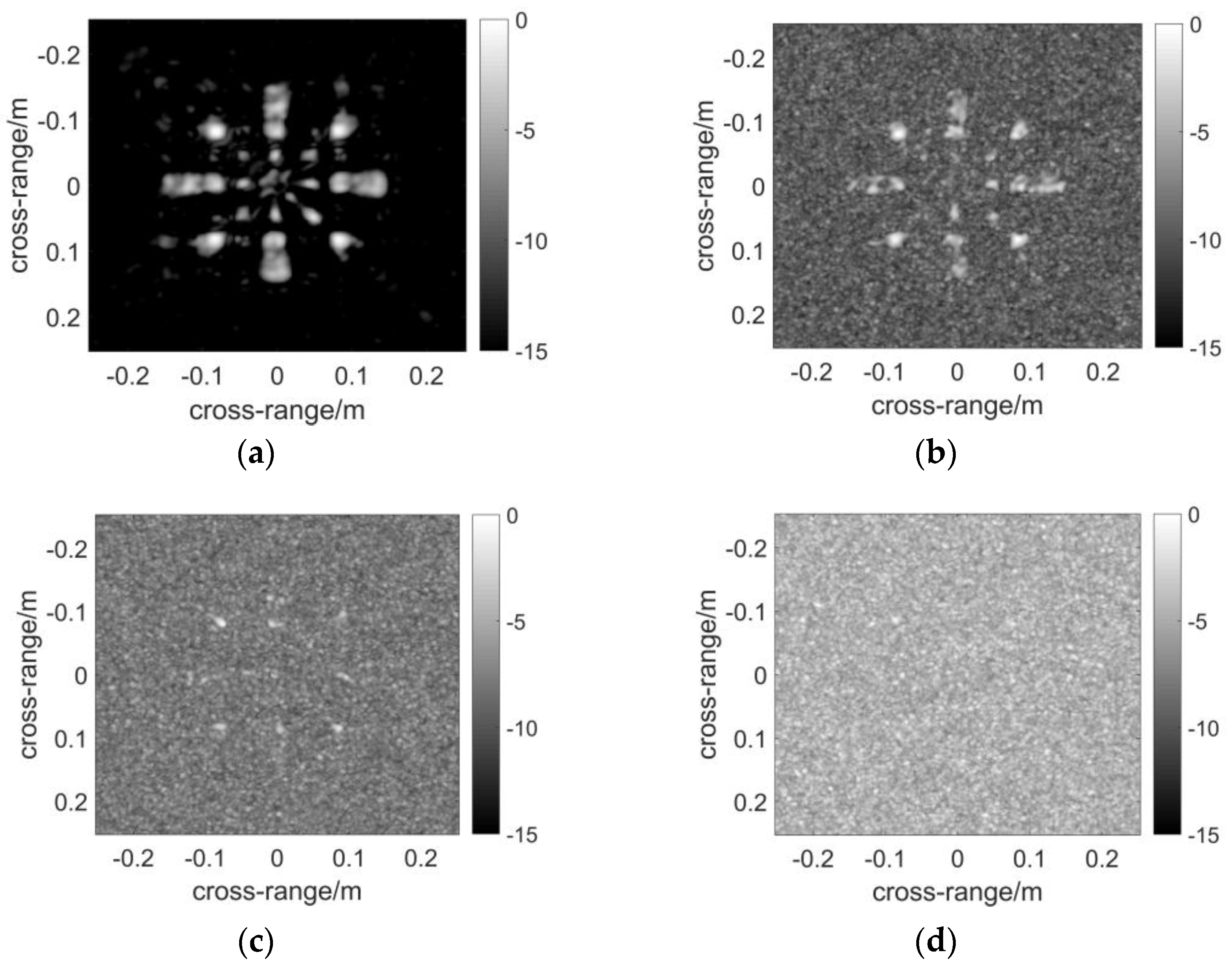
| Parameters | Value |
|---|---|
| Operating frequency range | 30 GHz–35 GHz |
| The range from the aperture to the scene center (Hc) | 500 mm |
| Number of samples in frequency | 64 |
| Processing Step | Complex Multiplications |
|---|---|
| 4D FFT | |
| Scene Center Compensation | |
| Piecewise Interpolation | |
| 3D inverse FFT (IFFT) |
| Processing Step | Complex Multiplications |
|---|---|
| 4D FFT | |
| Scene Center Compensation | |
| Piecewise Interpolation | |
| 3D IFFT | |
| Weight Multiplications |
| Method | Time Consumed (s) |
|---|---|
| DF-RMA | 10.243 |
| NUFFT based MIMO RMA | |
| Conventional MIMO RMA |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Wang, J.; Chang, T.; Cui, H.-L. Dimension-Factorized Range Migration Algorithm for Regularly Distributed Array Imaging. Sensors 2017, 17, 2549. https://doi.org/10.3390/s17112549
Guo Q, Wang J, Chang T, Cui H-L. Dimension-Factorized Range Migration Algorithm for Regularly Distributed Array Imaging. Sensors. 2017; 17(11):2549. https://doi.org/10.3390/s17112549
Chicago/Turabian StyleGuo, Qijia, Jie Wang, Tianying Chang, and Hong-Liang Cui. 2017. "Dimension-Factorized Range Migration Algorithm for Regularly Distributed Array Imaging" Sensors 17, no. 11: 2549. https://doi.org/10.3390/s17112549
APA StyleGuo, Q., Wang, J., Chang, T., & Cui, H.-L. (2017). Dimension-Factorized Range Migration Algorithm for Regularly Distributed Array Imaging. Sensors, 17(11), 2549. https://doi.org/10.3390/s17112549





