Matched Field Processing Based on Least Squares with a Small Aperture Hydrophone Array
Abstract
:1. Introduction
2. Least Squares MFP Model Formulation
2.1. Acoustic Fields with Normal Mode
2.2. Estimation of Mode Amplitudes by Least Squares
- Decompose the augmented matrix by SVD: .
- Let L is the elements of small array, M is the mode number in a shallow waveguide, k is the number of main singular value. If L is less than M, then let k equal to L, else let k equal to M.
- Let , it is obviously that consists of the latter column of , so the dimension of is .
- Let denotes the first row of , consists of the last rows of , viz. , so the dimension of is , and is a row less than . Then the TLS solution in the sense of minimum norm can be expressed as:
2.3. Matched Field Processing Based on Least Squares
3. Numerical Experiments and Performance Analysis
3.1. Environmental Model
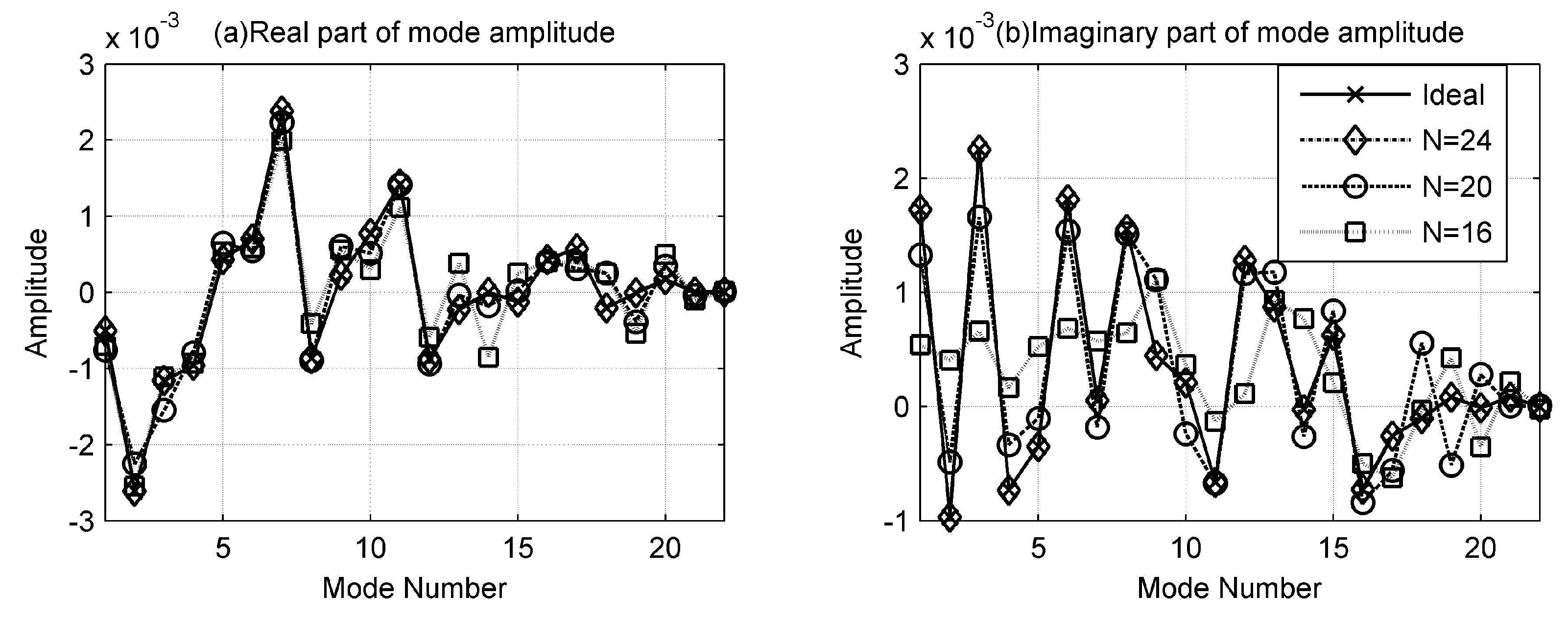
3.2. Results of Localization
3.3. Performance Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baggeroer, A.; Kuperman, W.; Mikhalevsky, P. An overview of matched field methods in ocean acoustics. IEEE J. Ocean. Eng. 1993, 18, 401–424. [Google Scholar] [CrossRef]
- Cox, H.; Pitre, R.; Lai, H. Robust adaptive matched field processing. In Proceedings of the Conference Record of the Thirty-Second Asilomar Conference on Signals, Systems AMP, Computers, Pacific Grove, CA, USA, 1–4 November 1998; pp. 127–131.
- Gingras, D.F.; Gerstoft, P. Inversion for geometric and geoacoustic parameters in shallow water: Experimental results. J. Acoust. Soc. Am. 1995, 97, 3589–3598. [Google Scholar] [CrossRef]
- Porter, M.B.; Tolstoy, A. The matched field processing benchmark problems. J. Comput. Acoust. 1994, 2, 161–185. [Google Scholar] [CrossRef]
- Hamson, R.M.; Heitmeyer, R.M. Environmental and system effects on source localization in shallow water by the matched field processing of a vertical array. J. Acoust. Soc. Am. 1989, 86, 1950–1959. [Google Scholar] [CrossRef]
- Shang, E.C.; Wang, Y.Y. Environmental mismatching effects on source localization processing in mode space. J. Acoust. Soc. Am. 1991, 89, 2285–2290. [Google Scholar] [CrossRef]
- Tolstoy, A. An improved broadband matched field processor for geoacoustic inversion (L). J. Acoust. Soc. Am. 2012, 132, 2151–2154. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Ma, Y.; Zou, S.; Yan, S. Adaptive matched field processing with mismatch environment and moving sources. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 18–23 September 2005; pp. 1175–1180.
- Dosso, S.E.; Morley, M.G.; Giles, P.M.; Brooke, G.H.; McCammon, D.F.; Pecknold, S.; Hines, P.C. Spatial field shifts in ocean acoustic environmental sensitivity analysis. J. Acoust. Soc. Am. 2007, 122, 2560–2570. [Google Scholar] [CrossRef] [PubMed]
- Cox, H.; Zeskind, R.M.; Myers, M. A subarray approach to matched field processing. J. Acoust. Soc. Am. 1990, 87, 168–178. [Google Scholar] [CrossRef]
- Mantzel, W.; Romberg, J.; Sabra, K.G.; Kuperman, W. Compressive matched field processing. J. Acoust. Soc. Am. 2010, 127. [Google Scholar] [CrossRef]
- Wilson, G.R.; Koch, R.A.; Vidmar, P.J. Matched mode localization. J. Acoust. Soc. Am. 1988, 84, 310–320. [Google Scholar] [CrossRef]
- Yang, T.C. A method of range and depth estimation by modal decomposition. J. Acoust. Soc. Am. 1987, 82, 1736–1745. [Google Scholar] [CrossRef]
- Porter, M.; Reiss, E.L. A numerical method for ocean acoustic normal modes. J. Acoust. Soc. Am. 1984, 76, 244–252. [Google Scholar] [CrossRef]
- Markovsky, I.; Huffel, S.V. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Hirakawa, K.; Parks, T. Image denoising using total least squares. IEEE Trans. Image Process. 2006, 15, 2730–2742. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; O’Leary, D.P. Implicitly-weighted total least squares. Linear Algebra Appl. 2011, 435, 560–577. [Google Scholar] [CrossRef]
- Dasgupta, K.; Soman, S. Line parameter estimation using phasor measurements by the total least squares approach. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5.
- Golub, G.H.; van Loan, C.F. An Analysis of the Total Least Squares Problem. SIAM J. Numer. Anal. 1980, 17, 883–893. [Google Scholar] [CrossRef]
- Fialkowski, L.T.; Perkins, J.S.; Collins, M.D.; Nicholas, M.; Fawcett, J.A.; Kuperman, W.A. Matched-field source tracking by ambiguity surface averaging. J. Acoust. Soc. Am. 2001, 110, 739–746. [Google Scholar] [CrossRef]

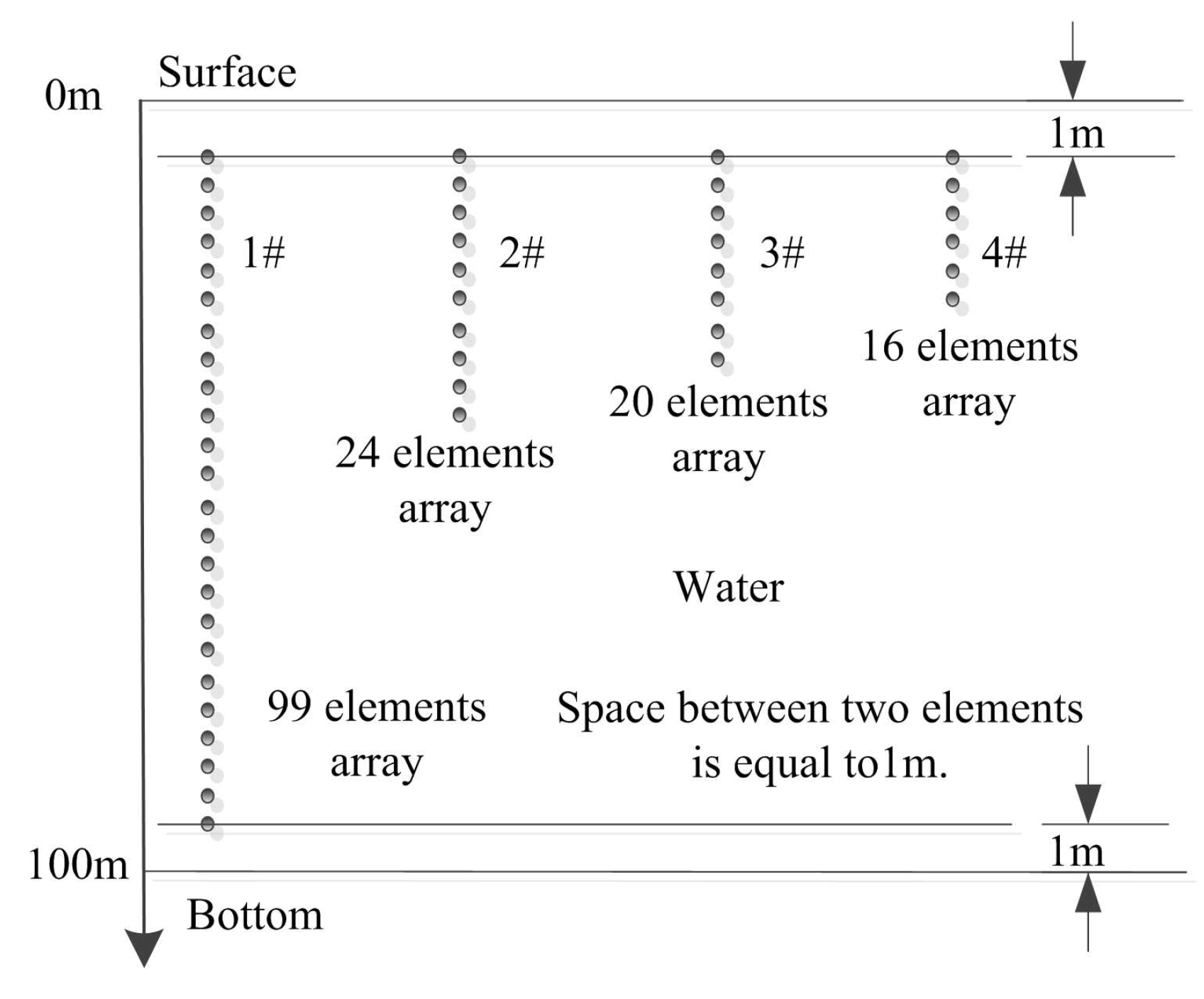
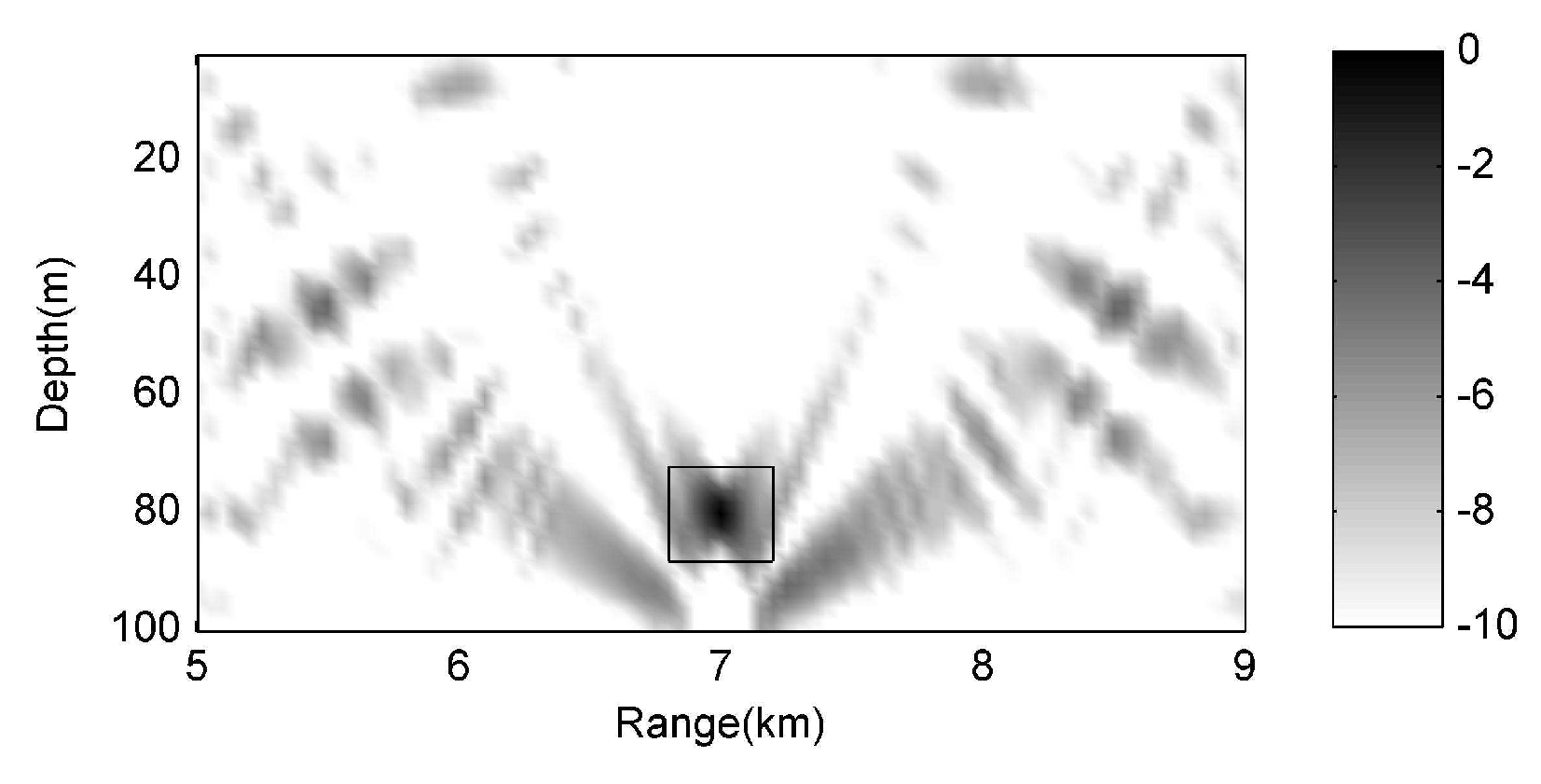
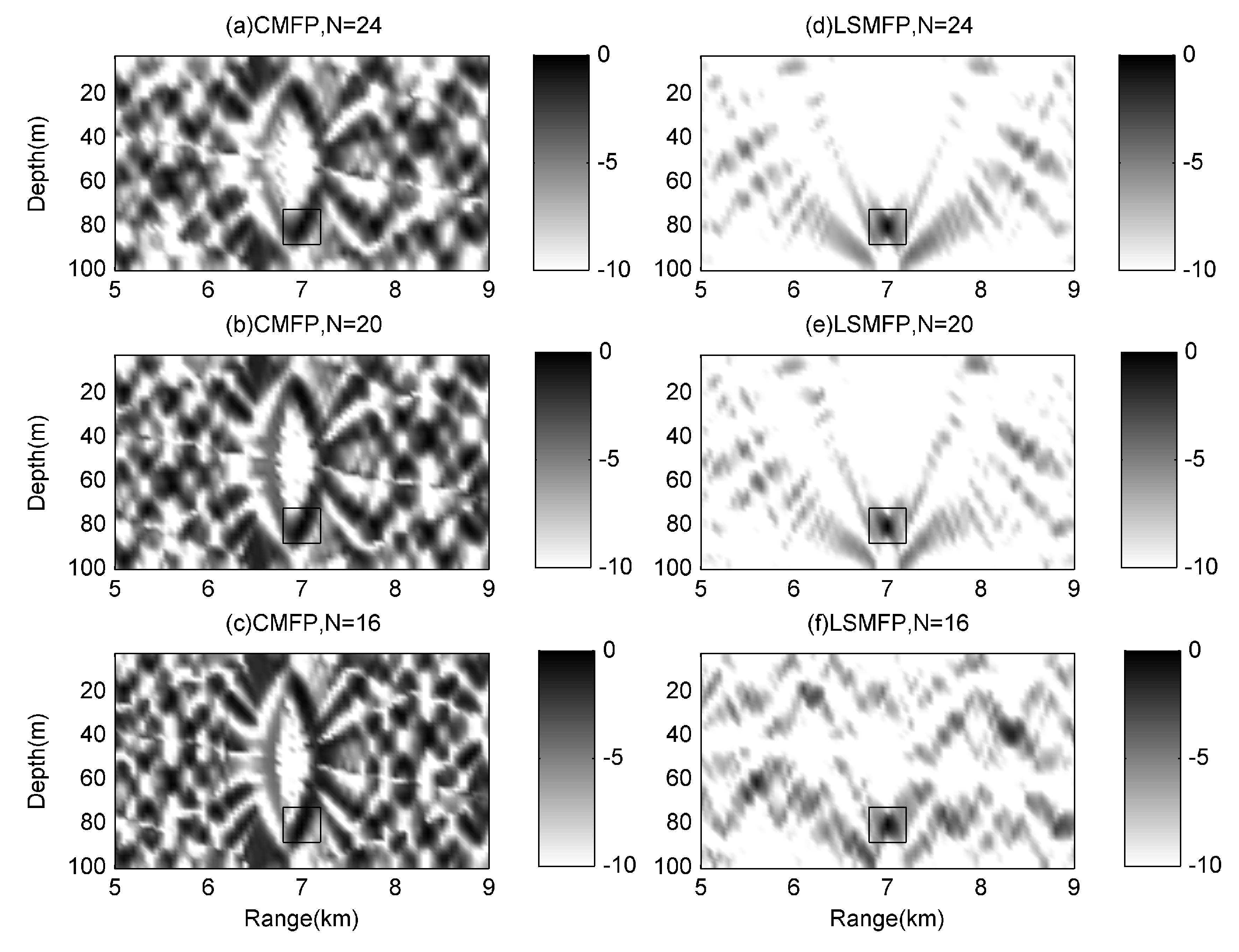
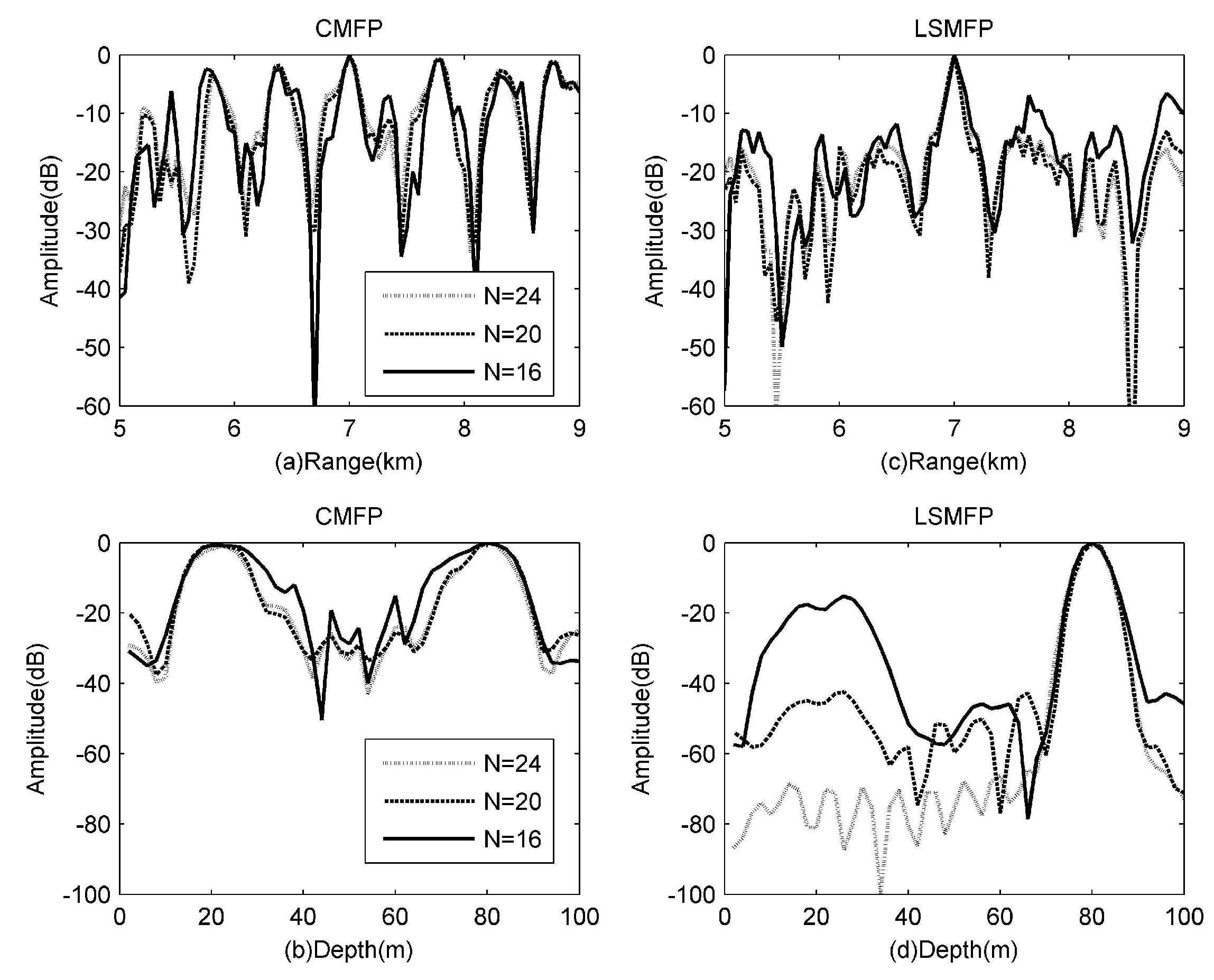
| Array | Hydrophones | Range (m) | Depth (m) | SINR (dB) | PBR (dB) | GCOS |
|---|---|---|---|---|---|---|
| 1# | 99 | 7000 | 80 | 16.65 | 10.49 | 1.0 |
| 2# | 24 | 7000 | 80 | 8.60 | 3.41 | 0.6866 |
| 3# | 20 | 7000 | 80 | 8.22 | 2.80 | 0.5002 |
| 4# | 16 | 7000 | 80 | 7.95 | 2.40 | 0.3247 |
| Array | Hydrophones | Range (m) | Depth (m) | SINR (dB) | PBR (dB) | GCOS |
|---|---|---|---|---|---|---|
| 1# | 99 | 7000 | 80 | 16.65 | 10.49 | 1.0 |
| 2# | 24 | 7000 | 80 | 16.32 | 10.34 | 0.9917 |
| 3# | 20 | 7000 | 80 | 15.78 | 10.22 | 0.8928 |
| 4# | 16 | 7000 | 80 | 13.58 | 8.12 | 0.5887 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wang, Y.; Zhu, G. Matched Field Processing Based on Least Squares with a Small Aperture Hydrophone Array. Sensors 2017, 17, 71. https://doi.org/10.3390/s17010071
Wang Q, Wang Y, Zhu G. Matched Field Processing Based on Least Squares with a Small Aperture Hydrophone Array. Sensors. 2017; 17(1):71. https://doi.org/10.3390/s17010071
Chicago/Turabian StyleWang, Qi, Yingmin Wang, and Guolei Zhu. 2017. "Matched Field Processing Based on Least Squares with a Small Aperture Hydrophone Array" Sensors 17, no. 1: 71. https://doi.org/10.3390/s17010071
APA StyleWang, Q., Wang, Y., & Zhu, G. (2017). Matched Field Processing Based on Least Squares with a Small Aperture Hydrophone Array. Sensors, 17(1), 71. https://doi.org/10.3390/s17010071





