A Machine Learning Approach to Pedestrian Detection for Autonomous Vehicles Using High-Definition 3D Range Data
Abstract
:1. Introduction
1.1. Pedestrian Detection
1.2. Pedestrian Detection Using 3D LIDAR Information
2. Materials and Methods
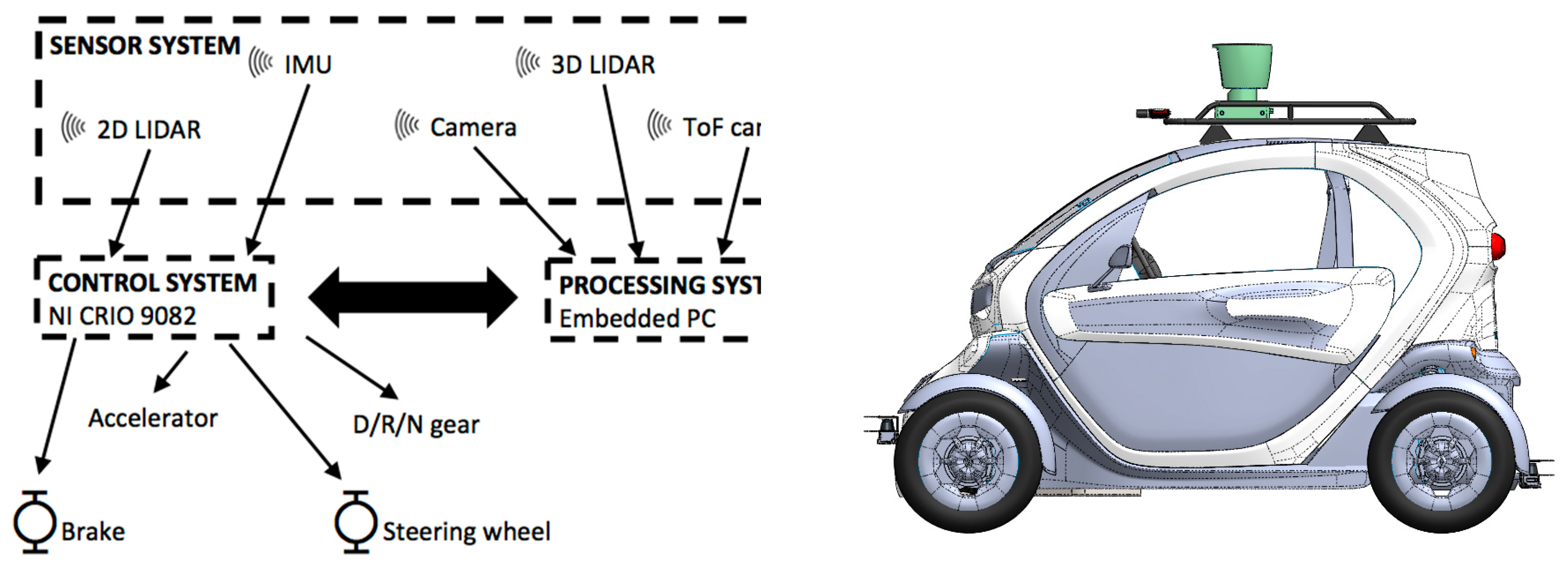
2.1. CIC Autonomous Vehicle
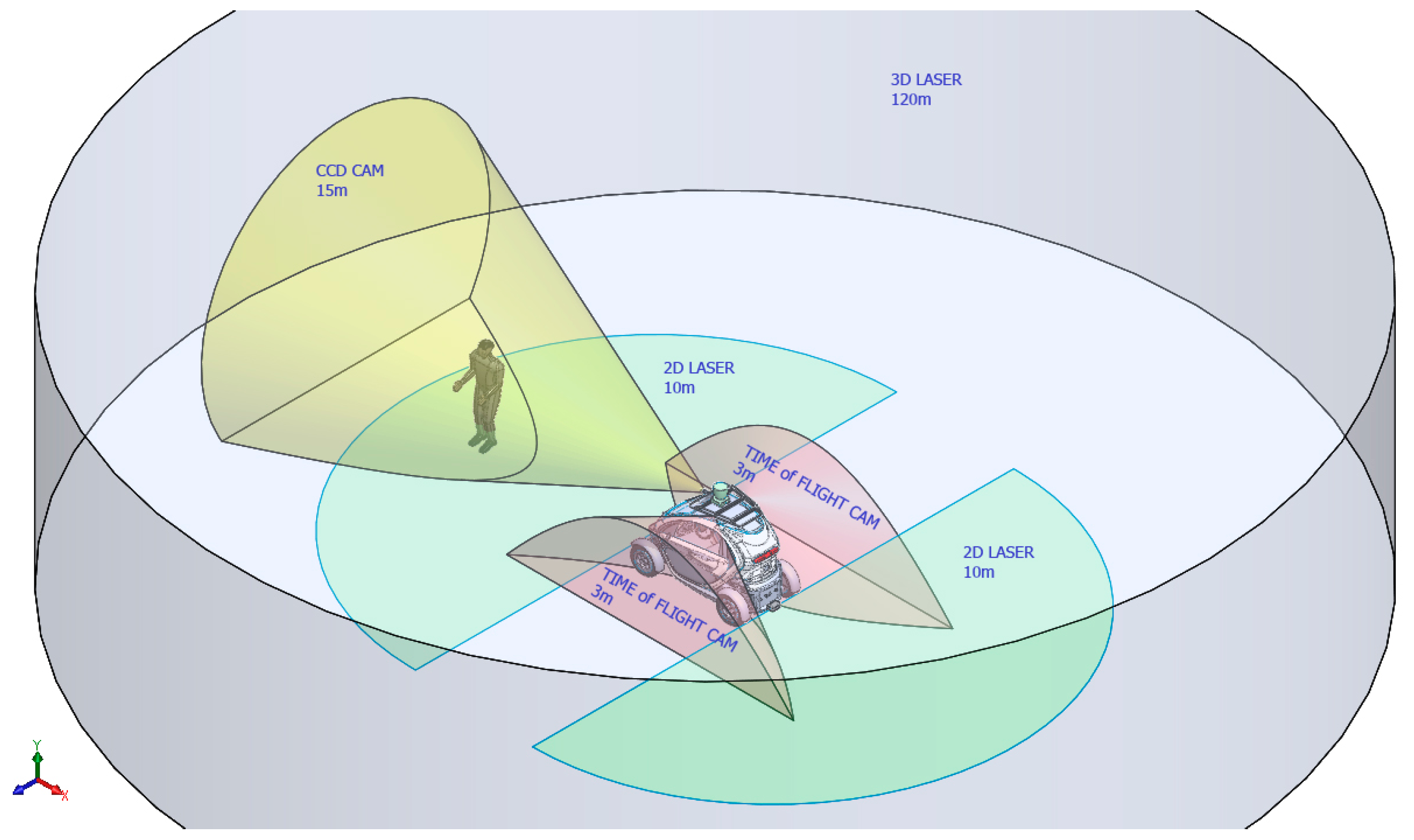
2.1.1. Sensor System
2.1.2. Control System
2.1.3. Processing System
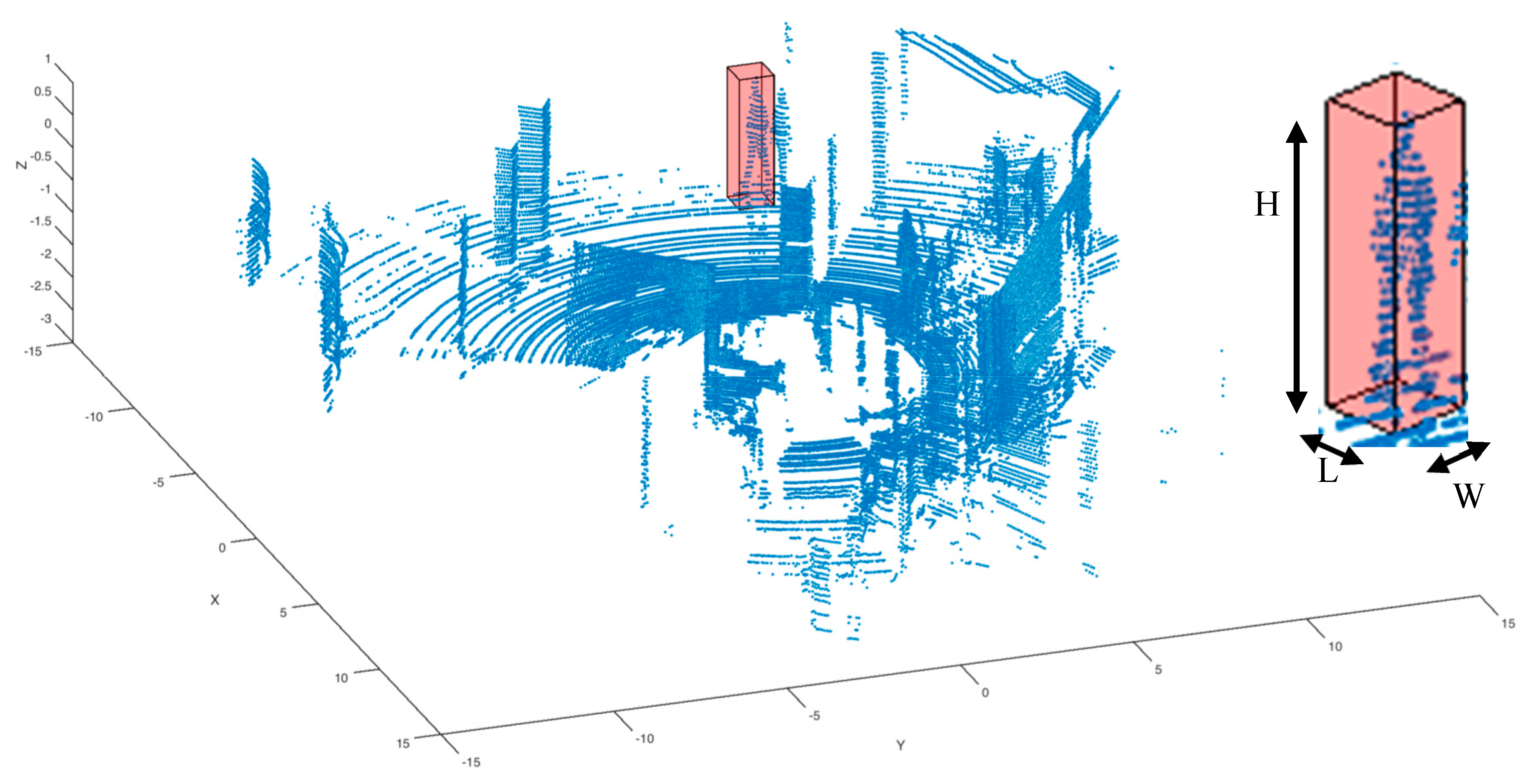
2.2. 3D LIDAR Cloud of Points
2.3. Pedestrian Detection Algorithm
- Select those cubes that contain a certain number of points, inside a threshold. This allows to eliminate objects with a reduced number of points which could produce false positives. Also, it reduces the computing time.
- Generate XY, YZ and XZ axonometric projections of the points contained inside the cube.
- Generate binary images of each projection, and then pre-process them.
- Extract features from each axonometric projection and 3D LIDAR raw data.
- Send the feature vector to a machine learning algorithm to decide whether it is a pedestrian or not.
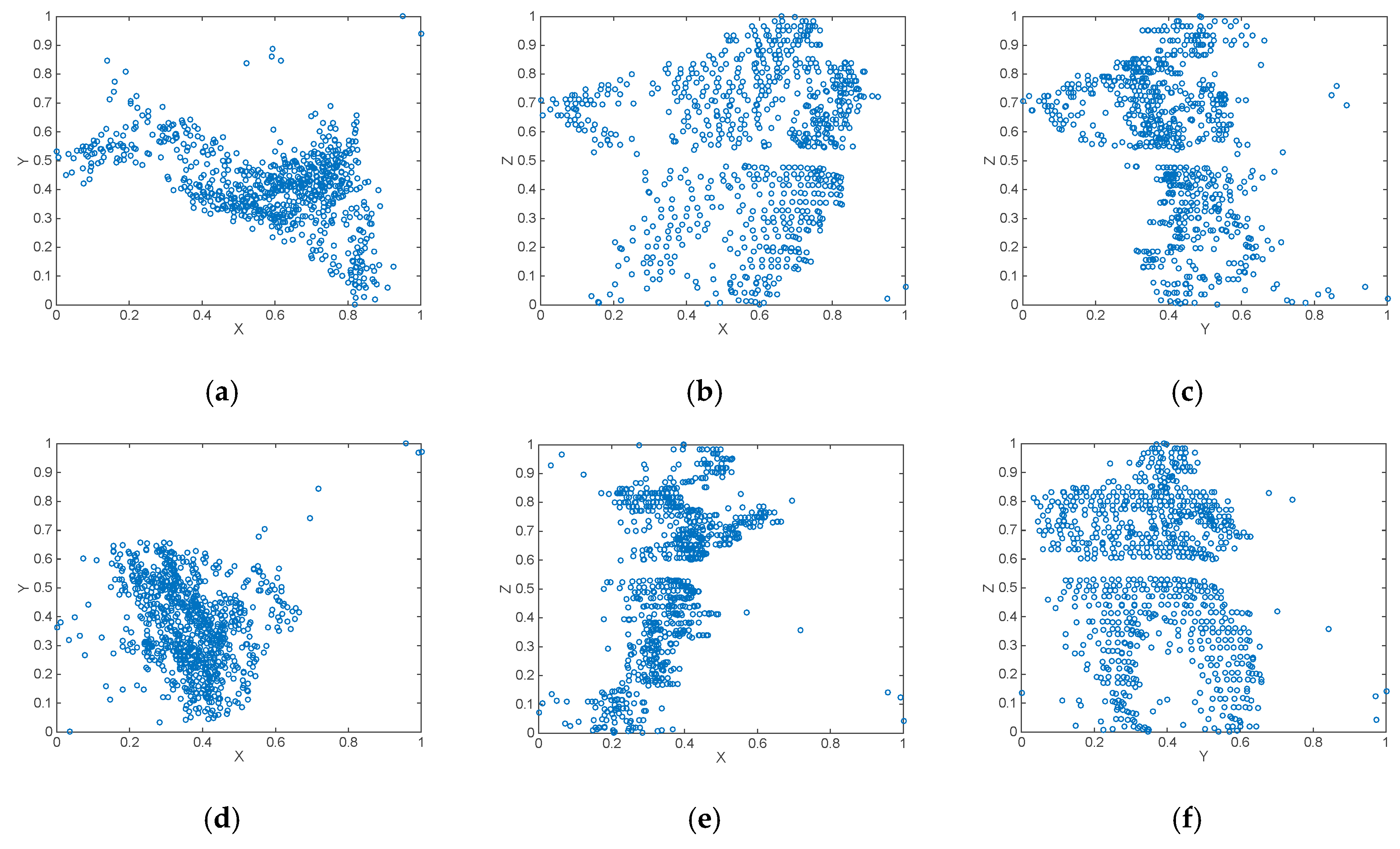
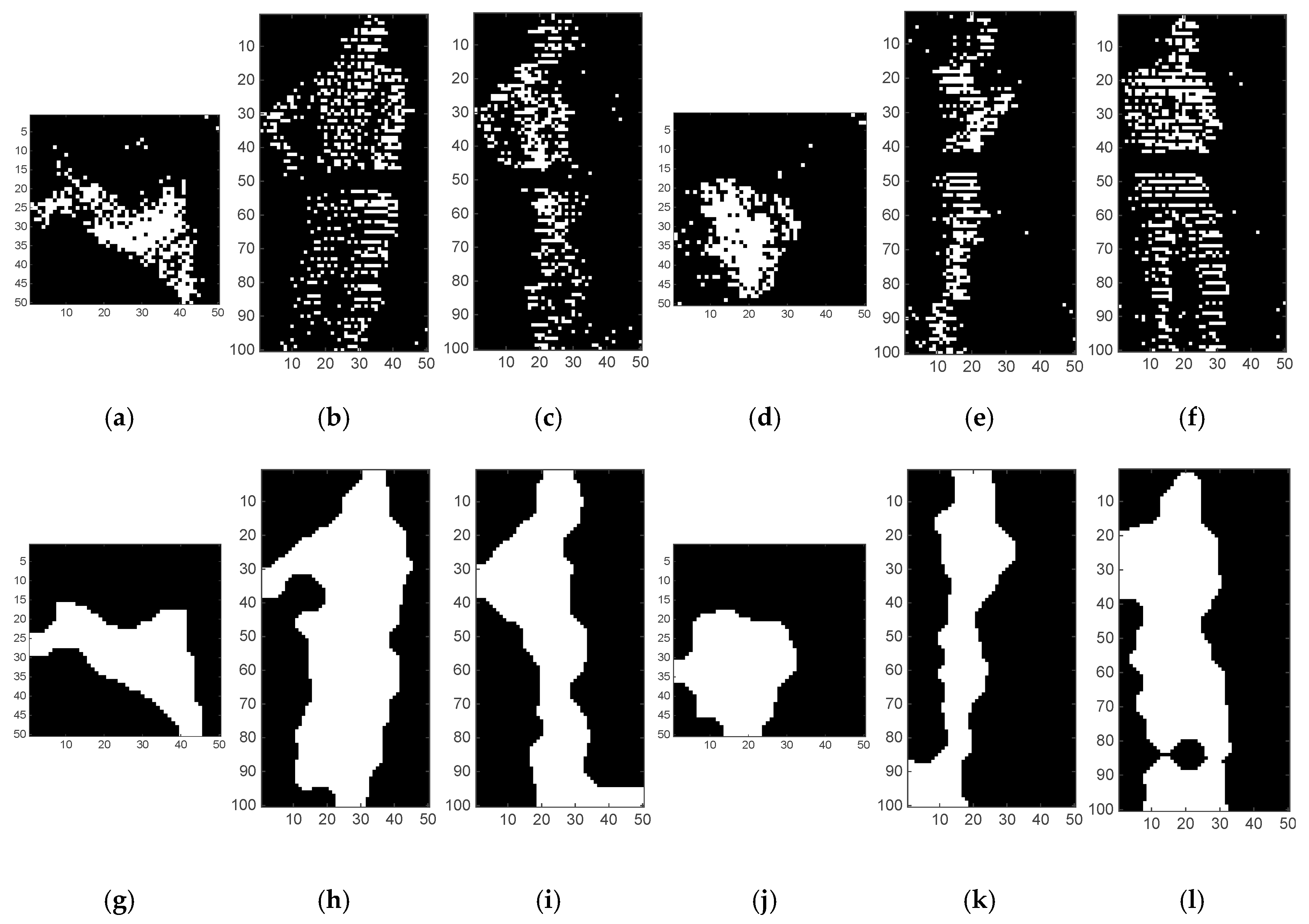
2.3.1. Step 2: Generation of XY, YZ and XZ Axonometric Projections
2.3.2. Step 3: Generation and Pre-processing of Binary Images of Axonometric Projections
2.3.3. Step 4: Compute Features Vector
- Area: number of pixels of the object.
- Perimeter: specifies the distance around the boundary of the region.
- Solidity: proportion of the pixels in the convex hull that are also in the region.
- Equivalent diameter: Specifies the diameter of a circle with the same area as the object (see Equation (3)):
- Eccentricity: Ratio of the distance between the foci of the ellipse and its major axis length. The value is between 0 and 1.
- Length of major/minor axis. A scalar that specifies the length (in pixels) of the major/minor axis of the ellipse that has the same normalized second central moments as the region under consideration.
2.3.4. Step 5: Machine Learning Algorithm
3. Results and Discussion
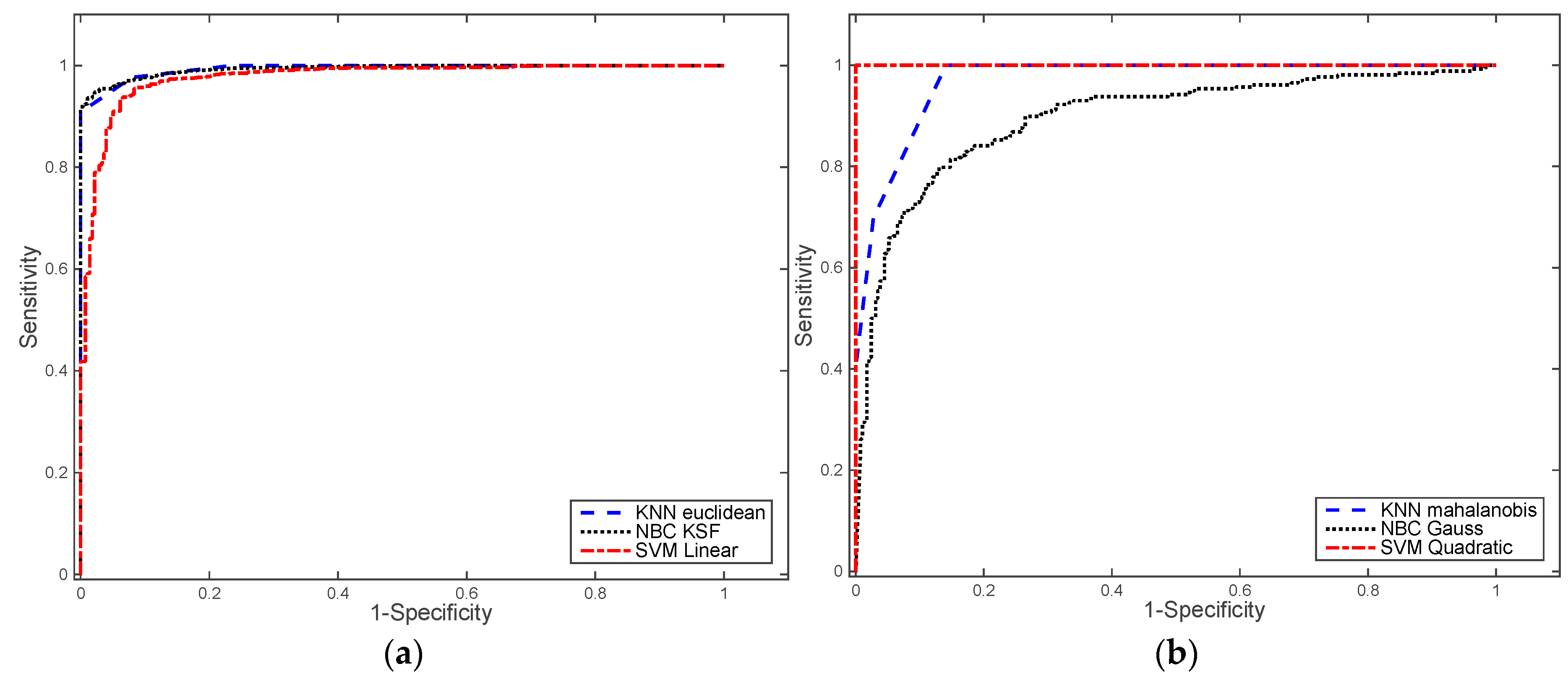
3.1. Performance of Machine Learning Algorithms
3.2. Performance of the Complete Pedestrian Detection Algorithm
4. Conclusions and Future Work
- Unlike other works [18,20,22], a novel set of elements is used to construct the feature vector the machine learning algorithm will use to discriminate pedestrians from other objects in its surroundings. Axonometric projections of cloud points samples are used to create binary images, which has allowed us to employ computer vision algorithms to compute part of the feature vector. The feature vector is composed of three kind of features: shape features, invariant moments and statistical features of distances and reflexivity from the 3D LIDAR.
- An exhaustive analysis of the performance of three different machine learning algorithms have been carried out: k-Nearest Neighbours (kNN), Naïve Bayes classifier (NBC), and Support Vector Machine (SVM). Each algorithm was trained with a training set comprising tool 277 pedestrians and 1654 no pedestrian samples and different kernel functions: kNN with Euclidean and Mahalanobis distances, NBC with Gauss and KSF functions and SVM with linear and quadratic functions. LOOCV and ROC analysis were used to detect the best algorithm to be used for pedestrian detection. The proposed algorithm has been tested in real traffic scenarios with 16 samples of pedestrians and 469 samples of non-pedestrians. The results obtained were used to validate theoretical results obtained in the Table 3. An overfitting problem in the SVM with quadratic kernel was found. Finally, SVM with linear function was selected since it offers the best results.
- A comparison of the proposed method with five other works that also use High Definition 3D LIDAR to carry-out the pedestrian detection, comparing the AUC and Fscore metrics. We can conclude that the proposed method obtains better performance results in every case.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ADAS | Advance Driver Assistance Systems |
| AUC | Area under curve |
| AV | Autonomous vehicles |
| CIC | Cloud Incubator Car |
| kNN | k-nearest neighbour |
| KSF | Kernel smoothing function |
| LOOCV | Leave-one-out cross validation method |
| MLA | Machine learning algorithms |
| NBC | Naïve Bayes classifier |
| SVM | Support vector machines |
References
- Thrun, S. Toward robotic cars. Commun. ACM 2010, 53, 99. [Google Scholar] [CrossRef]
- IEEE Expert Members of IEEE Identify Driverless Cars as Most Viable Form of Intelligent Transportation, Dominating the Roadway by 2040 and Sparking Dramatic Changes in Vehicular Travel. Available online: http://www.ieee.org/about/news/2012/5september_2_2012.html (accessed on 13 October 2016).
- Fagnant, D.J.; Kockelman, K. Preparing a nation for autonomous vehicles: Opportunities, barriers and policy recommendations. Transp. Res. Part A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Comission, E. Statistics of Road Safety. Available online: http://ec.europa.eu/transport/road_safety/specialist/statistics/index_en.htm (accessed on 1 December 2016).
- 2015 Motor Vehicle Crashes: Overview. Available online: https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/812318 (accessed on 1 December 2016).
- Dollar, P.; Wojek, C.; Schiele, B.; Perona, P. Pedestrian Detection: An Evaluation of the State of the Art. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 743–761. [Google Scholar] [CrossRef] [PubMed]
- Benenson, R.; Omran, M.; Hosang, J.; Schiele, B. Ten Years of Pedestrian Detection, What Have We Learned? In Computer Vision—ECCV 2014 Workshops; Springer International Publishing: Cham, Switzerland, 2015; pp. 613–627. [Google Scholar]
- Zhao, T.; Nevatia, R.; Wu, B. Segmentation and Tracking of Multiple Humans in Crowded Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1198–1211. [Google Scholar] [CrossRef] [PubMed]
- Kristoffersen, M.; Dueholm, J.; Gade, R.; Moeslund, T. Pedestrian Counting with Occlusion Handling Using Stereo Thermal Cameras. Sensors 2016, 16, 62. [Google Scholar] [CrossRef] [PubMed]
- Satake, J.; Chiba, M.; Miura, J. Visual person identification using a distance-dependent appearance model for a person following robot. Int. J. Autom. Comput. 2013, 10, 438–446. [Google Scholar] [CrossRef]
- Tsutsui, H.; Miura, J.; Shirai, Y. Optical flow-based person tracking by multiple cameras. In Proceedings of the International Conference on Multisensor Fusion and Integration for Intelligent Systems, MFI 2001, Baden-Baden, Germany, 20–22 August 2001; pp. 91–96.
- Dalal, N.; Triggs, W. Histograms of Oriented Gradients for Human Detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005; pp. 886–893.
- Szarvas, M.; Sakait, U.; Ogata, J. Real-Time Pedestrian Detection Using LIDAR and Convolutional Neural Networks. In Proceedings of the 2006 IEEE Intelligent Vehicles Symposium, Tokyo, Japan, 13–15 June 2006; pp. 213–218.
- Zhu, Q.; Chen, L.; Li, Q.; Li, M.; Nüchter, A.; Wang, J. 3D LIDAR point cloud based intersection recognition for autonomous driving. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium (IV), Madrid, Spain, 3–7 June 2012; pp. 456–461.
- Arastounia, M. Automated As-Built Model Generation of Subway Tunnels from Mobile LiDAR Data. Sensors 2016, 16, 1486. [Google Scholar] [CrossRef] [PubMed]
- Hämmerle, M.; Höfle, B. Effects of Reduced Terrestrial LiDAR Point Density on High-Resolution Grain Crop Surface Models in Precision Agriculture. Sensors 2014, 14, 24212–24230. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Liu, H.; Tan, J.; Li, Z.; Xie, H.; Chen, C. Scan Line Based Road Marking Extraction from Mobile LiDAR Point Clouds. Sensors 2016, 16, 903. [Google Scholar] [CrossRef] [PubMed]
- Premebida, C.; Batista, J.; Nunes, U. Pedestrain Detection Combining RGB and Dense LiDAR Data. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 4112–4117.
- Spinello, L.; Arras, K.; Triebel, R.; Siegwart, R. A Layered Approach to People Detection in 3D Range Data. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 1625–1630.
- Navarro-Serment, L.E.; Mertz, C.; Hebert, M. Pedestrian Detection and Tracking Using Three-dimensional LADAR Data. Int. J. Robot. Res. 2010, 29, 1516–1528. [Google Scholar] [CrossRef]
- Ogawa, T.; Sakai, H.; Suzuki, Y.; Takagi, K.; Morikawa, K. Pedestrian detection and tracking using in-vehicle LiDAR for automotive application. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 734–739.
- Kidono, K.; Miyasaka, T.; Watanabe, A.; Naito, T.; Miura, J. Pedestrian recognition using high-definition LIDAR. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 405–410.
- Toews, M.; Arbel, T. Entropy-of-likelihood feature selection for image correspondence. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 1041–1047.
- Chan, C.-H.; Pang, G.K.H. Fabric defect detection by Fourier analysis. IEEE Trans. Ind. Appl. 2000, 36, 1267–1276. [Google Scholar] [CrossRef]
- Chen, L.; Lu, G.; Zhang, D.S. Effects of different gabor filter parameters on image retrieval by texture. In Proceedings of the 10th International Multimedia Modeling Conference (MMM 2004), Brisbane, Australia, 5–7 January 2004; pp. 273–278.
- Fernández-Isla, C.; Navarro, P.J.; Alcover, P.M. Automated Visual Inspection of Ship Hull Surfaces Using the Wavelet Transform. Math. Probl. Eng. 2013, 2013, 12. [Google Scholar] [CrossRef]
- Navarro, P.J.; Pérez, F.; Weiss, J.; Egea-Cortines, M. Machine learning and computer vision system for phenotype data acquisition and analysis in plants. Sensors 2016, 16, 641. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.Q.; Nixon, M.S.; Thomas, D.W. Statistical geometrical features for texture classification. Pattern Recognit. 1995, 28, 537–552. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 610–621. [Google Scholar] [CrossRef]
- Zucker, S.W.; Terzopoulos, D. Finding structure in Co-occurrence matrices for texture analysis. Comput. Graph. Image Process. 1980, 12, 286–308. [Google Scholar] [CrossRef]
- Aggarwal, N.; Agrawal, R.K. First and Second Order Statistics Features for Classification of Magnetic Resonance Brain Images. J. Signal Inf. Process. 2012, 3, 146–153. [Google Scholar] [CrossRef]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- Zhang, Y.; Wang, S.; Sun, P. Pathological brain detection based on wavelet entropy and Hu moment invariants. Bio-Med. Mater. Eng. 2015, 26, S1283–S1290. [Google Scholar] [CrossRef] [PubMed]
- Alexa Internet. Available online: http://www.alexa.com/siteinfo/google.com (accessed on 1 December 2016).
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA; London, UK, 2012. [Google Scholar]
- Lantz, B. Machine Learning with R; Packt Publishing Ltd.: Birmingham, UK, 2013. [Google Scholar]
- Navarro, P.J.; Alonso, D.; Stathis, K. Automatic detection of microaneurysms in diabetic retinopathy fundus images using the L*a*b color space. J. Opt. Soc. Am. A. Opt. Image Sci. Vis. 2016, 33, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Hand, D. Measuring classifier performance: A coherent alternative to the area under the ROC curve. Mach. Learn. 2009, 77, 103–123. [Google Scholar] [CrossRef]






| Shape Features | Invariant Moments | Statistical Features |
|---|---|---|
| f1, f2, f3: Areas of XY, XZ, YZ projections | f22, f23, f24: Hu moment 1 over XY, XZ, YZ projections | f43, f44: Means of distances and reflexivity |
| f4, f5, f6: Perimeters of XY, XZ, YZ projections | f25, f26, f27: Hu moment 2 over XY, XZ, YZ projections | f45, f46: Standard deviations of distances and reflexivity |
| f7, f8, f9: Solidity of XY, XZ, YZ projections | f28, f29, f30: Hu moment 3 over XY, XZ, YZ projections | f47, f48: Kurtosis of distances and reflexivity |
| f10, f11, f12: Equivalent diameters of XY, XZ, YZ projections | f31, f32, f33: Hu moment 4 over XY, XZ, YZ projections | f49, f50: Skewness of distances and reflexivity |
| f13, f14, f15: Eccentricity of XY, XZ, YZ projections | f34, f35, f36: Hu moment 5 over XY, XZ, YZ projections | |
| f16, f17, f18: Length major axis of XY, XZ, YZ projections | f37, f38, f39: Hu moment 6 over XY, XZ, YZ projections | |
| f19, f20, f21: Length minor axis of XY, XZ, YZ projections | f40, f41, f42: Hu moment 7 over XY, XZ, YZ projections |
| Configuration | kNN | NBC | SVM |
|---|---|---|---|
| Method | Euclidean, Mahalanobis | Gauss (2), KSF (3) | Linear (4), quadratic (5) |
| Data normalisation | Yes (1) | No | Yes (1) |
| Metrics | LOOCV, ROC | LOOCV, ROC | LOOCV, ROC |
| Classes | 2 | 2 | 2 |
| MLA | kNN | NBC | SVM | ||||
|---|---|---|---|---|---|---|---|
| Configuration | Euclidean | Mahalanobis | KSF | Gauss | Linear | Quadratic | |
| LOOCV | Error | 0.0653 | 0.0673 | 0.1361 | 0.6769 | 0.0528 | 0.0451 |
| ROC curves | AUC | 0.9935 | 0.9916 | 0.9931 | 0.9317 | 0.9764 | 1.0000 |
| Sensivity | 0.9764 | 0.9727 | 0.9304 | 0.2122 | 0.9758 | 1.0000 | |
| Specificity | 0.9205 | 0.9169 | 0.9891 | 0.9855 | 0.8194 | 1.0000 | |
| Precision | 0.9865 | 0.985907 | 0.9980 | 0.9887 | 0.9699 | 1.0000 | |
| Accuracy | 0.9684 | 0.964785 | 0.9388 | 0.3231 | 0.9533 | 1.0000 | |
| Fscore | 0.9814 | 0.9793 | 0.9630 | 0.3494 | 0.9728 | 1.0000 | |
| kNN–Euclidean | SVM–Linear | SVM–Quadratic | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frame | Samples | Pedestrians in the Sample | TP | FP | TN | FN | TP | FP | TN | FN | TP | FP | TN | FN |
| 1 | 100 | 1 | 1 | 7 | 92 | 0 | 1 | 2 | 97 | 0 | 1 | 14 | 85 | 0 |
| 2 | 53 | 1 | 1 | 5 | 47 | 0 | 1 | 2 | 50 | 0 | 0 | 3 | 49 | 1 |
| 3 | 47 | 1 | 1 | 4 | 42 | 0 | 1 | 1 | 45 | 0 | 1 | 10 | 36 | 0 |
| 4 | 58 | 3 | 1 | 7 | 48 | 2 | 1 | 3 | 52 | 2 | 2 | 6 | 49 | 1 |
| 5 | 79 | 4 | 3 | 5 | 70 | 1 | 3 | 3 | 72 | 1 | 4 | 9 | 66 | 0 |
| 6 | 45 | 4 | 4 | 5 | 36 | 0 | 4 | 1 | 40 | 0 | 4 | 2 | 39 | 0 |
| 7 | 103 | 2 | 2 | 9 | 92 | 0 | 2 | 3 | 98 | 0 | 2 | 6 | 95 | 0 |
| Sum | 485 | 16 | 13 | 42 | 427 | 3 | 13 | 15 | 454 | 3 | 14 | 50 | 419 | 2 |
| Metric | kNN–Euclidean | SVM–Linear | SVM–Quadratic |
|---|---|---|---|
| Sensivity | 0.8125 | 0.8125 | 0.8750 |
| Specificity | 0.9104 | 0.9680 | 0.8934 |
| Precision | 0.2364 | 0.4643 | 0.2188 |
| Accuracy | 0.9072 | 0.9629 | 0.8928 |
| Fscore | 0.3662 | 0.5909 | 0.3500 |
| Author/Year [Ref.] | MLA | Metric | Performance | |
|---|---|---|---|---|
| Graphical | Numeric | |||
| Proposed 2016 | Linear SVM | ROC curve | LOOCV, AUC, sensitivity, specificity, precision, accuracy, Fscore | 0.0528, 0.9764, 0.9758, 0.8194, 0.9699, 0.9533, 0.9728 |
| Premebida 2014 [18] | Deformable Part-based Model (DPM) | Precision-Recall curve of the areas of the pedestrian correctly identified. | Authors report a mean | 0.3950 |
| Spinello 2010 [19] | Multiple AdaBoost classifiers | Precision-Recall curve, Equal Error Rates (EER) | Authors report a mean | 0.7760 |
| Navarro-Serment 2010 [20] | Two SVMs in cascade | Precision-Recall and ROC curves | AUC estimate | 0.8500 |
| Ogawa 2011 [21] | Interacting Multiple Model filter | Recognition rate | Authors report a mean | 0.8000 |
| Kidono 2011 [22] | SVM | ROC curve | AUC estimate | 0.9000 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, P.J.; Fernández, C.; Borraz, R.; Alonso, D. A Machine Learning Approach to Pedestrian Detection for Autonomous Vehicles Using High-Definition 3D Range Data. Sensors 2017, 17, 18. https://doi.org/10.3390/s17010018
Navarro PJ, Fernández C, Borraz R, Alonso D. A Machine Learning Approach to Pedestrian Detection for Autonomous Vehicles Using High-Definition 3D Range Data. Sensors. 2017; 17(1):18. https://doi.org/10.3390/s17010018
Chicago/Turabian StyleNavarro, Pedro J., Carlos Fernández, Raúl Borraz, and Diego Alonso. 2017. "A Machine Learning Approach to Pedestrian Detection for Autonomous Vehicles Using High-Definition 3D Range Data" Sensors 17, no. 1: 18. https://doi.org/10.3390/s17010018
APA StyleNavarro, P. J., Fernández, C., Borraz, R., & Alonso, D. (2017). A Machine Learning Approach to Pedestrian Detection for Autonomous Vehicles Using High-Definition 3D Range Data. Sensors, 17(1), 18. https://doi.org/10.3390/s17010018






