Efficient Data Gathering Methods in Wireless Sensor Networks Using GBTR Matrix Completion
Abstract
:1. Introduction
- (1)
- The features of sensor datasets are analyzed in consideration of their topology information, which reveals that the data matrix is sparse under the graph based transform.
- (2)
- The graph based transform regularized (GBTR) Matrix Completion problem is formulated. To reconstruct the missing values efficiently, the GBTR by Alternating Direction Method of Multipliers (GBTR-ADMM) algorithm is proposed. Simulation results reveal that GBTR-ADMM outperforms the state of art algorithms in view of the recovery accuracy and the energy consumption.
- (3)
- To accelerate the convergence of GBTR-ADMM, GBTR-A2DM2 algorithm is proposed, which benefits from a restart rule and the fusion of multiple constraints.
- (4)
- The time complexity of our proposed algorithms is analyzed, which shows that the complexity is low.
2. Problem Formulation
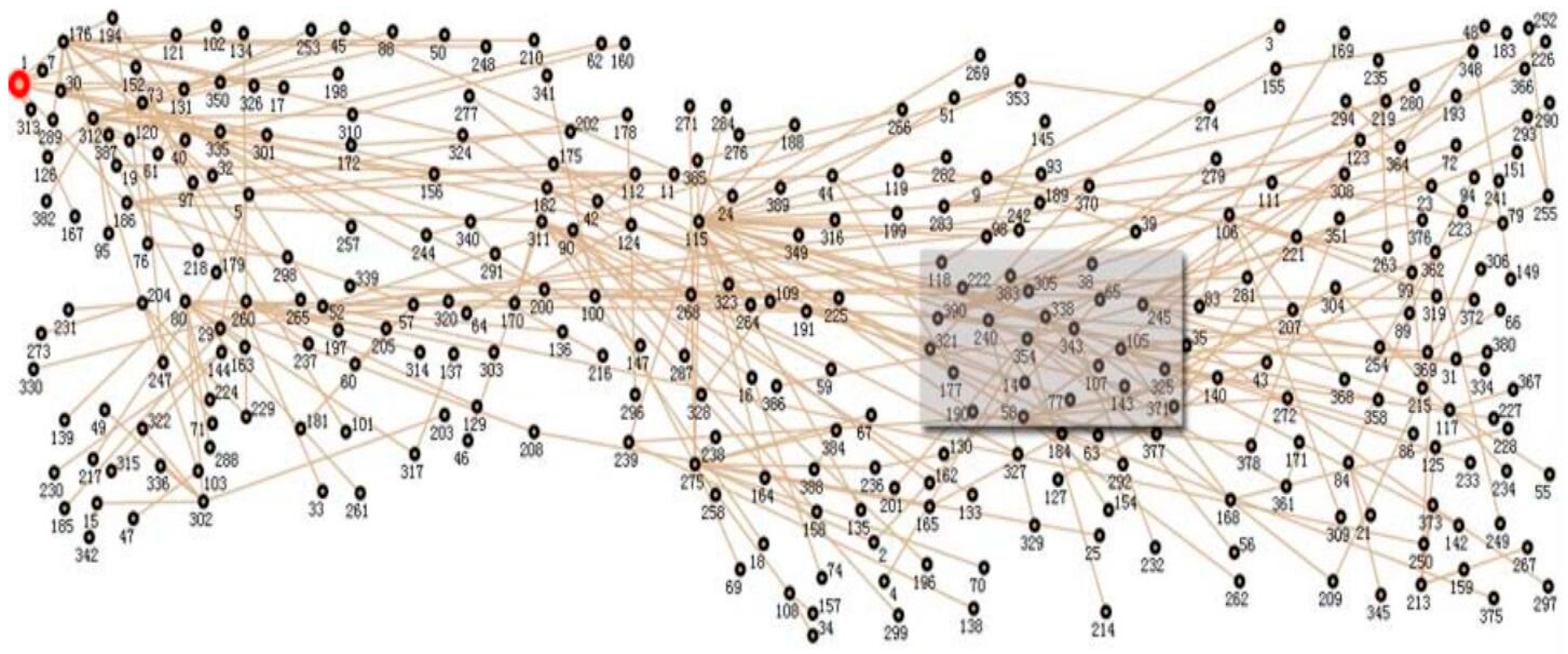
3. Exploring the Features of Datasets
3.1. Low-Rank Property
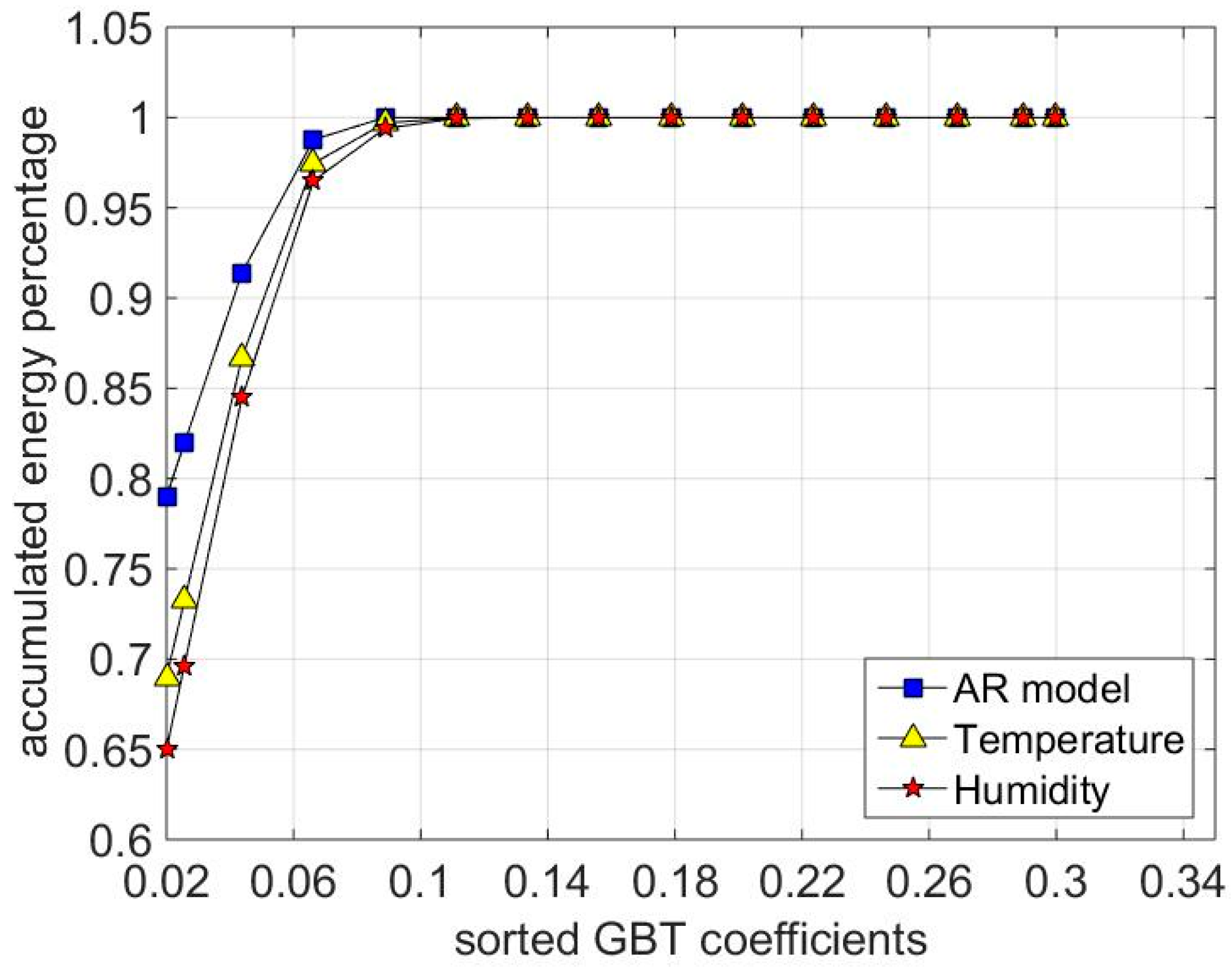
3.2. GBT Sparsity
4. The Proposed Optimization Algorithm
| Algorithm 1: The proposed GBTR-ADMM algorithm. |
| Initialization: |
| While do |
| 1: |
| 2: |
| In consideration of the constraint in Problem (6) |
| 3: |
5. The Proposed Method for Accelerated Convergence
5.1. The Fusion of Two Constraints
| Algorithm 2: GBTR-A2DM2 algorithm using restarting rule. |
| Initialization |
| While do |
| 1: Update by Equation (29) |
| 2: Update by Equation (30) |
| 3: Update by Equation (31) |
| 4: |
| If Then |
| 5: |
| 6: |
| 7: |
| Else |
| 8: |
| 9: |
| End if |
| End While |
5.2. The Accelerated Technique
6. Time Complexity Analysis
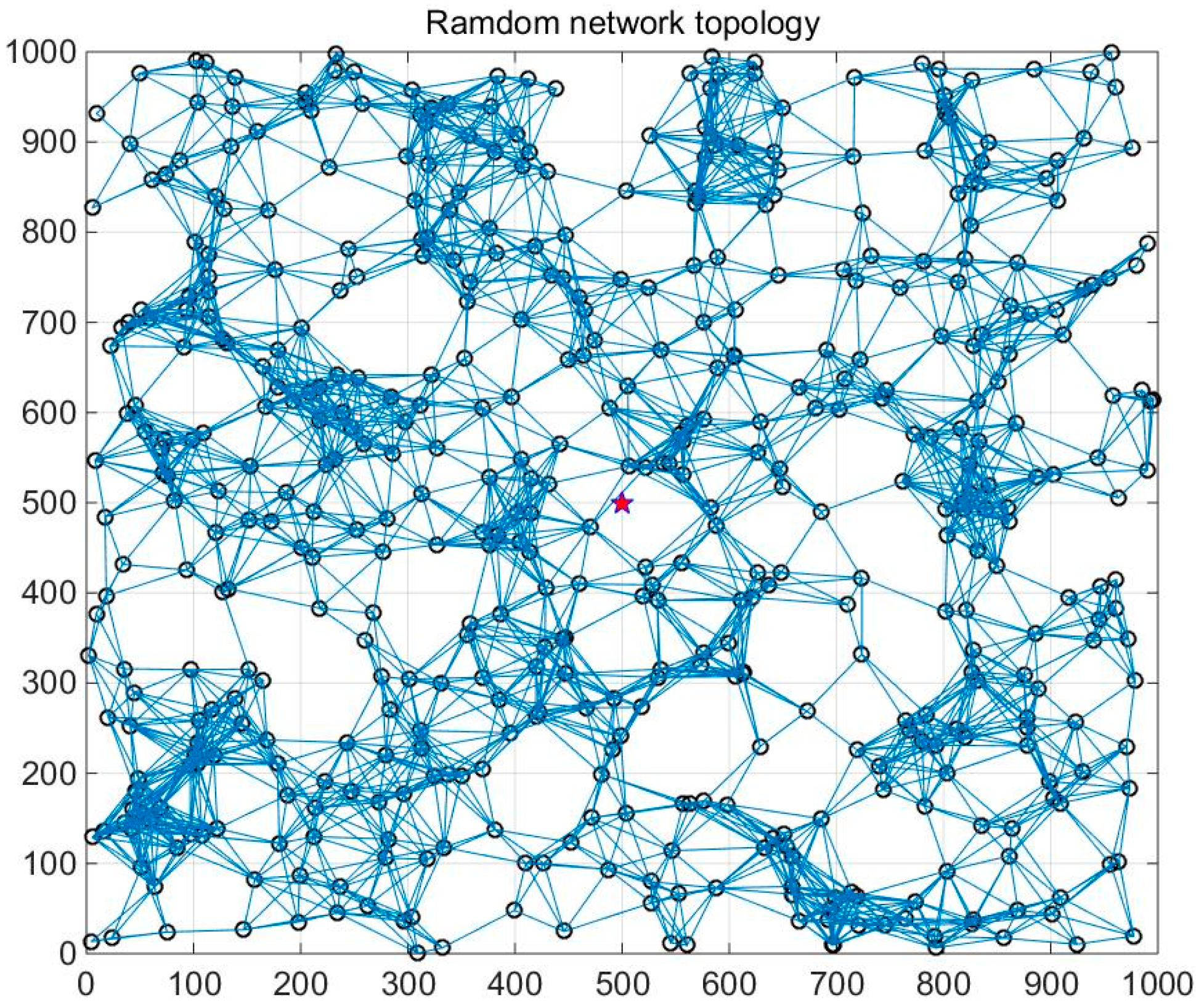
7. Performance Evaluation
7.1. Parameter Setting
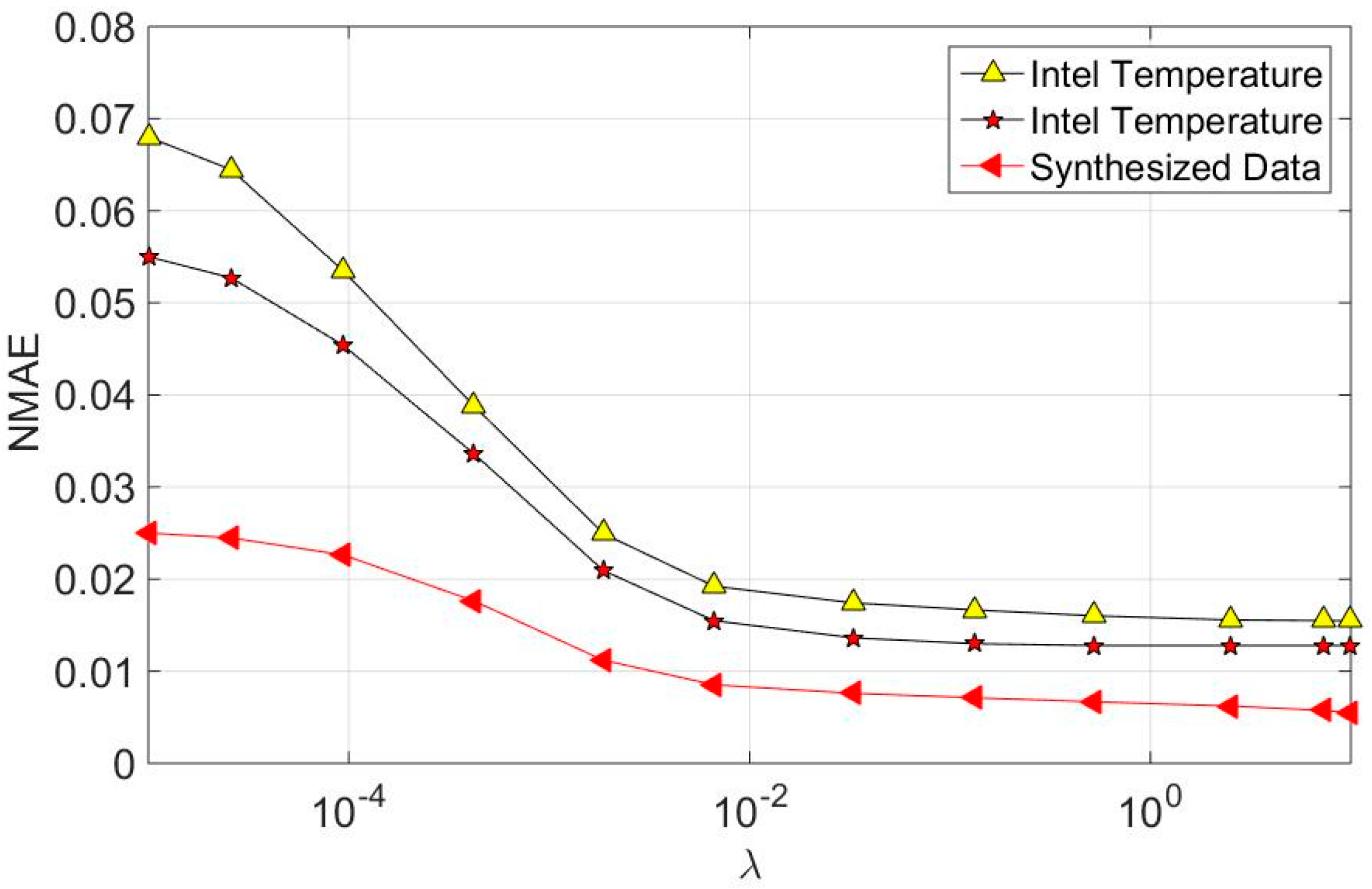
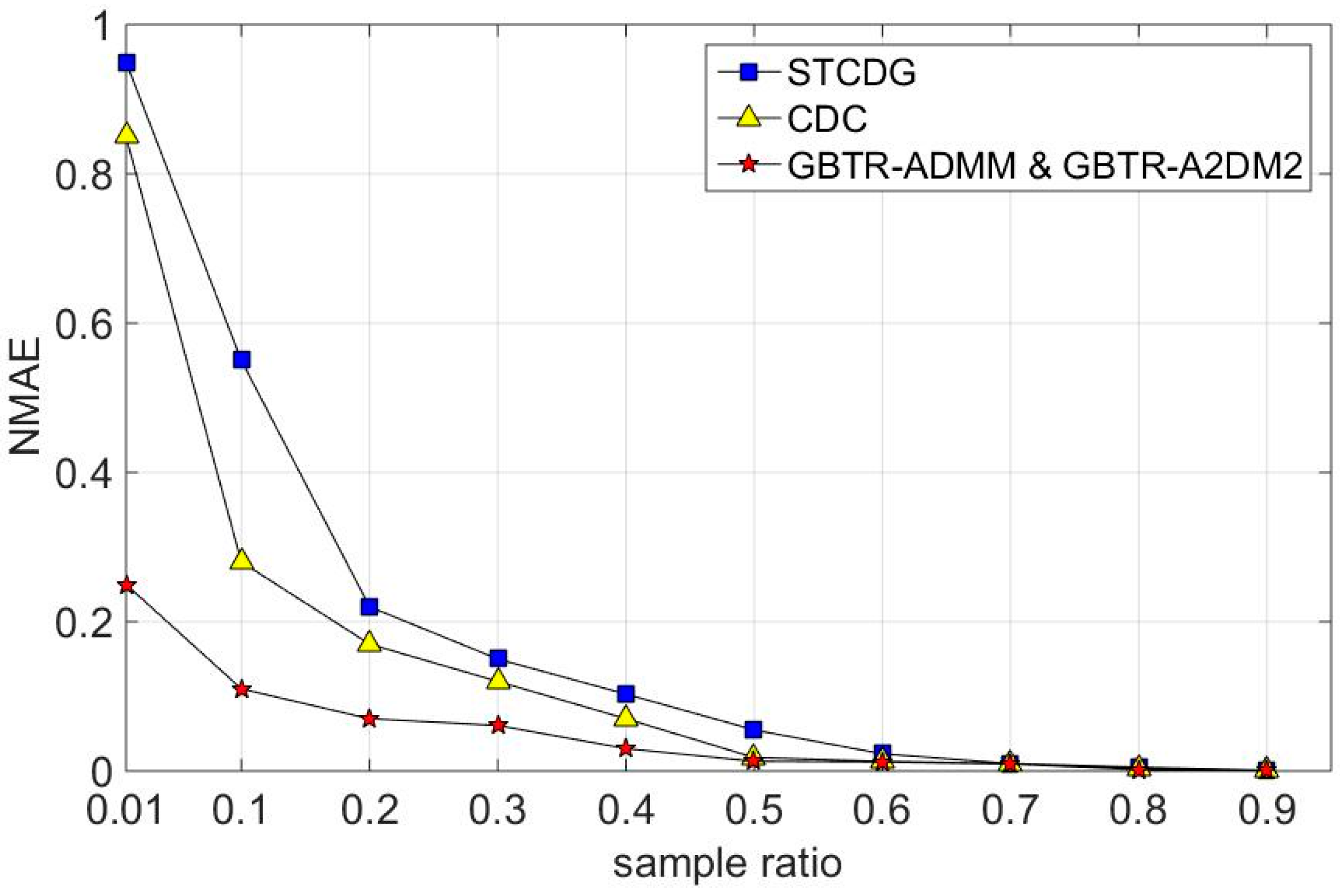
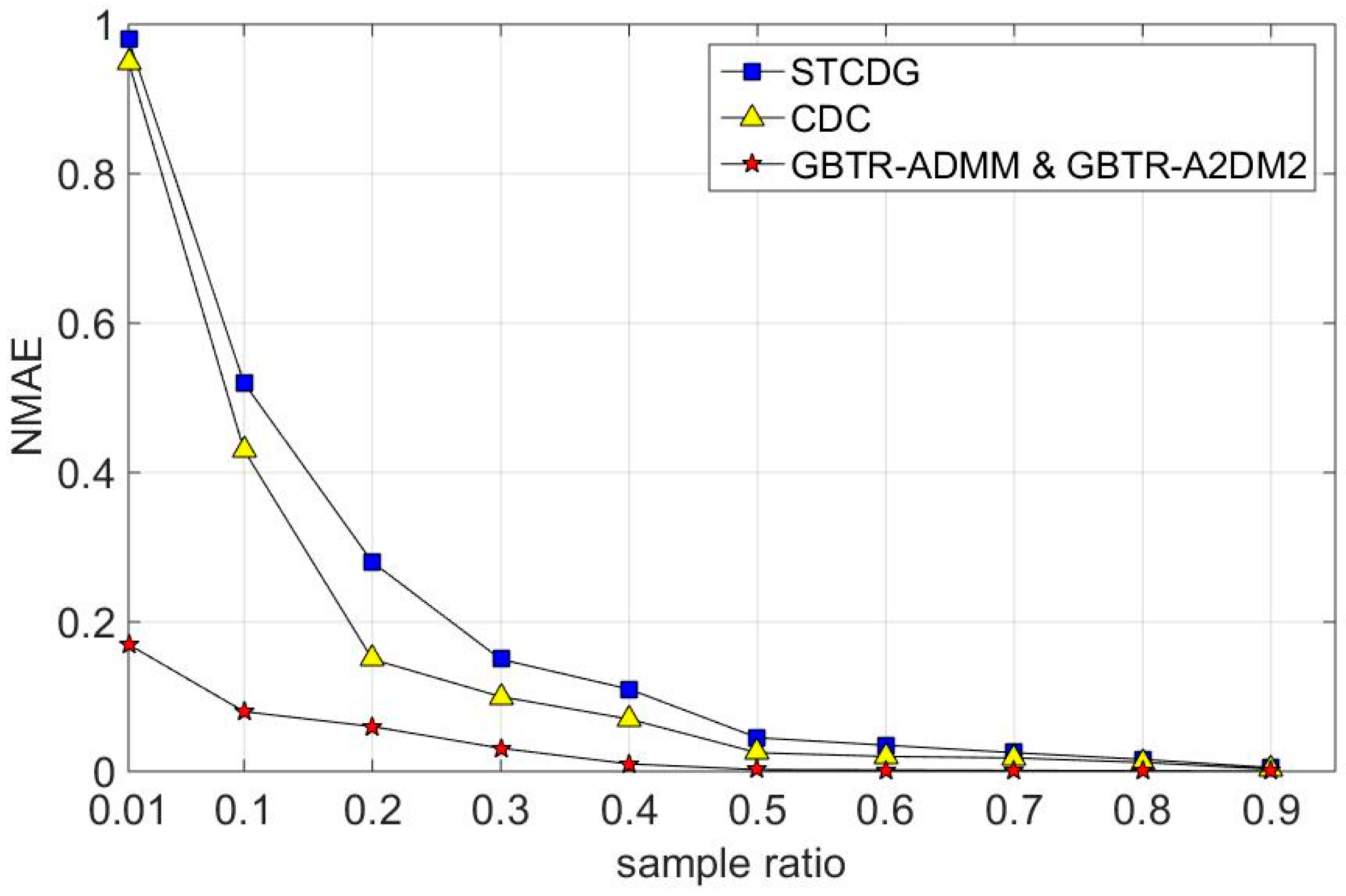
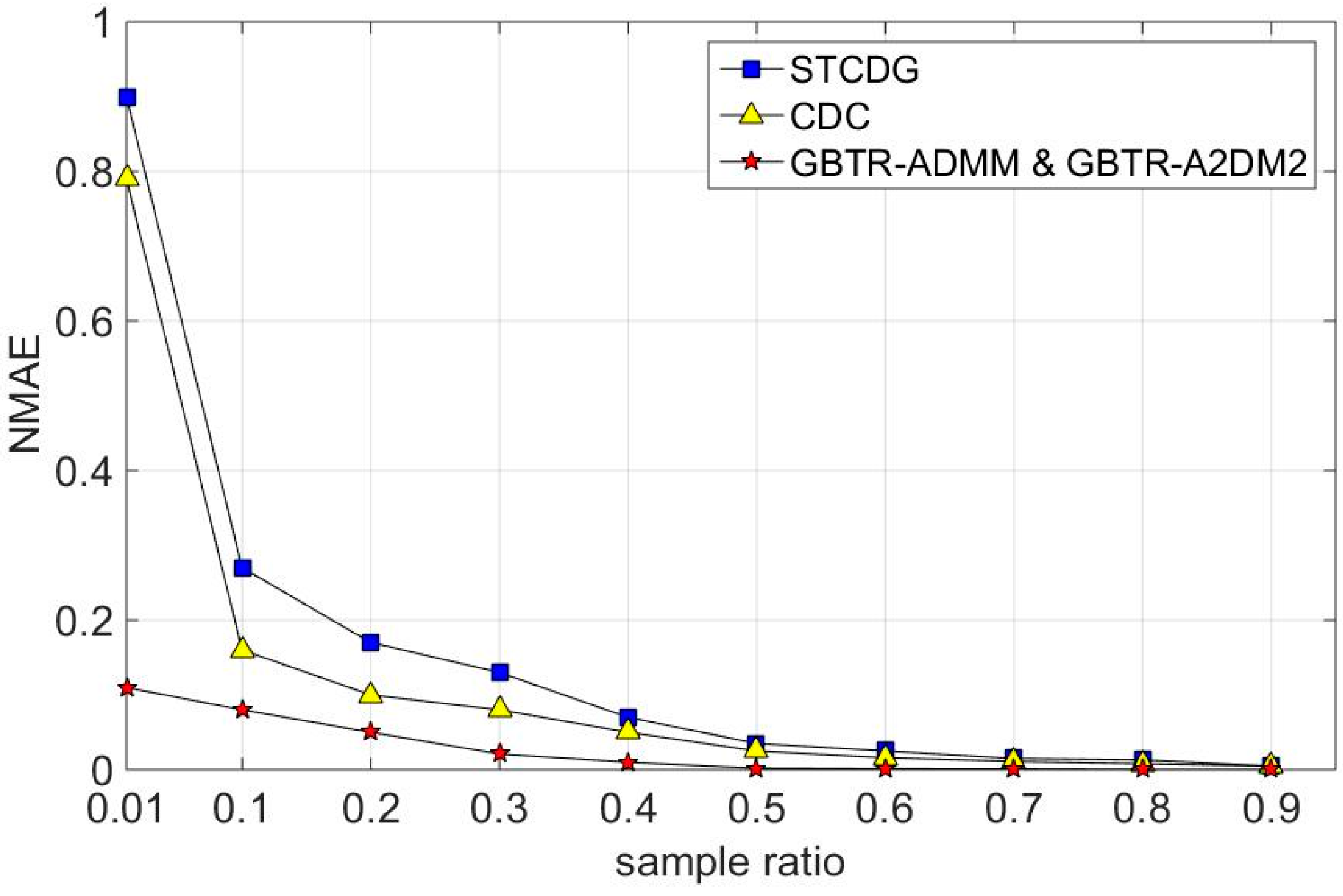
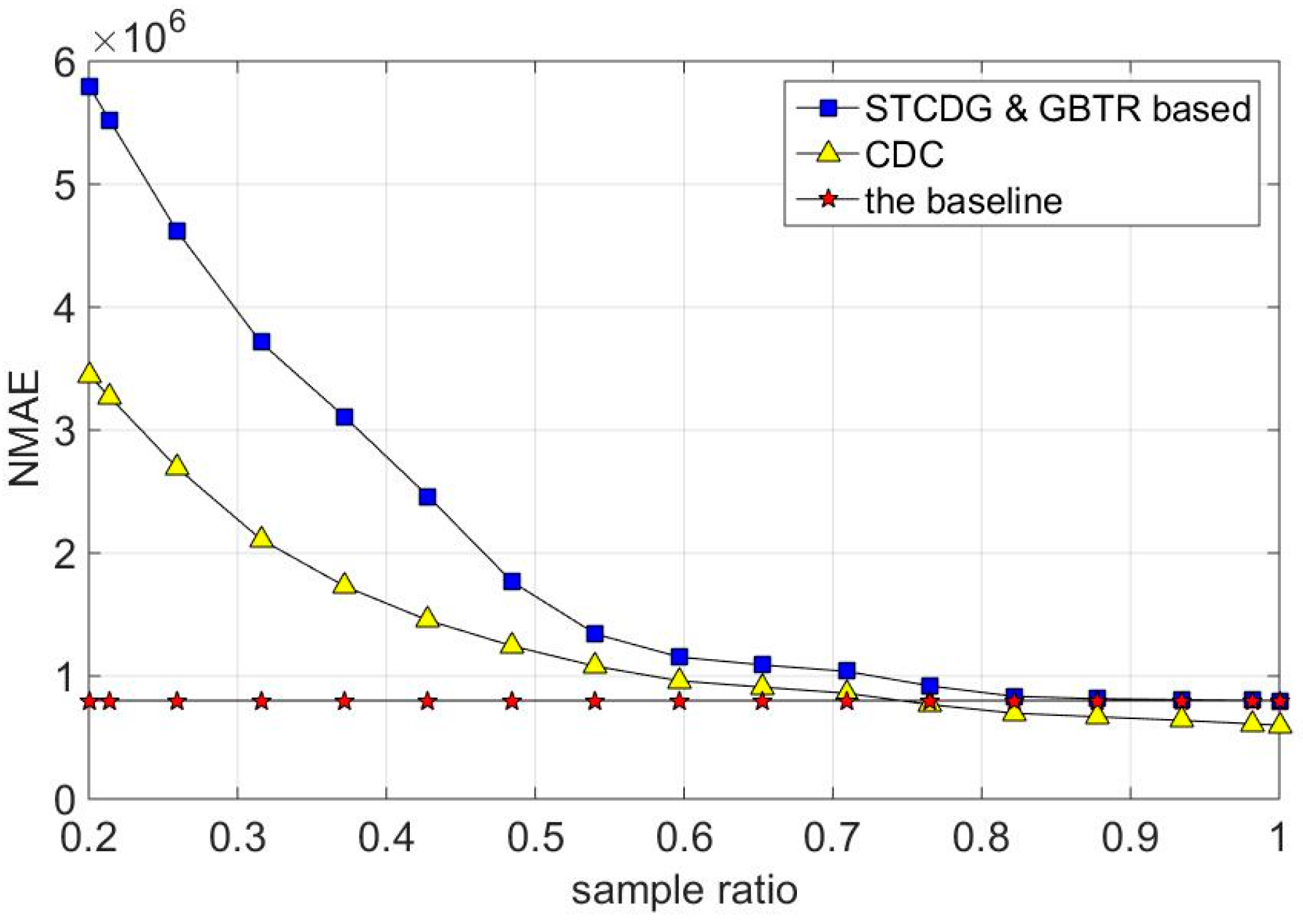
7.2. Recovery Accuracy
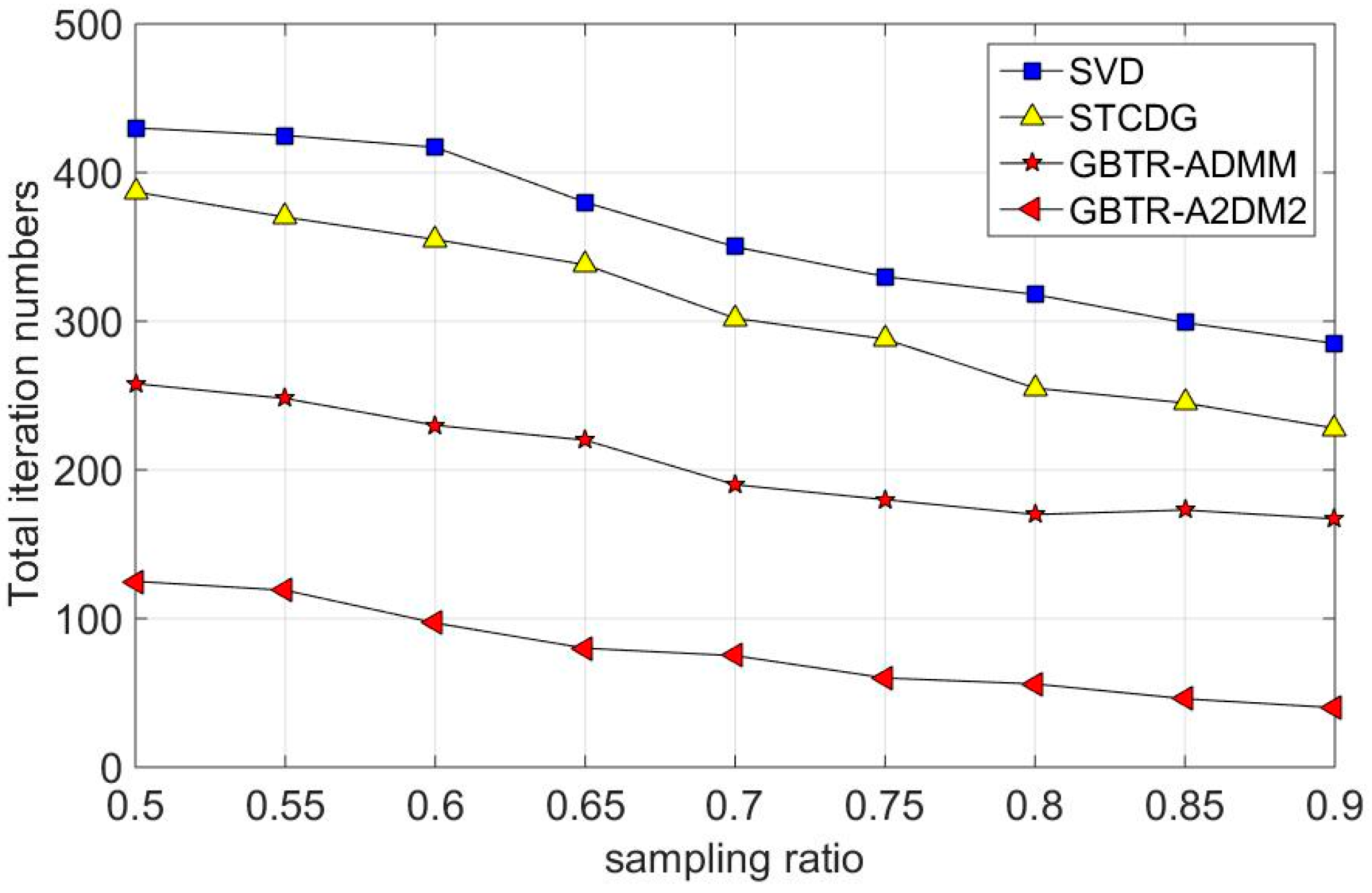
7.3. Convergence Behavior Analysis
7.4. Energy Consumption and Network Lifetime
8. Conclusions and Future Works
Acknowledgments
Author Contributions
Conflicts of interest
References
- Yoon, S.; Shahabi, C. The Clustered AGgregation (CAG) technique leveraging spatial and temporal correlations in wireless sensor networks. ACM Trans. Sens. Netw. 2007, 3, 3. [Google Scholar] [CrossRef]
- Pham, N.D.; Le, T.D.; Park, K.; Choo, H. SCCS: Spatiotemporal clustering and compressing schemes for efficient data collection applications in WSNs. Int. J. Commun. Syst. 2010, 23, 1311–1333. [Google Scholar] [CrossRef]
- Lachowski, R.; Pellenz, M.E.; Penna, M.C.; Jamhour, E.; Souza, R.D. An efficient distributed algorithm for constructing spanning trees in wireless sensor networks. Sensors 2015, 15, 1518–1536. [Google Scholar] [CrossRef] [PubMed]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Gleichman, S.; Eldar, Y.C. Blind compressed sensing. IEEE Trans. Inf. Theory 2011, 57, 6958–6975. [Google Scholar] [CrossRef]
- Li, S.X.; Gao, F.; Ge, G.N.; Zhang, S.Y. Deterministic construction of compressed sensing matrices via algebraic curves. IEEE Trans. Inf. Theory 2012, 58, 5035–5041. [Google Scholar] [CrossRef]
- Luo, C.; Wu, F.; Sun, J.; Chen, C.W. Compressive data gathering for large-scale wireless sensor networks. In Proceedings of the 15th ACM International Conference on Mobile Computing and Networking, Beijing, China, 20–25 September 2009; pp. 145–156.
- Caione, C.; Brunelli, D.; Benini, L. Distributed compressive sampling for lifetime optimization in dense wireless sensor networks. IEEE Trans. Ind. Inf. 2012, 8, 30–40. [Google Scholar] [CrossRef]
- Xiang, L.; Luo, J.; Rosenberg, C. Compressed data aggregation: Energy-efficient and high-fidelity data collection. IEEE ACM Trans. Netw. 2013, 21, 1722–1735. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhu, Y.; Kong, L.; Liu, C.; Gu, Y.; Vasilakos, A.V.; Wu, M.Y. CDC: Compressive data collection for wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 2188–2197. [Google Scholar] [CrossRef]
- Candes, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Cai, J.F.; Candes, E.J.; Shen, Z.W. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Roughan, M.; Zhang, Y.; Willinger, W.; Qiu, L.L. Spatio-temporal compressive sensing and internet traffic matrices. IEEE ACM Trans. Netw. 2012, 20, 662–676. [Google Scholar] [CrossRef]
- Cheng, J.; Ye, Q.; Jiang, H.; Wang, D.; Wang, C. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks. IEEE Trans. Wirel. Commun. 2013, 12, 850–861. [Google Scholar] [CrossRef]
- Liu, Y.; He, Y.; Li, M.; Wang, J.; Liu, K.; Li, X. Does wireless sensor network scale? A measurement study on GreenOrbs. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1983–1993. [Google Scholar] [CrossRef]
- Kong, L.; Xia, M.; Liu, X.Y.; Chen, G.; Gu, Y.; Wu, M.Y.; Liu, X. Data loss and reconstruction in wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2818–2828. [Google Scholar] [CrossRef]
- Candes, E.; Recht, B. Exact matrix completion via convex optimization. Commun. ACM 2012, 55, 111–119. [Google Scholar] [CrossRef]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- He, B.; Tao, M.; Yuan, X. Alternating direction method with Gaussian back substitution for separable convex programming. SIAM J. Optim. 2012, 22, 313–340. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, D.; Ye, J.; Li, X.; He, X. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, T.; O′Donoghue, B.; Setzer, S.; Baraniuk, R. Fast alternating direction optimization methods. SIAM J. Imaging Sci. 2014, 7, 1588–1623. [Google Scholar] [CrossRef]
- Kadkhodaie, M.; Christakopoulou, K.; Sanjabi, M.; Banerjee, A. Accelerated alternating direction method of multipliers. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 497–506.
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2012. [Google Scholar]
- Larsen, R.M. PROPACK-Software for Large and Sparse SVD Calculations. Available online: http://sun.stanford.edu/~rmunk/PROPACK (accessed on 19 September 2016).
- Toh, K.C.; Yun, S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems. Pac. J. Optim. 2010, 6, 615–640. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Siences, Maui, HI, USA, 4–7 Jauary 2000; p. 223.


| Number of time slots | |
| Number of sensor nodes | |
| The observed ratio | |
| The matrix rank | |
| The GBT sparsity regularization parameter | |
| The Lagrange penalty parameter | |
| The original data matrix | |
| The reconstructed data matrix | |
| The observed data matrix | |
| The degree matrix | |
| The adjacency matrix | |
| The Laplacian matrix | |
| The GBT matrix | |
| The introduced auxiliary variable | |
| The Lagrange multiplier |
| Data Name | Data Types | Selected Data Matrix | Time Interval |
|---|---|---|---|
| GreenOrbs | Temperature | 5 min | |
| GreenOrbs | Humidity | 5 min | |
| Synthesized | AR model | - |
| Parameter Name | λ | β |
|---|---|---|
| Set Value | 0.01 |
| Parameter Name | Value |
|---|---|
| Nodes number | 500 |
| Transmission range | 100 m |
| Initial energy | 2 J |
| Data Size | 64 bits |
| 100 nJ/bit | |
| 120 nJ/bit | |
| 0.1 nJ/( bit·m2) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Wan, J.; Nie, Z.; Zhang, Q.; Fei, Z. Efficient Data Gathering Methods in Wireless Sensor Networks Using GBTR Matrix Completion. Sensors 2016, 16, 1532. https://doi.org/10.3390/s16091532
Wang D, Wan J, Nie Z, Zhang Q, Fei Z. Efficient Data Gathering Methods in Wireless Sensor Networks Using GBTR Matrix Completion. Sensors. 2016; 16(9):1532. https://doi.org/10.3390/s16091532
Chicago/Turabian StyleWang, Donghao, Jiangwen Wan, Zhipeng Nie, Qiang Zhang, and Zhijie Fei. 2016. "Efficient Data Gathering Methods in Wireless Sensor Networks Using GBTR Matrix Completion" Sensors 16, no. 9: 1532. https://doi.org/10.3390/s16091532
APA StyleWang, D., Wan, J., Nie, Z., Zhang, Q., & Fei, Z. (2016). Efficient Data Gathering Methods in Wireless Sensor Networks Using GBTR Matrix Completion. Sensors, 16(9), 1532. https://doi.org/10.3390/s16091532





