Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China
Abstract
:1. Introduction
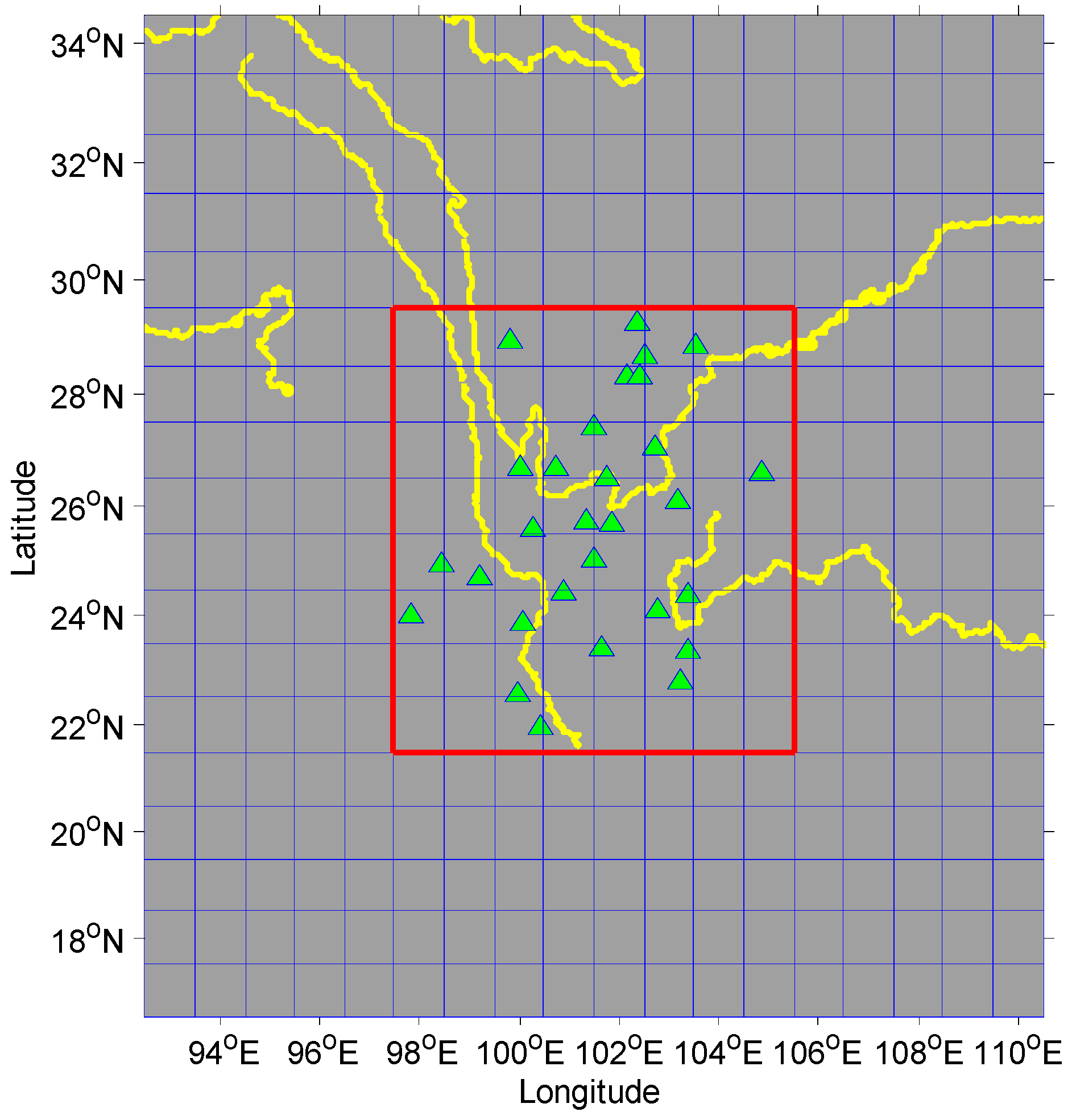
2. GPS Data Analysis
2.1. Data Pre-Processing with GAMIT/GLOBK
2.2. Post-Processing of Coordinates Time Series
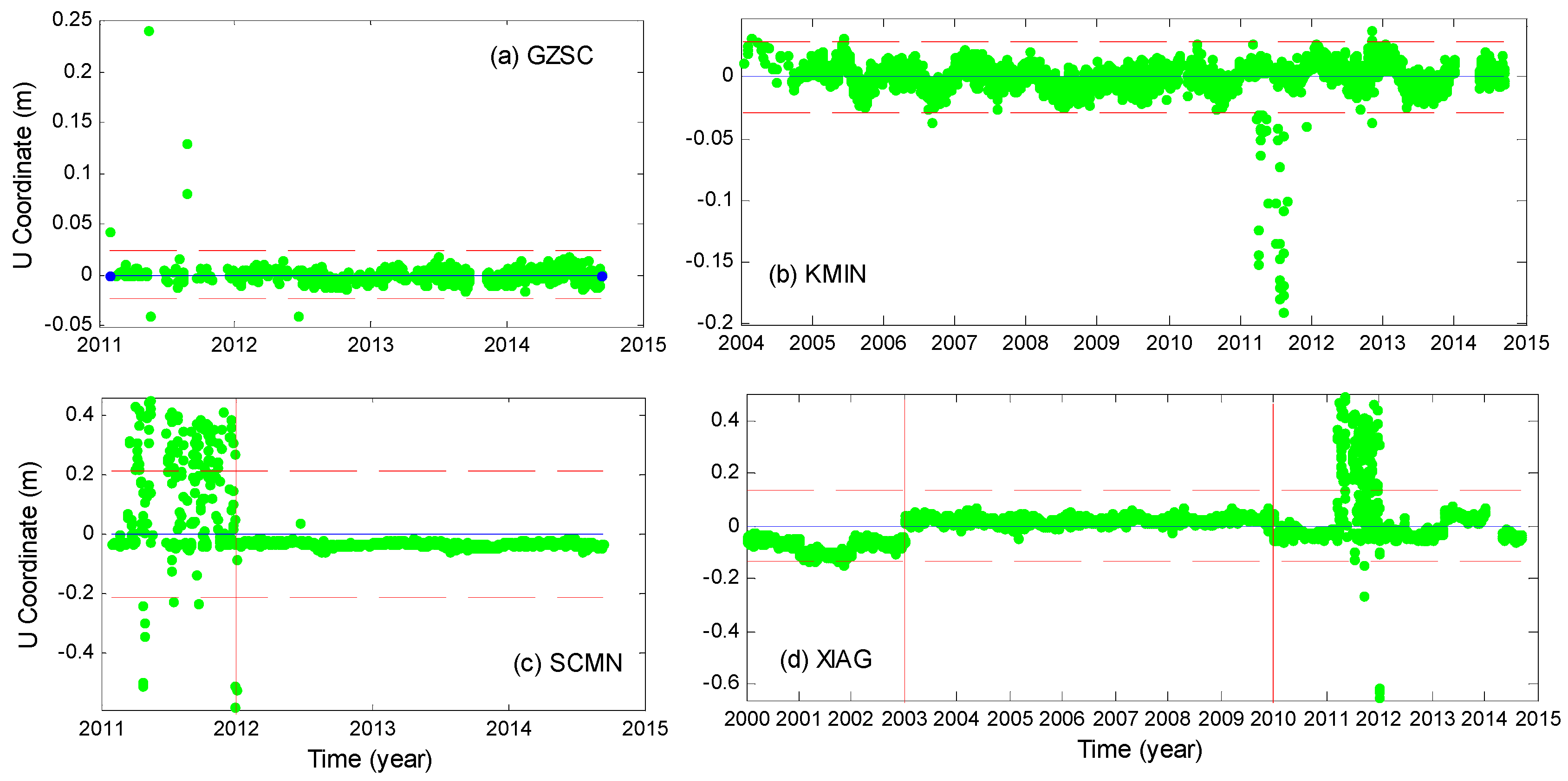
2.2.1. Outlier Rejection of GPS Data
- Step 1:
- Calculate the mean position and standard deviation and remove data that are beyond the range of ±2σ;
- Step 2:
- Find those stations belong to Group (c) and remove data before year 2012;
- Step 3:
- Find those stations belong to Group (d) and estimate the antenna offset; in fact, antenna offset is still present in XIAG station after Step 2. Hence, data before 2003 and after 2010 were removed.
- Step 4:
- Redo Step 1.
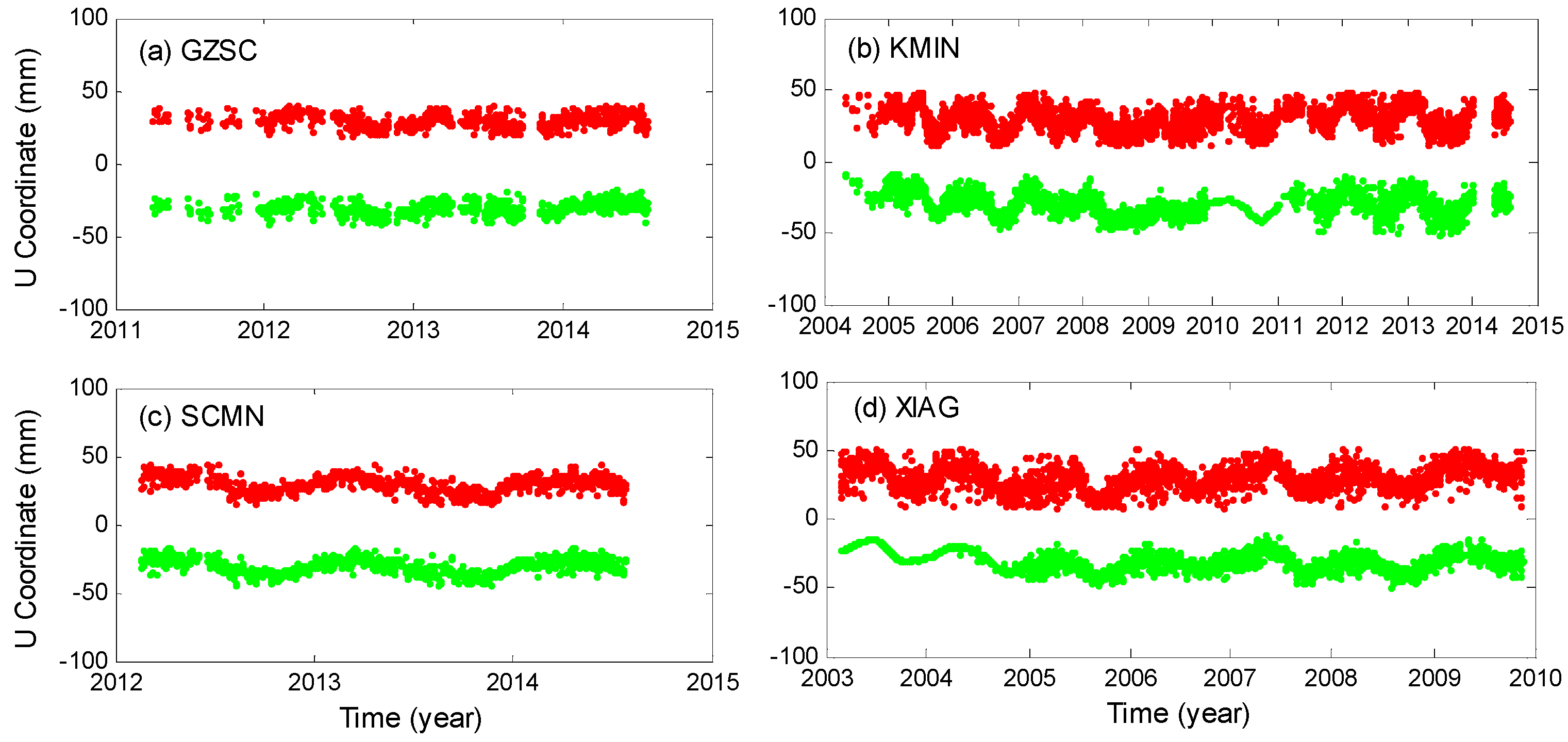
2.2.2. Regional Filtering of the GPS Data
2.2.3. Validation of Seasonal Signals
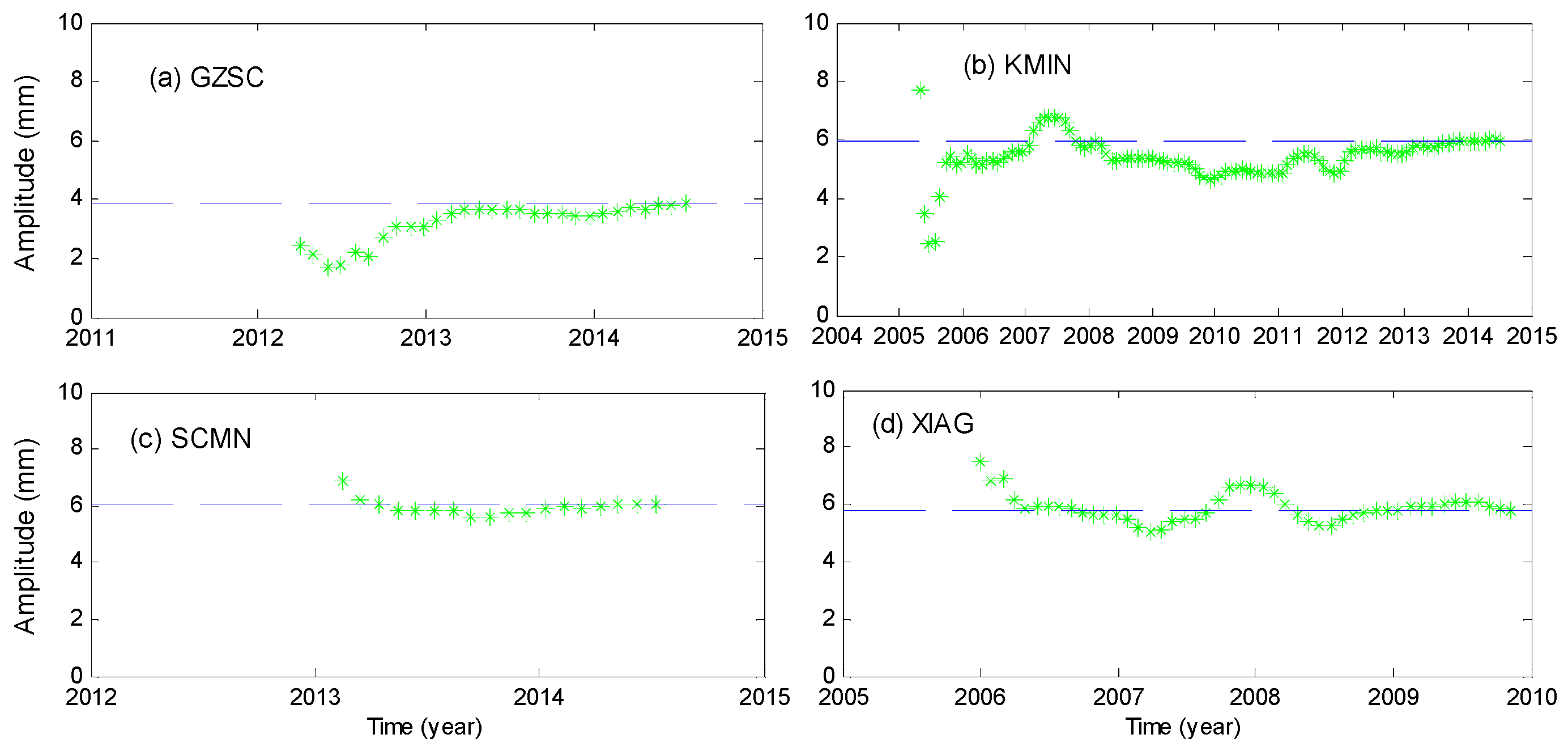
2.3. Annual Amplitude Estimation
3. Determination of Water Thickness from GPS
4. Equivalent Water Height from GRACE and GLDAS Hydrological Model
5. Results and Validation
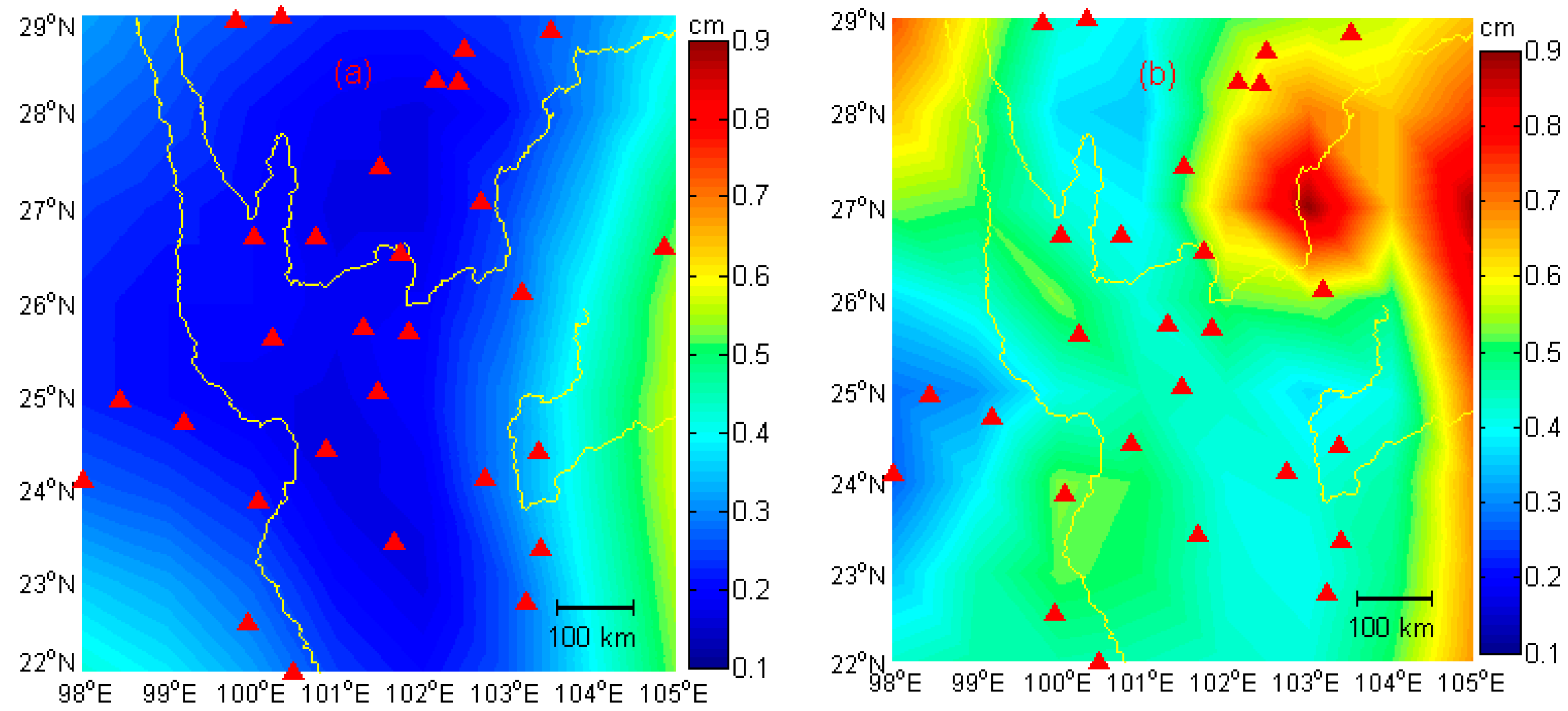
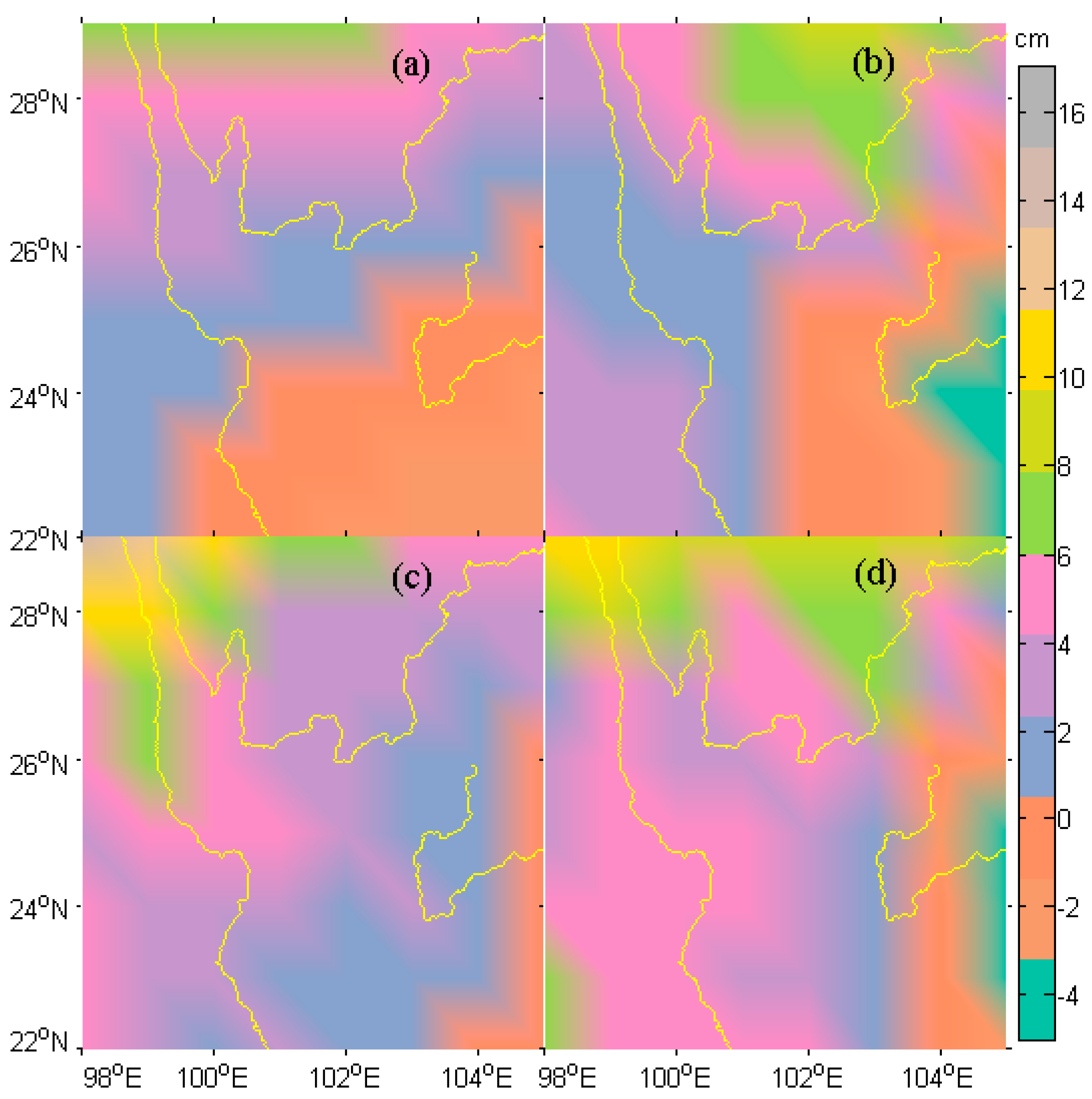
5.1. Results from GPS, GRACE and GLDAS
5.2. Quantitative Comparisons among GPS-, GRACE- and GLDAS-Inferred EWH
5.3. Potential Discrepancy and Error Sources
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, G.; Hu, H.; Li, T. The influence of freeze–thaw cycles of active soil layer on surface runoff in a permafrost watershed. J. Hydrol. 2009, 375, 438–449. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Xia, J.; Hua, D. Temporal and spatial variation of the main water balance components in the three rivers source region, China from 1960 to 2000. Environ. Earth Sci. 2013, 68, 973–983. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field’ hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Hu, X.; Chen, J.; Zhou, Y.; Huang, C.; Liao, X. Seasonal water storage change of the Yangtze River basin detected by GRACE. Sci. China Ser. D 2006, 49, 483–491. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A new global mode of Earth deformation: Seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [PubMed]
- Van Dam, T.; Wahr, J.; Milly, P.C.D.; Shmakin, A.B.; Blewitt, G.; Lavallée, D.; Larson, K.M. Crustal displacements due to continental water loading. Geophys. Res. Lett. 2001, 28, 651–654. [Google Scholar] [CrossRef]
- Bevis, M.; Alsdorf, D.; Kendrick, E.; Fortes, L.P.; Forsberg, B.; Smalley, R.; Becker, J. Seasonal fluctuations in the mass of the Amazon River system and Earth’s elastic response. Geophys. Res. Lett. 2005, 32, L16308. [Google Scholar] [CrossRef]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.E.; van Dam, T.; et al. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.L.; Elósegui, P.; Mitrovica, J.X.; Tamisiea, M.E. Climate-driven deformation of the solid earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Tregoning, P.; Watson, C.; Ramillien, G.; McQueen, H.; Zhang, J. Detecting hydrologic deformation using GRACE and GPS. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J.T.; Jensen, T. Seasonal hydrological loading in southern Alaska observed by GPS and GRACE. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Bouin, M.N.; Santamaría-Gómez, A.; Boy, J.P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; de Linage, C.; et al. Hydrological deformation induced by the West African Monsoon: Comparison of GPS, GRACE and loading models. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Steckler, M.S.; Nooner, S.L.; Akhter, S.H.; Chowdhury, S.K.; Bettadpur, S.; Seeber, L.; Kogan, M.G. Modeling Earth deformation from monsoonal flooding in Bangladesh using hydrographic, GPS, and Gravity Recovery and Climate Experiment (GRACE) data. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Terrestrial water storage response to the 2012 drought estimated from GPS vertical position anomalies. Geophys. Res. Lett. 2014, 41, 6145–6151. [Google Scholar] [CrossRef]
- Birhanu, Y.; Bendick, R. Monsoonal loading in Ethiopia and Eritrea from vertical GPS displacement time series. J. Geophys. Res. Solid Earth 2015, 120, 7231–7238. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.; Landerer, F.W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA, 2008. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Petrie, E.J.; King, M.A.; Moore, P.; Lavallée, D.A. Higher-order ionospheric effects on the GPS reference frame and velocities. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. GAMIT Reference Manual, Release 10.4; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L025546. [Google Scholar] [CrossRef]
- Steigenberger, P.; Boehm, J.; Tesmer, V. Comparison of GMF/GPT with VMF1/ECMWF and implications for atmospheric loading. J. Geod. 2009, 83, 943–951. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; van Dam, T.; Ding, W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- Khan, S.A.; Wahr, J.; Leuliette, E.; van Dam, T.; Larson, K.M.; Francis, O. Geodetic measurements of postglacial adjust ments in Greenland. J. Geophys. Res. 2008, 113, B02402. [Google Scholar] [CrossRef]
- Khan, S.A.; Liu, L.; Wahr, J.; Howat, I.; Joughin, I.; van Dam, T.; Fleming, K. GPS measurements of crustal uplift near Jakobshavn Isbræ due to glacial ice mass loss. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California Permanent GPS Geodetic Array: Error analysis of daily position estimates and site velocities. J. Geophys. Res. Solid Earth 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.G.; Dixon, T.H. Noise in GPS coordinate time series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1983. [Google Scholar]
- Agnew, D. The time domain behavior of power law noise. Geophys. Res. Lett. 1992, 19, 333–336. [Google Scholar] [CrossRef]
- Williams, S.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Ammar, G.; Gragg, W.B. Superfast solution of real positive defi-nite Toeplitz systems. SIAM J. Matrix Anal. Appl. 1988, 9, 61–76. [Google Scholar] [CrossRef]
- William, S. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Guo, J.Y.; Li, Y.B.; Huang, Y.; Deng, H.T.; Xu, S.Q.; Ning, J.S. Green’s function of the deformation of the Earth as a result of atmospheric loading. Geophys. J. Int. 2004, 159, 53–68. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference earth model. Phys. Earth Planet Int. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization tools: A matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 1994, 6, 1–35. [Google Scholar] [CrossRef]
- Xu, P. Determination of surface gravity anomalies using gradiometric observables. Geophys. J. Int. 1992, 110, 321–332. [Google Scholar] [CrossRef]
- Xu, P.; Rummel, R. A simulation study of smoothness methods in recovery of regional gravity fields. Geophys. J. Int. 1994, 117, 472–486. [Google Scholar] [CrossRef]
- Akaike, H. Likelihood and the Bayes procedure. Trab. Estad. Investig. Oper. 1980, 31, 143–166. [Google Scholar] [CrossRef]
- Xu, C.; Ding, K.; Cai, J.; Grafarend, E.W. Methods of determining weight scaling factors for geodetic–geophysical joint inversion. J. Geodyn. 2009, 47, 39–46. [Google Scholar] [CrossRef]
- Fok, H.S. Ocean Tides Modeling Using Satellite Altimetry. Ph.D. Thesis, School of Earth Sciences, Ohio State University, Columbus, OH, USA, 2012. [Google Scholar]
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variabilityin the earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Tapley, B.D. Variations in the earth’s oblatenessduring the past 28 years. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Cazenave, A.; Güntner, A. Time variations of land water storage froman inversion of 2 years of GRACE geoids. Earth Planet Sci. Lett. 2005, 235, 283–301. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Mitchell, K.E.; Lohmann, D.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, A.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A. On the nature of GPS draconitic year periodic pattern in multivariate position time series. J. Geophys. Res. Solid Earth 2013, 118, 2500–2511. [Google Scholar] [CrossRef]
- Fang, M.; Dong, D.; Hager, B.H. Displacements due to surface temperature variation on a uniform elastic sphere with its centre of mass stationary. Geophys. J. Int. 2014, 196, 194–203. [Google Scholar] [CrossRef]
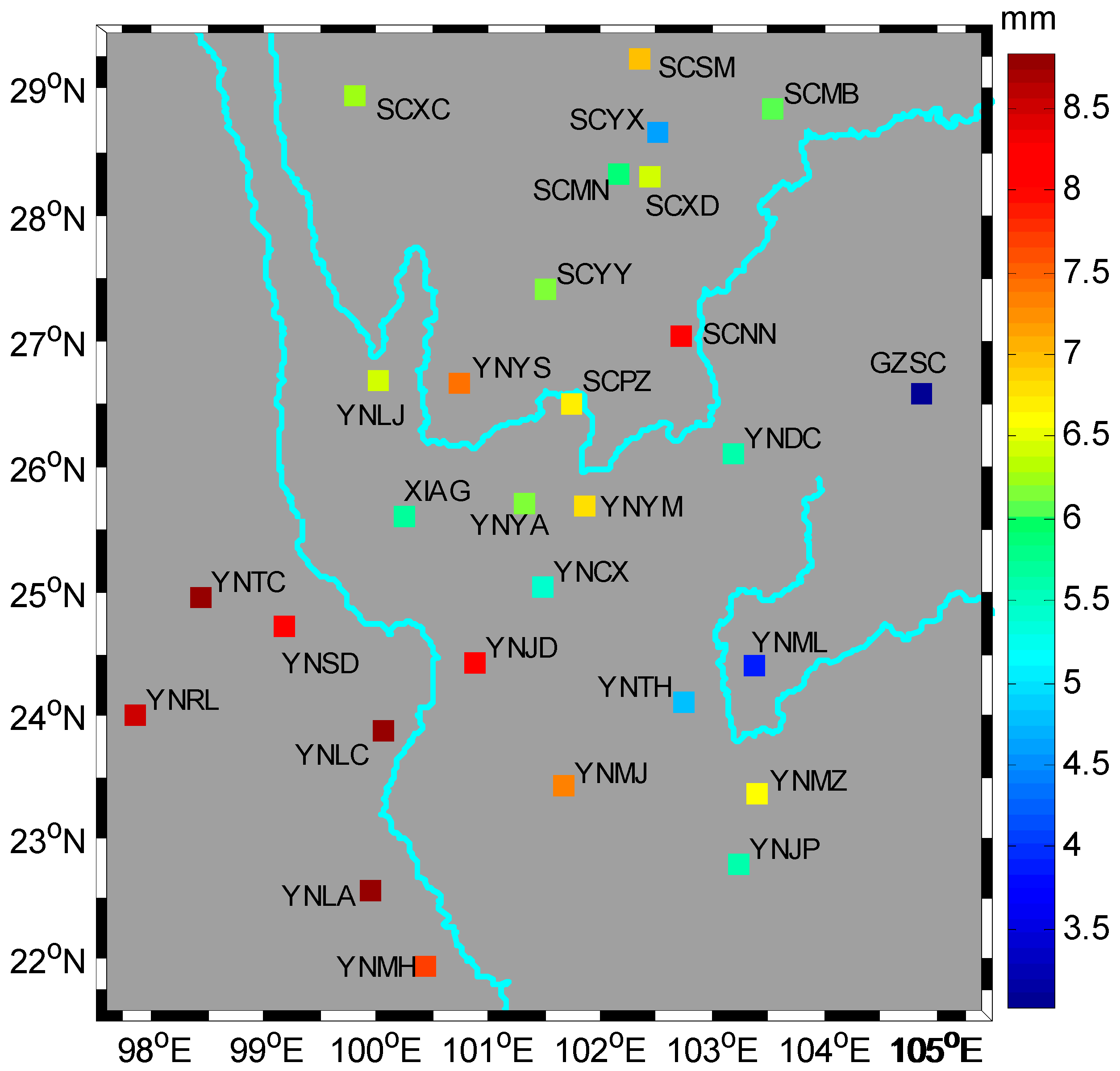

| Site | White Noise, mm | Power Law Noise, mm/year1/4 | Sepctra Index | Amplitude, mm |
|---|---|---|---|---|
| GZSC | 2.00 | 13.21 | −0.54 ± 0.23 | 3.03 ± 0.43 |
| SCMB | 2.45 | 11.49 | −0.67 ± 0.23 | 6.08 ± 0.51 |
| SCMN | 2.63 | 10.35 | −0.66 ± 0.21 | 5.93 ± 0.46 |
| SCNN | 4.75 | 9.80 | −1.00 ± 0.00 | 8.21 ± 0.95 |
| SCPZ | 2.91 | 7.21 | −0.77 ± 0.23 | 6.67 ± 0.41 |
| SCSM | 3.69 | 7.53 | −0.98 ± 0.24 | 6.98 ± 0.64 |
| SCXC | 2.64 | 6.12 | −1.10 ± 0.18 | 6.27 ± 0.66 |
| SCXD | 3.38 | 3.55 | −1.34 ± 0.25 | 6.39 ± 0.64 |
| SCYX | 3.48 | 7.96 | −0.97 ± 0.23 | 4.65 ± 0.66 |
| SCYY | 3.06 | 3.16 | −1.24 ± 0.27 | 6.19 ± 0.47 |
| XIAG | 3.02 | 9.96 | −0.94 ± 0.11 | 5.66 ± 0.54 |
| YNCX | 3.07 | 8.90 | −0.78 ± 0.19 | 5.40 ± 0.44 |
| YNDC | 4.64 | 12.85 | −0.60 ± 0.26 | 5.66 ± 0.46 |
| YNJD | 4.23 | 14.46 | −0.69 ± 0.21 | 8.10 ± 0.58 |
| YNJP | 4.08 | 8.70 | −1.09 ± 0.16 | 5.63 ± 0.78 |
| YNLA | 4.36 | 9.34 | −1.09 ± 0.17 | 8.82 ± 0.84 |
| YNLC | 4.43 | 9.08 | −0.82 ± 0.27 | 8.84 ± 0.51 |
| YNLJ | 2.52 | 5.90 | −0.95 ± 0.17 | 6.41 ± 0.40 |
| YNMH | 4.05 | 3.52 | −1.44 ± 0.23 | 7.72 ± 0.67 |
| YNMJ | 3.00 | 13.18 | −0.57 ± 0.20 | 7.30 ± 0.42 |
| YNML | 3.51 | 7.03 | −0.68 ± 0.31 | 3.87 ± 0.31 |
| YNMZ | 4.00 | 16.38 | −0.64 ± 0.19 | 6.57 ± 0.60 |
| YNRL | 3.96 | 3.53 | −1.21 ± 0.30 | 8.50 ± 0.43 |
| YNSD | 3.18 | 12.72 | −0.76 ± 0.17 | 8.17 ± 0.58 |
| YNTC | 3.68 | 14.69 | −0.68 ± 0.21 | 8.81 ± 0.57 |
| YNTH | 3.43 | 9.24 | −0.82 ± 0.19 | 4.77 ± 0.49 |
| YNYA | 3.43 | 4.82 | −1.14 ± 0.22 | 6.18 ± 0.49 |
| YNYM | 3.36 | 10.19 | −0.77 ± 0.19 | 6.81 ± 0.48 |
| YNYS | 3.01 | 9.93 | −0.55 ± 0.25 | 7.46 ± 0.32 |
| Mean | 3.28 | 9.60 | −0.86 | 6.59 |
| Method | k | (mm2) |
|---|---|---|
| MMSE | 1.95 × 10−5 | 0.86 |
| HVCE | 1.99 × 10−4 | 1.05 |
| Bias (cm) | SD (cm) | RMSE (cm) | Percentage Error (%) | |
|---|---|---|---|---|
| GPS_HVCE-GRACE | 1.9 | 2.6 | 3.2 | 16.6 |
| GPS_MMSE-GRACE | 2.1 | 3.3 | 3.9 | 18.0 |
| GPS_HVCE-GLDAS | 3.8 | 3.0 | 4.8 | 39.4 |
| GPS_MMSE-GLDAS | 4.0 | 3.4 | 5.2 | 41.2 |
| GPS_HVCE-GPS_MMSE | -0.2 | 2.0 | 2.0 | -1.3 |
| GRACE-GLDAS | 1.9 | 1.6 | 2.5 | 19.6 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Yao, Y.; Fok, H.S.; Hu, Y.; Chen, Q. Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China. Sensors 2016, 16, 1526. https://doi.org/10.3390/s16091526
Zhang B, Yao Y, Fok HS, Hu Y, Chen Q. Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China. Sensors. 2016; 16(9):1526. https://doi.org/10.3390/s16091526
Chicago/Turabian StyleZhang, Bao, Yibin Yao, Hok Sum Fok, Yufeng Hu, and Qiang Chen. 2016. "Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China" Sensors 16, no. 9: 1526. https://doi.org/10.3390/s16091526
APA StyleZhang, B., Yao, Y., Fok, H. S., Hu, Y., & Chen, Q. (2016). Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China. Sensors, 16(9), 1526. https://doi.org/10.3390/s16091526







