Spiking Cortical Model Based Multimodal Medical Image Fusion by Combining Entropy Information with Weber Local Descriptor
Abstract
:1. Introduction
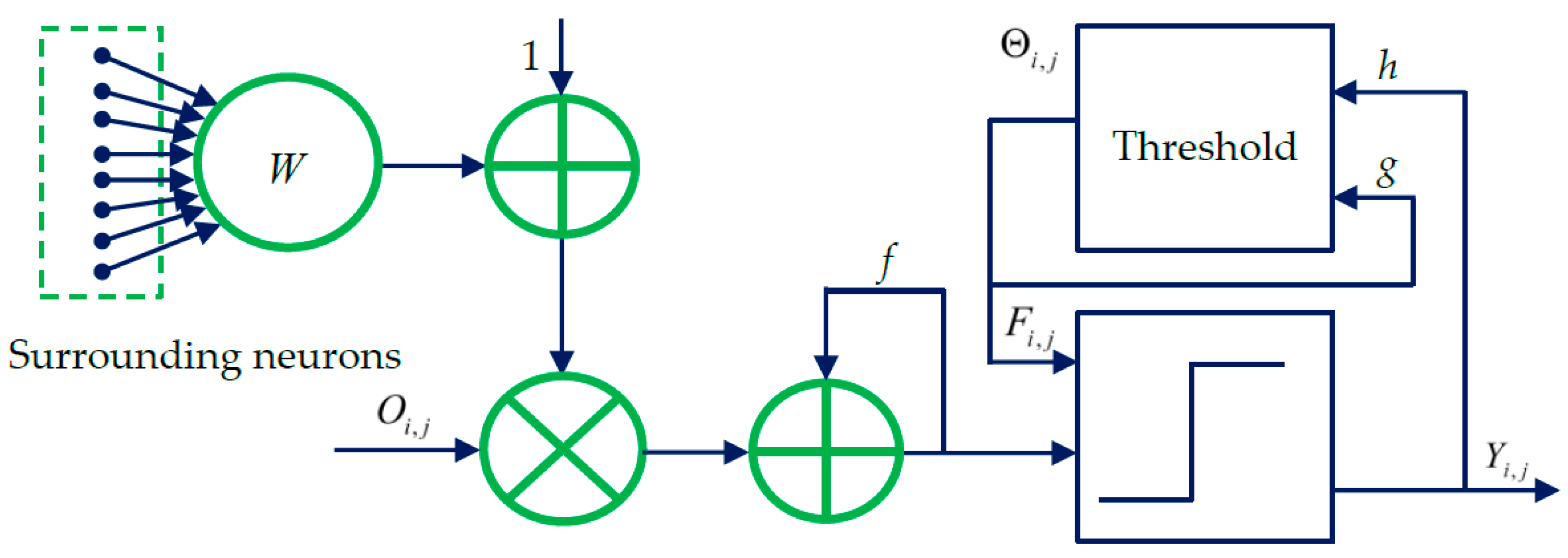
2. Spiking Cortical Model
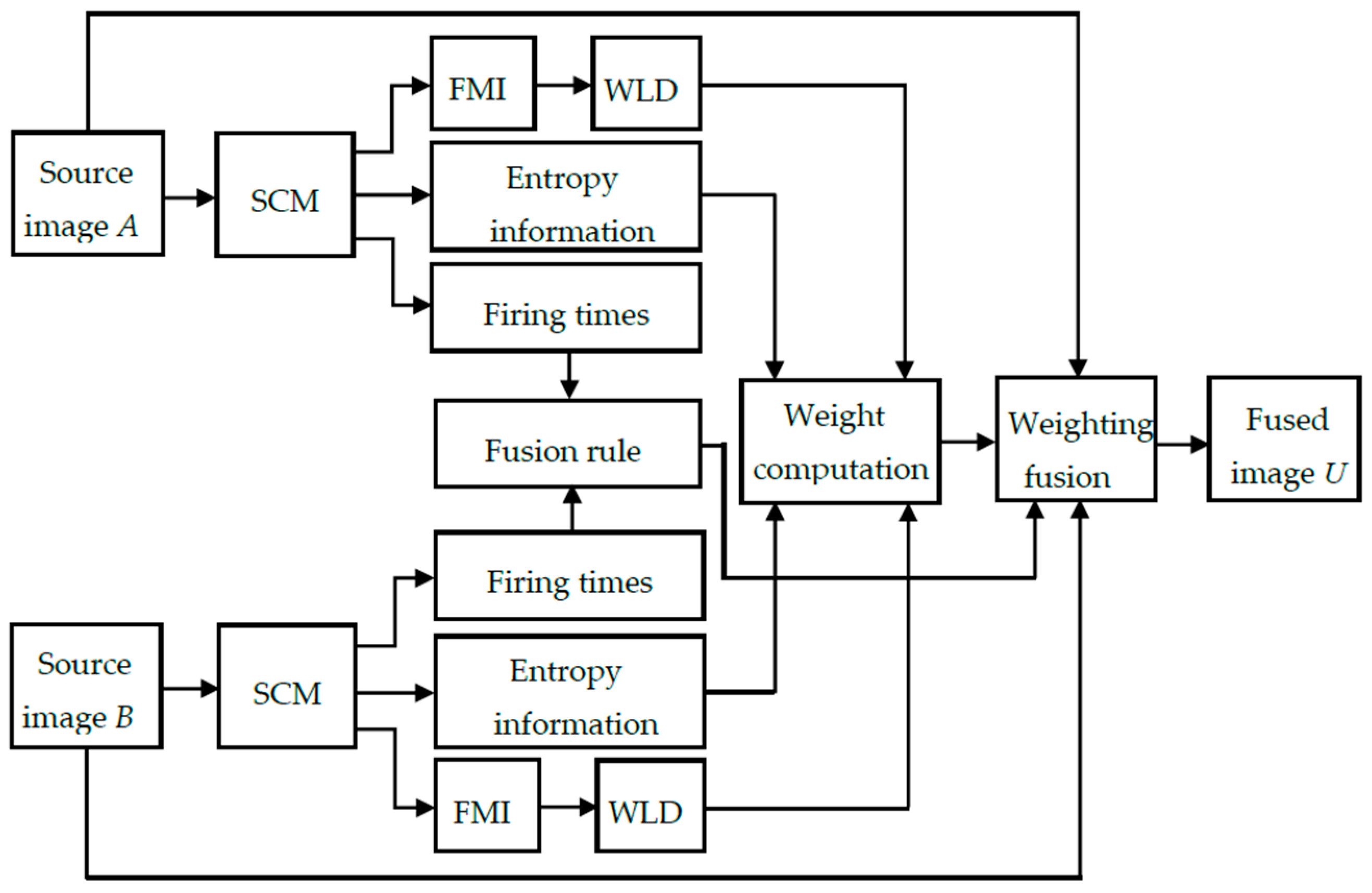
3. SCM Based Image Fusion
3.1. Fusion Rule
3.2. Weight Computation
3.2.1. Similarity Computation Based on the Entropy Information
3.2.2. Similarity Computation Based on the WLD
3.2.3. Weight Determining Based on the Combined Similarity
3.3. Implementation of the SCM-M Method
- (1)
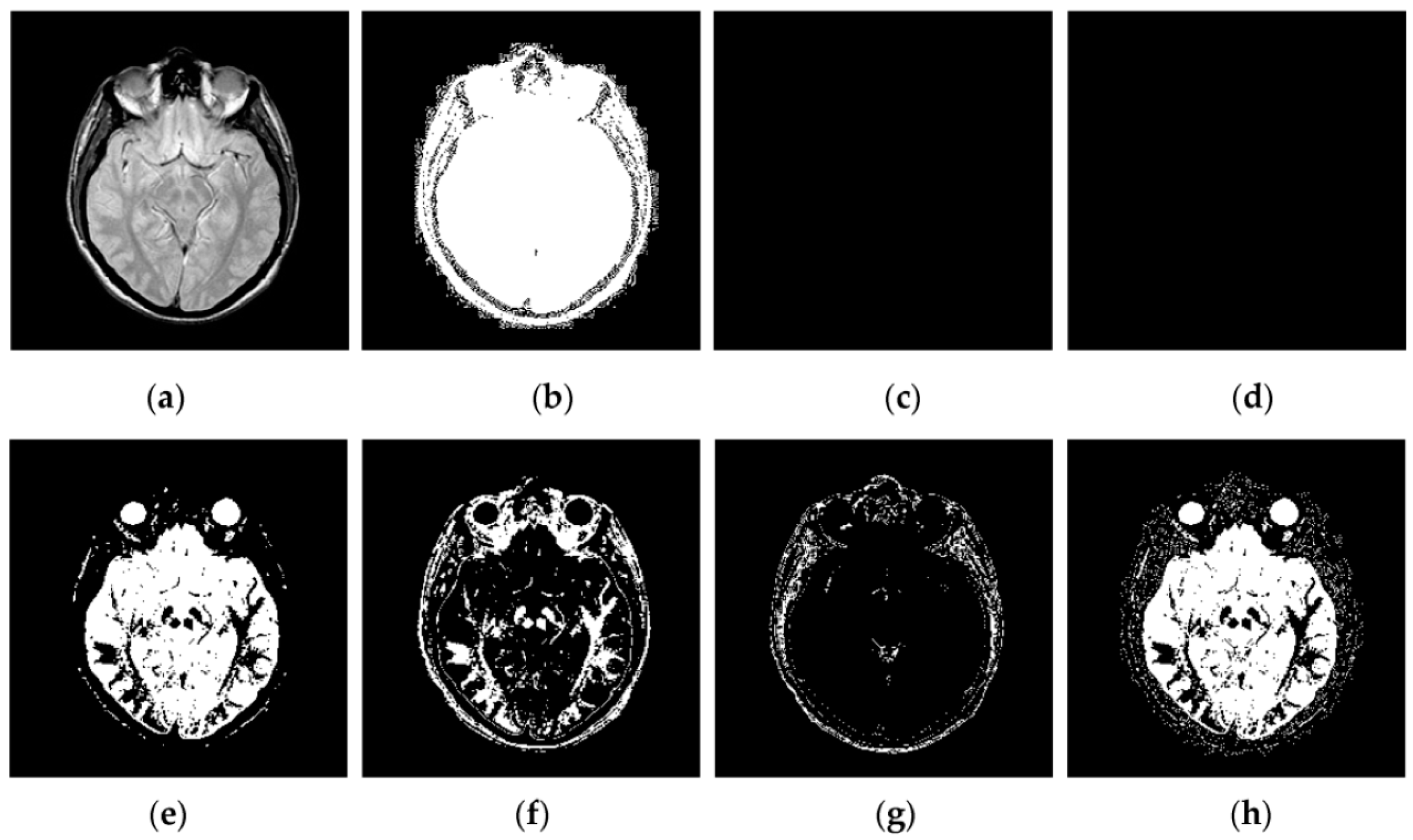
- The two source images A and B are input into two SCMs. After running the SCM for Nmax times, the series of binary pulse images will be obtained for the source images using Equations (1)–(4).
- (2)
- For each pixel at (i,j) in A and B, the Shannon entropy from the various iterations is computed on the output pulse images using Equation (10) to generate two feature vectors and . Based on the difference between the two feature vectors, the similarity between two image patches and centered at (i,j) is computed using Equation (13).
- (3)
- The output pulse images are utilized to generate the firing mapping images for two source images. For any pixel at (i,j) in two FMIs, the local energy and are computed on the considered two image patches centered at this pixel using Equations (7) and (8), respectively. Meanwhile, the WLD is computed for the two image patches using Equation (15) to determine the similarity between and using Equation (16).
- (4)
- The weight is determined by and using Equation (17).
- (5)
- According to the relationship between and , the fused image is produced by the weighted sum of two source images using Equation (9).
4. Experimental Results and Discussions
4.1. Parameter Settings
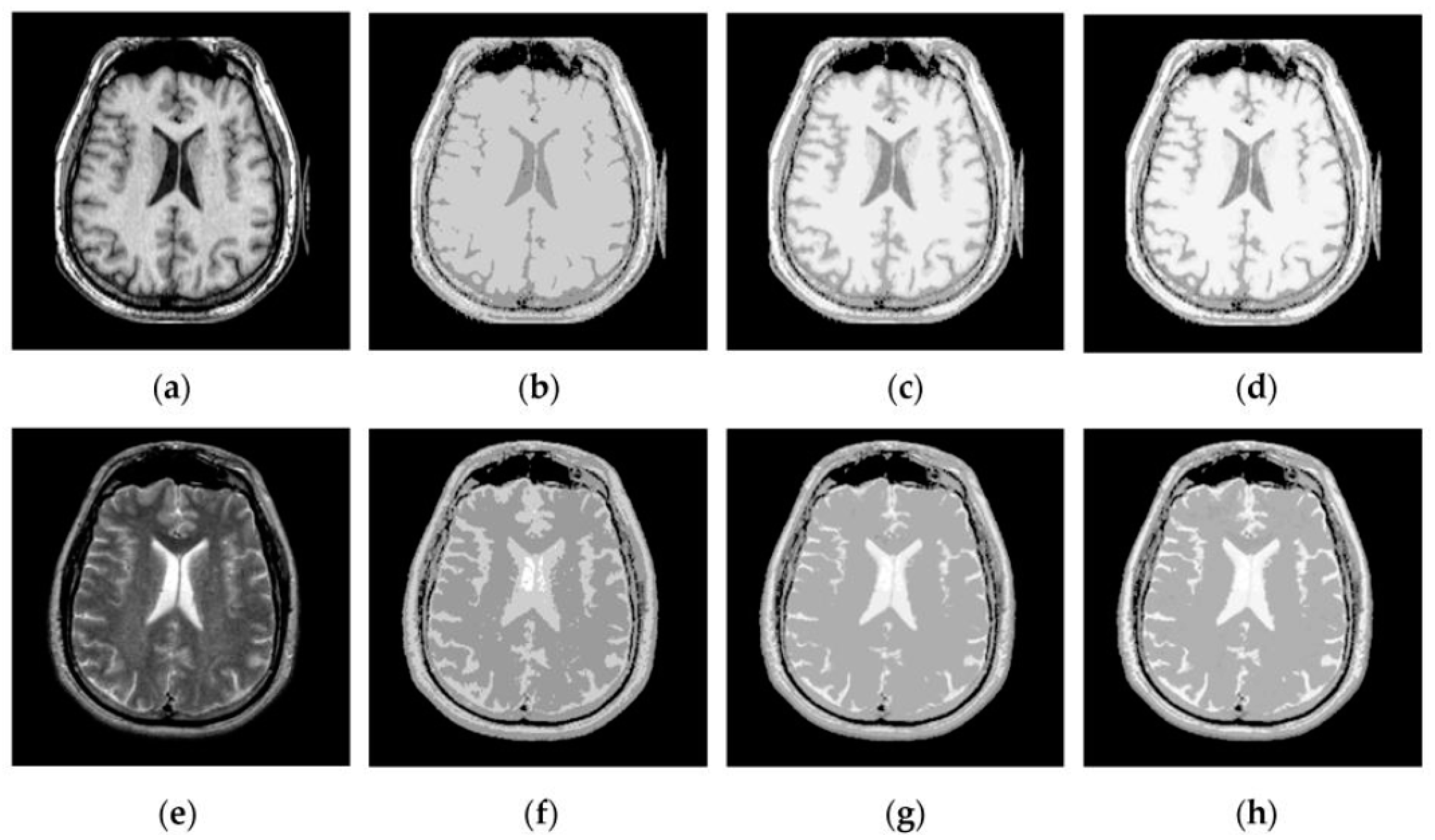
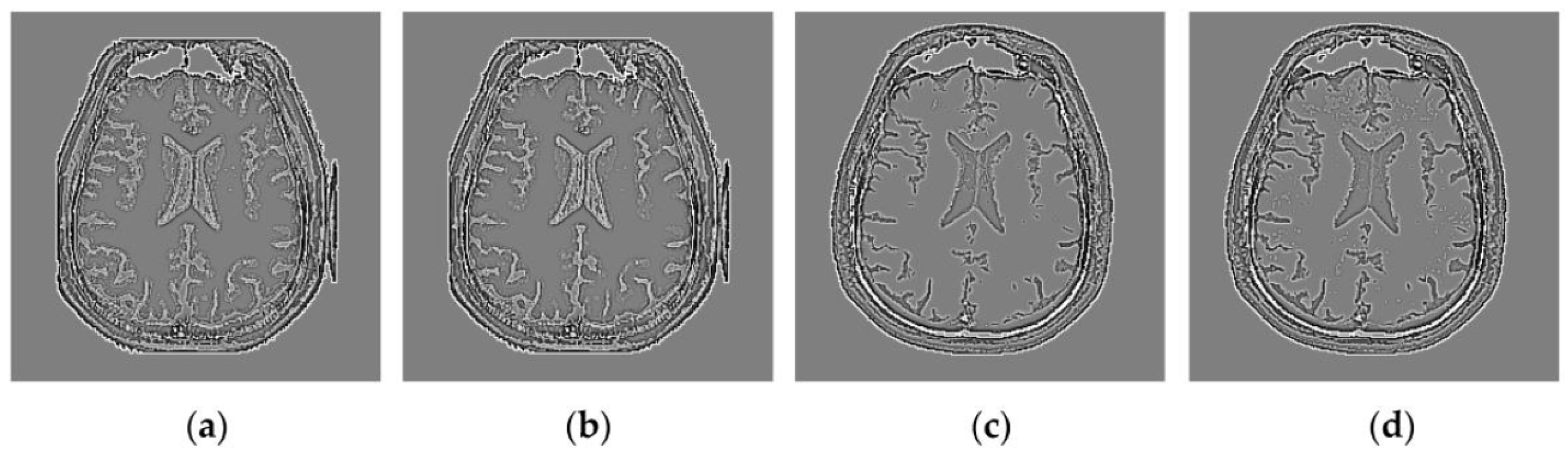
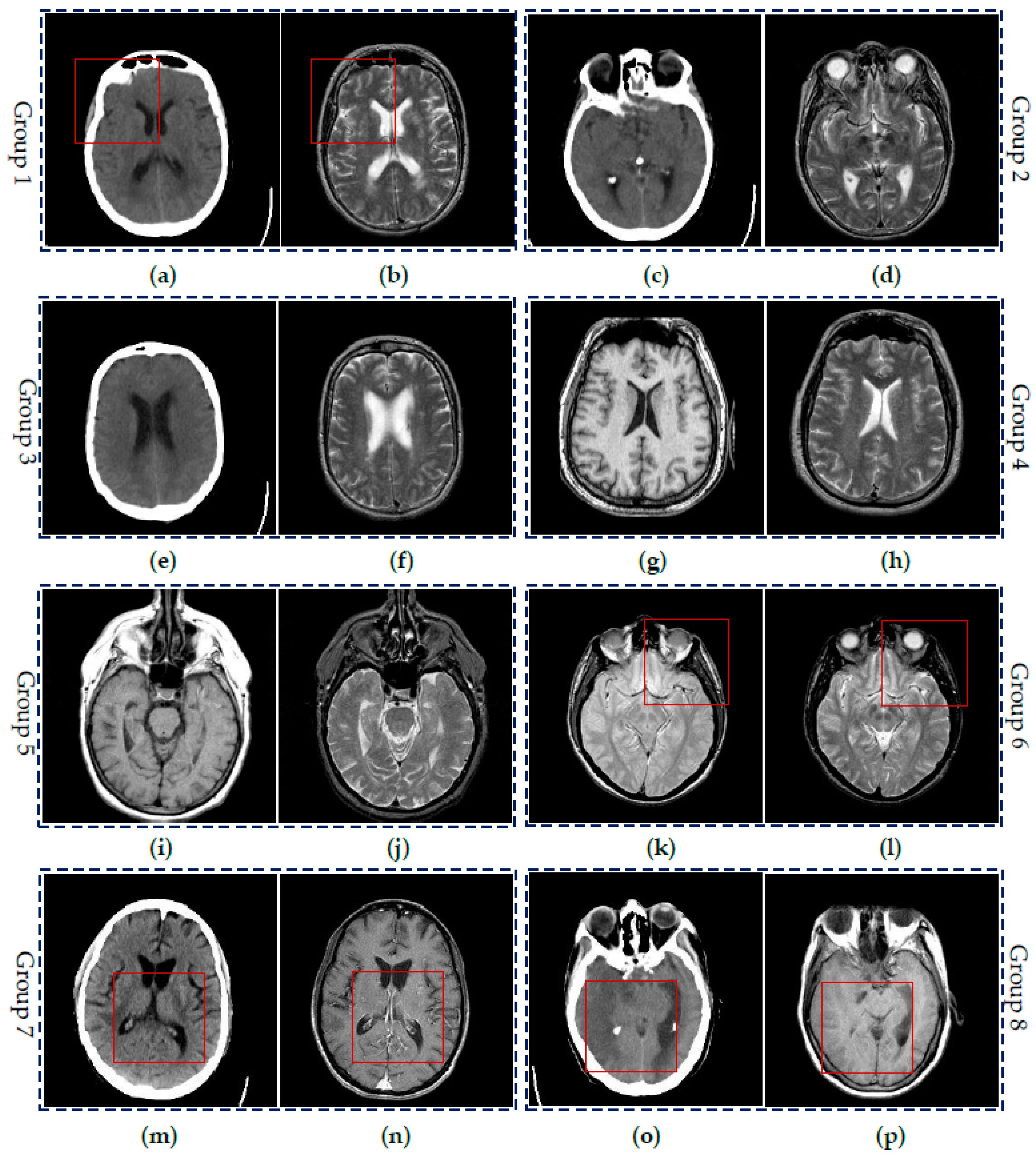
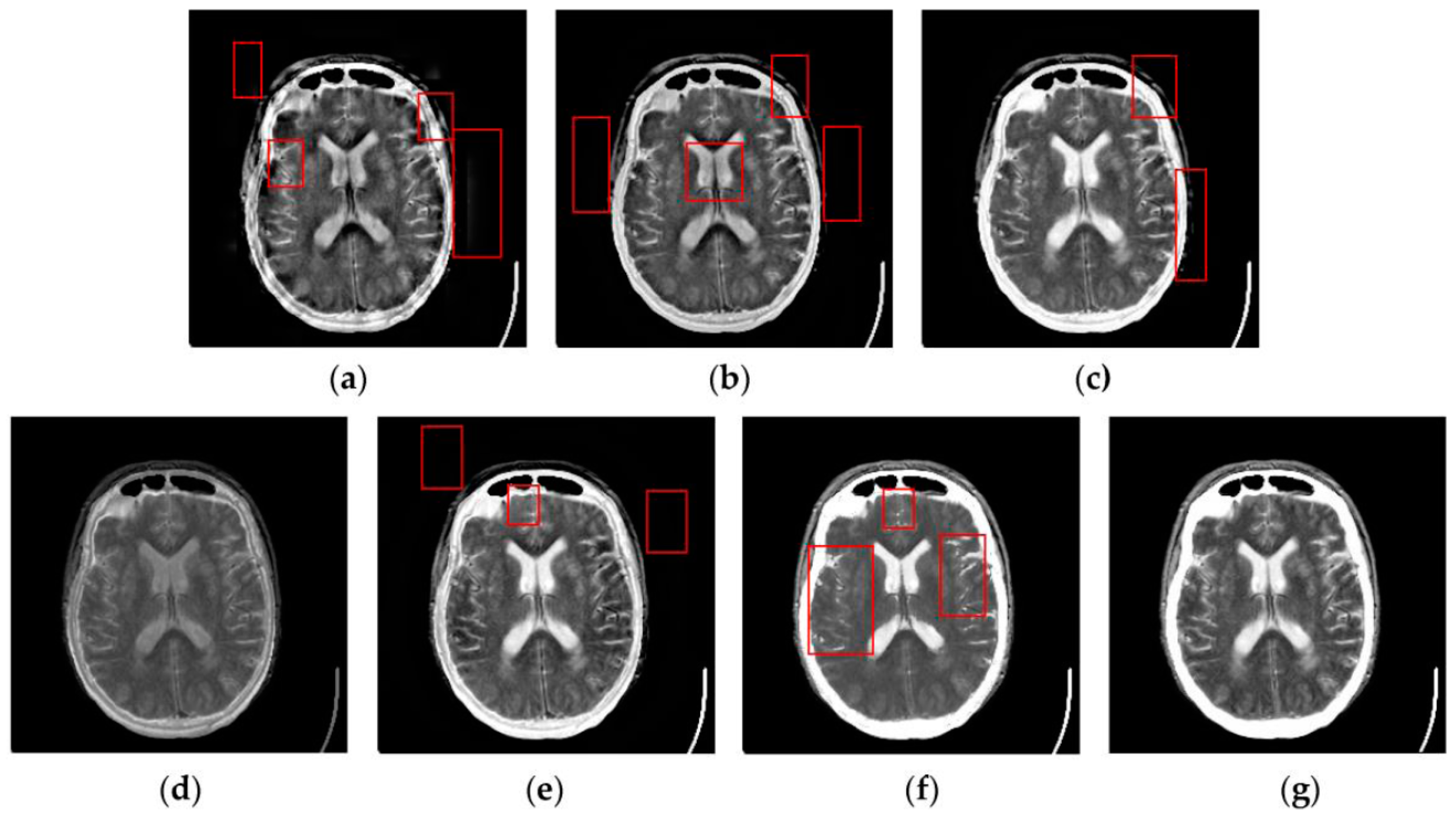
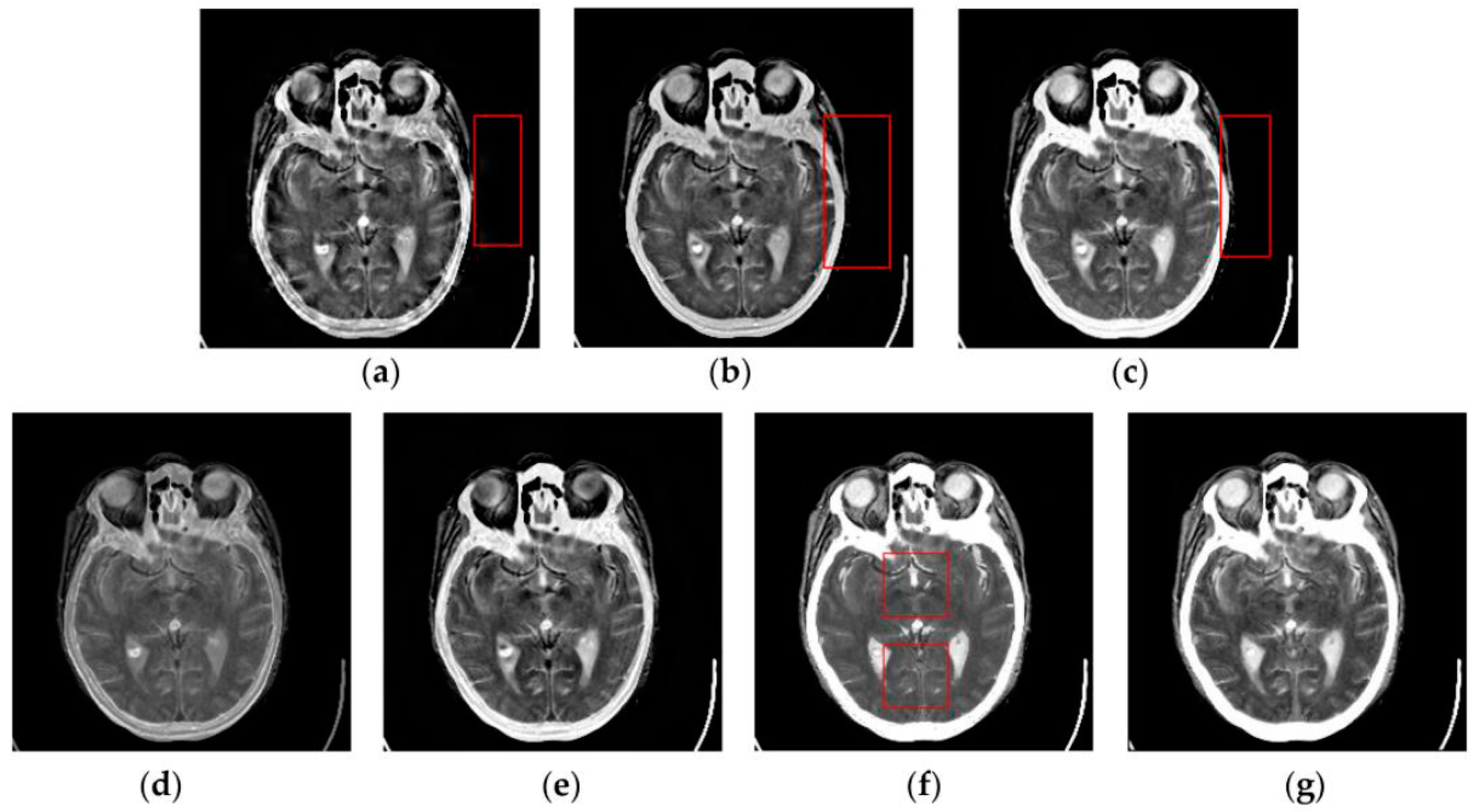
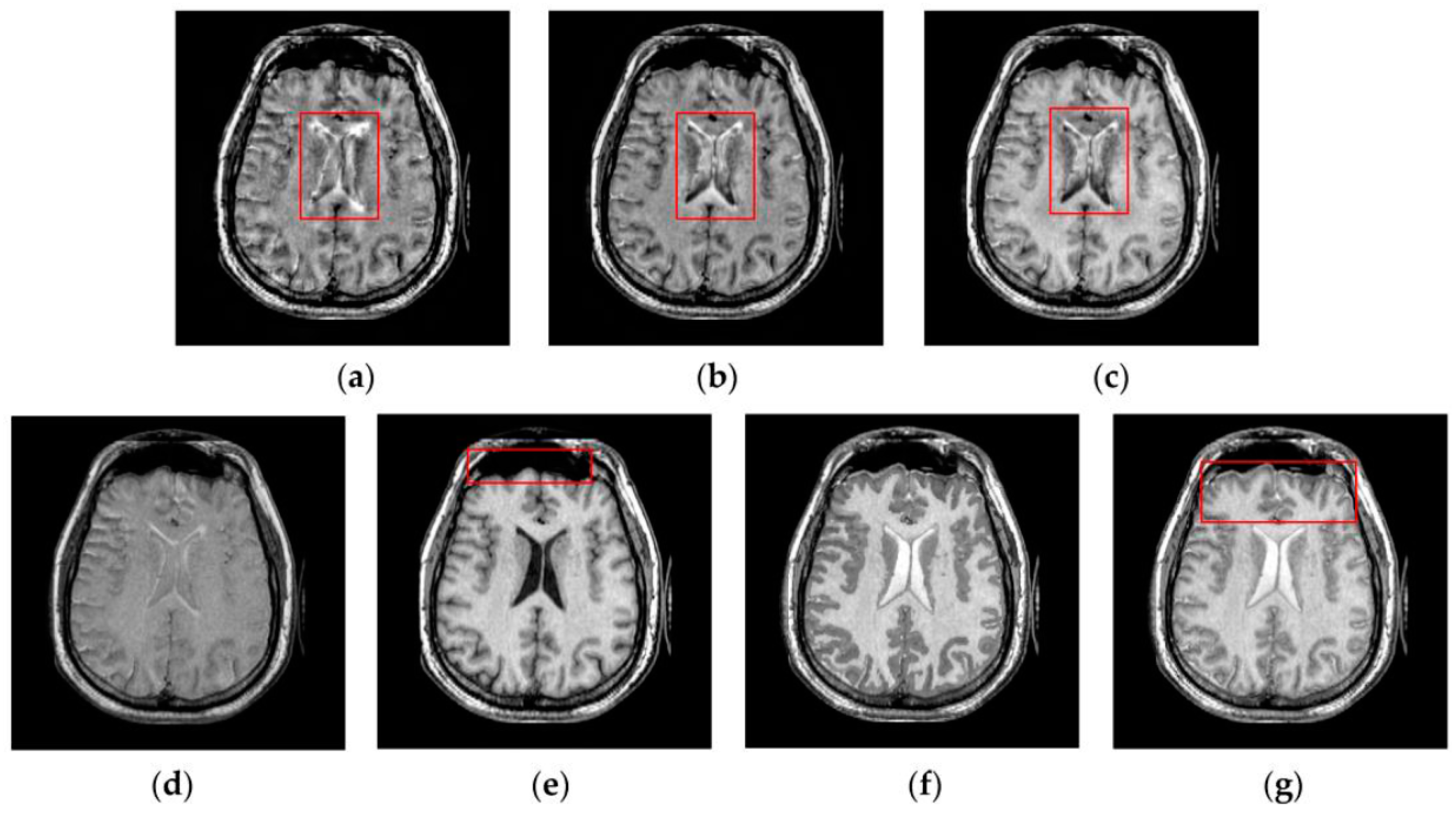
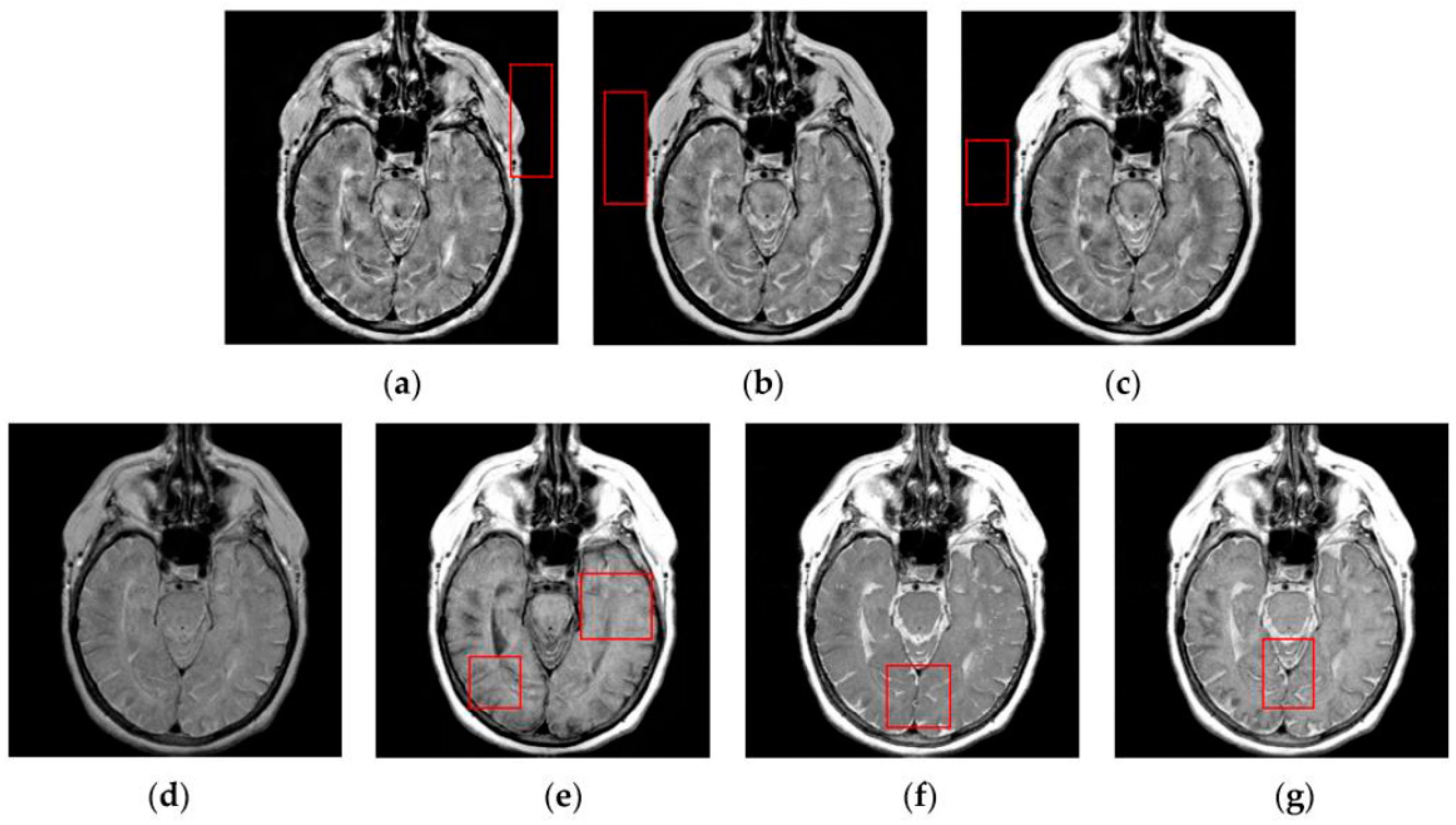
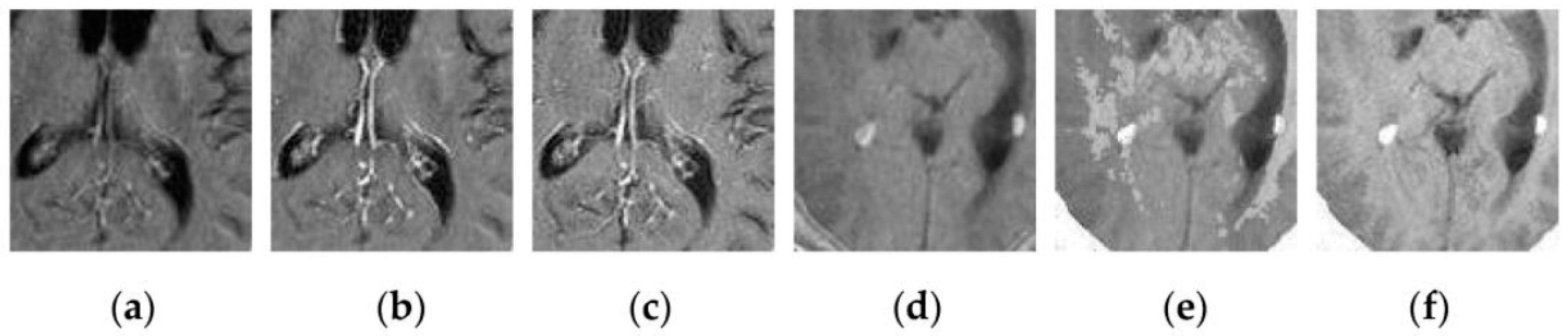
4.2. Visual Comparisons of Fused Results
4.3. Quantitative Comparison of Fused Results
(1)
(2)
(3)
(4) s
(5)
(6)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kaplan, I.; Oldenburg, N.E.; Meskell, P.; Blake, M.; Church, P.; Holupka, E.J. Real time MRI-ultrasound image guided stereotactic prostate biopsy. Magn. Reson. Imaging 2002, 20, 295–299. [Google Scholar] [CrossRef]
- Buck, A.K.; Herrmann, K.; Schreyögg, J. PET/CT for staging lung cancer: Costly or cost-saving? Eur. J. Nucl. Med. Mol. Imaging 2011, 38, 799–801. [Google Scholar] [CrossRef] [PubMed]
- Barra, V.; Boire, J.Y. A general framework for the fusion of anatomical and functional medical images. NeuroImage 2001, 13, 410–424. [Google Scholar] [CrossRef] [PubMed]
- Van der Ploeg, I.M.C.; Valdés Olmos, R.A.; Nieweg, O.E.; Rutgers, E.J.T.; Kroon, B.B.R.; Hoefnagel, C.A. The additional value of SPECT/CT in lymphatic mapping in breast cancer and melanoma. J. Nucl. Med. 2007, 48, 1756–1760. [Google Scholar] [CrossRef] [PubMed]
- Redondo, R.; Sroubek, F.; Fischer, S.; Cristoba, G. Multifocus image fusion using the log-Gabor transform and a multisize windows technique. Inf. Fusion 2009, 10, 163–171. [Google Scholar] [CrossRef]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Daneshvar, S.; Ghassemian, H. MRI and PET image fusion by combining IHS and retina-inspired models. Inf. Fusion 2010, 11, 114–123. [Google Scholar] [CrossRef]
- Wang, H.Q.; Xing, H. Multi-mode medical image fusion algorithm based on principal component analysis. In Proceedings of the International Symposium on Computer Network and Multimedia Technology, Wuhan, China, 18–20 January 2009; pp. 1–4.
- Toet, A.; van Ruyven, J.J.; Valeton, J.M. Merging thermal and visual images by a contrast pyramid. Opt. Eng. 1989, 28, 789–792. [Google Scholar] [CrossRef]
- Petrovic, V.S.; Xydeas, C.S. Gradient-based multiresolution image fusion. IEEE Trans. Image Process. 2004, 13, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Ehsan, S.; Abdullah, S.M.U.; Akhtar, M.J.; Mandic, D.P.; McDonald-Maier, K.D. Multi-scale pixel-based image fusion using multivariate empirical mode decomposition. Sensors 2015, 15, 10923–10947. [Google Scholar]
- Qu, G.; Zhang, D.; Yan, P. Medical image fusion by wavelet transform modulus maxima. Opt. Express 2001, 92, 184–190. [Google Scholar]
- Yang, Y.; Park, D.S.; Huang, S.; Rao, N. Medical image fusion via an effective wavelet-based approach. EURASIP J. Adv. Signal Process. 2010, 2010, 579341. [Google Scholar] [CrossRef]
- Singh, R.; Khare, A. Fusion of multimodal medical images using Daubechies complex wavelet transform—A multiresolution approach. Inf. Fusion 2014, 19, 49–60. [Google Scholar] [CrossRef]
- Ali, F.E.; El-Dokany, I.M.; Saad, A.A.; Abd El-Samie, F.E. Curvelet fusion of MR and CT images. Prog. Electromagn. Res. C 2008, 3, 215–224. [Google Scholar] [CrossRef]
- Das, S.; Chowdhury, M.; Kundu, M.K. Medical image fusion based on ripplet transform type-I. Prog. Electromagn. Res. B 2011, 30, 355–370. [Google Scholar] [CrossRef]
- Yang, L.; Guo, B.L.; Ni, W. Multimodality medical image fusion based on multiscale geometric analysis of contourlet transform. Neurocomputing 2008, 72, 203–211. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y. Biological image fusion using a NSCT based variable-weight method. Inf. Fusion 2011, 12, 85–92. [Google Scholar] [CrossRef]
- Liu, C.; Chen, S.; Fu, Q. Multi-modality image fusion using the nonsubsampled contourlet transform. IEICE Trans. Inf. Syst. 2013, 96, 2215–2223. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Wu, Q.M.J.; Liu, Z. Directive contrast based multimodal medical image fusion in NSCT domain. IEEE Trans. Multimed. 2013, 15, 1014–1024. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Z. A general framework for image fusion based on multi-scale transform and sparse representation. Inf. Fusion 2015, 24, 147–164. [Google Scholar] [CrossRef]
- Wang, J.; Lai, S.; Li, M. Improved image fusion method based on NSCT and accelerated NMF. Sensors 2012, 12, 5872–5887. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, B.; Tian, L. Multi-modal medical image fusion using the inter-scale and intra-scale dependencies between image shift-invariant shearlet coefficients. Inf. Fusion 2014, 19, 20–28. [Google Scholar] [CrossRef]
- Wang, L.; Li, B.; Tian, L. EGGDD: An explicit dependency model for multi-modal medical image fusion in shift-invariant shearlet transform domain. Inf. Fusion 2014, 19, 29–37. [Google Scholar] [CrossRef]
- Jiang, H.; Tian, Y. Fuzzy image fusion based on modified self-generating neural network. Expert Syst. Appl. 2011, 38, 8515–8523. [Google Scholar] [CrossRef]
- Eckhorn, R.; Reitboeck, H.J.; Arndt, M.; Dicke, P.W. Feature linking via synchronization among distributed assemblies: Simulation of results from cat cortex. Neural Comput. 1990, 2, 293–307. [Google Scholar] [CrossRef]
- Eckhorn, R.; Frien, A.; Bauer, R.; Woelbern, T.; Kehr, H. High frequency (60–90 Hz) oscillations in primary visual cortex of awake monkey. Neuroreport 1993, 4, 243–246. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Cai, W.; Tan, Z. A region-based multi-sensor image fusion scheme using pulse coupled neural network. Pattern Recognit. Lett. 2006, 27, 1948–1956. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y. Medical image fusion using m-PCNN. Inf. Fusion 2008, 9, 176–185. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Q.; Hao, A. Multimodal medical image fusion using improved multi-channel PCNN. Bio-Med. Mater. Eng. 2014, 24, 221–228. [Google Scholar]
- Chai, Y.; Li, H.F.; Qu, J.F. Image fusion scheme using a novel dual-channel PCNN in lifting stationary wavelet domain. Opt. Commun. 2010, 283, 3591–3602. [Google Scholar] [CrossRef]
- Qu, X.; Yan, J.; Xiao, H.; Zhu, Z. Image fusion algorithm based on spatial frequency-motivated pulse coupled neural networks in nonsubsampled contourlet transform domain. Acta Autom. Sin. 2008, 34, 1508–1514. [Google Scholar] [CrossRef]
- Kong, W.W.; Lei, Y.J.; Lei, Y.; Lu, S. Image fusion technique based on non-subsampled contourlet transform and adaptive unit-fast-linking pulse-coupled neural network. IET Image Process. 2011, 5, 113–121. [Google Scholar] [CrossRef]
- El-taweel, G.S.; Helmy, A.K. Image fusion scheme based on modified dual pulse coupled neural network. IET Image Process. 2013, 7, 407–414. [Google Scholar] [CrossRef]
- Das, S.; Kundu, M.K. NSCT-based multimodal medical image fusion using pulse-coupled neural network and modified spatial frequency. Med. Biol. Eng. Comput. 2012, 50, 1105–1114. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Kundu, M.K. A neuro-fuzzy approach for medical image fusion. IEEE Trans. Biomed. Eng. 2013, 60, 3347–3353. [Google Scholar] [CrossRef] [PubMed]
- Ganasala, P.; Kumar, V. Feature-motivated simplified adaptive PCNN-based medical image fusion algorithm in NSST domain. J. Digit. Imaging 2016, 29, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Geng, P.; Wang, Z.; Zhang, Z.; Xiao, Z. Image fusion by pulse couple neural network with shearlet. Opt. Eng. 2012, 51, 067005. [Google Scholar] [CrossRef]
- Feng, K.; Zhang, X.; Li, X. A novel method of medical image fusion based on bidimensional empirical mode decomposition. J. Converg. Inf. Technol. 2011, 6, 84–89. [Google Scholar]
- Zhan, K.; Zhang, H.; Ma, Y. New spiking cortical model for invariant texture retrieval and image processing. IEEE Trans. Neural Netw. 2009, 20, 1980–1986. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wu, Y.; Ding, M.; Zhang, X. Medical image fusion based on spiking cortical model. In Proceedings of the SPIE 8676, Medical Imaging 2013: Digital Pathology, Lake Buena Vista, FL, USA, 9–14 February 2013.
- Chen, J.; Shan, S.; He, C.; Zhao, G.; Pietikäinen, M.; Chen, X.; Gao, W. WLD: A robust local image descriptor. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1705–1720. [Google Scholar] [CrossRef] [PubMed]
- The Whole Brain Atlas. Available online: http://www.med.harvard.edu/aanlib/home.html (accessed on 1 July 2016).
- Image Fusion Toolbox. Available online: http://www.metapix.de/toolbox.html (accessed on 1 July 2016).
- NSCT-SF-PCNN-ImageFusion-Toolbox. Available online: http://dspace.xmu.edu.cn/dspace/handle/2288/8332 (accessed on 1 July 2016).
- MST_SR_Fusion_Toolbox. Available online: http://home.ustc.edu.cn/~liuyu1/publications/MST_SR_fusion_toolbox (accessed on 1 July 2016).
- Qu, G.; Zhang, D.; Yan, P. Information measurement for performance of image fusion. Electron. Lett. 2002, 38, 313–315. [Google Scholar] [CrossRef]
- Xydeas, C.S.; Petrovic, V. Objective image fusion performance measure. Electron. Lett. 2000, 36, 308–309. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, J.; Wang, X.; Liu, X. A novel similarity based quality metric for image fusion. Infusion Fusion 2008, 9, 156–160. [Google Scholar] [CrossRef]
- Piella, G.; Heijmans, H. A new quality metric for image fusion. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Barcelona, Spain, 14–18 September 2003; pp. 173–176.
- Cvejic, N.; Loza, A.; Bull, D.; Canagarajah, N. A similarity metric for assessment of image fusion algorithms. Int. J. Signal Process. 2005, 2, 178–182. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]


| Image Pairs | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F | SCM-M |
|---|---|---|---|---|---|---|---|
| Group 1 | 2.7762 | 3.0183 | 3.3993 | 3.7837 | 3.1382 | 4.0495 | 5.0609 |
| Group 2 | 2.7632 | 3.0260 | 3.2706 | 3.9376 | 3.0969 | 4.2426 | 5.1302 |
| Group 3 | 2.7708 | 3.0362 | 3.3459 | 3.6843 | 3.2681 | 3.9568 | 4.9279 |
| Group 4 | 2.5753 | 2.8873 | 3.1128 | 3.6600 | 4.6146 | 4.6320 | 5.4548 |
| Group 5 | 3.0404 | 3.1078 | 3.4823 | 3.8007 | 3.8178 | 4.9843 | 6.1422 |
| Group 6 | 3.4840 | 3.7787 | 3.5974 | 3.9726 | 3.9684 | 4.2431 | 5.5556 |
| Group 7 | 2.9382 | 3.1397 | 3.2482 | 3.5257 | 3.2624 | 3.9406 | 5.3860 |
| Group 8 | 2.8822 | 3.0045 | 3.0446 | 3.7121 | 3.0854 | 4.2942 | 5.0863 |
| Image Pairs | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F | SCM-M |
|---|---|---|---|---|---|---|---|
| Group 1 | 0.5131 | 0.6044 | 0.6256 | 0.3416 | 0.5750 | 0.5344 | 0.6357 |
| Group 2 | 0.5049 | 0.5972 | 0.6127 | 0.3662 | 0.5464 | 0.5378 | 0.6224 |
| Group 3 | 0.4753 | 0.5482 | 0.5772 | 0.3173 | 0.5255 | 0.4919 | 0.5867 |
| Group 4 | 0.4569 | 0.5704 | 0.5741 | 0.3929 | 0.6579 | 0.5461 | 0.6298 |
| Group 5 | 0.4544 | 0.5592 | 0.5606 | 0.3366 | 0.4815 | 0.5193 | 0.5937 |
| Group 6 | 0.6584 | 0.7048 | 0.7010 | 0.6974 | 0.6679 | 0.6639 | 0.7045 |
| Group 7 | 0.4834 | 0.5676 | 0.5653 | 0.4174 | 0.5030 | 0.4770 | 0.5503 |
| Group 8 | 0.4383 | 0.5651 | 0.5634 | 0.3627 | 0.4878 | 0.4587 | 0.5104 |
| Image Pairs | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F | SCM-M |
|---|---|---|---|---|---|---|---|
| Group 1 | 0.6369 | 0.4501 | 0.5484 | 0.7877 | 0.6017 | 0.9081 | 0.9671 |
| Group 2 | 0.6550 | 0.4551 | 0.5374 | 0.7772 | 0.5432 | 0.9077 | 0.9542 |
| Group 3 | 0.6264 | 0.4510 | 0.5316 | 0.7887 | 0.5874 | 0.9089 | 0.9693 |
| Group 4 | 0.6515 | 0.5172 | 0.6109 | 0.7586 | 0.8935 | 0.9118 | 0.9467 |
| Group 5 | 0.6401 | 0.5221 | 0.6423 | 0.6717 | 0.7193 | 0.8645 | 0.9234 |
| Group 6 | 0.7543 | 0.6456 | 0.6612 | 0.9170 | 0.6405 | 0.9347 | 0.9753 |
| Group 7 | 0.6426 | 0.4753 | 0.6007 | 0.8028 | 0.5866 | 0.8790 | 0.9500 |
| Group 8 | 0.6250 | 0.4473 | 0.5053 | 0.7742 | 0.5958 | 0.8524 | 0.9315 |
| Image Pairs | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F | SCM-M |
|---|---|---|---|---|---|---|---|
| Group 1 | 0.3333 | 0.4217 | 0.5045 | 0.4913 | 0.2817 | 0.6523 | 0.7323 |
| Group 2 | 0.3533 | 0.4551 | 0.5098 | 0.4724 | 0.2378 | 0.6271 | 0.6931 |
| Group 3 | 0.3138 | 0.3937 | 0.4628 | 0.4834 | 0.2676 | 0.6405 | 0.7156 |
| Group 4 | 0.3006 | 0.4366 | 0.4797 | 0.4420 | 0.4479 | 0.5357 | 0.5854 |
| Group 5 | 0.3280 | 0.5095 | 0.5723 | 0.2928 | 0.3018 | 0.4922 | 0.5096 |
| Group 6 | 0.5355 | 0.6659 | 0.7189 | 0.7681 | 0.3318 | 0.7845 | 0.7719 |
| Group 7 | 0.3290 | 0.4314 | 0.5102 | 0.5183 | 0.2677 | 0.5685 | 0.5700 |
| Group 8 | 0.2972 | 0.3684 | 0.3935 | 0.4488 | 0.2754 | 0.4622 | 0.5142 |
| Image Pairs | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F | SCM-M |
|---|---|---|---|---|---|---|---|
| Group 1 | 0.6100 | 0.4164 | 0.5159 | 0.7729 | 0.5640 | 0.8734 | 0.9337 |
| Group 2 | 0.6254 | 0.4160 | 0.5023 | 0.7590 | 0.5177 | 0.8672 | 0.9163 |
| Group 3 | 0.5984 | 0.4199 | 0.4988 | 0.7750 | 0.5645 | 0.8745 | 0.9351 |
| Group 4 | 0.6155 | 0.4740 | 0.5689 | 0.7390 | 0.8404 | 0.8628 | 0.8991 |
| Group 5 | 0.5935 | 0.4608 | 0.5778 | 0.6417 | 0.6516 | 0.7996 | 0.8515 |
| Group 6 | 0.7240 | 0.4541 | 0.6085 | 0.9022 | 0.5810 | 0.9075 | 0.9135 |
| Group 7 | 0.6042 | 0.4343 | 0.5587 | 0.7853 | 0.5496 | 0.8355 | 0.8952 |
| Group 8 | 0.5928 | 0.4058 | 0.4662 | 0.7575 | 0.5628 | 0.7981 | 0.8773 |
| Image Pairs | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F | SCM-M |
|---|---|---|---|---|---|---|---|
| Group 1 | 66.6193 | 66.1906 | 79.5626 | 52.5581 | 74.3848 | 79.8346 | 81.0782 |
| Group 2 | 67.9753 | 69.5841 | 82.3969 | 55.5187 | 74.2025 | 82.5708 | 83.7441 |
| Group 3 | 64.6307 | 67.8026 | 79.8704 | 49.3479 | 74.1064 | 79.7935 | 80.8798 |
| Group 4 | 69.9537 | 70.2955 | 79.6350 | 64.9548 | 82.0193 | 82.5526 | 85.1864 |
| Group 5 | 73.3412 | 74.7206 | 85.5797 | 57.8297 | 85.0754 | 86.0308 | 88.7634 |
| Group 6 | 72.6172 | 73.3028 | 73.2137 | 64.9728 | 64.6814 | 72.4982 | 80.1262 |
| Group 7 | 68.7288 | 70.7589 | 79.8773 | 55.9421 | 74.2269 | 79.7173 | 82.8038 |
| Group 8 | 79.2868 | 81.8019 | 88.7306 | 64.8613 | 75.6456 | 93.8168 | 96.9955 |
| Metrics | DWT | NSCT | NSCT-SR | m-PCNN | PCNN-NSCT | SCM-F |
|---|---|---|---|---|---|---|
| p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | |
| p < 0.01 | p > 0.05 | p > 0.05 | p < 0.01 | p < 0.01 | p < 0.01 | |
| p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | |
| p < 0.01 | p < 0.01 | 0.01 < p < 0.05 | p < 0.01 | p < 0.01 | 0.01 < p < 0.05 | |
| p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | |
| p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ren, J.; Huang, Z.; Zhu, F. Spiking Cortical Model Based Multimodal Medical Image Fusion by Combining Entropy Information with Weber Local Descriptor. Sensors 2016, 16, 1503. https://doi.org/10.3390/s16091503
Zhang X, Ren J, Huang Z, Zhu F. Spiking Cortical Model Based Multimodal Medical Image Fusion by Combining Entropy Information with Weber Local Descriptor. Sensors. 2016; 16(9):1503. https://doi.org/10.3390/s16091503
Chicago/Turabian StyleZhang, Xuming, Jinxia Ren, Zhiwen Huang, and Fei Zhu. 2016. "Spiking Cortical Model Based Multimodal Medical Image Fusion by Combining Entropy Information with Weber Local Descriptor" Sensors 16, no. 9: 1503. https://doi.org/10.3390/s16091503
APA StyleZhang, X., Ren, J., Huang, Z., & Zhu, F. (2016). Spiking Cortical Model Based Multimodal Medical Image Fusion by Combining Entropy Information with Weber Local Descriptor. Sensors, 16(9), 1503. https://doi.org/10.3390/s16091503







