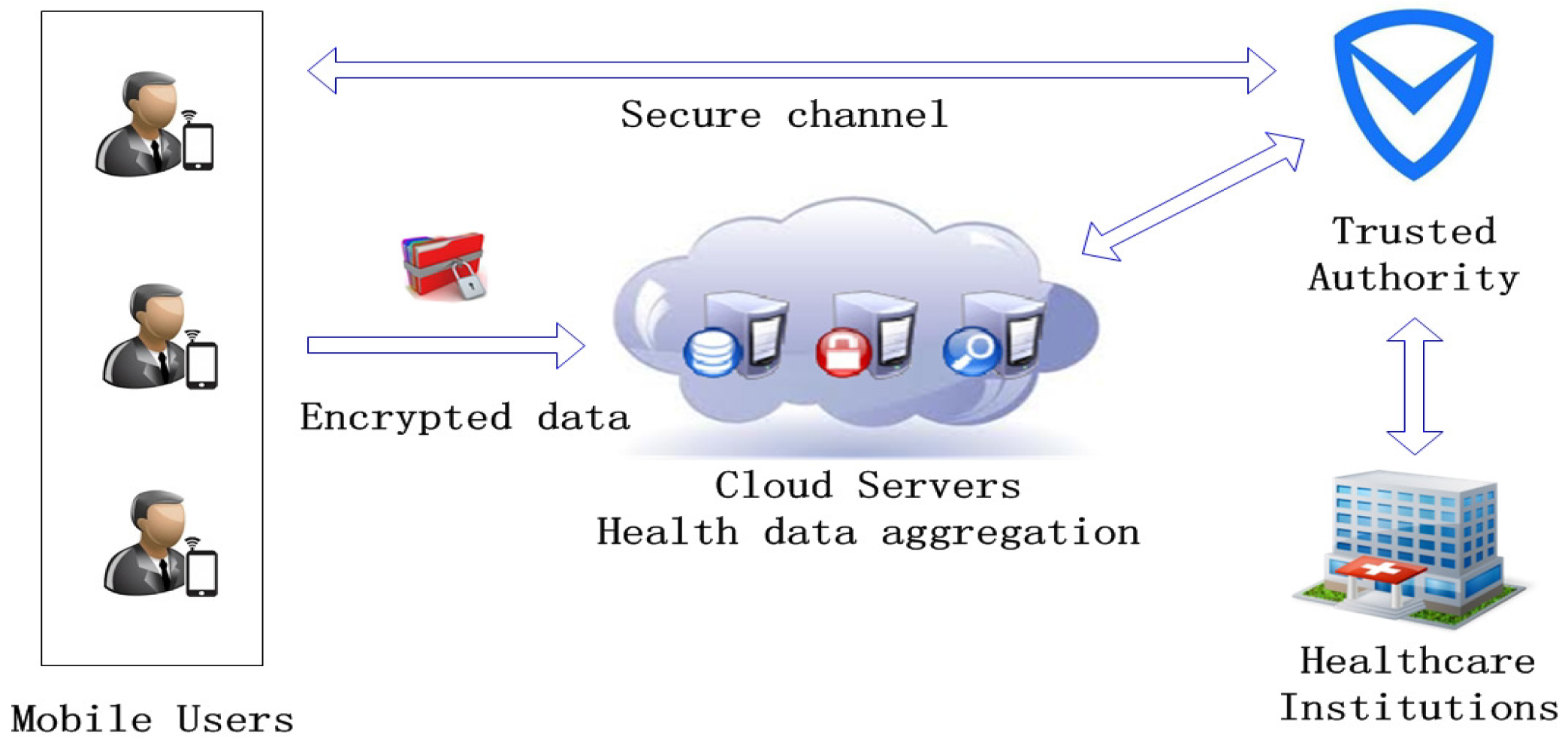
Here, we will give a detailed discussion on the dataset. As we know, once the differential privacy mechanism is chosen, the noise scale is also calibrated. In this paper, we utilize the Laplace mechanism as the building block of the scheme. Hence, the sensitivity of the aggregation function is the only parameter that can directly affect the noise scale (i.e., the accuracy of the result). In reality, there are many different health data, such as the blood pressure, body temperature, heart rate, and so on. Different data types lead to different data ranges and typical sizes. For instance, usually, body temperature is within the range of 35–45 degrees Celsius. For a common person, the mean value of the body temperature is 36.9 Celsius. However, for another kind of health data, such as blood pressure, the data range must be totally different from the body temperature. The maximum of blood pressure should be less than 180 mmHg. In this paper, the maximum of the message should be less than T. Hence, our scheme can be applied for different data types as long as the max value is less than T. In this paper, we only consider the size of the largest message to evaluate the sensitivity and the error of the result. Therefore, the error of each protocol is irrelevant to the type of data. Specifically, we vary the size of the message w () from {12, 13, 14, 15, 16, 17, 18, 19, 20, 21} (w is the length of a message). Once the maximum value and the message amount are both established, we can calculate the mathematical expectation of the square difference of the Laplace mechanism.
6.2. Computational Overhead
For additive aggregation schemes, the computation overhead is clear. Because, the process of the encryption and decryption of the whole aggregation system can be divided into some basic calculations, in this paper, we mainly consider four different kinds of calculations. As shown in
Table 3, we use some symbols to denote the time of each operation.
In our system, there are three entities that share the total computational overhead: MUs (mobile users), TA and CSs. Consequently, we analyze the computational overhead of and three different additive aggregation protocols of PMHA-DP in the above three aspects. Details are shown as follows.
In this paper, the TA has to bear some computational tasks. We have tried our best to reduce the computational burden of TA. As we know, the encrypted data are outsourced to the public cloud. Most aggregation operations are finished by the cloud. However, the cloud servers are honest-but-curious, which may learn the content of the data. Therefore, some sensitive information of the dataset should not be disclosed to the cloud servers. TA is assigned to add noises to the original query result, such as the summation of the data. Due to the property of the Laplace mechanism, the noise scale is proportional to the sensitivity of the aggregation function. Once the privacy budget is set, it is easy to obtain the sensitivity. The sensitivity of an aggregation function can directly reflect the distribution of a dataset. For instance, if the sensitivity of a function is about 37, we can deduce that the dataset is the body temperature. Furthermore, the TA only needs to add noises to the final result, and it is irrelevant regarding the number of users. The time complexity of adding noises is O(1).
For WAAS, TA needs to store the weights of the users and encrypt them before sending them to the cloud servers. Each user’s weight is personal information, and it should be protected from the public cloud. When the system is running for the first time, TA needs to encrypt all of the users’s weights. After the first time, TA only needs to do some partial modifications, which can significantly reduce the computational burden.
For PAAS, the additional calculation of TA is computing the summation of the data. TA can obtain the sum by calculating a simple polynomial. The time complexity is O(1).
Computation overhead of BAAS: Each MU encrypts the health data with one modular multiplication and two modular exponential operations. Therefore, each MU’s total computational overhead is . One of the working CSs gathers all of the MUs’ messages by taking modular multiplication, that is . Then, all of the working CSs calculate the decryption shares with modular exponential operations. Next, one randomly chosen CS gathers the decryption, shares and decrypts it using Pollard’s lambda method, which takes . Therefore, the total computational overhead of working CSs is . TA’s computation burden is light and negligible in the basic scheme.
Computation overhead of WAAS: Each MU encrypts the private data with time . TA encrypts each MU’s weight with time , and there are k users. Therefore, the total time of TA is . Then, all of the working CSs calculate the encrypted weighted sum of the dataset with k bilinear map operations and modular multiplication, that is . At last, CSs jointly decrypt the aggregated data with the same time of the basic scheme: . Therefore, the total computation overhead of CSs is .
Computation overhead of PAAS: Each user encrypts the message with time . Then, the user preprocesses the additional private keys with time . Finally, the user generates the ciphertext of with two bilinear map operations. Thus, the total time of each user is . In the privacy-enhanced scheme, working CSs need to calculate the sum of all users’ messages twice and jointly decrypt them. Therefore, the total computational overhead of CSs is two times that of the basic scheme, that is . TA’s computation burden is negligible and is irrelevant to the scale of the dataset.
Computation overhead of
: In
[
6], each individual MU encrypts the health data with two modular exponential operations and one modular multiplication. Therefore, the total overhead of an MU is
. The aggregator SP’soverhead is
. The working CSs jointly decrypt the aggregated data with time
.
The comparison of the computational overhead is shown in
Table 4.
We utilize OpenSSL Library [
19] to conduct our experiment on a 2.65-GHz processor, 4 GB memory, computing machine. We let the security parameter
and set message’s bit length as
. Besides, we let the user number range from 10,000–100,000. One CS can provide service for 2500 users at most. The result of the experiment showed that the bilinear map operation and Pollard’s lambda method are quit time consuming. Specifically, we have the results
ms,
ms and
ms. Besides,
is directly proportional to
. When
,
ms. Based on these results, we depict the variation of computational overheads in terms of
k in
Figure 3 and
Figure 4.
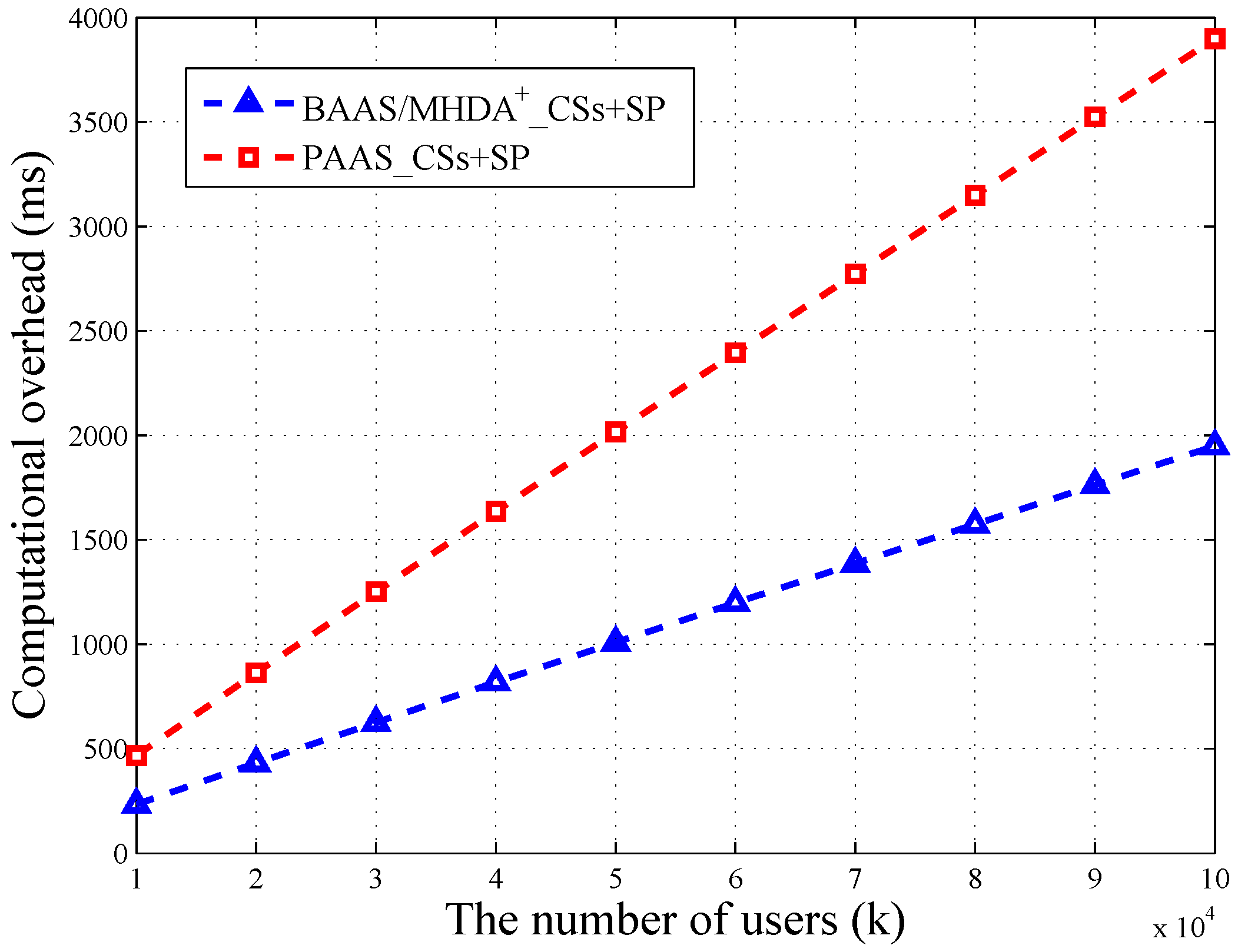
As shown in
Figure 3, the computational overhead of CSs + SP in the basic scheme (BAAS) is exactly the same as
. Therefore, we use the same line to depict the variation. We can find that the overhead of the privacy-enhanced scheme (PAAS) is two times that of BAAS and
. When the user number is 100,000, PAAS’s computational overhead is 3898.80 ms, nearly 4 s. Besides,
’s overhead is 1949.40 ms, nearly 2 s. Therefore, the privacy-enhanced scheme takes up an extra 2 s of calculating time, which is acceptable. Even in the big data environment, suppose the user number reaches 10 million; the calculating time of PAAS is 363,159.64 ms, nearly six minutes. Consider that the high-performance servers in the cloud and part of the computation burden can be uniformly distributed; it is possible to reduce the running time into the acceptable range. Thus, PAAS protects the aggregated data at a low price.
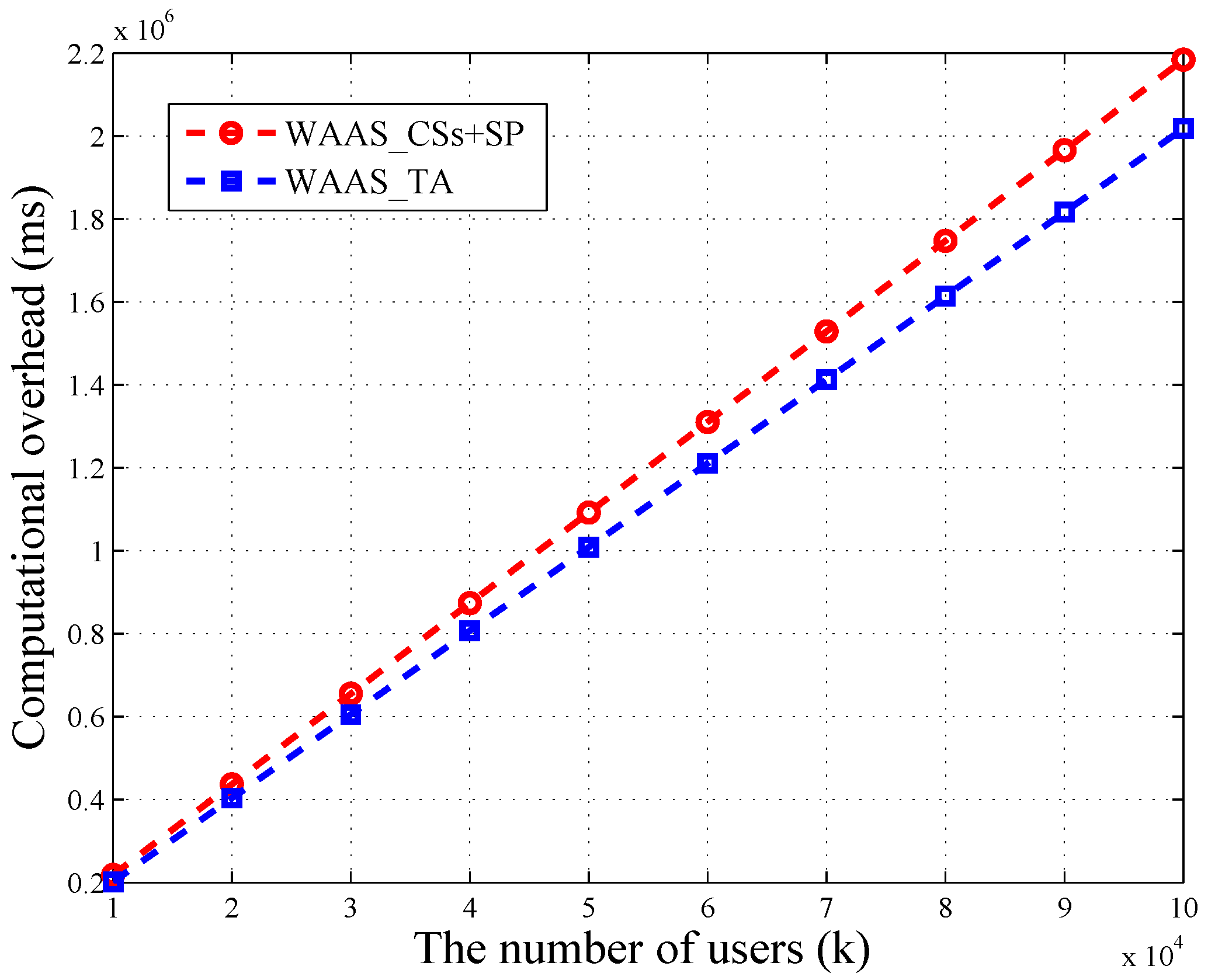
As depicted in
Figure 4, the time consumption of TA and CSs + SP in WAAS increases linearly with the number of users. Besides, the loads of TA and CSs are balanced. When the amount of users reaches 100,000, the computational overhead of TA is 2018 s, which is close to CSs’ 2184 s. In WAAS, CSs need to do
k bilinear map operations, and TA is required to take
modular exponential operations. These two calculations are time consuming, but both of them can be completed in parallel. Thus, it is possible to reduce the running time.
6.3. Communication Overhead
First, we compare the communication overhead of the proposed additive aggregation schemes with . As we know, the length of the ciphertext directly reflects the communication overhead. Therefore, the communication cost of each entity (TA MUs CSs) in BAAS is the same as . In WAAS, the additional communication burden is carried by TA. TA needs to send all of the encrypted weights of MUs to CSs. Actually, in a system, one user’s weight cannot be set by himself or herself. Thus, some control centers like TA are bound to manage all of the users’ weight, and the communication cost is inevitable. In PAAS, each user needs to generate two ciphertexts for one message. Thus, the communication cost of MU is two times that of .
For the proposed non-additive aggregation schemes (NAS) and , the communication overhead can be considered in the communication of each MU. In NAS, MU reports its own encrypt message to CSs. However, MU in submits the ciphertext to SP instead. The length of MU’s ciphertext in is a linear function of the size of the plaintext w. That is , where τ is the security parameter. However, the size of MU’s ciphertext in NAS is a constant .
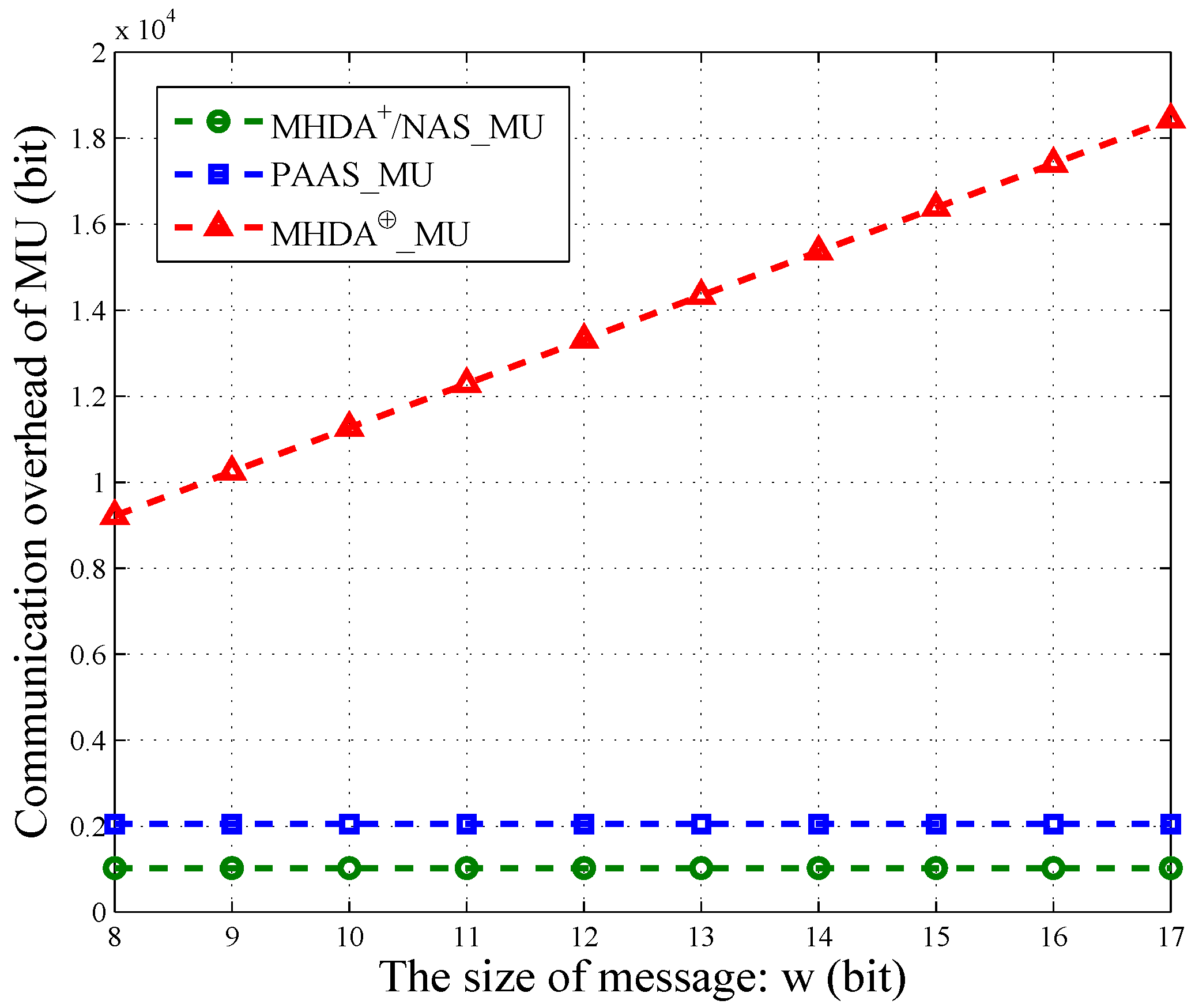
Actually, each MU’s packet also contains some other information, such as time stamp, user ID, and so on. However, the message occupies the most space of one packet. Therefore, we only consider the message’s communication overhead. As shown in
Figure 5, we vary
w from
and illustrate the communication cost of PAAS, NAS,
and
in terms of
w. The size of MU’s encrypted data in NAS is the same as
. Thus, we use the same line to depict them. Similarly, the communication overhead of MU in PAAS is also a constant and is irrelevant to
w. However, each MU in PAAS needs to generate two ciphertext for one message. Therefore, PAAS has twice the communication overhead of NAS and
, that is
. For
, the overhead of MU increases linearly with the growing of
w. Namely, the longer the message, the larger the communication overhead. Thus, NAS and PAAS are more practical when the message’s size is large.
6.4. Error Analysis
In our additive schemes, we directly add noise
to the result
M. Then, we obtain the noisy answer
, where
. In this section, we use
to represent any aggregation function’s sensitivity. Thus, the mathematical expectation of the square difference of the Laplace mechanism is
, which simplifies to:
. Since
, we have
. As discussed in
Section 4.1, the aggregation functions of BAAS and PAAS are the same, and the sensitivity of both functions is
. In WAAS,
. Thus, the errors of BAAS and PAAS are
. We also have
.
In our non-additive scheme, we choose not to add noise to the result of max/min and median aggregations; because the sensitivity of the function will be too large and is irrelevant to k, that is . However, in , the authors choose to add noises with a large scale. Therefore, we can deduce that the error of max/min and median aggregation in is . In the reality, the number of the users (k) is much larger than 10,000 or even more. Therefore, the error of max/min and median in should be larger than , which is unacceptable. For our histogram aggregation scheme HMH, the sensitivity is , where t is the level of the query tree T. Thus, we have , where m is the length of the query vector .
In
, the authors directly add noise to the sum of the health data. Therefore, the sensitivity is
T. However, in
, the noisy sum is divided by
k to acquire the noisy average. Therefore, we can deduce that the sensitivity of the mean value function in
is
. Note that the noises in
are sampled from the geometric distribution
. Its probability density function is:
where
and
. Let
X be the noise sampled from
. Then, the error of
is
, which is calculated as follows.
Let
, and
. We can deduce
. Then, we have
. Since
and
, the final result can be calculated as:
The errors of PMHA-DP and
[
6] are clearly listed in
Table 5.
In
Table 5,
is the largest weight of all of the mobile users. Therefore,
must be larger than the average of all of the users’ weights. Then,
, which can be transformed into
. Therefore, the error of WAAS is greater than or equal to that of PAAS and BAAS. The noise of
is sampled from the symmetric geometric distribution, which is a discrete approximation of the Laplace distribution. Consequently, the errors of
, BAAS and PAAS can be considered equivalent approximate. Let
. We vary
k from {10,000, 20,000, 30,000, 40,000, 50,000, 60,000, 70,000, 80,000, 90,000, 100,000} and vary
w (
) from {12,13,14,15,16,17,18,19,20,21} to calculate the error of
and BAAS/PAAS. All of the error values of
and BAAS/PAAS are listed in
Table 6. Apparently, the difference between
and
is negligible.
Here, we give a detailed discussion on the dataset. As mentioned above, the sensitivity of the average aggregation function and the number of the messages are the only parameters that can directly affect the noise scale. In reality, there are many different health data, such as blood pressure, body temperature, heart rate, and so on. Different data types lead to different data ranges and typical sizes. For instance, usually, the body temperature is within the range 35 °C–45 °C. For a common person, the mean value of the body temperature is 36.9 °C. However, for another kind of health data, such as blood pressure, the data range must be totally different from the body temperature. The maximum of blood pressure should be less than 180 mmHg. In this paper, the maximum of the message should be less than
T. We only consider the size of the largest message to evaluate the sensitivity and the error of the result. Therefore, the error listed in
Table 6 is irrelevant to the type of data. Specifically, once the maximum value and the message amount are both established, we can calculate the mathematical expectation of the square difference of the Laplace mechanism.
In HMH, we improve the accuracy of the query through consistency. According to [
12],
for all query sequences, and there exists a query sequence with
. As depicted in
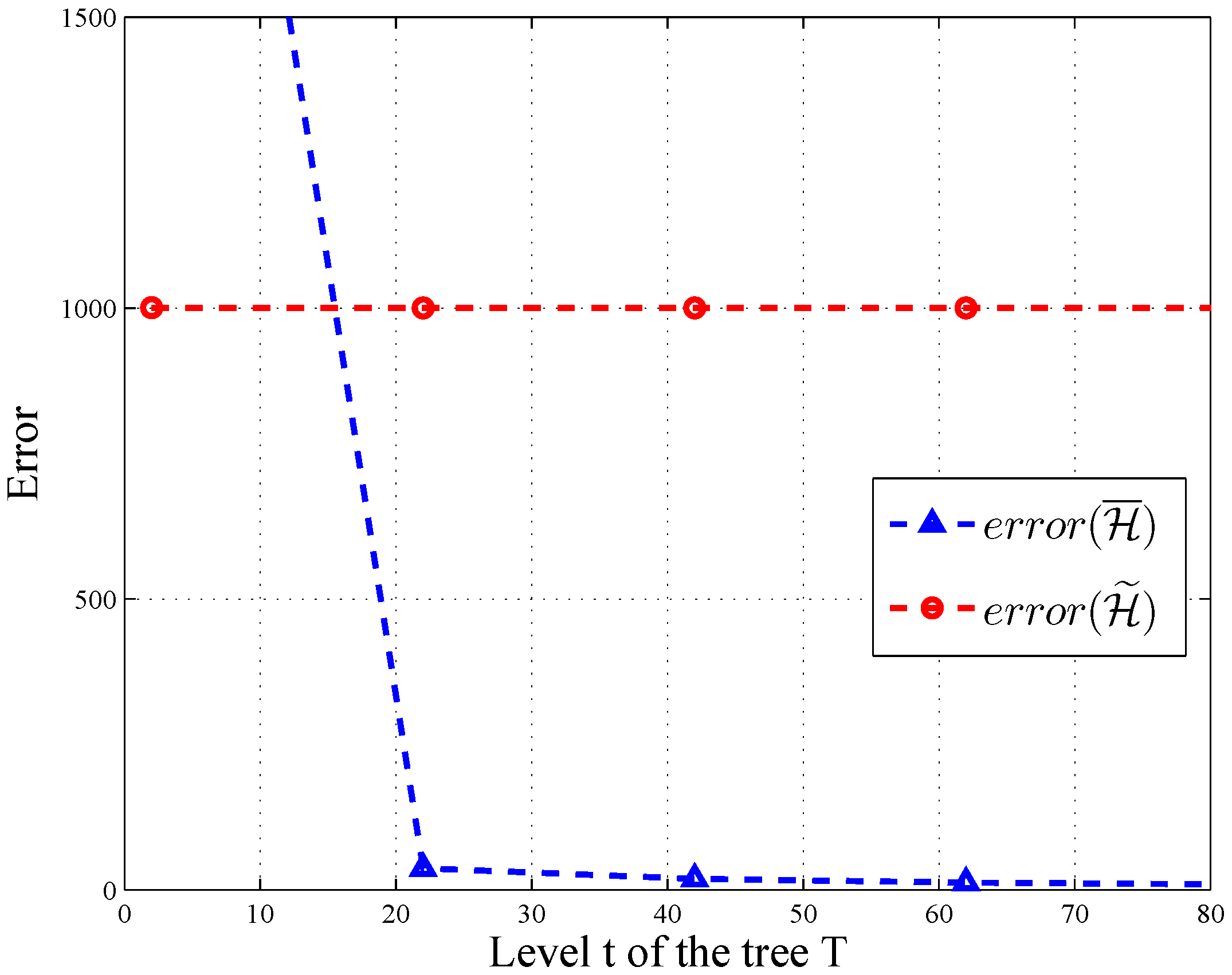
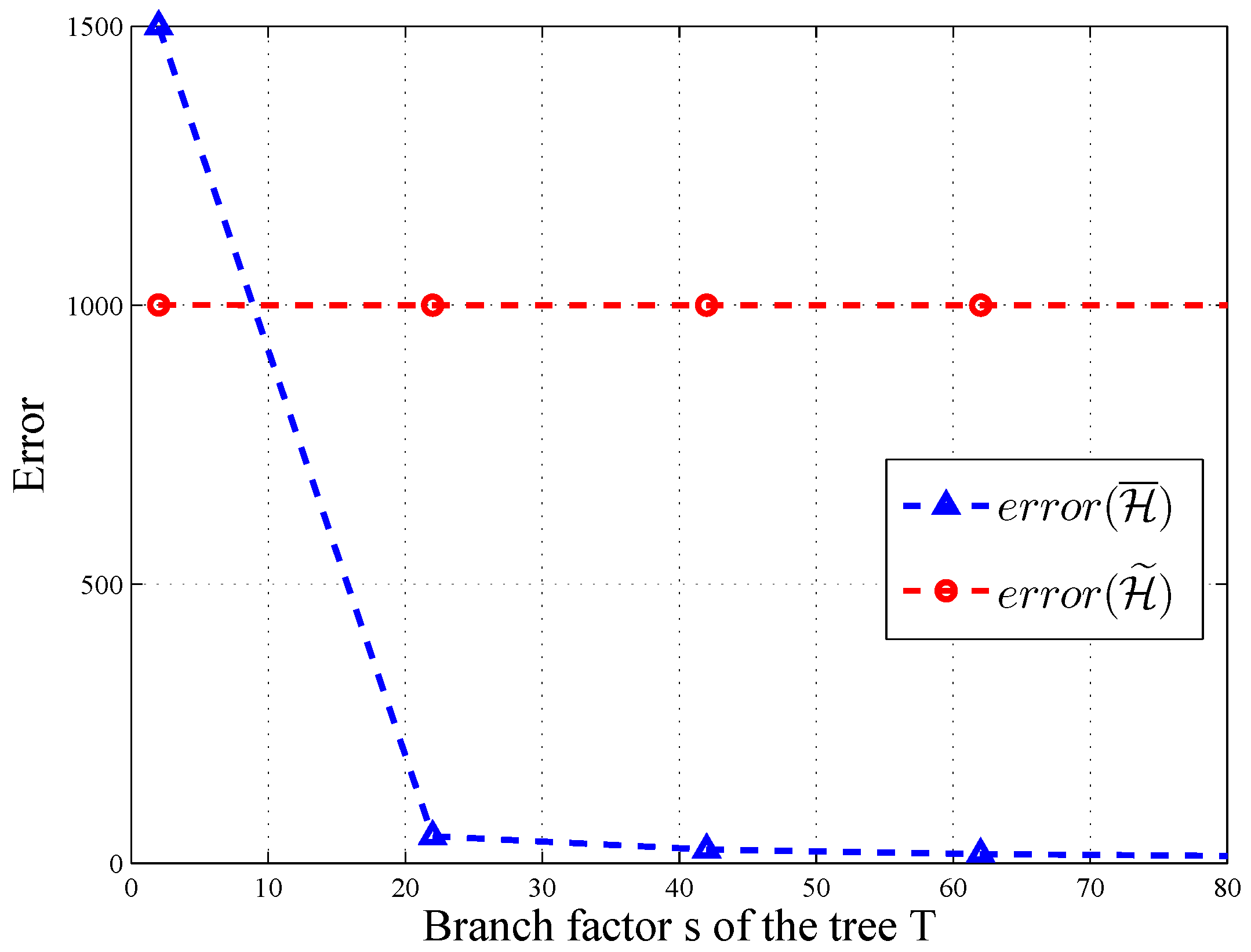
Figure 6 and
Figure 7, the error of
changes significantly along with the level and branch of query tree
T, when
and
. Thus, post-processing makes
more accurate on some query sequences.
Another typical way to evaluate the error is to issue queries on the data before and after using differential privacy and measuring the difference between these query results. Therefore, we also give a further analysis of the error by leveraging a popular metric called the relative error [
6]. This metric can directly reflect the difference between the original result and the permutated result. The mathematical expectation of the relative error
η is calculated as follows.
where
. Therefore, the relative error is
. As the sensitivity of the aggregation functions are already discussed, we can easily calculate
η. Additionally, the relative errors of each scheme are listed in
Table 7.
As analyzed above, the error of WAAS is greater than or equal to that of PAAS and BAAS. Moreover, the errors of , BAAS and PAAS can be considered equivalent approximately. Here, we assume that the data type is the body temperature. Let , T = 45 °C (i.e., the maximum temperature of human) and the average temperature M = 37 °C. Suppose the number of users is . Then, the relative error of BAAS/PAAS is , which is almost the same as , that is . Therefore, the difference between BAAS/PAAS and is negligible.