1. Introduction
The pedagogical rationale for hands-on laboratory explorations in science and engineering education is well established and includes improvement in students’ conceptual understanding as well as opportunities to hone design, professional, and social skills [
1]. However, instructional laboratories are increasingly burdened by the costs of purchasing and maintaining equipment. Test-bed peripherals, including hardware and software used to collect and process experimental measurements, can often contribute to significant costs. Efforts to provide valuable educational experiences that avoid such large costs have included the deployment of virtual laboratories that operate on simulations of physical processes, thus obviating the need for sensing, actuation, and data acquisition [
2]. An alternative approach has allowed students to remotely perform experiments and collect data from test-beds using a web browser, reducing the number of test-beds required at the laboratory site and allowing students “anytime, anywhere” access to laboratory-grade equipment [
3]. Despite the advantages of virtual and remote labs, studies suggest that the loss of physical presence with actual equipment frequently causes learners to: have difficulty in achieving learning outcomes, experience lack of motivation, and express preference for hands-on labs [
4]. To provide cost-effective, readily-accessible solutions that allow measurement, control, and enhanced interaction with real equipment, developers of platforms for science and engineering courses, as well as educators of such courses, can leverage the smartphones that learners already bring with them to the laboratory.
The pervasive adoption of smartphones has launched a new era of personal computing in which the ability to sense, store, process, and communicate information is available in the palm of one’s hand. The sensing, storage, computation, and communication (SSCC) capabilities of smartphones have enabled them to serve as lightweight, portable, and inexpensive platforms for a variety of measurement applications [
5]. For example, the inertial sensors of smartphones have been used for positioning applications in indoor environments where GPS signal is weak [
6] and to encourage independent navigation of the visually impaired [
7]. Mobile applications have analyzed inertial data to recognize user activity, e.g., walking, jogging, and ascending or descending stairs [
8]. In the medical field, applications include processing and integrating data from smartphone inertial sensors to measure the Cobb angle in both kyphoses [
9] and scoliosis [
10], analyze gait characteristics [
11], characterize Parkinson’s disease tremor [
12], and notify emergency services if a user has fallen [
13]. A smartphone implementation may also yield cost reductions
vis-a-vis conventional hardware. For instance, a system that processes accelerometer data from a smartphone to detect potholes has been proposed as a substitute for high-cost equipment [
14]. A study that used a smartphone to detect traffic collisions and notify emergency services [
15] noted that similar in-vehicle systems are infeasible to retrofit into older vehicles and too expensive to include in newer vehicles.
Several innovative mobile applications have leveraged smartphone cameras for vision-based measurement, e.g., to recognize fingerprints [
16], to enable farmers to remotely classify fish species [
17], and to assist the visually impaired in both indoor and outdoor navigation [
18]. Moreover, a system has been developed that fuses information from several different smartphone sensors, including both front- and rear-facing cameras, to monitor driving conditions [
19]. Computer vision and machine learning algorithms are performed on the phone to detect the head pose and eye states of the driver to infer his/her attentiveness and drowsiness during driving, as well as to detect unsafe conditions such as tailgating, lane weaving, or drifting. It has been noted that similar built-in features are only found in the most expensive of cars [
19].
The use of smartphone-collected sensor data in the closed-loop networked control of physical systems remains largely unexplored. A notable exception is the construction of an artificial pancreas system using a smartphone to process wireless data from a continuous glucose monitoring system worn by patients with type 1 diabetes [
20], improving the mobility of users compared to previous prototypes, which were tethered to a PC. Additional examples include smartphone-controlled robots and unmanned vehicles, in which the multi-core processors and real-time operating systems of smartphones have been leveraged to handle large computational loads [
21]. Mounted smartphones have been used for obstacle avoidance of a marine vehicle [
22] and for the stabilization and control of unmanned aerial vehicles [
23]. These studies use the device camera to capture video and computer vision techniques such as template matching, feature tracking with random sampling consensus, and color segmentation to enable the autonomous guidance and navigation of the vehicle. In this role, smartphones use embedded sensors to detect obstacles in the environment, sense collisions, estimate the pose of the vehicle, and compute vehicle velocities.
Advancements in mobile technology provide a unique opportunity for the integration of smartphones into test-beds for science and engineering laboratories. Specifically, there exist test-beds that are amenable to housing a mounted smartphone that performs some of the required sensing, control, and user interface tasks. Such smartphone-mounted laboratory test-beds (SMLTBs) can enable learners to quickly and seamlessly perform experiments with increased portability and reduced cost. Moreover, having learners mount their personal devices onto equipment and interact with the test-bed through an interface on a mobile application can stimulate engagement in laboratory work, changing learners’ views of their devices from consumer products to technological tools.
Despite their promising potential, the development of SMLTBs presents several challenges related to the mounting of the smartphone, modeling and designing the controller for the SMLTB, and programming the back end (computing) and front end (user interface) of the mobile application. This study investigates the factors that can have a significant impact on the stability of the SMLTB’s physical dynamics and the responsiveness of the user interface, and describes guidelines and efficient algorithms to address them for three illustrative SMLTBs in which mounted smartphones provide sensing, control, and user interfaces for the system. These three SMLTBs are based on classic platforms that exhibit rotational and/or translational motion and have consistently been used in feedback control research and education, as well as in investigations of new technologies for feedback control. Specifically, the study explores the position control of a DC motor, a naturally stable system whose full state is measured directly from a smartphone’s inertial sensors, the use of an efficient vision-based technique to balance an inverted pendulum on a cart (IPC), a naturally unstable and underactuated system that imposes stricter demands on processing time and sampling rate than the motor, and the integration of both inertial and vision-based sensing to stabilize a ball and beam, an even more complex system that requires a multi-rate estimation and control approach. For each case, a discussion is provided on the smartphone mounting, sensing approach, system model, control design, and user interface. Simulations and experiments are conducted to validate the feasibility of mounted smartphones as measurement and feedback control platforms for engineering laboratories, to report the measurement precision and closed-loop performance achieved with such platforms, and to address major challenges and considerations encountered in the development of the platforms.
2. Motivation: Smartphones as Laboratory Tools
As society experiences changes in the economic and technological landscape, educational institutions are expected to adapt the format of their laboratory instruction. For institutions with limited resources, maintaining hands-on laboratories has posed a serious economic burden. Meanwhile, the potential of mobile hardware and software to deliver valuable educational experiences is beginning to be explored and is inspiring novel educational technology formats, e.g., mobile learning [
24] and mobile-assisted seamless learning [
25]. Development of novel mobile applications is beginning to transform smartphones into powerful tools for science education, allowing students to collect, analyze, and share data right from the devices in their pockets both in and out of classrooms [
26]. Recent advances include educational applications that utilize the capabilities of mobile devices to provide learning experiences fueled by interactive augmented reality [
27], simulated physical dynamics [
28], real-world measurement and portable experimentation [
29], and mobile access to remote laboratories [
30]. Thus, the SSCC capabilities of mobile devices have been leveraged to different degrees to provide learners with the information, tools, data, visualizations, measurements, and remote access needed for effective learning.
A majority of people now own smartphones. Since students and educators already bring smartphones into the laboratory with them, large costs can be eliminated by replacing laboratory-grade sensing and PC-based DAC hardware, which can cost thousands of dollars per laboratory station, with these devices, which institutions will not need to purchase. For a diverse array of laboratory test-beds, a smartphone can be readily mounted and its SSCC capabilities integrated to measure and control the state of the test-bed while hosting a user interface for interaction with the test-bed. This is because, due to advances in MEMS technology and the availability of affordable and compact cameras, smartphones can provide measurements that are comparable to those from laboratory-grade sensors in some feedback control applications. Moreover, smartphones provide the capacity to develop graphically rich, intuitive user interfaces that may be distributed to students to enhance their interactions with test-beds. In spite of their promising potential, no study has yet investigated smartphone-mounted solutions for measurement and feedback control of laboratory test-beds.
3. Smartphone-Mounted Laboratory Approach
When attempting to visualize and develop a deeper understanding of abstract concepts, students benefit greatly by seeing and interacting with concrete, physical demonstrations [
31]. In engineering fields such as automatic control, laboratory test-beds are developed that often undergo some form of motion [
32]. Fortunately, several different technologies that can sense motion are housed in smartphones. Laboratory test-beds that display rotational or translational motion are thus amenable to being fitted with smartphones that serve as platforms for contactless sensing and wireless control of the test-beds. The suggested implementation has the advantages of reduced wiring, lower cost, and smaller form factor. Moreover, allowing learners to leverage their personal devices in the experimental process can provide them with more engaging and convenient laboratory experiences.
3.1. Mounting a Smartphone
In securing a smartphone to a test-bed so that its embedded sensors can be used to obtain accurate measurements of the system’s state, it is critical to examine where and how the smartphone is to be mounted. At the scale of the cases considered in this study, the added volume and inertia of the mounted smartphone is not negligible. In fact, the placement of the smartphone will affect several other stages of the development, including the modeling of the system and design of the controller. Moreover, the placement of the smartphone needs to be chosen with consideration for the sensing approach to be taken. It will be shown that if the placement and sensing strategies as well chosen, then subsequent phases of development can be simplified considerably.
3.2. Sensing Modalities
While deciding the placement of the smartphone on the test-bed, developers are confronted with the question of how the smartphone will be used to capture the state of the system. Mobile applications have been developed that utilize the embedded sensors of smartphones to monitor a wide variety of user activities and physical states [
33]. Some of the most powerful and popular of these sensors are the inertial sensors and digital cameras. In this study, both of these sensing modalities are considered for measuring the motions exhibited by the test-beds.
3.2.1. Inertial Measurement
Inertial measurement units (IMUs) have become a standard sensor on board smartphones, often being used in applications with gesture-based interactions. They consist of 3-axis gyroscopes, accelerometers, and magnetometers, whose raw data can be used directly or processed by sensor fusion algorithms to estimate the attitude of the device. Device attitude is represented with Euler angles and defined as the rotation between the device’s current reference frame and the initially established reference frame when the mobile application is initialized. By rigidly mounting the smartphone to a test-bed, the attitude readings of the smartphone indicate the attitude of the test-bed. Since the test-beds considered in this study exhibit planar motion, only orientation about one axis is of interest. Choosing the rate that the IMU is sampled at is an important design consideration since it has a significant impact on the system model, the controller design, and the performance of the closed-loop system. The mobile applications developed in this study support IMU sampling rates of up to 100 Hz to detect high-frequency motions such as impacts and quick shakes. However, developers must keep in mind that although a faster sampling rate yields a more stable system response, it significantly increases battery consumption.
Because the smartphone’s attitude estimates are relative measurements that tend to drift with time, calibration of the readings is an important consideration. Calibration of attitude estimates can be performed using either the smartphone’s magnetometer, which is a source of absolute measurement, or an inexpensive external sensor such as a potentiometer or encoder. For the purposes of evaluating characteristics of measurements collected on the smartphone (e.g., accuracy, noise, drift), in this paper, experimental data from the smartphone-based measurement is compared with corresponding data from potentiometers and encoders embedded on the test-beds. The experiments are initiated at the orientation corresponding to the external sensor’s zero measurement. Thus, the angular position readings from the smartphone and the external sensors can be compared.
3.2.2. Vision-Based Measurement
Vision-based sensing offers a data-rich, affordable, contactless sensing mechanism for many measurement and control applications. Practically all modern smartphones now have integrated digital cameras that can capture high resolution video at frame rates as high as 60 fps (frames per second). Thus, smartphones are better equipped than ever to run fundamental computer vision algorithms that capture, in real time, a physical system’s state, which can be processed by the feedback control algorithms to apply actuation signals on the system. To extract system state, two main vision approaches can be used. The first approach utilizes algorithms that work with the pixel coordinates of features in the image. In the second approach, a calibrated camera is used to estimate the pose between the camera’s coordinate system and a real-world coordinate system so that algorithms can work with real-world coordinates of features in the scene. In this study, both image-based and pose-based approaches are explored in the stabilization of test-beds. Due to inherent nonlinearities, underactuation, large bandwidth, and open-loop instability of many automatic control test-beds, vision-based control of such systems poses challenging demands on processing time, frame rate, and image quality. Thus, to implement SMLTBs successfully, it is critical to investigate the effects of these parameters on the stability and performance of the systems.
3.3. System Modeling and Control Design
Because mounting a smartphone to the test-bed adds a significant inertia, which must be driven by the motor, the test-bed dynamics needs to be remodeled to take into account the presence of the smartphone. If the smartphone is placed such that it is aligned with the motor shaft, the new model will be relatively simple. However, as will be shown, the farther from the rotational axis the smartphone is placed, the larger will be the effects of nonlinear terms in the dynamic model. This can necessitate a change in the control algorithm needed to stabilize the SMLTB. Furthermore, a smartphone located far from the rotational axis contributes a large load on the motor, destabilizing the system and making control more difficult.
3.4. Communication
Once the application running on the smartphone has collected and processed all necessary measurements, it must communicate this data as feedback for driving the test-bed. This communication is chosen to be wireless to avoid cable entanglement that can result from the rotating smartphone. Communication of data between the smartphone and an external processor that drives the test-bed is performed over Wi-Fi using a client-server architecture. During experimentation, to validate the use of SMLTB, the client is executed on the smartphone and the server is executed on a PC and accessed via a wireless local area network maintained by a router. Data is sent and received using the TCP/IP protocol. To allow data to be sent and received in real time, the Nagle algorithm, which is built into the TCP/IP protocol to improve the efficiency of communication [
34], is disabled on both sides of the communication because it introduces latency.
3.5. User Interface Design
Mounting smartphones to laboratory test-beds not only allows for its on-board hardware to monitor and control the system, but also allows its software to provide an interactive user interface mounted directly to the experiment. In designing the front end of the mobile application, developers have the opportunity to present learners with educational content; instructions for the experimental process; and natural controls for adjusting system parameters, commanding the test-bed to a desired state, and saving collected data for post-processing. As the interface is the focus of the user’s attention and the means by which s/he interacts with the test-bed and conducts experiments, its design is critical to the quality of the user experience with the SMLTB.
6. Results
The prior sections have provided an overview of the development of three test-beds that utilize the on-board inertial sensors and cameras of mounted smartphones to measure motion. In addition to aforementioned challenges associated with integrating smartphones on laboratory test-beds, we must also examine the influence of noise, drift, and time delays on the smartphone-based measurements and their impact on the stability and performance of the system. These phenomena are associated with several factors, including the smartphone’s embedded hardware and software, the sensing modalities, the computational algorithms, and the wireless communication between the smartphone and the test-bed. Thus, several experiments are conducted to explore the effects of these factors on the behavior of the SMLTBs. We show that, in spite of the various challenges, the SMLTBs yield acceptable performances for use in engineering laboratory education.
6.1. DC Motor Test-Bed
6.1.1. Inertial Measurement
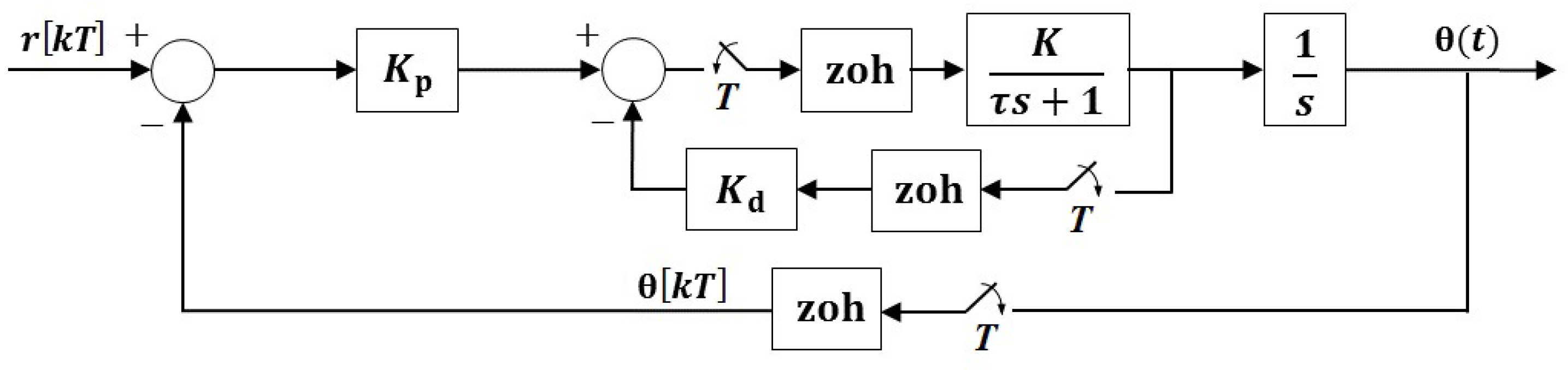
One of the most critical factors in guaranteeing the closed-loop stability of the test-beds is ensuring that measurements are sampled at a rate that is sufficiently fast relative to the dynamics of the test-bed. A commonly used rule of thumb in digital control design is for the sampling rate to be faster than 30 times the closed-loop bandwidth frequency,
, which can be calculated from values of damping ratio
ζ and natural frequency
of the system dynamics [
42]:
By designing a controller that regulates the motor to a desired orientation within one second without any overshoot ( and rad/s), the closed-loop bandwidth is calculated to be rad/s (0.4047 Hz). Thus, the smartphone needs to provide attitude measurement at a rate faster than ≈12.2 Hz. Although mobile applications developed for the iPhones utilized in this study support sampling rates of up to 100 Hz for detecting high-frequency motions, such as impacts and quick shakes, processing of the data by the application may impose an upper bound on the sampling rate. After performing an experiment involving the collection of 350 samples, the mean motion data computation time on the smartphone is determined to be 244.4 μs with a standard deviation of 91.168 μs. This gives a 95% confidence interval of [239.13, 258.36] μs, which is fast enough to support a 100 Hz sampling rate, if desired. Although this low-bandwidth system supports a large range of sampling rates, note that the battery consumption by the sensors and communication module becomes substantially larger at faster sampling rates.
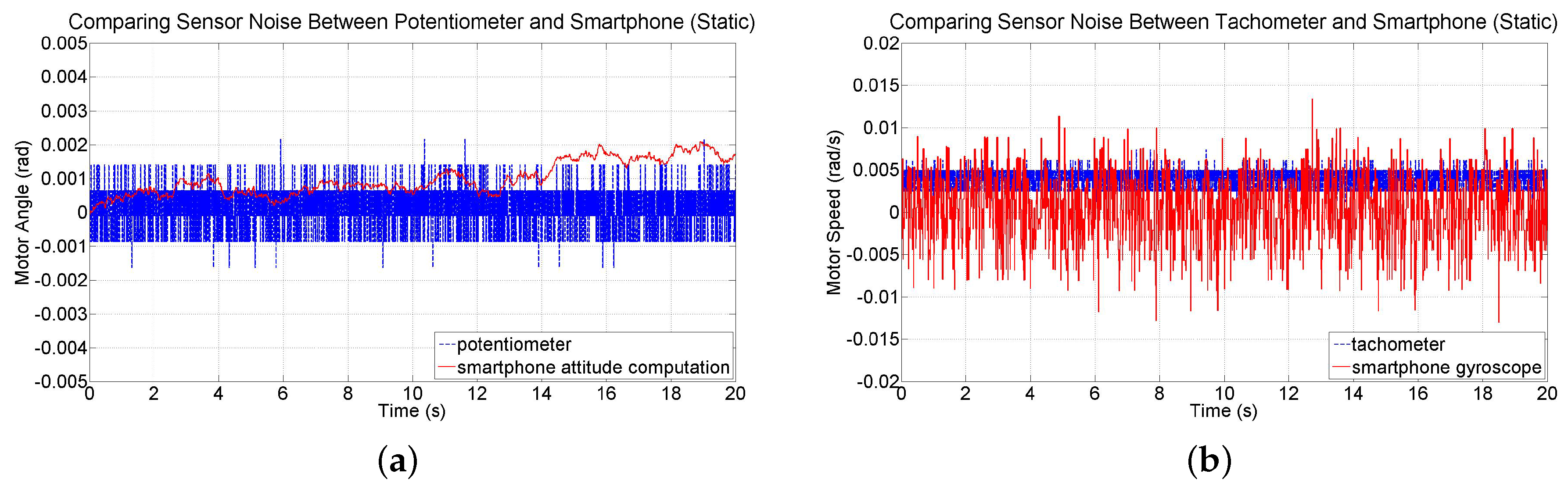
Drift errors associated with gyroscope data have been observed and documented [
43]. Even commercially available gyros have been found to provide reliable estimates of orientation only for up to one minute of operation [
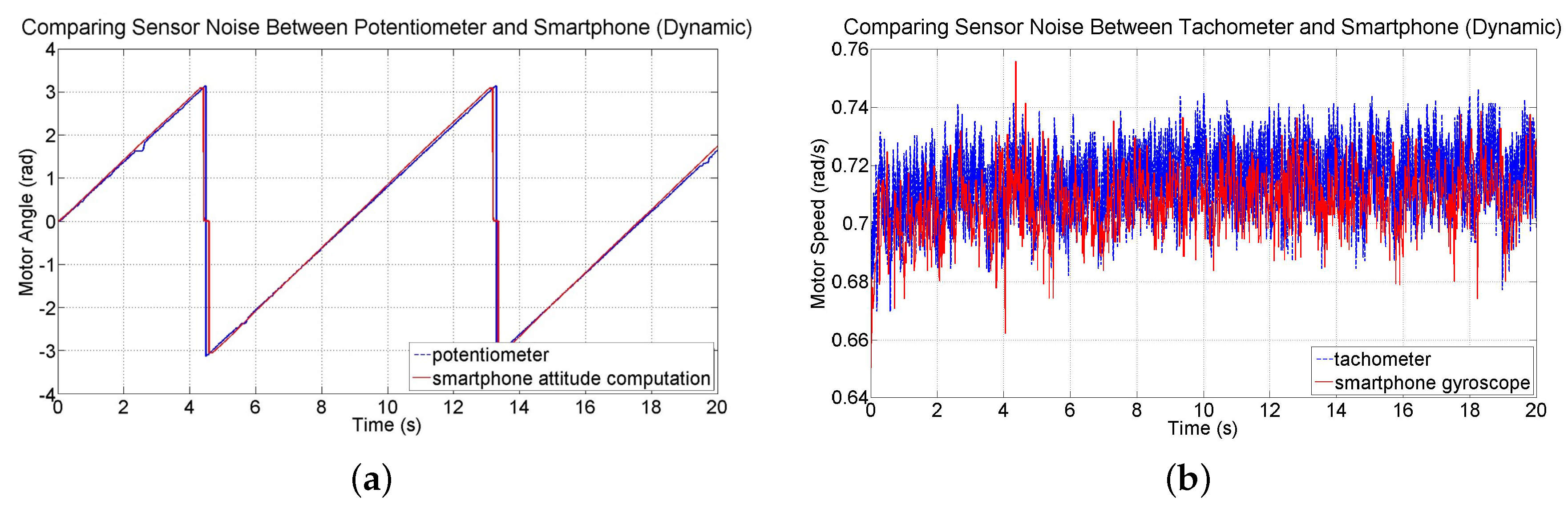
44]. Fortunately, the test-beds investigated in this study are expected to be stabilized within just a few seconds. Nevertheless, the noise and drift characteristics of device attitude and angular velocity measurements are investigated by conducting two 20 s tests in which the smartphone’s IMU is sampled at 60 Hz and its readings are compared to readings from the potentiometer and tachometer sensors on the test-bed. The first test involved collecting sensor data while the motor is held at the zero orientation without being driven. The angular position data from the smartphone sensors and potentiometer are shown in
Figure 10a for this static test. Smartphone attitude data has an average drift rate of 1.0297 × 10
−4 rad/s (0.0059 deg/s). Angular velocity data from the gyroscope and the tachometer are shown in
Figure 10b. Data from the tachometer has a slight bias; the mean of measurements from the gyroscope is −1.4439 × 10
−4 rad/s (−0.0083 deg/s) compared to 0.0038 rad/s (0.2177 deg/s) from the tachometer. However, data from the smartphone is noisier and causes drift in attitude. The standard deviation of the measurements from the gyroscope is 0.0044 rad/s (0.2521 deg/s) and 7.0937 × 10
−4 rad/s (0.0406 deg/s) from the tachometer.
A second test involved collecting data while the motor is driven at a constant speed. The angular position measurements from the smartphone and from the potentiometer of the test-bed are shown in
Figure 11a. At the beginning of the run, the difference between the angular position readings is 0.0030 rad (0.1719 deg) and at the end of the run, the difference is −0.0174 rad (−0.9969 deg). Over the course of the run, the mean difference between the two sensors is −0.0247 rad (−1.4152 deg). These results indicate a sufficiently small error as the motor is driven for a relatively long time period. Measurements from the gyroscope and from the tachometer are shown in
Figure 11b. The mean of the angular speed measurements from the gyroscope is 0.7070 rad/s (40.5081 deg/s) compared to 0.7163 rad/s (41.0410 deg/s) from the tachometer, indicating a difference of just 0.0093 rad/s (0.5329 deg/s). The standard deviation of the measurements from the gyroscope is 0.0113 rad/s (0.6474 deg/s) and from the tachometer 0.0107 rad/s (0.6131 deg/s), showing that the two sensors have noise of comparable magnitude.
6.1.2. Communication
To test the communication between a smartphone and a test-bed over a wireless network, a command is issued on the PC to ping the smartphone and another PC. After sending 100 echo requests with 32 byte packets, the average round trip times for the smartphone and the other PC are determined to be 78.11 ms and 30.79 ms, respectively. A paired t-test is conducted to test whether the two sets come from distributions with equal means. With a 95% confidence level, the null hypothesis can be rejected (with ). Thus, communication with a smartphone experiences larger latency than a typical PC on the same network. Network latency results in time delays between data collected by the sensors on the test-bed and the embedded sensors of the smartphone. These time delays in the closed-loop system can vary significantly, which can cause degradation in system stability and performance and complicate analysis and control design. Several control methodologies have been used over the last several decades to compensate for such effects, spanning the use of Smith predictors, optimal stochastic methods, fuzzy logic, and queuing and buffering. However, with a mean one-way communication delay of 39.055 ms, average delays in the system are only between 0 and 4 sampling periods, depending on the sampling rate used. As will be shown, this amount of delay is negligible when controlling the motor-based test-beds, whose bandwidths are sufficiently low.
6.1.3. System Response
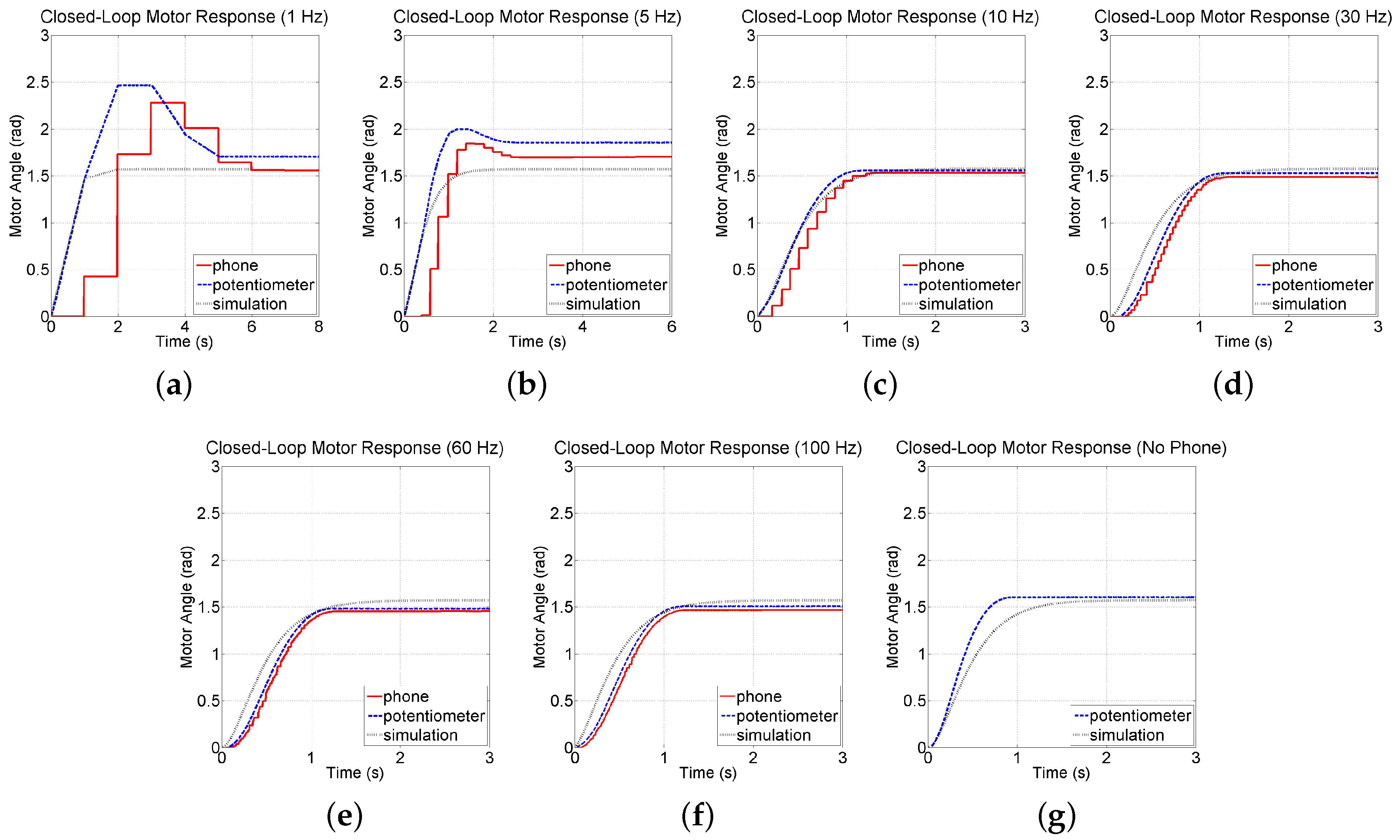
To explore the feasibility of controlling the motor test-bed using attitude and speed measurements collected by a smartphone and of running the PD-control algorithm directly on the smartphone, trials are conducted in which the motor is given a step command of 90 deg (1.5708 rad).
Figure 12a–f show the motor’s closed-loop response at several sampling rates. By plotting the angular position reported by the smartphone alongside those by the potentiometer, one can visualize the communication delay between the smartphone and computer as well as the drift in the smartphone sensor data. Note that simulation results are also plotted alongside the experimental results. For comparison,
Figure 12g shows the response when the PD controller is implemented on the PC using feedback from the potentiometer and tachometer sensors of the test-bed.
Table 3 shows the percent overshoot and settling time for each of the experimental responses. These results indicate an improvement in the responsiveness of the system as the sensors are sampled faster. Note that a loss in performance is observed from the motor when the smartphone-based controller is run slower than 10 Hz. This is because sampling at 5 Hz and 1 Hz, on the order of the closed-loop bandwidth frequency, leaves a large amount of inter-sample behavior uncaptured by the smartphone. Finally, each response exhibits varying degrees of steady-state error, which are attributed to friction in the motor and gearbox causing a deadzone in the motor’s sensitivity around 0 V that can be overcome by introducing an integral term to the controller. Note that the response of the motor at each sampling rate is consistent and varies little between sampling rates.
To confirm that time delays introduced by wireless communication may be neglected in the design of the SMLTB, a simulation of the sampled-data model is run with a constant delay of 39.055 ms introduced (the mean one-way communication time measured in
Section 6.1.2). As seen in
Figure 12, the experimental results match the simulated responses quite well, indicating that delays of 0–4 sampling periods are not significant when controlling a system with such a low bandwidth. Results of experiments with the IPC test-bed will explore the response of a high-bandwidth plant that utilizes smartphone sensing.
6.2. Inverted Pendulum Test-Bed
Unlike the motor test-bed, the IPC has nonlinear, high-bandwidth, open-loop unstable, and underactuated dynamics. In the vision-based control of such systems, limitations in image resolution, image processing speed, and frame rate supported by the camera of the smartphone can introduce noise and time delays that can degrade system stability and performance. A series of experiments are performed to obtain insights into the relationships between these factors.
6.2.1. Vision-Based Measurement
As seen with the motor test-bed, sampling rate has an important impact on stability and performance. In the vision-based control of a SMLTB, this sampling rate is equivalent to the frame rate of the smartphone camera. Using Equation (11), the closed-loop bandwidth of the IPC test-bed is calculated to be 7.0995 Hz (44.6072 rad/s), suggesting a frame rate of ≈213 Hz, or higher. This rate is not achievable with our SMLTB, thus the highest achievable frame rate should be used for this high-bandwidth system. Although the standard frame rate of most smartphones is 30 fps, a higher frame rate can be achieved at the cost of lower image resolution. A resolution of 192 × 144 is chosen for experiments with the IPC test-bed since it is the lowest available and it allows the fastest frame rate, 60 fps, supported by the iPhone 6 Plus. The time required to process each frame introduces a delay between the instant that the visual data is captured by the camera and the instant that the measurement interpreted from that data becomes available. With a 60 fps rate, a processing time of up to 16.667 ms is acceptable, however large processing times can cause noticeable effects on stability or performance. Moreover, if the processing time exceeds the upper bound per frame, subsequent frames are discarded, causing information about the state of the system to be delayed until processing is complete. To characterize the effect of image resolution on computation time, frames are captured at 10 fps to avoid discarding any frames.
Table 4 shows the computation times obtained for a variety of image resolutions. After performing an experiment in which 200 measurements are collected at a resolution of 192 × 144 (the lowest resolution supported by the iPhone 6 Plus), the mean computation time is found to be 5.09 ms with a standard deviation of 0.3609, which is fast enough to support a 60 fps rate. Thus, this resolution is chosen for the stabilization of the IPC (
s).
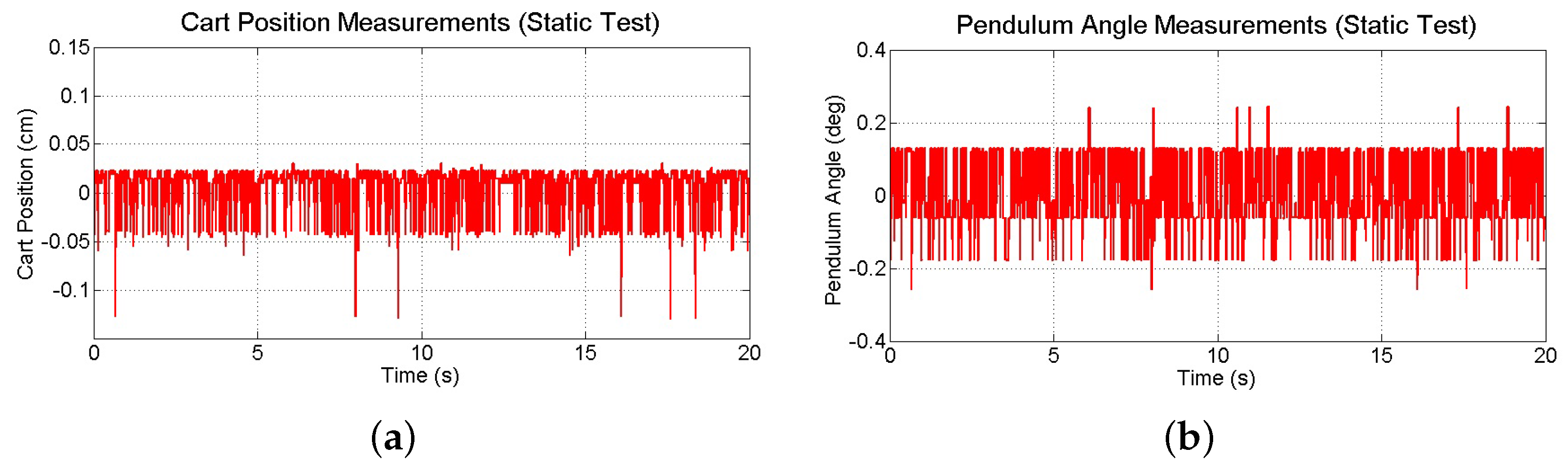
Although lower image resolutions allow for faster processing times, this comes at the expense of increased measurement noise, which may degrade the performance of the system. To investigate the effect of image resolution on the noise characteristics of the vision-based measurements, raw data is collected while the IPC is kept in its stable equilibrium configuration (see
Figure 13). Over the course of 20 s, standard deviations of cart position and pendulum angle measurements are determined to be 0.0258 cm and 0.1102 deg, respectively. Although this noise is larger than that observed with higher image resolutions, it will be shown to be acceptable for intended purpose of the smartphone.
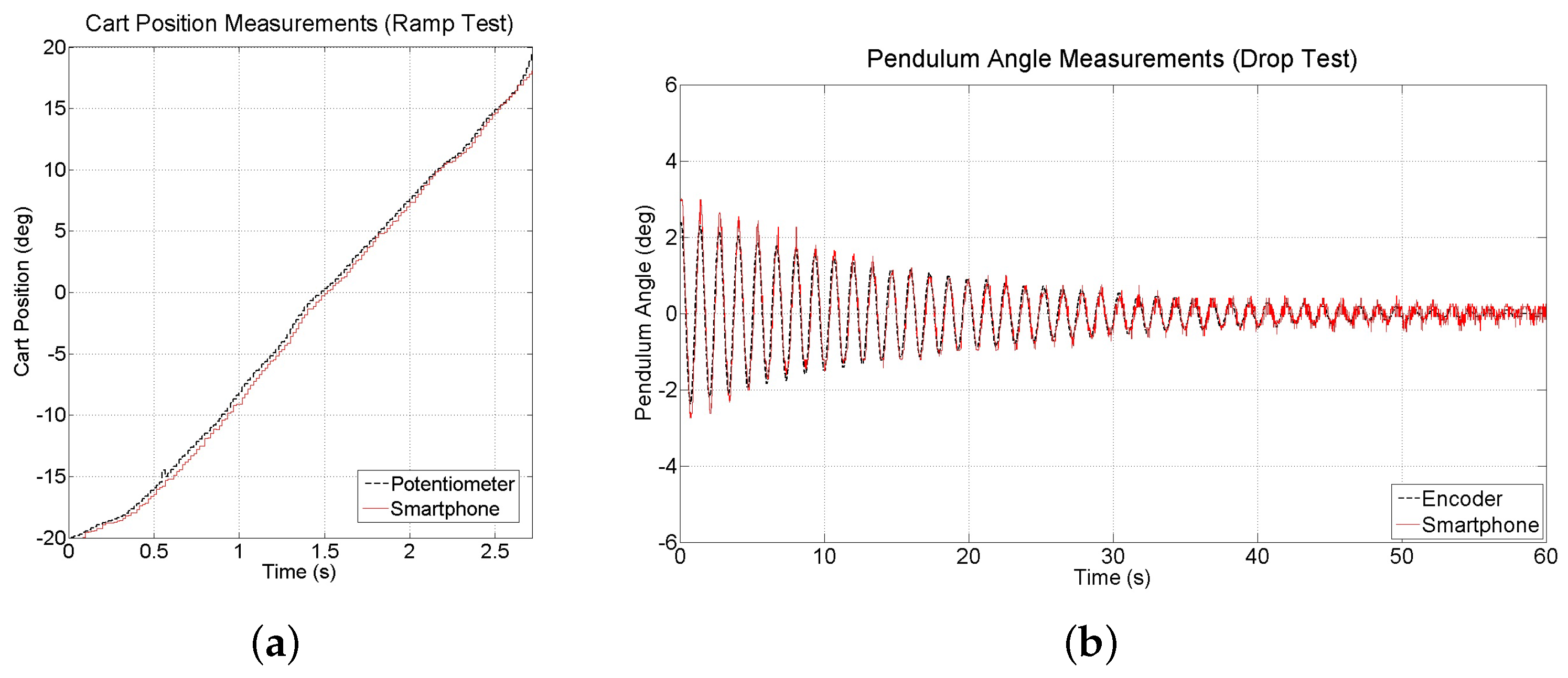
To further evaluate the accuracy and noise associated with the vision-based measurements, two additional experiments are conducted to compare these measurements to those obtained from the potentiometer connected to the motor and the encoder connected to the pendulum. The first experiment, a ramp test, examines cart position measurements as a ramp reference is applied to the cart position for approximately 3 s. Results (see
Figure 14a) confirm that the smartphone can accurately measure the position of the cart, although the measurements suffer from a time delay of approximately 30 ms. The second experiment, a drop test, is run by lifting the pendulum arm a small amount from its stable equilibrium and dropping it to allow it to swing to a stop. Results (see
Figure 14b) show that the smartphone measurements have acceptable levels of accuracy, however suffer from the same time delay as the position measurements.
6.2.2. System Response
To investigate the response of the IPC test-bed as it is controlled using vision-based measurements from the camera of the mounted smartphone, the IPC is first controlled using measurements from the standard potentiometer and encoder sensors on board the test-bed, as shown in
Figure 15. After approximately 10.5 s, the source of the measurements is switched to the vision-based measurements of the smartphone. Then, after 10 s, the measurement source is switched back to the potentiometer and encoder. The response of the IPC before, during, and after the use of the vision-based measurements is shown in
Figure 15. The system response remains stable with the smartphone measurements, and resembles the response with the standard sensors. Small variation between the response using smartphone camera and that using the test-bed sensors can be attributed to the small amounts of delay and noise introduced by the smartphone sensing. With more robust computer vision techniques and smartphones that can support faster frame rates and higher image resolutions, the performance of high-bandwidth systems like the IPC with mounted smartphones is expected to improve significantly.
6.3. Ball and Beam Test-Bed
The addition of the smartphone can add new challenges to the modeling, measurement, filtering, and control problems related to SMLTB. In the case of the ball and beam test-bed, nonlinear dynamics are introduced by the weight added on the beam, and limitations in image resolution, computation speed, and frame rate are again encountered, this time with the back-facing camera of the smartphone. A set of experiments show that, in spite of the challenges, the SMLTB yields acceptable stability and performance in tracking step references as compared to simulations and a benchmark experimental response obtained using a conventional measurement approach.
6.3.1. Measurement Precision
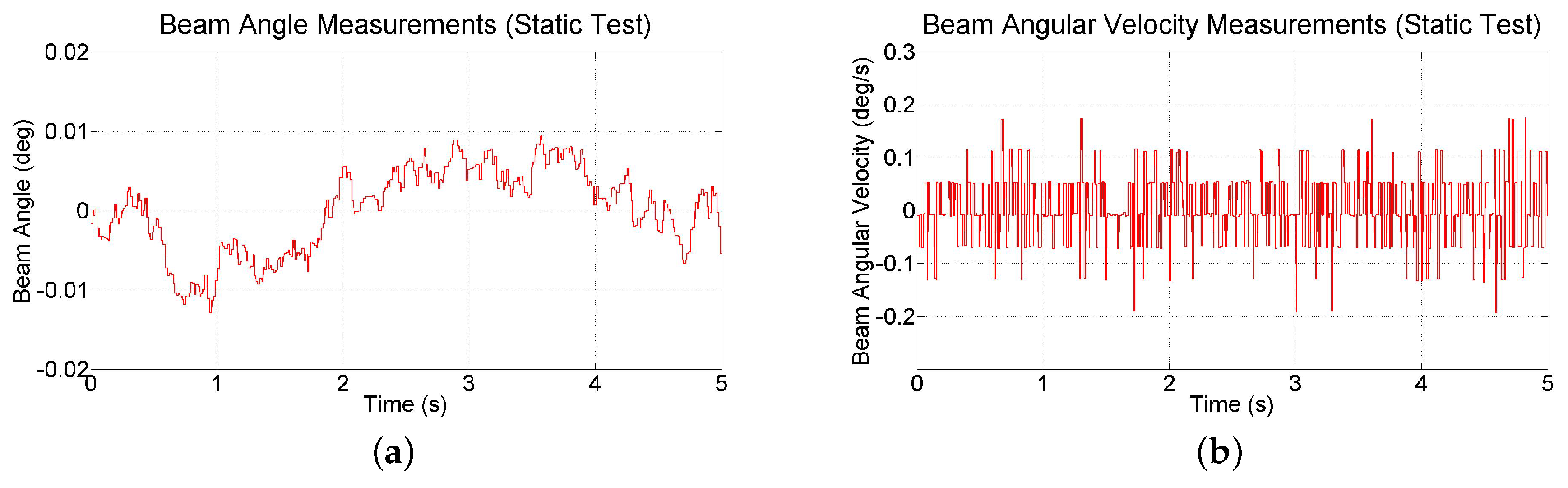
To explore the noise characteristics of the inertial measurements provided by the smartphone, raw data is collected at 90 Hz for 5 s while the test-bed is at rest at its zero state (see
Figure 16). A small amount of drift is observed in the orientation measurements. The range of beam angle measurements is 0.022 deg and variance of angular velocity is 0.0041 (deg/s)
2. For the image-based vision approach on the smartphone, frame rate of back-facing camera is restricted to 30 fps (33 ms processing time). Applying Equation (11), the bandwidth of the ball and beam test-bed is calculated to be 0.8848 Hz (5.559 rad/s), suggesting a frame rate of ≈26.5 Hz, or higher. Thus, although the back-facing camera of the iPhone 6 Plus only supports frame rates of 30 fps, this rate is sufficient for the ball and beam test-bed. At this frame rate, the highest allowable image resolution is 640 × 480 before the computation time exceeds the allowable range. An experiment indicates that at this resolution, the mean computation time is 30.24 ms, with a standard deviation of 0.6541 ms, and that the ball position can be measured to within 0.705 mm. This measurement resolution is approximately 25 times more coarse than the resolution of 0.028 mm that has been obtained with a measurement system consisting of a linear membrane potentiometer, an operational amplifier circuit, and a 14-bit analog-to-digital converter [
45]. While a lower image resolution reduces processing time, it also reduces precision by increasing the level of noise in the measurements. Alternatively, a higher image resolution improves precision, but also increases processing time, causing latency that can destabilize the system. For example, experiments in which the image resolution was lowered to 352 × 288 degraded measurement precision and experiments in which the image resolution was increased to 1280 × 720 yielded large computation delays, both of which rendered the system unstable.
6.3.2. System Response
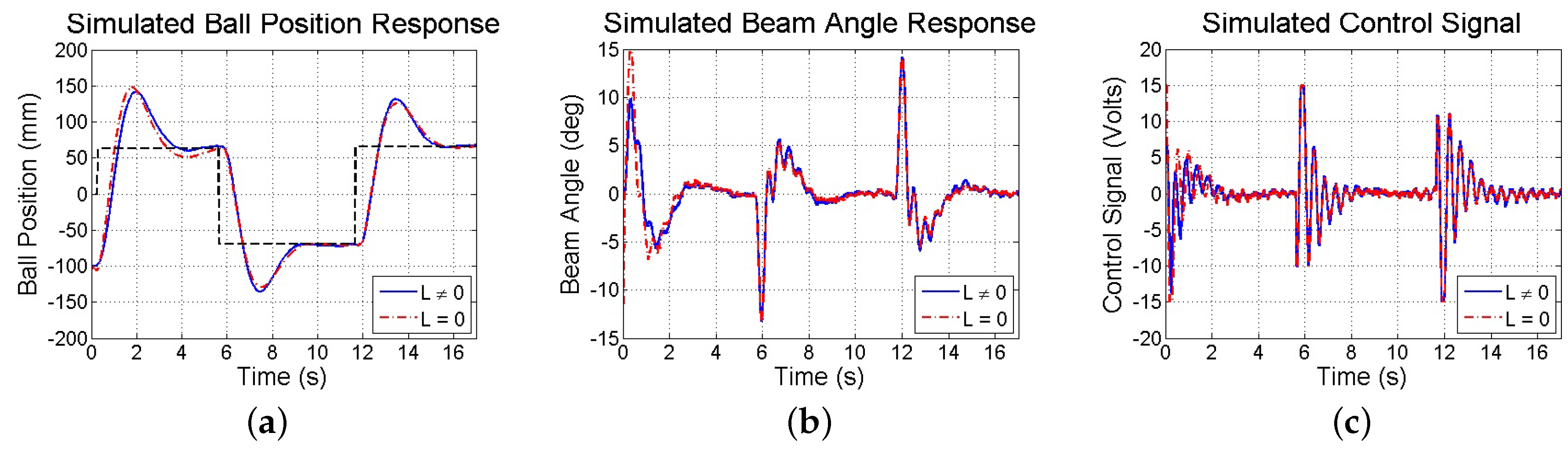
Limitations in resolution, precision, and sampling rate introduced by the smartphone’s visual and inertial sensors have consequences on the test-bed’s closed-loop response. Thus, simulations and experiments are performed to investigate the stability and performance of the smartphone-mounted ball and beam test-bed in response to reference commands. First, a simulation is run taking into account experimentally observed sensor noise, computation and communication delays, measurement resolution, sampling rates, and actuator saturation. Both methods of state estimation (discussed in
Section 4.3.2) are used and found to be comparable. The resulting closed-loop responses are shown in
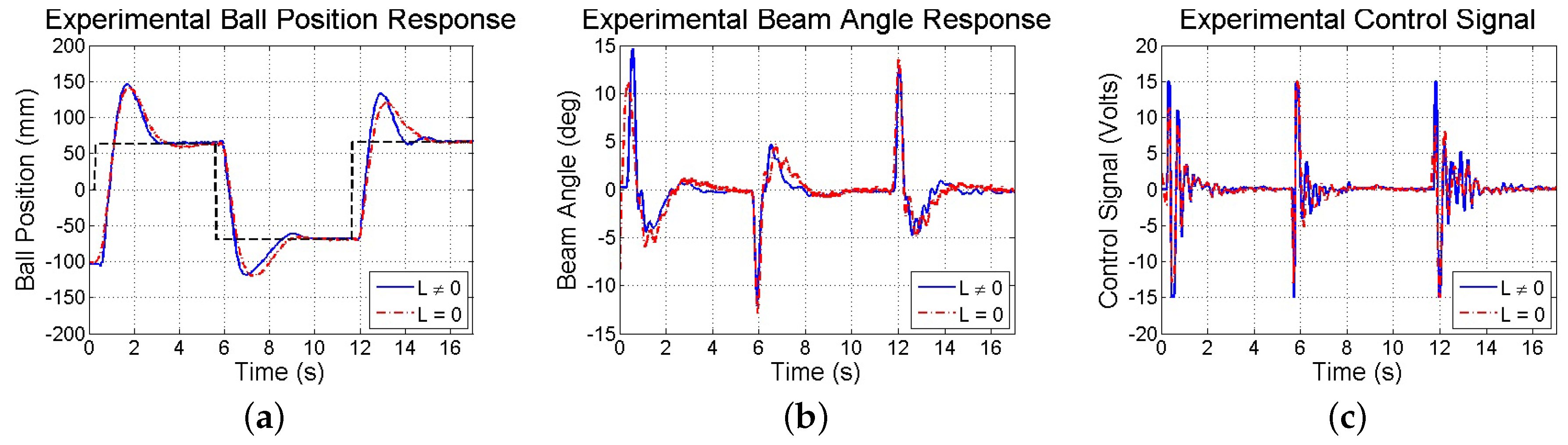
Figure 17. Next, in experiments, the same step commands generated from user taps on the touchscreen to drive a simulation are used to drive the actual test-bed utilizing the smartphone, whose responses are shown in
Figure 18. Furthermore,
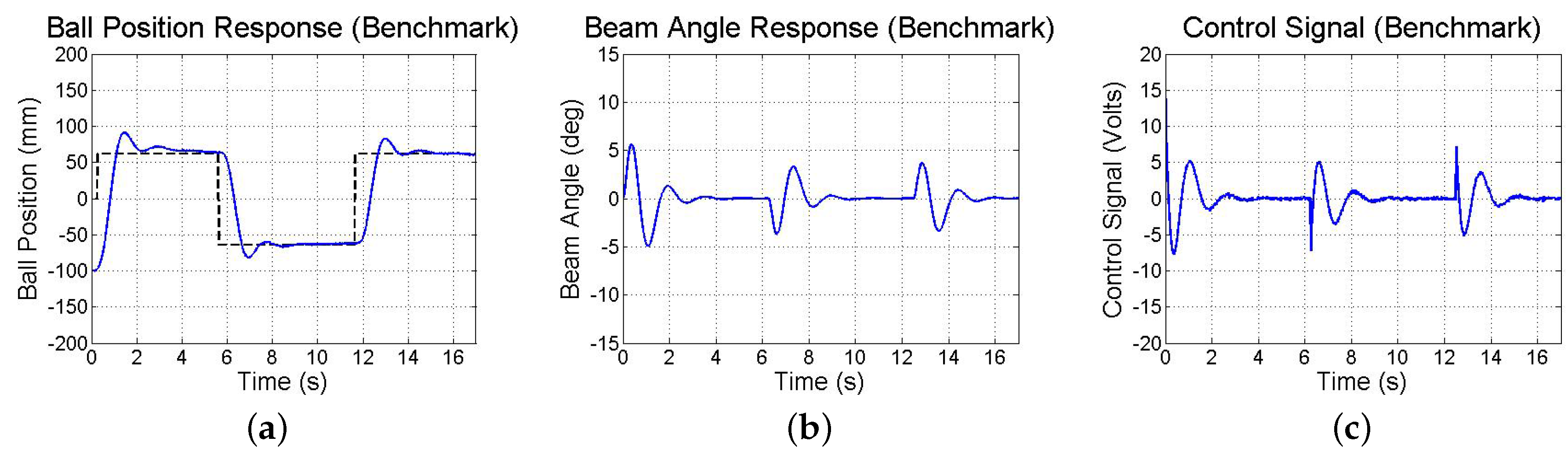
Figure 19 illustrates the response of the benchmark system that utilizes a conventional sensing approach (an encoder and tachometer to measure the beam angle and angular velocity, respectively, and a linear membrane potentiometer to measure the ball position, as described in [
45], all sampled at 1000 Hz). Although the system maintains stability and settles in approximately 3 s, the ball exhibits large overshoots as compared to the benchmark response due to limitations in smartphone-based sensing as discussed above.
6.4. Battery Consumption
To realize SMLTBs, researchers and learners mount to test-beds their personal devices and interact with them for extended periods. This necessitates a consideration of battery consumption of smartphones during operation. To investigate battery consumption rates, each SMLTB is run 3 times for 10 min using an iPhone 5 and an iPhone 6 Plus starting with a 100% charged battery. During each trial, all background applications and processes are closed so as not to affect results.
Table 5 shows the average battery consumption rate measured over three trials for each combination of smartphone and test-bed, in units of minutes taken for the battery power to drop by 1% (smaller numbers indicate faster battery drain). Measurements are collected from the DC motor with inertial sensors being sampled at 100 Hz sampling rate. Results show that the IPC, which utilizes the front-facing camera of the smartphone at 60 Hz, drains battery much faster than the DC motor, indicating that the camera drains battery faster than the IMU. Next, the ball and beam test-bed, which utilizes both the back-facing camera of the smartphone at a 30 Hz sampling rate and the IMU at a 90 Hz sampling rate, drains battery slightly faster than the IPC. Note that the iPhone 6 Plus, which runs on a 1810 mAh battery compared to the 1440 mAh battery of the iPhone 5 and contains a more power efficient processor, drains battery slower than the iPhone 5. The results of
Table 5 are promising since the average activity with the SMLTBs lasts approximately 30 min, even a 3-year old iPhone 5 whose battery has been recharged many times will lose only 14% of its battery during the course of an average activity with the most power draining experiment.