Subsea Cable Tracking by Autonomous Underwater Vehicle with Magnetic Sensing Guidance
Abstract
:1. Introduction
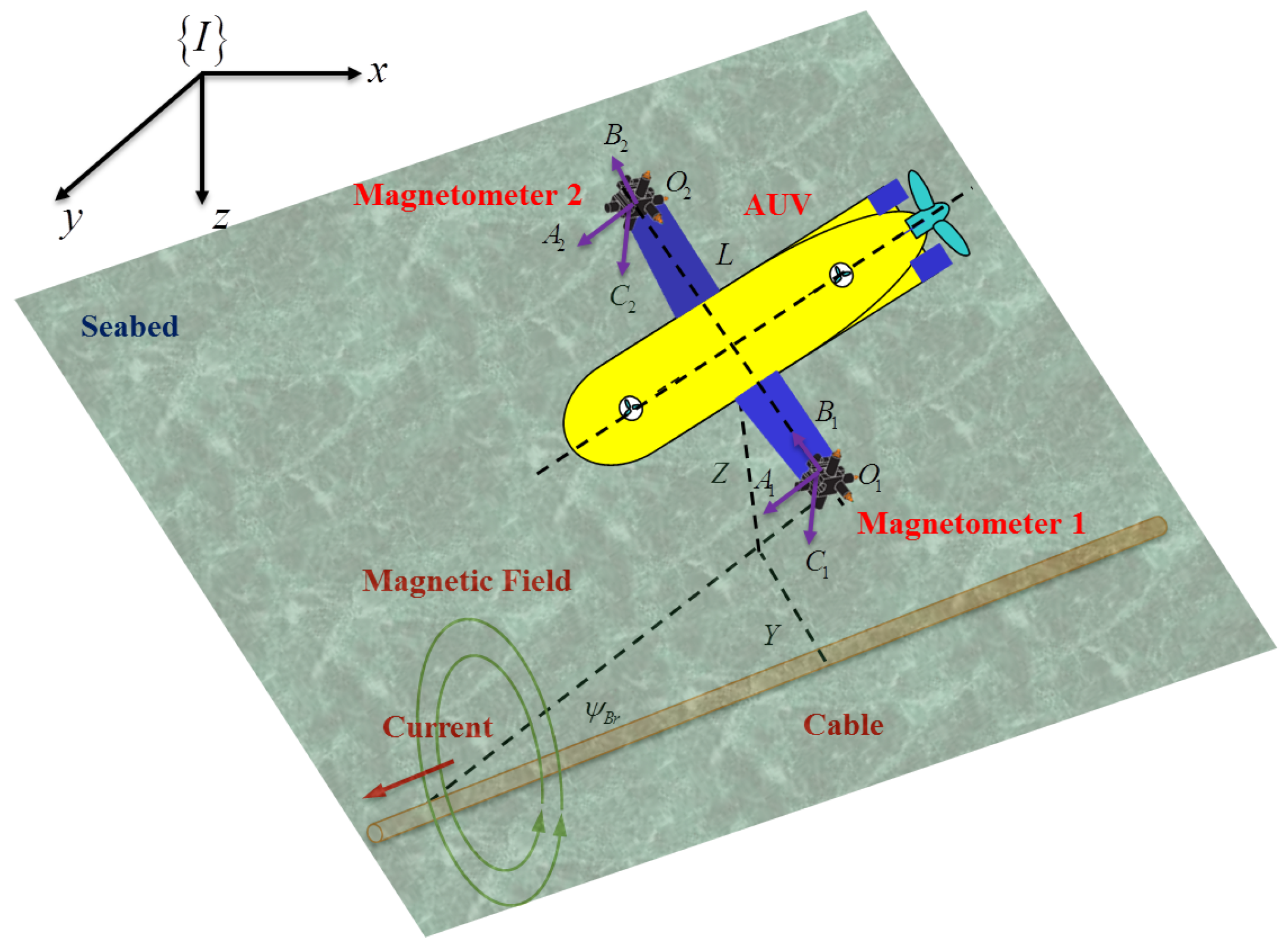
2. Magnetic Sensing and Cable Localization
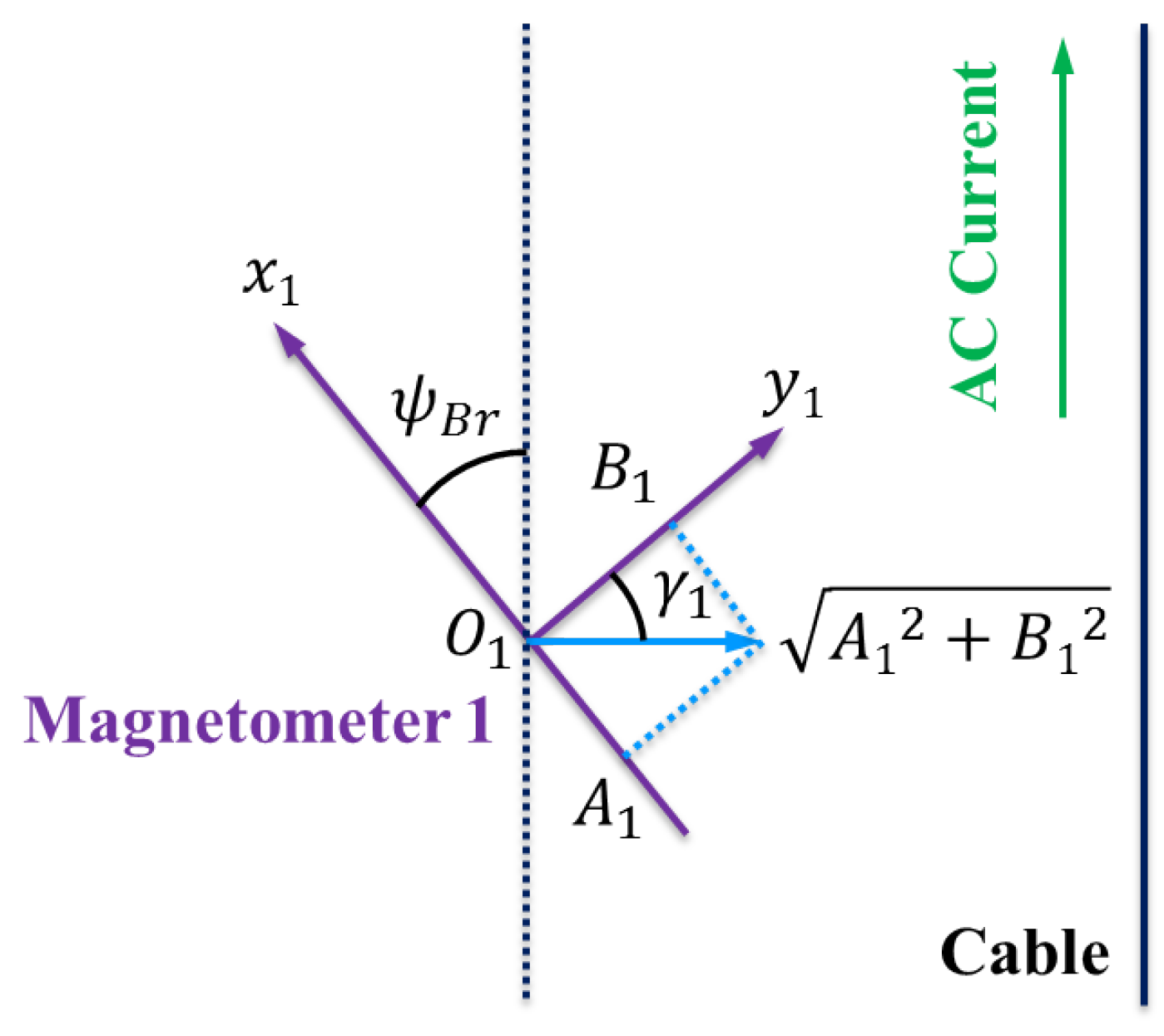
2.1. Passive Magnetic Sensing
2.2. Cable Location
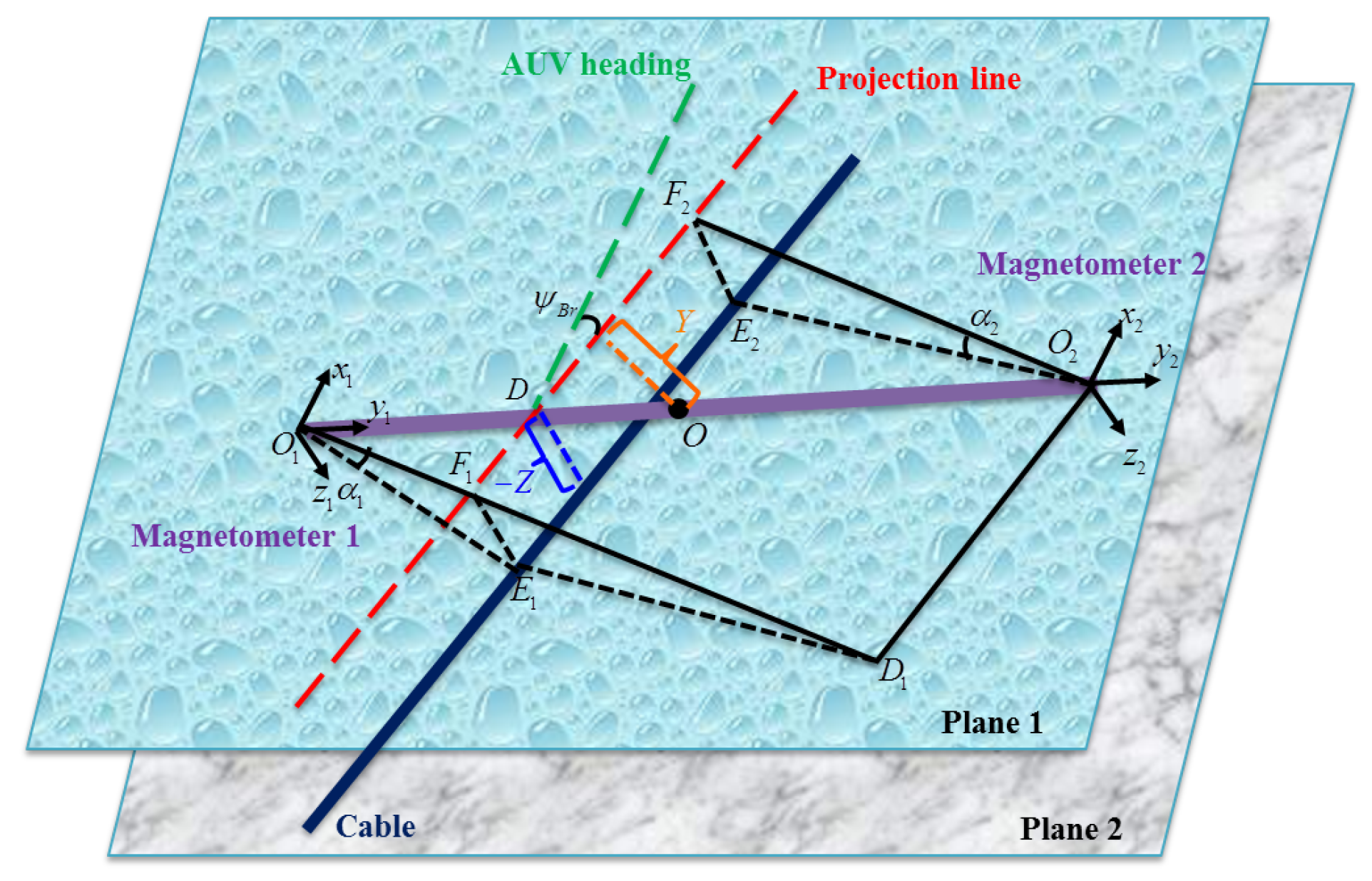
2.2.1. Heading Deviation
2.2.2. Buried Depth
2.2.3. Horizontal Offset
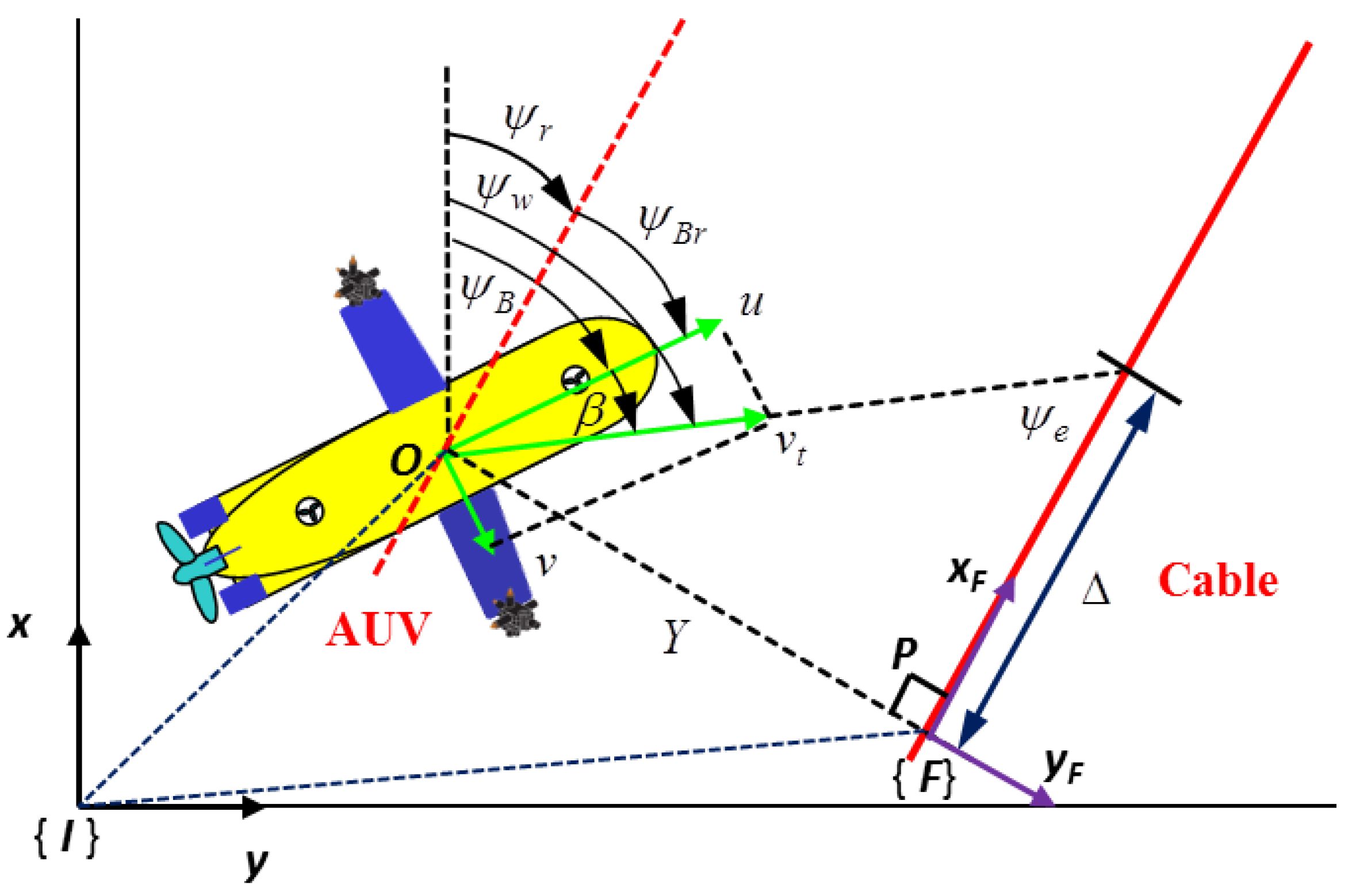
3. Magnetic Guidance and Tracking Control
3.1. AUV Modeling
3.2. Guidance and Control Design
3.2.1. Magnetic Guidance
3.2.2. Cable Tracking Control
4. Numerical Simulation
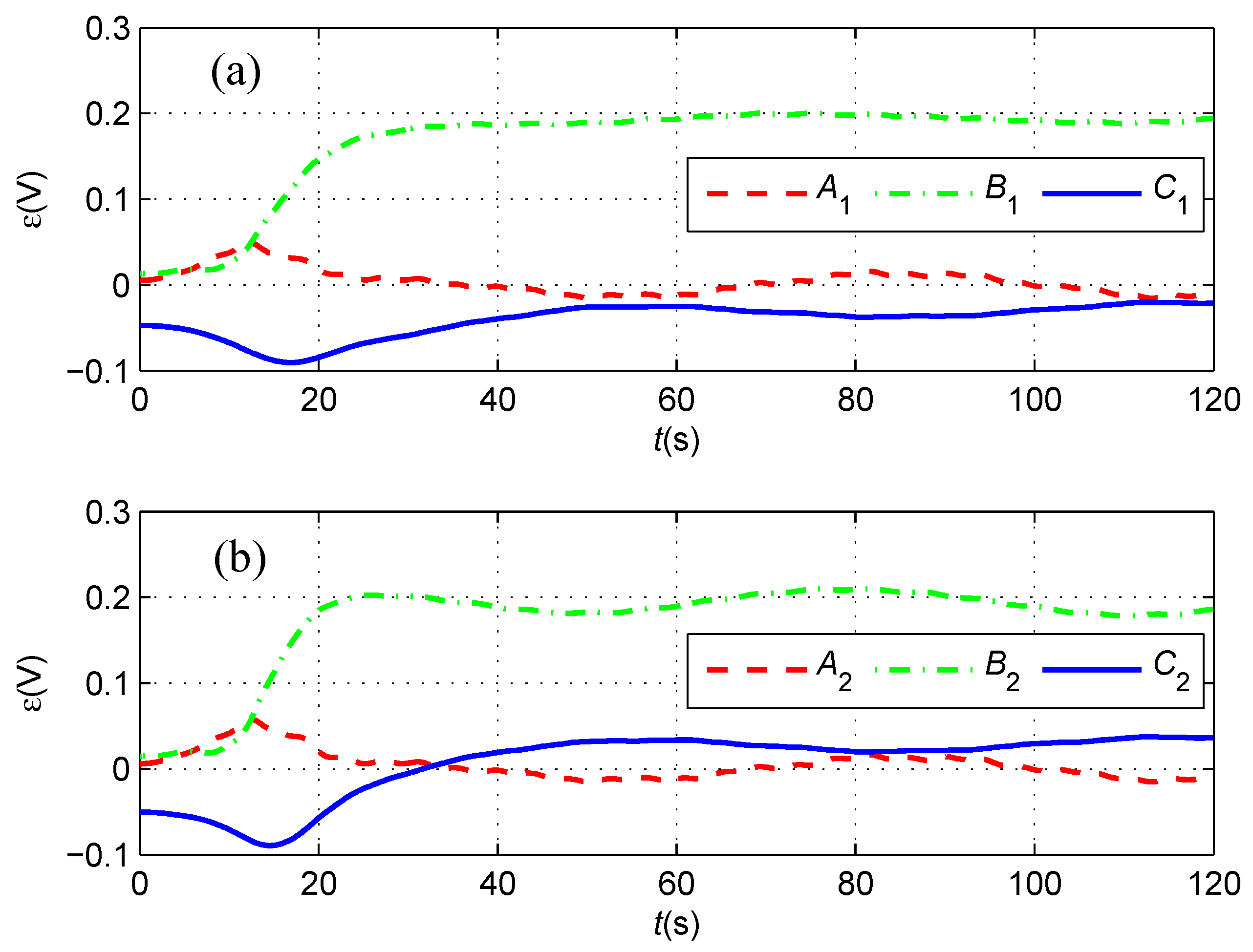
4.1. Magnetic Field Simulation
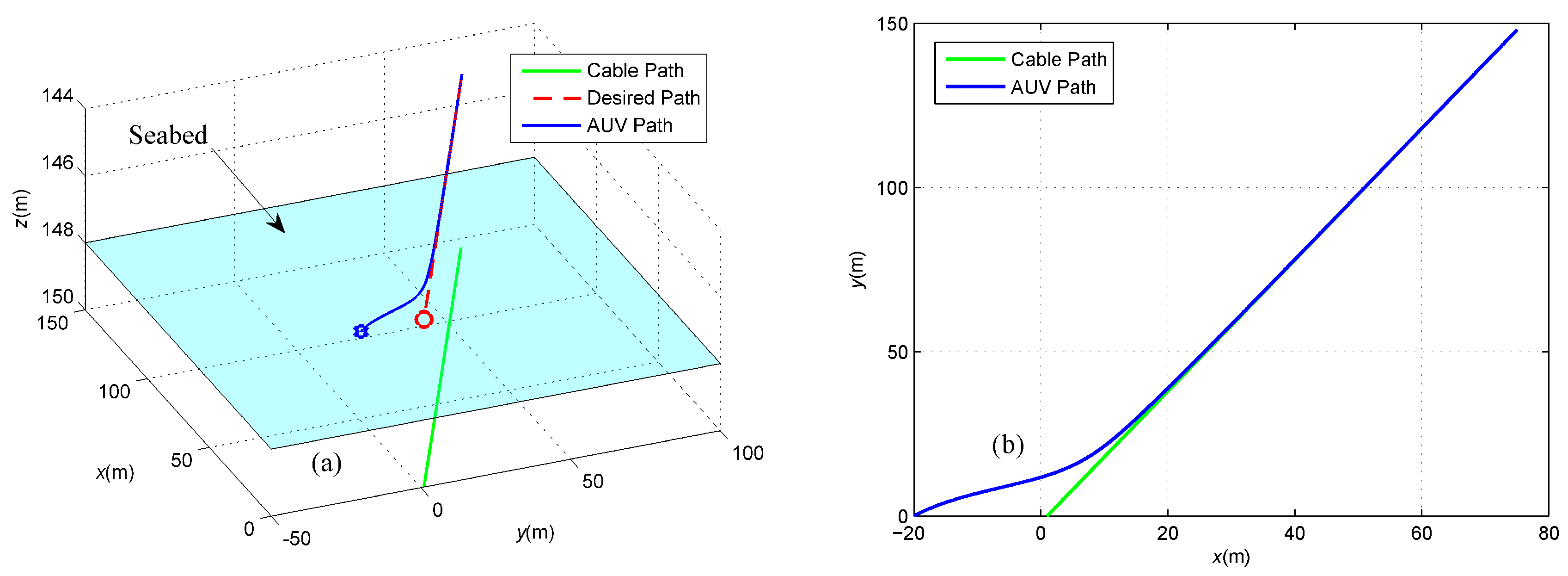
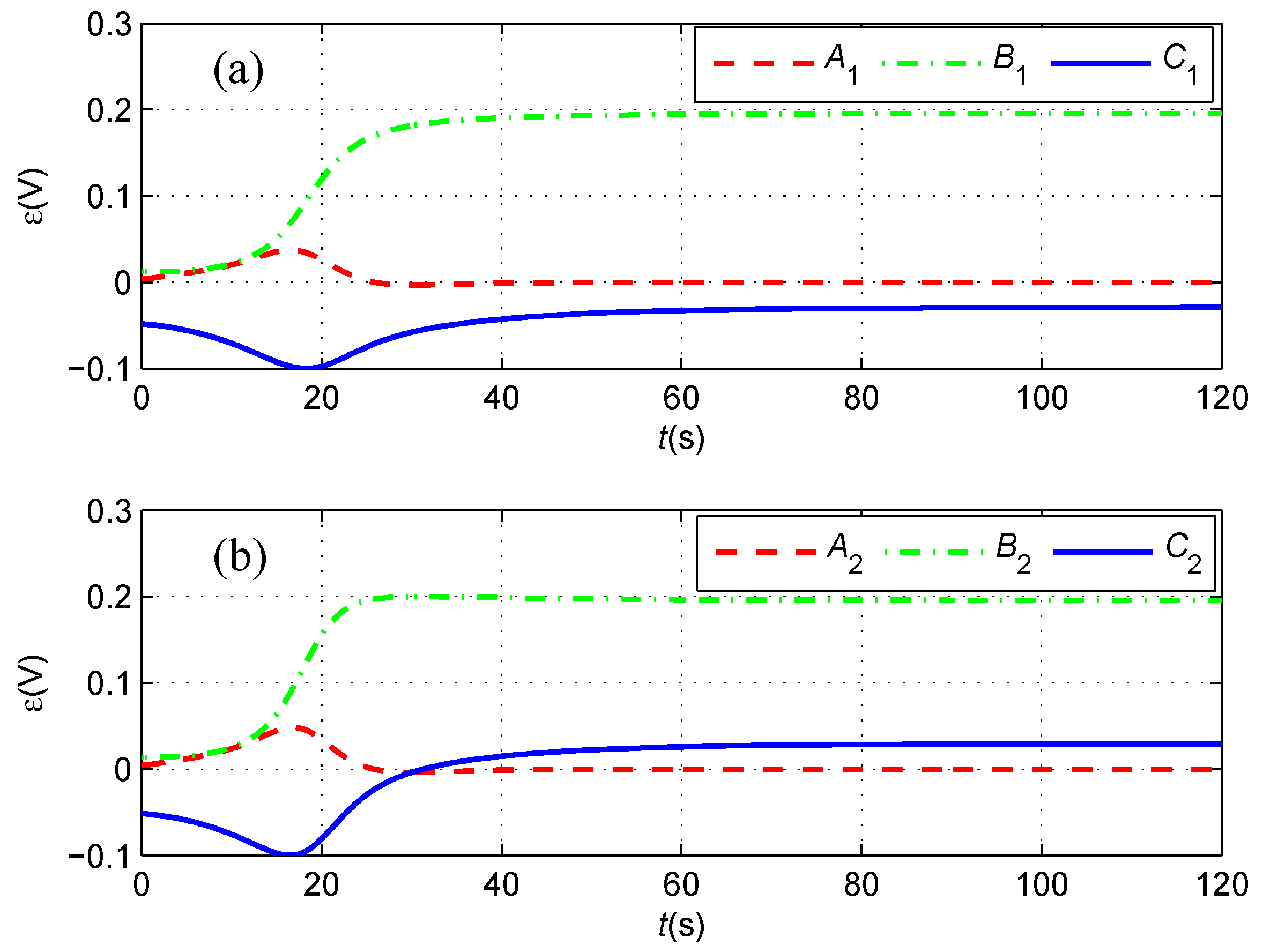
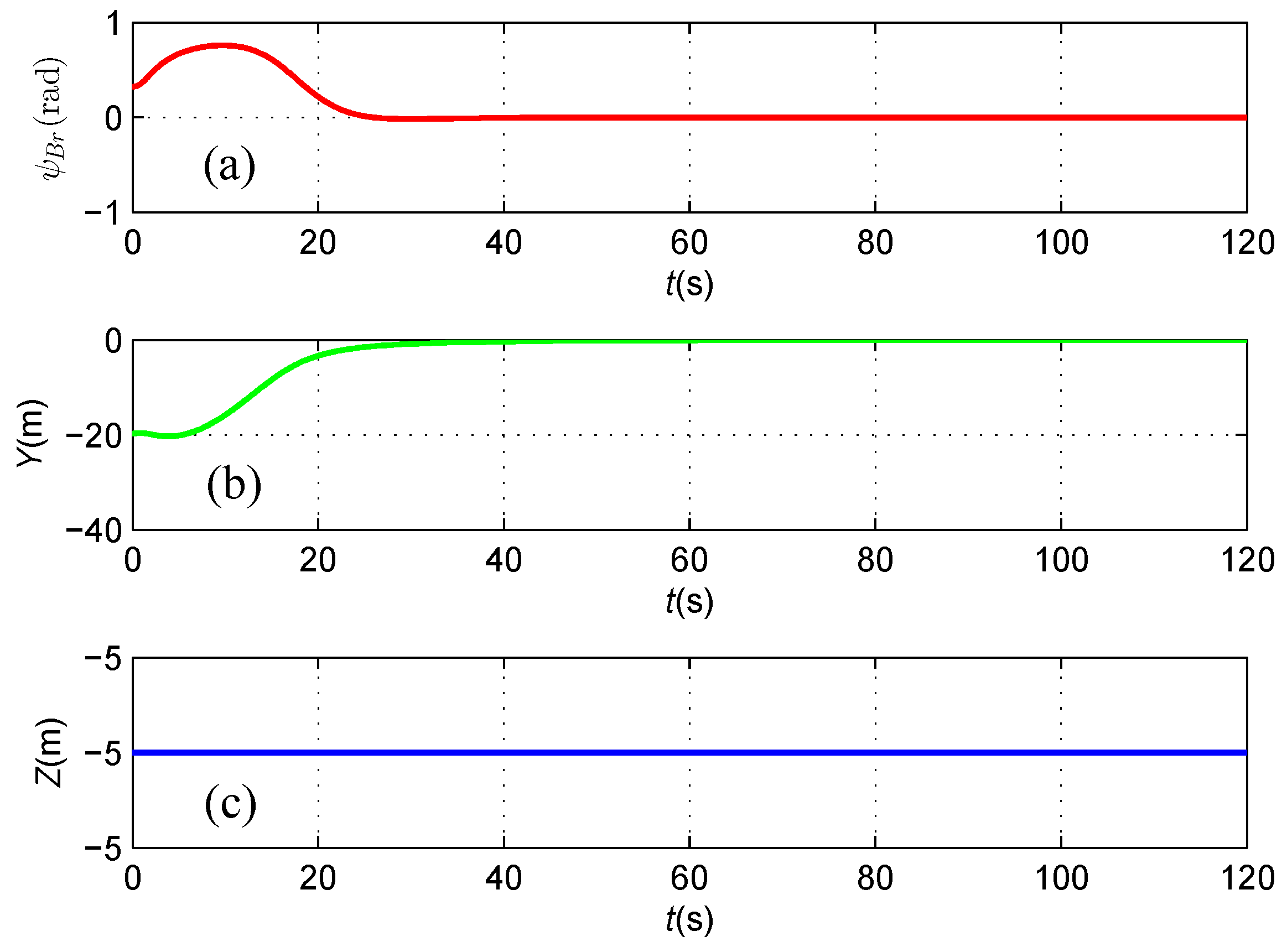
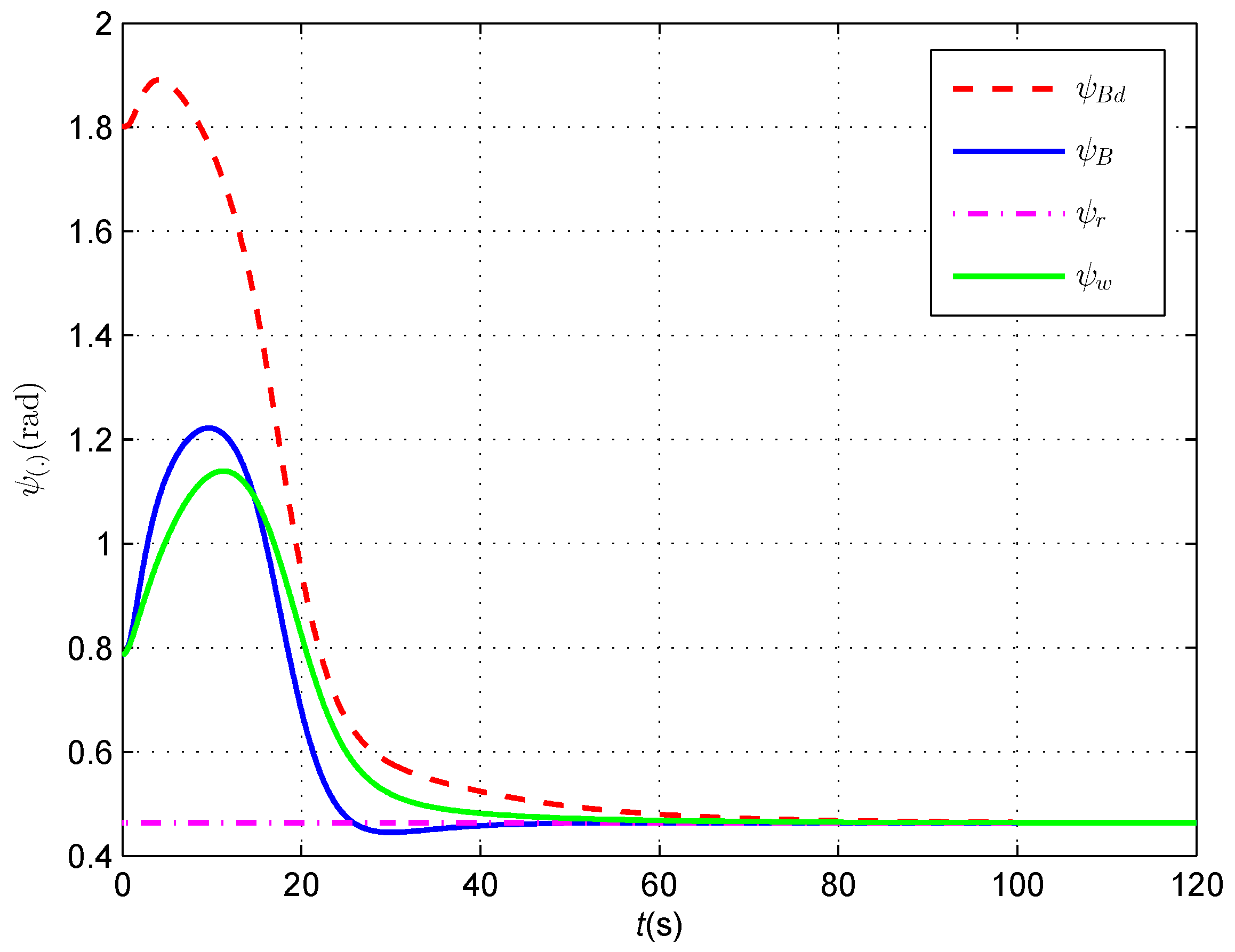
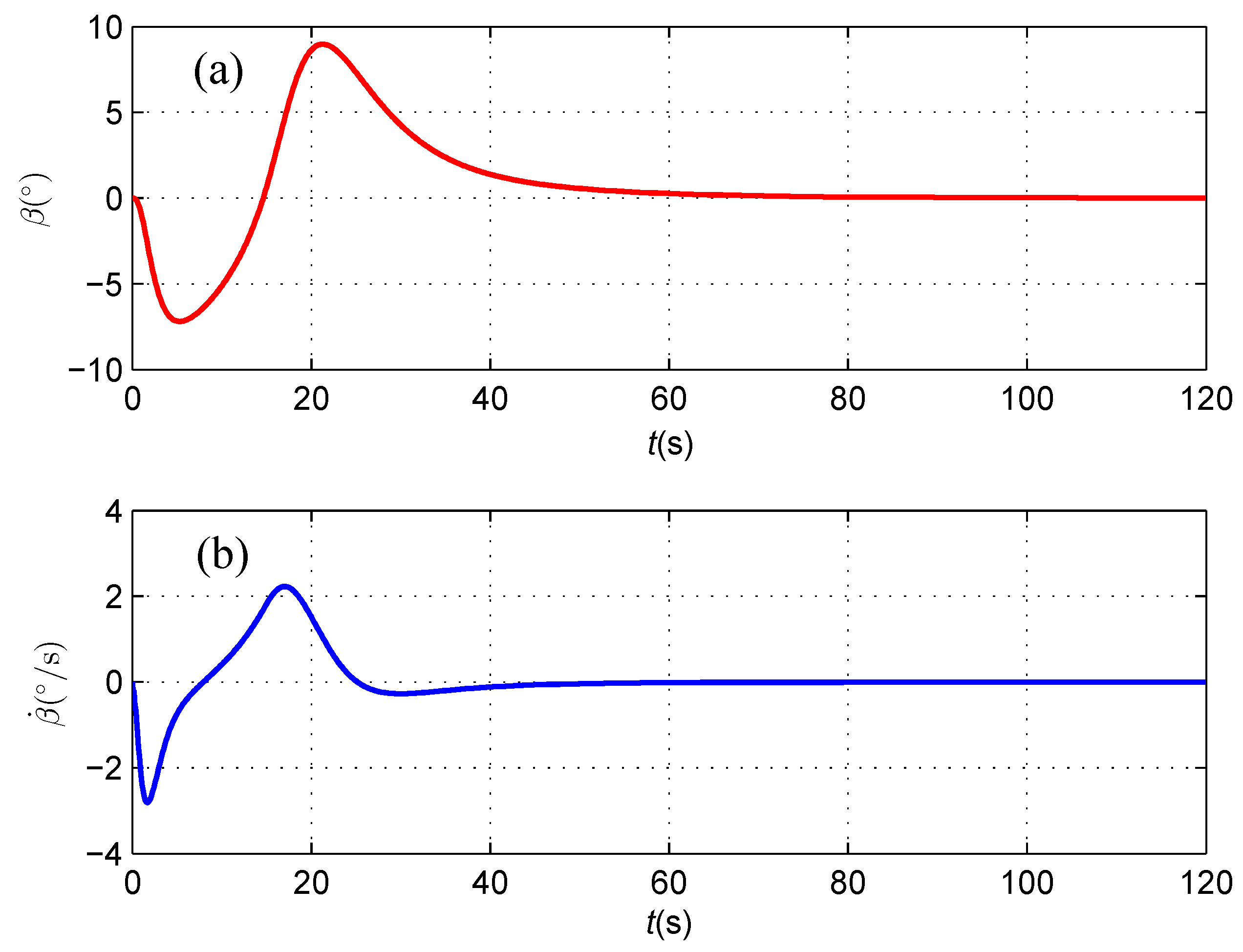
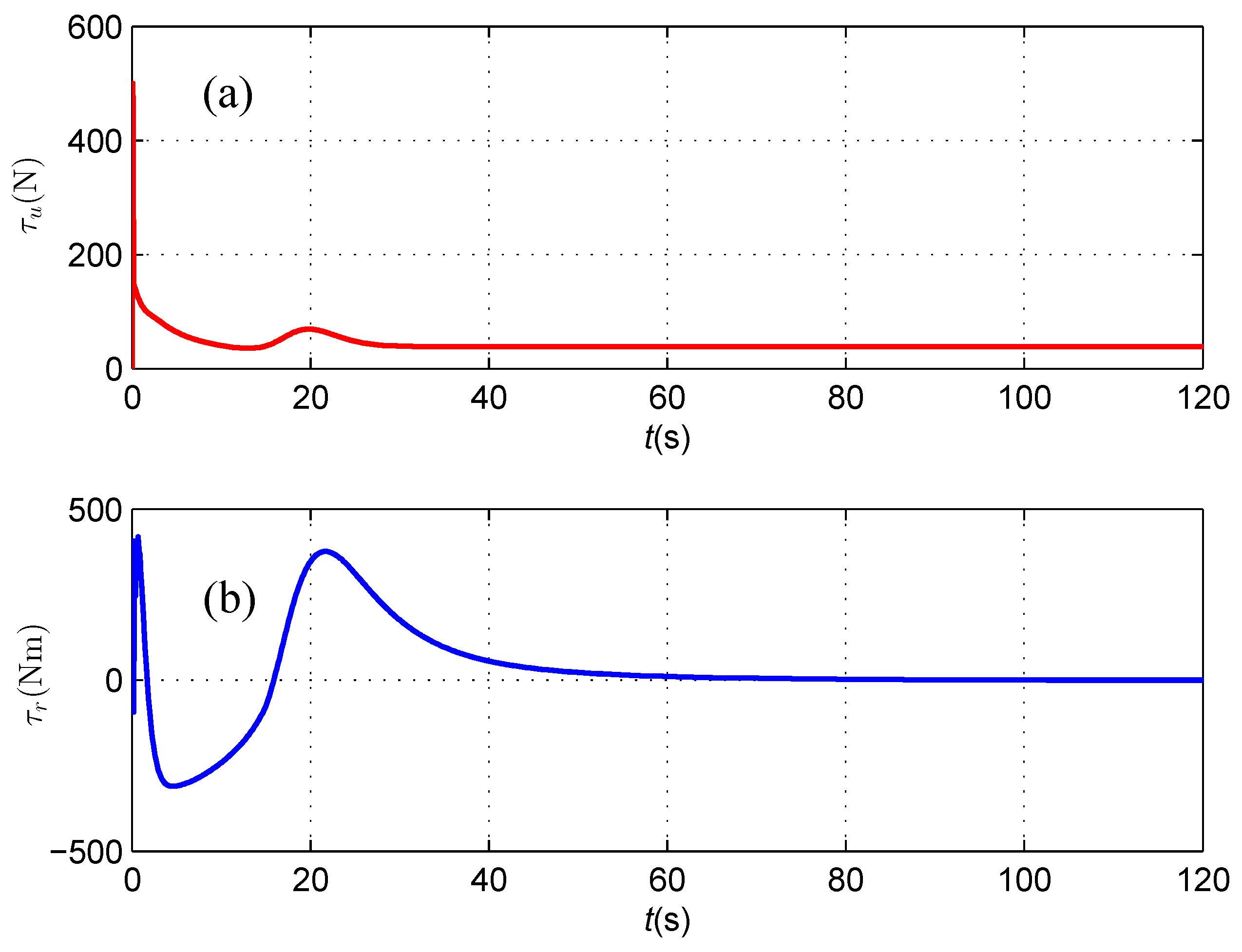
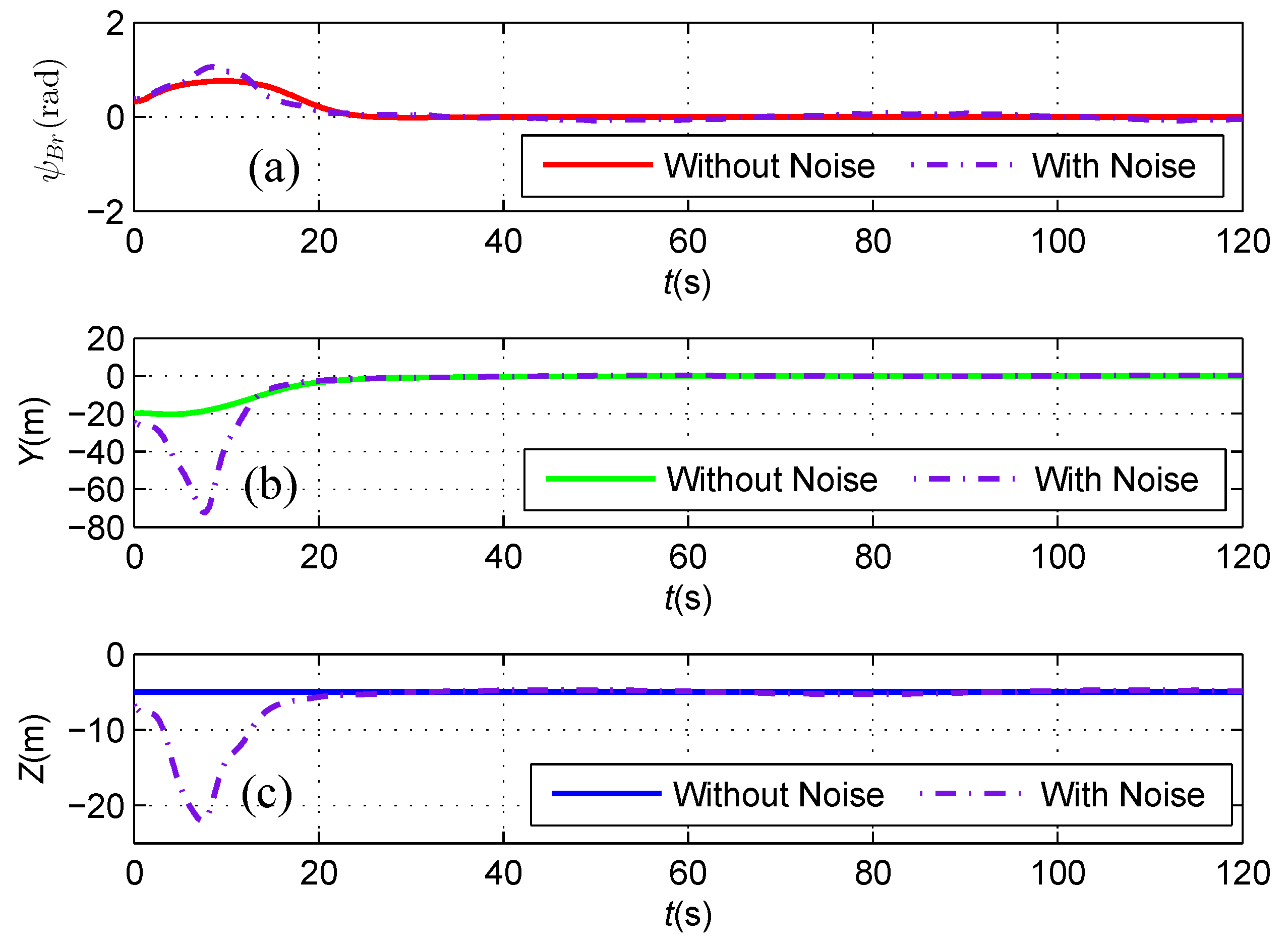
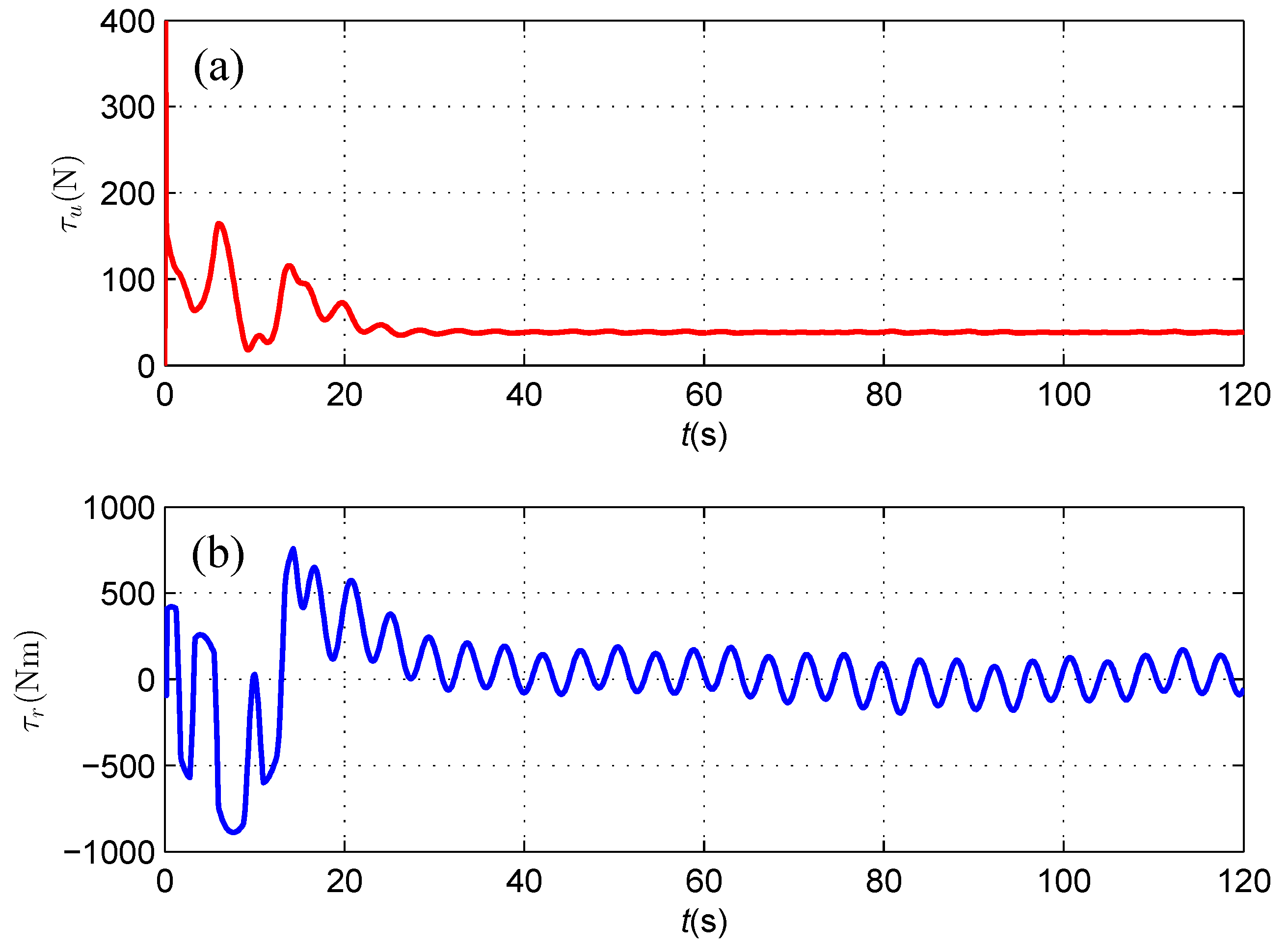
4.2. Cable Tracking Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ROV | Remotely-operated vehicle |
| 3-DOF | Three-degrees-of-freedom |
| AUV | Autonomous underwater vehicle |
| AC | Alternating current |
| AE | AQUA EXPLORER |
| LOS | Line-of-sight |
| ILOS | Integral line-of-sight |
| USV | Unmanned surface vessel |
References
- Ortiz, A.; Antich, J.; Oliver, G. A particle filter-based approach for tracking undersea narrow telecommunication cables. Mach. Vis. Appl. 2011, 22, 283–302. [Google Scholar] [CrossRef]
- Asakawa, K.; Kojima, J.; Kato, Y.; Matsumoto, S.; Kato, N.; Asai, T.; Iso, T. Design concept and experimental results of the autonomous underwater vehicle AQUA EXPLORER 2 for the inspection of underwater cables. Adv. Robot. 2002, 16, 27–42. [Google Scholar] [CrossRef]
- Sun, X.; Poon, C.K.; Chan, G.; Sum, C.L.; Lee, W.K.; Jiang, L.; Pong, P.W.T. Operation-state monitoring and energization-status identification for underground power cables by magnetic field sensing. IEEE Sens. J. 2013, 13, 4527–4533. [Google Scholar] [CrossRef]
- Szyrowski, T.; Sharma, S.K.; Sutton, R.; Kennedy, G.A. Subsea cable tracking in an uncertain environment using particle filters. J. Mar. Eng. Technol. 2015, 14, 1–13. [Google Scholar] [CrossRef]
- Maldonado-Lopez, R.; Christen, R. Position-controlled data acquisition embedded system for magnetic NDE of bridge stay cables. Sensors 2011, 11, 162–179. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Duan, Y.; Or, S.W.; Zhao, Y. Smart elasto-magneto-electric (EME) sensors for stress monitoring of steel cables: design theory and experimental validation. Sensors 2014, 14, 13644–13660. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Wu, X.; Jiang, X.; Jian, L. Enhancement of the excitation efficiency of the non-contact magnetostrictive sensor for pipe inspection by adjusting the alternating magnetic field axial length. Sensors 2014, 14, 1544–1563. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.Y.; Liu, D.J.; Pan, Q.; Zhang, Y.Y. Forward modeling of total magnetic anomaly over a pseudo-2D underground ferromagnetic pipeline. J. Appl. Geophys. 2015, 113, 14–30. [Google Scholar] [CrossRef]
- Szyrowski, T.; Sharma, S.K.; Sutton, R.; Kennedy, G.A. Developments in subsea power and telecommunication cables detection: Part 2—Electromagnetic detection. Underw. Technol. 2013, 31, 133–143. [Google Scholar] [CrossRef]
- Ortiz, A.; Simo, M.; Oliver, G. Image sequence analysis for real-time underwater cable tracking. In Proceedings of the Fifth IEEE Workshop on Applications of Computer Vision, Palm Springs, CA, USA, 4–6 December 2000; pp. 230–236.
- Budiyono, A. Advances in unmanned underwater vehicles technologies: Modeling, control and guidance perspectives. Indian J. Geo-Mar. Sci. 2009, 38, 282–295. [Google Scholar]
- Xiang, X.; Jouvencel, B.; Parodi, O. Coordinated formation control of multiple autonomous underwater vehicles for pipeline inspection. Int. J. Adv. Robot. Syst. 2010, 7, 75–84. [Google Scholar] [CrossRef]
- Wynn, R.B.; Huvenne, V.A.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous underwater vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Sato, Y.; Maki, T.; Kume, A.; Matsuda, T.; Sakamaki, T.; Ura, T. Path replanning method for an AUV in natural hydrothermal vent fields: Toward 3D imaging of a hydrothermal chimney. Mar. Technol. Soc. J. 2014, 48, 104–114. [Google Scholar] [CrossRef]
- Xiang, X.; Niu, Z.; Lapierre, L.; Zuo, M. Hybrid underwater robotic vehicles: The state-of-the-art and future trends. HKIE Trans. 2015, 22, 103–116. [Google Scholar] [CrossRef]
- Zhang, F.; Marani, G.; Smith, R.N.; Choi, H.T. Future trends in marine robotics [TC Spotlight]. IEEE Robot. Autom. Mag. 2015, 22, 14–122. [Google Scholar] [CrossRef]
- Schofield, O.; Jones, C.; Kohut, J.; Kremer, U.; Miles, T.; Saba, G.; Webb, D.; Glenn, S. Developing coordinated communities of autonomous gliders for sampling coastal ecosystems. Mar. Technol. Soc. J. 2015, 49, 9–16. [Google Scholar] [CrossRef]
- Bibuli, M.; Pascoal, A.; Ridao, P.; Zereik, E. Introduction to the special section on navigation, control, and sensing in the marine environment. Annu. Rev. Control 2015, 40, 127–128. [Google Scholar] [CrossRef]
- Campos, R.; Gracias, N.; Ridao, P. Underwater multi-vehicle trajectory alignment and mapping using acoustic and optical constraints. Sensors 2016, 16, 387. [Google Scholar] [CrossRef] [PubMed]
- Ito, Y.; Kato, N.; Kojima, J.; Takagi, S.; Asakawa, K.; Shirasaki, Y. Cable tracking for autonomous underwater vehicle. In Proceedings of the 1994 Symposium on Autonomous Underwater Vehicle Technology (AUV ’94), Cambridge, MA, USA, 19–20 July 1994; pp. 218–224.
- Kojima, J.; Kato, Y.; Asakawa, K.; Kato, N. Experimental results of autonomous underwater vehicle ‘AQUA EXPLORER 2’ for inspection of underwater cables. In Proceedings of the OCEANS ’98 Conference, Nice, France, 28 September–1 October 1998; pp. 113–117.
- Choi, J.; Shiraishi, T.; Tanaka, T.; Sakai, H. A practical and useful autonomous towed vehicle for port area inspection. Adv. Robot. 2012, 21, 351–370. [Google Scholar] [CrossRef]
- Breivik, M.; Fossen, T. Principles of guidance-based path following in 2D and 3D. In Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC’05), Seville, Spain, 12–15 December 2005; pp. 627–634.
- Jantapremjit, P.; Wilson, P.A. Optimal control and guidance for homing and docking tasks using an autonomous underwater vehicle. In Proceedings of the International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 243–248.
- Malisoff, M.; Zhang, F. Robustness of adaptive control under time delays for three-dimensional curve tracking. SIAM J. Control Optim. 2015, 53, 2203–2236. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Zhang, Q.; Xu, G. Path-following control of an AUV: Fully actuated versus under-actuated configuration. Mar. Technol. Soc. J. 2016, 50, 34–47. [Google Scholar] [CrossRef]
- Peymani, E.; Fossen, T.I. Path following of underwater robots using Lagrange multipliers. Robot. Auton. Syst. 2015, 67, 44–52. [Google Scholar] [CrossRef]
- Encarnacao, P.; Pascoal, A. 3D path following for autonomous underwater vehicle. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; Volume 3, pp. 2977–2982.
- Lapierre, L.; Soetanto, D.; Pascoal, A. Nonlinear path following with applications to the control of autonomous underwater vehicles. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; Volume 2, pp. 1256–1261.
- Lapierre, L.; Soetanto, D. Nonlinear path-following control of an AUV. Ocean Eng. 2007, 34, 1734–1744. [Google Scholar] [CrossRef]
- Lapierre, L.; Jouvencel, B. Robust nonlinear path-following control of an AUV. IEEE J. Ocean. Eng. 2008, 33, 89–102. [Google Scholar] [CrossRef]
- Ghommam, J.; Saad, M. Backstepping-based cooperative and adaptive tracking control design for a group of underactuated AUVs in horizontal plan. Int. J. Control 2014, 87, 1076–1093. [Google Scholar] [CrossRef]
- Xiang, X.; Lapierre, L.; Jouvencel, B. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration. Robot. Auton. Syst. 2015, 67, 14–22. [Google Scholar] [CrossRef]
- Zhu, D.; Zhao, Y.; Yan, M. A bio-inspired neurodynamics-based backstepping path-following control of an AUV with ocean current. Int. J. Robot. Autom. 2012, 27, 298–307. [Google Scholar] [CrossRef]
- Zheng, Z.; Yan, K.; Yu, S.; Zhu, B.; Zhu, M. Path following control for a stratospheric airship with actuator saturation. Trans. Inst. Meas. Control 2016. [Google Scholar] [CrossRef]
- Guo, J.; Chiu, F.C.; Huang, C.C. Design of a sliding mode fuzzy controller for the guidance and control of an autonomous underwater vehicle. Ocean Eng. 2003, 30, 2137–2155. [Google Scholar] [CrossRef]
- Zhang, L.J.; Qi, X.; Pang, Y.J. Adaptive output feedback control based on DRFNN for AUV. Ocean Eng. 2009, 36, 716–722. [Google Scholar] [CrossRef]
- Ishii, K.; Ura, T. An adaptive neural-net controller system for an underwater vehicle. Control Eng. Pract. 2000, 8, 177–184. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Wilson, P.A.; Liu, X. Adaptive neural network-based backstepping fault tolerant control for underwater vehicles with thruster fault. Ocean Eng. 2015, 110, 15–24. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Shi, Y.; Wang, H.; Wang, W. Containment control of networked autonomous underwater vehicles with model uncertainty and ocean disturbances guided by multiple leaders. Inf. Sci. 2015, 316, 163–179. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Yang, S.X. Real-time hybrid design of tracking control and obstacle avoidance for underactuated underwater vehicles. J. Intell. Fuzzy Syst. 2016, 30, 2541–2553. [Google Scholar] [CrossRef]
- Chu, Z.; Zhu, D.; Yang, S.X. Observer-based adaptive neural network trajectory tracking control for remotely operated vehicle. IEEE Trans. Neural Netw. Learn. Syst. 2016. [Google Scholar] [CrossRef] [PubMed]
- Lekkas, A.M.; Fossen, T.I. Integral LOS path following for curved paths based on a monotone cubic Hermite spline parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Fossen, T.I.; Lekkas, A.M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents. Int. J. Adapt. Control Signal Process. 2015. [Google Scholar] [CrossRef]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Gravdahl, J.T.; Sorensen, A.J.; Milovanovic, M.; Bruzzone, G. Integral line-of-sight guidance and control of underactuated marine vehicles: Theory, simulations, and experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef]
- Ghommam, J.; Mnif, F. Coordinated path-following control for a group of underactuated surface vessels. IEEE Trans. Ind. Electron. 2009, 56, 3951–3963. [Google Scholar] [CrossRef]
- Bibuli, M.; Bruzzone, G.; Caccia, M.; Lapierre, L. Path-following algorithms and experiments for an unmanned surface vehicle. J. Field Robot. 2009, 26, 669–688. [Google Scholar] [CrossRef]
- Almeida, J.; Silvestre, C.; Pascoal, A. Cooperative control of multiple surface vessels in the presence of ocean currents and parametric model uncertainty. Int. J. Robust Nonlinear Control 2010, 20, 1549–1565. [Google Scholar] [CrossRef]
- Oh, S.R.; Sun, J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control. Ocean Eng. 2010, 37, 289–295. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J.; Sun, J.C.; Liu, Y.C. Adaptive robust online constructive fuzzy control of a complex surface vehicle system. IEEE Trans. Cybern. 2015, 46, 1511–1523. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, D.; Peng, Z. Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances. Neurocomputing 2015, 173, 799–808. [Google Scholar] [CrossRef]
- Do, K.D. Global path-following control of stochastic underactuated ships: A level curve approach. J. Dyn. Syst. Meas. Control 2015, 137. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J. Self-constructing adaptive robust fuzzy neural tracking control of surface vehicles with uncertainties and unknown disturbances. IEEE Trans. Control Syst. Technol. 2015, 23, 991–1002. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Tian, Y.P. Formation tracking and attitude synchronization control of underactuated ships along closed orbits. Int. J. Robust Nonlinear Control 2015, 25, 3023–3044. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Zhou, Y. Research on modeling and experimentation on detecting buried depth of optical fiber submarine cables based on active detection technique. In Proceedings of the 9th International Conference on Electronic Measurement & Instruments (ICEMI ’09), Beijing, China, 16–19 August 2009; pp. 1–94.
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles: Design for Underactuated and Nonlinear Marine Systems; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley: Trondheim, Norway, 2011. [Google Scholar]
- Pettersen, K.Y.; Lefeber, E. Way-point tracking control of ships. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 940–945.




| Parameter | Value | Unit |
|---|---|---|
| L | 1.5 | m |
| 1116 | kg | |
| 2133 | kg | |
| 4061 | kg·m2 | |
| 25.5 | kg·s−1 | |
| 138 | kg·s−1 | |
| 490 | kg·m2·s−1 | |
| 0 | kg·m−1 | |
| 0 | kg·m−2·s | |
| 920.1 | kg·m−1 | |
| 750 | kg·m−2·s | |
| 0 | kg·m2 | |
| 0 | kg·m2·s |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, X.; Yu, C.; Niu, Z.; Zhang, Q. Subsea Cable Tracking by Autonomous Underwater Vehicle with Magnetic Sensing Guidance. Sensors 2016, 16, 1335. https://doi.org/10.3390/s16081335
Xiang X, Yu C, Niu Z, Zhang Q. Subsea Cable Tracking by Autonomous Underwater Vehicle with Magnetic Sensing Guidance. Sensors. 2016; 16(8):1335. https://doi.org/10.3390/s16081335
Chicago/Turabian StyleXiang, Xianbo, Caoyang Yu, Zemin Niu, and Qin Zhang. 2016. "Subsea Cable Tracking by Autonomous Underwater Vehicle with Magnetic Sensing Guidance" Sensors 16, no. 8: 1335. https://doi.org/10.3390/s16081335
APA StyleXiang, X., Yu, C., Niu, Z., & Zhang, Q. (2016). Subsea Cable Tracking by Autonomous Underwater Vehicle with Magnetic Sensing Guidance. Sensors, 16(8), 1335. https://doi.org/10.3390/s16081335







