A Matrix-Based Proactive Data Relay Algorithm for Large Distributed Sensor Networks
Abstract
:1. Introduction
2. Related Work
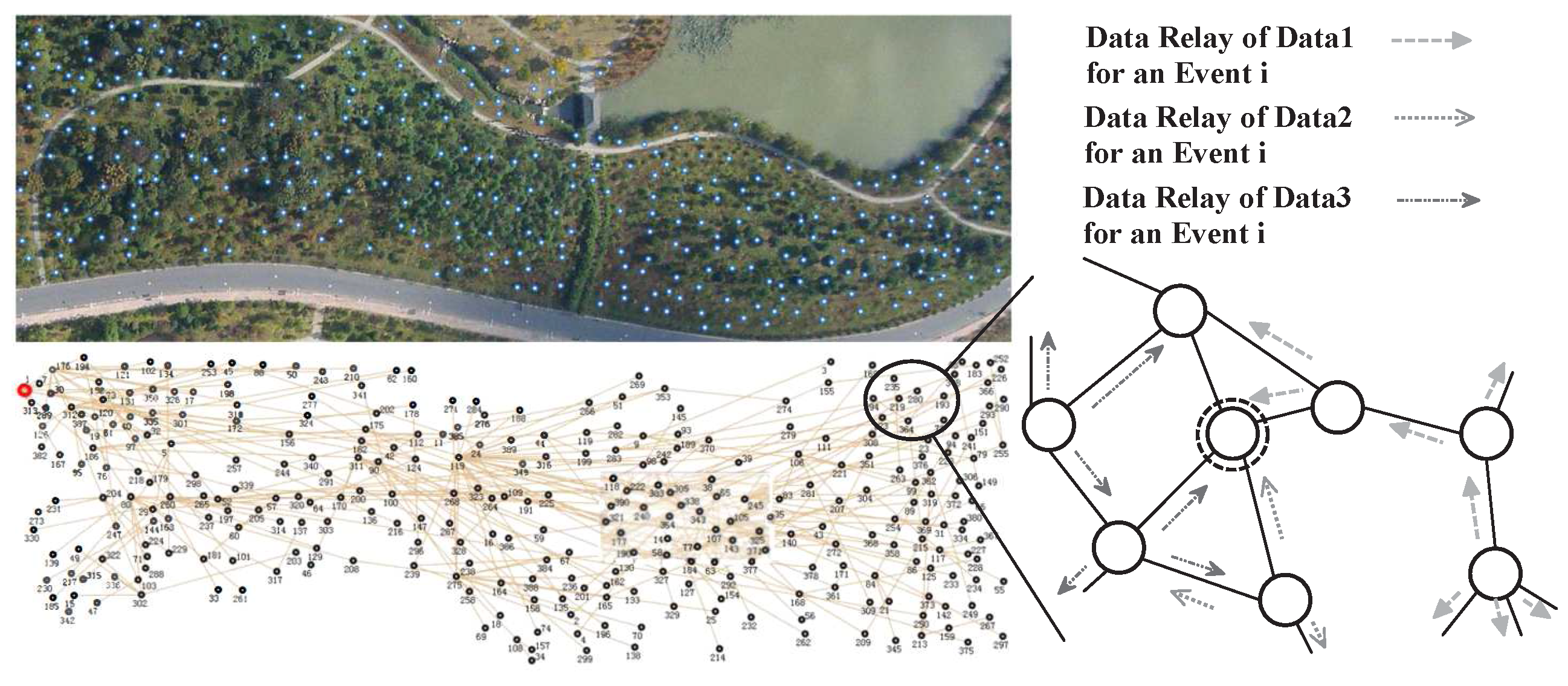
3. Problem Description
- is the ID of the sensor that senses this data.
- is the confidence hypotheses about the target identities , which can be expressed as An example is shown in Table 1.
- is the geographical location of the target when detected.
- is the system time when the target is detected.
- records sensors that pass this data.
| Algorithm 1 Distributed data relay process. |
| 1: while true do |
| 2: data received or sensed by |
| 3: for all data received or sensed by do |
| 4: Try to fuse it with relevant data in ; |
| 5: if the quality of the fused data meets the threshold then |
| 6: Fuse them into a piece of information; |
| 7: Inform other nodes data is outdated; |
| 8: else |
| 9: ; |
| 10: Make communication decisions for each data in ; |
3.1. Information Quality
3.2. Energy Consumption on Communication
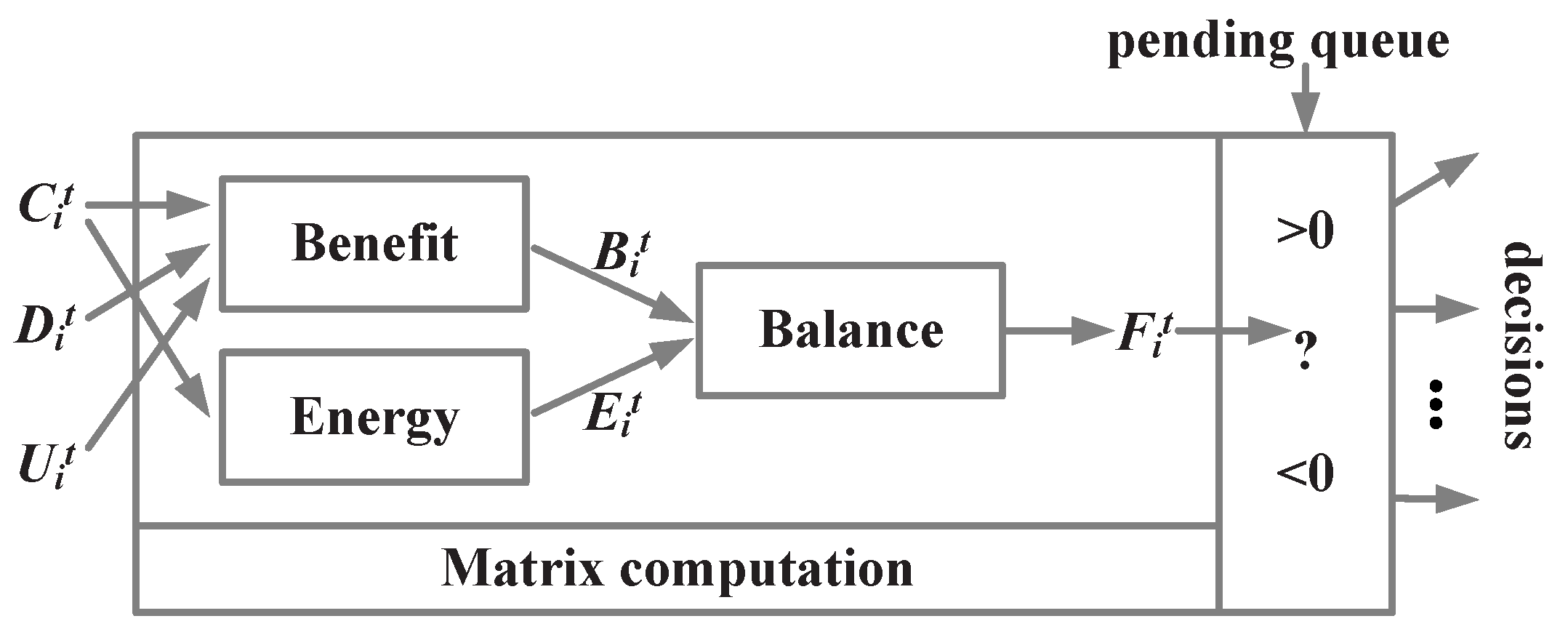
4. Matrix-Based Data Relay Algorithm
4.1. Basic Matrix Model
4.2. Benefit of Broadcasting
4.3. Energy Cost of Transmission
4.4. The Balance
- the data that has higher confidence (that can make a higher contribution to fuse into an information) has a higher priority to be broadcast, which can avoid the energy consumption on unnecessary data retransmission.
- the data that is more relative to data of neighbors has a high probability to be broadcast. This guarantees that the related data are only transmitted in a small part of the whole network and aggregated toward some node rather than blind coverage.
5. Model Maintenance Algorithm
5.1. Initialization
5.2. The Rules to Maintain The Dimensions
- will add an element in set : when receiving a data and is not in .
- will be removed from : when neither has positive connection probability with it nor has any knowledge of it, =0 and =0.
- will add an element into :
- −
- when receiving data that is not in .
- −
- when generating data based on its detection.
- will delete the element from : when , where stores data that has been fused or outdated.
5.3. Updating the Connection Matrix C
5.4. Updating the Data Distribution Matrix D
| Algorithm 2 |
| 1: for all do |
| 2: |
| 3: for all do |
| 4: ; |
| 5: for all do |
| 6: ; |
| 7: for all do |
| 8: ; |
| 9: ; |
5.5. Updating The Utility Matrix U
| Algorithm 3 |
| 1: for all do |
| 2: for all do |
| 3: if then |
| 4: |
| 5: else |
| 6: |
- For target A, , . After checking , can get . Doing the same for target B, can get
- The utility is a function of these two values. One possible way:
5.6. Integrated Algorithm
| Algorithm 4 Data relay process for a sensor . |
| 1: while do |
| 2: ; |
| 3: ; |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: for all do |
| 9: if then |
| 10: ; |
| 11: if then |
| 12: fuse into information ; |
| 13: ; |
| 14: else |
| 15: ; |
| 16: ; |
| 17: for all do |
| 18: if then |
| 19: ; |
| 20: ; |
| 21: |
6. Experimental Section
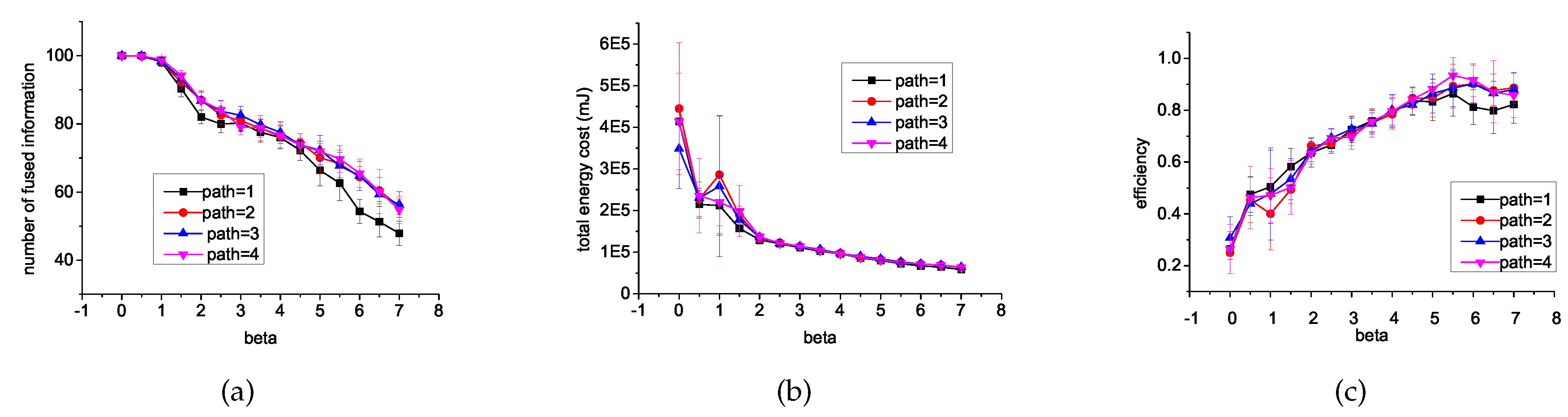
6.1. Different β and Different Length of Path
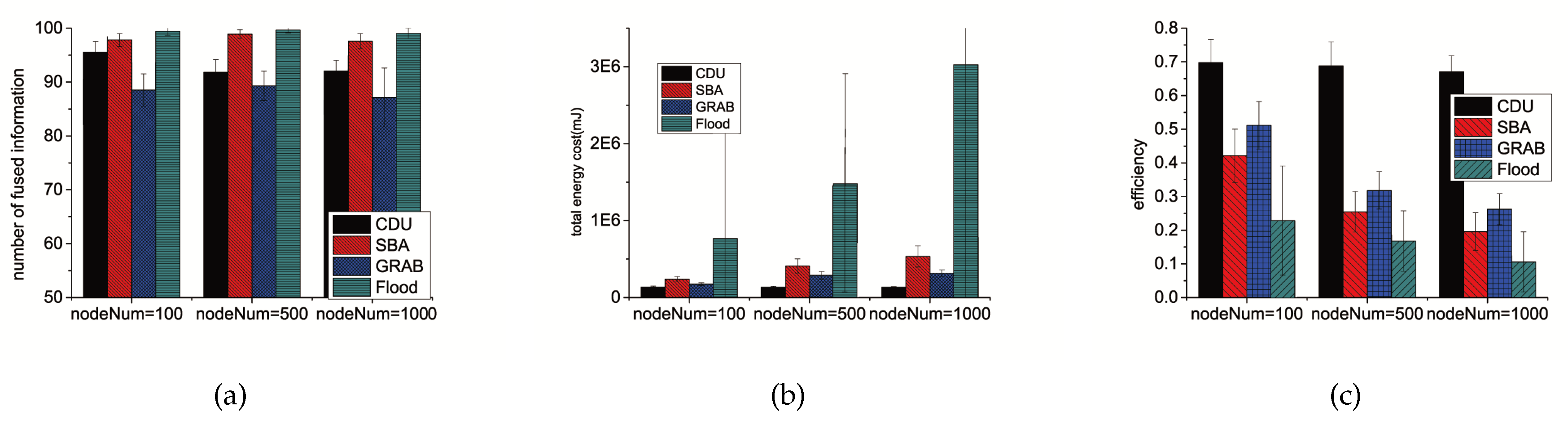
6.2. Different Algorithms
6.3. Impact of Environmental Settings
6.3.1. Network Size
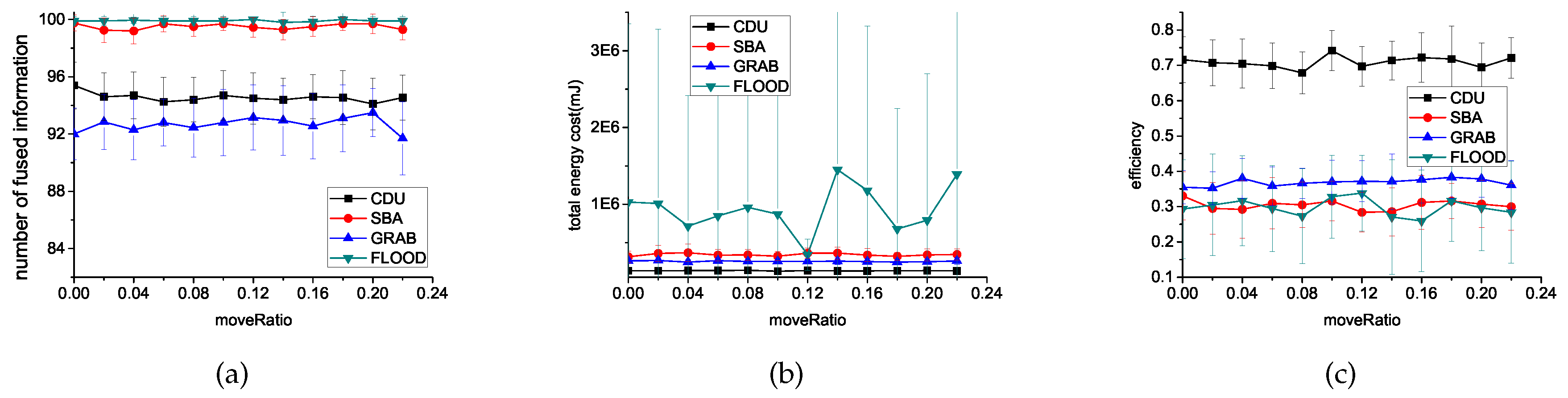
6.3.2. The Ratio of Moved Sensors
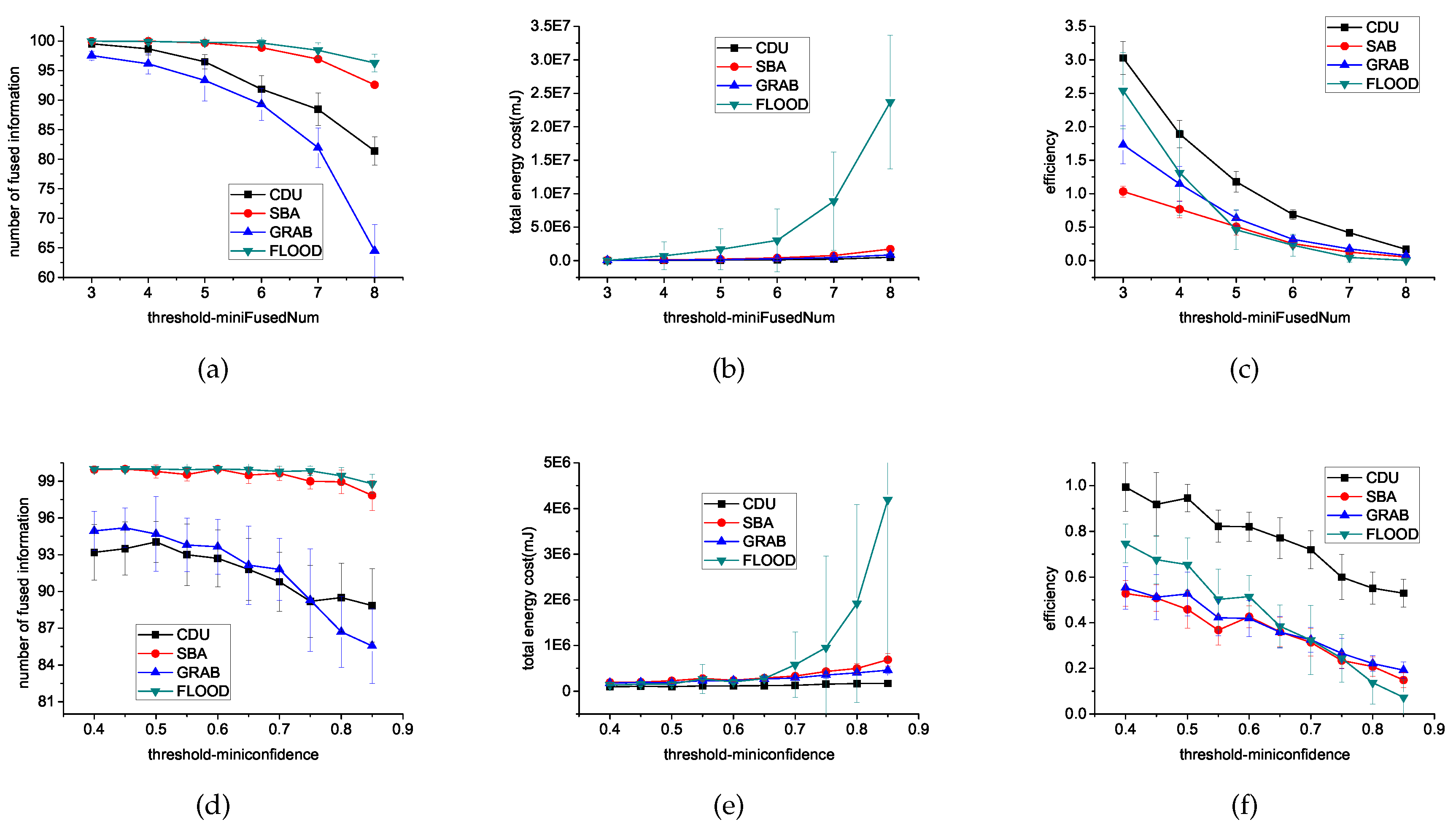
6.3.3. Threshold
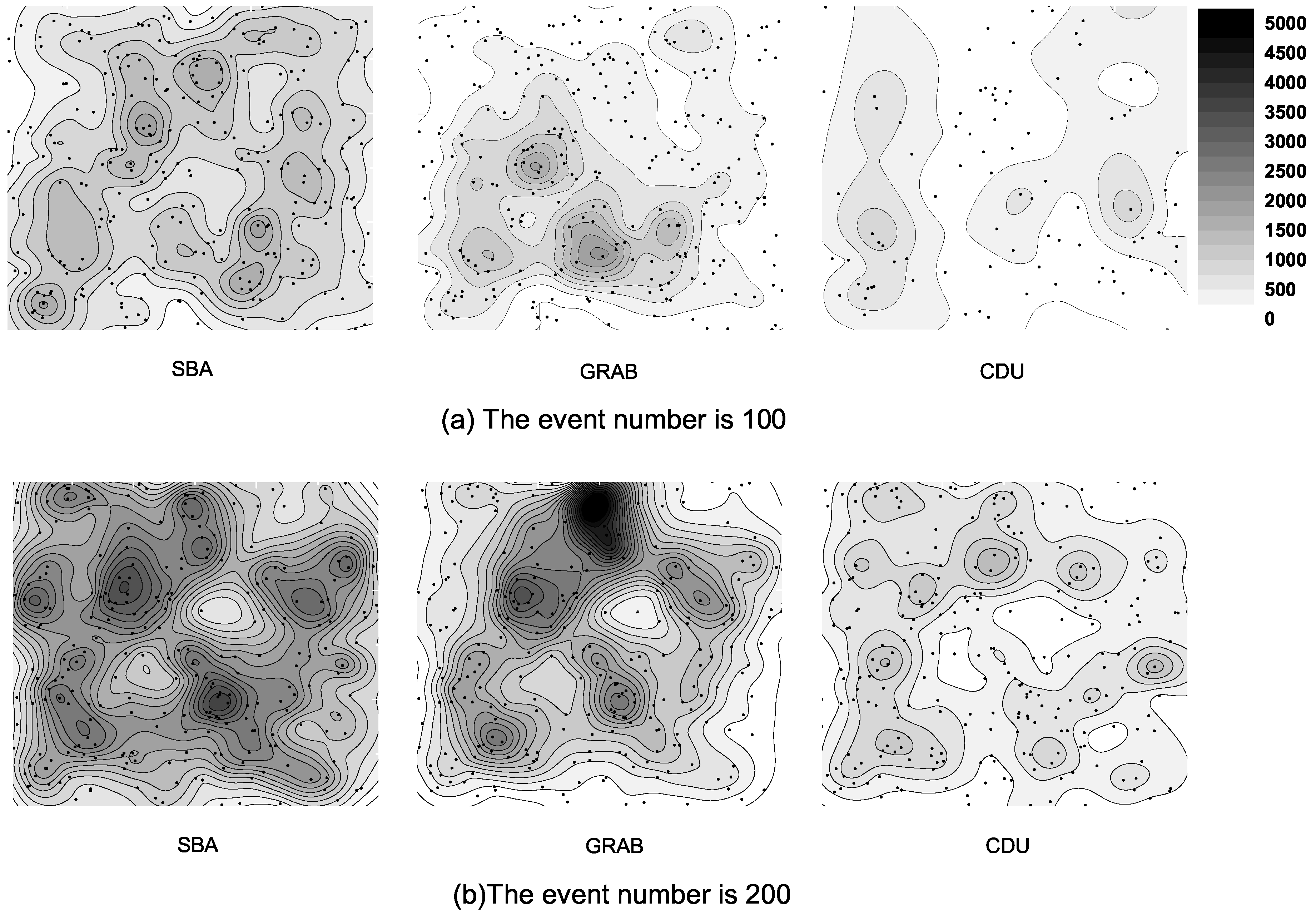
6.4. Energy Distribution
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tifenn, R.; Bouabdallah, A.; Challal, Y. Energy efficiency in wireless sensor networks: A top-down survey. Comput. Netw. 2014, 67, 104–122. [Google Scholar]
- Maurizio, B.; Ossi, K.; Neal, P.; Suresh, V. Multiple target tracking with RF sensor networks. IEEE Trans. Mobile Comput. 2014, 13, 1787–1800. [Google Scholar]
- George, S.M.; Zhou, W.; Chenji, H.; Won, M.; Lee, Y.O.; Pazarloglou, A.; Stoleru, R.; Barooah, P. DistressNet: A wireless ad hoc and sensor network architecture for situation management in disaster response. IEEE Commun. Mag. 2010, 48, 128–136. [Google Scholar] [CrossRef]
- Vicaire, P.; He, T.; Cao, Q.; Yan, T.; Zhou, G.; Gu, L.; Luo, L.; Stoleru, R.; Stankovic, J.A.; Abdelzaher, T.F. Achieving long-term surveillance in vigilnet. ACM Trans. Sens. Netw. 2009, 5. [Google Scholar] [CrossRef]
- Alexei, M.; Hugh, D.W. Decentralized data fusion and control in active sensor networks. In Proceedings of the Seventh International Conference on Information Fusion, Stockholm, Sweden, 28 June–1 July 2004; pp. 479–486.
- Ochoa, S.F.; Santos, R. Human-centric wireless sensor networks to improve information availability during urban search and rescue activities. Inf. Fus. 2015, 22, 71–84. [Google Scholar] [CrossRef]
- Daniela, B.; Sytze, D.B.; Bregt, A.K. Value of information and mobility constraints for sampling with mobile sensors. Comput. Geosci. 2012, 49, 102–111. [Google Scholar]
- Borges, L.M.; Velez, F.J.; Lebres, A.S. Survey on the characterization and classification of wireless sensor network applications. IEEE Commun. Surv. Tutor. 2014, 16, 1860–1890. [Google Scholar]
- Intanagonwiwat, C.; Govindan, R.; Estrin, D. Directed diffusion: A scalable and robust communication paradigm for sensor networks. In Proceedings of the 6th annual international conference on Mobile computing and networking, Boston, MA, USA, 6–11 August 2000; pp. 56–67.
- David, B.; Deborah, E. Rumor routing algorthim for sensor networks. In Proceedings of the 1st ACM international workshop on Wireless sensor networks and applications, Atlanta, GA, USA, 28 September 2002; pp. 22–31.
- Chu, M.; Haussecker, H.; Zhao, F. Scalable information-driven sensor querying and routing for ad hoc heterogeneous sensor networks. Int. J. High Perform. Comput. Appl. 2002, 16, 293–313. [Google Scholar] [CrossRef]
- Liu, M.; Xu, Y.; Mohammed, A.W. Decentralized Opportunistic Spectrum Resources Access Model and Algorithm toward Cooperative Ad-Hoc Networks. Available online: http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0145526 (accessed on 3 August 2016).
- Heinzelman, W.R.; Kulik, J.; Balakrishnan, H. Adaptive protocols for information dissemination in wireless sensor networks. In Proceedings of the 5th Annual ACM/IEEE International Conference On Mobile Computing and Networking, Seattle, WA, USA, 15–19 August 1999; pp. 174–185.
- Peng, W.; Lu, X.C. On the reduction of broadcast redundancy in mobile ad hoc networks. In Proceedings of the 1st ACM international symposium on Mobile ad hoc networking & computing, Boston, MA, USA, 11 August 2000; pp. 129–130.
- John, S.; Ivan, M. An Efficient Distributed Network-Wide Broadcast Algorithm for Mobile Ad Hoc Networks. Avaiable online: http://www.ece.rutgers.edu/~marsic/Publications/infocom2001nwb.pdf (accessed on 3 August 2016).
- Hyojun, L.; Chongkwon, K. Multicast tree construction and flooding in wireless ad hoc networks. In Proceedings of the 3rd ACM International Workshop on Modeling, Analysis and Simulation of Wireless and Mobile Systems, Boston, MA, USA, 20 August 2000; pp. 61–68.
- Hyocheol, J.; Hyeonjun, J.; Younghwan, Y. Dynamic probabilistic flooding algorithm based-on neighbor information in wireless sensor networks. In Proceedings of the International Conference on Information Network 2012, Bali, India, 1–3 Feburary 2012; pp. 340–345.
- Williamson, S.A.; Gerding, E.H.; Jennings, N.R. Reward shaping for valuing communications during multi-agent coordination. In International Foundation for Autonomous Agents and Multiagent Systems, Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems, Budapest, Hungary, 10–15 May 2009; Volume 1, pp. 641–648.
- Raphen, B.; Alan, C.; Victor, L.; Shlomo, Z. Analyzing myopic approaches for multi-agent communication. Comput. Intell. 2009, 25, 31–50. [Google Scholar]
- Karthikeyan, N.; Palanisamy, V.; Duraiswamy, K. Performance comparison of broadcasting methods in mobile ad hoc network. Int. J. Future Gener. Commun. Netw. 2009, 2, 47–58. [Google Scholar]
- Akkaya, K.; Younis, M. A survey on routing protocols for wireless sensor networks. Ad Hoc Netw. 2005, 3, 325–349. [Google Scholar] [CrossRef]
- Chen, W.; Guha, R.K.; Kwon, T.J.; Lee, J.; Hsu, Y.Y. A survey and challenges in routing and data dissemination in vehicular ad hoc networks. Wirel. Commun. Mobile Comput. 2011, 11, 787–795. [Google Scholar] [CrossRef]
- Nishi, S.; Vandna, V. Energy efficient LEACH protocol for wireless sensor network. Int. J. Inf. Netw. Secur. 2013, 2, 333–338. [Google Scholar]
- Heinzelman, W.B. Application-Specific Protocol Architectures for Wireless Networks. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Eriksson, O. Error Control in Wireless Sensor Networks: A Process Control Perspective. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2011. [Google Scholar]
- Bin, Y.; Paul, S.; Katia, S.; Yang, X.; Michael, L. Scalable and reliable data delivery in mobile ad hoc sensor networks. In Proceedings of the Fifth International Joint Conference On Autonomous Agents and Multiagent Systems, Hakodate, Japan, 8–12 May 2006; pp. 1071–1078.
- Ondrej, K.; Neuzil, J.; Smid, R. Quality-based multiple-sensor fusion in an industrial wireless sensor network for MCM. IEEE Trans. Ind. Electron. 2014, 61, 145–157. [Google Scholar]
- Wang, H.T.; Jia, Q.S.; Song, C.; Yuan, R.; Guan, X. Building occupant level estimation based on heterogeneous information fusion. Inf. Sci. 2014, 272, 145–157. [Google Scholar] [CrossRef]
- Ling, D.; Weili, W.; James, W.; Lidong, W.; Zaixin, L.; Wonjun, L. Constant-approximation for target coverage problem in wireless sensor networks. In Proceedings of the 31st Annual IEEE International Conference on Computer Communications, Orlando, FL, USA, 25–30 March 2012; pp. 1584–1592.
- Bin, Y.; Katia, S. Learning the quality of sensor data in distributed decision fusion. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8.

| Target | Confidence | Target Type | Confidence |
|---|---|---|---|
| USSR T80 | 0.4 | US M977 | 0.001 |
| WSSR T72M | 0.3 | US M35 | 0.001 |
| US M1 | 0.1 | US AVENGER | 0.001 |
| US M1A1 | 0.05 | US HMMWV | 0.001 |
| USSR 2S6 | 0.02 | USSR SA9 | 0.001 |
| USSR ZSU23 | 0.03 | CLUTTER | 0.095 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Hu, X.; Hu, H.; Liu, M. A Matrix-Based Proactive Data Relay Algorithm for Large Distributed Sensor Networks. Sensors 2016, 16, 1300. https://doi.org/10.3390/s16081300
Xu Y, Hu X, Hu H, Liu M. A Matrix-Based Proactive Data Relay Algorithm for Large Distributed Sensor Networks. Sensors. 2016; 16(8):1300. https://doi.org/10.3390/s16081300
Chicago/Turabian StyleXu, Yang, Xuemei Hu, Haixiao Hu, and Ming Liu. 2016. "A Matrix-Based Proactive Data Relay Algorithm for Large Distributed Sensor Networks" Sensors 16, no. 8: 1300. https://doi.org/10.3390/s16081300
APA StyleXu, Y., Hu, X., Hu, H., & Liu, M. (2016). A Matrix-Based Proactive Data Relay Algorithm for Large Distributed Sensor Networks. Sensors, 16(8), 1300. https://doi.org/10.3390/s16081300






