Time Domain Strain/Stress Reconstruction Based on Empirical Mode Decomposition: Numerical Study and Experimental Validation
Abstract
:1. Introduction
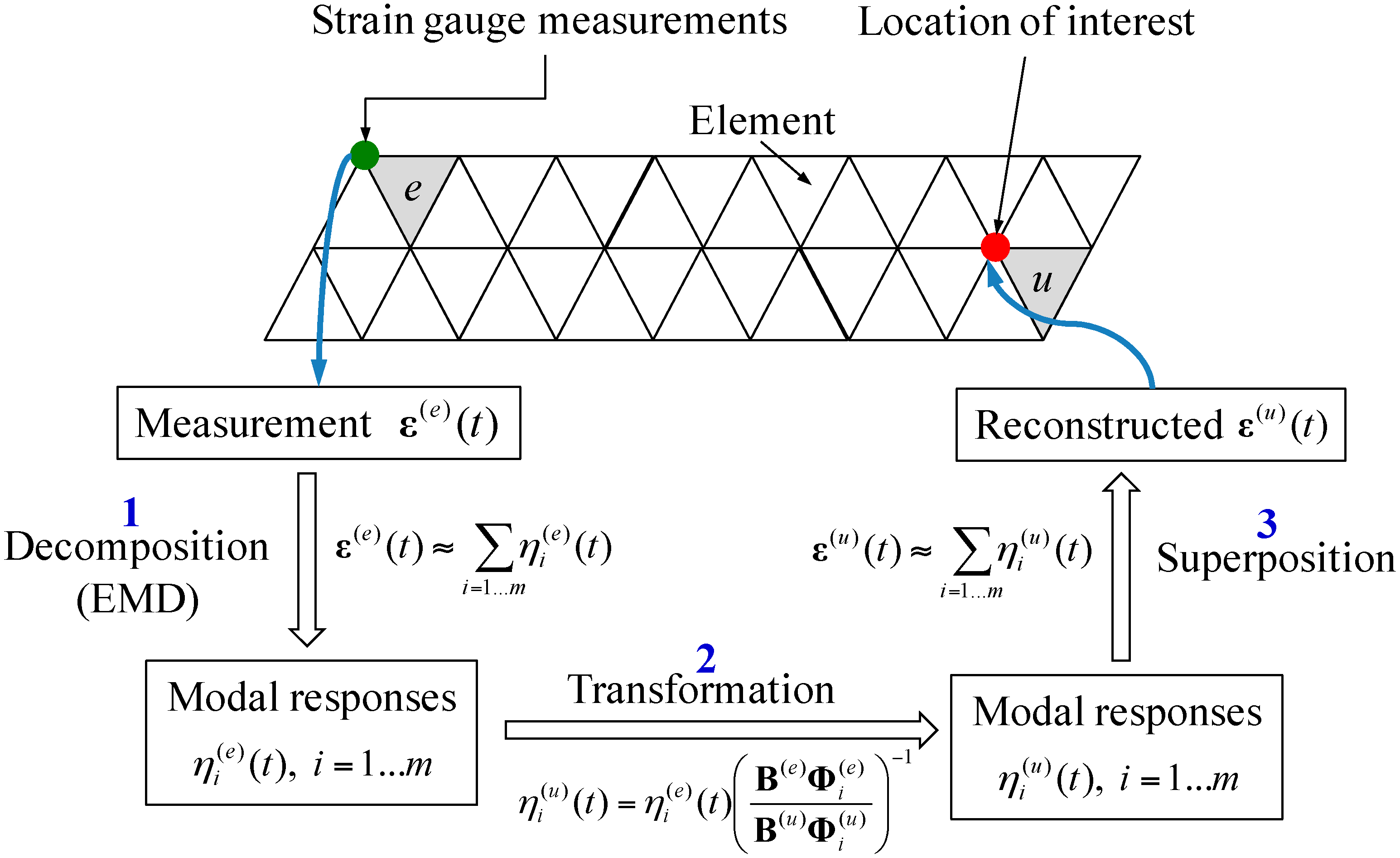
2. Strain and Stress Reconstruction Methodology
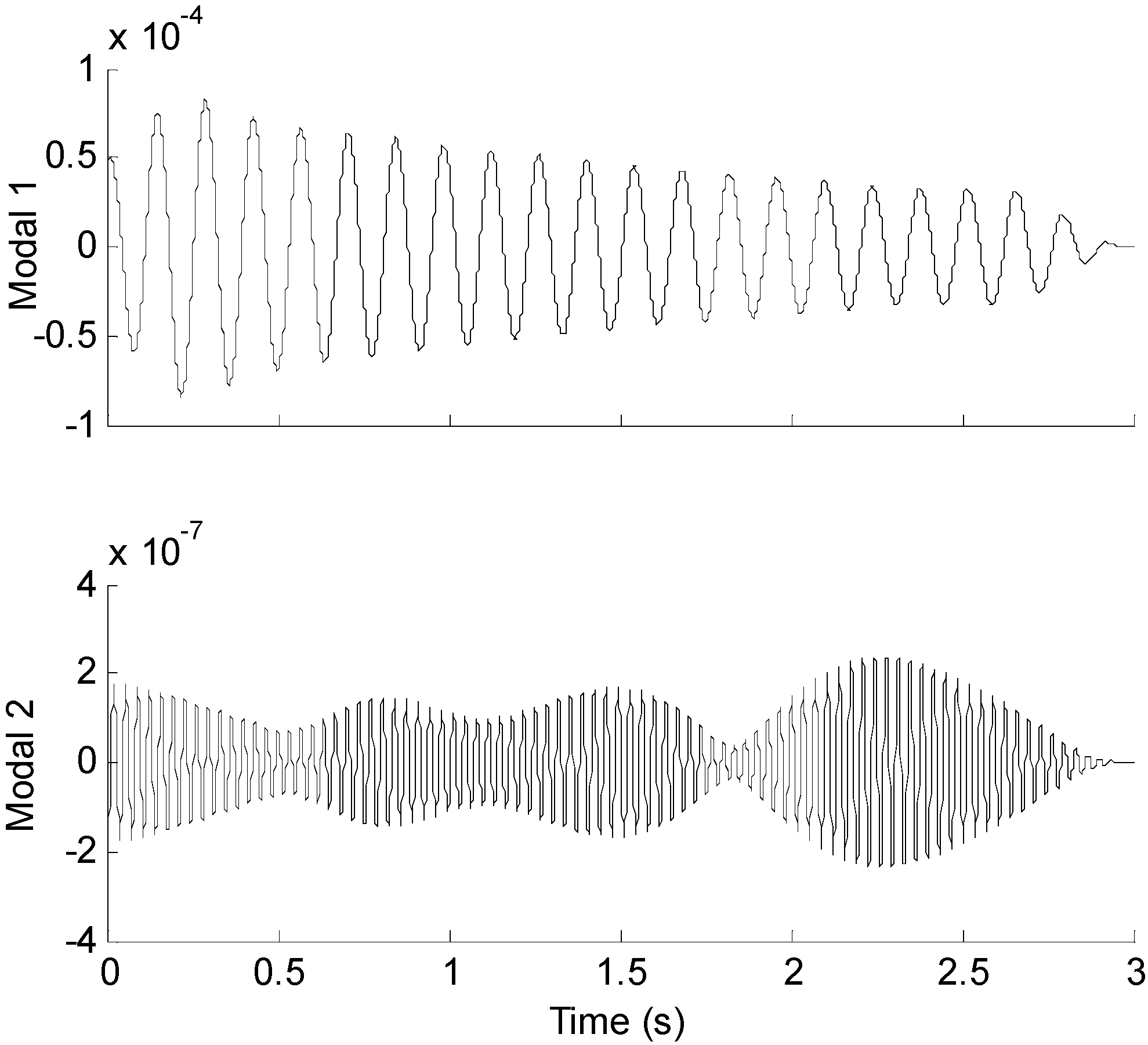
2.1. Extraction of Modal Responses from Measurement Data Using EMD Method
2.2. Transformation Equations for Strain and Stress Responses
3. Numerical Examples
3.1. Example 1: A Numerical Beam Structure Example
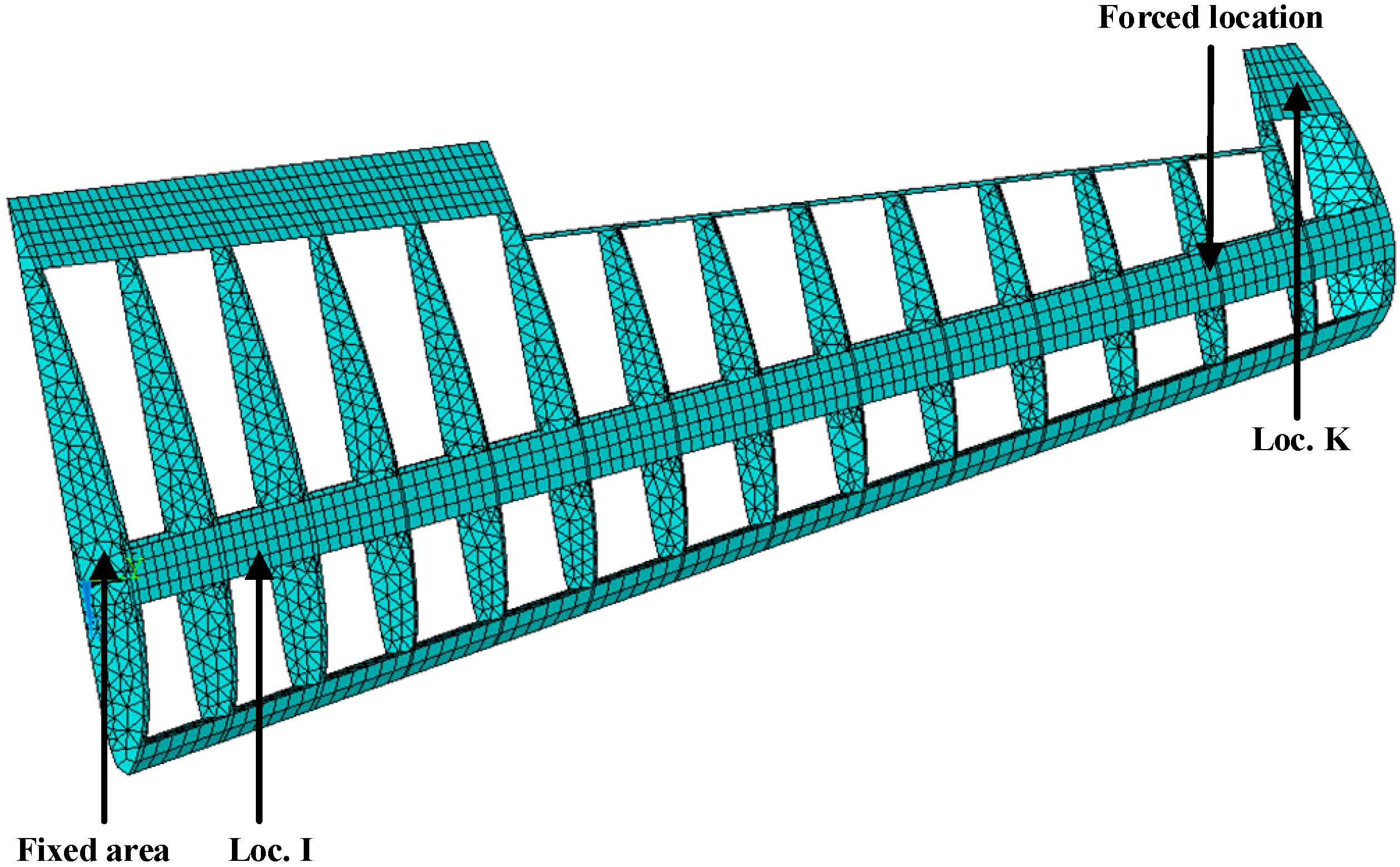
3.2. Example 2: A Simplified Airfoil Structure Model Example
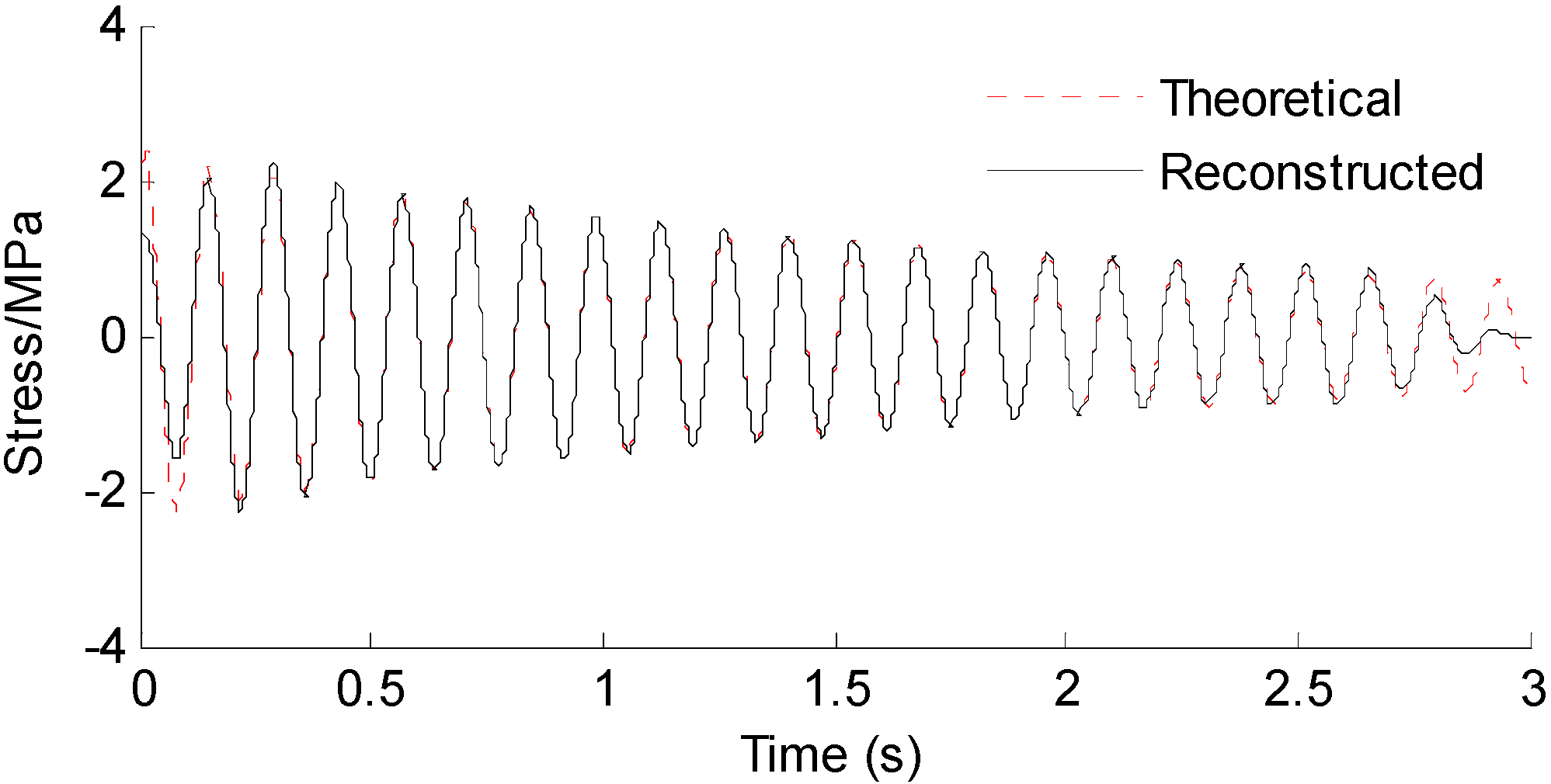
3.2.1. Strain and Stress Response Reconstruction
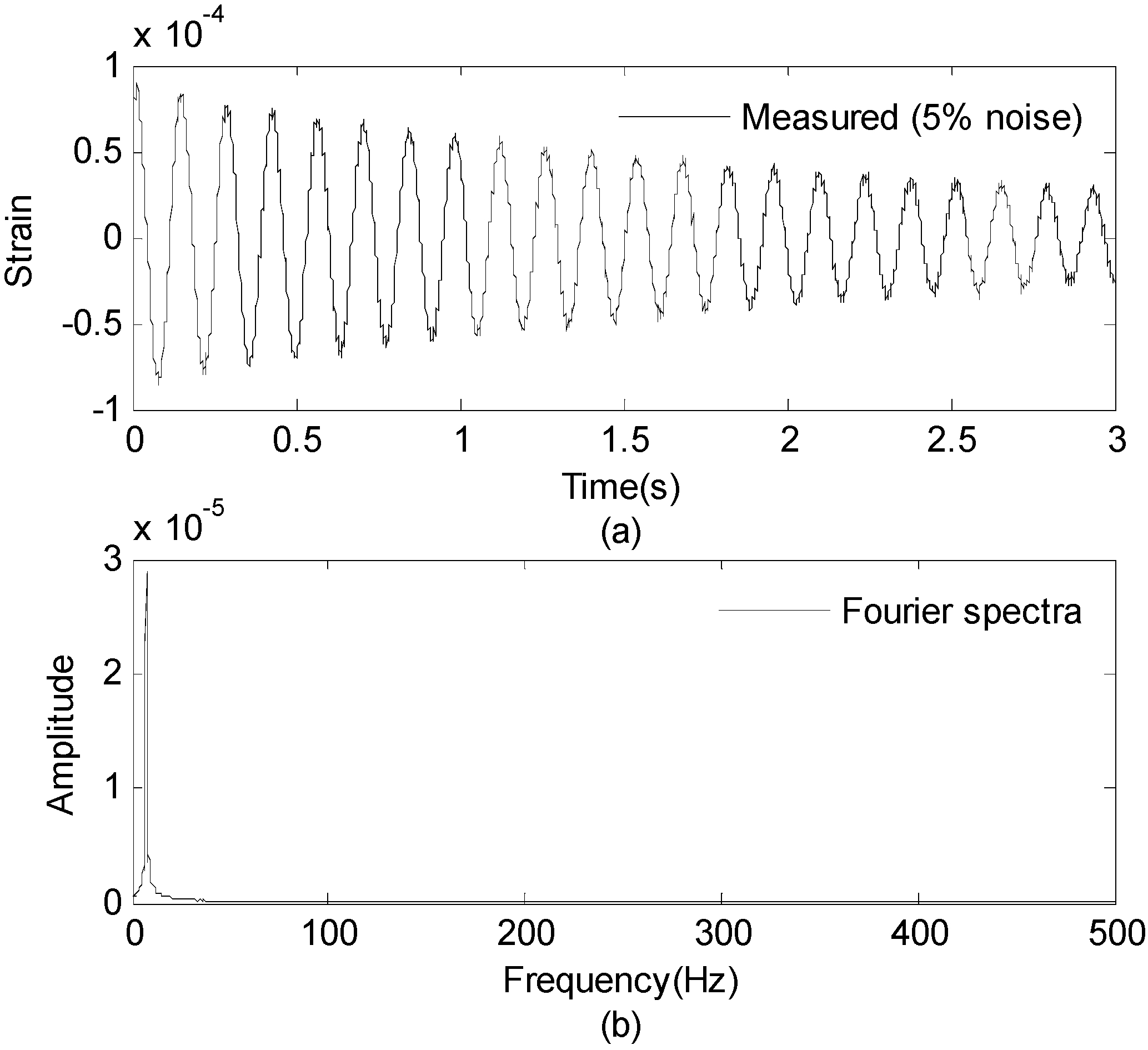
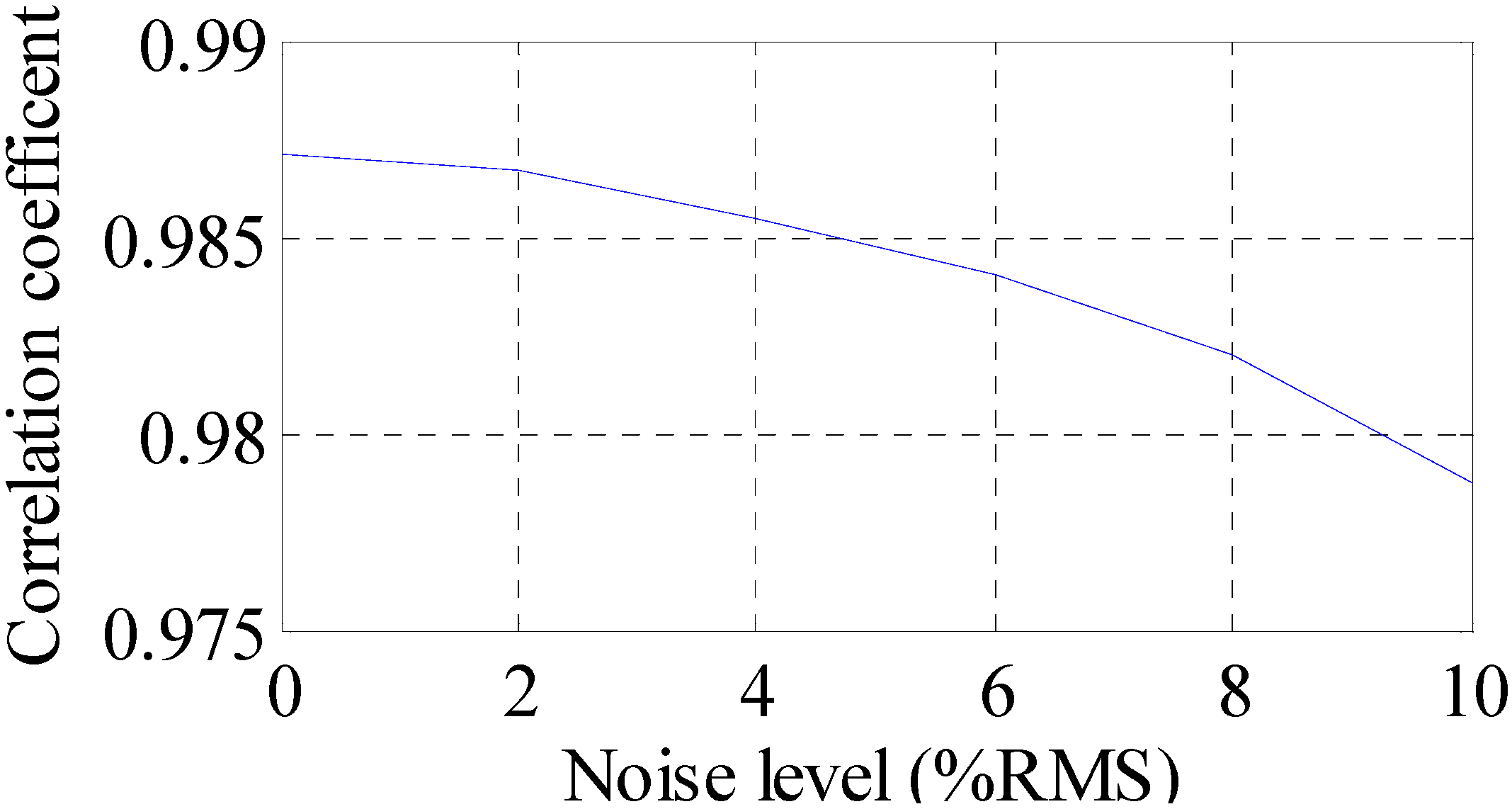
3.2.2. Effect of Measurement Noise to Reconstructed Strain and Stress Responses
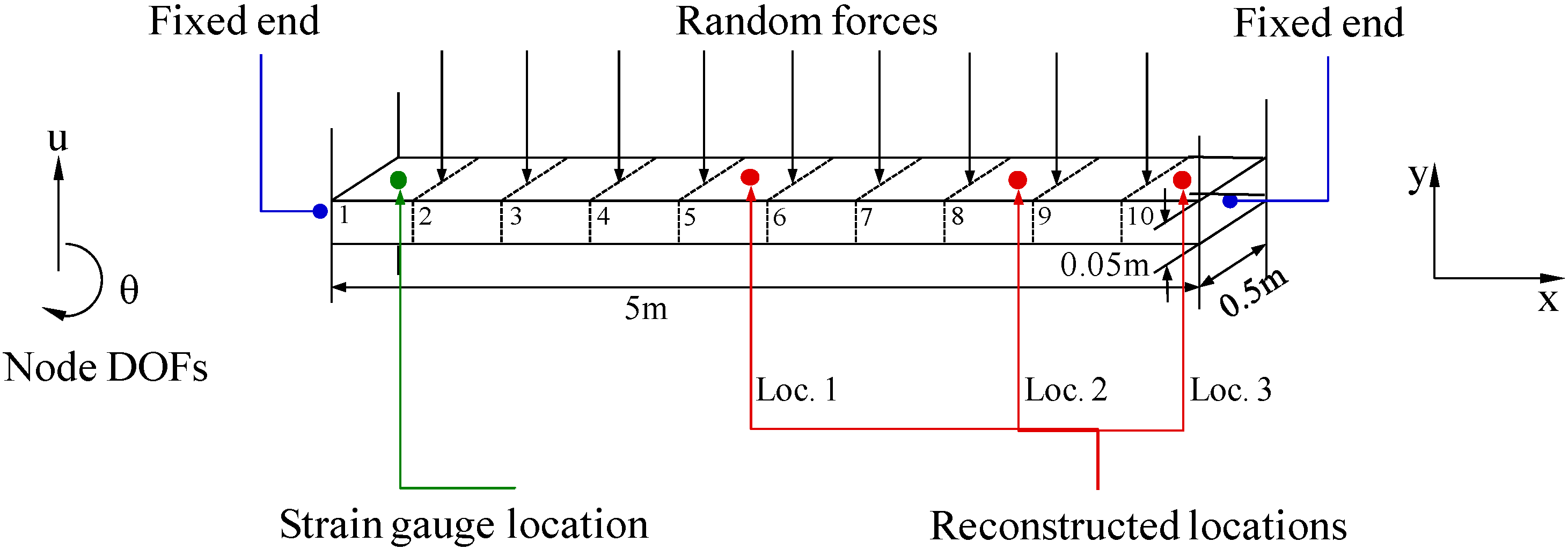
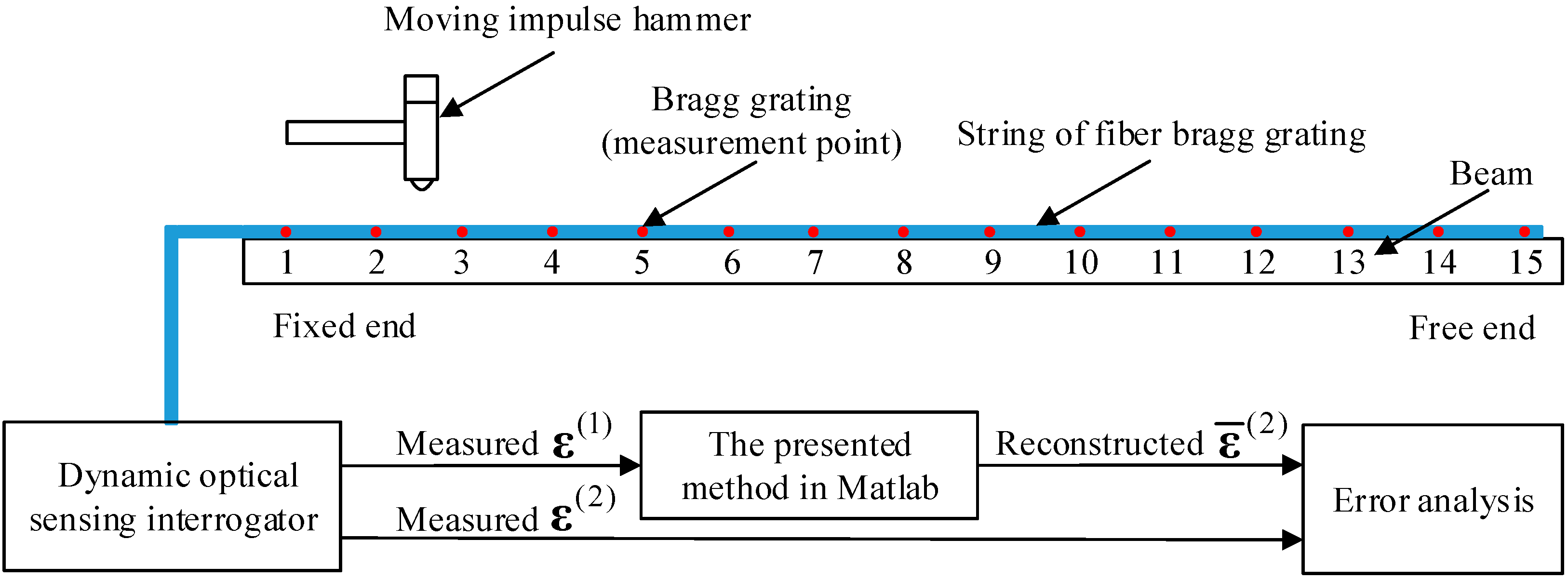
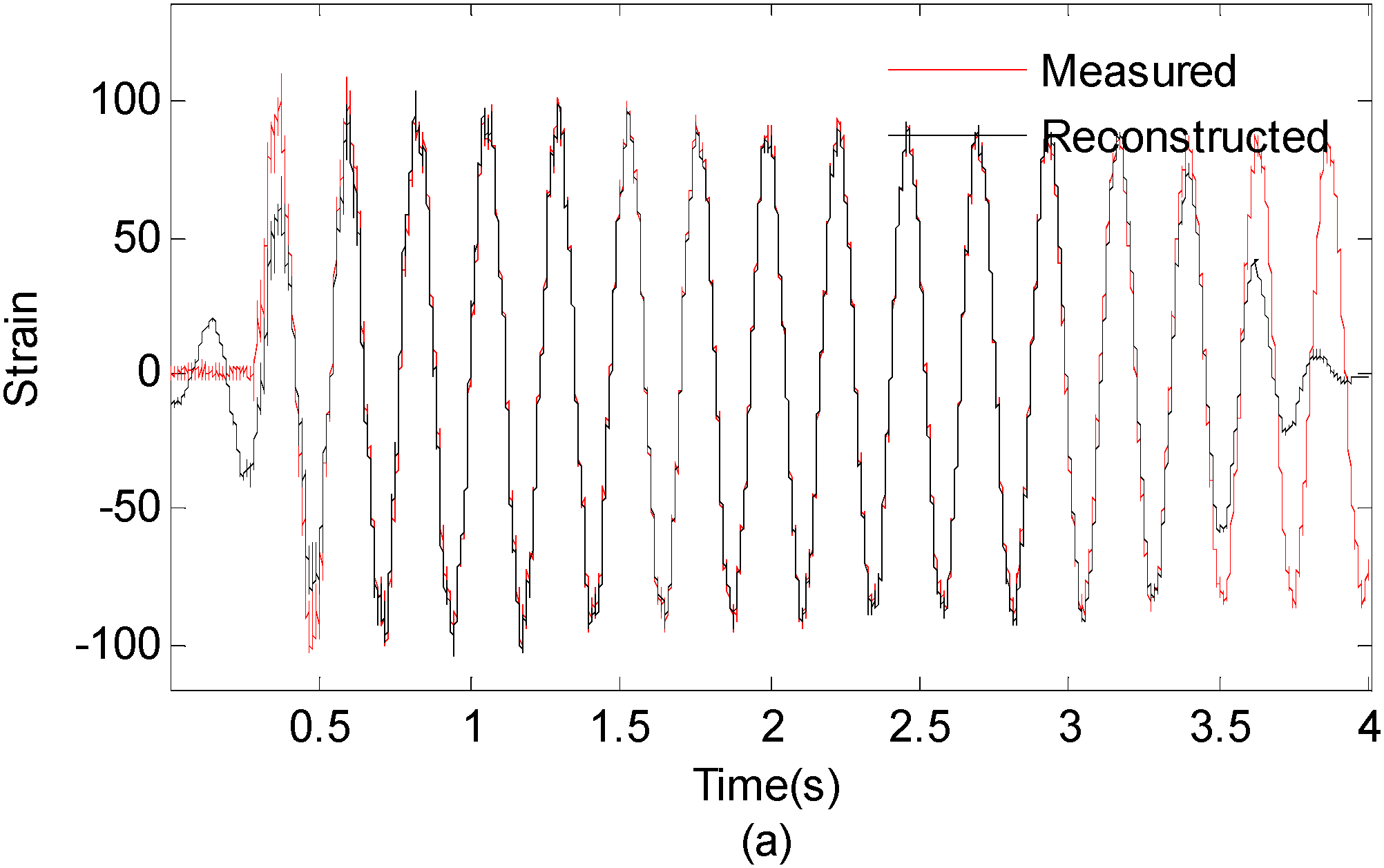
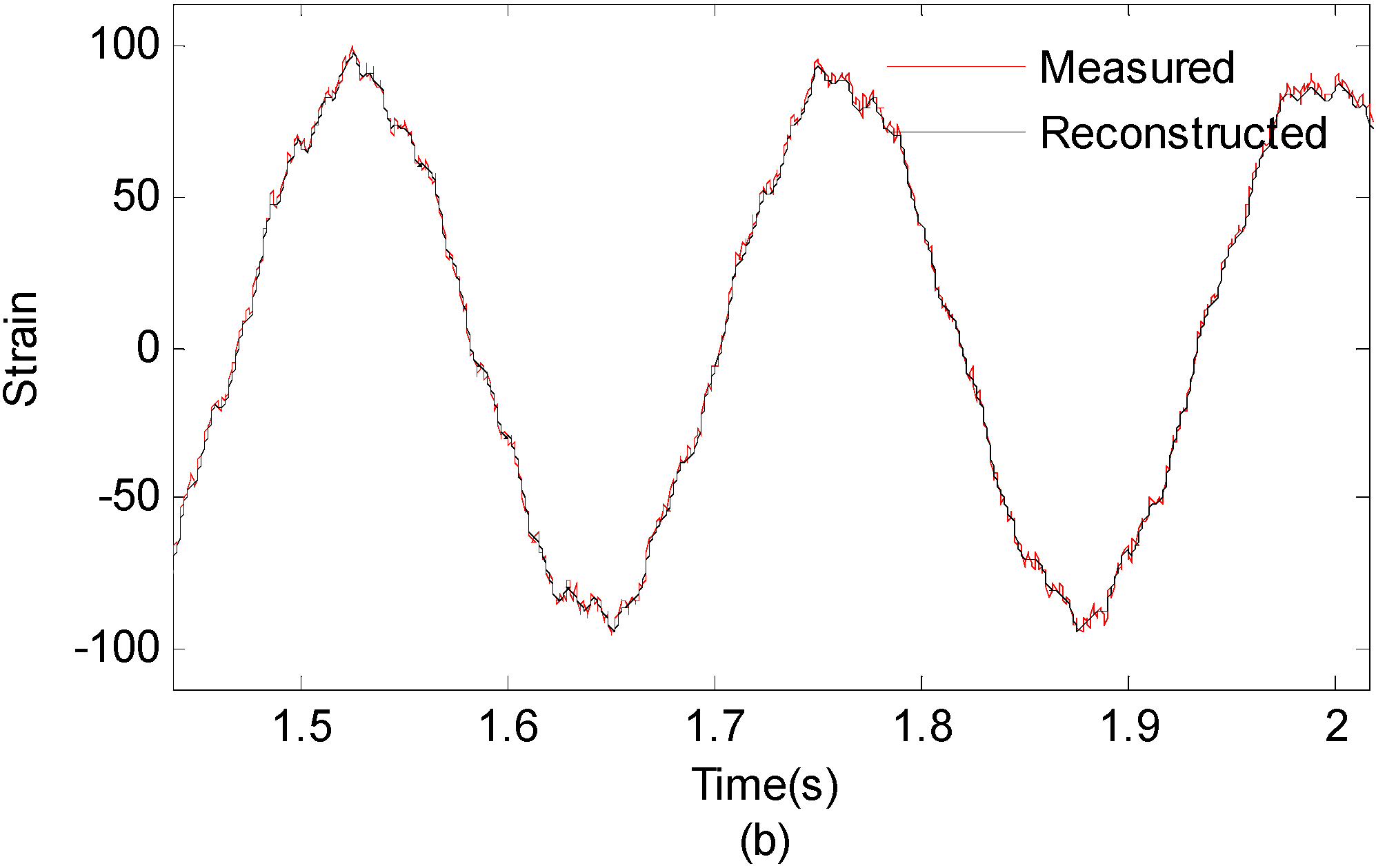
4. Experimental Validation
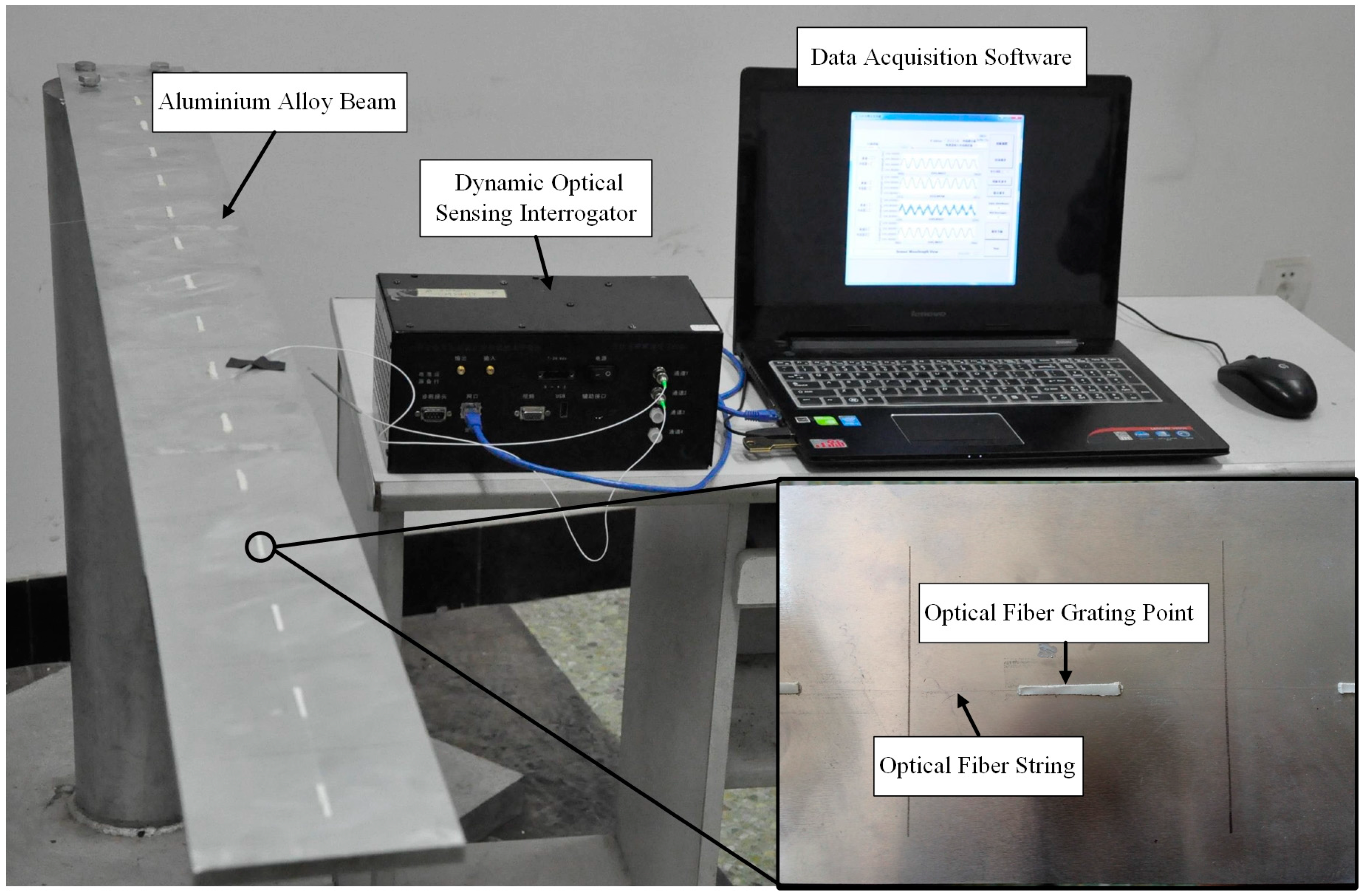
4.1. Experimental Setup
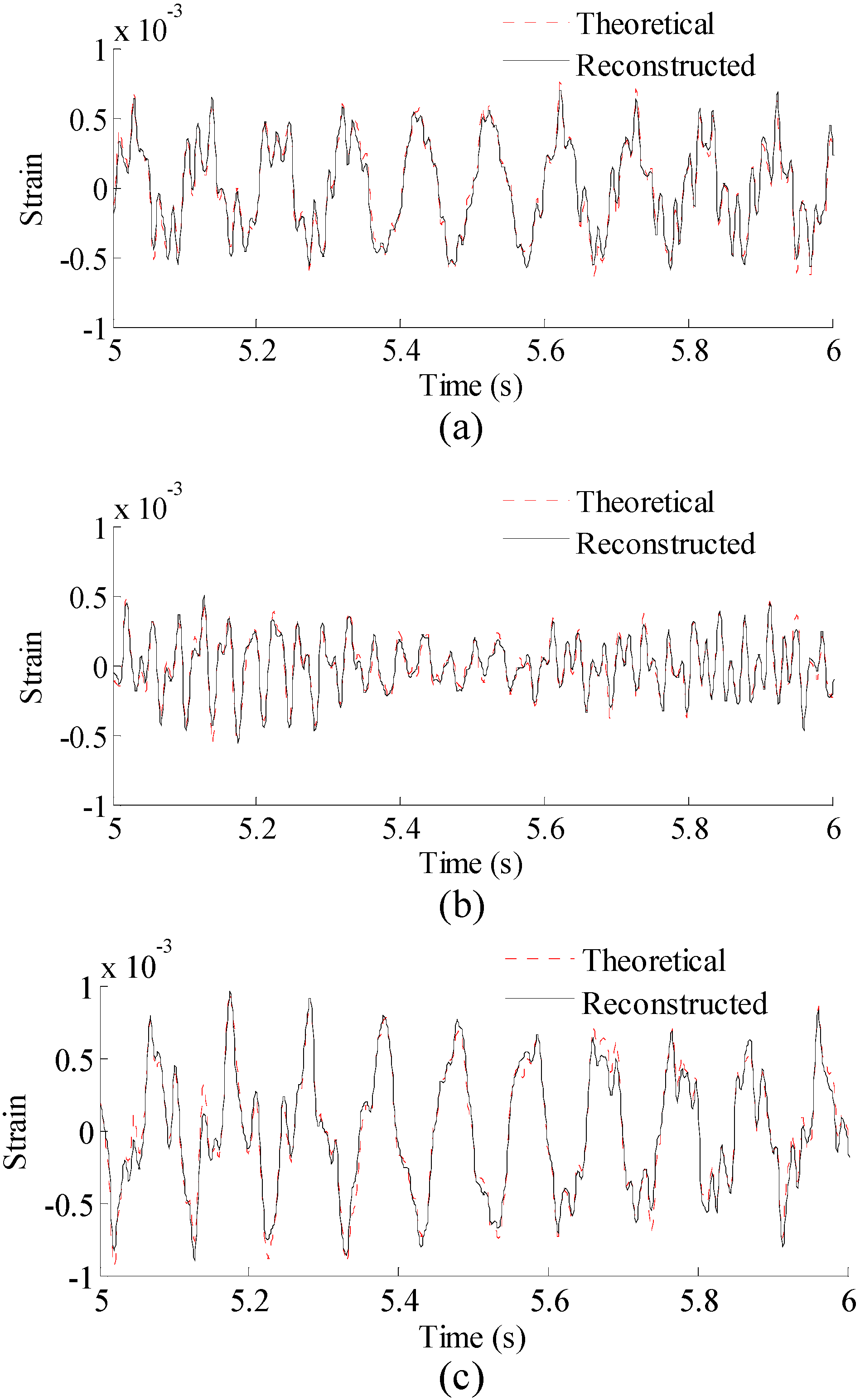
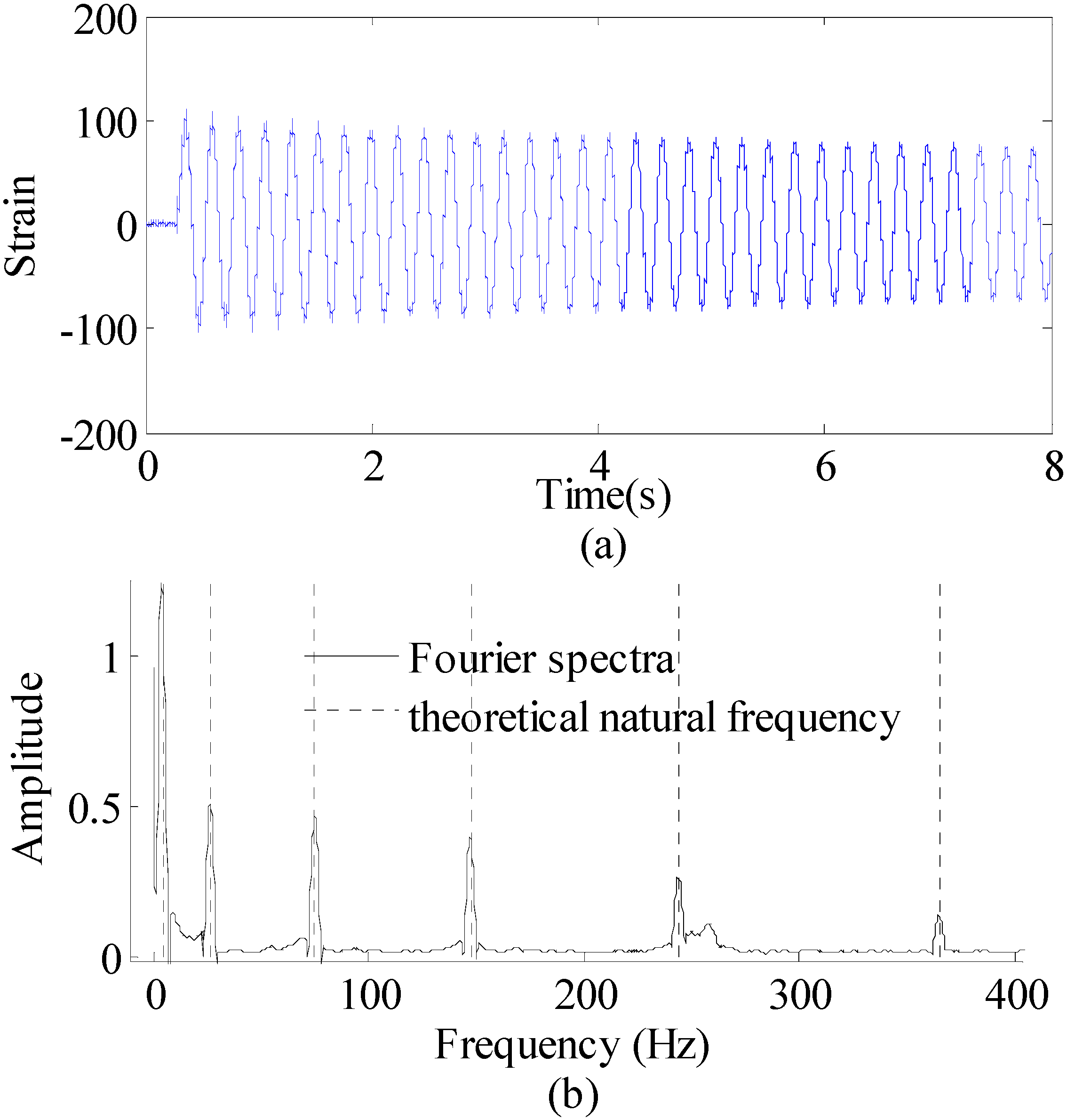
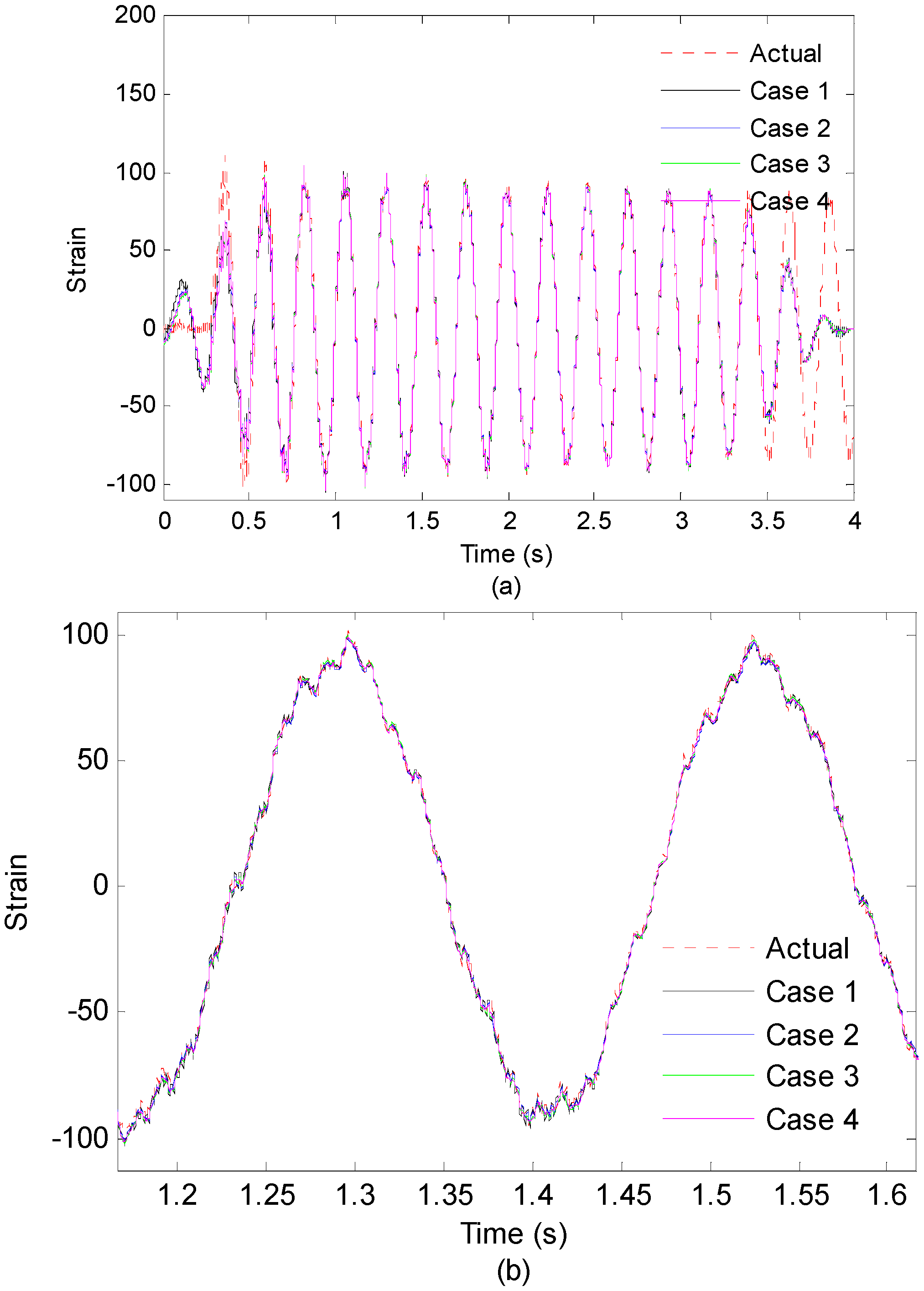
4.2. Results and Discussion
Case 1. Effect of Sensor Number
Case 2. Effect of Sensor Location
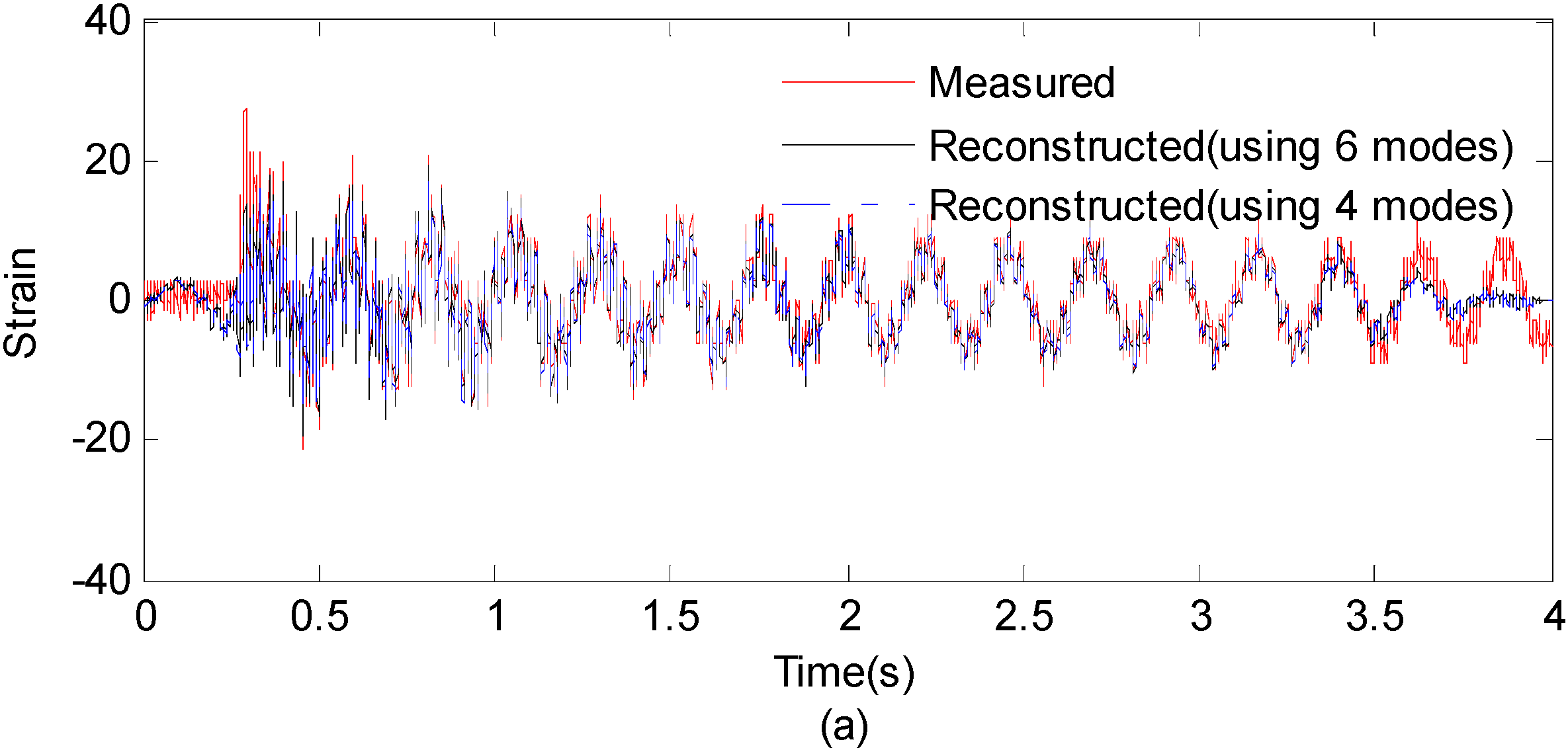
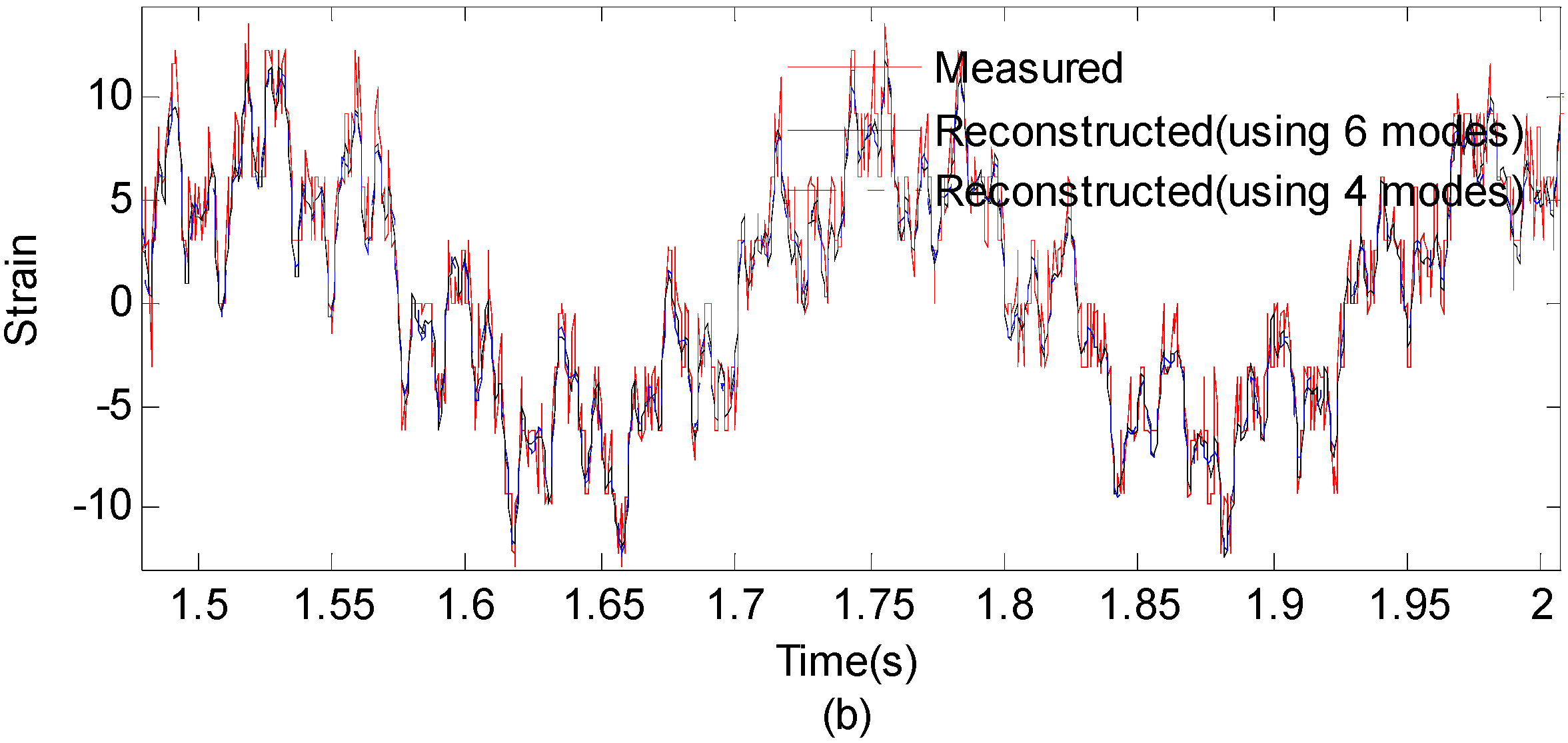
Case 3. Effect of Mode Number
5. Conclusions
- (1)
- In this study, a time domain strain/stress reconstruction method based on EMD is proposed. According to numerical analysis results, the proposed method can produce results which are very close to theoretical solutions considering a practical noisy measurement system. The reconstructed results have an overall correlation coefficient larger than 0.975 under 10% RMS noise settings. The discrepancy between actual measurements and reconstruction results at the boundary region are possibly caused by the end boundary effect of EMD method.
- (2)
- Four sets of experiments, associated with basic example, sensor number, sensor location and mode number, verified the effectiveness of the time domain strain/stress reconstruction method in successfully reconstructing the strain response in location of interested. The results indicate that increasing the number of the measurement points has trivial effects on the reconstruction accuracy under ideal experimental circumstance. However, increasing the number of the measurement points may decrease the uncertainty (imposed by measurement noise or mishandling) for real engineering applications. Thus, more sensor measurements will commonly lead to higher reconstruction accuracy.
- (3)
- For the sensor location, two specific sensor locations should be avoided for reliable strain/stress response reconstruction: (a) locations where have low signal-to-noise ratio. In such case, the measured strain data are corrupted by noise, which will lead to inaccurate reconstruction results; (b) locations at or near the nodal points. In such locations, it may not capture all excited modes of the strain responses.
- (4)
- For the mode number, the higher modes will have little influence on the accuracy of the reconstruction, because of their low participation factors in Fourier spectra. Only dominant modes are efficient for accurate reconstructions.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Johnson, T.J.; Brown, R.L.; Adams, D.E.; Schiefer, M. Distributed structural health monitoring with a smart sensor array. Mech. Syst. Signal Process. 2004, 18, 555–572. [Google Scholar] [CrossRef]
- Pines, D.; Salvino, L. Structural health monitoring using empirical mode decomposition and the hilbert phase. J. Sound Vib. 2006, 294, 97–124. [Google Scholar] [CrossRef]
- Hurlebaus, S.; Gaul, L. Smart structure dynamics. Mech. Syst. Signal Process. 2006, 20, 255–281. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Los Alamos National Lab NM: Los Alamos, NM, USA, 1996. [Google Scholar]
- Kulkarni, S.; Achenbach, J. Structural health monitoring and damage prognosis in fatigue. Struct. Health Monit. 2008, 7, 37–49. [Google Scholar] [CrossRef]
- Beral, B.; Speckmann, H. Structural Health Monitoring (Shm) for Aircraft Structures: A Challenge for System Developers and Aircraft Manufactures. In Proceedings of the 4th International Workshop on Structural Health Monitoring Structural Health Monitoring 2003: From Diagnostics & Prognostics to Structural Health Management, Stanford University, Stanford, CA, USA, 15–17 September 2003; Chang, F.K., Ed.; Stanford University: Stanford, CA, USA, 2003; pp. 12–29. [Google Scholar]
- Verboven, P.; Parloo, E.; Guillaume, P.; Van Overmeire, M. Autonomous structural health monitoring—Part I: Modal parameter estimation and tracking. Mech. Syst. Signal Process. 2002, 16, 637–657. [Google Scholar] [CrossRef]
- Parloo, E.; Verboven, P.; Guillaume, P.; Van Overmeire, M. Autonomous structural health monitoring—Part II: Vibration-based in-operation damage assessment. Mech. Syst. Signal Process. 2002, 16, 659–675. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Cuc, A. Embedded non-destructive evaluation for structural health monitoring, damage detection, and failure prevention. Shock Vib. Dig. 2005, 37, 83–105. [Google Scholar] [CrossRef]
- Chang, P.C.; Flatau, A.; Liu, S. Review paper: Health monitoring of civil infrastructure. Struct. Health Monit. 2003, 2, 257–267. [Google Scholar] [CrossRef]
- Katsikeros, C.E.; Labeas, G. Development and validation of a strain-based structural health monitoring system. Mech. Syst. Signal Process. 2009, 23, 372–383. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- He, J.; Guan, X.; Liu, Y. Structural response reconstruction based on empirical mode decomposition in time domain. Mech. Syst. Signal Process. 2012, 28, 348–366. [Google Scholar] [CrossRef]
- Law, S.; Li, J.; Ding, Y. Structural response reconstruction with transmissibility concept in frequency domain. Mech. Syst. Signal Process. 2011, 25, 952–968. [Google Scholar] [CrossRef]
- Kammer, D. Estimation of structural response using remote sensor locations. J. Guid. Control Dyn. 1997, 20, 501–508. [Google Scholar] [CrossRef]
- Ribeiro, A.; Silva, J.; Maia, N. On the generalisation of the transmissibility concept. Mech. Syst. Signal Process. 2000, 14, 29–36. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Eriten, M.; Kurt, M.; Luo, G.Y.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Nonlinear system identification of frictional effects in a beam with a bolted joint connection. Mech. Syst. Signal Process. 2013, 39, 245–264. [Google Scholar] [CrossRef]
- Kurt, M.; Chen, H.; Lee, Y.S.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Nonlinear system identification of the dynamics of a vibro-impact beam: Numerical results. Arch. Appl. Mech. 2012, 82, 1461–1479. [Google Scholar] [CrossRef]
- Chen, H.; Kurt, M.; Lee, Y.S.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Experimental system identification of the dynamics of a vibro-impact beam with a view towards structural health monitoring and damage detection. Mech. Syst. Signal Process. 2014, 46, 91–113. [Google Scholar] [CrossRef]
- Lei, Y.G.; Lin, J.; He, Z.J.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Deering, R.; Kaiser, J.F. The use of a masking signal to improve empirical mode decomposition. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, (ICASSP ’05), Philadelphia, PA, USA, 18–23 March 2005; Volume 484, pp. iv/485–iv/488.
- WU, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Kurt, M.; Eriten, M.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Strongly nonlinear beats in the dynamics of an elastic system with a strong local stiffness nonlinearity: Analysis and identification. J. Sound Vib. 2014, 333, 2054–2072. [Google Scholar] [CrossRef]
- Kurt, M. Identification, Reduced Order Modeling and Model Updating of Nonlinear Mechanical Systems. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2014. [Google Scholar]
- Senroy, N.; Suryanarayanan, S. Two techniques to enhance empirical mode decomposition for power quality applications. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; IEEE: New York, NY, USA, 2007; Volumes 1–10, pp. 3354–3359. [Google Scholar]
- Yang, J.N.; Lei, Y.; Pan, S.; Huang, N. System identification of linear structures based on hilbert-huang spectral analysis—Part 1: Normal modes. Earthq. Eng. Struct. Dyn. 2003, 32, 1443–1467. [Google Scholar] [CrossRef]
- Bao, C.; Hao, H.; Li, Z.X.; Zhu, X. Time-varying system identification using a newly improved HHT algorithm. Comput. Struct. 2009, 87, 1611–1623. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The hilbert spectrum 1. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
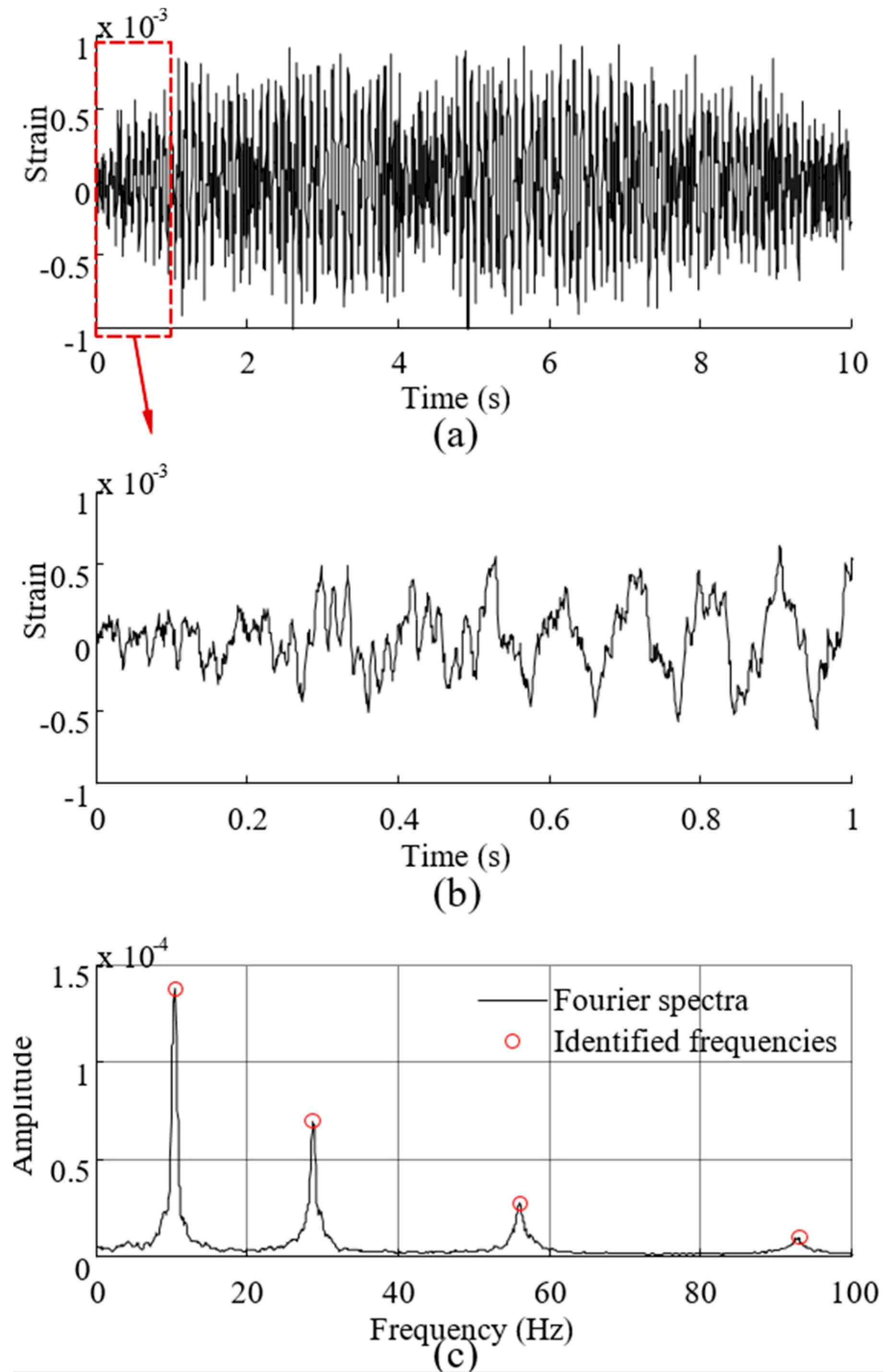






| Mode | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Identified frequency | 10.38 | 28.69 | 56.22 | 93.15 |
| Passband corner frequency (Hz) | [8–9] | [22–26] | [46–52] | [80–87] |
| Stopband corner frequency (Hz) | [11.5–13] | [31–36] | [61–67] | [98–105] |
| Property | Value |
|---|---|
| Material | Aluminum 7075 |
| Element type | Solid185 |
| Young’s modulus E (GPa) | 72 |
| Poisson’s ratio ν | 0.33 |
| Mass per unit volume ρ (kg/m3) | 2.81 × 103 |
| Number of elements | 14,951 |
| Property | Value |
|---|---|
| Material | Aluminum 7050 |
| Length | 1.36 m |
| Width | 0.12 m |
| Thick | 0.01 m |
| Young’s modulus E (GPa) | 7.17 |
| Poisson’s ratio ν | 0.33 |
| Mass per unit volume ρ (kg/m3) | 2.81 × 103 |
| Mode | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Identified frequency | 4.39 | 27.23 | 75.69 | 148.22 | 244.15 | 365.26 |
| Passband corner frequency (Hz) | [3–4] | [25–26] | [65–70] | [135–140] | [226–231] | [350–355] |
| Stopband corner frequency (Hz) | [5–6] | [27.5–28.5] | [80–85] | [160–165] | [257–262] | [375–380] |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Measurement points for reconstruction | 7-th | 3-th, 12-th | 3-th, 7-th, 12-th | the rest points except 5-th |
| Correlation coefficient | 0.9497 | 0.9516 | 0.9519 | 0.9519 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Zhou, Y.; Guan, X.; Zhang, W.; Zhang, W.; Liu, Y. Time Domain Strain/Stress Reconstruction Based on Empirical Mode Decomposition: Numerical Study and Experimental Validation. Sensors 2016, 16, 1290. https://doi.org/10.3390/s16081290
He J, Zhou Y, Guan X, Zhang W, Zhang W, Liu Y. Time Domain Strain/Stress Reconstruction Based on Empirical Mode Decomposition: Numerical Study and Experimental Validation. Sensors. 2016; 16(8):1290. https://doi.org/10.3390/s16081290
Chicago/Turabian StyleHe, Jingjing, Yibin Zhou, Xuefei Guan, Wei Zhang, Weifang Zhang, and Yongming Liu. 2016. "Time Domain Strain/Stress Reconstruction Based on Empirical Mode Decomposition: Numerical Study and Experimental Validation" Sensors 16, no. 8: 1290. https://doi.org/10.3390/s16081290
APA StyleHe, J., Zhou, Y., Guan, X., Zhang, W., Zhang, W., & Liu, Y. (2016). Time Domain Strain/Stress Reconstruction Based on Empirical Mode Decomposition: Numerical Study and Experimental Validation. Sensors, 16(8), 1290. https://doi.org/10.3390/s16081290





