Frequency Splitting Analysis and Compensation Method for Inductive Wireless Powering of Implantable Biosensors
Abstract
:1. Introduction
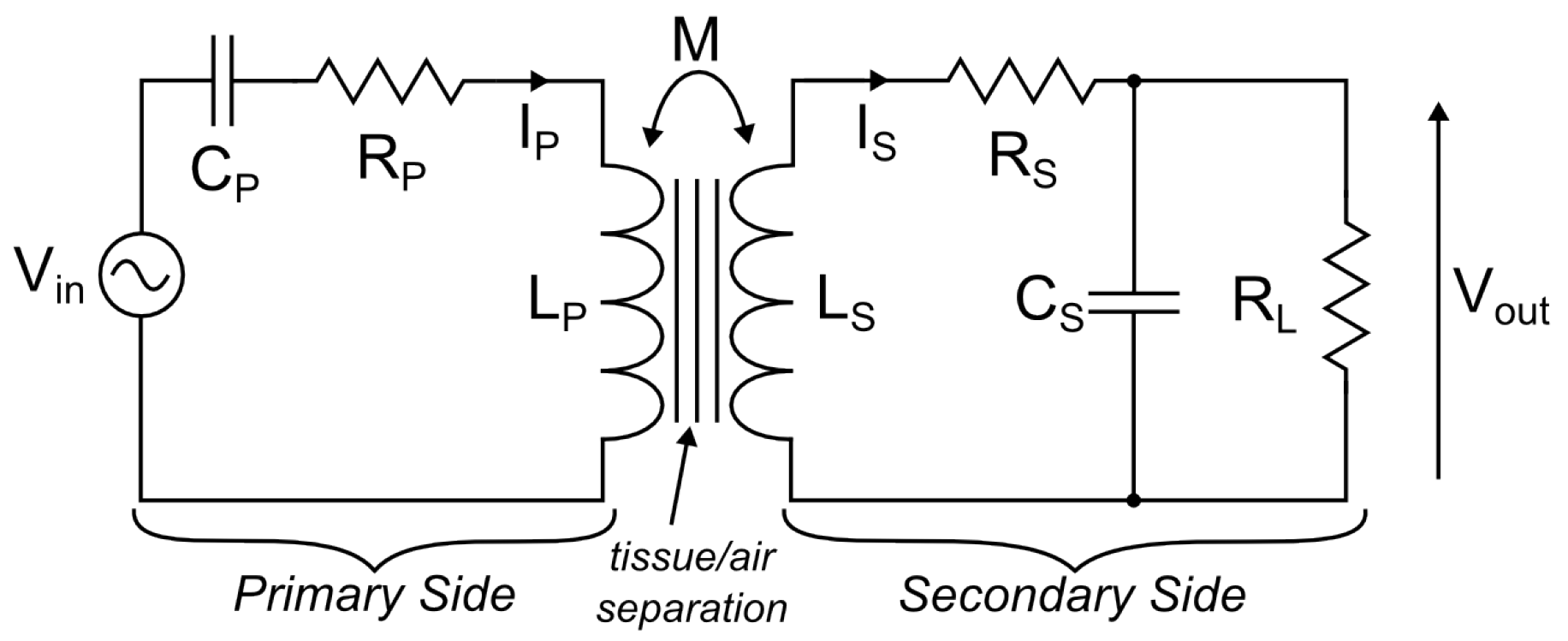
2. Inductive Link Theory
2.1. Inductive Link Fundamentals
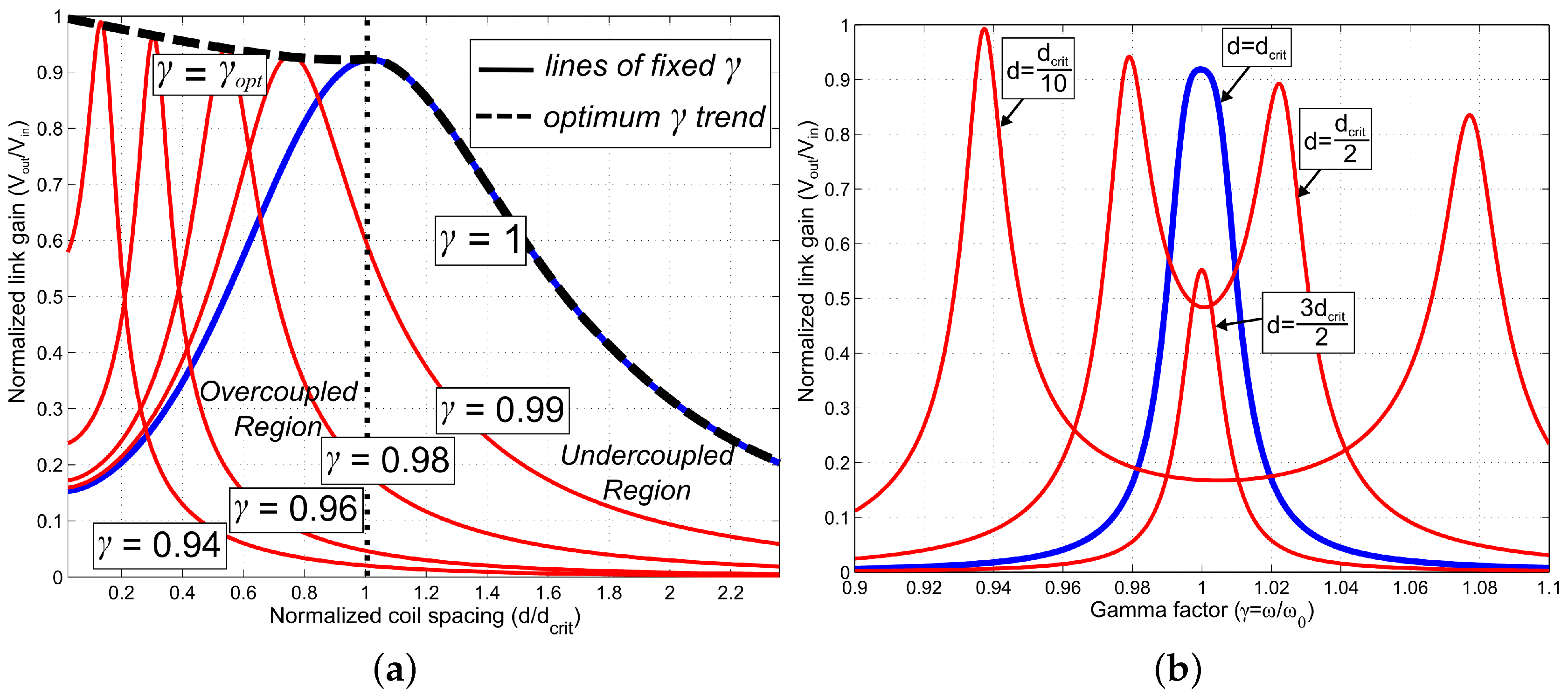
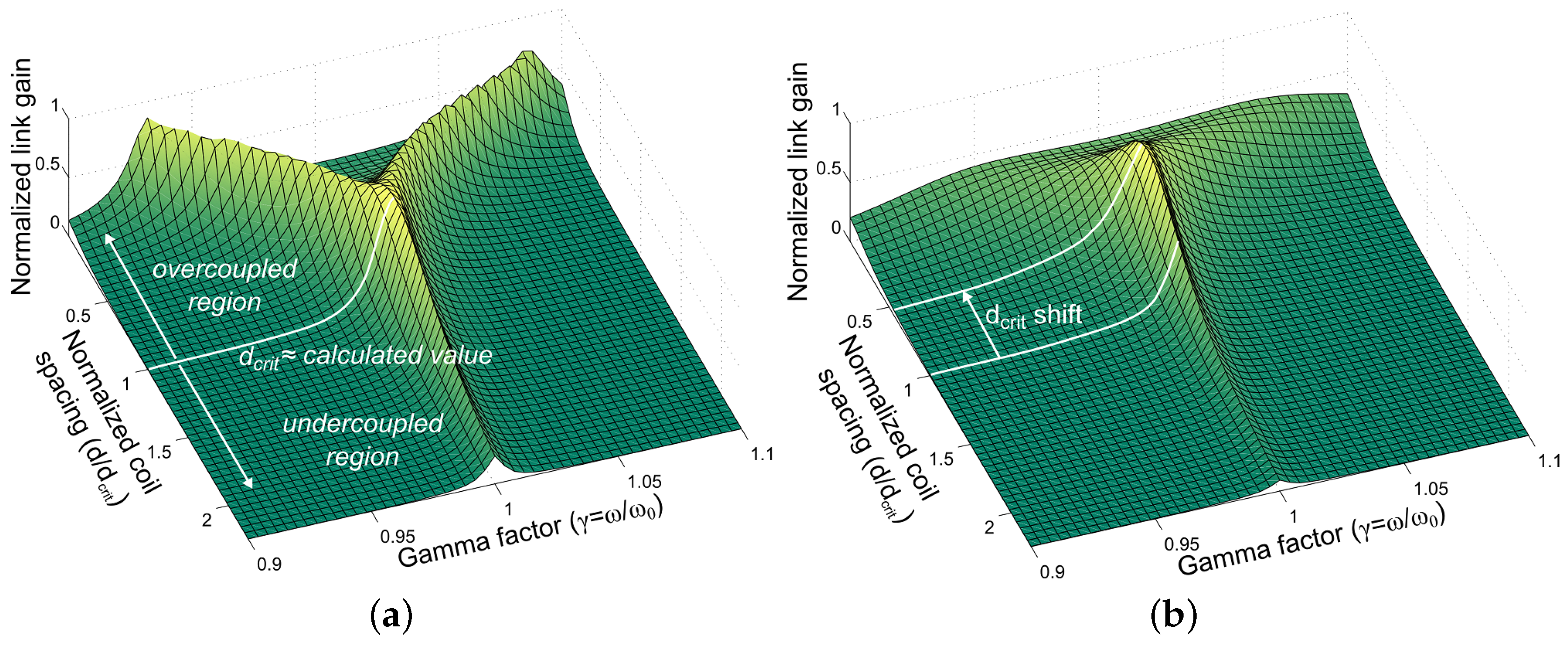
2.2. Frequency Splitting in Overcoupled Inductive Links
2.3. Relationship between Coupling and Coil Separation
2.4. Effects of Frequency Splitting
2.5. Effects of
2.6. Considerations for Tracking
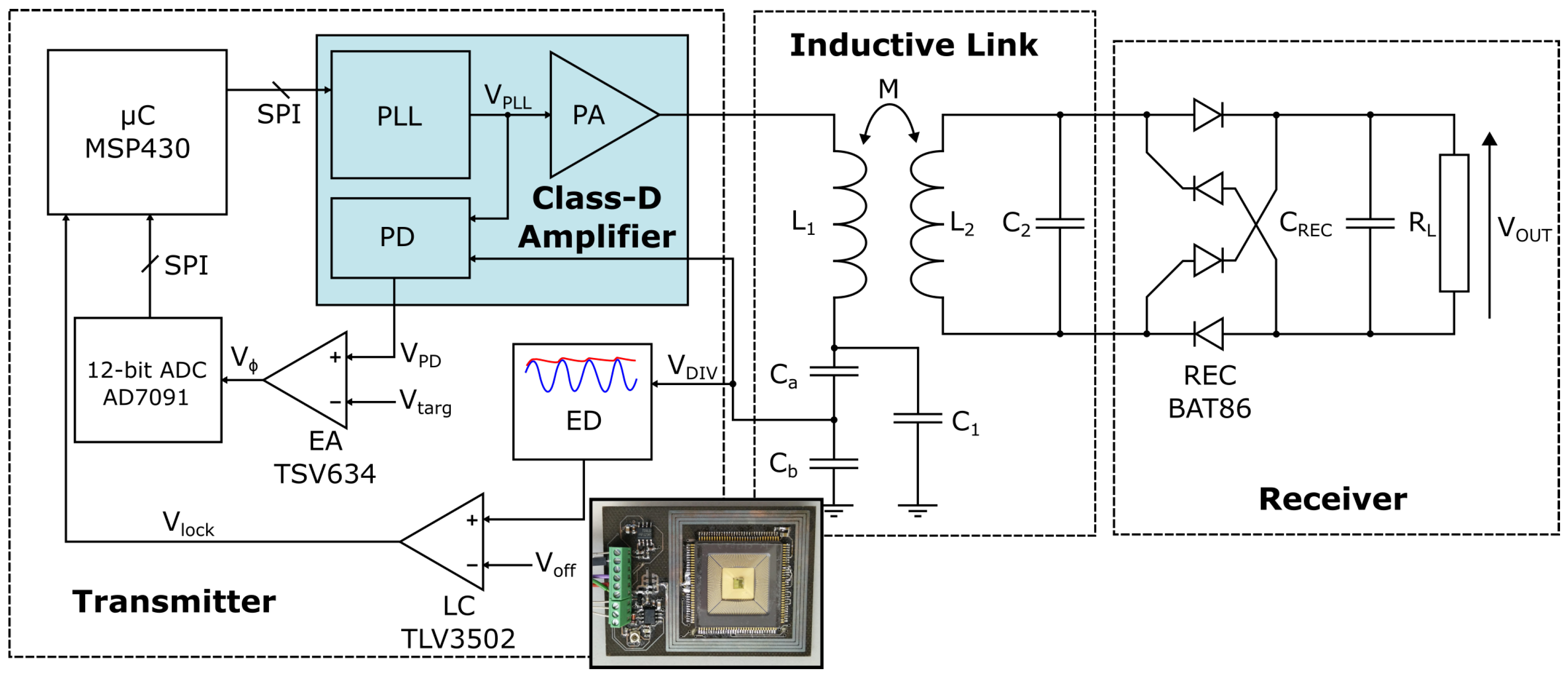
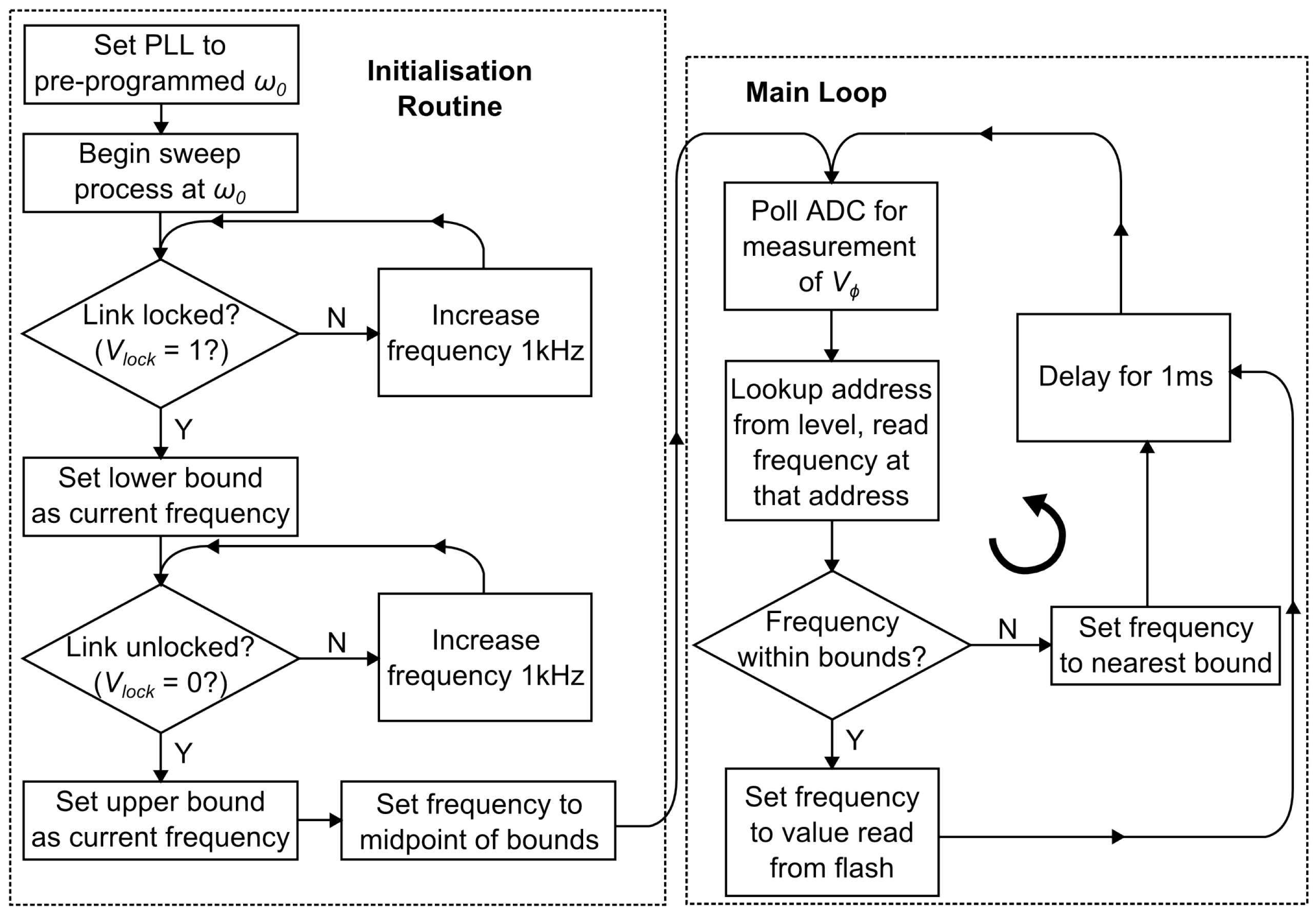
3. Frequency Tracking System
3.1. Transmitter System Operation
3.2. Coil Design and Implementation
4. Testing and Results
4.1. Test Procedure
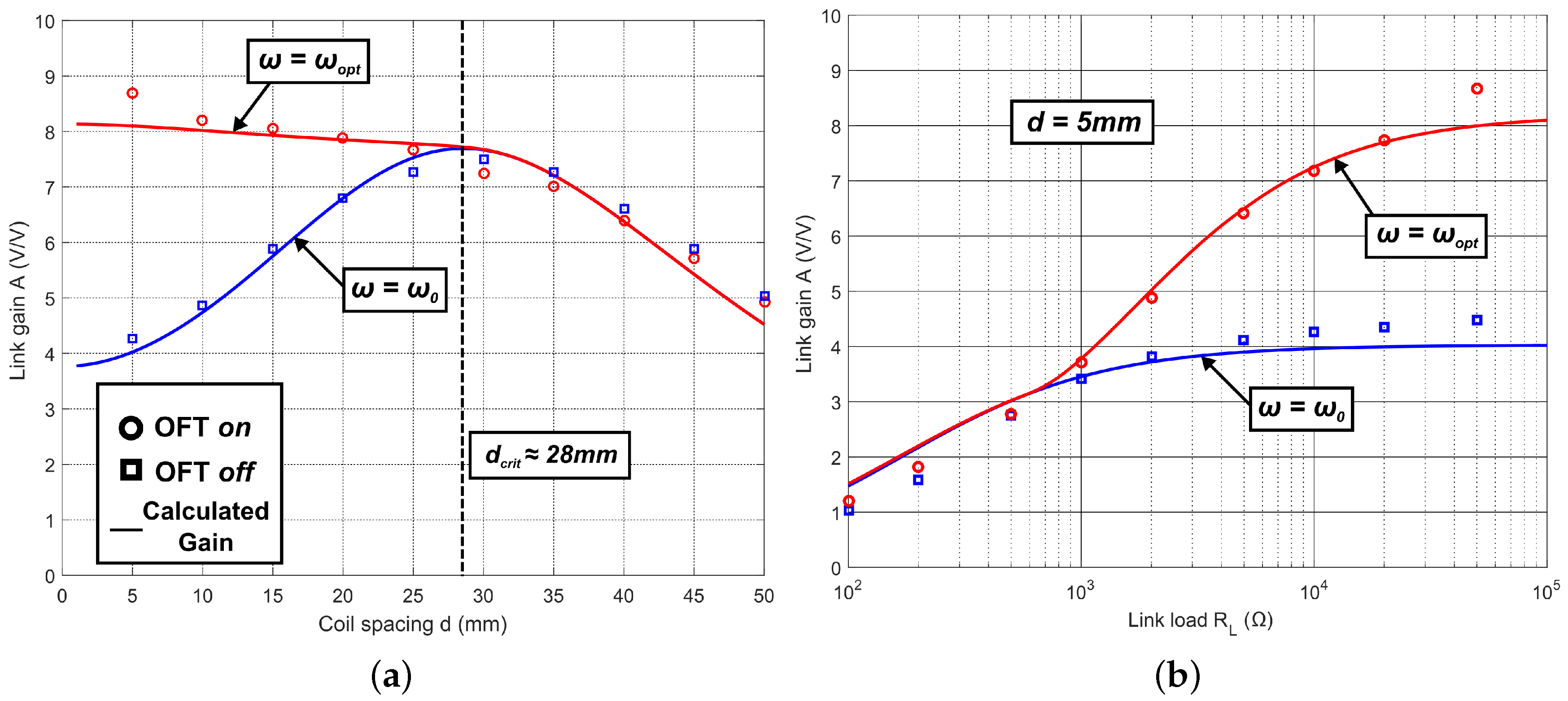
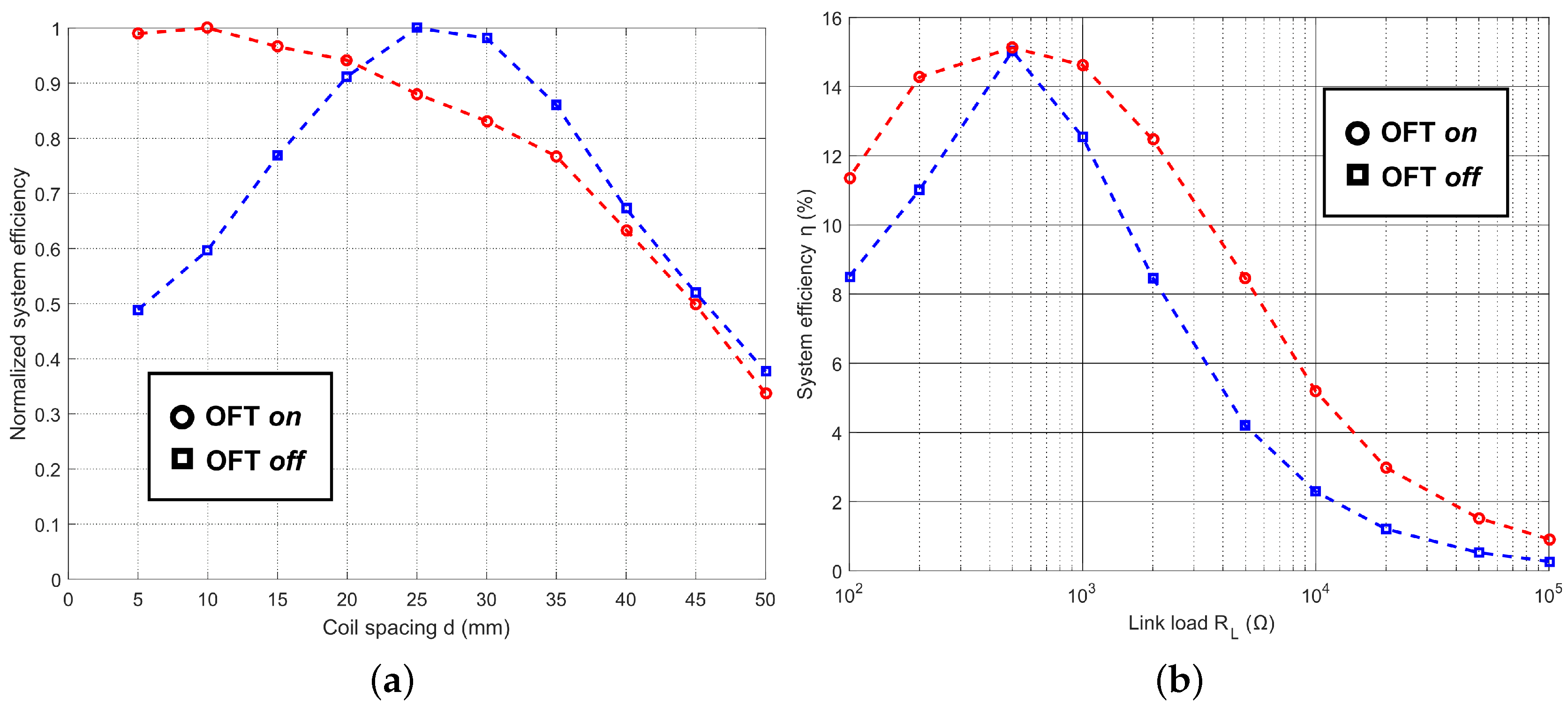
4.2. Link Measurements
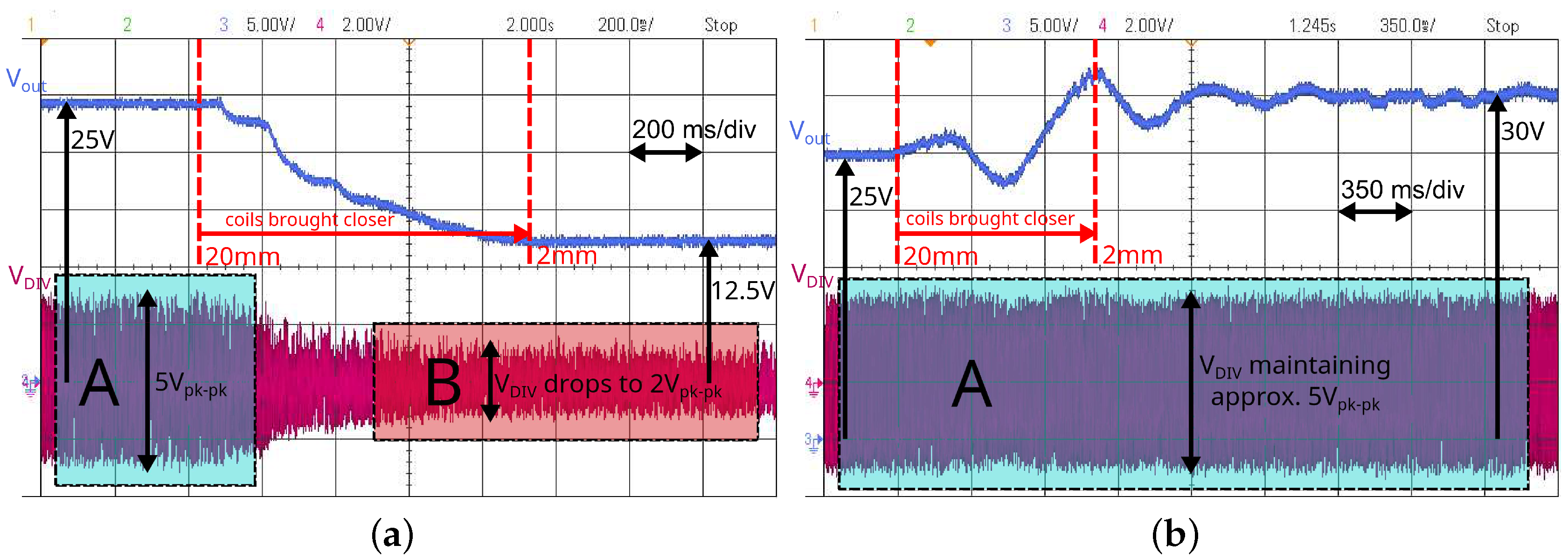
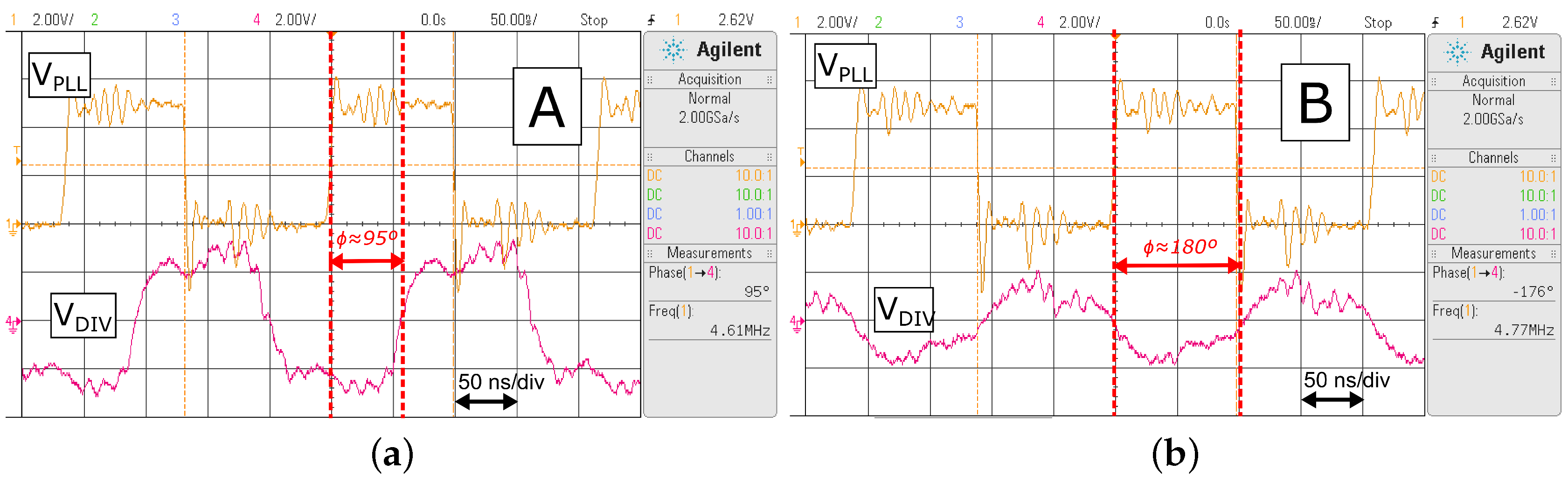
4.3. Real-Time System Operation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| WPT | Wireless Power Transfer |
| IMD | Implanted Medical Device |
| OFT | Optimum Frequency Tracking |
| PA | Power Amplifier |
| ED | Envelope Detector |
| PD | Phase Detector |
| LC | Lock Comparator |
| PLL | Phase-Locked Loop |
| EA | Error Amplifier |
| ADC | Analogue to Digital Converter |
References
- Rhew, H.G.; Jeong, J.; Fredenburg, J.A.; Dodani, S.; Patil, P.G.; Flynn, M.P. A fully self-contained logarithmic closed-loop deep brain stimulation SoC with wireless telemetry and wireless power management. IEEE J. Solid-St. Circ. 2014, 49, 2213–2227. [Google Scholar] [CrossRef]
- Lee, B.; Ahn, D.; Ghovanloo, M. Three-phase time-multiplexed planar power transmission to distributed implants. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Stoecklin, S.; Yousaf, A.; Volk, T.; Reindl, L. Efficient wireless powering of biomedical sensor systems for multichannel brain implants. IEEE Trans. Instrum. Meas. 2015, 65, 754–764. [Google Scholar] [CrossRef]
- Moradi, E.; Björninen, T.; Sydänheimo, L.; Rabaey, J.M. Analysis of wireless powering of mm-size neural recording tags in rfid-inspired wireless brain- machine interface systems. In Proceedings of the IEEE International Conference on RFID, Penang, Malaysia, 30 April–2 May 2013; pp. 8–15.
- Lin, Y.P.; Yeh, C.Y.; Huang, P.Y.; Wang, Z.Y.; Cheng, H.H.; Li, Y.T.; Chuang, C.F.; Huang, P.C.; Tang, K.T.; Ma, H.P.; et al. A Battery-Less, Implantable Neuro-Electronic Interface for Studying the Mechanisms of Deep Brain Stimulation in Rat Models. IEEE Trans. Biomed. Circuits Syst. 2015, 10, 98–112. [Google Scholar] [CrossRef] [PubMed]
- Cleven, N.J.; Müntjes, J.A.; Fassbender, H.; Urban, U.; Görtz, M.; Vogt, H.; Gräfe, M.; Göttsche, T.; Penzkofer, T.; Schmitz-Rode, T.; et al. A novel fully implantable wireless sensor system for monitoring hypertension patients. IEEE Trans. Biomed. Eng. 2012, 59, 3124–3130. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.; Chiou, J.C. A wireless and batteryless microsystem with implantable grid electrode/3-dimensional probe array for ECoG and extracellular neural recording in rats. Sensors 2013, 13, 4624–4639. [Google Scholar] [CrossRef] [PubMed]
- Laskovski, A.N.; Yuce, M.R.; Dissanayake, T. Stacked spirals for biosensor telemetry. IEEE Sens. J. 2011, 11, 1484–1490. [Google Scholar] [CrossRef]
- Kang, S.K.; Murphy, R.K.J.; Hwang, S.W.; Lee, S.M.; Harburg, D.V.; Krueger, N.A.; Shin, J.; Gamble, P.; Cheng, H.; Yu, S.; et al. Bioresorbable silicon electronic sensors for the brain. Nature 2016, 530, 71–76. [Google Scholar] [CrossRef] [PubMed]
- Niu, W.Q.; Chu, J.X.; Gu, W.; Shen, A.D. Exact analysis of frequency splitting phenomena of contactless power transfer systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1670–1677. [Google Scholar] [CrossRef]
- Bocan, K.; Sejdić, E. Adaptive transcutaneous power transfer to implantable devices: A state of the art review. Sensors 2016, 16, 393. [Google Scholar] [CrossRef] [PubMed]
- Kiani, M.; Ghovanloo, M. An RFID-based closed-loop wireless power transmission system for biomedical applications. IEEE Trans. Circ. Syst. II Exp. Briefs 2010, 57, 260–264. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Liu, W.; Sivaprakasam, M.; Kendir, G.A. Design and analysis of an adaptive transcutaneous power telemetry for biomedical implants. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 2109–2117. [Google Scholar] [CrossRef]
- Li, X.; Tsui, C.Y.; Ki, W.H. A 13.56 MHz wireless power transfer system with reconfigurable resonant regulating rectifier and wireless power control for implantable medical devices. IEEE J. Solid-St. Circ. 2015, 50, 978–989. [Google Scholar] [CrossRef]
- Lyu, Y.I.; Meng, F.Y.; Yang, G.H.; Che, B.J.; Wu, Q.; Sun, L.; Erni, D.; Li, J.L.W. A method of using nonidentical resonant coils for frequency splitting elimination in wireless power transfer. IEEE Trans. Power Electron. 2015, 30, 6097–6107. [Google Scholar] [CrossRef]
- Lenaerts, B.; Peeters, F.; Puers, R. Closed-loop transductor-compensated Class-E driver for inductive links. In Proceedings of the TRANSDUCERS and EUROSENSORS 2007–4th International Conference on Solid-State Sensors, Actuators and Microsystems, Lyon, France, 10–14 June 2007; pp. 65–68.
- Aldhaher, S.; Chi-kwong Luk, P.; Whidborne, J.F. Tuning class E inverters applied in inductive links using saturable reactors. IEEE Trans. Power Electron. 2014, 29, 2969–2978. [Google Scholar] [CrossRef]
- Si, P.; Hu, A.P.; Malpas, S.; Budgett, D. A frequency control method for regulating wireless power to implantable devices. IEEE Trans. Biomed. Circuits Syst. 2008, 2, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Kiani, M.; Ghovanloo, M. A triple-loop inductive power transmission system for biomedical applications. IEEE Trans. Biomed. Circuits Syst. 2015, 10, 138–148. [Google Scholar] [CrossRef] [PubMed]
- Hannan, M.A.; Hussein, H.A.; Mutashar, S.; Samad, S.A.; Hussain, A. Automatic frequency controller for power amplifiers used in bio-implanted applications: Issues and challenges. Sensors 2014, 14, 23843–23870. [Google Scholar] [CrossRef] [PubMed]
- Schormans, M.; Valente, V.; Demosthenous, A. Efficiency optimization of class-D biomedical inductive wireless power transfer systems by means of frequency adjustment. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5473–5476.
- Sample, A.P.; Meyer, D.A.; Smith, J.R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer. IEEE Trans. Ind. Electron. 2011, 58, 544–554. [Google Scholar] [CrossRef]
- Valente, V.; Eder, C.; Donaldson, N.; Demosthenous, A. A high-power CMOS class-D amplifier for inductive-link medical transmitters. IEEE Trans. Power Electron. 2014, 30, 1–12. [Google Scholar] [CrossRef]
- Terman, F.E. Radio Engineers’ Handbook; McGraw-Hill Book Company: New York, NY, USA, 1943. [Google Scholar]
- Van Schuylenbergh, K.; Puers, R. (Eds.) Inductive Powering; Springer Netherlands: Dordrecht, The Netherlands, 2009.
- Donaldson, N.D.N.; Perkins, T.A. Analysis of resonant coupled coils in the design of radio frequency transcutaneous links. Med. Biol. Eng. Comput. 1983, 21, 612–627. [Google Scholar] [CrossRef] [PubMed]
- Jow, U.M.M.; Ghovanloo, M. Design and optimization of printed spiral coils for efficient inductive power transmission. In Proceedings of the IEEE International Conference on Electronics, Circuits, and Systems, Marrakech, Morocco, 11–14 December 2007; Volume 1, pp. 70–73.
- Chandrakasan, A.P.; Verma, N.; Daly, D.C. Ultralow-power electronics for biomedical applications. Ann. Rev. Biomed. Eng. 2008, 10, 247–274. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Handwerker, J.; Ortmanns, M. Telemetry for implantable medical devices. IEEE Solid-St. Circ. Mag. 2014, 6, 60–63. [Google Scholar] [CrossRef]
- Lenaerts, B.; Puers, R. An inductive power link for a wireless endoscope. Biosens. Bioelectron. 2007, 22, 1390–1395. [Google Scholar] [CrossRef] [PubMed]
- Ha, S.; Khraiche, M.L.; Silva, G.A.; Cauwenberghs, G. Direct inductive stimulation for energy-efficient wireless neural interfaces. In Proceedings of the 2012 IEEE-EMBS International Conference on Biomedical and Health Informatics, Hong Kong, China, 5–7 January 2012; pp. 883–886.
- Mirbozorgi, S.A.; Bahrami, H.; Sawan, M.; Gosselin, B. A smart multi-receiver power transmission system for long-term biological monitoring. In Proceedings of the 2014 IEEE Biomedical Circuits and Systems Conference (BioCAS), Lausanne, Switzerland, 22–24 October 2014; pp. 412–415.
| Tx Coil | Rx Coil | ||
|---|---|---|---|
| Outer Diameter | 64.7 mm | 20.0 mm | |
| Inner Diameter | 37.2 mm | 4.7 mm | |
| Number of Turns | n | 12 | 13 |
| Inductance | L | 10.150 | 2.255 |
| Q-factor | Q | 47.5 | 26.0 |
| [13] | [12] | [19] | [31] | This Work | |
|---|---|---|---|---|---|
| Operating Frequency | 1 MHz | 13.56 MHz | 13.56 MHz | 10 MHz | Variable (4.5–5.5 MHz) |
| Effective Range | 15 mm | 20 mm | 20 mm | N/A | 30 mm |
| Compensation Parameter | Supply Voltage | Supply Voltage | , , and Supply Voltage | None | Drive Frequency |
| System Efficiency (Best) | 65.8% | 14% | 14% | N/A | 15% |
| Component Mismatch Insensitive | No | No | Yes | No | Yes |
| Passive Implant Compatible | No | No | No | Yes | Yes |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schormans, M.; Valente, V.; Demosthenous, A. Frequency Splitting Analysis and Compensation Method for Inductive Wireless Powering of Implantable Biosensors. Sensors 2016, 16, 1229. https://doi.org/10.3390/s16081229
Schormans M, Valente V, Demosthenous A. Frequency Splitting Analysis and Compensation Method for Inductive Wireless Powering of Implantable Biosensors. Sensors. 2016; 16(8):1229. https://doi.org/10.3390/s16081229
Chicago/Turabian StyleSchormans, Matthew, Virgilio Valente, and Andreas Demosthenous. 2016. "Frequency Splitting Analysis and Compensation Method for Inductive Wireless Powering of Implantable Biosensors" Sensors 16, no. 8: 1229. https://doi.org/10.3390/s16081229
APA StyleSchormans, M., Valente, V., & Demosthenous, A. (2016). Frequency Splitting Analysis and Compensation Method for Inductive Wireless Powering of Implantable Biosensors. Sensors, 16(8), 1229. https://doi.org/10.3390/s16081229






