1. Introduction
The face image is widely used to discriminate and identify people, in lip reading and to understand one’s emotion and intentions based on the facial expressions [
1,
2,
3]. This paper aims to develop a 3D facial movement tracking framework for real time human computer interface applications such as expression recognition, intention prediction, mental state estimation, etc. In such contexts, the 3D facial movement includes: (a) rigid global head movement and (b) non-rigid facial muscle movement. The rigid global head movement or the head pose consists of a continuous angular measurement of three degree-of-freedom (3-DOF) and a continuous translation measurement of 3-DOF. The non-rigid face movement includes eyelid movement and mouth movement, which play an important role in interpreting the face expression.
State-of-the-art techniques demonstrate impressive real-time facial animation tracking results by using the depth data from an RGBD camera [
4,
5]. Video cameras, however, are more widely available on PCs and mobile devices than RGBD cameras, and video-based facial tracking remains a challenging problem.
The video-based face tracker can be categorized as either motion-based or model-based [
6]. The motion-based tracker estimates the displacements of pixels (or blocks of pixels) from one frame to another. The motion field is used to estimate the face motion, but it accumulates motion errors and eventually will lose face tracking. The model-based tracker, on the other hand, uses the prior knowledge of the face structure and motion and tries to update the object’s model parameters to fit new frames.
Video-based face trackers can also be categorized as either appearance-based or feature-based [
6]. Appearance-based trackers match a parameterized model of the entire facial appearance with the test image, trying to find optimal parameters that minimize the distance between the image generated from the synthesized face model and the test image. To search for the optimal parameters in a high-dimensional space brings high computational complexity. Feature-based trackers firstly extract a few facial feature points and then optimize the face pose (and possibly shape) using these feature points. The facial feature points are the fiducial landmarks surrounding facial components: brows, eyes, nose, and mouth. They encode critical information about facial expression and face movement.
From the perspective of error suppression and computation complexity, the Model-Based & Feature-Based framework is a better choice. For a Feature-Based Tracker the facial landmark localization is a crucial stage.
Active Shape Models (ASM) [
7], Active Appearance Models (AAM) [
8] and Constrained Local Models (CLM) [
9] are classical model based methods for facial landmark localization. In ASM, firstly Procrustes Analysis [
10] is applied to the training data to remove similarity transformations, then PCA is utilized to obtain a shape model defined by mean shape and eigenvectors. AAM is an extension of ASM, which contains both the shape statistical model and appearance statistical model. The fitting of AAM can be viewed as an optimization process and Gauss-Newton iterative algorithm is often used to solve this problem. Some modified algorithms have been proposed in the past years to improve the performance of ASM and AAM [
11,
12,
13]. However, most fitting algorithms are sensitive to pose and illumination changes. The initial location in the test image has a significant impact on the result of ASM or AAM, which makes the algorithm less robust. CLM utilizes the same shape model as ASM and AAM, except that the appearance model in CLM is constructed by local facial landmark patches instead of the entire face region. In addition, the appearance model in CLM is used to generate feature templates instead of approximating the image pixels directly. Wang et al. [
14] proposed an enforcing convexity strategy at each local patch response surface to optimize a global warp update in an efficient way. This local patch response was obtained by linear SVM and the parametric vector was updated using convex quadratic curve fitting method. Saragih et al. [
15] pointed that the effect of ambiguous landmark detections in CLM could be reduced by posing a constraint on joint motion. The non-parametric mean-shift approach was applied over all landmarks simultaneously to impose a global prior over the joint motion.
Some unified frameworks were proposed to detect the face and landmark simultaneously to handling large facial pose variations. Zhu and Ramanan [
16] proposed a unified tree structured part model for face detection, pose and landmark estimation. A mixture-of-trees model was encoded based on the topological changes of viewpoint, and each facial landmark was described by deformable part model. The dynamic programming algorithm was utilized to find global optimal solutions. Yu et al. [
17] proposed an optimized part mixtures by using the most significant anchor points while omitting the intermediate landmarks, which reduces the risk of error propagation from misaligned landmarks. However, both the method in [
16,
17] cannot run in real-time.
In the last few years Discriminative Shape Regression (DSR) has been widely used to locate facial landmarks across different persons, illuminations, and viewpoints in real-time [
18,
19]. These techniques predict a 2D face shape in a cascade manner: They begin with an initial guess about shape and then progressively refine that guess by regressing a shape update step-by-step from the feature space. Feature spaces can be either global features such as pixel-difference features and Haar-like features in the face region [
19,
20,
21], or local features such as SIFT and local binary features with respect to the landmarks [
22,
23,
24]. The regression function can be either a Ferns regression [
19,
20], regression trees [
21], regression forest [
25] or linear regression [
22,
23,
24]. Compared with the model-based methods such as AAM or CLM, the regression based method utilizes the pre-trained regressor to solve the complex, high dimensional, non-linear optimization problem (such as SDM [
22]), this regression process is simple and achieves real-time performance. In addition, regression based method directly uses the location of landmarks to describe the face shape.
While most previous face alignment work has emphasized on 2D face tracking and registration, recovering 3D facial movement information from 2D video has not been studied intensively. Only recently [
26,
27] proposed to recover the 3D face pose and facial animation through regression methodology. Because this kind of approach requires extra scanned 3D face datasets and uses both 2D and 3D annotations, a correction step is needed to resolve inconsistency in the landmark positions across different poses and self-occlusions.
Inspired by the structure from motion methodology, this paper proposes an analytical approach to estimate 3D facial movement using 2D landmarks in real time. The framework adopts Discriminative Shape Regression to locate the 2D facial feature points on the image and uses an Extended Kalman Filter (EKF) tracking kernel to estimate the 3D facial movement.
The paper’s main contribution is the development of a framework that combines a 2D facial feature point extraction and a 3D EKF tracking kernel. The framework expands 2D facial landmarks into 3D facial movement information. Given actual face scale the framework could output real world metric. Moreover the framework could register the face shape automatically for different persons.
The arrangement of the paper is as follow:
Section 2 presents the algorithm of facial feature point extraction on images;
Section 3 gives the 3D face model and its projection model;
Section 4 develops the Extended Kalman Filter tracking kernel;
Section 5 presents the experiment evaluation of the proposed framework;
Section 6 makes a conclusion and gives the future work’s direction.
2. Facial Feature Point Extraction
This section presents the discriminative shape regression for facial feature point extraction. We first introduce the training and testing processes of DSR. Then after a quantitative comparison of DSRs with different feature mapping functions and regression functions, we propose to implement the DSR with SIFT feature function and linear regression function since it balances accuracy and real-time processing.
2.1. Training
Given
training images
and the corresponding annotated shapes
with
, where
is the number of landmarks. The training procedure of DSR can be summarized as following steps, for details please refer to [
22,
23,
24]:
Step 1. Training Data Augmentation. Each image in the training data is initialized by randomly sampling multiple shapes of other annotated images, the training samples can be expressed by triplets of face image, initial shape estimation and target shape. The triplet can be represented as , where and (, where is the number of augmentation). By randomly selecting other annotated shapes as the initial training shapes, one training image can produce different triplets, this can be viewed as an augmented process, and the total number of these augmented samples is .
Step 2. Feature Mapping. The shape-indexed feature is generated by the feature mapping function , where , is the feature dimensionality. SIFT features is adopted as the feature mapping function in DSR. It is a kind of local feature that extract only the local region feature coordinated with the facial landmarks.
Step 3.
Regressor Learning. A regressor in stage
is learned by minimizing the error between the estimated shape
and ground truth shape
in image
as:
For a linear regressor,
has the form of:
where
and
. Then, Equation (2) becomes a least squares problem and has a closed solution as:
where
is the feature matrix,
is the identity matrix,
is used to avoid the inversion of singular matrix and
is the error matrix between the ground truth shapes and the current estimated shapes.
Step 4. Shape Update.
where
.
Step 2–Step 4 iterate in a gradient boosting framework until converged to the target shapes.
2.2. Runtime Regreesion
Given a new image
with an initial shape
, the landmark is regressed by the learned cascaded regressor
stage by stage as:
where
is the input image,
is the shape with
facial landmarks in
at stage
,
is the shape-indexed feature mapping function depends on both image
and previous estimated shape
,
is the regression function in stage
and
is the number of cascade level.
The success of discriminative regression method is mainly due to the following properties: (1) the shape-indexed feature in each stage makes a re-sampling at the previous estimation of the landmark location. This feature extract method compensates the effect of large appearance variations and increases the robustness and accuracy; (2) gradient boosting framework is incorporated in the training procedure of regression functions. In each stage the regression function is learned based on the previously estimated shape error and the shape-indexed feature. Thus, the output error in each stage monotonically decreases and converges in 4 or 5 stages; (3) the output of the regressor is a linear combination of training shapes which inherently guarantees the output is a reasonable face shape without any extra constraints.
2.3. Feature Mapping Functions and Regression Functions
The feature mapping and regressor learning are the two main steps in DSR. The selection of feature mapping function and regression function may affect the DSR performance. In this section, we compare different DSR implementations to find a better one. Candidate feature mapping functions include pixel-difference features and SIFT features and candidate regression functions include ferns regression, regression trees and linear regression. The LFPW dataset [
28] and COFW dataset [
20] are utilized to make a quantitative comparison.
Pixel-difference Features (PFs) calculate the intensity difference of (here in our implementation) pairs of pixels in the face region. These pixel intensities are obtained by interpolated shape-indexed features, the correlation-based feature selection is utilized to select the final features (128 dimensions in our paper) for regression. SIFT Features (SFs) are obtained by resizing the width of face in the training image into 255 pixel width and then a pixel region around each facial landmark is used to extract SIFT features. The feature dimensions of SFs for a single landmark is 128. The final features are composed by the cascade of these local SIFT features and with the dimension of .
Ferns Regressor (FR) is implemented with depth of 5 and two-level cascaded regression with T = 100 and K = 50. T is the number of cascade level and K is the number of regressors that used in each cascade level. Trees Regressor (TR) is with depth of 5 and the minimum samples for each leaf node is set to 5, two-level cascaded regression is adopted with T = 10 and K = 10 similar as ferns regressor. Linear Regressor (LR) is utilized as described in
Section 2.1 with T = 5 in LFPW dataset and T = 10 in COFW dataset for more complex environment.
All the datasets for the experiments are initialized with L = 20 and the initial shape is selected as the mean shape for testing. Actually, SFs has high-dimension feature space (
) and not suitable for ferns and tree regression, so we didn’t implement DSR with these combinations.
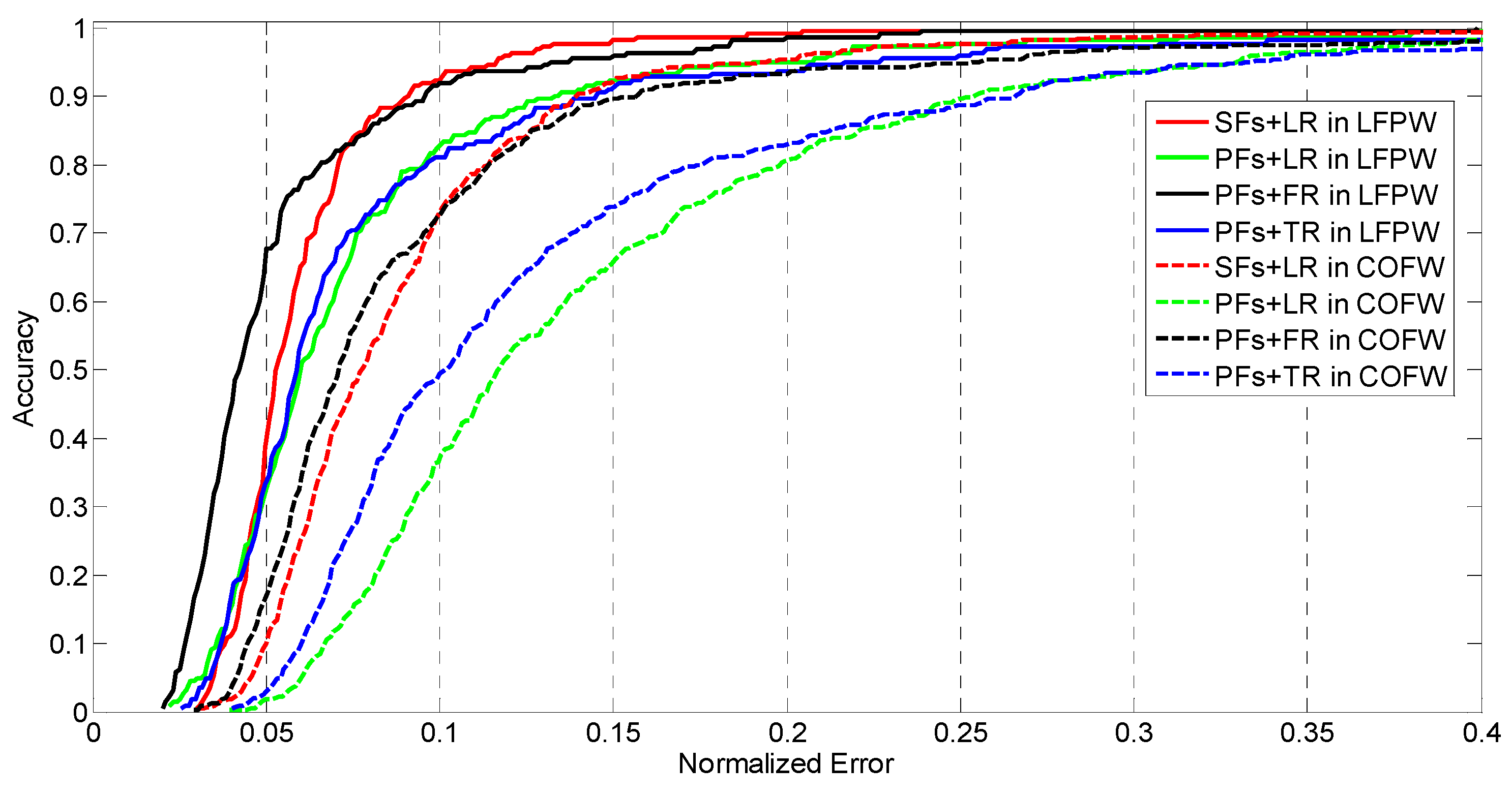
Figure 1 shows the CED curve of these comparisons.
Figure 1 shows that the combination of PFs and FR gives the best performance. This method uses simple features but large number of weak regressors (5000 in our application) to obtain good results. However, its computation cost is high. TR is stronger than ferns and linear regression. Actually, ferns can be viewed as a simplified version of tree regression with randomly split features chosen. The number and depth of TR have significant effect on the regression result, which cause the regressor tend to be under-fitting or over-fitting. SFs contain more information (such as gradient and directional information) but its computation cost is higher than PFs. However, this strong features need fewer iterations for shape regression (
in LFPW and
in COFW), which decreases the computation time of regressor. Considering the balance of accuracy and computation efficiency, we propose to implement DSR with SIFT features and linear regression.
4. Tracking Kernel
Given
facial feature points
obtained from the facial feature point extraction module and their corresponding vertex in the face model
, the 3D facial movement tracking problem can be solved by minimizing the following function:
This cost function minimizes the Euclidean distance between the projected points of the model vertexes and the extracted points in the image.
Normally different persons have different face shapes and the face would take random global or local motions. So every parameter in vector
is a random variable. But the evolution of vector
from time
to time
can be approximated by some classical dynamic model plus additive noise. Here a zero-order evolution model is adopted, where the object’s motion is considered as static evolution. The state evolution equation is:
where
is the state vector and is defined as
,
and
is the value of the state vector at time
and
,
is an identity matrix,
equals to the sampling time
, and the process noise
is a zero-mean Gaussian white noise vector. Assume the initial state error covariance matrix is
, the noise distribution satisfy
and
,
is the covariance matrix of process noise and
is the covariance matrix of measurement noise. The paper utilizes the Extended Kalman Filter (EKF) algorithm to recursively solve the facial movement problem as follow:
Firstly, predict the a priori of state vector and its covariance matrix at
using the evolution model as Equation (15a,b):
where
is the posterior state vector value at time
,
is the prior state vector value at time
,
is the posterior covariance matrix of state error at time
,
is the prior covariance at time
,
is the covariance matrix of process noise at time
.
In Equation (14), a zero-order static evolution system model is adopted to approximate the face movement dynamics. There exist some modeling errors for the approximation inevitably, which would result inaccuracy estimation. To compensate these modeling errors the fading-memory filter is introduced. The fading-memory filter is identical to the standard Kalman filter, except that the prediction of
has a factor
in its first term as in Equation (15c). This factor serves to increase the uncertainty in the state prediction, which gives more credence to the measurement. In most applications,
is only slightly greater than 1 (for example, 1.01):
When new measurement arrives we have to correct the a priori using the new measured facial feature points
(
is the vector of the measured facial feature points,
is the total number of feature points). Given the a priori we could derive the facial feature points using the projection model
as in Equation (11), where
is the corresponding vertex of
in the basic face model. The difference between the measured points
and the projected points
is used as the residual to correct the predicted a priori:
and
. The correction equation is (16a) and (16b):
where
is the posterior state vector at time
,
is the posterior covariance matrix of state error at time
,
is the Kalman gain factor and
is the Jacobean matrix of measurement to state vector.
The state error covariance matrix
should be a symmetric positive definite matrix. Because of numerical computing problems, the posterior update of covariance matrix
in Equation (16b) does not guarantee
is positive definite even when
and
are positive definite. So Equation (16b) is replaced with Equation (16c), which guarantees
is positive definite:
The Kalman gain factor
is obtained using Equation (17):
Observing Equations (16b,c) and (17) it is easy to find that
is already available from the a priori,
can be determined from the facial feature point extraction module as covariance of measurement noise,
is the Jacobean matrix of measurement to state vector. Equation (11) is the measurement model for Kalman filter, which project the state vector to the facial feature points. Since the projecting process is nonlinear we have to linearize the measurement model at the current state point and compute the
at every time step, which is called Extended Kalman Filter. The Jacobean matrix is defined as:
Using the chain rule of partial differential,
can be written as:
can be derived from Equation (10) as:
can be derived from Equation (9) as:
,
,
and
can be derived from Equation (8) as:
and
can be derived from Equation (7) as:
Substituting Equation (20a–h) into Equation (19) yields the partial differential of one facial feature point to the state vector. Then the Jacobean matrix of Equation (18) can be obtained by padding all the partial differential of the measured feature points along the row. Jacobean matrix should be computed every step using the a priori value.
Given Equations (15)–(18) we could estimate the face 3D movement recursively using newly measured facial feature points.
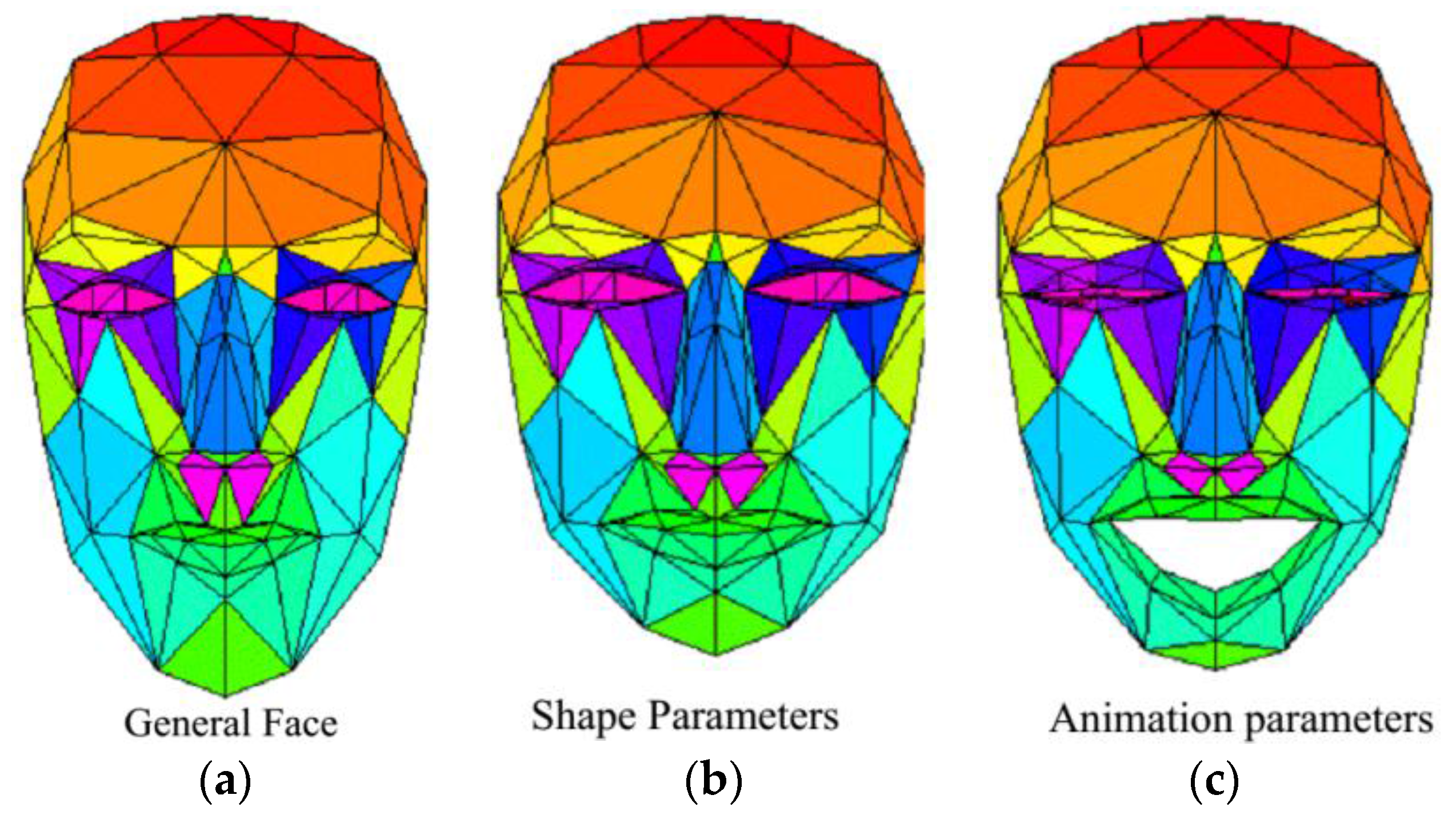
During implementation the pose (), shape () and animation () parameters are optimized using an alternating strategy. Firstly the pose is optimized then the shape is optimized and finally the animation is optimized. The alternating strategy could reduce the coupling problem between the parameters and fit to different persons more accurately.
6. Conclusions and Future Work
This paper develops a 3D facial movement tracking framework for real time human computer interface applications such as expression recognition, intention prediction, mental state estimation, etc. In such contexts, the 3D facial movement includes: (a) rigid global head movement and (b) non-rigid facial muscle movement. The proposed framework combines a DSR facial landmark localization module and an EKF 3D face tracking kernel. After comparing different DSR implementations quantitatively the framework decide to implement DSR with SIFT features and linear regression considering its accuracy and real time performance. An analytical EKF 3D face movement tracking kernel is derived, which could track the 3D face pose and animation parameters using 2D facial feature points. During implementation the pose, shape and animation parameters are optimized using an alternating strategy. Firstly the pose is optimized then the shape is optimized and finally the animation is optimized. The alternating strategy could reduce the coupling problem between the parameters and fit to different persons more accurately.
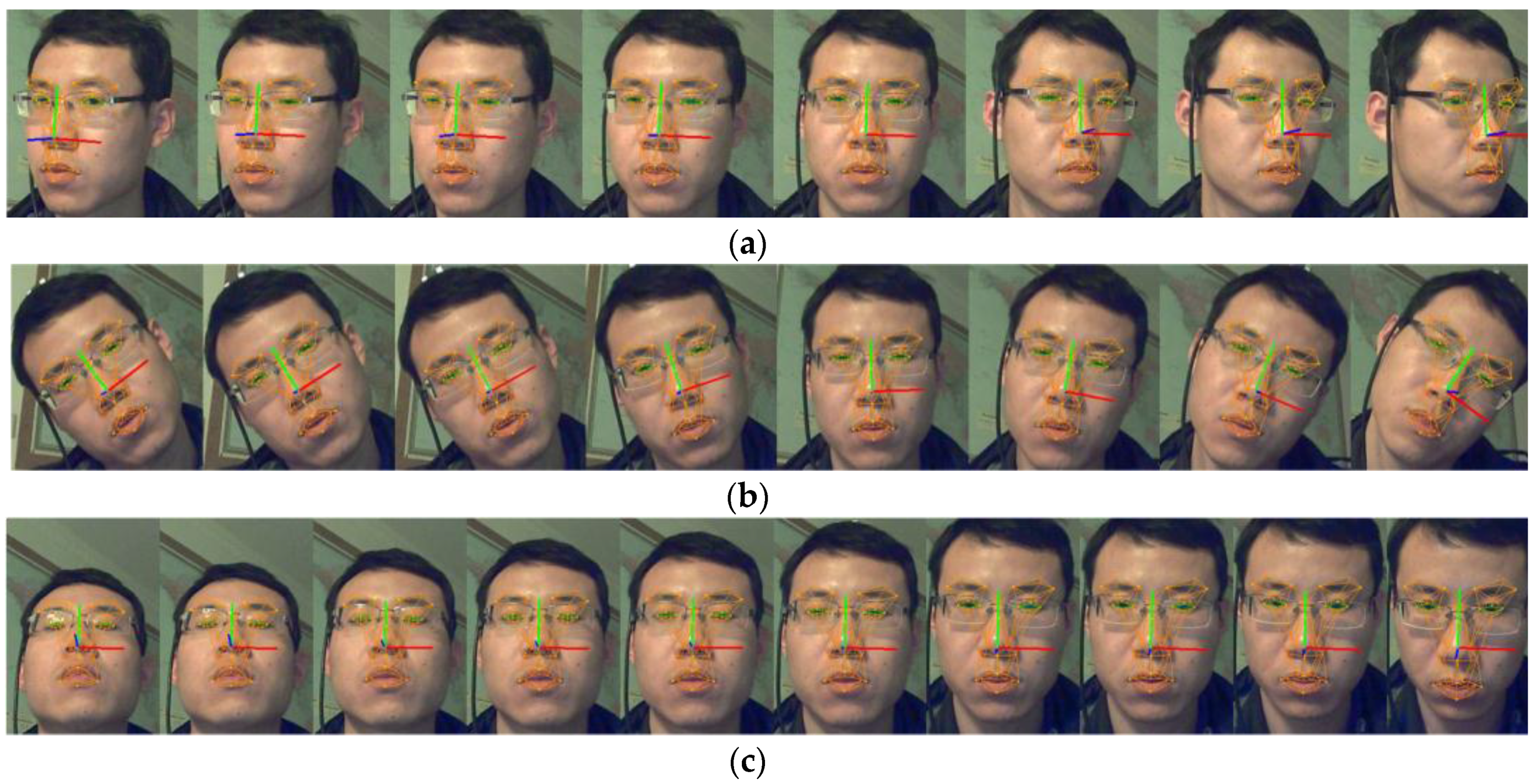
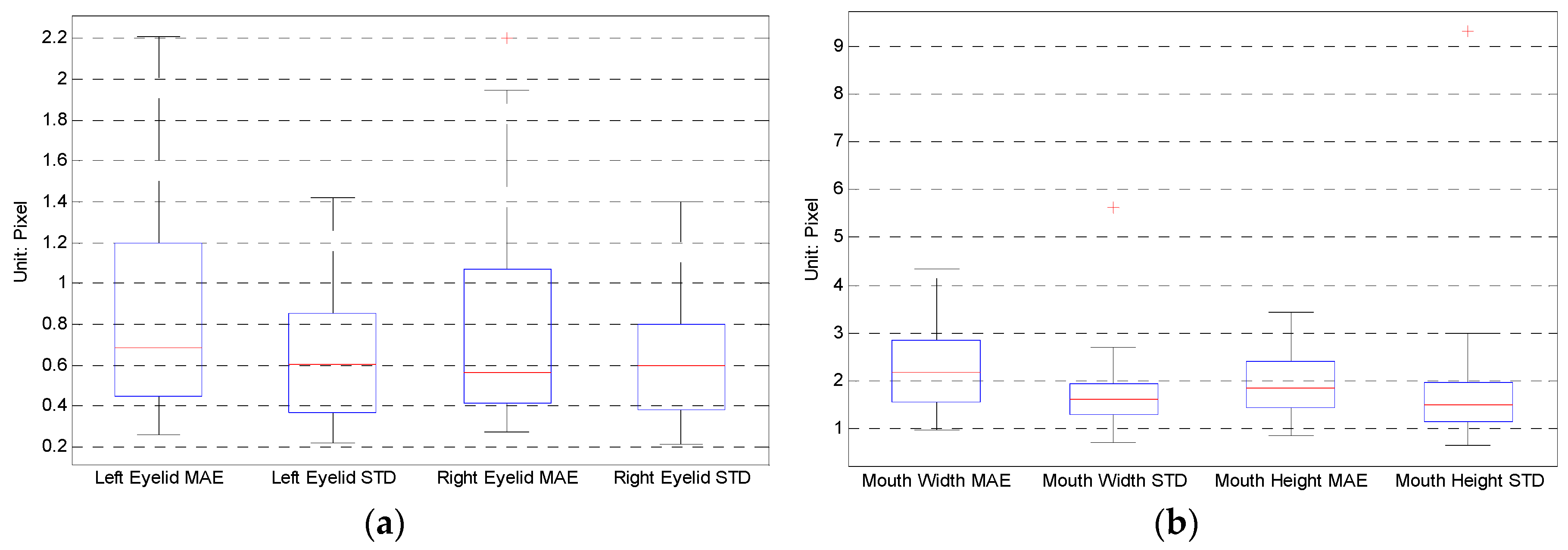
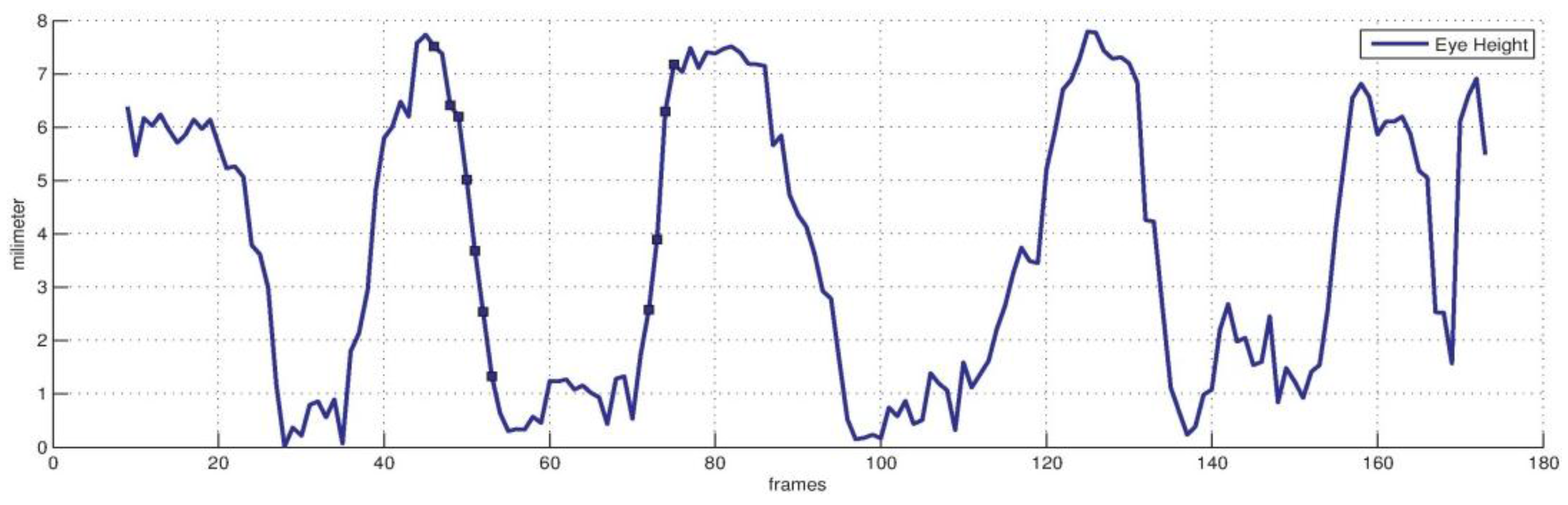
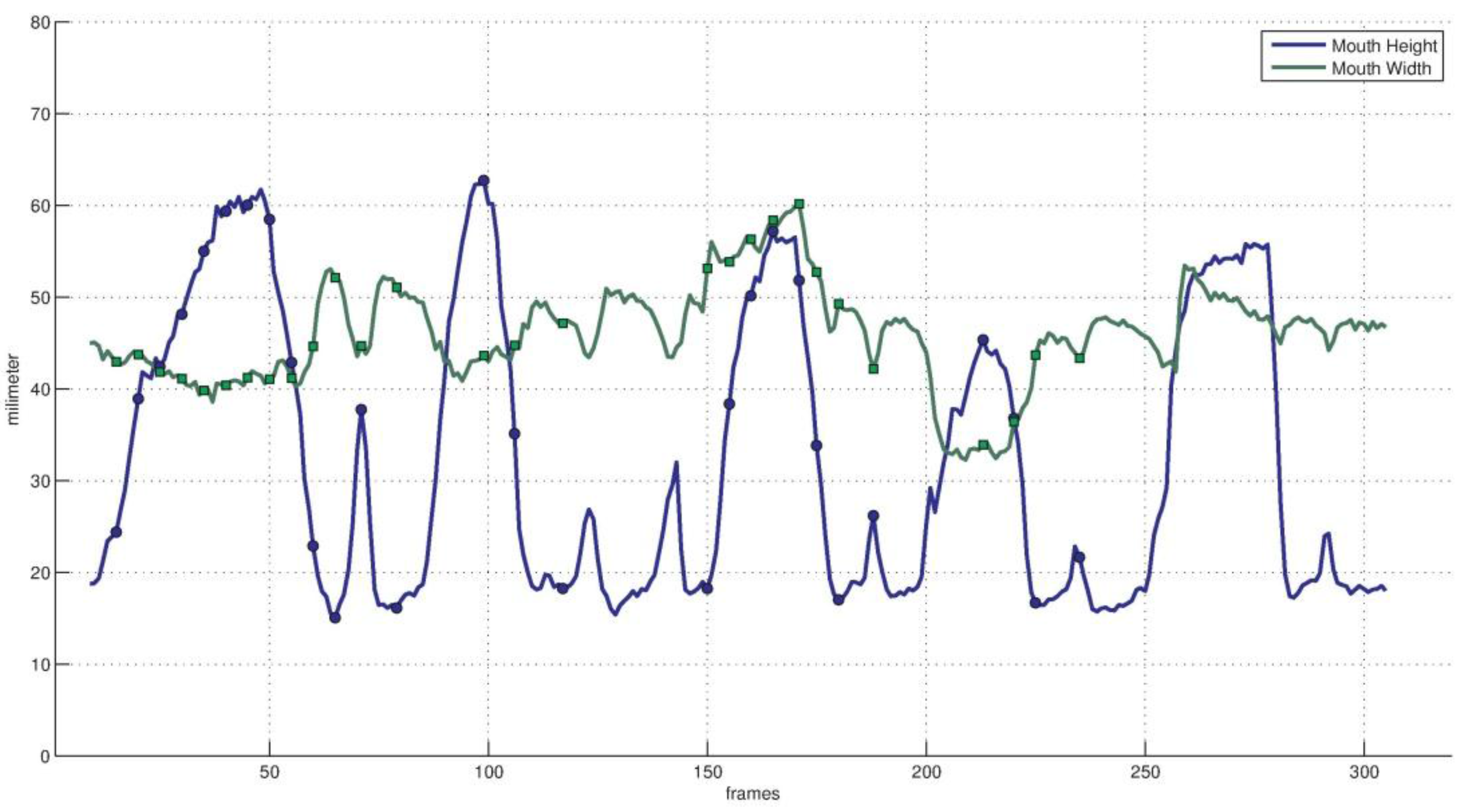
Experiments show that the proposed framework could track the face rotation with MAE of 4.23 (yaw), 5.65 (roll) and 2.36 (pitch) degree for BUFT datasets and 2.8 (yaw), 2.3 (roll) and 2.2 (pitch) degree for our laboratory datasets. The MAE of the eyelid distance tracking mainly locates within 1.2 pixels, while the MAE of the mouth width and height tracking mainly locate within 2.8 pixels on 300-VW database. Given registered face scale the framework could produce eyelid distance and mouth width/height with a metric of millimeter. The eyelid tracking error is 1 mm while the mouth width/height tracking error is 2 mm. Experiments on 300-VW and our laboratory dataset also show the framework could fit to different persons automatically and accurately thanks to the alternating optimizing strategy.
In the future we will conduct research on the following aspects: increasing the working range of yaw rotation, enhancing the robustness against partial occlusion, pose-free gaze estimation and solving the variable coupling problem to increase the accuracy.