Verification of Geometric Model-Based Plant Phenotyping Methods for Studies of Xerophytic Plants
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
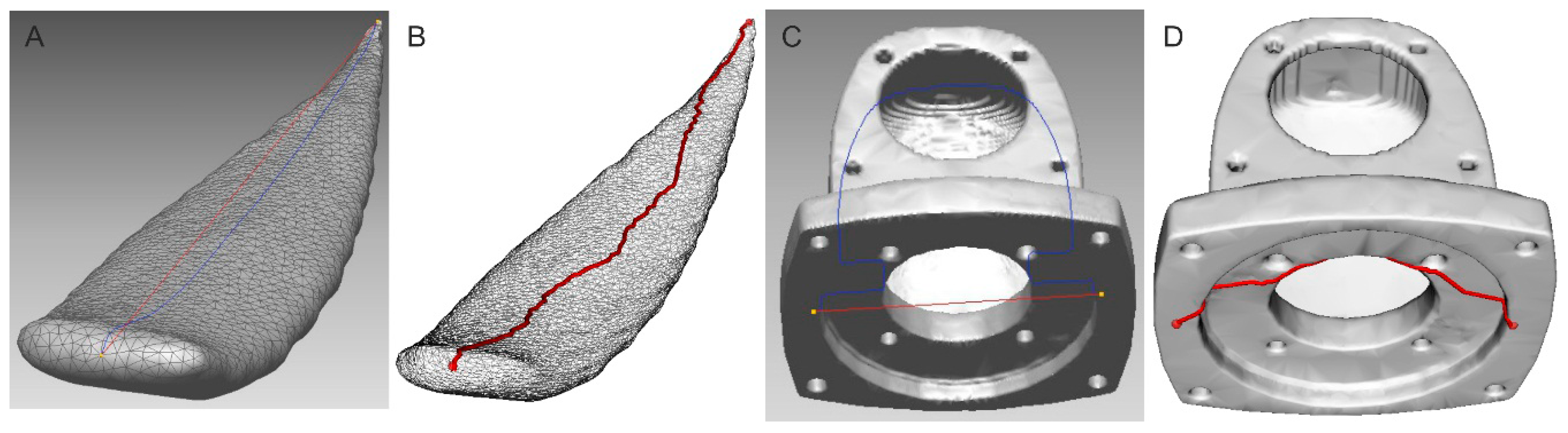
2.2.1. Distance Measurement between Two Points
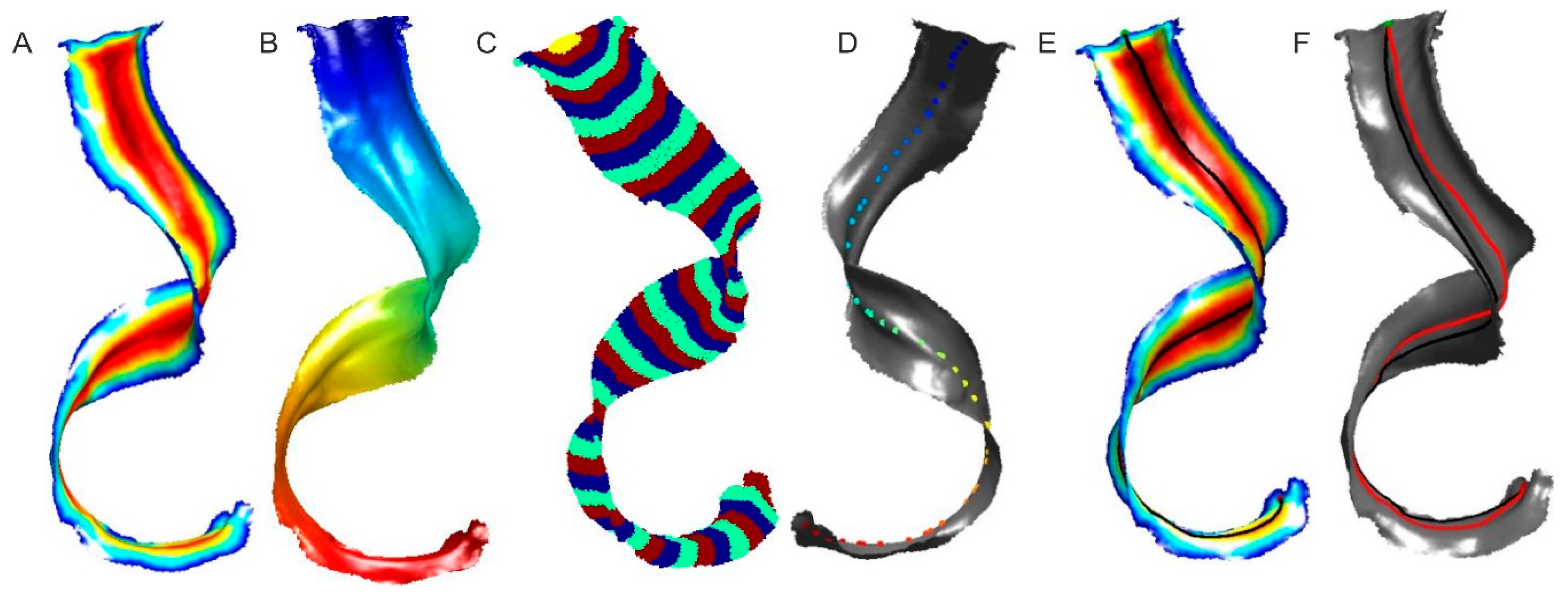
2.2.2. Leaf’s Length Estimation as a Center Line
- finding the outer edges of the leaf,
- mapping the distances between all vertices in the triangular mesh from the starting point using the FMM method and division into a given number of areas (Figure 4B,C),
- determining the vertices that are furthest from the object’s edges in every area except the one containing the starting point and the endpoint (Figure 4D),
- determining the shortest routes between vertices set in the previous step, taking into account the starting point and the endpoint, then summing them (Figure 4E).
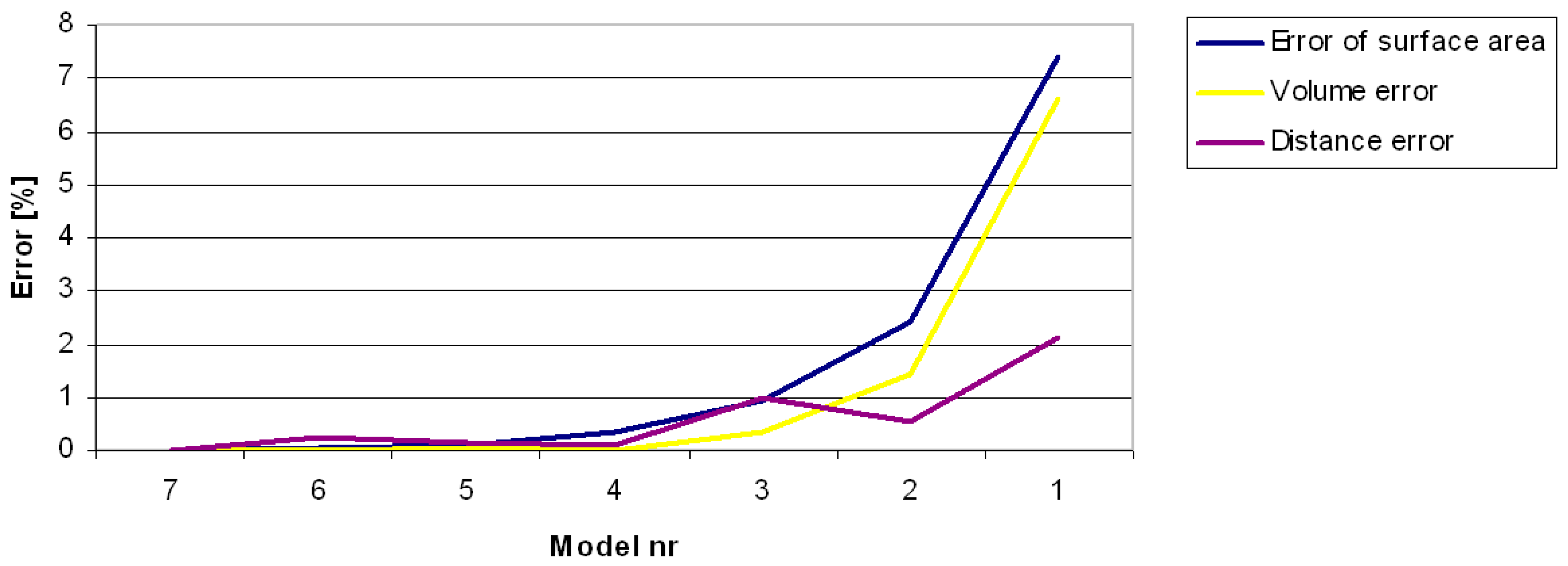
2.2.3. Errors of Measurement Based on Computer Models
3. Results
3.1. Errors in Measurement of Distances, Areas and Volumes on the Basis of Computer Models
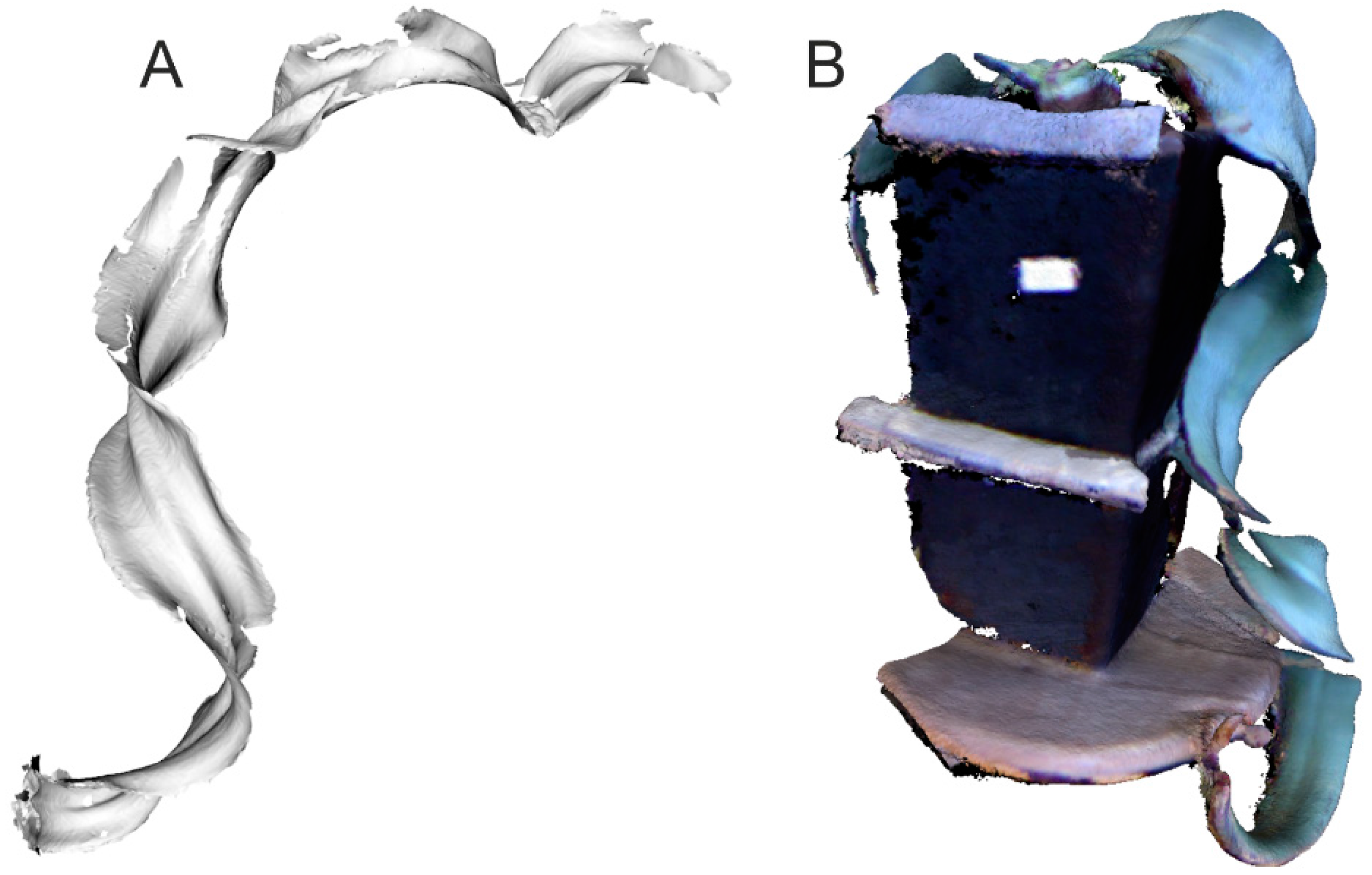
3.2. DAVID Laserscanner Scanning Results and Data Processing
3.3. Hand-Held and Kinect Scanning Results
3.4. Geometric Models of Large-Size Plants
3.5. Detecting the Effect of Different Kinds of Surfaces on Effective Plant Scanning
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, L.; Zhang, Q.; Huang, D. A Review of Imaging Techniques for Plant Phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef] [PubMed]
- Chéné, Y.; Rousseau, D.; Lucidarme, P.; Bertheloot, J.; Caffier, V.; Morel, P.; Belin, E.; Chapeau-Blondeau, F. On the use of depth camera for 3D phenotyping of entire plants. Comput. Electron. Agric. 2012, 82, 122–127. [Google Scholar] [CrossRef]
- Von Willert, D.J.; Brinckmann, E.; Scheitler, B.; Eller, B.M. Availability of water controls Crassulacean acid metabolism in succulents of the Richtersveld (Namib desert, South Africa). Planta 1985, 164, 44–55. [Google Scholar] [CrossRef] [PubMed]
- Gaff, D.F. Desiccation tolerant vascular plants of southern Africa. Oecologia 1977, 31, 95–109. [Google Scholar] [CrossRef]
- Schulze, E.-D.; Lange, O.L.; Buschbom, U.; Kappen, L.; Evenari, M. Stomatal responses to changes in humidity in plants growing in the desert. Planta 1972, 108, 259–270. [Google Scholar] [CrossRef] [PubMed]
- Von Willert, D.J.; Wagner-Douglas, U. Water relations, CO2 exchange, water-use efficiency and growth of Welwitschia mirabilis Hook. fil. in three contrasting habitats of the Namib desert. Bot. Acta 1994, 107, 291–299. [Google Scholar] [CrossRef]
- Henschel, J.R.; Seely, M.K. Long-term growth patterns of Welwitschia mirabilis, a long-lived plant of the Namib Desert (including a bibliography). Plant Ecol. 2000, 150, 7–26. [Google Scholar] [CrossRef]
- Ehleringer, J. Leaf morphology and reflectance in relation to water and temperature stress. In Adaptation of Plants to Water and High Temperature Stress; John Wiley & Sons, Inc.: New York, NY, USA, 1980; pp. 293–308. [Google Scholar]
- Bruce, W.G.G. Medicinal properties in the Aloe. Excelsa 1975, 5, 57–68. [Google Scholar]
- Spickett, A.; Van der Merwe, D.; Matthee, O. The effect of orally administered Aloe marlothii leaves on Boophilus decoloratus tick burdens on cattle. Exp. Appl. Acarol. 2007, 41, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Grace, O.M.; Simmonds, M.S.J.; Smith, G.F.; van Wyk, A.E. Therapeutic uses of Aloe L. (Asphodelaceae) in southern Africa. J. Ethnopharmacol. 2008, 119, 604–614. [Google Scholar] [CrossRef]
- Liége, R.; de Souza, A.; Santana, M.F.S.; de Macedo, E.M.S.; de Brito, E.S.; Correia, R.T.P. Physicochemical, bioactive and functional evaluation of the exotic fruits Opuntia ficus-indica and Pilosocereus pachycladus Ritter from the Brazilian caatinga. J. Food Sci. Technol. 2015, 52, 7329–7336. [Google Scholar]
- Goettsch, B.; Hilton-Taylor, C.; Cruz-Piñón, G.; Duffy, J.P.; Frances, A.; Hernández, H.M.; Inger, R.; Pollock, C.; Schipper, J.; Superina, M.; et al. High proportion of cactus species threatened with extinction. Nat. Plants 2015. [Google Scholar] [CrossRef] [PubMed]
- Convention on International Trade in Endangered Species of Wild Fauna and Flora. Available online: https://www.cites.org/sites/default/files/eng/disc/CITES-Convention-EN.pdf (accessed on 24 November 2015).
- The IUCN Red List of Threatened Species Version 2014. 1. Available online: http://www.iucnredlist.org (accessed on 24 November 2015).
- Rahaman, M.M.; Chen, D.; Gillani, Z.; Klukas, C.; Chen, M. Advanced phenotyping and phenotype data analysis for the study of plant growth and development. Front. Plant Sci. 2015, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- DAVID 3D Scanning. Available online: http://www.david-3d.com (accessed on 24 November 2015).
- Suk, J.; Kim, S.; Ryoo, I. Non-contact plant growth measurement method and system based on ubiquitous sensor network technologies. Sensors 2011, 11, 4312–4334. [Google Scholar] [CrossRef] [PubMed]
- Kicherer, A.; Herzog, K.; Pflanz, M.; Wieland, M.; Rüger, P.; Kecke, S.; Kuhlmann, H.; Töpfer, R. An Automated Field Phenotyping Pipeline for Application in Grapevine Research. Sensors 2015, 15, 4823–4836. [Google Scholar] [CrossRef] [PubMed]
- Fanourakis, D.; Briese, C.; Max, J.F.J.; Kleinen, S.; Putz, A.; Fiorani, F.; Ulbrich, A.; Schurr, U. Rapid determination of leaf area and plant height by using light curtain arrays in four species with contrasting shoot architecture. Plant Methods 2014, 10, 9. [Google Scholar] [CrossRef] [PubMed]
- Walter, A.; Liebisch, F.; Hund, A. Plant phenotyping: From bean weighing to image analysis. Plant Methods 2015, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, D.; Chéné, Y.; Belin, E.; Semaan, G.; Trigui, G.; Boudehri, K.; Franconi, F.; Chapeau-Blondeau, F. Multiscale imaging of plants: Current approaches and challenges. Plant Methods 2015, 11, 6. [Google Scholar] [CrossRef] [PubMed]
- Humplík, J.F.; Lazár, D.; Husičková, A.; Spíchal, L. Automated phenotyping of plant shoots using imaging methods for analysis of plant stress responses—A review. Plant Methods 2015, 11, 29. [Google Scholar] [CrossRef]
- Mankoff, K.; Russo, T. The Kinect: A low-cost, high-resolution, short-range, 3D camera. Earth Surf. Process. Landf. 2013, 38, 926–936. [Google Scholar] [CrossRef]
- Barsanti, S.G.; Remondino, F.; Visintini, D. Photogrammetry and Laser Scanning for Archaeological Site 3D Modeling—Some Critical Issues. In Proceedings of the 2nd Workshop on the New Technologies for Aquileia, Aquileia, Italy, 25 June 2012; pp. B1–B10.
- Paulus, S.; Behmann, J.; Mahlein, A.-K.; Plümer, L.; Kuhlmann, H. Low-Cost 3D Systems: Suitable Tools for Plant Phenotyping. Sensors 2014, 14, 3001–3018. [Google Scholar] [CrossRef] [PubMed]
- Kempthorne, D.M.; Barry, M.; Zabkiewicz, J.A.; Young, J. 3D digitisation of plant leaves. ANZIAM J. 2014, 55, C138–C152. [Google Scholar]
- Artec 3D Scanners. Available online: http://www.artec3d.com (accessed on 24 November 2015).
- HandyScan 3D. Available online: http://www.creaform3d.com/en/metrology-solutions/products/portable-3d-scanner/technical-specifications-handyscan-3d (accessed on 24 November 2015).
- Perceptron. Available online: http://www.perceptron.com (accessed on 24 November 2015).
- Hexagon Metrology. Available online: https://hexagonmetrology.us/news-and-events/press-releases/116-romer-inc-unveils-all-new-infinite-20-series-measuring-arm (accessed on 24 November 2015).
- Portable Living Leaf Area Meter. Available online: http://www.instrumentsmart.com/plant-testing-instrument.html#portable-living-leaf-area-meter (accessed on 24 November 2015).
- Plant database. Available online: www.tropicos.org (accessed on 12 March 2016).
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed.; MIT Press and McGraw-Hill: Cambridge, MA, USA, 2001; pp. 595–601. [Google Scholar]
- Rapidform. Available online: http://www.rapidform.com/evaluations/rapidform-2006-evaluation (accessed on 24 November 2015).
- Kimmel, R.; Setian, J.A. Computing geodesic Paths on Manifolds. Proc. Natl. Acad. Sci. USA 1998, 95, 8431–8435. [Google Scholar] [CrossRef] [PubMed]
- Korecki, D. Software and Hardware Setup for Scanning and Plants Phenotyping. Master’s Thesis, Poznan University of Technology, Poznan, Poland, 2015. [Google Scholar]
- Schroeder, W.; Martin, K.; Lorencen, M. The Visualization Toolkit. In An Object-Oriented Approach to 3D Graphics; Prentice-Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- The Visualization Toolkit. Available online: http://www.vtk.org (accessed on 24 November 2015).
- Wu, C. VisualSFM: A Visual Structure from Motion System. Available online: http://ccwu.me/vsfm (accessed on 24 November 2015).
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the 3DV 2013 International Conference on 3D Vision, Seattle, WA, USA, 29 June–1 July 2013; pp. 127–134.
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. Eurogr. Symp. Geom. Process. 2006, 61–70. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Slaughter, D.C.; Max, N.; Maloof, J.N.; Sinha, N. Structured Light-Based 3D Reconstruction System for Plants. Sensors 2015, 15, 18587–18612. [Google Scholar] [CrossRef] [PubMed]
- Mauseth, J.D. Theoretical Aspects of Surface-to-Volume Ratios and Water-Storage Capacities of Succulent Shoots. Am. J. Bot. 2000, 87, 1107–1115. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Xu, L.; Tan, C.; Goodman, E.D.; Fu, D.; Xin, L. Digitization and Visualization of Greenhouse Tomato Plants in Indoor Environments. Sensors 2015, 15, 4019–4051. [Google Scholar] [CrossRef] [PubMed]





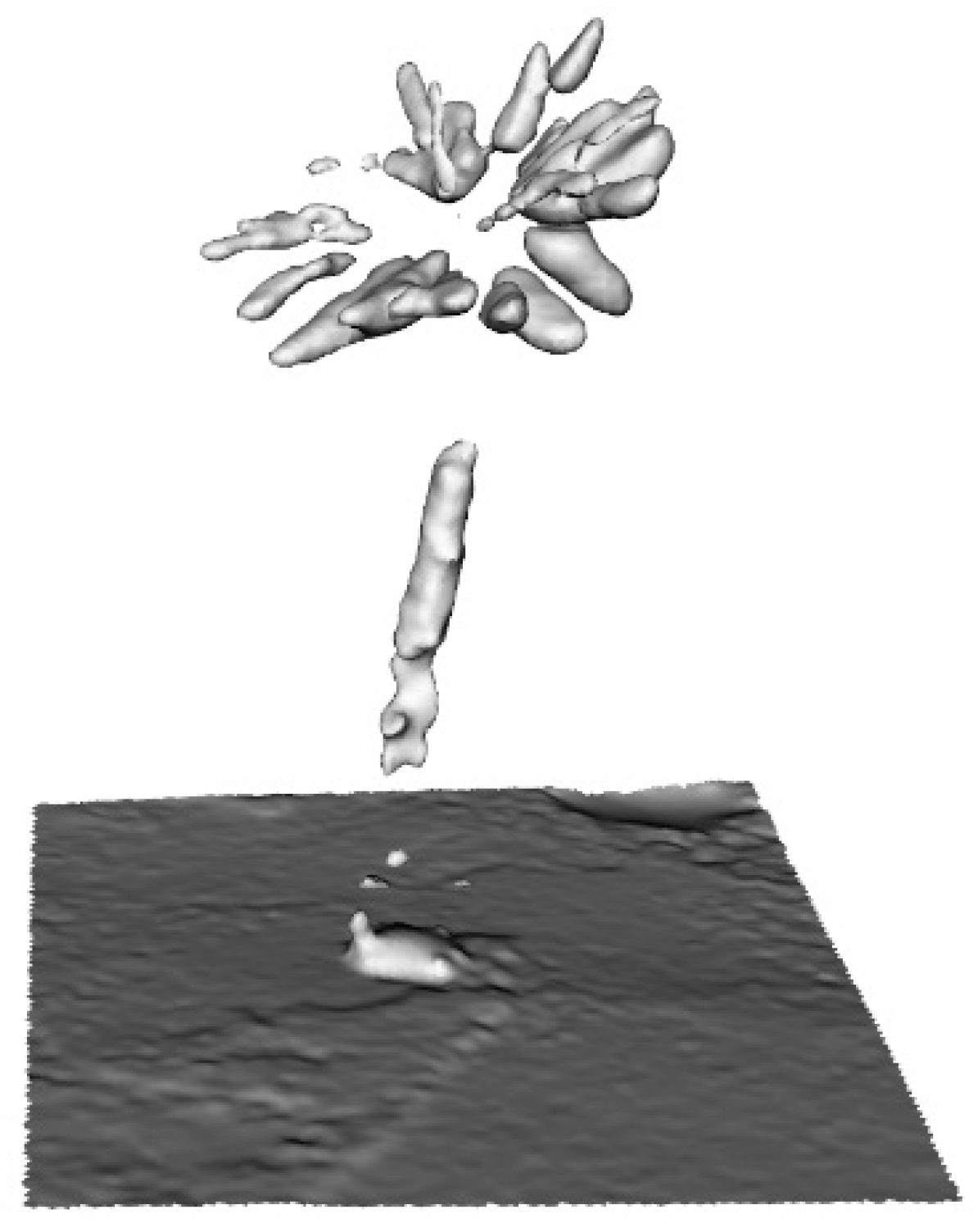


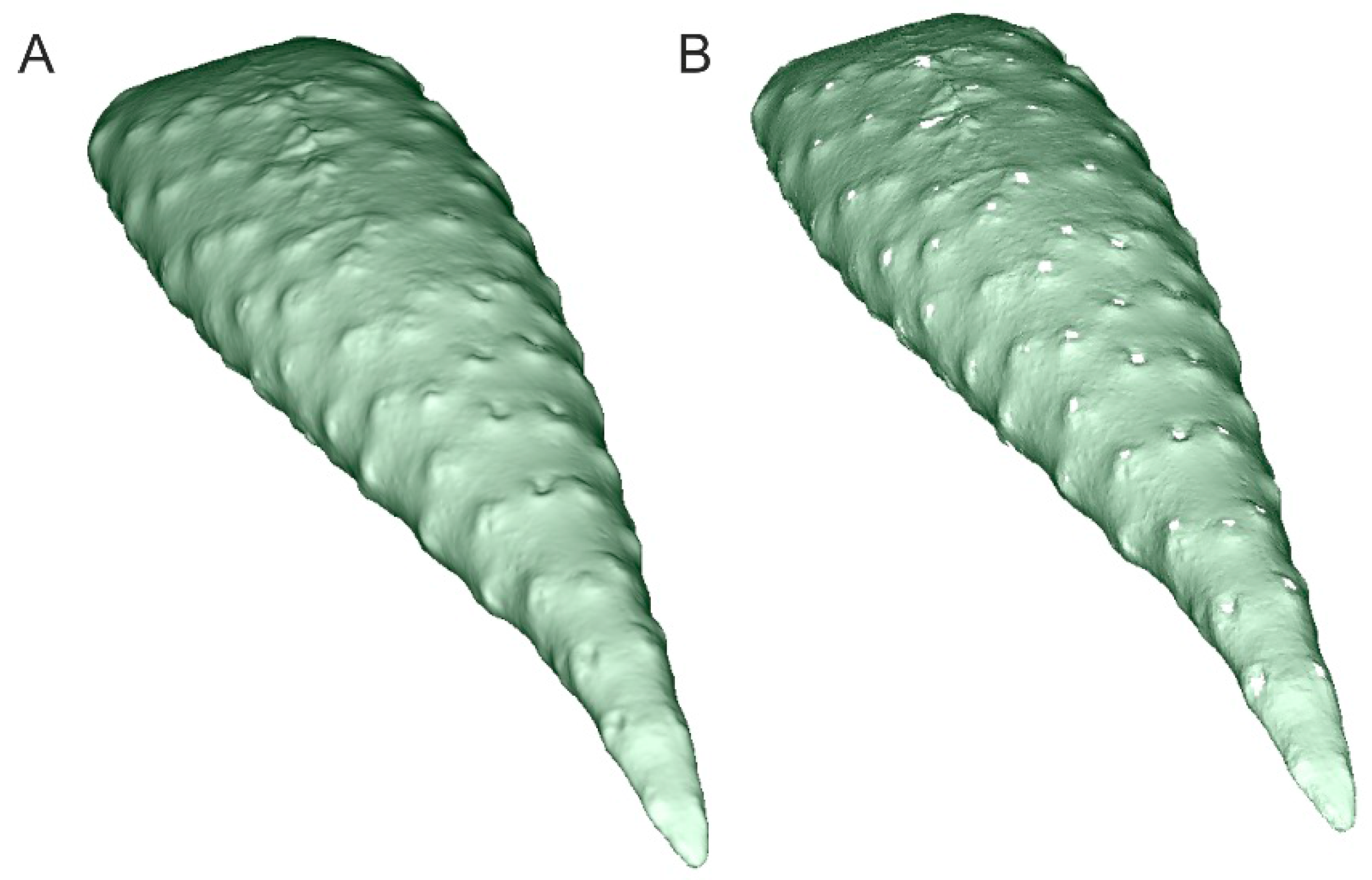
| Family | Species | AMU BG Accession Number | CITES Appen. | Ecological Form |
|---|---|---|---|---|
| Aloaceae | Aloe marlothii A. Berger | I_I004_002_0000_6010_4570 | II | leaf succulent |
| Apocynaceae | Pachypodium lamerei Drake | I_I004_002_0000_6997_3368 | II | stem succulent |
| Cactaceae | Astrophytum capricorne (A. Dietr.) Britton et Rose | I_I002_003_0000_6996_4580 | II | stem succulent |
| Cactaceae | Astrophytum myriostigma Lem. | I_I002_003_0000_6996_4581 | II | stem succulent |
| Cactaceae | Echinopsis leucantha (Gillies ex Salm-Dyck) Walp. | I_I002_003_0000_6996_4571 | II | stem succulent |
| Cactaceae | Leuchtenbergia principis Hook. | I_I002_003_0000_6997_4590 | II | stem succulent |
| Cactaceae | Mammillaria magnimamma Haw. | I_I002_003_0000_6999_4573 | II | stem succulent |
| Cactaceae | Pilosocereus pachycladus F. Ritter | I_I002_003_0000_6998_4572 | II | stem succulent |
| Welwitschiaceae | Welwitschia mirabilis Hook.f. | I_I004_001_0000_6998_4560 | I | true xerophyte |
| Model Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Mean distance between vertices [mm] | 3.97 | 2.03 | 1.09 | 0.56 | 0.28 | 0.20 | 0.14 |
| Number of points | 859 | 3442 | 12,013 | 48,159 | 191,352 | 370,824 | 713,645 |
| Number of triangles | 1664 | 6852 | 24,022 | 96,314 | 382,700 | 741,632 | 1,427,286 |
| Area [mm2] | 11,314 | 11,919 | 12,100 | 12,175 | 12,206 | 12,209 | 12,216 |
| Error % | 7.38 | 2.43 | 0.95 | 0.34 | 0.08 | 0.06 | 0.00 |
| Volume [mm3] | 52,463 | 55,364 | 55,993 | 56,167 | 56,206 | 56,172 | 56,174 |
| Error % | 6.61 | 1.44 | 0.32 | 0.01 | 0.06 | 0.00 | 0.00 |
| Distance–triangular mesh [mm] | 179.7 | 184.5 | 181.7 | 183.8 | 183.8 | 183.1 | 183.5 |
| Error % | 2.10 | 0.53 | 0.99 | 0.12 | 0.16 | 0.23 | 0.00 |
| Distance–segment projection [mm] | 169.3 | 175.7 | 176.2 | 176.0 | 176.4 | 177.0 | 177.2 |
| Error % | 6.13 | 5.01 | 3.17 | 4.39 | 4.21 | 3.45 | 3.60 |
| S/V ratio | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drapikowski, P.; Kazimierczak-Grygiel, E.; Korecki, D.; Wiland-Szymańska, J. Verification of Geometric Model-Based Plant Phenotyping Methods for Studies of Xerophytic Plants. Sensors 2016, 16, 924. https://doi.org/10.3390/s16070924
Drapikowski P, Kazimierczak-Grygiel E, Korecki D, Wiland-Szymańska J. Verification of Geometric Model-Based Plant Phenotyping Methods for Studies of Xerophytic Plants. Sensors. 2016; 16(7):924. https://doi.org/10.3390/s16070924
Chicago/Turabian StyleDrapikowski, Paweł, Ewa Kazimierczak-Grygiel, Dominik Korecki, and Justyna Wiland-Szymańska. 2016. "Verification of Geometric Model-Based Plant Phenotyping Methods for Studies of Xerophytic Plants" Sensors 16, no. 7: 924. https://doi.org/10.3390/s16070924
APA StyleDrapikowski, P., Kazimierczak-Grygiel, E., Korecki, D., & Wiland-Szymańska, J. (2016). Verification of Geometric Model-Based Plant Phenotyping Methods for Studies of Xerophytic Plants. Sensors, 16(7), 924. https://doi.org/10.3390/s16070924





