1. Introduction
The existence of a tradeoff between physical size and performance has always been a key aspect in UHF-RFID tag design. In fact, since the free-space wavelength at the UHF-RFID band (840–960 MHz) is of the order of 30 cm, and tag antennas usually work like resonant dipoles, meandering has always been an extensively used technique in order to avoid excessive tag dimensions, thus allowing the tagging of small items. However, it is well known that dipole meandering decreases the radiation efficiency due to current cancellation [
1,
2], and thus tag performance in terms of read range is also degraded. Moreover, it is well known that bandwidth is limited by the electrical size of the antenna [
3,
4] (hence, size reduction goes against worldwide tag functionality). In addition, whereas meandering reduces tag length, it tends to increase tag width, which can be a clear limitation, depending on the aspect ratio of the tagged item.
Whereas for many applications a tradeoff between tag dimensions and performance is necessary, there are some applications where tag performance optimization (i.e., read range) is a due, even at the expense of tag dimensions. Such applications may include, for instance, inventory of boxes in a large warehouse, and pallet tagging, among others. In general, when a high read range is required and the dimensions of the tagged objects are relatively large, oversized (as compared to the usual sizes) tags with optimized read range might be preferred. Moreover, other applications might take advantage of the form factor of a non-meandered wire. For example, the tag could be sewn into the seams of garments, towels, robe and other textile items, or even directly embedded in their fabric by using conductive thread.
In this work, performance optimization of passive UHF-RFID tags without size limitation is studied for the first time, yet keeping the overall size of the tag within reasonable limits for the applications mentioned above. The paper is organized as follows. In
Section 2, the tag design principle is discussed. In
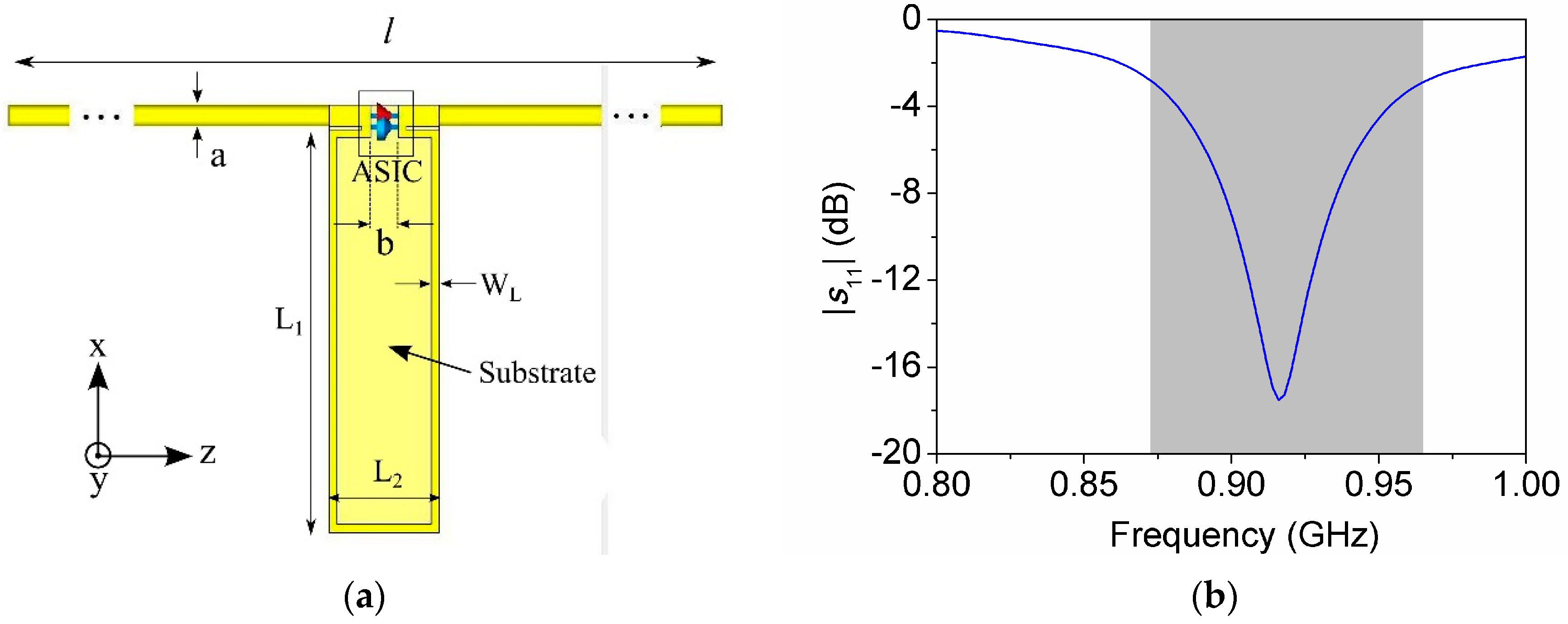
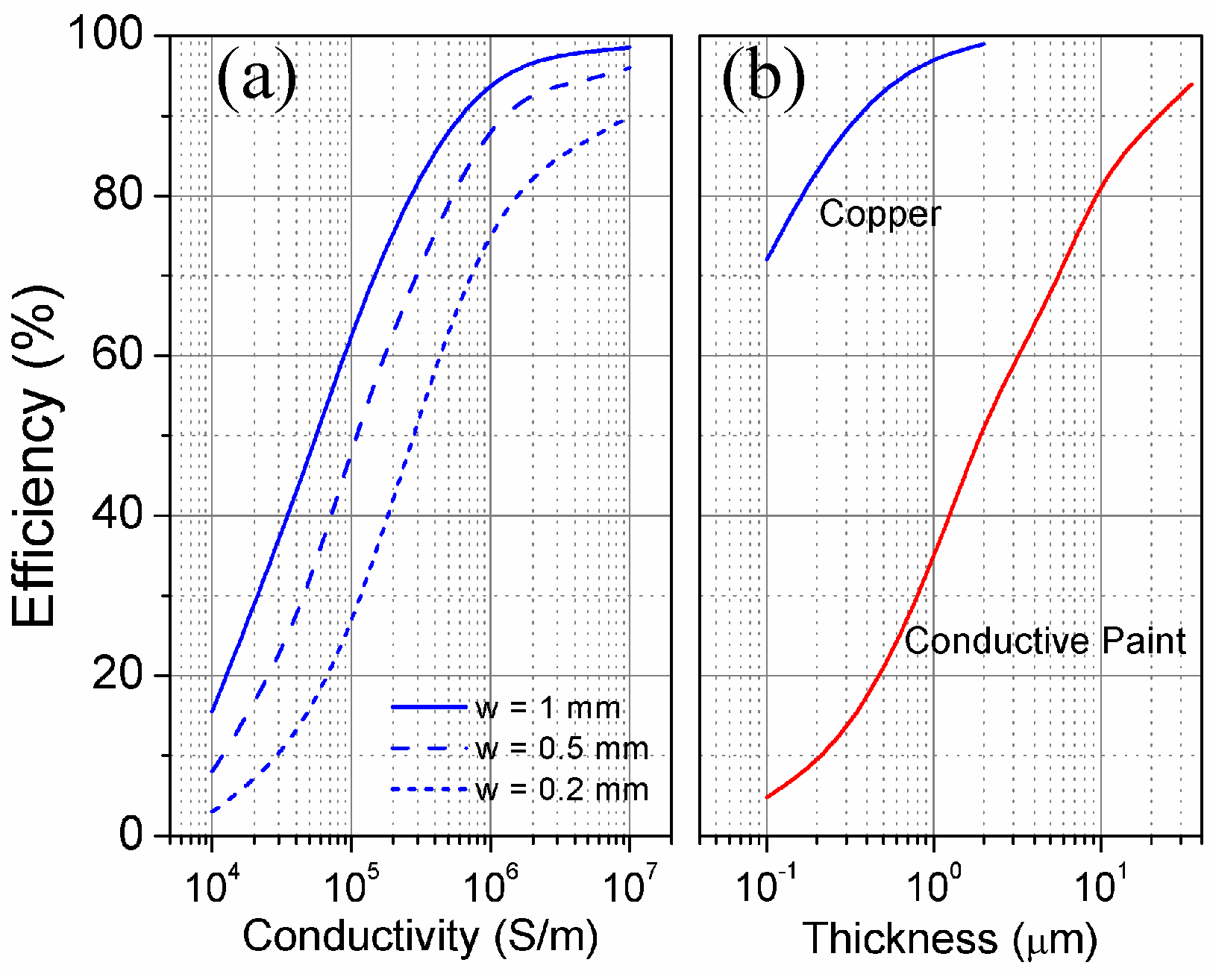
Section 3, a tag prototype based on a wire antenna and a matching network is presented, along with the electromagnetic simulation results. The discussion is then extended to a case of practical interest in RFID, where the antenna is implemented by means of standard planar technology, providing simulations for the radiation efficiency as a function of the geometry and metal layer conductivity. Finally, the experimental results are reported in
Section 4.
2. Strategy to Optimize the Read Range
The field radiated by an infinitely thin wire antenna of a given length
l oriented along the
z-axis can be calculated by integrating the radiation of the infinitesimal current element
dI over the length of the antenna. As reported in many classical analyses of the problem [
5,
6], it is a good approximation to consider the current over the antenna as a perfect harmonic function of the position, with zeroes at both ends of the wire, thus neglecting the second order effects on the current distribution. The resulting expression for the directivity, as a function of the wire length, can be written as [
6]:
where
F(
θ,
l) is a function proportional to the radiated power density, and can be expressed as:
where
θ is the inclination angle and
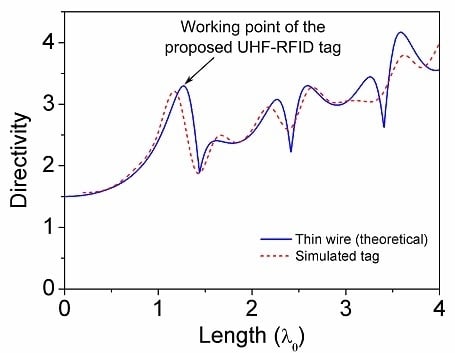
β is the free-space phase constant at the working frequency. A graphical representation of Equation (1) for wire lengths up to four free-space wavelengths is depicted at
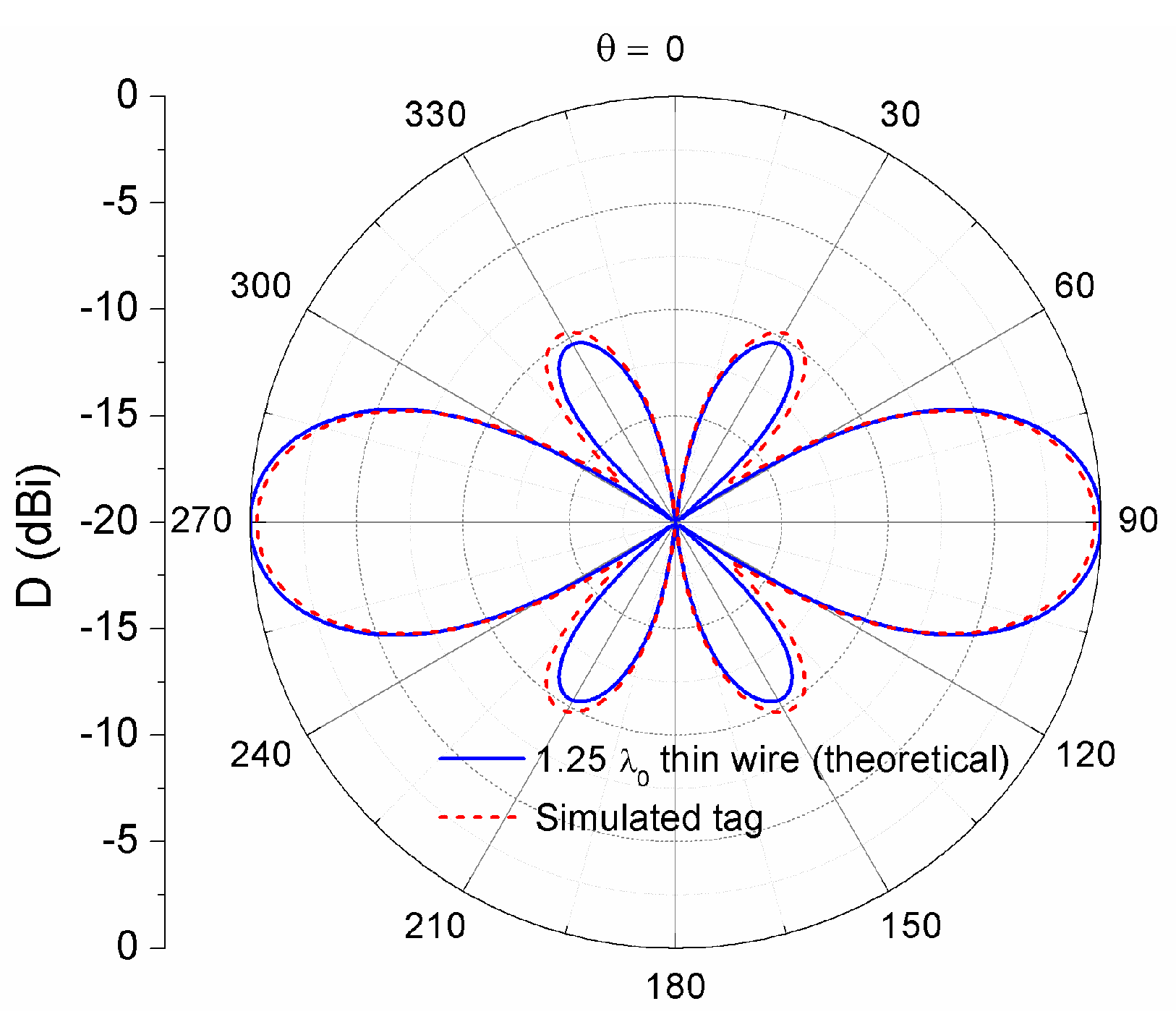
Figure 1. It can be clearly seen from the graph that the directivity increases monotonically with the antenna length up to approximately 1.25 wavelengths, where a peak value of
D0 = 3.3 (5.2 dBi) results. Above that length, the increase of the side lobes produces a sudden degradation of the directivity, leading to a minimum located at approximately 1.5 wavelengths. A further increase of the antenna length results in periodical directivity peaks and minima, of which levels tend to increase linearly with the antenna length.
Nonetheless, the radiation pattern above the first peak is characterized by a crescent number of lobes, and radiation zeros. Such a kind of radiation pattern is not useful for a general purpose RFID tag, since it produces undesired blind spots in the tag read range. From
Figure 1 it is also clear that, above the first directivity peak, the following major peak occurs at 3.6 wavelengths, which implies tag lengths exceeding one meter.
For the above reasons, we found reasonable to design the tag to work at 1.25 wavelengths, corresponding to an overall length of
l = 410 mm at the frequency
f0 = 915 MHz. The theoretical power radiation pattern, obtained from Equation (1) and normalized to 5.2 dBi, is depicted in
Figure 2. It is composed of a main lobe with a maximum at
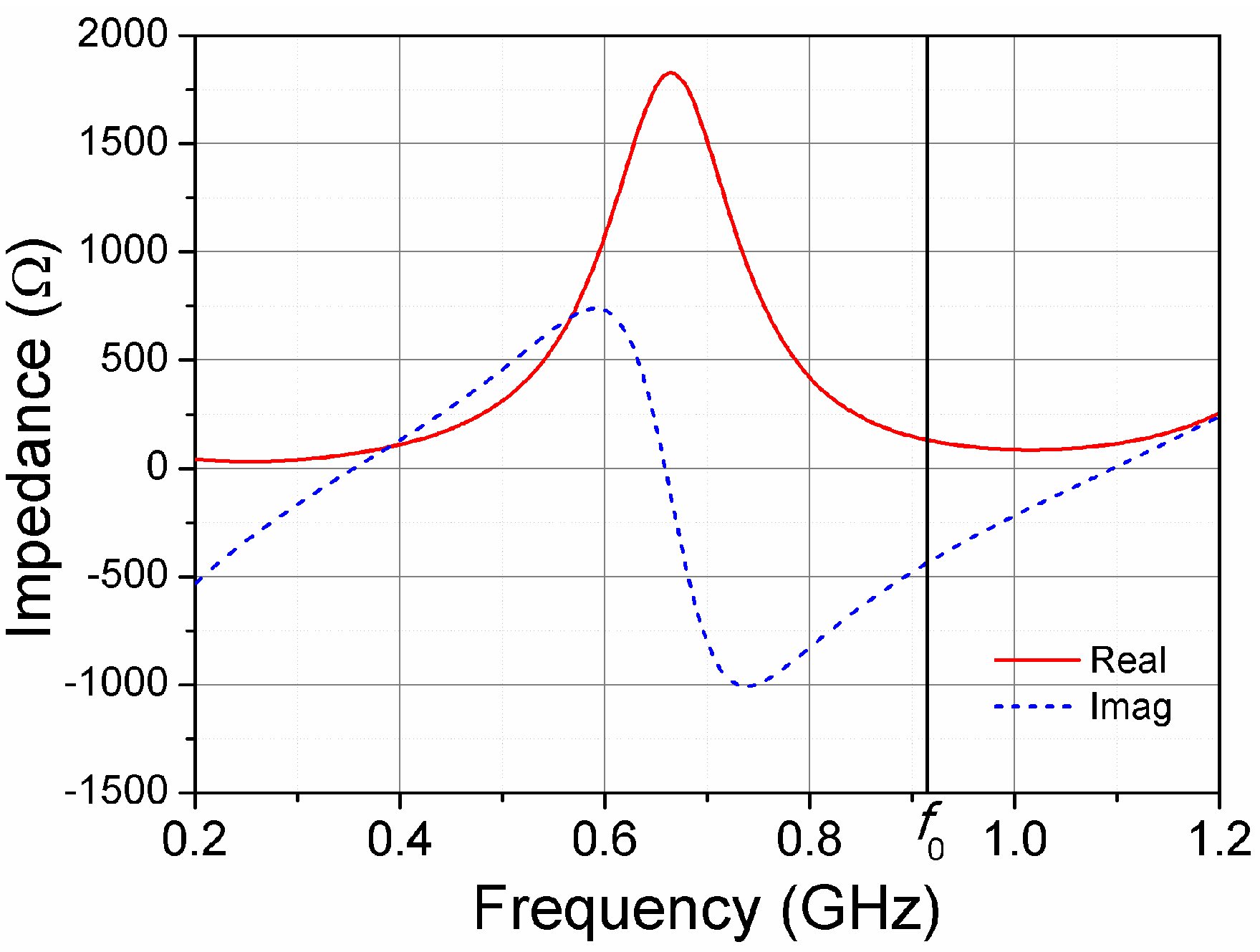
θ = 90°, and two side lobes of magnitude −10 dB. The half-power beamwidth is 34°, and the null-to-null beamwidth is 74°. Since the read range of an RFID tag is proportional to the square root of the receiving antenna gain (see Equation (3)), it is interesting to quantify the quarter-power beamwidth, thus corresponding to the half-read-range beamwidth, whose value in our case is 46°. It is worth mentioning that, for a non-zero radius wire, the effective antenna length can differ slightly from the theoretical value of 1.25 wavelengths.
Let us now quantify the maximum theoretical read range which can be obtained with this kind of tag. This can be accomplished by using the very well-known read range formula [
7]:
where
EIRP is the equivalent isotropic radiated power,
λ is the free-space wavelength at the working frequency,
Gr is the gain of the tag antenna,
τ = (1 − |
s|
2) is the power transmission coefficient and
Pth is the chip sensitivity. By neglecting ohmic and mismatch losses, and considering an
EIRP level of 4 W and a sensitivity of −17 dBm (e.g., Alien Higgs-3 chip, SOT-323), the maximum predicted read range is
r0 = 21 m. Such value, qualitative since losses have been neglected, is very promising since it doubles the maximum read range of general-purpose commercial UHF-RFID tags (e.g., the Alien ALN9640 “Squiggle” tag [
8]), which is of the order of 10–11 m.
It is worth mentioning that, according to the previous analysis, the read range is increased by making the tag more directive. Hence, due to its reduced beamwidth, the tag performance is more dependent on its orientation with respect to the reader antenna. Although this is generally an undesired behavior in general purpose UHF-RFID tags (where the tag orientation is not known a priori), it is not necessarily an issue for many applications requiring read range optimization (e.g., when the tag orientation is known, as in many scenarios of pallet and box inventory). In other applications, like passive RFID sensing, the orientation dependence can even be an advantage, so that a long distance passive orientation sensor could be built based on the proposed antenna. In this latter case, however, ambiguous result may arise due to the presence of the side lobes. Nevertheless, the spurious read range is only 30% (on the basis of Equation (3), and considering a simulated side lobe level of −10 dB) of the peak read range, so that ambiguity could be eliminated by properly distancing the objects from the reader.
4. Experimental Results
In order to validate the simulated results, the tag layout described in
Section 3.1 was fabricated and its read range was measured. The measurement setup consisted of a commercial Motorola FX7400 UHF-RFID reader matched to a half-wave dipole antenna, obtaining a transmission
EIRP = 1.5 W. The tag was measured in an outdoor environment, with the ground as a unique nearby scatterer. The read range was measured in the 865–868 MHz (Europe) and 902–928 MHz (USA and others) bands available from the reader.
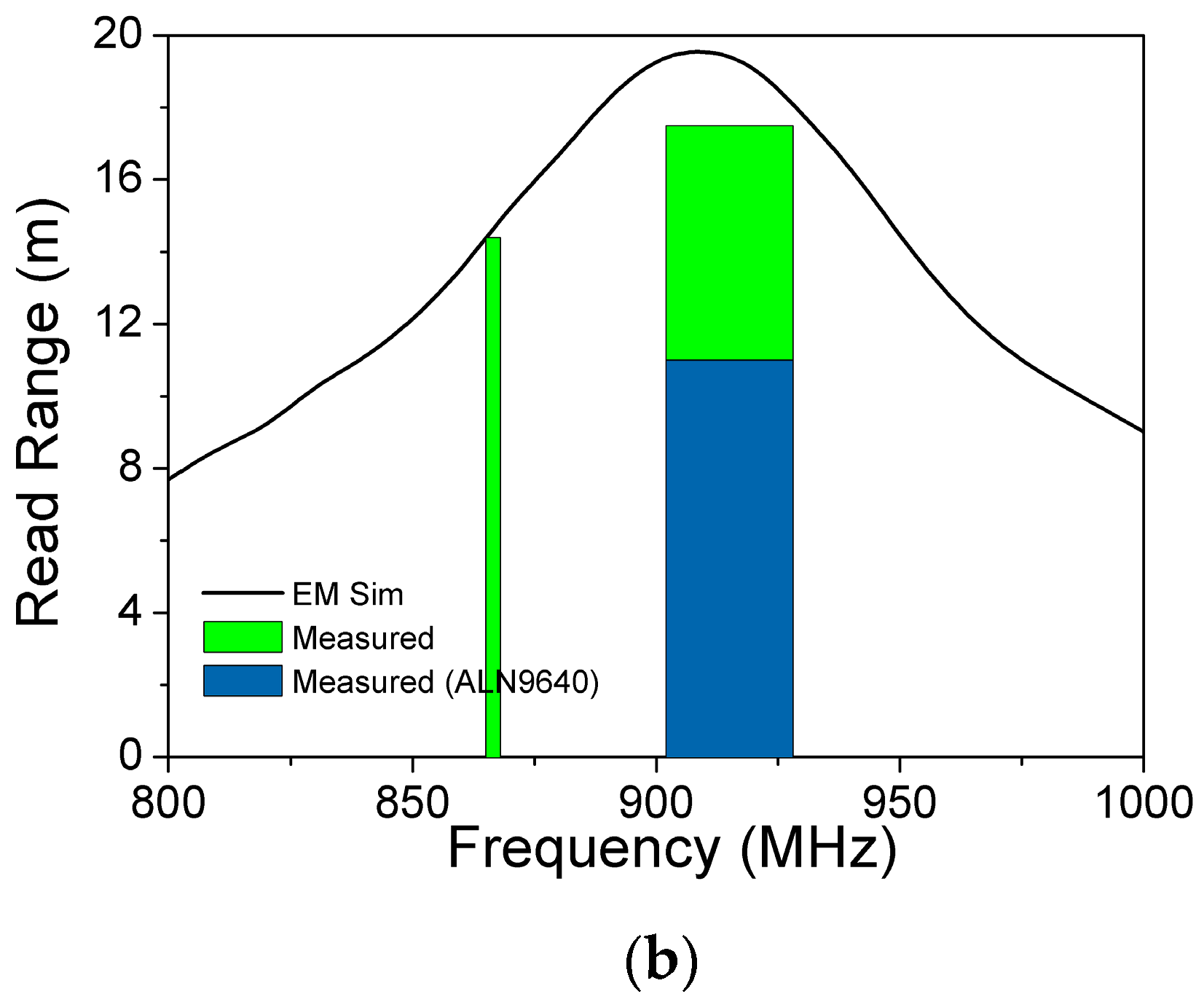
The results, normalized to
EIRP = 4 W (which is the value used for the simulated read range, and the maximum
EIRP value in USA [
12]), and compared to the simulated read range curve, are depicted in
Figure 6b. The data is in very good agreement in the 865–868 MHz band, where 14.4 m were obtained. On the other hand, the measured peak read range is 17.5 m in the 902–928 MHz band, which is 10% lower as compared to the simulated value. This discrepancy can be attributed to the fact that the actual chip sensitivity tends to be smaller [
13,
14] than the manufacturer nominal value. Indeed, each dB decrease in the chip sensitivity leads to 10% reduction of the read range, according to Equation (3). Nonetheless, when compared to one of the best performing available commercial tags in terms of read range, i.e., the Alien ALN9640 “Squiggle”, the tag presented in this work provides a measured read range in the 902–928 MHz band that represents an increase of almost 60% (
Figure 6). This improved read range has been achieved despite the fact that the nominal sensitivity (−18 dBm [
15]) of the unpackaged Higgs-3 chip used in the ALN9640 inlay is better than the one of the
SOT-323 version used in this work (−17 dBm). This improvement of read range is a remarkable aspect of this paper. It is also remarkable that the read range measured when the proposed tag is attached to a wooden pallet (1 m above the ground) is 16.4 m, pointing out the potential of these tags for such application.