1. Introduction
In recent years, universal high-temperature piezoresistive pressure sensors have been extensively applied in the fields of petrochemicals, energy and electric power, and aerospace. Thus, improving the measurement accuracy is likely to play an increasingly important role in various industries, especially those that encounter high-temperature environments [
1]. Among the current applications, sensors are expected to deliver consistent performance and accuracy under temperature increases of up to 220 °C. In such situations, however, a continuous drift in the sensor’s output voltage is inevitable, because the piezoresistance increases with temperature, whereas the piezoresistive coefficient decreases [
2], which adversely affects testing precision. Hence, it is critical to achieve effective temperature compensation for high-temperature piezoresistive pressure sensors.
The main measuring principle used by high-temperature piezoresistive pressure sensors is the Wheatstone bridge. The output voltage of a Wheatstone bridge must be compensated in terms of the offset voltage, the temperature coefficient of the offset, and the temperature coefficient of the sensitivity. Current bridge temperature compensation methods can be divided into hardware, software, or hybrid techniques. Hardware methods typically use an extra thermistor, a low-temperature coefficient resistor network, a diode, a triode, an adjustable gain operational amplifier, and so on [
3]. The software methods are based on data processing according to an inverse function algorithm or artificial neural networks [
4,
5]. Hybrid techniques combine the hardware and software approaches to obtain higher compensation accuracy. Compared with other techniques, hardware compensation is simpler, more efficient, more economical, and easier to implement in industrial production and manufacturing; hence, hardware compensation is widely used.
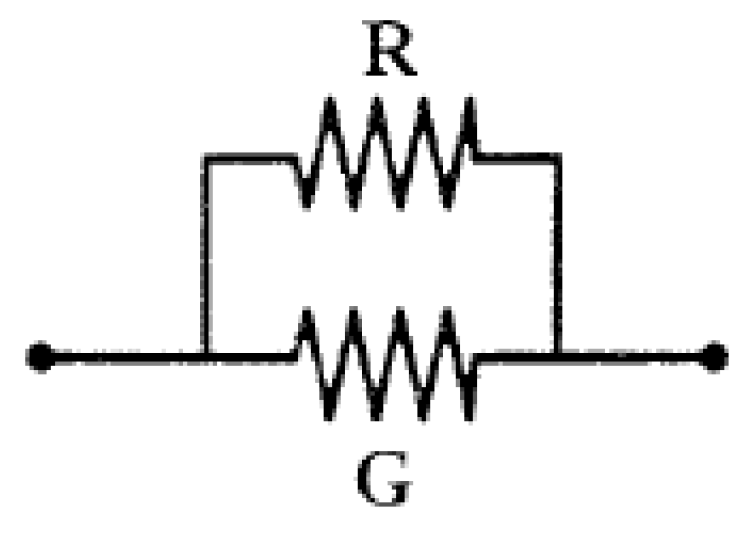
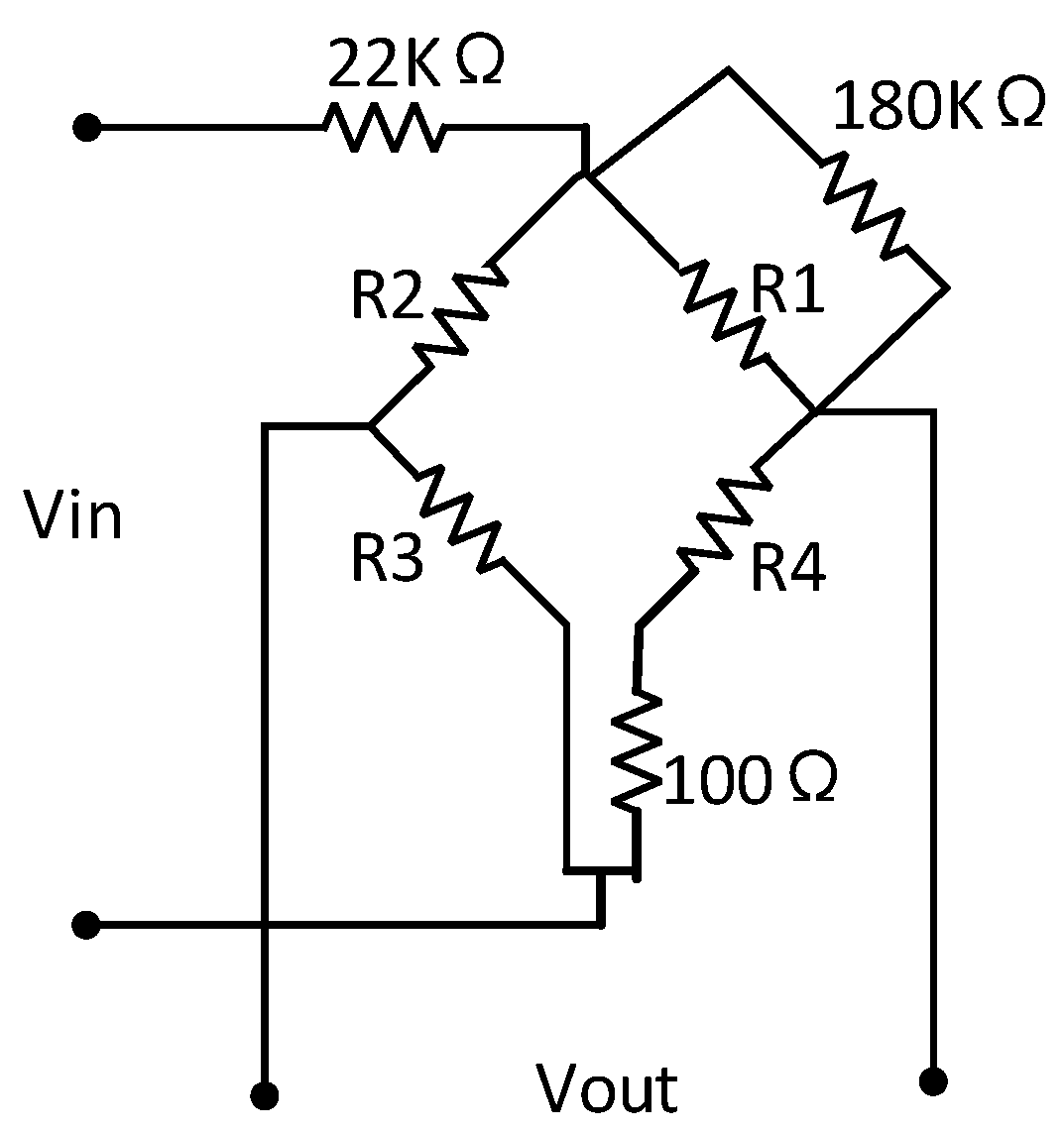
In this study, we describe a passive resistor temperature compensation technique that uses a low-temperature coefficient resistance network. Unlike other hardware methods, which require the compensation circuit to be in the same temperature field as the bridge arm piezoresistor, our passive resistor temperature compensation circuit does not need to be at the working temperature of the bridge arm piezoresistor, allowing more flexibility and convenience in packing. Moreover, the compensation accuracy of the proposed method is independent of the temperature difference between the compensation circuit and the bridge arm piezoresistor. A typical circuit diagram of a low-temperature coefficient resistor network model is shown in
Figure 1.
The traditional theoretical compensation formulas for the offset voltage and temperature coefficient of the offset are given in Equations (1) and (2), respectively; the compensation formula for the temperature coefficient of the sensitivity is given in Equation (3).
where R
B is the bridge arm resistance, TCR
B is the temperature coefficient of R
B, V
OS is the bridge zero output voltage, and α is the temperature coefficient of the output voltage sensitivity [
6].
These equations assume that the four bridge arm resistances and their temperature coefficients have almost the same initial values, and neglect the influence of residual stress caused by the fabrication process. Otherwise, the compensation applied to the temperature coefficient of the offset and the sensitivity would be invalid [
7,
8]. In contrast, the passive resistor temperature compensation algorithm proposed in the next section uses actual sensor measurement data, and is independent of residual stress and deviations in the bridge parameters. This results in high compensation precision and extensive applicability.
3. Model and Algorithm for Passive Resistor Temperature Compensation
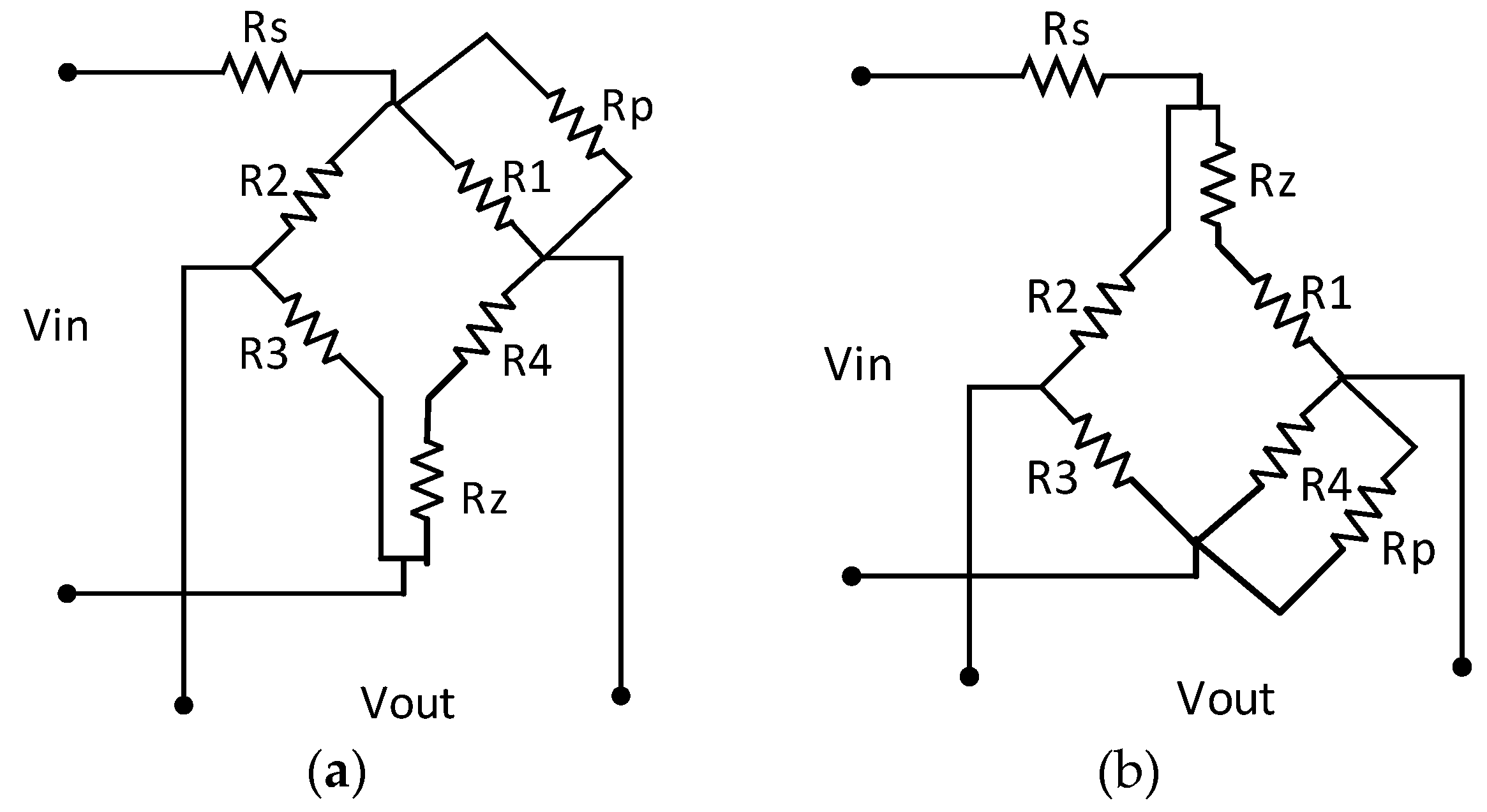
Our model for passive resistor temperature compensation is based on the principles described above. As a simple supply circuit is best suited to high-temperature applications, a constant voltage supply is usually adopted by high-temperature pressure sensors. The following describes the model and algorithm for passive resistor temperature compensation with a constant voltage supply.
Figure 5 illustrates the model.
The sensor output voltage is:
where K
+ (T, P) and K
- (T, P) are the positive and negative voltage division factors, respectively, and V
B(T, P) is the supply voltage of the bridge, which can be written as:
According to the initial offset voltage and sensor test data, we select the compensation model in
Figure 5a or that in
Figure 5b and the corresponding computational formula. The measurement parameters of the compensation model, which should be tested in advance, involve the four bridge arm resistances at the two compensation temperature thresholds of the high-temperature pressure sensor T0, T1 (T0 < T1) and two load pressures P0, P1 (P0 < P1). These values are presented in
Table 1.
The compensation model in
Figure 5a can be analyzed as follows:
Voltage division factors:
The output voltage expression of the model in
Figure 5a can be described by substituting Equations (10)–(13) into Equation (9). The output voltage expression of the model in
Figure 5b can be described in a similar way. This gives:
where R
Z, R
P, R
S are the model parameters to be determined, and R
i(T, P) (i = 1, 2, 3, 4) are the known measurement parameter values in
Table 1.
According to the demands of the bridge temperature compensation, the algorithm for passive resistor temperature compensation can be written as:
It can be seen from these equations that compensating for the temperature coefficient of offset (sensitivity) requires the sensor output voltage under the initial (higher) load pressure P0 (P1) to be independent of the temperature. This means that the partial derivatives of VOUT (T, P0) and VOUT (T, P1) with respect to temperature T must remain equal to zero.
The values of R
Z, R
P, R
S in the passive resistor temperature compensation model can be determined from Equation (15) using computer software such as MATLAB [
10].
4. Experiments and Data Processing
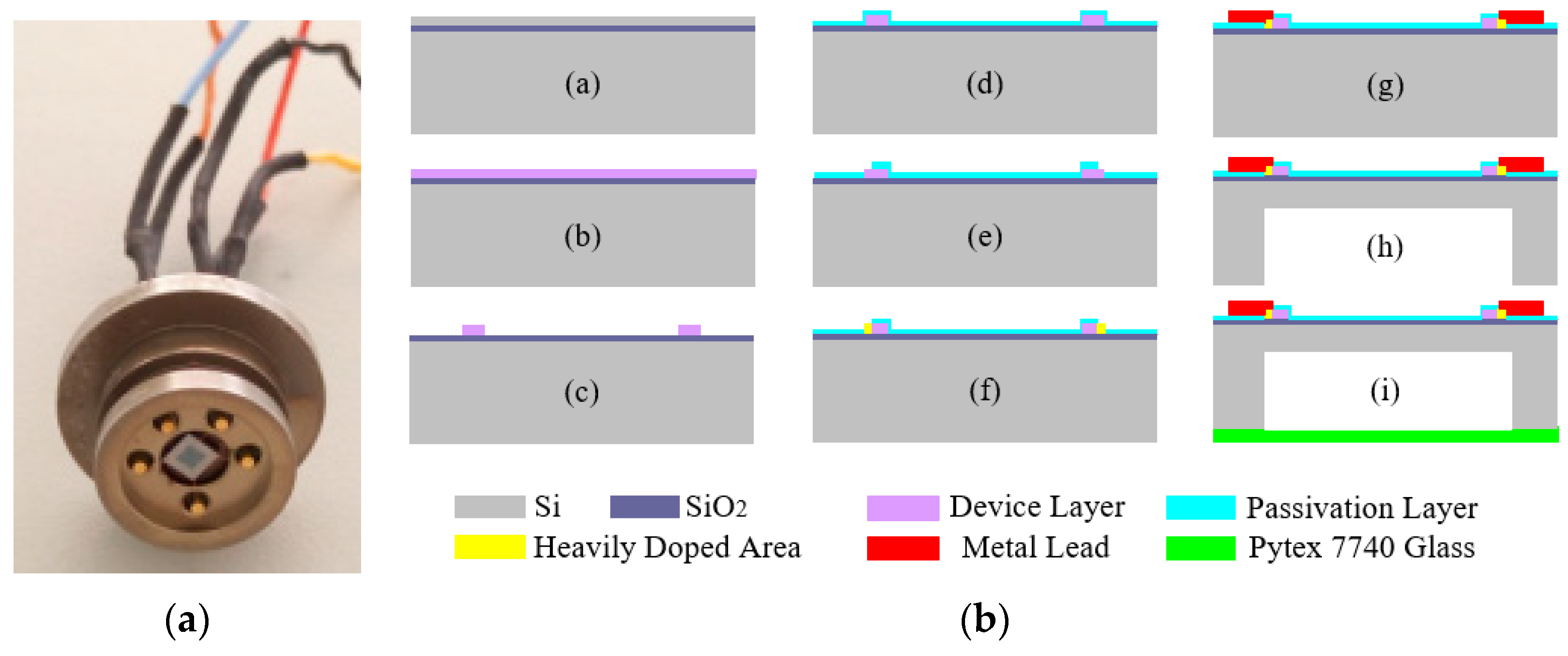
Figure 6a shows an uncompensated high-temperature pressure sensor based on silicon on insulation (SOI) material that can work for long periods within a temperature range of 220 °C. The standard microelectromechanical system (MEMS) processes shown in
Figure 6b were used to fabricate this pressure-sensitive chip.
The uncompensated high-temperature pressure sensor can be tested using the high-temperature and pressure calibration device shown in
Figure 7. The sensor was calibrated in the ranges of 20–220 °C and 100–2000 kPa.
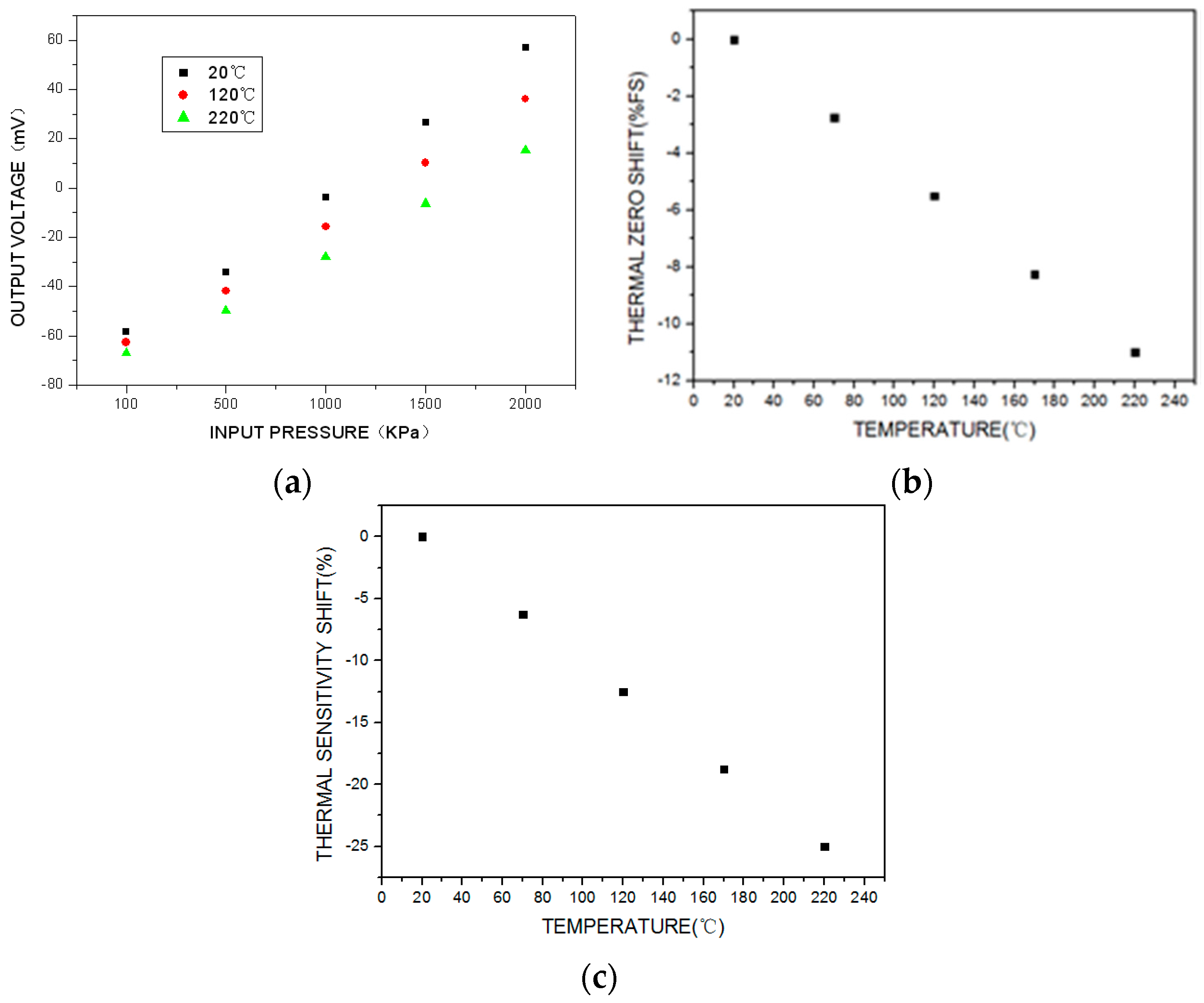
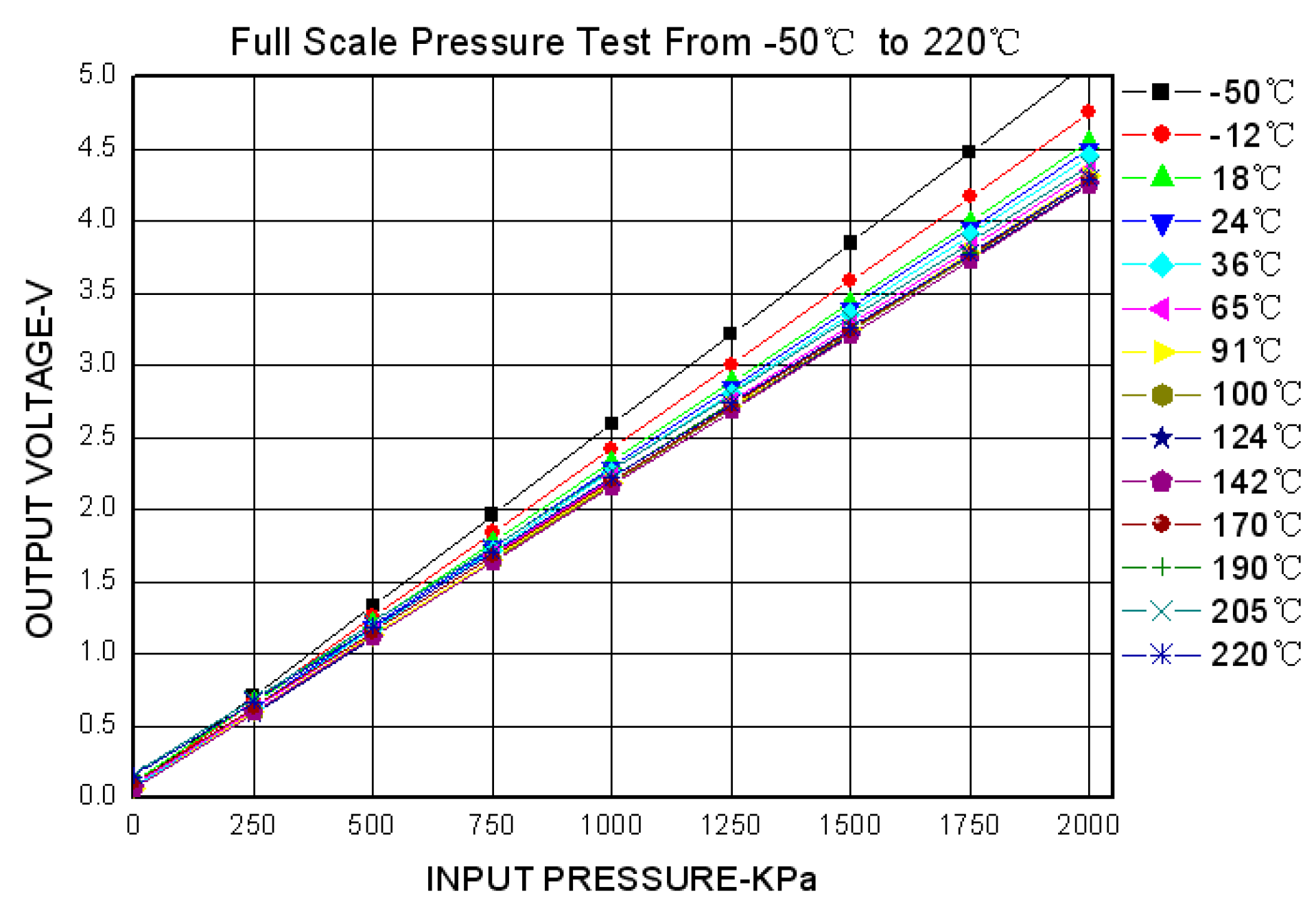
The test results are shown in
Figure 8. Because of the parameter deviation among the piezoresistors of the MEMS pressure sensor and the residual stress caused by the fabrication process or a mismatch in the thermal expansion coefficients, the sensor’s initial offset voltage is negative and the output voltage decreases significantly as the temperature increases, as shown in
Figure 8a. The thermal zero shift and thermal sensitivity shift are shown in
Figure 8b,c. Over the working temperature range, the total accuracy is ±18%FS (full scale), the maximum thermal zero shift is −11%FS, and the maximum thermal sensitivity shift is −25%. The uncompensated high-temperature pressure sensor exhibits significant parameter drift over the whole working temperature range, which greatly affects the measurement accuracy.
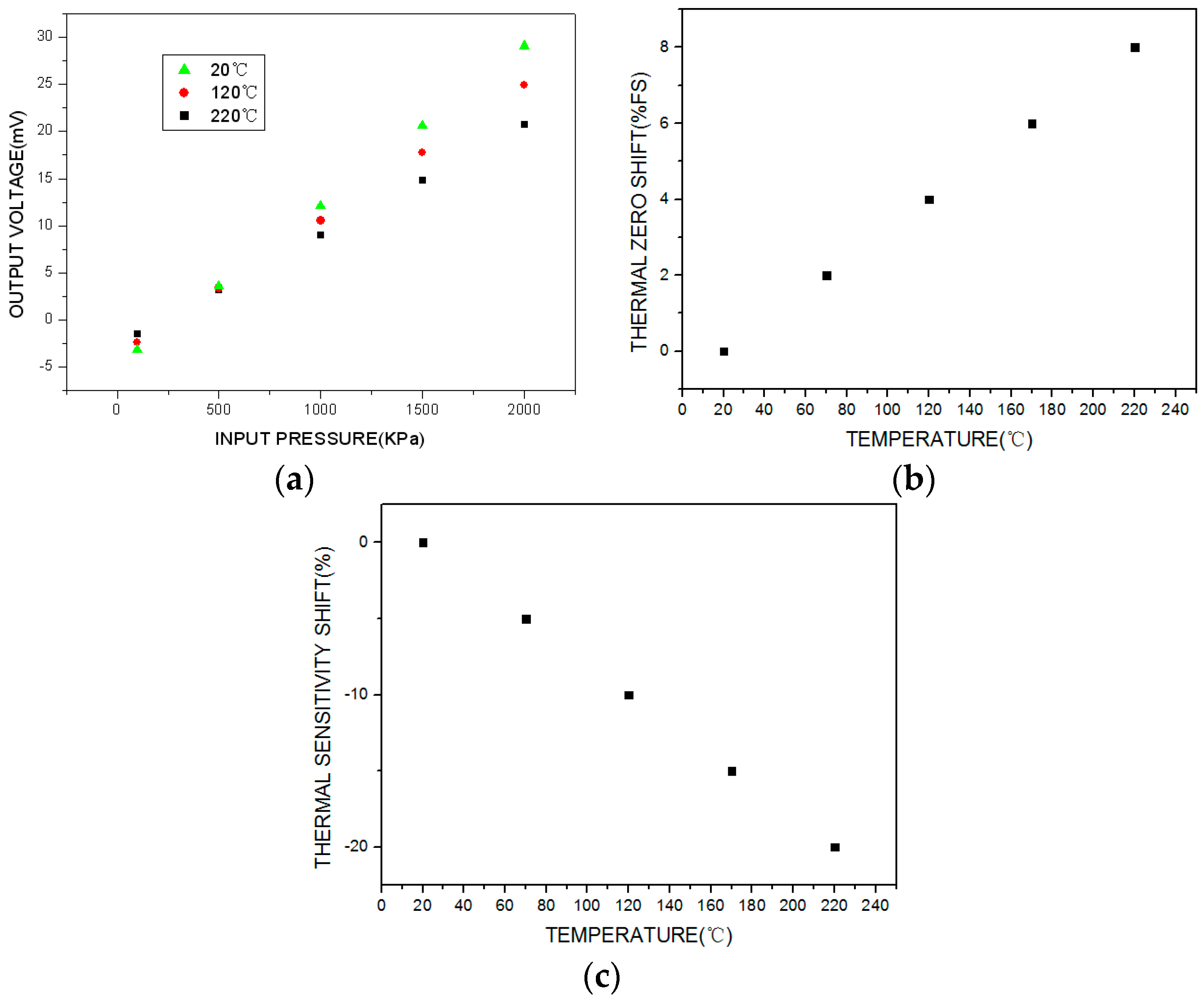
The traditional temperature compensation model and experiential arithmetic shown in
Figure 1 and Equations (1)–(3) were used to compensate for the output voltage temperature. The test results for the compensated sensor are shown in
Figure 9. Over the working temperature range, it can be seen that the total accuracy is ±12%FS, the maximum thermal zero shift is +8%FS, and the maximum thermal sensitivity shift is −20%. Thus, traditional temperature compensation is relatively ineffective.
The passive resistor temperature compensation model and differential equations derived in this paper were applied to the bridge arm resistors at temperature thresholds of 20 °C and 220 °C and load pressures of 200 kPa and 600 kPa. The results are listed in
Table 2. There are clearly large differences between the four initial bridge arm resistances, and some variation in resistance with load pressure and temperature coefficient due to process variables (such as photolithography) or the residual stress caused by the fabrication process.
Because of the negative initial offset output voltage, the compensation model circuit shown in
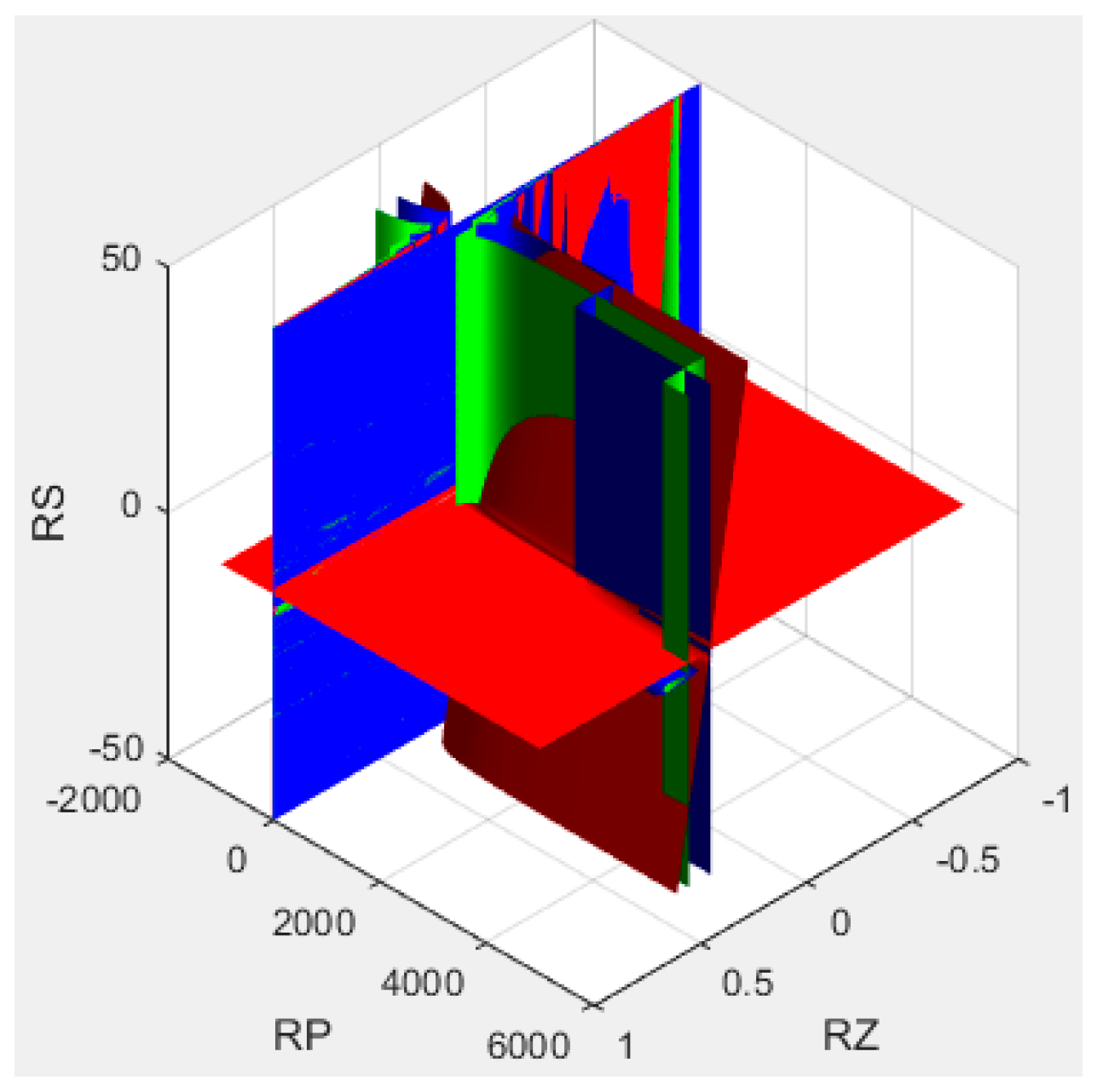
Figure 5a should be adopted. The algorithm for passive resistor temperature compensation shown in Equation (15) can be solved by examining the diagram in
Figure 10, which was constructed using MATLAB from the test data in
Table 2 (setting the offset output voltage U
0 = 4 mV).
In the
Figure 10, the red surface is drawn according to the first equation in Equation (15), representing the compensation of the offset voltage U
0; the green surface is drawn according to the second equation in Equation (15), representing the compensation of the temperature coefficient of offset; the blue surface is drawn according to the third equation in Equation (15), representing the compensation of the temperature coefficient of sensitivity.
The parameter values were varied within the following compensation resistance ranges:
From this, we obtained the minimal compensation resistance parameters:
The passive resistor temperature compensation circuit was then established using the data in
Table 2. The resulting circuit is shown in
Figure 11.
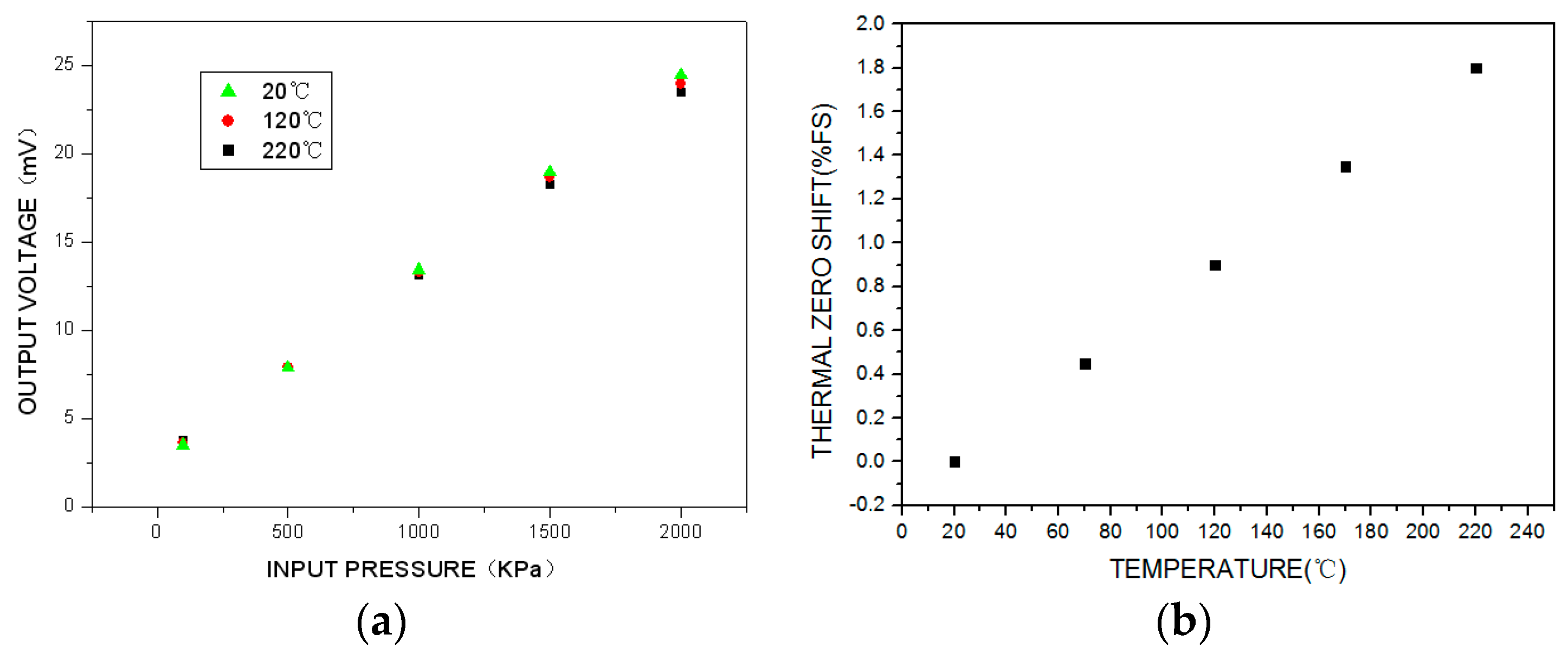
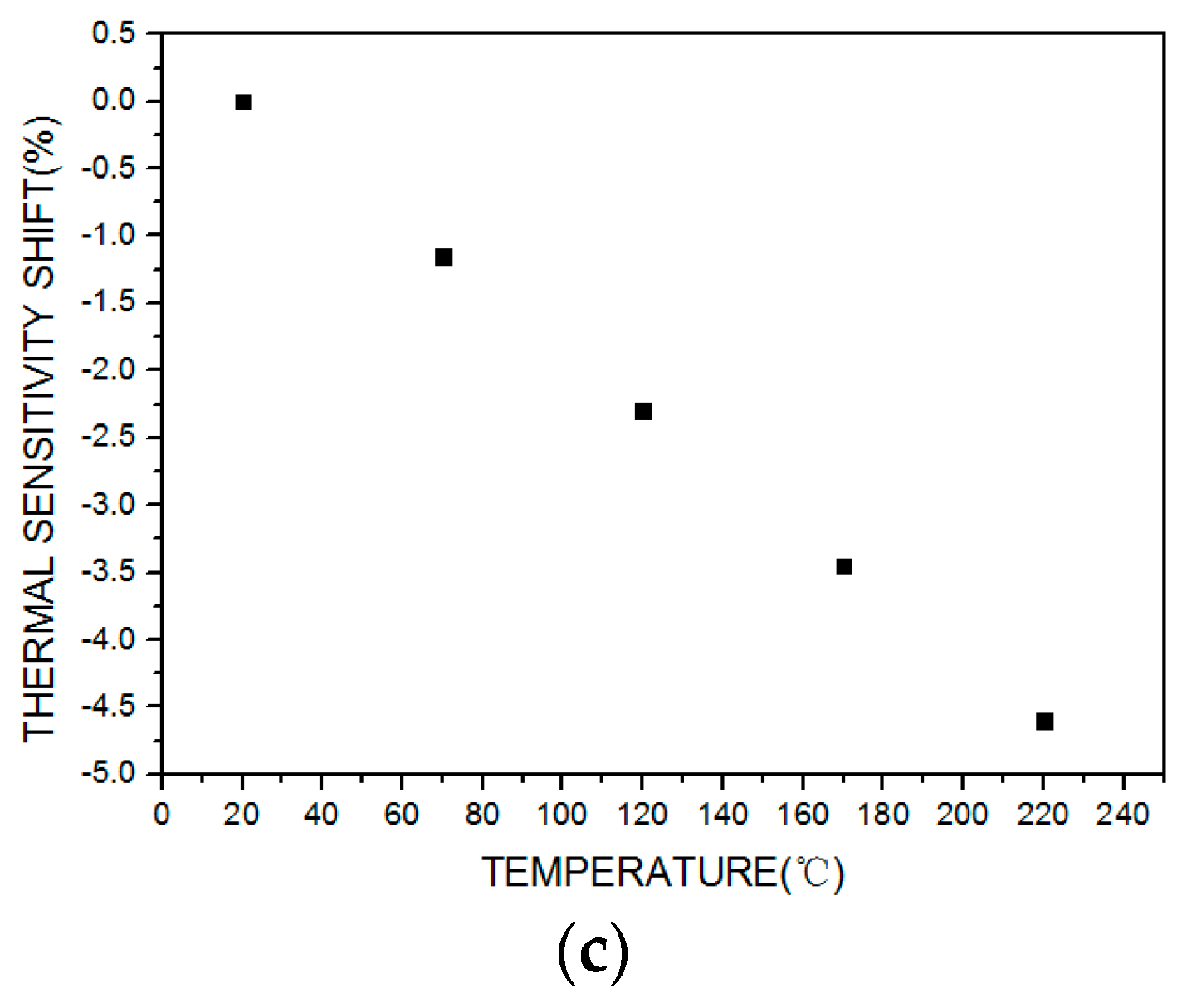
The test results for the sensor under passive resistor temperature compensation are shown in
Figure 12. Over the working temperature range, the total accuracy is ±1.5%FS, the maximum thermal zero shift is +1.8%FS, and the maximum thermal sensitivity shift is −4.6%.
From the above results, it is clear that the uncompensated sensor calibration curve (
Figure 8) shows significant variation over the temperature range. The sensor calibration curve compensated by the traditional method has an improved total accuracy over the temperature range (
Figure 9). However, the sensor calibration curve compensated by the proposed passive resistor temperature compensation (
Figure 12) clearly exhibits the best accuracy over the whole temperature range. It is obvious that passive resistor temperature compensation is more effective than the traditional temperature compensation, as it resulted in higher measurement accuracy across the experimental temperature range.
One limitation of this compensation approach is its effect on the output sensitivity. As can be seen by comparing
Figure 8 and
Figure 12, the output sensitivity falls by 70% under the proposed method. To ameliorate this problem, we can use a high-temperature signal-conditioning circuit to improve the sensor’s output sensitivity, as shown in
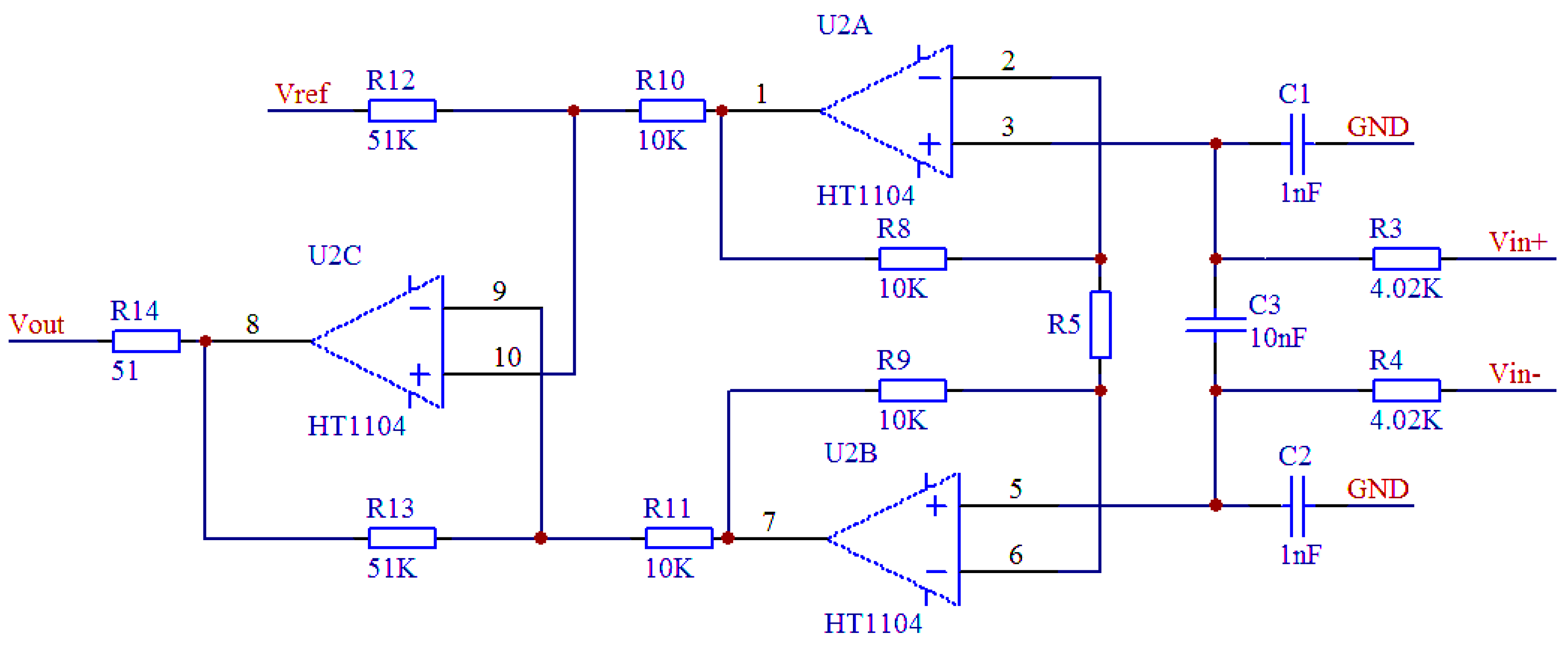
Figure 13. The main function of the circuit is to amplify the sensor output voltage signal from tens of millivolts to 0–5 V.
In
Figure 13, V
in+ and V
in- are the output voltages of the bridge, V
ref is the output zero reference voltage of the circuit, and R5 (the gain adjustment resistor) determines the output voltage of the high-temperature signal-conditioning circuit, which can be expressed as:
The test results for the high-temperature piezoresistive pressure sensor with passive resistor temperature compensation and the high-temperature signal-conditioning circuit are shown in
Figure 14, and a performance comparison with the corresponding XTE-190 sensor (produced by KULITE) is listed in
Table 3.
As can be seen from these results, the uncompensated high-temperature pressure sensor suffers from a significant degree of parameter drift across the whole working temperature range, but the sensor with passive resistor temperature compensation and the high-temperature signal-conditioning circuit can achieve similar levels of accuracy and temperature drift as the XTE-190.
Additionally, in order to fully verify the effect of passive resistor temperature compensation, the same batch of six sensors has completed the temperature compensation calibration test by the same method, and the compensation effect reaches the same level. The sensor device pictures are shown in
Figure 15.