Force-Sensing Silicone Retractor for Attachment to Surgical Suction Pipes †
Abstract
:1. Introduction
2. Related Work
3. Force-Sensing System
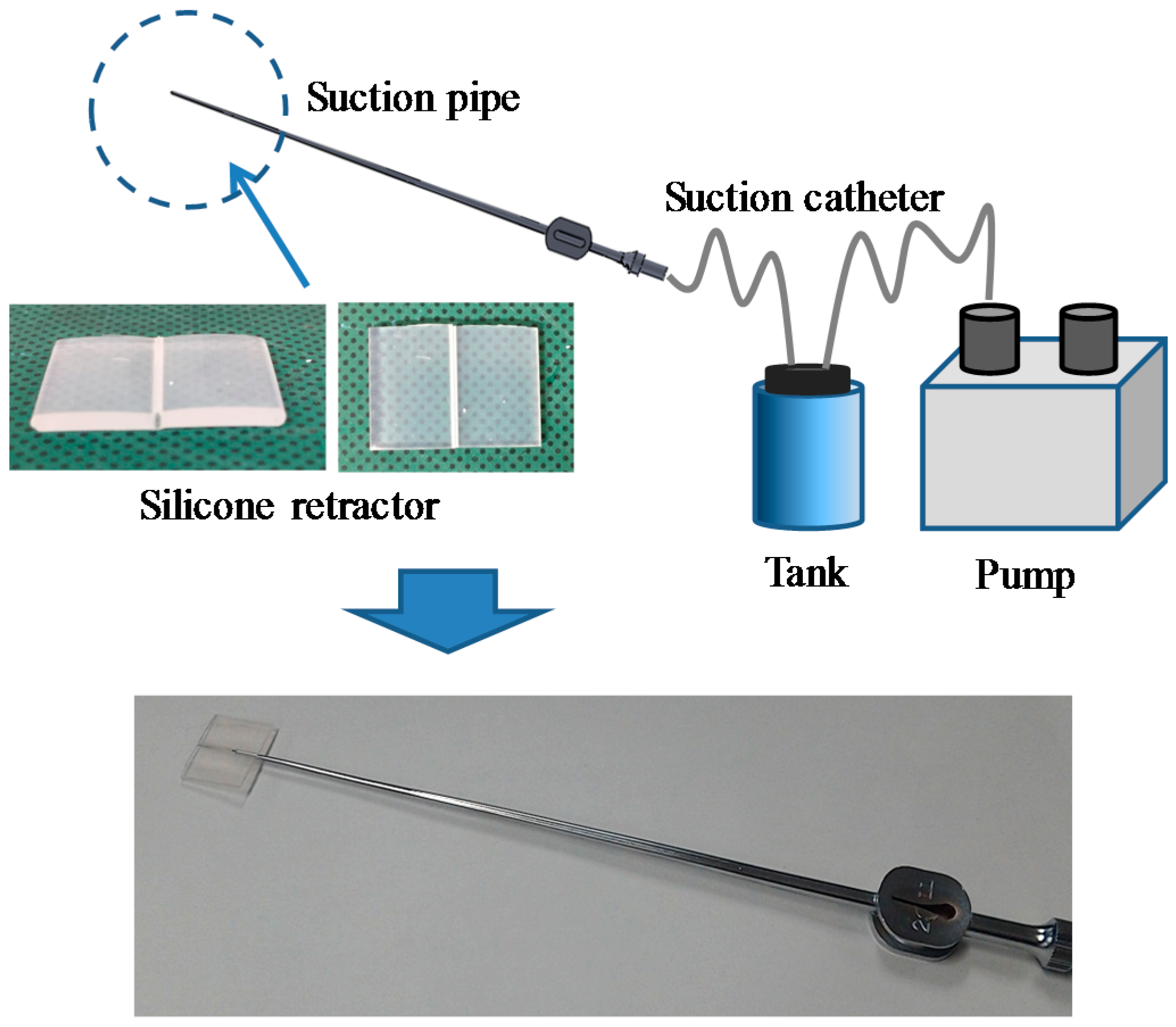
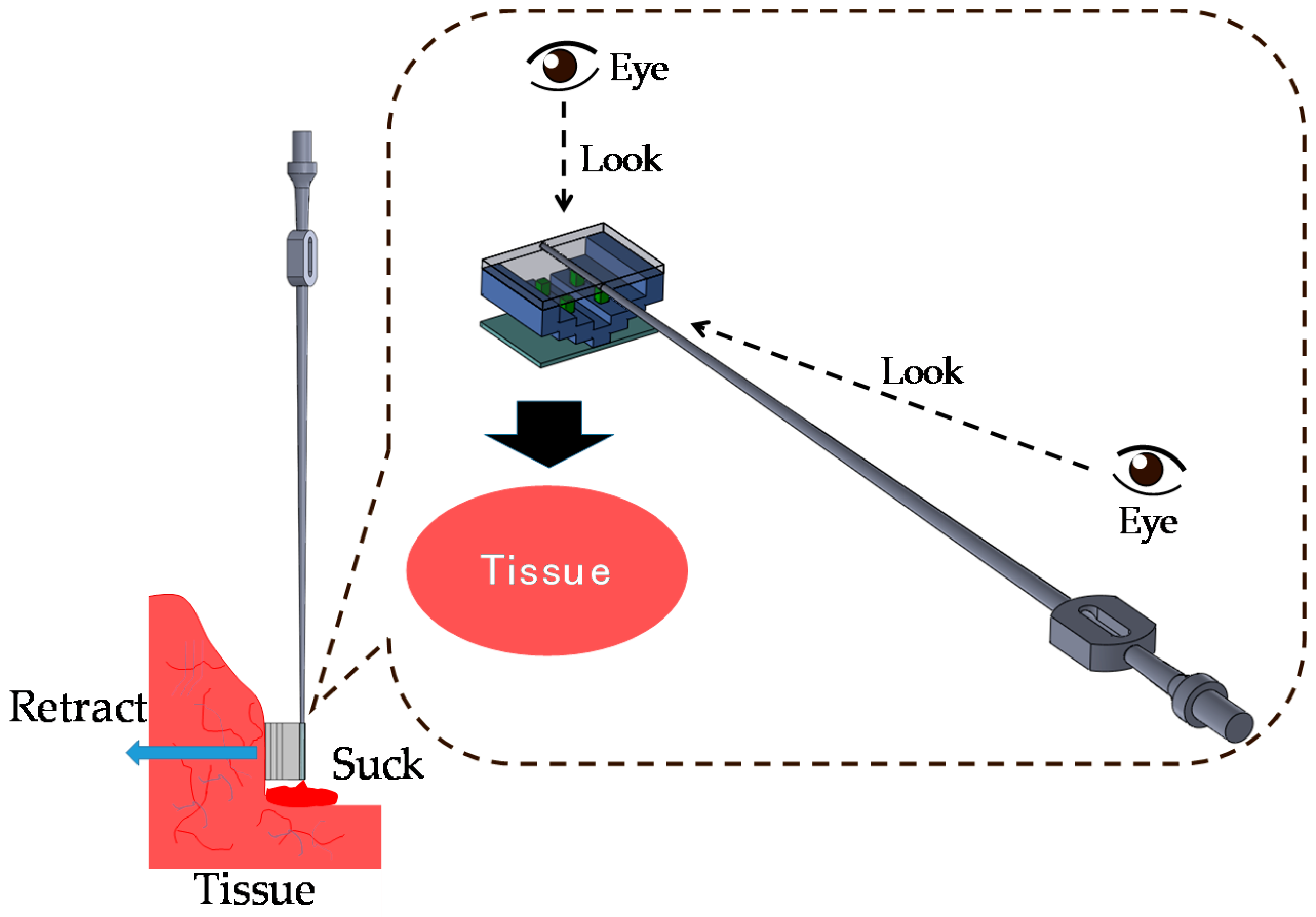
3.1. Target Situation
3.2. Design Requirements
- The retraction force can be visualized.
- The retraction force can be measured while retraction is being performed.
- The device can be attached to suction pipes.
- The device does not include any electric components.
- The device dimensions should be as follows: a width of less than 30 mm, length of less than 20 mm, and thickness of less than 15 mm.
- The force can be measured over a range of 0–0.3 N, with a resolution of 0.05 N.
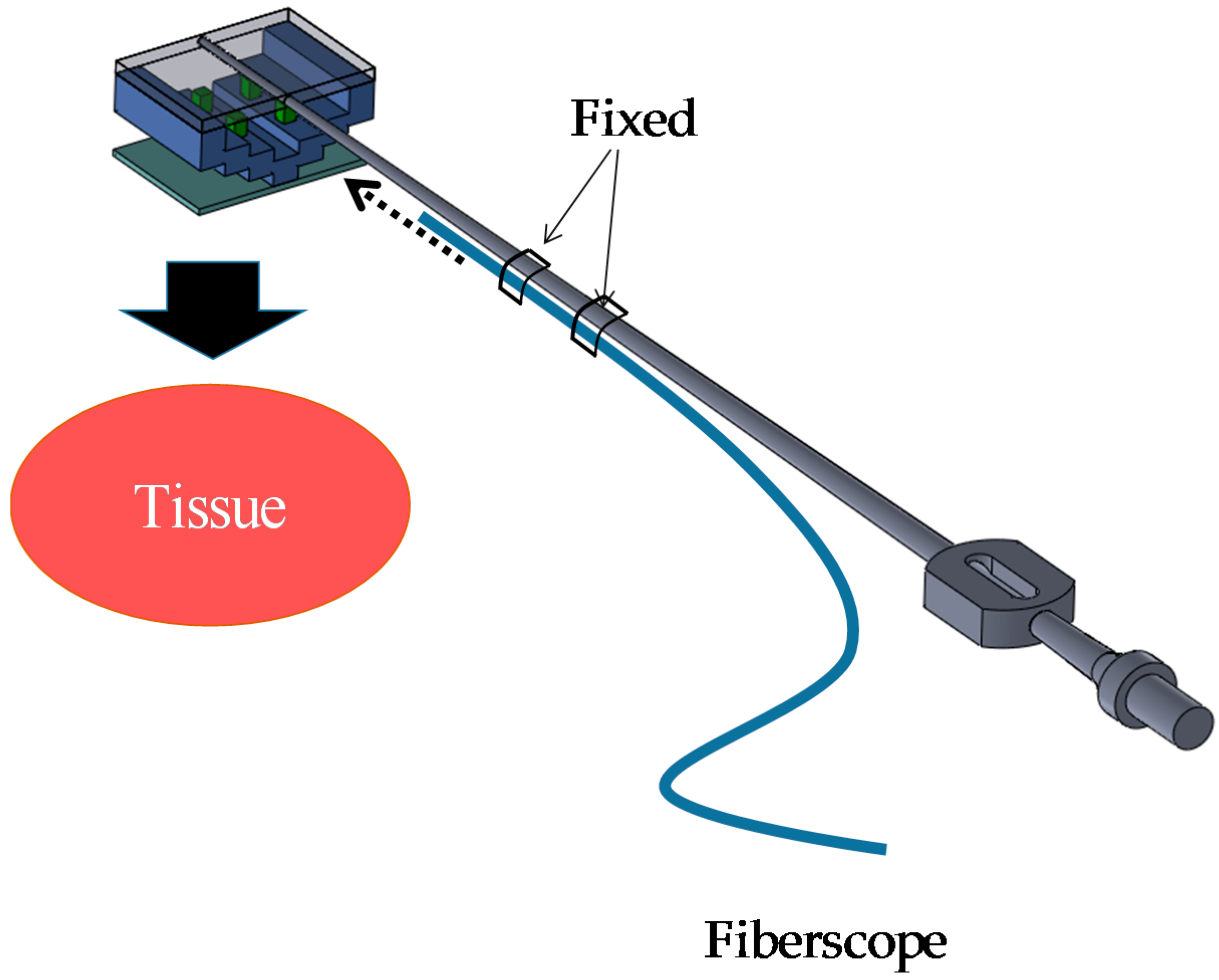
3.3. Principle of Force Sensing
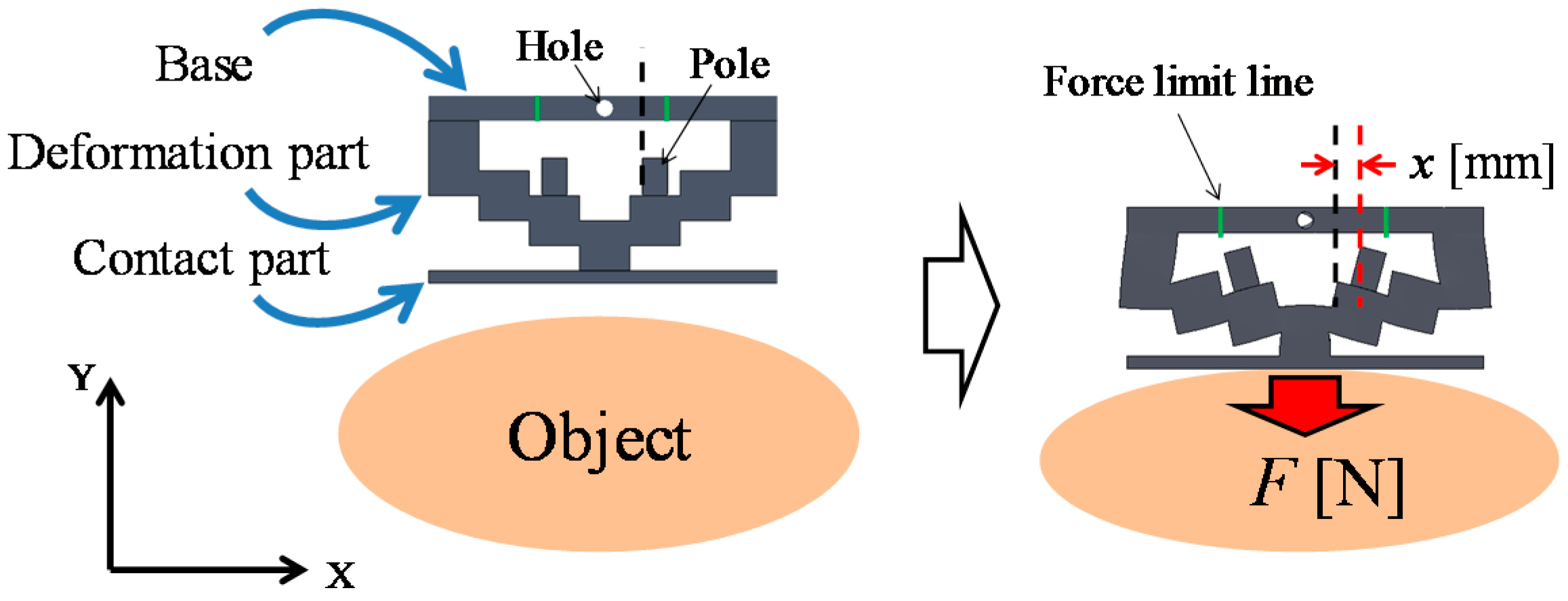
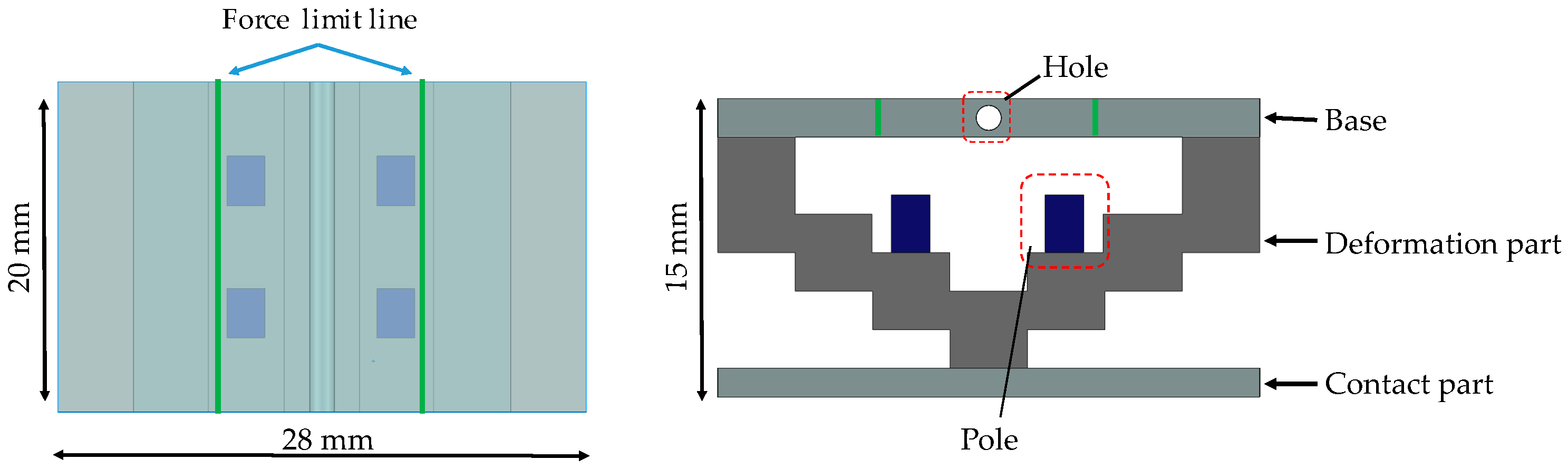
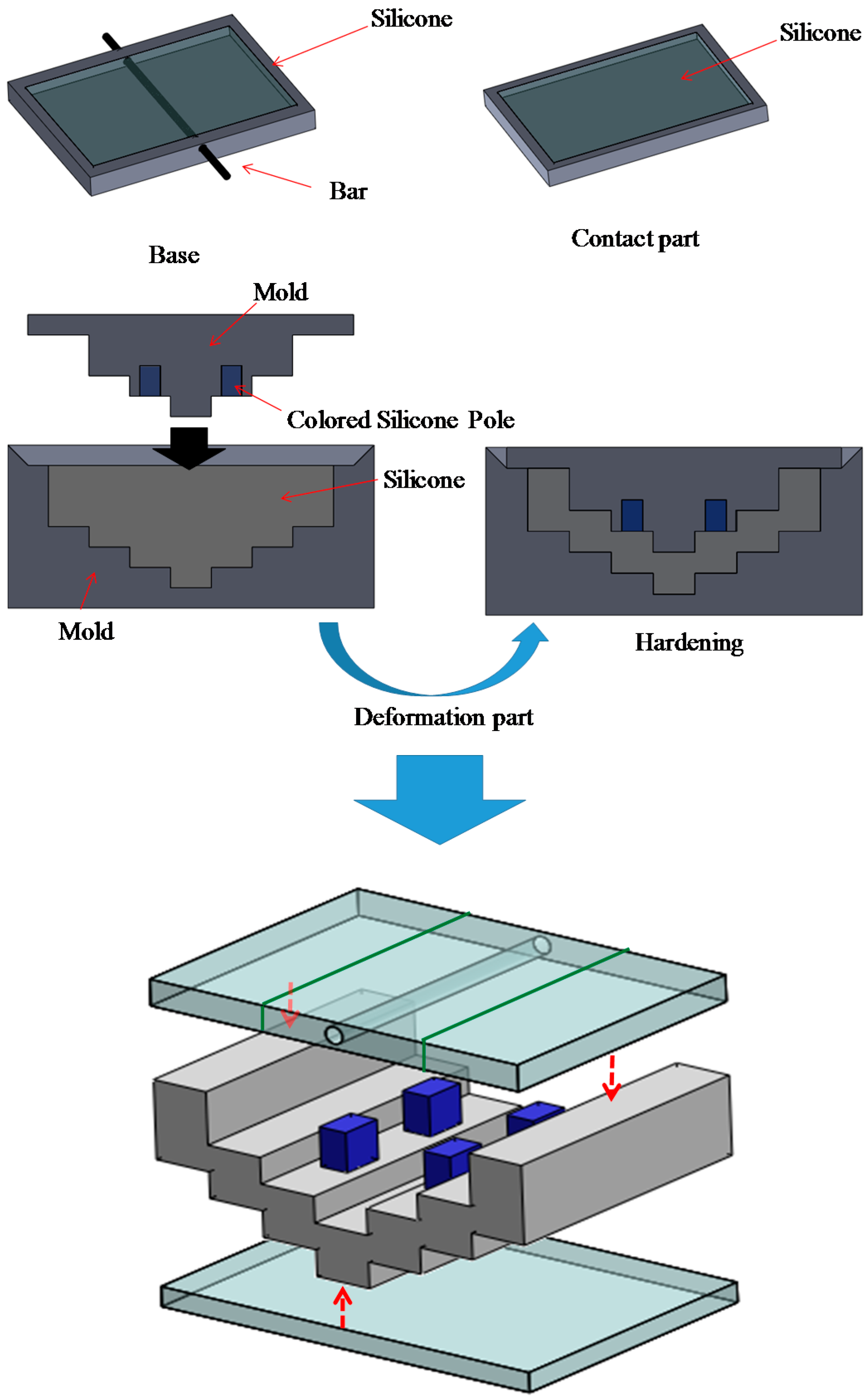
3.4. Structure of Silicone Retractor with Embedded Force-Sensing System
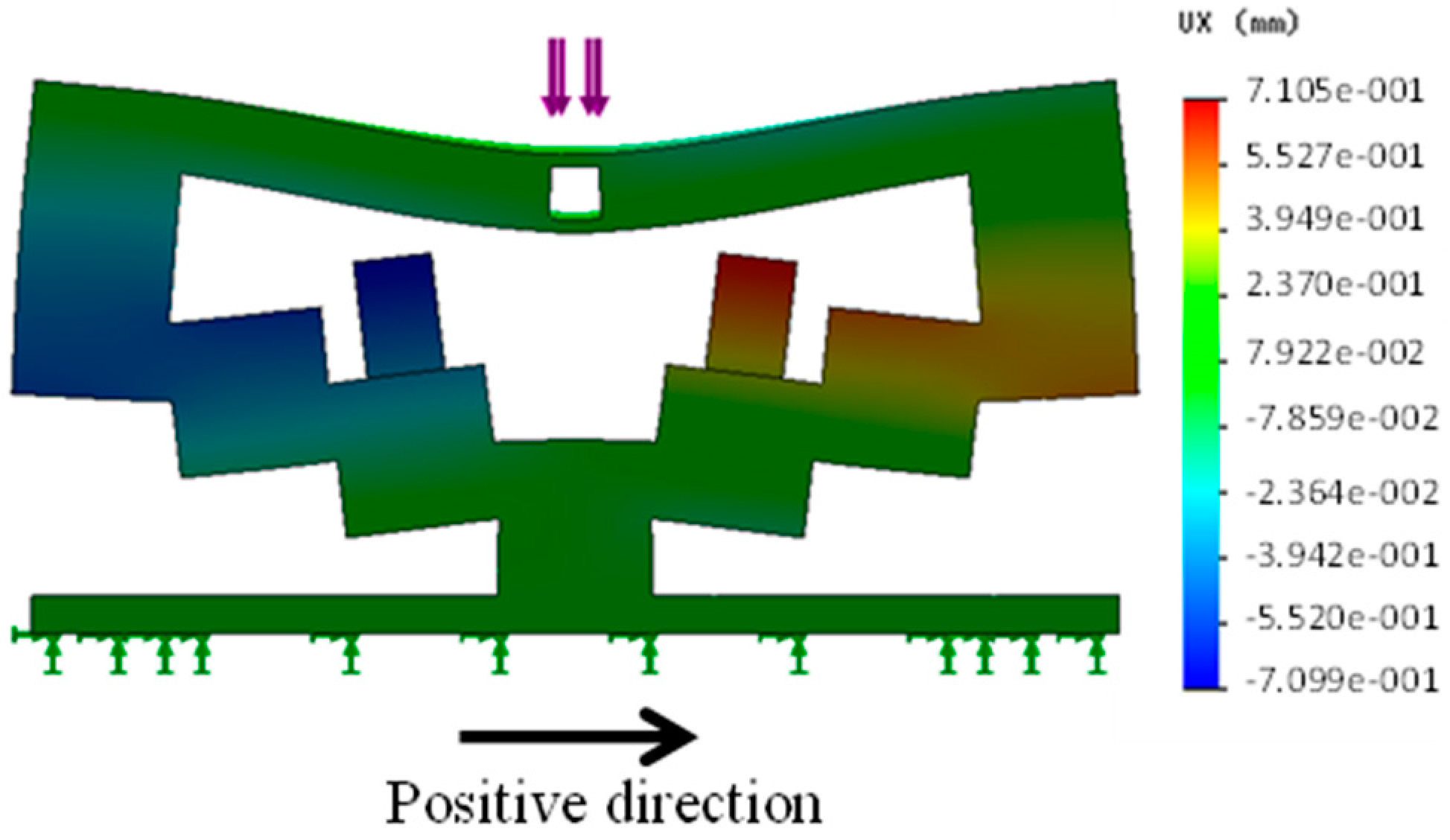
3.5. FEM Analysis of Relationship between Retraction Force and Distance Moved by Pole Tip
4. Experimental Evaluation
4.1. Case of Retracting a Flat and Solid Surface
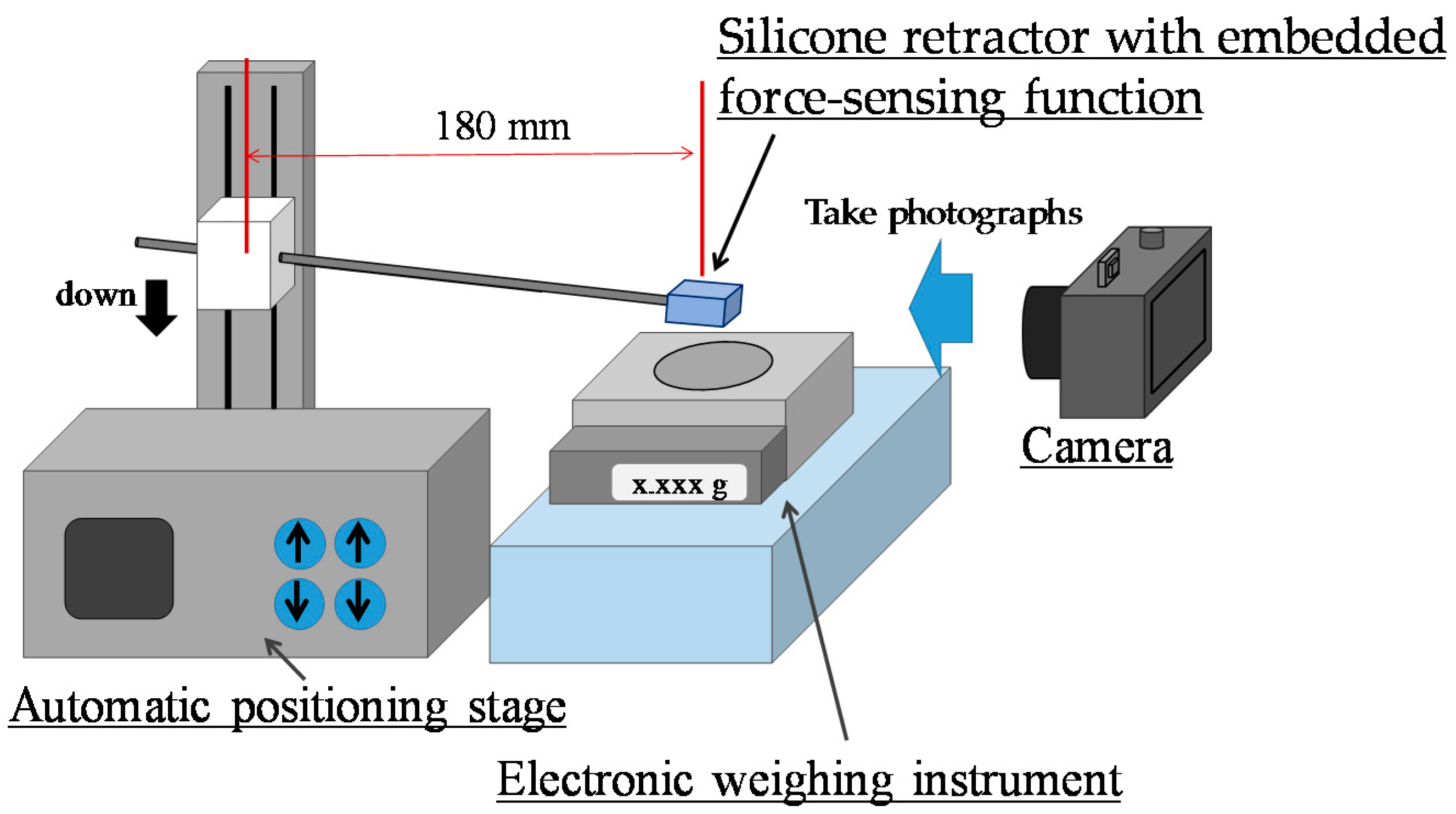
4.1.1. Procedure
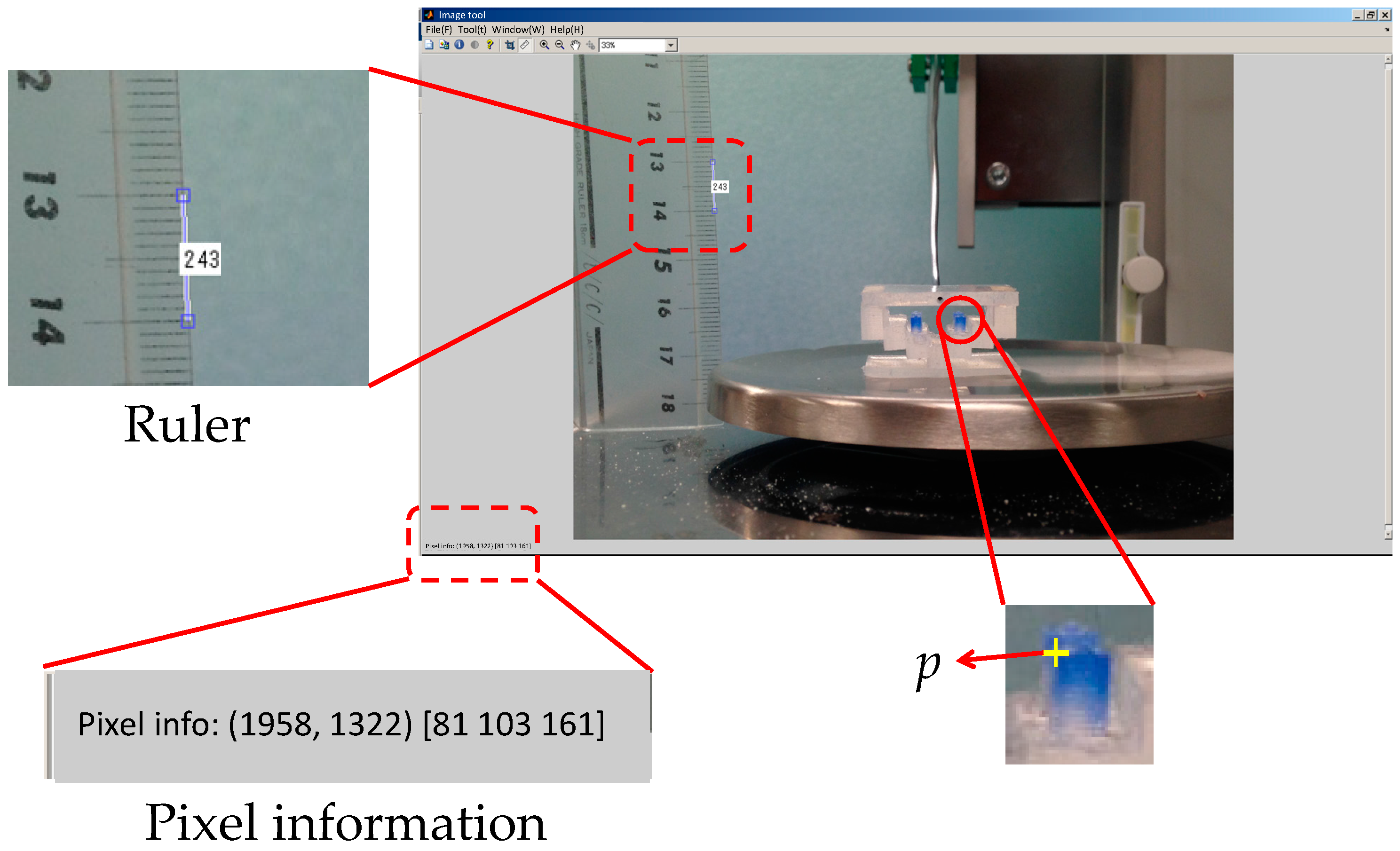
4.1.2. Derivation of Distance Moved by Pole Tip in Silicone Retractor
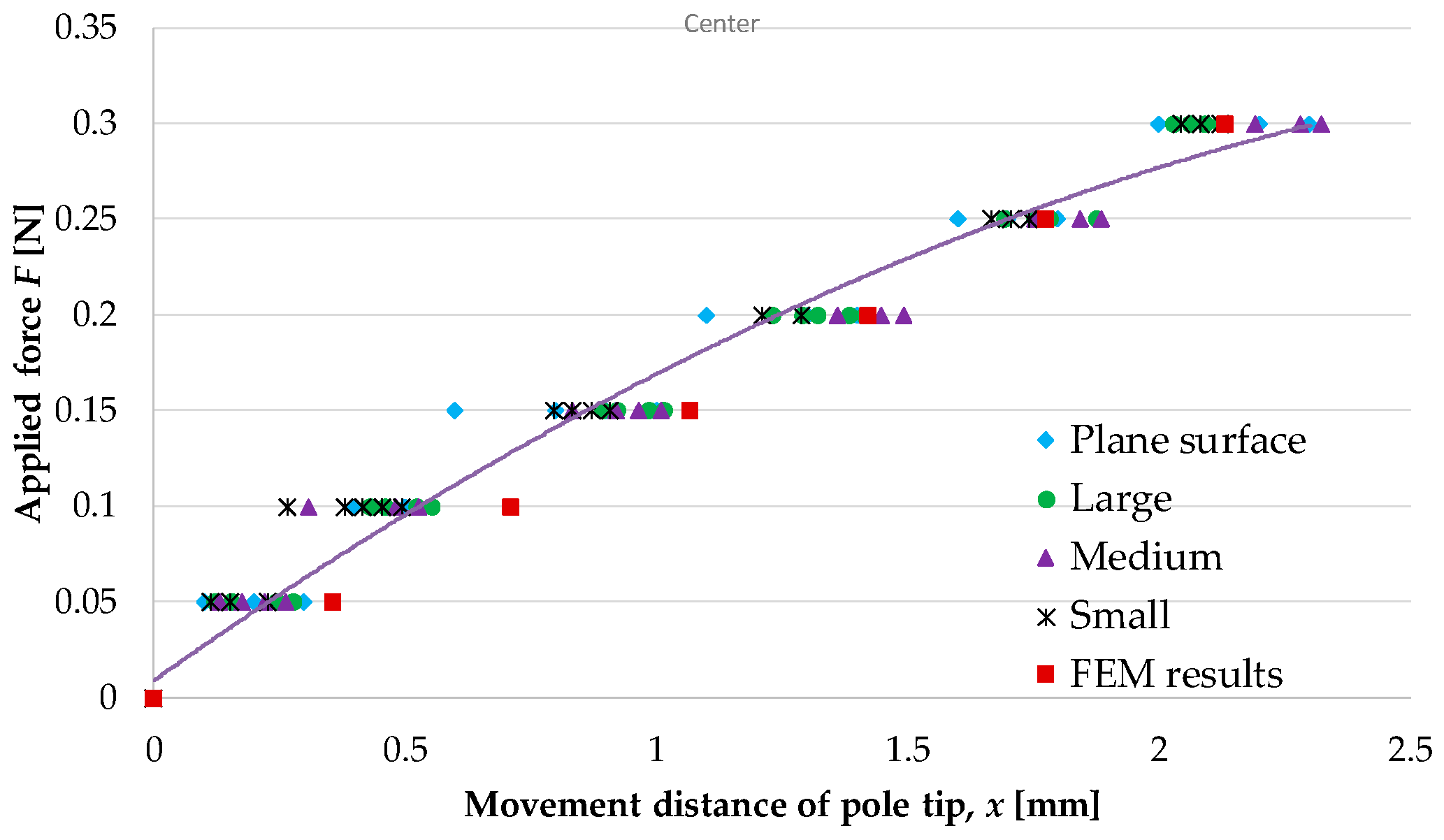
4.1.3. Relationship between Retraction Force and Distance Moved by Pole Tip
4.1.4. Discussion
4.2. Case of Retraction of Curved and Soft Surfaces
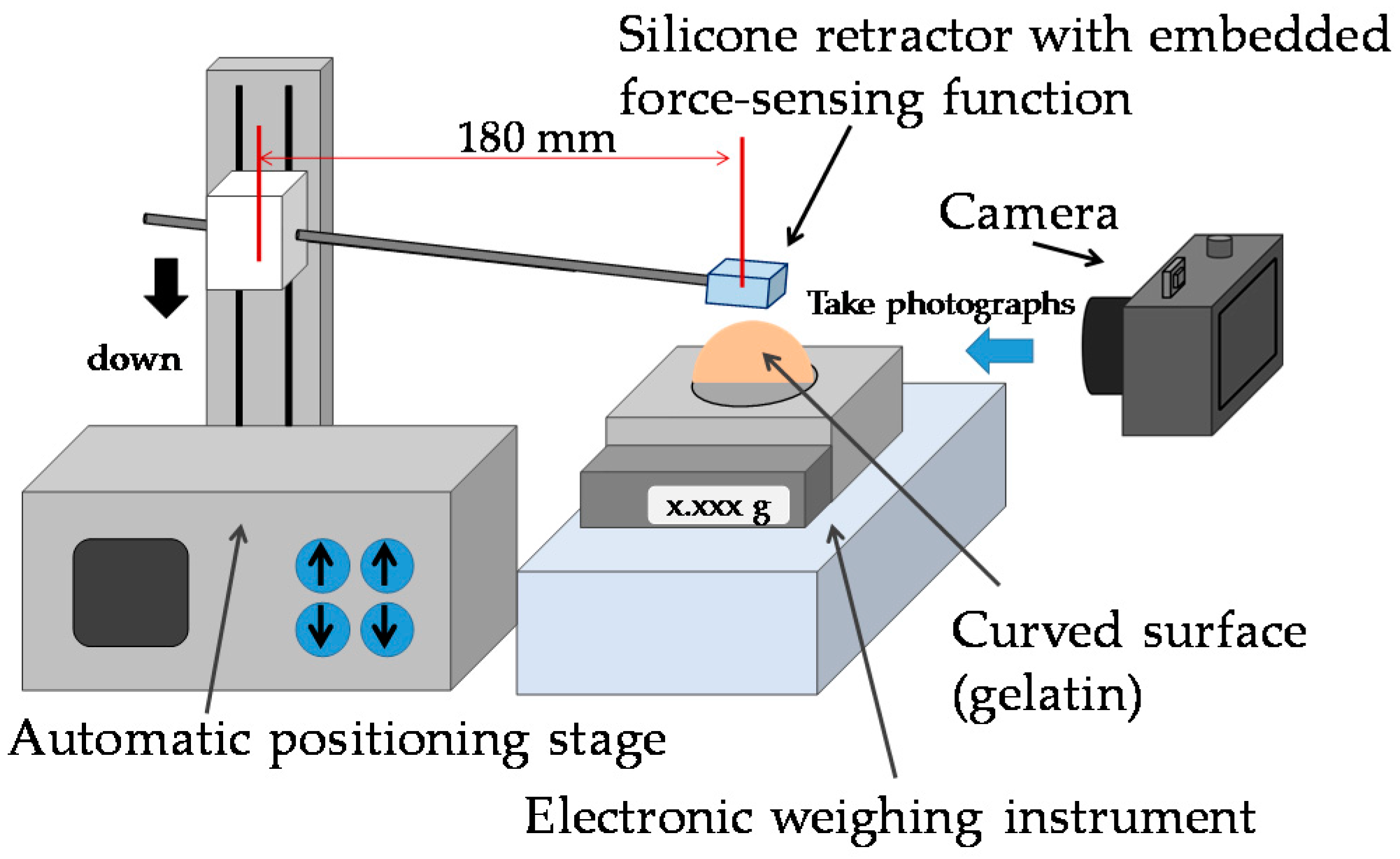
4.2.1. Procedure
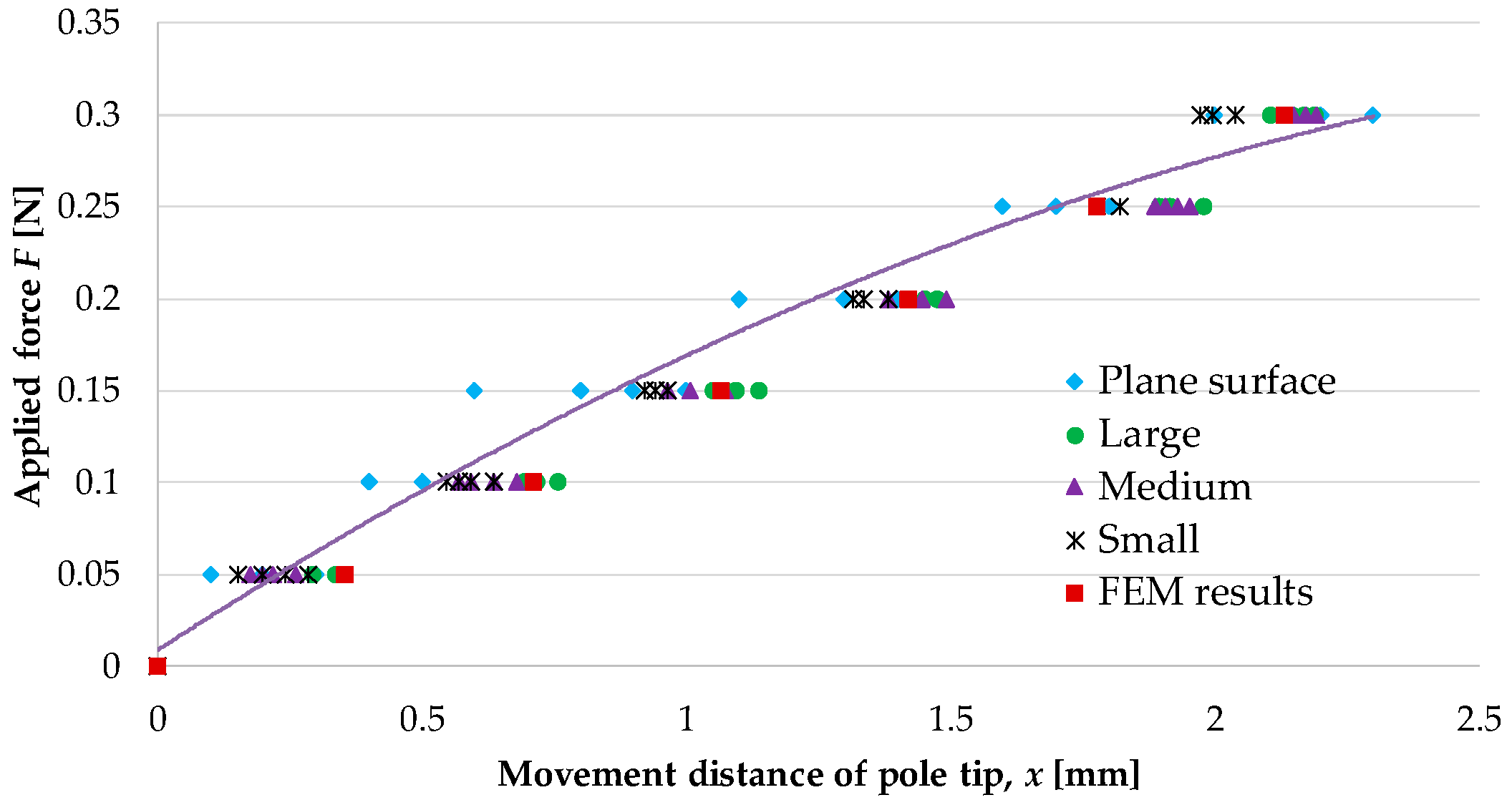
4.2.2. Relationship between Retraction Force and Distance Moved by Pole Tip
4.2.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Koyama, T.; Iwai, T.; Yoneyama, T.; Kagawa, H.; Hayashi, Y.; Nakada, M.; Watanabe, T. Silicone Retractor with Embedded Force-Sensing Function for Attachment to Surgical Suction Pipes. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Korea, 7–11 July 2015; pp. 145–150. [CrossRef]
- Puangmali, P.; Althoefer, K.; Seneviratne, L.D.; Murphy, D.; Dasgupta, P. State-of-the-Art in Force and Tactile Sensing for Minimally Invasive Surgery. IEEE Sens. J. 2008, 8, 371–381. [Google Scholar] [CrossRef]
- Westebring-van der Putten, E.P.; Goossens, R.H.M.; Jakimowicz, J.J.; Dankelman, J. Haptics in Minimally Invasive Surgery—A Review. Minim. Invasive Ther. Allied Technol. 2008, 17, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Okamura, A.M. Haptic Feedback in Robot-Assisted Minimally Invasive Surgery. Curr. Opin. Urol. 2009, 19, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Vander Poorten, E.V.B.; Demeester, E.; Lammertse, P. Haptic Feedback for Medical Applications, A Survey. In Proceedings of the 13th International Conference on New Actuators, Bremen, Germany, 18–21 June 2012; pp. 18–20.
- Tiwana, M.I.; Redmond, S.J.; Lovell, N.H. A Review of Tactile Sensing Technologies with Applications in Biomedical Engineering. Sens. Actuators A Phys. 2012, 179, 17–31. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile Sensing-From Humans to Humanoids. IEEE Trans. Robot. 2010, 26, 1–20. [Google Scholar] [CrossRef]
- Back, J.; Dasgupta, P.; Seneviratne, L.; Althoefer, K.; Liu, H. Feasibility Study-Novel Optical Soft Tactile Array Sensing for Minimally Invasive Surger. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1528–1533. [CrossRef]
- Yoneyama, T.; Watanabe, T.; Kagawa, H.; Hamada, J.; Hayashi, Y.; Nakada, M. Force-Detecting Gripper and Force Feedback System for Neurosurgery Applications. Int. J. Comput. Assist. Radiol. Surg. 2013, 8, 819–829. [Google Scholar] [CrossRef] [PubMed]
- Kanada, Y.; Yoneyama, T.; Watanabe, T.; Kagawa, H.; Sugiyama, N.; Tanaka, K.; Hanyu, T. Force Feedback Manipulating System for Neurosurgery. Procedia CIRP 2013, 5, 133–136. [Google Scholar] [CrossRef]
- Fujihira, Y.; Hanyu, T.; Kanada, Y.; Yoneyama, T.; Watanabe, T.; Kagawa, H. Gripping Force Feedback System for Neurosurgery. Int. J. Autom. Technol. 2014, 8, 83–94. [Google Scholar]
- Tomo, T.P.; Somlor, S.; Schmitz, A.; Jamone, L.; Huang, W.; Kristanto, H.; Sugano, S. Design and Characterization of A Three-Axis Hall Effect-Based Soft Skin Sensor. Sensors 2016, 16, 491. [Google Scholar] [CrossRef] [PubMed]
- Jamone, L.; Natale, L.; Metta, G.; Sandini, G. Highly Sensitive Soft Tactile Sensors for an Anthropomorphic Robotic Hand. IEEE Sens. J. 2015, 15, 4226–4233. [Google Scholar] [CrossRef]
- Takaki, T.; Omasa, Y.; Ishii, I.; Kawahara, T.; Okajima, M. Force Visualization Mechanism Using a Moire; Fringe Applied to Endoscopic Surgical Instruments. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3648–3653. [CrossRef]
- Tadano, K.; Kawashima, K. Development of 4-DOFs Forceps with Force Sensing using Pneumatic Servo System. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 2250–2255. [CrossRef]
- Kawahara, T.; Tanaka, S.; Kaneko, M. Non-Contact Stiffness Imager. Int. J. Rob. Res. 2006, 25, 537–549. [Google Scholar] [CrossRef]
- Peirs, J.; Clijnen, J.; Reynaerts, D.; Brussel, H.; Van Herijgers, P.; Corteville, B.; Boone, S. A Micro Optical Force Sensor for Force Feedback during Minimally Invasive Robotic Surgery. Sens. Actuators A Phys. 2004, 115, 447–455. [Google Scholar] [CrossRef]
- Tada, M.; Sasaki, S.; Ogasawara, T. Development of an Optical 2-axis Force Sensor Usable in MRI Environments. IEEE Sens. Proc. 2002, 2, 984–989. [Google Scholar]
- Puangmali, P.; Liu, H.; Seneviratne, L.D.; Dasgupta, P.; Althoefer, K. Miniature 3-Axis Distal Force Sensor for Minimally Invasive Surgical Palpation. IEEE/ASME Trans. Mechatron. 2012, 17, 646–656. [Google Scholar] [CrossRef]
- Polygerinos, P.; Seneviratne, L.D.; Razavi, R.; Schaeffter, T.; Althoefer, K. Triaxial Catheter-Tip Force Sensor for MRI-Guided Cardiac Procedures. IEEE/ASME Trans. Mechatron. 2013, 18, 386–396. [Google Scholar] [CrossRef]
- Polygerinos, P.; Ataollahi, A.; Schaeffter, T.; Razavi, R.; Seneviratne, L.D.; Althoefer, K. MRI-Compatible Intensity-Modulated Force Sensor for Cardiac Catheterization Procedures. IEEE Trans. Biomed. Eng. 2011, 58, 721–726. [Google Scholar] [CrossRef] [PubMed]
- Polygerinos, P.; Zbyszewski, D.; Schaeffter, T.; Razavi, R.; Seneviratne, L.D.; Althoefer, K. MRI-Compatible Fiber-Optic Force Sensors for Catheterization Procedures. IEEE Sens. J. 2010, 10, 1598–1608. [Google Scholar] [CrossRef]
- Polygerinos, P.; Seneviratne, L.D.; Althoefer, K. Modeling of Light Intensity-Modulated Fiber-Optic Displacement Sensors. IEEE Trans. Instrum. Meas. 2011, 60, 1408–1415. [Google Scholar] [CrossRef]
- Liu, H.; Puangmali, P.; Zbyszewski, D.; Elhage, O.; Dasgupta, P.; Dai, J.S.; Seneviratne, L.; Althoefer, K. An Indentation Depth-Force Sensing Wheeled Probe for Abnormality Identification during Minimally Invasive Surgery. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2010, 224, 751–763. [Google Scholar] [CrossRef]
- Ahmadi, R.; Packirisamy, M.; Dargahi, J.; Cecere, R. Discretely Loaded Beam-Type Optical Fiber Tactile Sensor for Tissue Manipulation and Palpation in Minimally Invasive Robotic Surgery. IEEE Sens. J. 2012, 12, 22–32. [Google Scholar] [CrossRef]
- Xie, H.; Liu, H.; Seneviratne, L.D.; Althoefer, K. An Optical Tactile Array Probe Head for Tissue Palpation During Minimally Invasive Surgery. IEEE Sens. J. 2014, 14, 3283–3291. [Google Scholar] [CrossRef]
- Tan, U.X.; Yang, B.; Gullapalli, R.; Desai, J.P. Tri-Axial MRI Compatible Fiber-Optic Force Sensor. IEEE Trans. Robot. 2011, 27, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Fischer, G.S. A 3-Axis Optical Force/Torque Sensor for Prostate Needle Placement in Magnetic Resonance Imaging Environments. In Proceedings of the 2009 IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 9–10 November 2009; pp. 5–9. [CrossRef]
- Turkseven, M.; Ueda, J. Design of an MRI Compatible Haptic Interface. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2139–2144. [CrossRef]
- Su, H.; Zervas, M.; Furlong, C.; Fischer, G.S. A Miniature Mri-Compatible Fiber-Optic Force Sensor Utilizing Fabry-Perot Interferometer. In Mems and Nanotechnology; Springer: New York, NY, USA, 2011; pp. 131–136. [Google Scholar] [CrossRef]
- Su, H.; Zervas, M.; Cole, G.A.; Furlong, C.; Fischer, G.S. Real-Time MRI-Guided Needle Placement Robot with Integrated Fiber Optic Force Sensing. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1583–1588. [CrossRef]
- Liu, X.; Iordachita, I.I.; He, X.; Taylor, R.H.; Kang, J.U. Miniature Fiber-Optic Force Sensor based on Low-Coherence Fabry-Pérot Interferometry for Vitreoretinal Microsurgery. Biomed. Opt. Express 2012, 3, 1062–1076. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Iwai, T.; Fujihira, Y.; Wakako, L.; Kagawa, H.; Yoneyama, T. Force Sensor Attachable to Thin Fiberscopes/Endoscopes Utilizing High Elastic Fabric. Sensors 2014, 14, 5207–5220. [Google Scholar] [CrossRef] [PubMed]
- Iwai, T.; Fujihira, Y.; Wakako, L.; Kagawa, H.; Yoneyama, T.; Watanabe, T. Three-Axis Force Visualizing System for Fiberscopes Utilizing Highly Elastic Fabric. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Besacon, France, 8–11 July 2014; pp. 1110–1115. [CrossRef]
- Watanabe, T.; Iwai, T.; Koyama, T.; Yoneyama, T. Stiffness Measurement System Using Endoscopes With a Visualization Method. IEEE Sens. J. 2016, 16, 5889–5897. [Google Scholar] [CrossRef]
- Ohka, M.; Mitsuya, Y.; Matsunaga, Y.; Takeuchi, S. Sensing Characteristics of an Optical Three-Axis Tactile Sensor under Combined Loading. Robotica 2004, 22, 213–221. [Google Scholar] [CrossRef]
- Kamiyama, K.; Vlack, K.; Mizota, T.; Kajimoto, H.; Kawakami, K.; Tachi, S. Vision-based Sensor for Real-Time Measuring of Surface Traction Fields. IEEE Comput. Graph. Appl. 2005, 25, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Winstone, B.; Griffiths, G.; Pipe, T.; Melhuish, C.; Rossiter, J. TACTIP—Tactile Fingertip Device, Texture Analysis through Optical Tracking of Skin Features. In Biomimetic and Biohybrid Systems; Springer: Berlin, Germany; Heidelberg, Germany, 2013; pp. 323–334. [Google Scholar] [CrossRef]
- Gan, L.S.; Zareinia, K.; Lama, S.; Maddahi, Y.; Yang, F.W.; Sutherland, G.R. Quantification of Forces during a Neurosurgical Procedure: A Pilot Study. World Neurosurg. 2015, 84, 537–548. [Google Scholar] [CrossRef] [PubMed]
- Marcus, H.J.; Zareinia, K.; Gan, L.S.; Yang, F.W.; Lama, S.; Yang, G.Z.; Sutherland, G.R. Forces Exerted during Microneurosurgery: a Cadaver Study. Int. J. Med. Robot. Comput. Assist. Surg. 2014, 10, 251–256. [Google Scholar] [CrossRef] [PubMed]
- Payne, C.J.; Marcus, H.J.; Yang, G.Z. A Smart Haptic Hand-Held Device for Neurosurgical Microdissection. Ann. Biomed. Eng. 2015, 43, 2185–2195. [Google Scholar] [CrossRef] [PubMed]
- Allin, S.; Matsuoka, Y.; Klatzky, R. Measuring just Noticeable Differences for Haptic Force Feedback: Implications for Rehabilitation. In Proceedings of the 10th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Orlando, FL, USA, 24–25 March 2002; pp. 299–302. [CrossRef]








| Part | Young’s Modulus MPa | Poisson’s Ratio |
|---|---|---|
| Base | 0.5 | 0.3 |
| Deformation part | 0.2 | 0.3 |
| Contact part | 0.5 | 0.3 |
| Device | Camera | Electronic Weighing Instrument | Automatic Positioning Stage |
|---|---|---|---|
| Resolution | 2816 × 2112 pixels | 0.001 g | 0.01 mm |
| Speed | - | - | 10 (mm/min) |
| Dimension of Polynomial Function | Coefficient of Determination, R2 | RMSE |
|---|---|---|
| 2 | 0.98 | 0.014 |
| Retraction Position | Large | Medium | Small |
|---|---|---|---|
| Center | 0.013 N | 0.017 N | 0.012 N |
| At a distance of 5 mm from center | 0.026 N | 0.020 N | 0.014 N |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, T.; Koyama, T.; Yoneyama, T.; Nakada, M. Force-Sensing Silicone Retractor for Attachment to Surgical Suction Pipes. Sensors 2016, 16, 1133. https://doi.org/10.3390/s16071133
Watanabe T, Koyama T, Yoneyama T, Nakada M. Force-Sensing Silicone Retractor for Attachment to Surgical Suction Pipes. Sensors. 2016; 16(7):1133. https://doi.org/10.3390/s16071133
Chicago/Turabian StyleWatanabe, Tetsuyou, Toshio Koyama, Takeshi Yoneyama, and Mitsutoshi Nakada. 2016. "Force-Sensing Silicone Retractor for Attachment to Surgical Suction Pipes" Sensors 16, no. 7: 1133. https://doi.org/10.3390/s16071133
APA StyleWatanabe, T., Koyama, T., Yoneyama, T., & Nakada, M. (2016). Force-Sensing Silicone Retractor for Attachment to Surgical Suction Pipes. Sensors, 16(7), 1133. https://doi.org/10.3390/s16071133





