Novel Intersection Type Recognition for Autonomous Vehicles Using a Multi-Layer Laser Scanner
Abstract
:1. Introduction
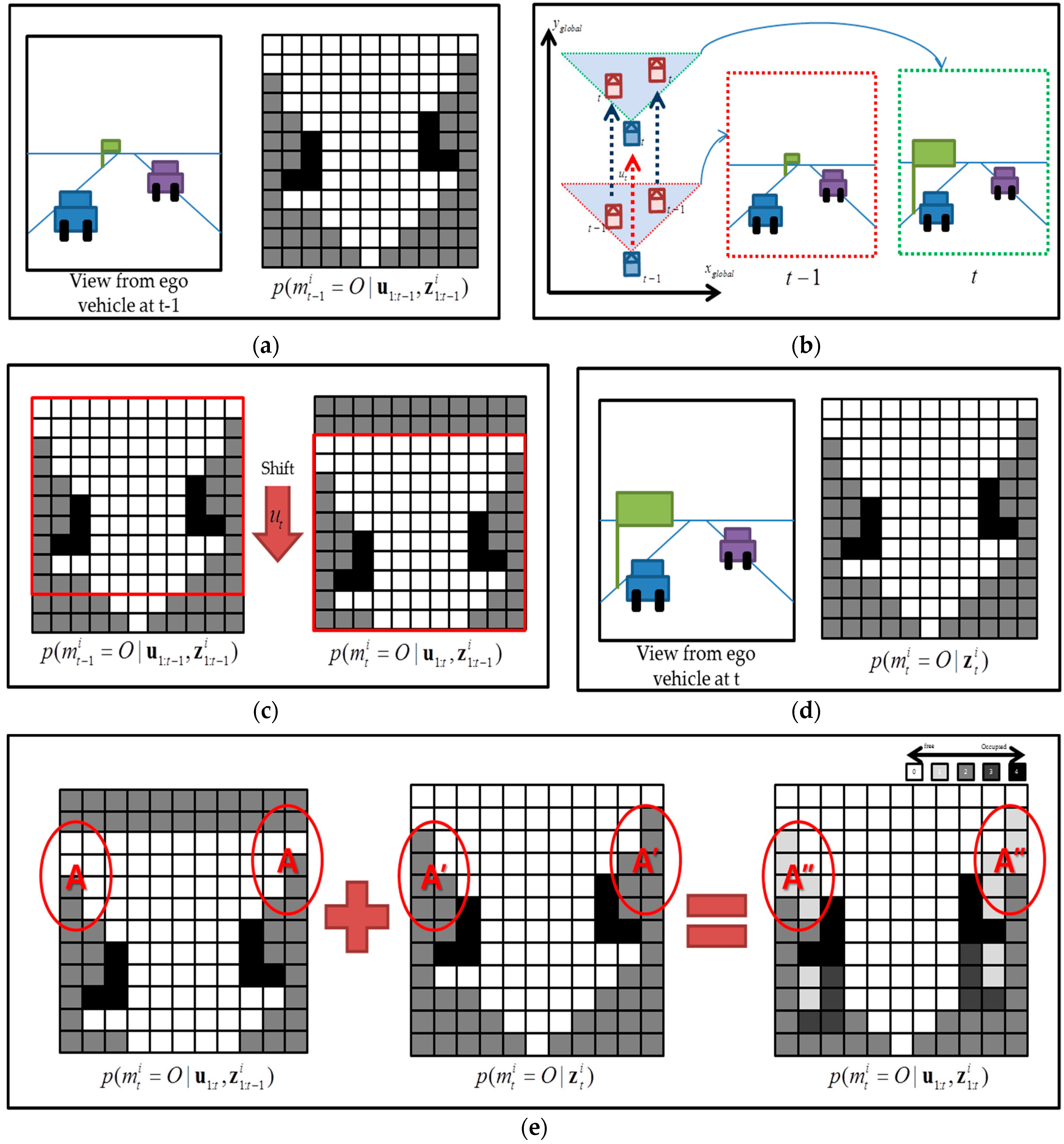
2. Static Local Coordinate Occupancy Grid Map
2.1. Motivation
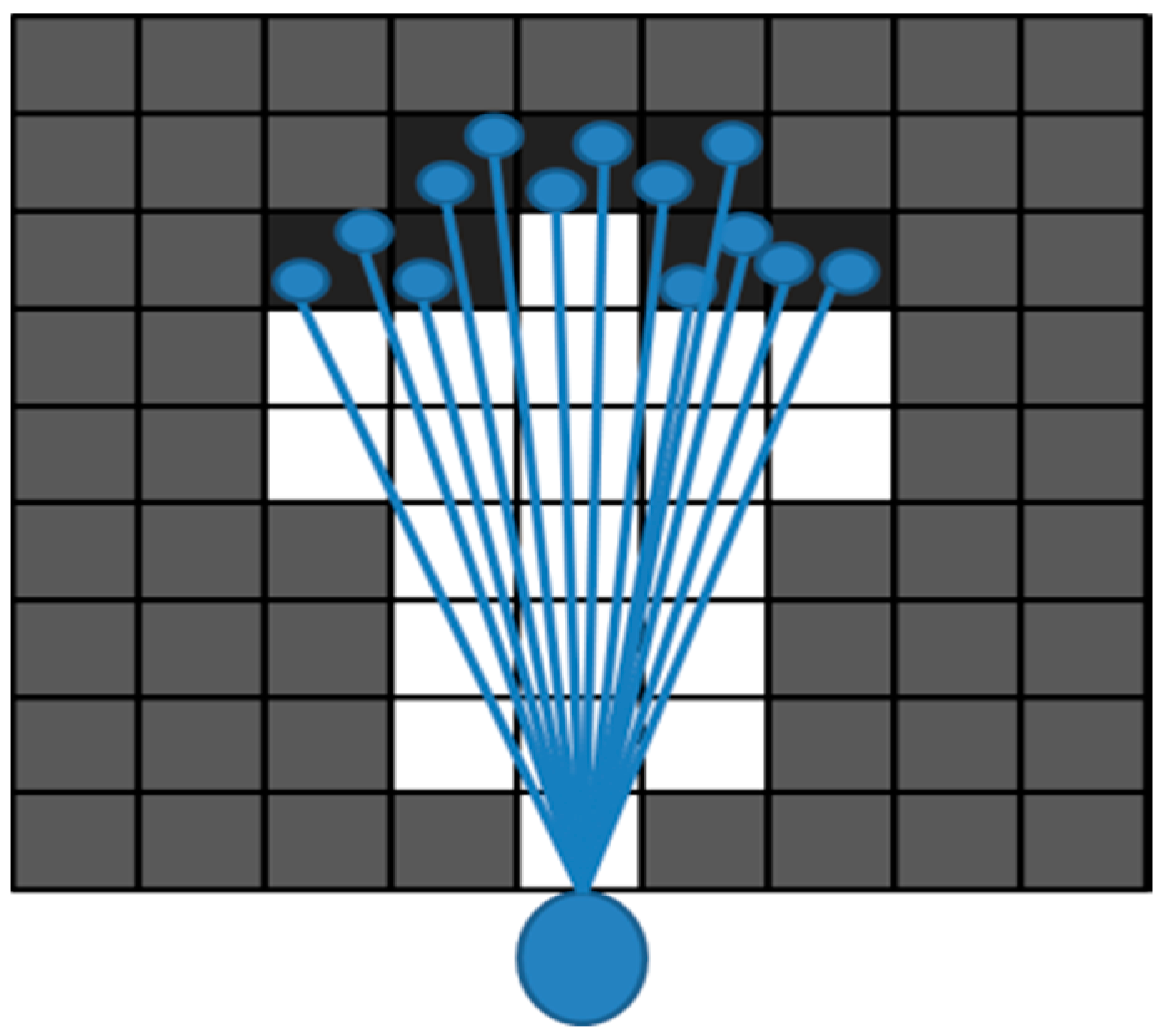
2.2. Occupancy Grid Mapping Relative to Autonomous Vehicles
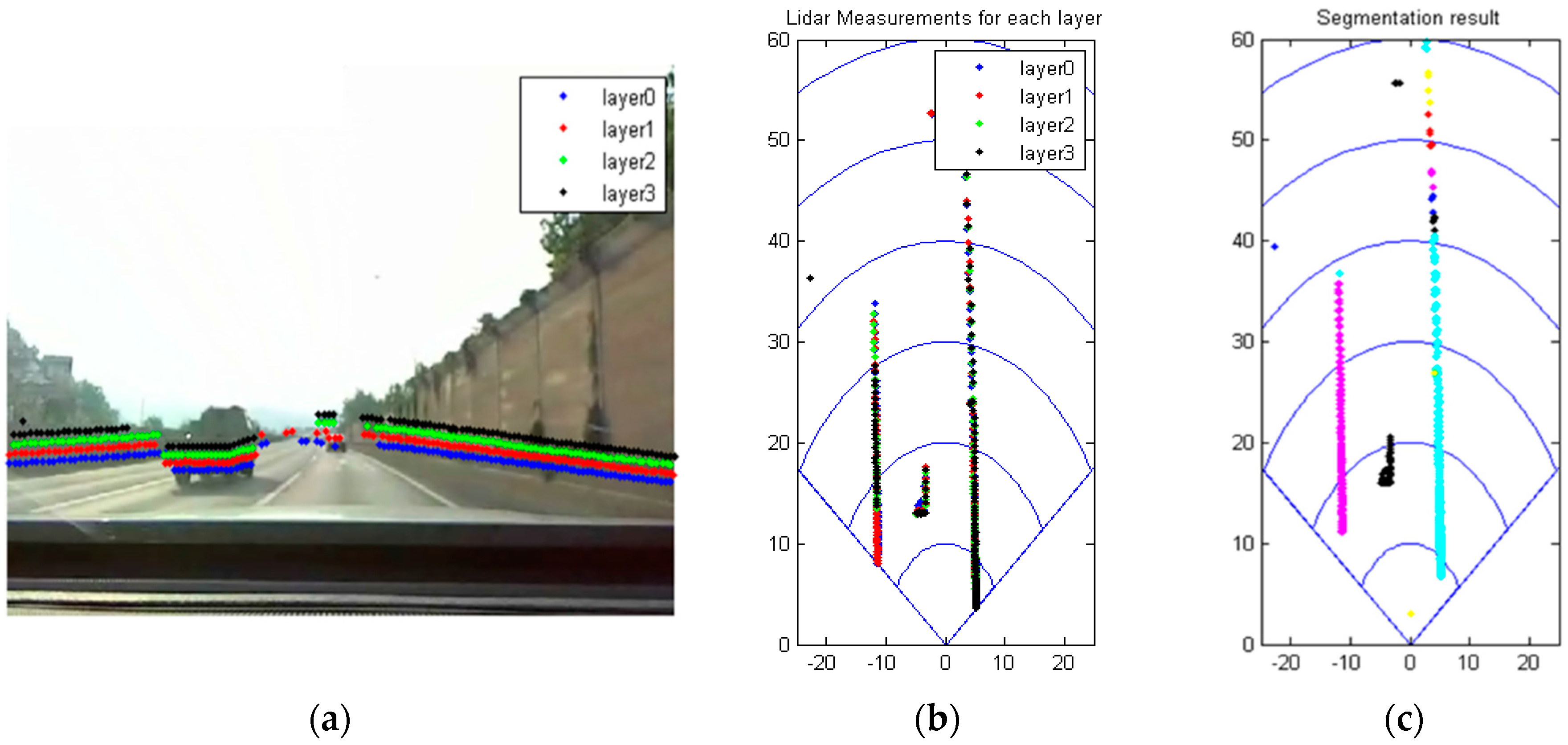
2.3. Dynamic Object Removal
3. Intersection Type Recognition Using the SLOGM
3.1. Intersection Types
3.2. New Similarity Measure and Nearest Neighbor Classifier
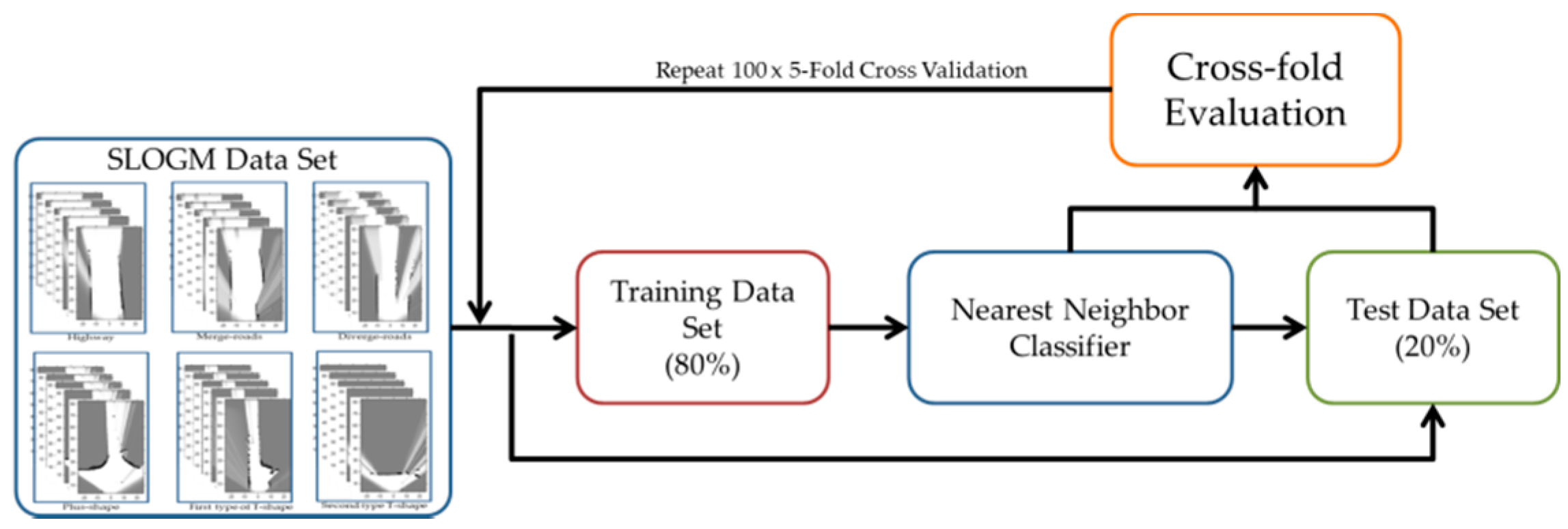
4. Experiment Setup
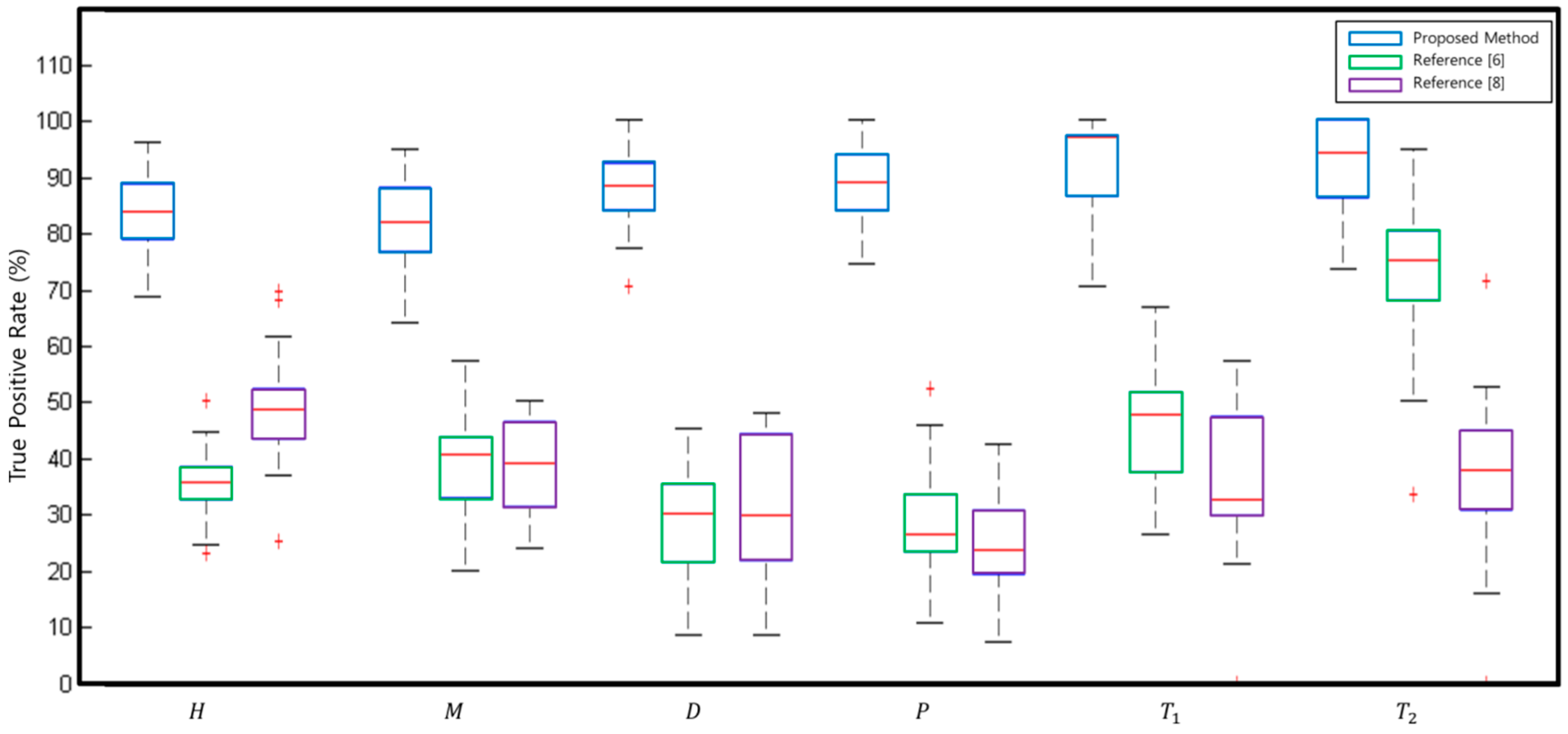
5. Experiment Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alberto, B. Parallel and local feature extraction: A real-time approach to road boundary detection. IEEE Trans. Image Process. 1995, 4, 217–223. [Google Scholar]
- Kong, H.; Audibert, J.-Y.; Ponce, J. General road detection from a single image. IEEE Trans. Image Process. 2010, 19, 2211–2220. [Google Scholar] [PubMed]
- Karl, K. Extracting road curvature and orientation from image edge points without perceptual grouping into features. In Proceedings of the IEEE Intelligent Vehicles Symposium, Paris, France, 24–26 October 1994; pp. 109–114.
- Danescu, R.; Oniga, F.; Nedevschi, S. Modeling and tracking the driving environment with a particle-based occupancy grid. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1331–1342. [Google Scholar] [CrossRef]
- Homm, F.; Kaempchen, N.; Ota, J.; Burschka, D. Efficient occupancy grid computation on the GPU with lidar and radar for road boundary detection. In Proceedings of the IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 1006–1013.
- Zhu, Q.; Chen, L.; Li, Q.Q.; Li, M.; Nüchter, A.; Wang, J. 3D lidar point cloud based intersections recognition for autonomous driving. In Proceedings of the IEEE Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012; pp. 456–461.
- Zhu, Q.; Mao, Q.; Chen, L.; Li, M.; Li, Q. Veloregistration based intersections detection for autonomous driving in challenging urban scenarios. In Proceedings of the 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 1191–1196.
- Hata, A.Y.; Habermann, D.; Osorio, F.S.; Wolf, D.F. Road geometry classification using ANN. In Proceedings of the IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 1319–1324.
- Chen, T.; Dai, B.; Liu, D.; Liu, Z. Lidar-based long range road intersections detection. In Proceedings of the 2011 Sixth International Conference on Image and Graphics (ICIG), Hefei, China, 12–15 August 2011; pp. 754–759.
- Ryu, K.-J.; Park, S.-K.; Hwang, J.-P.; Kim, E.-T.; Park, M. On-road Tracking using Laser Scanner with Multiple Hypothesis Assumption. Int. J. Fuzzy Logic. Intell. Syst. 2009, 9, 232–237. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H.; Kim, S. Positioning and Driving Control of Fork-Type Automatic Guided Vehicle with Laser Navigation. Int. J. Fuzzy Logic. Intell. Syst. 2013, 13, 307–314. [Google Scholar] [CrossRef]
- Kim, B.; Choi, B.; Park, S.; Kim, H.; Kim, E. Pedestrian/Vehicle Detection Using a 2.5-dimensional Multi-layer Laser Scanner. IEEE Sens. J. 2016, 16, 400–408. [Google Scholar] [CrossRef]
- Weiss, T.; Schiele, B.; Dietmayer, K. Robust Driving Path Detection in Urban and Highway Scenarios Using a Laser Scanner and Online Occupancy Grids. In Proceedings of the IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007; pp. 184–189.
- Konrad, M.; Szczot, M.; Dietmayer, K. Road course estimation in occupancy grids. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 412–417.
- Konrad, M.; Szczot, M.; Schüle, F.; Dietmayer, K. Generic grid mapping for road course estimation. In Proceedings of the IEEE Intelligent Vehicles Symposium, Baden-Baden, Germany, 5–9 June 2011; pp. 851–856.
- Thrun, S.; Fox, D.; Burgard, W. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Lee, H.; Hong, S.; Kim, E. Probabilistic background subtraction in a video-based recognition system. KSII Trans. Internet Inf. Syst. 2011, 5, 782–804. [Google Scholar] [CrossRef]
- Kim, B.; Choi, B.; Yoo, M.; Kim, H.; Kim, E. Robust Object Segmentation Using a Multi-layer Laser Scanner. Sensors 2014, 14, 20400–20418. [Google Scholar] [CrossRef] [PubMed]


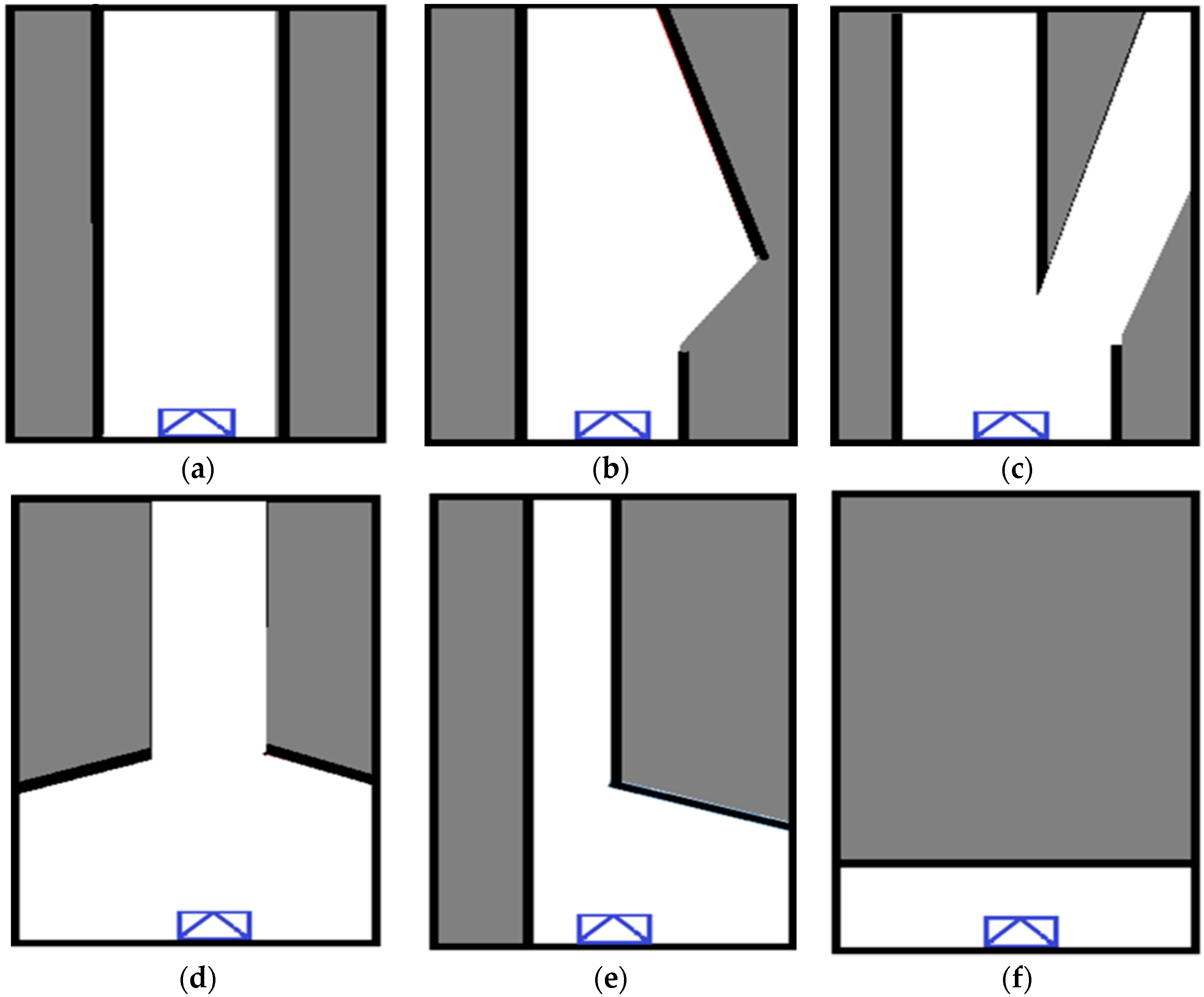


| Class | Type of Intersections |
|---|---|
| Highways | |
| Merge-roads | |
| Diverge-roads | |
| Plus-shape intersections | |
| First type T-shape junctions | |
| Second type T-shape junctions |
| Prediction | |||||||
|---|---|---|---|---|---|---|---|
| Actual | |||||||
| 82.76% | 4.01% | 8.11% | 2.75% | 1.05% | 1.33% | ||
| 3.96% | 81.06% | 8.23% | 1.63% | - | 5.12% | ||
| 2.29% | 1.89% | 87.63% | 2.64% | 1.15% | 4.41% | ||
| - | - | 0.24% | 87.43% | 0.54% | 11.79% | ||
| - | - | - | - | 91.58% | 8.43% | ||
| - | - | - | 5.53% | 2.94% | 91.53% | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, J.; Choi, B.; Sim, K.-B.; Kim, E. Novel Intersection Type Recognition for Autonomous Vehicles Using a Multi-Layer Laser Scanner. Sensors 2016, 16, 1123. https://doi.org/10.3390/s16071123
An J, Choi B, Sim K-B, Kim E. Novel Intersection Type Recognition for Autonomous Vehicles Using a Multi-Layer Laser Scanner. Sensors. 2016; 16(7):1123. https://doi.org/10.3390/s16071123
Chicago/Turabian StyleAn, Jhonghyun, Baehoon Choi, Kwee-Bo Sim, and Euntai Kim. 2016. "Novel Intersection Type Recognition for Autonomous Vehicles Using a Multi-Layer Laser Scanner" Sensors 16, no. 7: 1123. https://doi.org/10.3390/s16071123
APA StyleAn, J., Choi, B., Sim, K.-B., & Kim, E. (2016). Novel Intersection Type Recognition for Autonomous Vehicles Using a Multi-Layer Laser Scanner. Sensors, 16(7), 1123. https://doi.org/10.3390/s16071123









