Exploiting Outage and Error Probability of Cooperative Incremental Relaying in Underwater Wireless Sensor Networks
Abstract
:1. Introduction
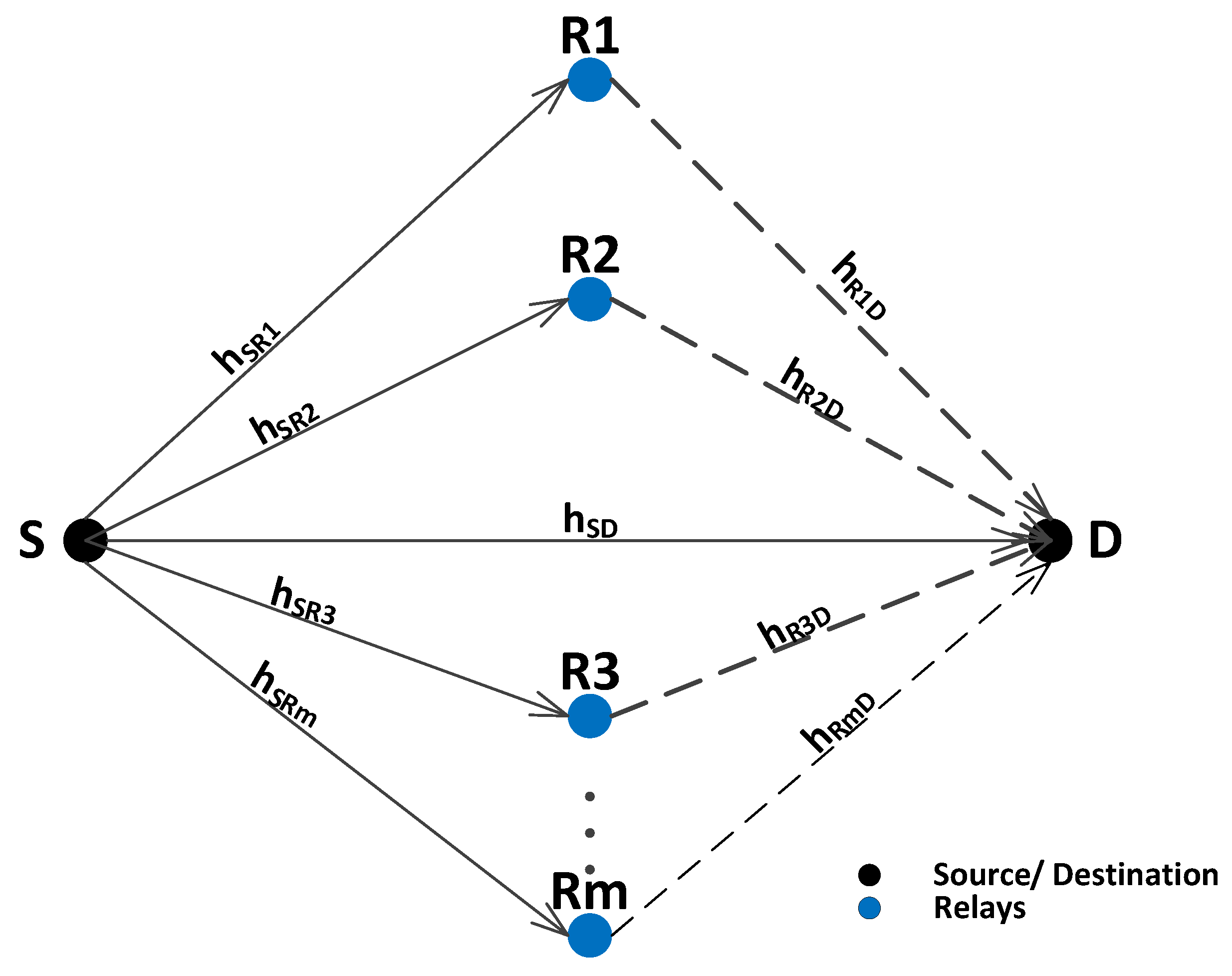
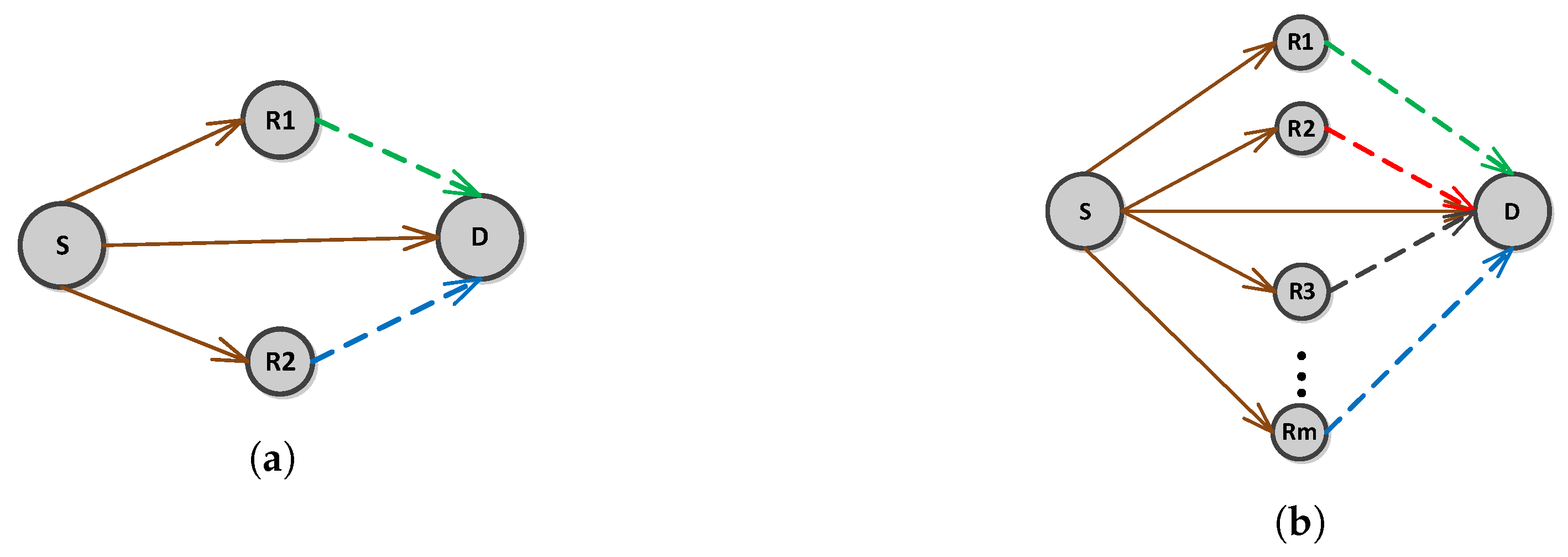
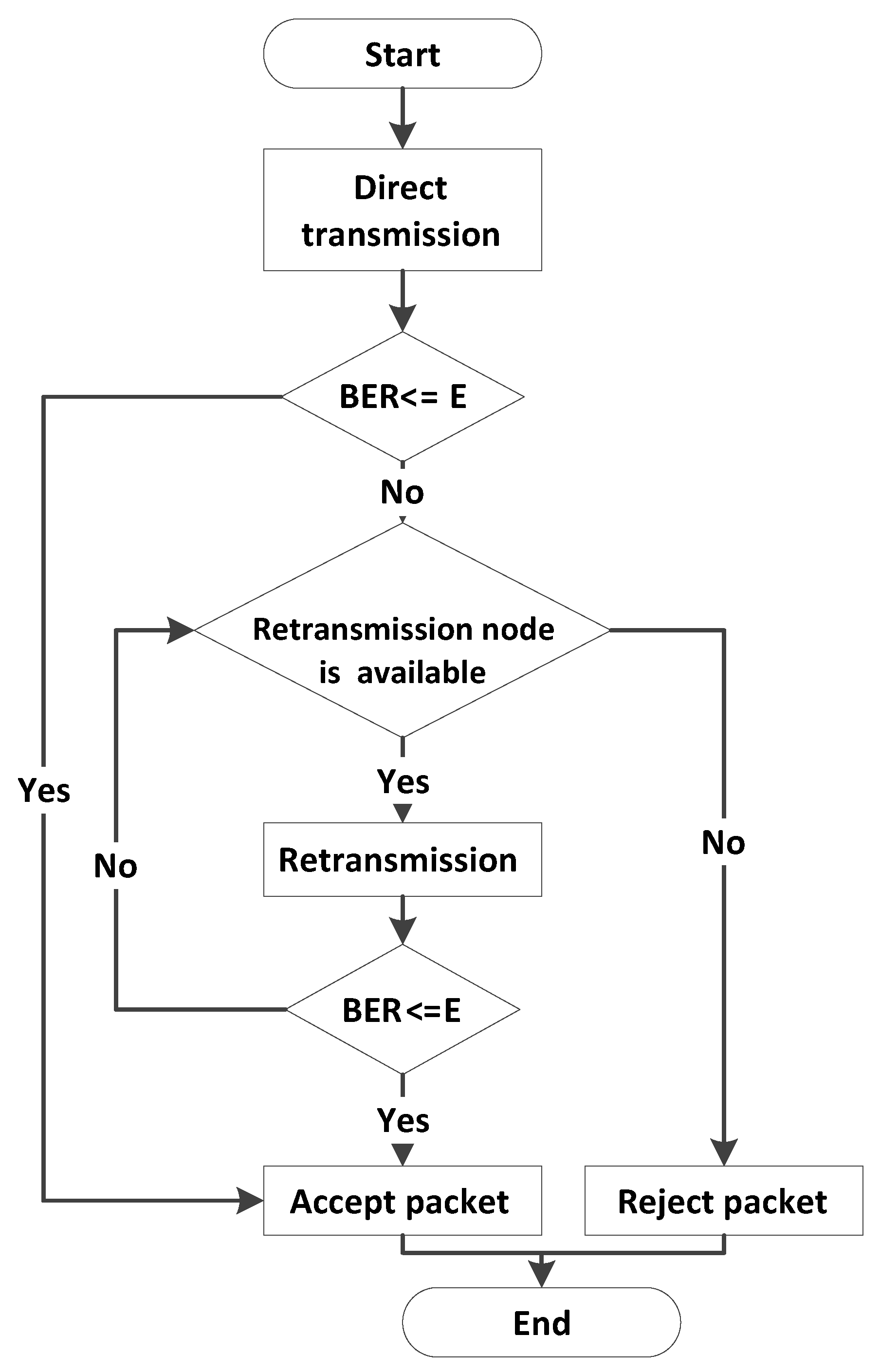
- We proposed incremental relaying cooperative diversity scheme based on multiple number of relays. In our proposed scheme, source broadcasts data to destination and relays. If destination receives an erroneous signal, then relay is responsible to retransmit the signal. Both direct and relayed signals are combined at destination using a diversity combining technique. If signal quality is still not sufficient, second relay is held responsible to retransmit the data. This process continues till either of the two termination criteria are reached; the destination receives a signal with an acceptable quality or all available relays are expired.
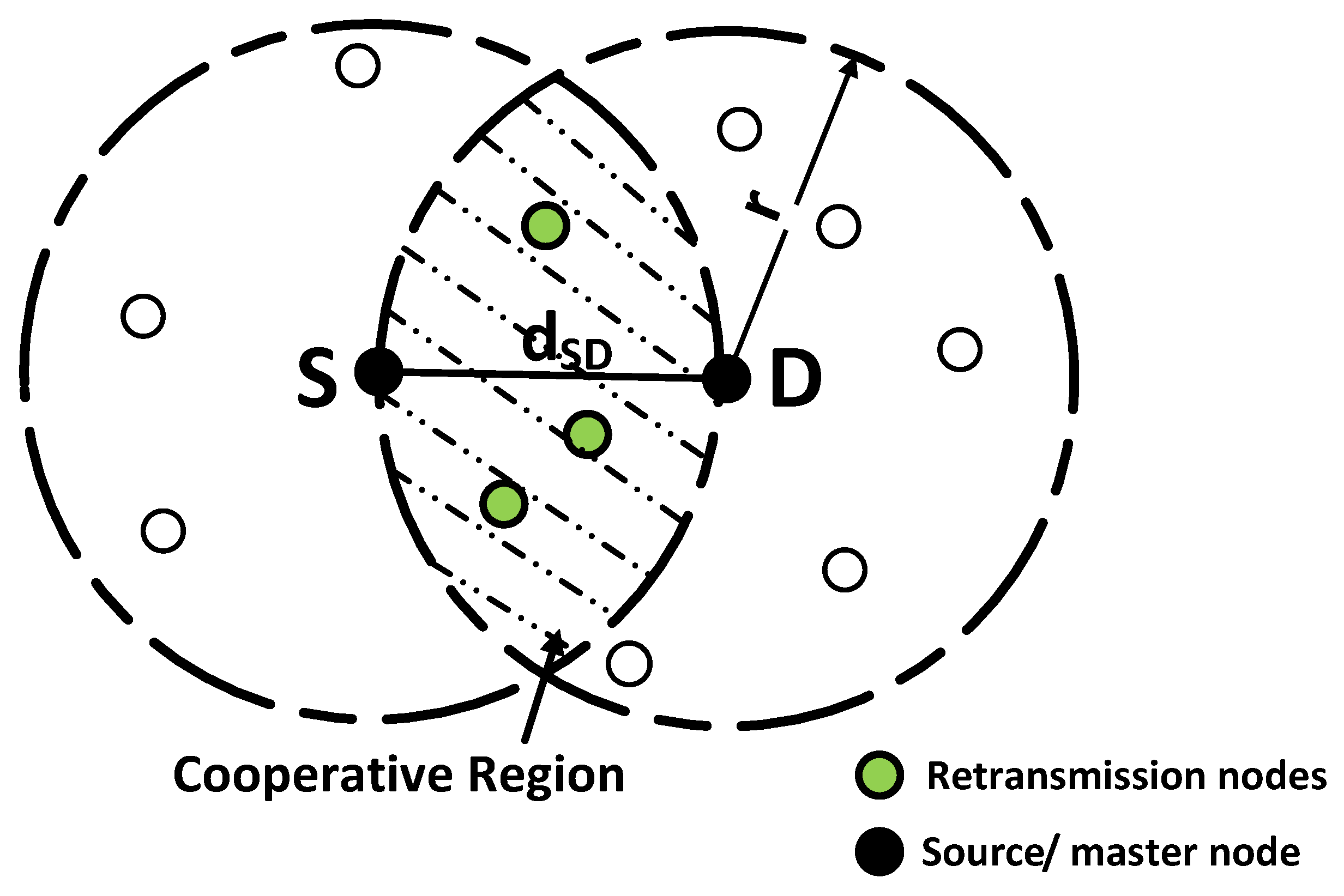
- We proposed two routing protocols for UWSN; ACE [10] and E-ACE. In ACE protocol, retransmission mechanism is incorporated in a cooperative manner to enhance reliability of an existing routing protocol; Energy Efficient Depth Based Routing (EEDBR) [3]. ACE allows only two retransmissions in case of erroneous data reception at destination. However, in noisy underwater environment, two retransmissions may not be sufficient. Therefore, enhanced version of ACE, E-ACE is proposed. In E-ACE, all nodes present in common region of source and destination’s transmission range perform retransmission. Increased number of retransmissions improves reliability and throughput.
- In our work, the relays perform retransmissions in a cooperative manner. The idea of cooperative retransmissions is taken from CARQ scheme [11]. CARQ scheme is proposed for underwater channel. In this scheme, for a given source-destination pair, neighbor nodes make a cooperative nodes set. The cooperative nodes are selected to retransmit the erroneous packet in a closest one first manner. However, we introduced channel affects and different relay nodes selection criteria in our proposed scheme. For channel affects, BER is calculated at each destination to evaluate the signal quality. Additionally, we presented the cooperative nodes selection method, i.e., minimum depth and highest residual energy among the cooperative nodes. Furthermore, signal combining technique is incorporated in the proposed protocols to reduce Bit Error Rate.
2. Related Work
3. System Performance Analysis and Our Proposed Cooperative Routing Protocols
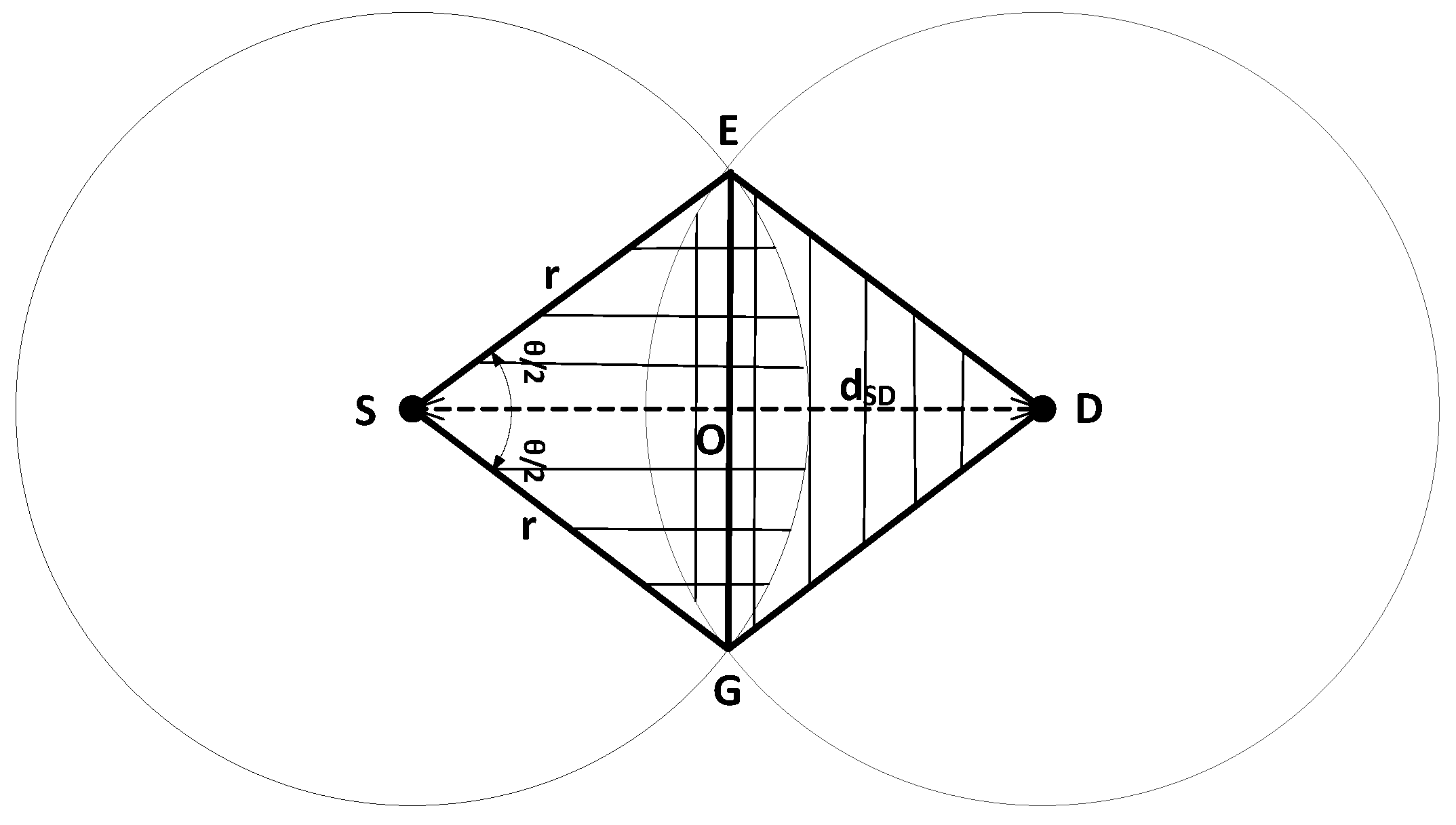
3.1. System Model and Performance Analysis
3.2. Determination of the Number of Available Relays
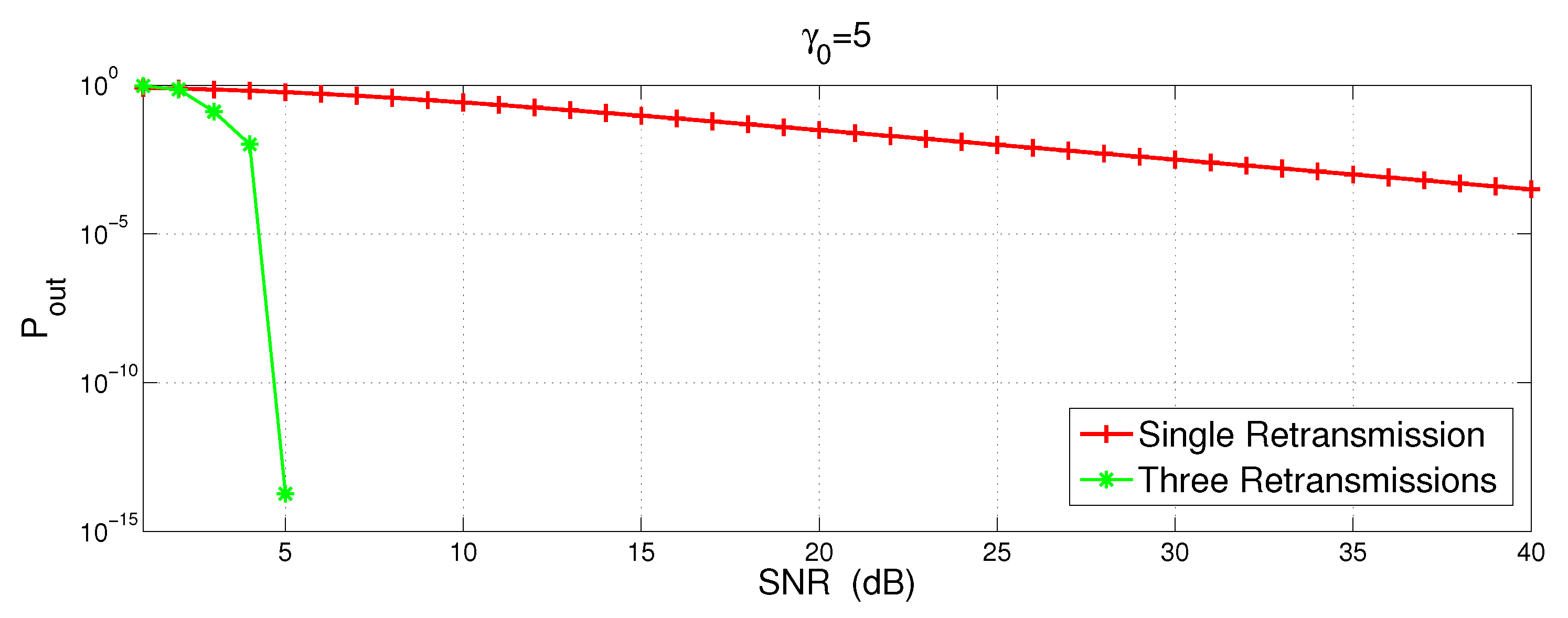
3.3. Outage Probability
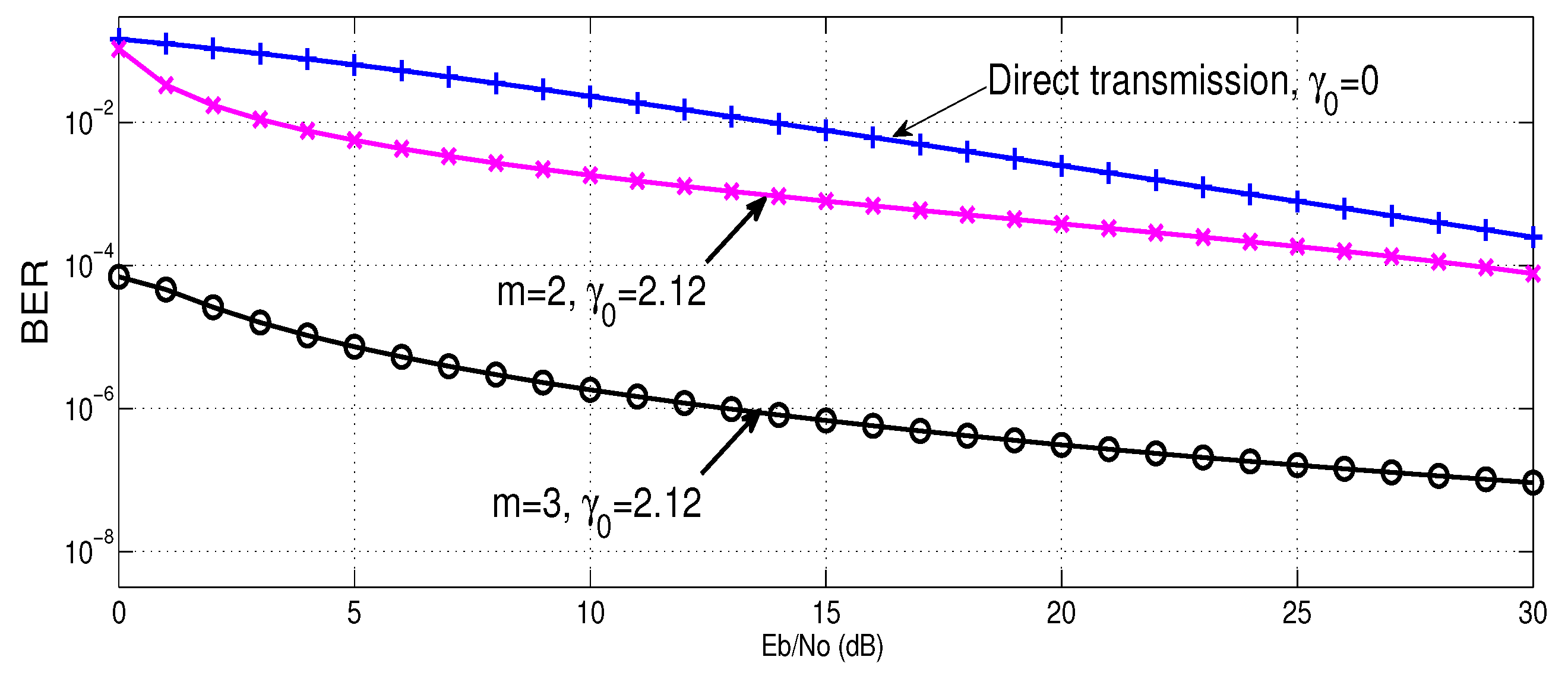
3.4. Error Probability
- Case 1:
- In this case, the relay, , performs re-transmission given that direct transmission is not successful. In this case, , where represents output SNR at D and is defined in Equation (B2). can be written asis a random variable whose PDF is the convolution of the PDFs of and . is derived in Appendix B in Equation (B3). The conditional PDF of output SNR at D, is derived as:where, is defined in Equation (21). Now, the closed-form expression for is obtained by putting Equation (26) in Equation (25) and performing integration. We need to integrate from 0 to for case .
- Case 2:
- In this case, relays, and , perform retransmission given that first retransmission was not successful. Here, , where represents output SNR at D and is given in Equation (B2). can be written as:The PDF of random variable, , will be the convolution of the PDFs of , and . Hence, for case is derived as:where . is defined in Appendix B in Equation (B4). is obtained by integrating Equation (B3) from 0 to .
- Case 3:
- For this case, relays, and , perform retransmission given that second retransmission was not successful and third retransmission is required from . Here, , where represents output SNR at D and is from Equation (B2). can be written asThe PDF of random variable, , in this case will be the convolution of the PDFs of , , and . So, for case is given by:where:and. is derived in Equation (B5) in Appendix B and is obtained by integration Equation (B4) from 0 to . By substituting the above equation in Equation (34) and integrating, we get closed-form expression for as:
3.5. Proposed Scheme 1: ACE
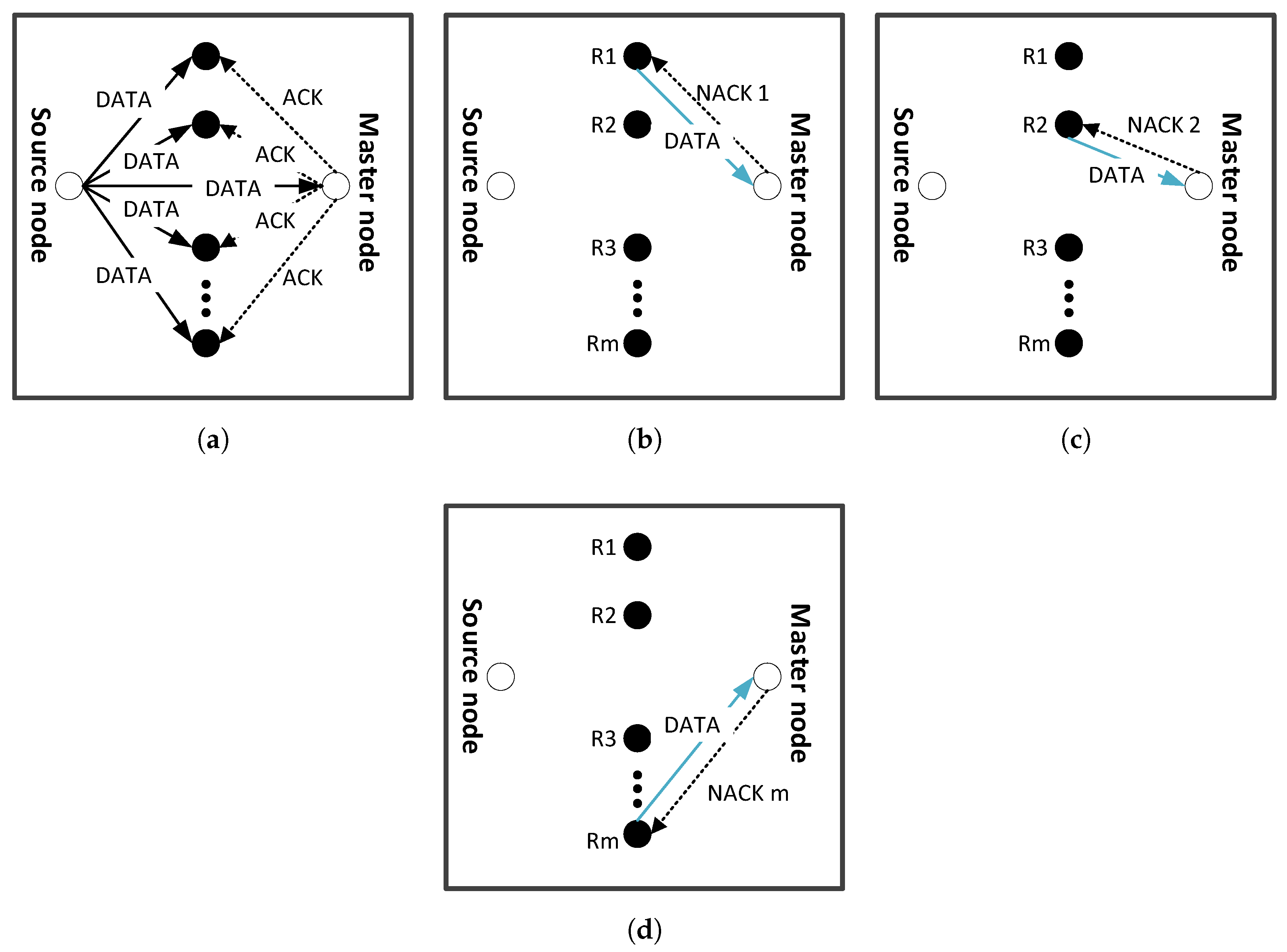
- Information exchange phase
- Path establishment phase
- Data transmission phase
3.5.1. Information Exchange Phase
3.5.2. Path Establishment Phase
3.5.3. Data Transmission Phase
3.6. Proposed Scheme 2: E-ACE
3.6.1. Information Exchange Phase
3.6.2. Path Establishment Phase
3.6.3. Data Transmission Phase
3.7. Energy Consumption Analysis
4. Simulation Results and Discussions
4.1. Network Performance Parameters—Definitions
- Network lifetime: It is the time duration from the start of the network till the death of the last node.
- Total energy consumption: It is the total energy consumed by all the nodes during transmission, reception, and idle time. It is measured in Joules.
- Throughput: It is defined as the total number of successfully received packets at the sink and is measured in packets/time slot.
- Packet drop: It is the number of packets that are not successfully received at the sink.
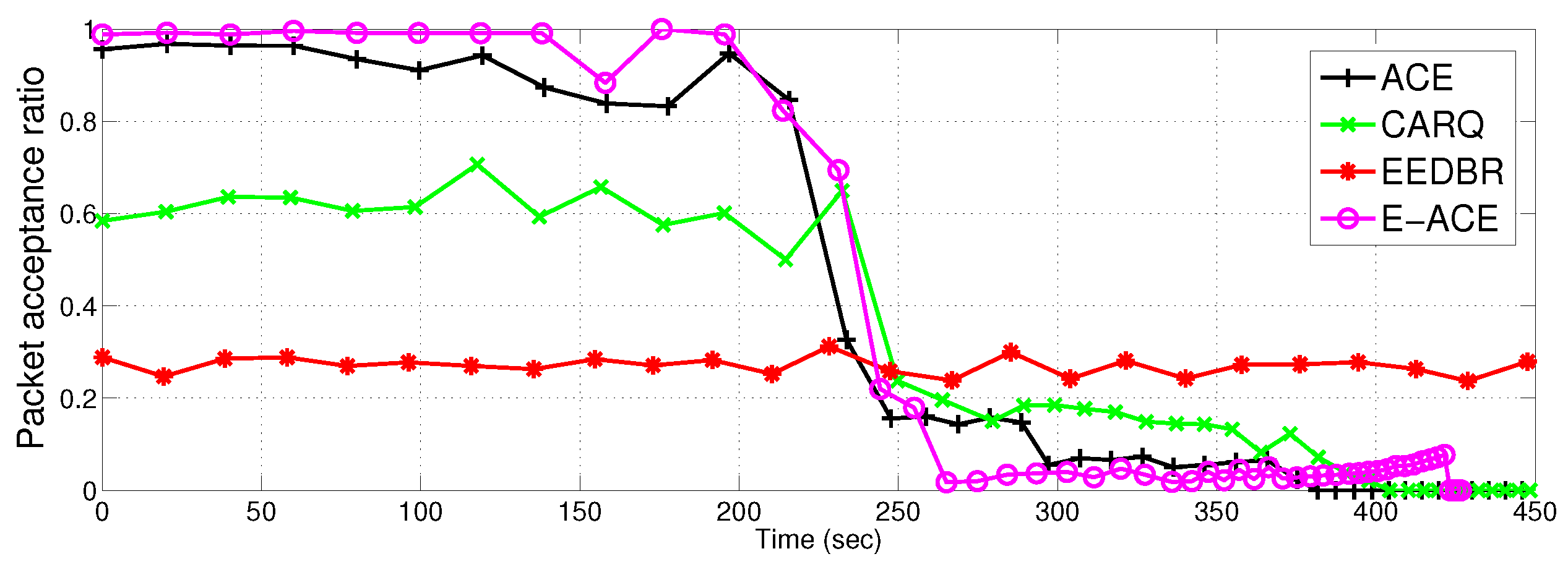
- Packet acceptance ratio: It is the ratio of packets received at sink to the total number of packets sent towards sink.
4.2. Network Performance Parameters—Discussion
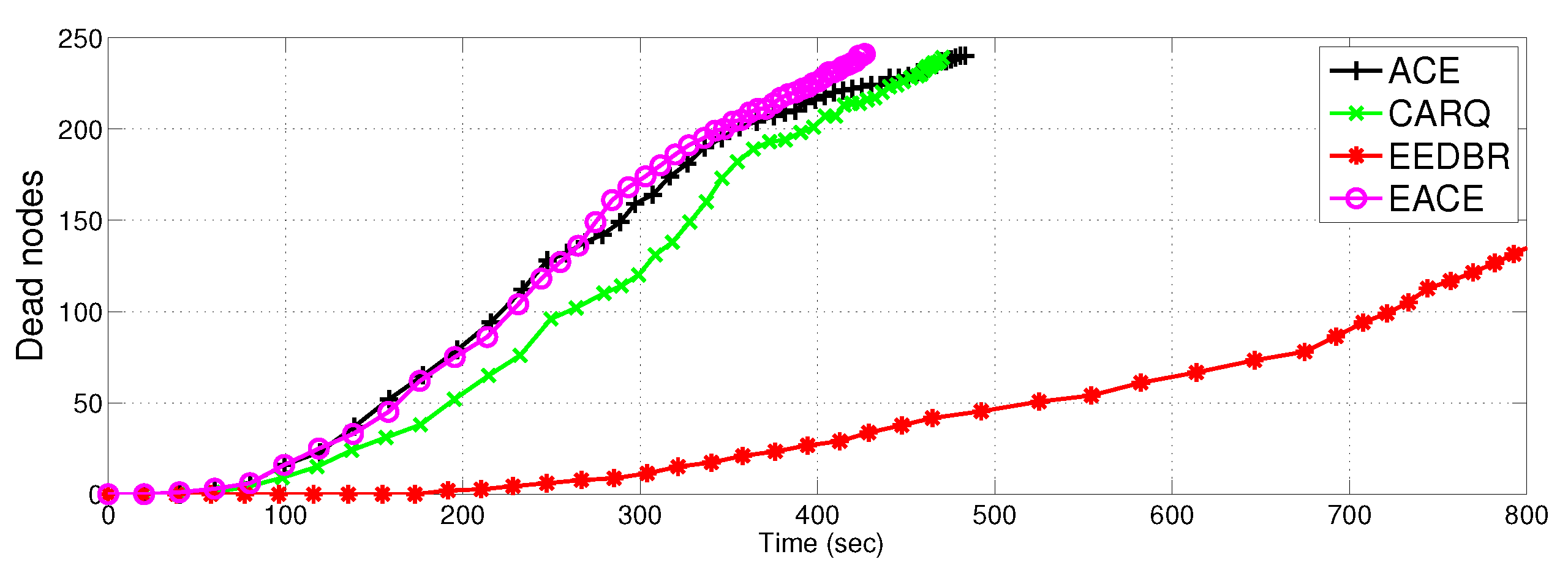
4.2.1. Network Lifetime
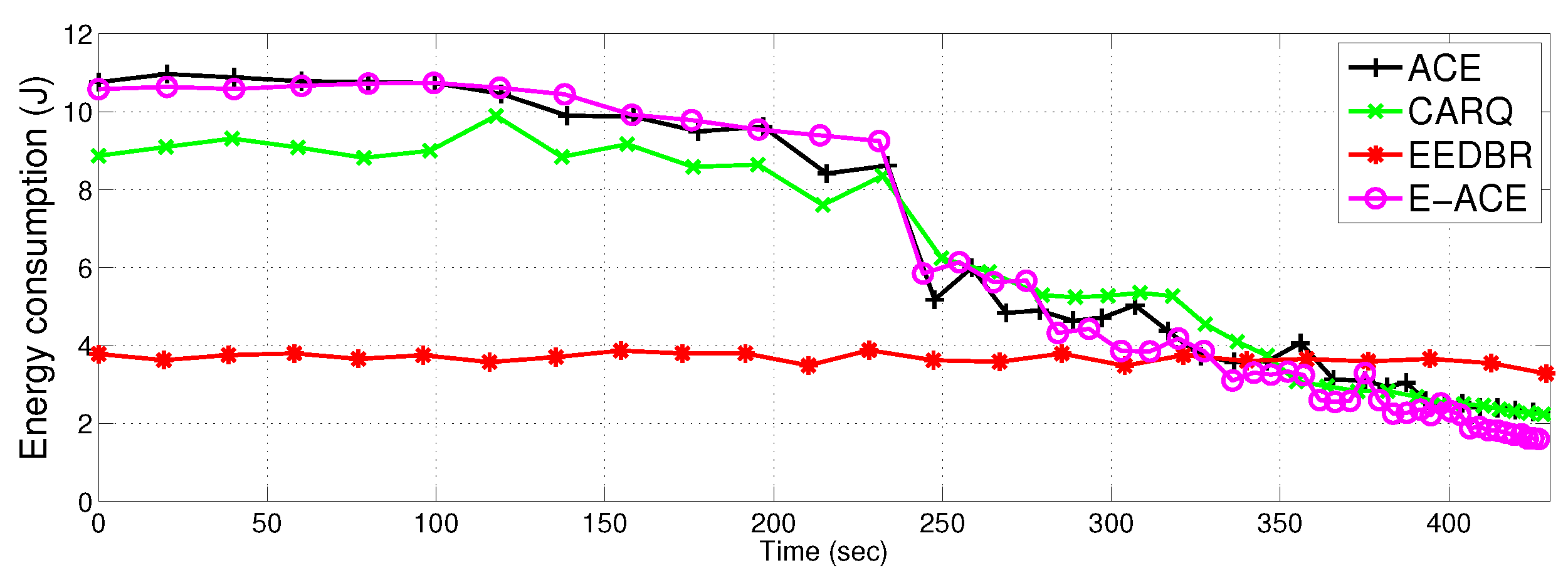
4.2.2. Total Energy Consumption
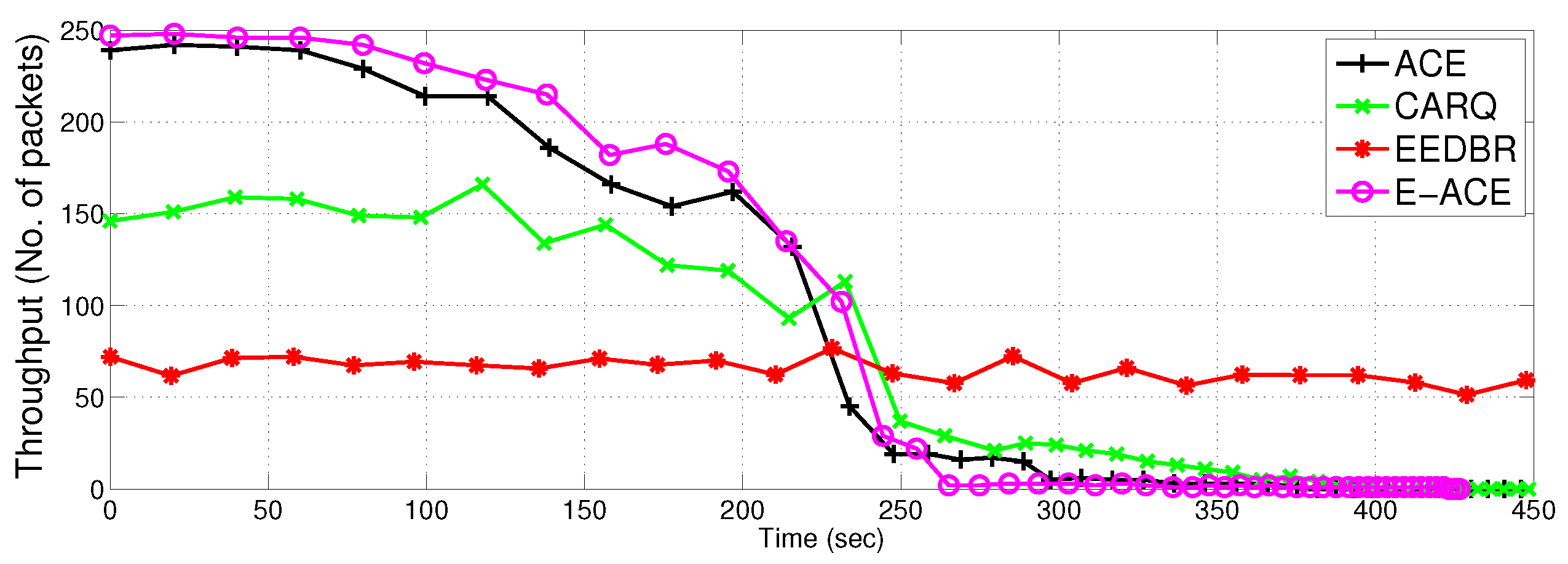
4.2.3. Throughput
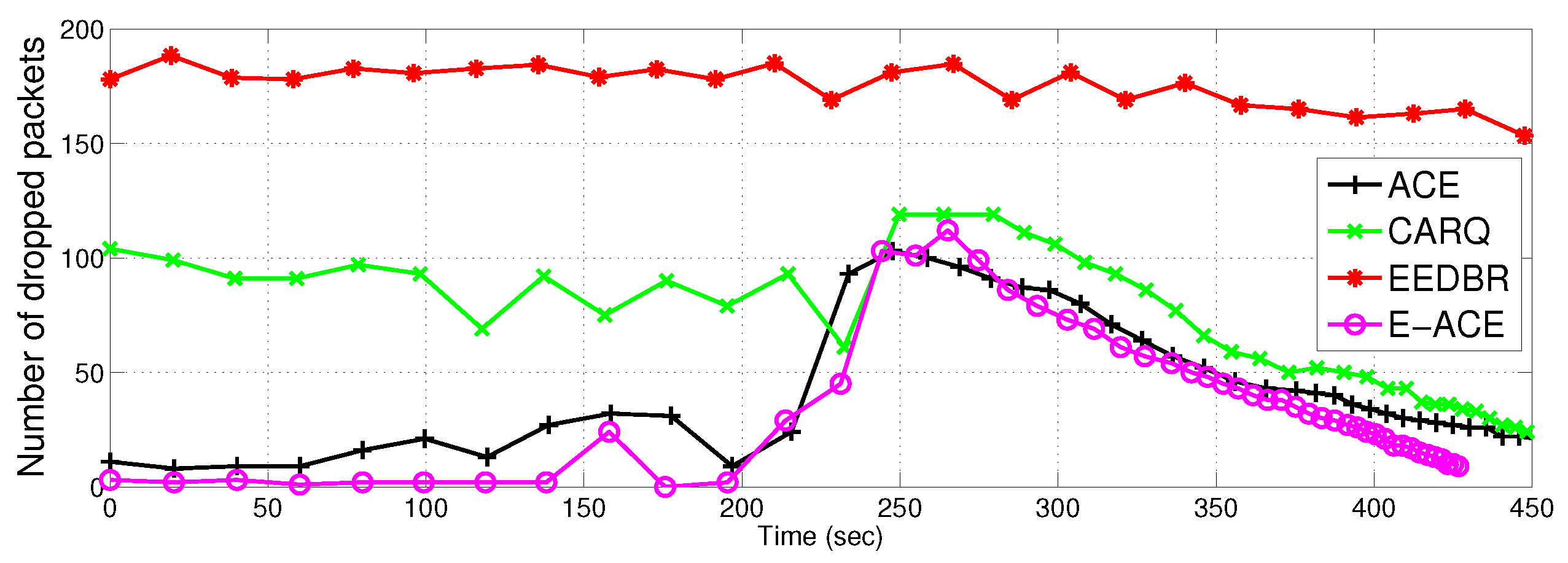
4.2.4. Packet Drop
4.2.5. Packet Acceptance Ratio
4.3. Performance Trade-offs
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Area of Overlapping Region
Appendix B. Derivation of fγd
Appendix C. Derivation of Pout
References
- Akyildiz, I.F.; Dario, P.; Tommaso, M. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 10, 257–279. [Google Scholar] [CrossRef]
- Yan, H.; Shi, Z.J.; Cui, J.H. DBR: Depth-Based Routing for Underwater Sensor Networks. In Networking: Ad Hoc and Sensor Networks, Wireless Networks, Next Generation Internet; Springer: Berlin, Germany, 2008; pp. 72–86. [Google Scholar]
- Wahid, A.; Kim, D. An energy efficient localization-free routing protocol for underwater wireless sensor networks. Int. J. Distrib. Sens. Netw. 2012. [Google Scholar] [CrossRef]
- Babiker, A.; Nordin, Z. Energy Efficient Communication for Underwater Wireless Sensors Networks. In Energy Efficiency in Communications and Networks; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Fareed, M.M.; Mohamed-Slim, A. Efficient Incremental Relaying. In Proceedings of the IEEE International Symposium on Information Theory Proceedings (ISIT); Istanbul, Turkey, 7–12 July 2013; pp. 1964–1668.
- Al-Dharrab, S.; Uysal, M.; Duman, T.M. Cooperative underwater acoustic communications. IEEE Commun. Mag. 2013, 51, 146–153. [Google Scholar] [CrossRef]
- Jannati, M.J.; Abdollah, D.A.; Vahid, T.V. Implementation of cooperative virtual MISO communication in underwater acoustic wireless sensor networks. Int. J. Comput. Sci. Issues 2011, 8, 124–130. [Google Scholar]
- Ikki, S.S.; Ahmed, M.H. Performance analysis of cooperative diversity with incremental-best-relay technique over Rayleigh fading channels. IEEE Trans. Commun. 2011, 59, 2152–2161. [Google Scholar] [CrossRef]
- Duy, T.T.; Kong, H.Y. Performance analysis of hybrid decode-amplify-forward incremental relaying cooperative diversity protocol using SNR-based relay selection. J. Commun. Netw. 2012, 14, 703–709. [Google Scholar] [CrossRef]
- Nasir, H.; Javaid, N.; Murtaza, M.; Manzoor, S.; Khan, Z.A.; Qasim, U.; Sher, M. ACE: Adaptive Cooperation in EEDBR for Underwater Wireless Sensor Networks. In Proceedings of the Ninth International Conference on Broadband and Wireless Computing, Communication and Applications, Guangdong, China, 8–10 November 2014; pp. 8–10.
- Lee, J.W.; Cheon, J.Y.; Cho, H.S. A cooperative ARQ scheme in underwater acoustic sensor networks. In Proceedings of the IEEE OCEANS, Sydney, Australia, 24–27 May 2010; pp. 1–5.
- Mansourkiaie, F.; Ahmed, M. Optimal and Near-Optimal Cooperative Routing and Power Allocation for Collision Minimization in Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 1398–1411. [Google Scholar] [CrossRef]
- Michalopoulos, D.S.; Suraweera, HA.; Schober, R. Relay selection for simultaneous information transmission and wireless energy transfer: A tradeoff perspective. IEEE J. Sel. Areas Commun. 2015, 33, 1578–1594. [Google Scholar] [CrossRef]
- Coutinho, R.; Boukerche, A.; Menezes Vieira, L.; Loureiro, A. Geographic and Opportunistic Routing for Underwater Sensor Networks. IEEE Sens. J. 2016, 65, 548–561. [Google Scholar] [CrossRef]
- Ikki, S.S.; Ahmed, M.H. Performance analysis of incremental-relaying cooperative-diversity networks over Rayleigh fading channels. Commun. IET 2011, 5, 337–349. [Google Scholar] [CrossRef]
- Madan, R.; Mehta, N.B.; Molisch, A.F.; Zhang, J. Energy-efficient cooperative relaying over fading channels with simple relay selection. IEEE Trans. Wirel. Commun. 2008, 7, 3013–3025. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, S.; Cui, J.H.; Cui, S. Energy-efficient cooperative communication based on power control and selective single-relay in wireless sensor networks. IEEE Trans. Wirel. Commun. 2008, 7, 3066–3078. [Google Scholar] [CrossRef]
- Razeghi, B.; Okati, N.; Abed Hodtani, G. A novel multi-criteria relay selection scheme in cooperation communication networks. In Proceedings of the IEEE 49th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 18–20 March 2015; pp. 1–4.
- Wang, X.; Zhang, H.; Gulliver, T.A.; Shi, W.; Zhang, H. Performance analysis of two-way AF cooperative relay networks over Weibull fading channels. J. Commun. 2013, 8, 372–377. [Google Scholar] [CrossRef]
- Hikmat, Q.A.; Dai, B.; Khaji, R.; Huang, B. Performance Analysis of Best Relay Selection in Cooperative Wireless Networks. Int. J. Future Gener. Commun. Netw. 2015, 8, 43–56. [Google Scholar] [CrossRef]
- Sharma, S.; Shi, Y.; Hou, Y.T.; Sherali, H.D.; Kompella, S. Cooperative communications in multi-hop wireless networks: Joint flow routing and relay node assignment. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9.
- Hsu, C.C.; Liu, H.H.; Gomez, J.L.; Chou, C.F. Delay-Sensitive Opportunistic Routing for Underwater Sensor Networks. IEEE Sens. J. 2015, 15, 6584–6591. [Google Scholar] [CrossRef]
- Mansourkiaie, F.; Ahmed, M.H. Joint Cooperative Routing and Power Allocation for Collision Minimization in Wireless Sensor Networks With Multiple Flows. IEEE Wirel. Commun. Lett. 2015, 4, 6–9. [Google Scholar] [CrossRef]
- Habibi, J.; Ghrayeb, A.; Aghdam, A.G. Energy-efficient cooperative routing in wireless sensor networks: A mixed-integer optimization framework and explicit solution. IEEE Trans. Commun. 2013, 61, 3424–3437. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, S.; Cui, S.; Cui, J.H. Energy-efficient cooperative communication in a clustered wireless sensor network. IEEE Trans. Veh. Technol. 2008, 57, 3618–3628. [Google Scholar] [CrossRef]
- Fang, W.; Liu, F.; Yang, F.; Shu, L.; Nishio, S. Energy-efficient cooperative communication for data transmission in wireless sensor networks. IEEE Trans. Consum. Electron. 2010, 56, 2185–2192. [Google Scholar] [CrossRef]
- Zhou, Z.; Cui, J.H. Energy efficient multi-path communication for time-critical applications in underwater sensor networks. In Proceedings of the 9th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Hong Kong, China, 26–30 May 2008; pp. 221–230.
- Carbonelli, C.; Mitra, U. Cooperative multihop communication for underwater acoustic networks. In Proceedings of the 1st ACM International Workshop on Underwater Networks, Los Angeles, CA, USA, 25 September 2006; Volume 1, pp. 97–100.
- Hasna, M.O.; Alouini, M.S. End-to-end performance of transmission systems with relays over Rayleigh-fading channels. IEEE Trans. Wirel. Commun. 2003, 2, 1126–1131. [Google Scholar] [CrossRef]
- Ikki, S.; Ahmed, M.H. Performance analysis of cooperative diversity wireless networks over Nakagami-m fading channel. IEEE Commun. Lett. 2007, 11, 334–336. [Google Scholar] [CrossRef]
- Stojanovic, M. On the relationship between capacity and distance in an underwater acoustic communication channel. In Proceedings of the ACM SIGMOBILE Mobile Computing and Communications Review, New York, NY, USA, 1 October 2007; Volume 11, pp. 34–43.
- Huang, X.; Zhai, H.; Fang, Y. Robust cooperative routing protocol in mobile wireless sensor networks. IEEE Trans. Wirel. Commun. 2008, 7, 5278–5285. [Google Scholar] [CrossRef]
| Ref. | Issues Addressed | Technique | Relaying Technique | Flaws/ Deficiencies | Achievements | Cost | |
|---|---|---|---|---|---|---|---|
| [12] | WSNs | packet collision minimization, Collision caused by source and relay | Branch and bound, Mixed integer non-linear programming, CSMA-CA | Incremental decode and forward | only a single cost function is used | Minimum collision probability, minimized total transmission power | Energy consumption |
| [13] | WSNs | Dependence of the ergodic capacity, outage probability | Pareto efficient scheme, channel state information | Decode and forward | Only single relay is used | Increase in channel capacity | Overhead |
| [14] | UWSNs | Overloading of acoustic channel, Hidden terminal problem | Greedy algorithm, Opportunistic routing | Decode and forward | Longer Delay, Additional energy consumption | Fraction of void node is decreased, Reduced redundant packets | End-to-end delay, Energy consumption |
| [15] | WSNs | Inefficient utilization of channel | Incremental relaying cooperative diversity | Amplify and forward | No end-to-end delay analysis | Reduced bit error rate, High throughput | Outage increases |
| [16] | WSNs | Energy consumption for acquiring CSI | Relay cooperative beam forming, Channel state information | Decode and forward | Tradeoff between energy consumption and data transmission | Energy efficiency | Overhead of channel state information |
| [17] | WSNs | Energy consumption per data packet, Maximize the network lifetime | RTS/CTS signaling | Decode and forward | Overhead of RTS/CTS signaling | Energy efficiency, Prolonged network lifetime | Delay |
| [18] | WSNs | Relaying selection parameter | Onion layered cooperation, Information theory | Decode and forward, Amplify and forward | Increase overhead and extensive computation | New relaying mechanism | High energy consumption |
| [19] | WSNs | Overall outage probability, Average symbol error rate | Binary phase shift keying, Monte carlos simulations | Amplify and forward | Optimal values for OOP and ASEP | ||
| [20] | WSNs | Relay selection technique, Optimal power for source and relay nodes | Channel state information, Orthogonal channel model | Decode and forward | To decrease SER, Number of relays must be increased | New SER method, Throughput | Network lifetime |
| [21] | WSNs | Single hop cooperation, Relay node assignment | Branch and cut, Orthogonal channel model, Linear integer programming | Amplify and forward | Interference between two or more sessions | Throughput | Delay, Network lifetime |
| [22] | UWSNs | Good put and end-to-end latency | Opportunistic routing | Direct method | SNR,PER,BER not taken as a performance metrics | Less end-to-end delay | Energy consumption |
| [23] | WSNs | Packet collision minimization | Cooperative routing, Bellman-ford equation | incremental adaptive decode and forward | No optimal selection of relays | Optimal power allocation | Energy consumption |
| [24] | WSNs | Optimal transmission policy, Low computational complexity | Multi parametric programming, QPSK | Decode and forward | Less power efficient for large scale networks | Low BER, Low transmission power | Not suitable for higher throughput applications |
| [25] | WSNs | Total energy consumption in clustered network | Space time block code, BPSK | Decode and forward | Short network lifetime | Minimizing overall energy consumption | Packet error rate |
| [26] | WSNs | Saving energy | Reducing total number of transmissions, Shortening delay | Node cooperation, Cross layer | Direct relay system | No residual energy check procedure, Not suitable for sparse network | Energy saving, Ack exchange overhead |
| Serial. No. | Protocol Name | Dead Nodes | |||||
|---|---|---|---|---|---|---|---|
| 0 | 50 | 100 | 150 | 200 | 250 | ||
| 1 | E-ACE | 247 | 182 | 102 | 26 | 3 | 0 |
| 2 | ACE | 239 | 166 | 46 | 15 | 3 | 0 |
| 3 | EEDBR | 72 | 59 | 17 | 2 | 1 | 0 |
| 4 | CARQ | 146 | 119 | 29 | 15 | 1 | 0 |
| Protocol | Achieved Performance Parameter | Cost Paid |
|---|---|---|
| E-ACE | Highest throughput, least packet drop, | Highest delay, short network lifetime, |
| highest reliability. | high energy consumption, high complexity. | |
| ACE | High throughput, less packet drop, | High delay, short network lifetime, |
| high packet acceptance ratio, high reliability. | high energy consumption, complexity. | |
| EEDBR | Low throughput, low reliability, | Low delay, long network lifetime, |
| high packet drop. | less energy consumption, low complexity. | |
| CARQ | Medium throughput, medium reliability, | Low delay, short network lifetime, |
| medium packet drop. | high energy consumption, medium complexity. |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasir, H.; Javaid, N.; Sher, M.; Qasim, U.; Khan, Z.A.; Alrajeh, N.; Niaz, I.A. Exploiting Outage and Error Probability of Cooperative Incremental Relaying in Underwater Wireless Sensor Networks. Sensors 2016, 16, 1076. https://doi.org/10.3390/s16071076
Nasir H, Javaid N, Sher M, Qasim U, Khan ZA, Alrajeh N, Niaz IA. Exploiting Outage and Error Probability of Cooperative Incremental Relaying in Underwater Wireless Sensor Networks. Sensors. 2016; 16(7):1076. https://doi.org/10.3390/s16071076
Chicago/Turabian StyleNasir, Hina, Nadeem Javaid, Muhammad Sher, Umar Qasim, Zahoor Ali Khan, Nabil Alrajeh, and Iftikhar Azim Niaz. 2016. "Exploiting Outage and Error Probability of Cooperative Incremental Relaying in Underwater Wireless Sensor Networks" Sensors 16, no. 7: 1076. https://doi.org/10.3390/s16071076
APA StyleNasir, H., Javaid, N., Sher, M., Qasim, U., Khan, Z. A., Alrajeh, N., & Niaz, I. A. (2016). Exploiting Outage and Error Probability of Cooperative Incremental Relaying in Underwater Wireless Sensor Networks. Sensors, 16(7), 1076. https://doi.org/10.3390/s16071076







