Physical Layer Security Using Two-Path Successive Relaying
Abstract
:1. Introduction
2. Secrecy Two-Path Successive Relaying Network
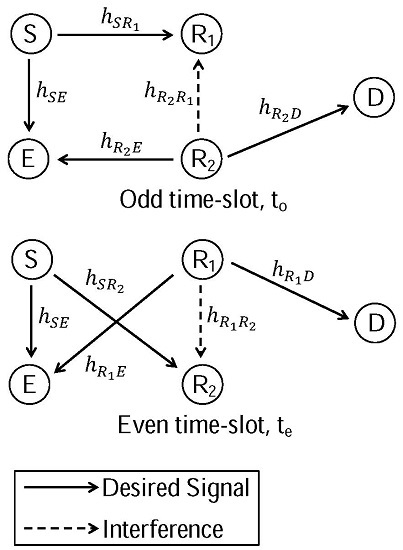
2.1. System Model
2.2. Transmission Protocol
- In odd time-slots, S transmits and forwards . receives from S while being interfered by (inter-relay interference) and D receives from . E receives both and simultaneously.
- In even time-slots, S transmits and forwards . receives from S while being interfered by (inter-relay interference) and D receives from . E receives both and simultaneously.
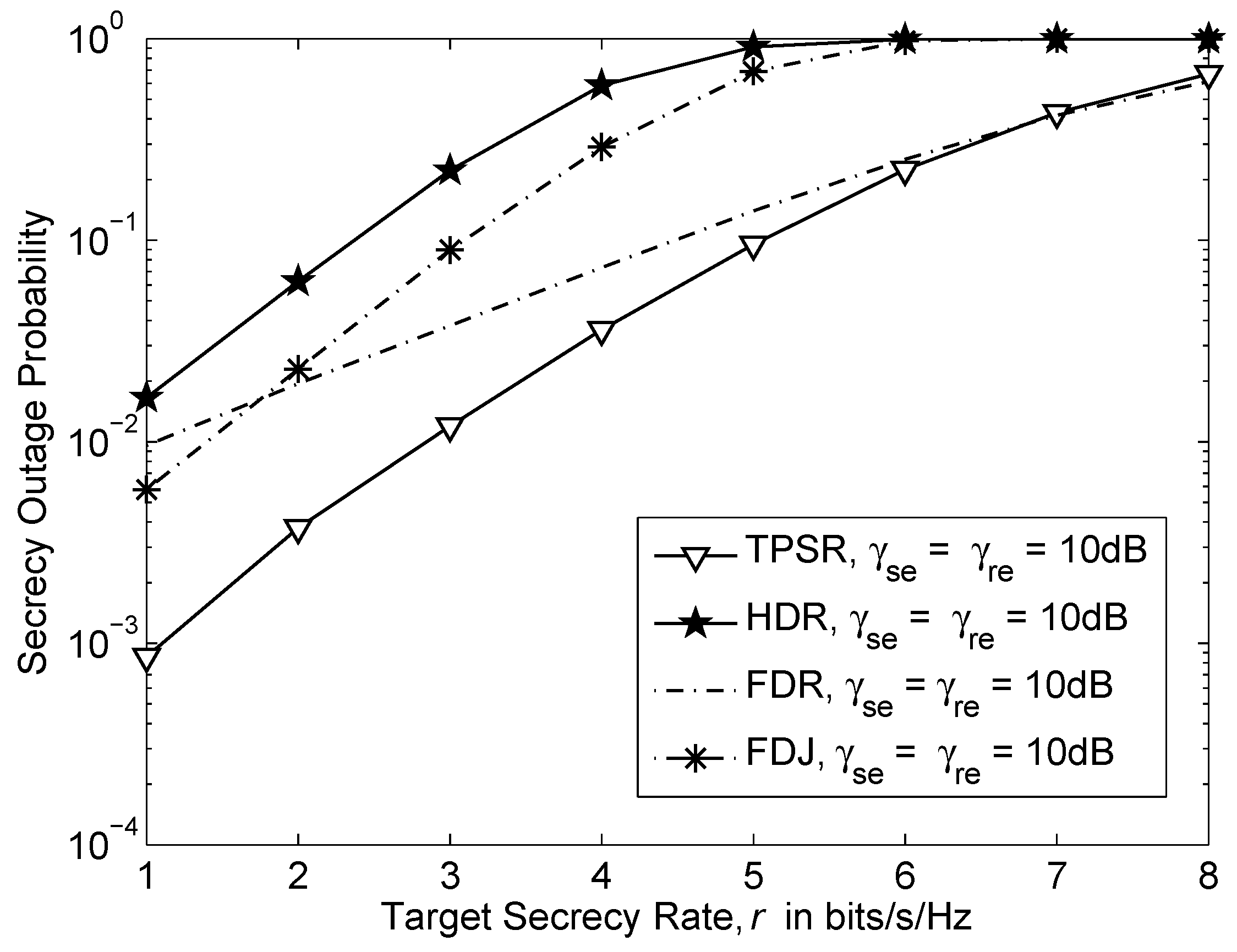
2.3. Achievable Secrecy Rates
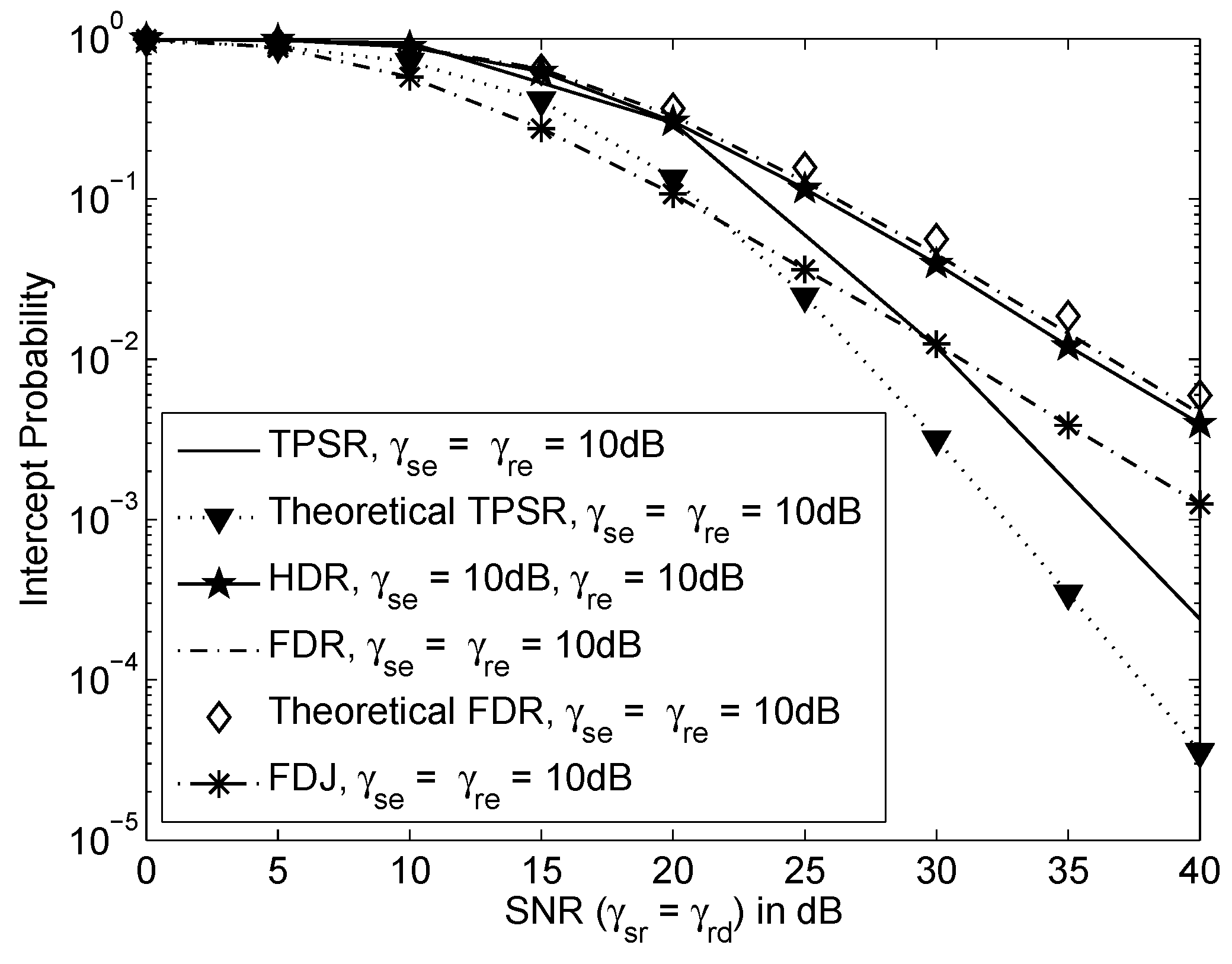
3. Analysis on Intercept Probability
4. Comparable Schemes
4.1. Secrecy Half-Duplex Relaying Network
4.2. Secrecy Full-Duplex Relaying Network
4.3. Secrecy Full-Duplex Jamming Network
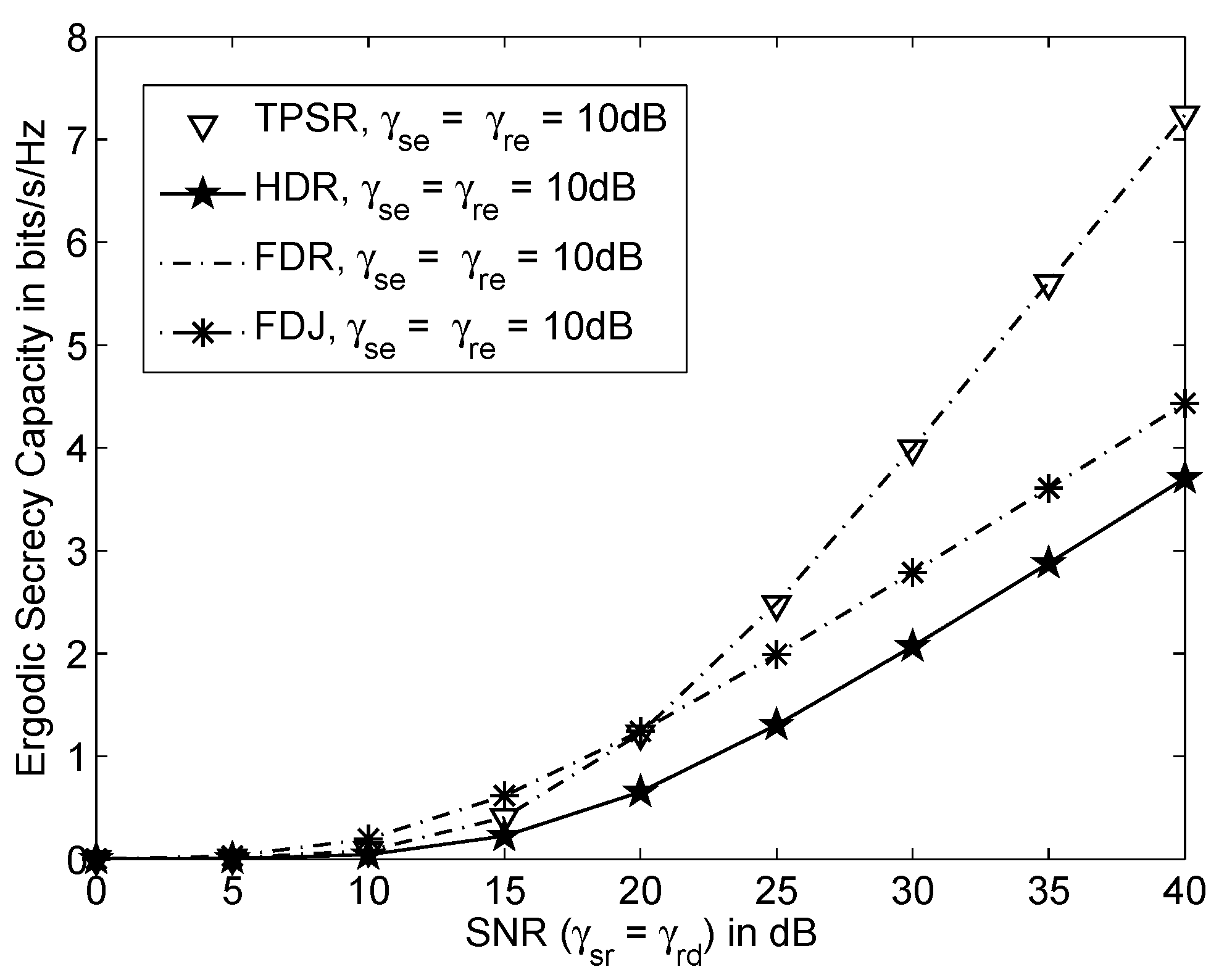
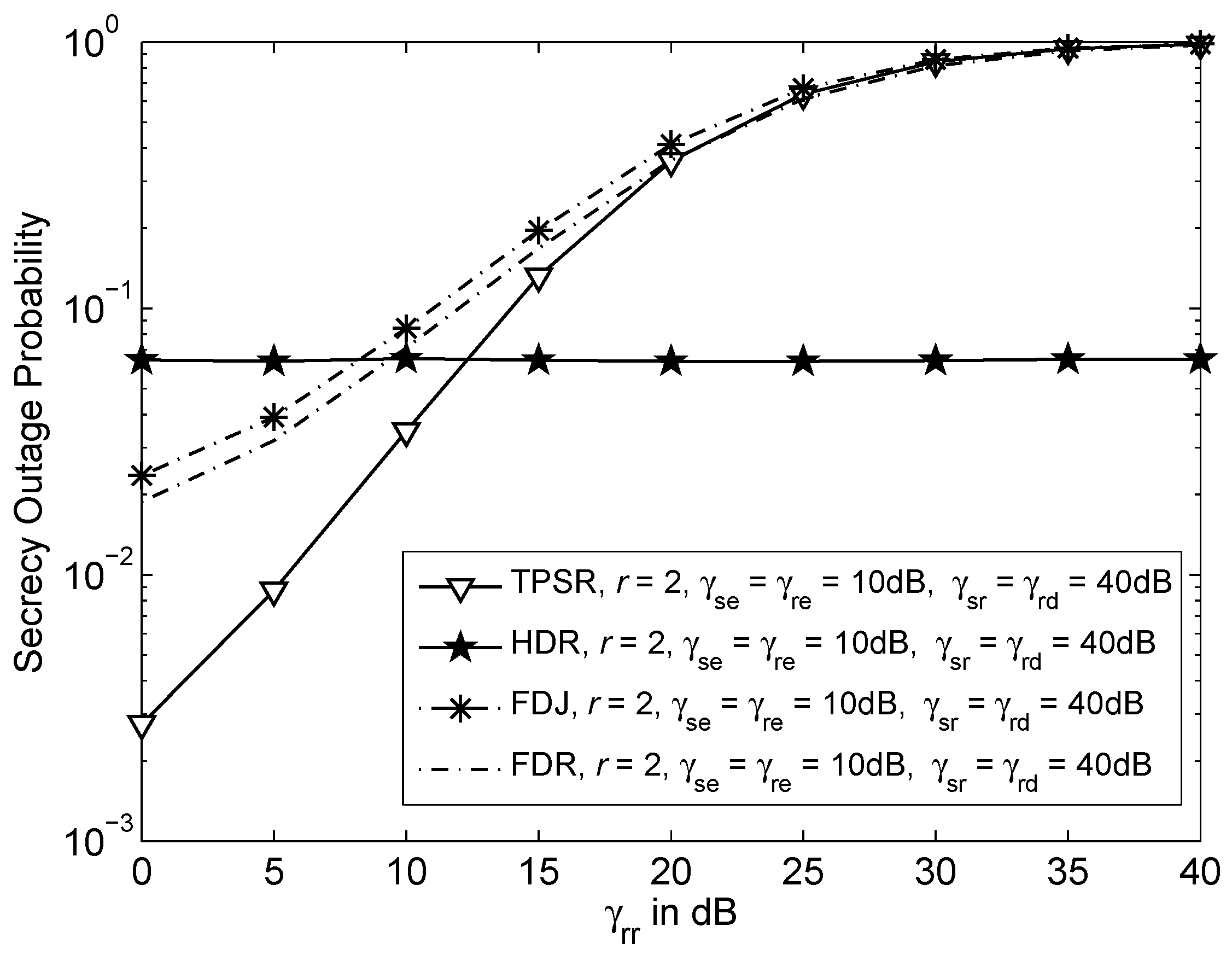
5. Numerical Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, G.; Huang, L.; Xu, H.; Li, J. Relay Node Placement for Maximizing Network Lifetime in Wireless Sensor Networks. In Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–5.
- Zhu, Y.; Zhang, Y.; Xie, J.; Bai, C. A new optimal power allocation scheme for opportunistic cooperative multicast transmission and network coding in wireless sensor networks. In Proceedings of the IEEE 4th International Conference on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, 15–17 November 2013; pp. 329–332.
- Prathibha, V.; Aruna, T. Enhancing the network lifetime of cooperative wireless sensor networks using energy harvesting technique. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 18–20 December 2014; pp. 1–4.
- Demestichas, P.; Georgakopoulos, A.; Karvounas, D.; Tsagkaris, K.; Stavroulaki, V.; Lu, J.; Xiong, C.; Yao, J. 5G on the Horizon: Key Challenges for the Radio-Access Network. IEEE Vehicul. Technol. Mag. 2013, 8, 47–53. [Google Scholar] [CrossRef]
- Hellman, M. An overview of public key cryptography. IEEE Commun. Soc. Mag. 1978, 16, 24–32. [Google Scholar] [CrossRef]
- Kartalopoulos, S. A primer on cryptography in communications. IEEE Commun. Mag. 2006, 44, 146–151. [Google Scholar] [CrossRef]
- Liang, Y.; Poor, H.; Shamai, S. Secure Communication Over Fading Channels. IEEE Trans. Inf. Theory 2008, 54, 2470–2492. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodrigues, M.; McLaughlin, S. Wireless Information-Theoretic Security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Gopala, P.K.; Lai, L.; El Gamal, H. On the Secrecy Capacity of Fading Channels. IEEE Trans. Inf. Theory 2008, 54, 4687–4698. [Google Scholar] [CrossRef]
- Khisti, A.; Tchamkerten, A.; Wornell, G.W. Secure Broadcasting Over Fading Channels. IEEE Trans. Inf. Theory 2008, 54, 2453–2469. [Google Scholar] [CrossRef]
- Shannon, C. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Deng, H.; Wang, H.M.; Guo, W.; Wang, W. Secrecy Transmission With a Helper: To Relay or to Jam. IEEE Trans. Inf. Forens. Secur. 2015, 10, 293–307. [Google Scholar] [CrossRef]
- Hui, H.; Swindlehurst, A.; Li, G.; Liang, J. Secure Relay and Jammer Selection for Physical Layer Security. IEEE Signal Process. Lett. 2015, 22, 1147–1151. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Petropulu, A. Destination Assisted Cooperative Jamming for Wireless Physical-Layer Security. IEEE Trans. Inf. Forens. Secur. 2013, 8, 682–694. [Google Scholar] [CrossRef]
- Popovski, P.; Simeone, O. Wireless Secrecy in Cellular Systems With Infrastructure-Aided Cooperation. IEEE Trans. Inf. Forens. Secur. 2009, 4, 242–256. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, X.; Shen, W. Physical-Layer Security with Multiuser Scheduling in Cognitive Radio Networks. CoRR 2013, 61, 5103–5113. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, J.; Wang, X.; Leung, V. Improving physical-layer security in wireless communications using diversity techniques. IEEE Netw. 2015, 29, 42–48. [Google Scholar] [CrossRef]
- Wang, H.M.; Luo, M.; Yin, Q.; Xia, X.G. Hybrid Cooperative Beamforming and Jamming for Physical-Layer Security of Two-Way Relay Networks. IEEE Trans. Inf. Forens. Secur. 2013, 8, 2007–2020. [Google Scholar] [CrossRef]
- Zheng, T.X.; Wang, H.M.; Liu, F.; Lee, M.H. Outage Constrained Secrecy Throughput Maximization for DF Relay Networks. IEEE Trans. Commun. 2015, 63, 1741–1755. [Google Scholar] [CrossRef]
- Wang, H.M.; Xia, X.G. Enhancing wireless secrecy via cooperation: signal design and optimization. IEEE Commun. Mag. 2015, 53, 47–53. [Google Scholar] [CrossRef]
- Li, W.; Rikkinen, K.; Pirinen, P.; Tapio, V.; Lavin, C.; Gonzáles, L.; Debaillie, B.; van Liempd, B.; Klumperink, E.; van den Broek, D.J.; et al. System Scenarios and Technical Requirements for Full-Duplex Concept; Technical Report; DUPLO: Surrey, UK, 2013. [Google Scholar]
- Bliss, D.; Hancock, T.; Schniter, P. Hardware phenomenological effects on cochannel full-duplex MIMO relay performance. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 4–7 November 2012; pp. 34–39.
- Riihonen, T.; Werner, S.; Wichman, R. Mitigation of Loopback Self-Interference in Full-Duplex MIMO Relays. IEEE Trans. Signal Process. 2011, 59, 5983–5993. [Google Scholar] [CrossRef]
- Taghizadeh, O.; Mathar, R. Full-Duplex Decode-and-Forward Relaying with Limited Self-Interference Cancellation. In Proceedings of the 2014 18th International ITG Workshop on Smart Antennas (WSA), Erlangen, Germany, 12–13 March 2014; pp. 1–7.
- Vermeulen, T.; Rosas, F.; van Liempd, B.; Verhelst, M.; Pollin, S. An energy-scalable in-band full duplex architecture. In Proceedings of the 2015 IEEE 20th International Workshop on Computer Aided Modelling and Design of Communication Links and Networks (CAMAD), Guildford, UK, 7–9 September 2015; pp. 22–26.
- Alves, H.; Souza, R.D.; Pellenz, M.E. Brief survey on full-duplex relaying and its applications on 5G. In Proceedings of the 2015 IEEE 20th International Workshop on Computer Aided Modelling and Design of Communication Links and Networks (CAMAD), Guildford, UK, 7–9 September 2015; pp. 17–21.
- Chen, G.; Gong, Y.; Xiao, P.; Chambers, J. Physical Layer Network Security in the Full-Duplex Relay System. IEEE Trans. Inf. Forens. Secur. 2015, 10, 574–583. [Google Scholar] [CrossRef]
- Rankov, B.; Wittneben, A. Spectral efficient protocols for half-duplex fading relay channels. IEEE J. Sel. Areas Commun. 2007, 25, 379–389. [Google Scholar] [CrossRef]
- Liau, Q.Y.; Leow, C.Y. Performance of Two-Path Successive Relaying in the Presence of Inter-Relay Interference. J. Theor. Appl. Inf. Technol. 2015, 74, 82–87. [Google Scholar]
- Liau, Q.Y.; Leow, C.Y. Study of relay position in two-path successive relaying with interference cancellation. In Proceedings of the 2014 IEEE Asia Pacific Conference on Wireless and Mobile, Bali, France, 28–30 August 2014; pp. 254–259.
- Nomikos, N.; Vouyioukas, D. A successive opportunistic relaying protocol with inter-relay interference mitigation. In Proceedings of the 8th International Wireless Communications and Mobile Computing Conference (IWCMC), Limassol, Cyprus, 27–31 August 2012; pp. 228–233.
- Hu, Y.; Li, K.H.; Teh, K.C. An Efficient Successive Relaying Protocol for Multiple-Relay Cooperative Networks. IEEE Trans. Wirel. Commun. 2012, 11, 1892–1899. [Google Scholar] [CrossRef]
- Nomikos, N.; Vouyioukas, D.; Charalambous, T.; Krikidis, I.; Skoutas, D.; Johansson, M. Capacity improvement through buffer-aided successive opportunistic relaying. In Proceedings of the 3rd International Conference on Wireless Communications, Vehicular Technology, Information Theory and Aerospace Electronic Systems (VITAE), Atlantic City, NJ, USA, 24–27 June 2013; pp. 1–5.
- Nomikos, N.; Charalambous, T.; Krikidis, I.; Skoutas, D.; Vouyioukas, D.; Johansson, M. Buffer-aided successive opportunistic relaying with inter-relay interference cancellation. In Proceedings of the IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 1316–1320.
- Nomikos, N.; Vouyioukas, D.; Charalambous, T.; Krikidis, I.; Makris, P.; Skoutas, D.N.; Johansson, M.; Skianis, C. Joint relay-pair selection for buffer-aided successive opportunistic relaying. Trans. Emerg. Telecommun. Technol. 2014, 25, 823–834. [Google Scholar] [CrossRef]
- Leung-Yan-Cheong, S.; Hellman, M. The Gaussian wire-tap channel. IEEE Trans. Inf. Theory 1978, 24, 451–456. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007; pp. 1148–1171. [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liau, Q.Y.; Leow, C.Y.; Ding, Z. Physical Layer Security Using Two-Path Successive Relaying. Sensors 2016, 16, 846. https://doi.org/10.3390/s16060846
Liau QY, Leow CY, Ding Z. Physical Layer Security Using Two-Path Successive Relaying. Sensors. 2016; 16(6):846. https://doi.org/10.3390/s16060846
Chicago/Turabian StyleLiau, Qian Yu, Chee Yen Leow, and Zhiguo Ding. 2016. "Physical Layer Security Using Two-Path Successive Relaying" Sensors 16, no. 6: 846. https://doi.org/10.3390/s16060846
APA StyleLiau, Q. Y., Leow, C. Y., & Ding, Z. (2016). Physical Layer Security Using Two-Path Successive Relaying. Sensors, 16(6), 846. https://doi.org/10.3390/s16060846