Local Strategy Combined with a Wavelength Selection Method for Multivariate Calibration
Abstract
:1. Introduction
2. Materials and Methods
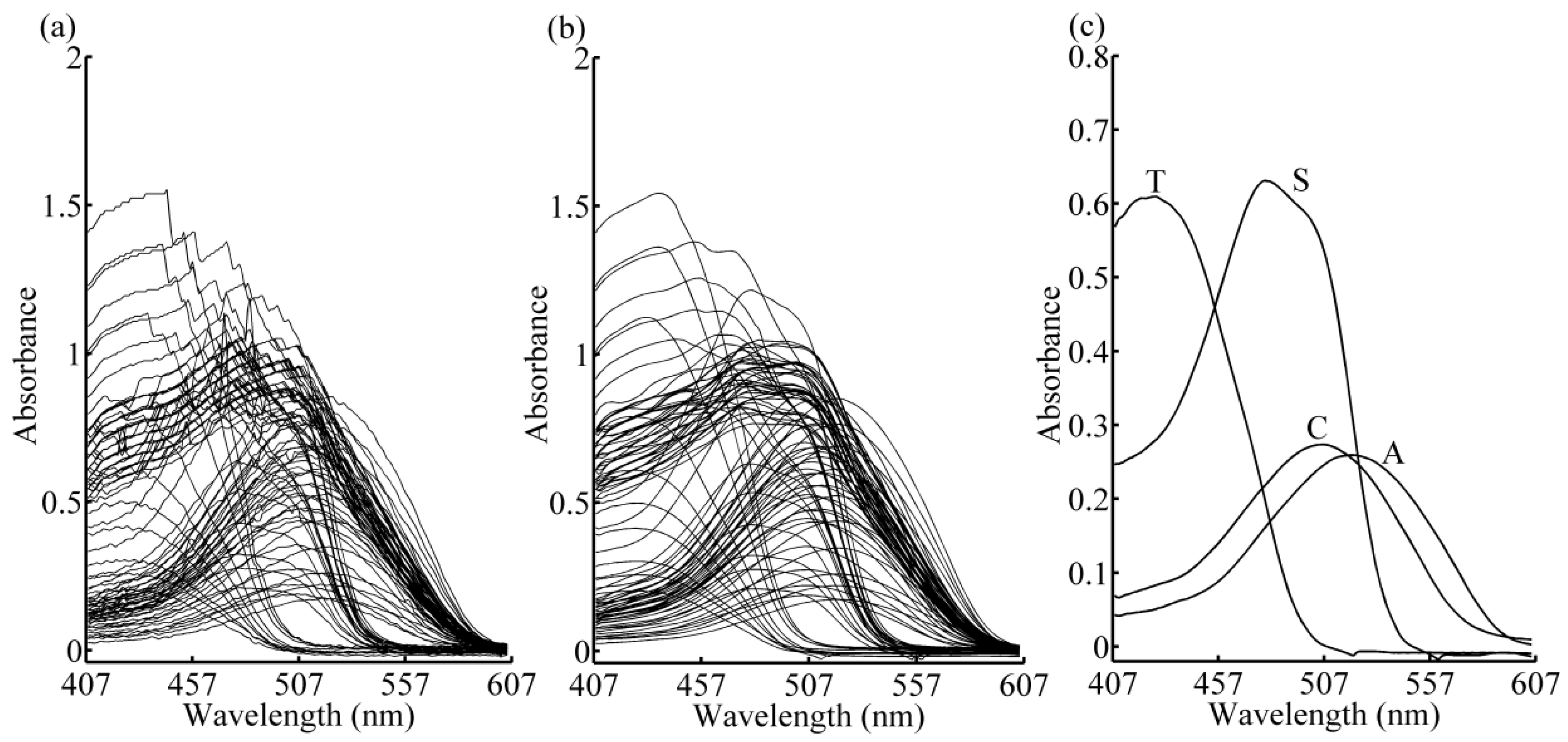
2.1. Experimental Setup
2.2. Data Pre-Processing
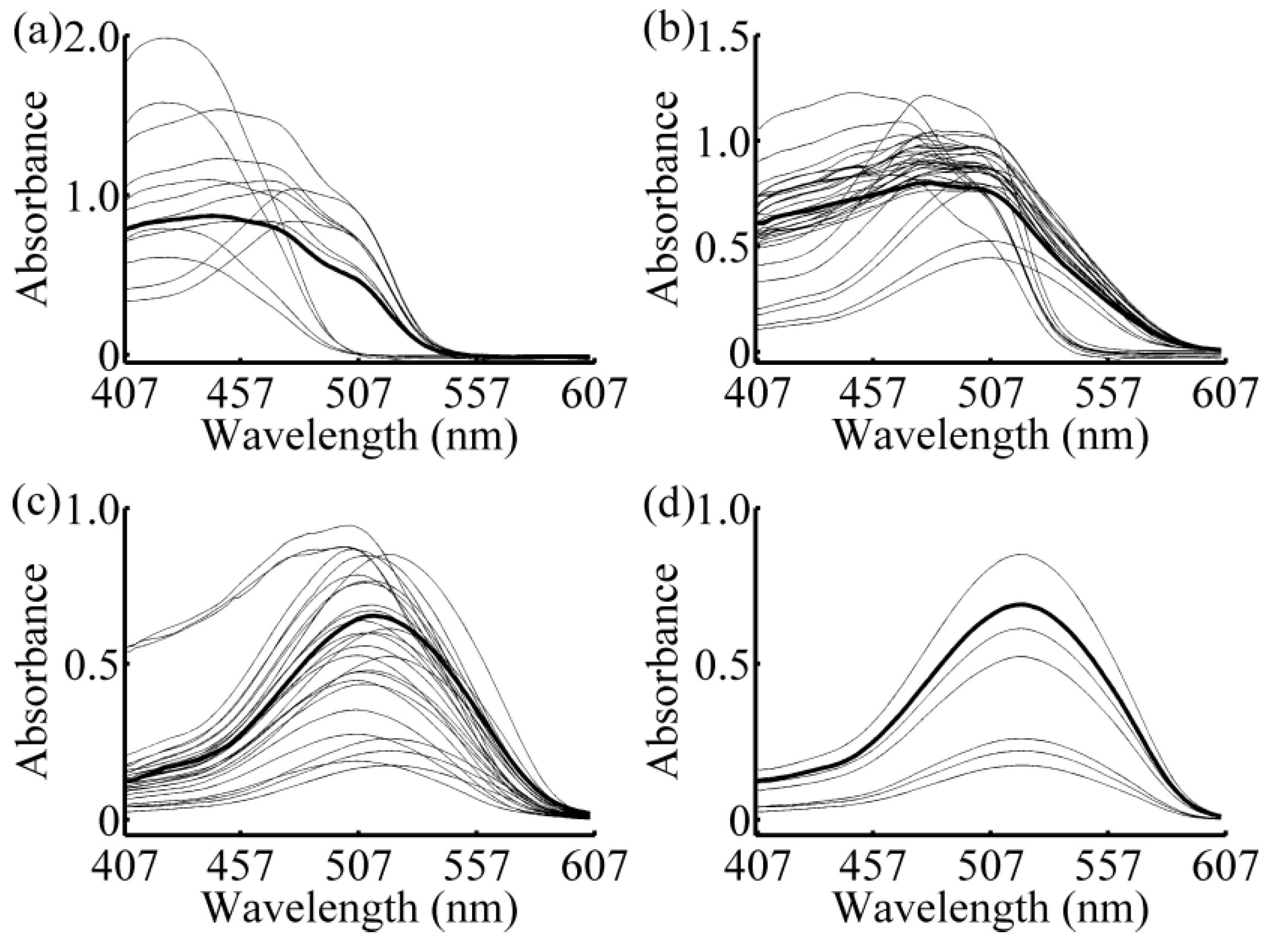
2.3. Local Strategy
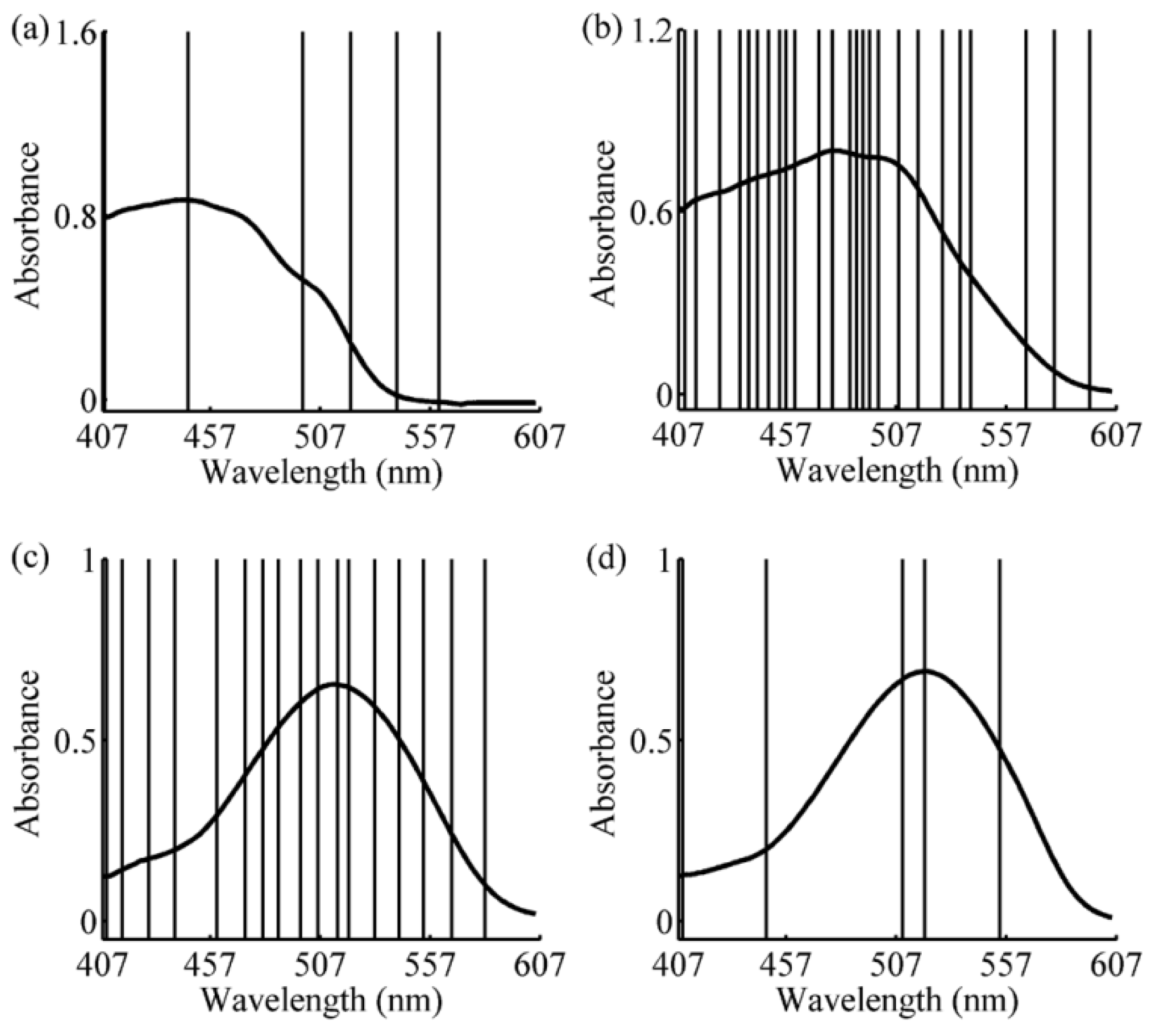
2.4. Wavelength Selection
2.5. Simple-to-Use Interactive Self-Modeling Mixture Analysis
2.6. Model Evaluation
3. Results and Discussion
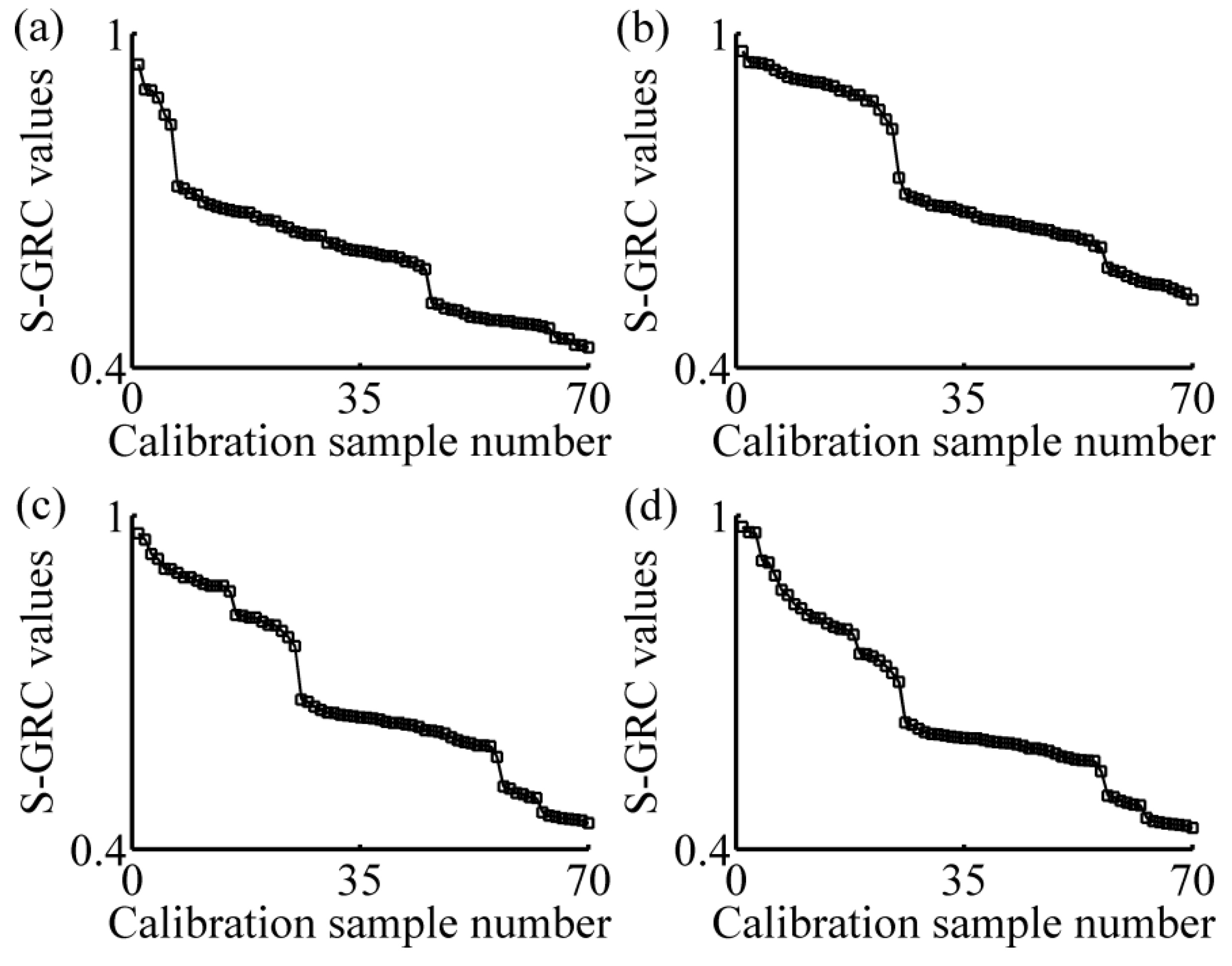
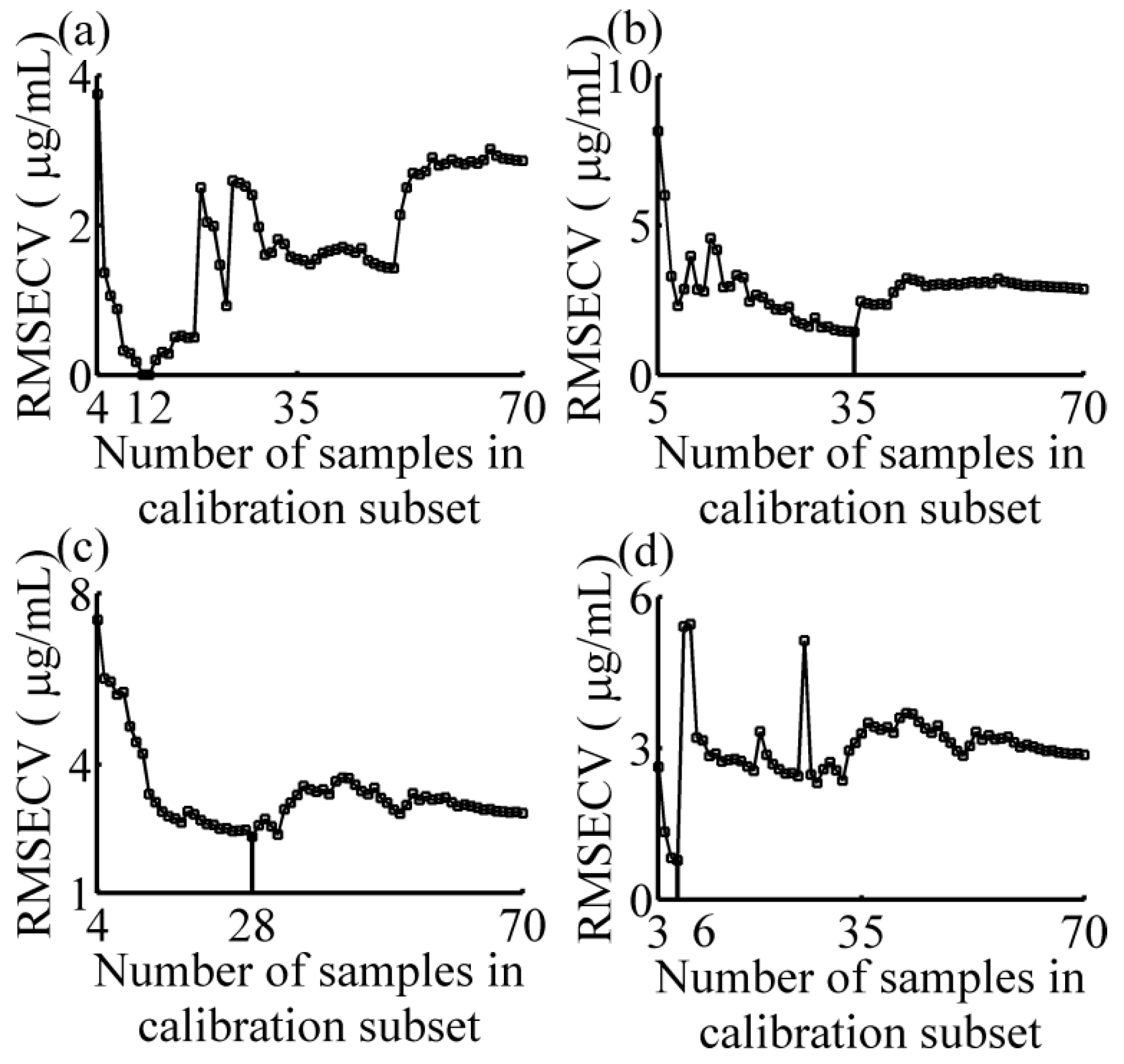
3.1. Calibration Subset Selection
- Sorting calibration set in the descending order of S-GRC values. Here, m = 70 and n = 198;
- Selecting the former Nsub samples of calibration set that compose calibration subset. Here, Nsub = 3 or 4 or 5;
- Applying the regression method, PLSR, on the absorbance data in the calibration subset using the LOOCV method, calculating the RMSECV; and
- Nsub = Nsub + 1, repeating the step (2) and (3) until Nsub > 70.
3.2. Wavelength Selection
3.3. Comparative Performance of the Various Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PCR | Principal Components Regression |
| PLSR | Partial Least Squares Regression |
| GA | Genetic Algorithms |
| UVE | Uninformative Variable Elimination |
| MWPLS | Moving Window Partial Least Squares |
| SPA | Successive Projections Algorithm |
| S-GRC | Synthetic degree of Grey Relation Coefficient |
| RMSEP | Root Mean Square Error of Prediction |
| RMSECV | Root Mean Square Error of Prediction in Cross-Validation |
| LOO | Leave-One-Out |
| SIMPLISMA | Simple-to-use Interactive Self-modeling Mixture Analysis |
| GRA | Grey Relation Analysis |
| LOOCV | Leave-One-Out Cross-Validation |
| PRESS | Prediction Residual Error Sum of Squares |
| UV-Vis | Ultraviolet-Visible |
| SG | Savitzky-Golay |
References
- Kalivas, J.H. Multivariate calibration, an overview. Anal. Lett. 2005, 38, 2259–2280. [Google Scholar] [CrossRef]
- Gao, L.; Ren, S.X. Simultaneous multicomponent analysis of overlapping spectrophotometric signals using a wavelet-based latent variable regression. Spectrochim. Acta. Part. A. 2008, 71, 959–964. [Google Scholar] [CrossRef] [PubMed]
- Jolliffe, I.T. Principal Component Analysis; Springer-Verlag: New York, NY, USA, 1986; pp. 63–76. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Analytica. Chimica. Acta. 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Martens, H.; Naes, T. Multivariate Calibration; Wiley: New York, NY, USA, 1989; pp. 72–236. [Google Scholar]
- Estienne, F.; Pasti, L.; Centner, V.; Walczak, B.; Despagne, F.; Rimbaud, D.J.; Noord, O.E.; Massart, D.L. A comparison of multivariate calibration techniques applied to experimental NIR data sets Part II. Predictive ability under extrapolation conditions. Chemom. Intell. Lab. Syst. 2001, 58, 195–211. [Google Scholar] [CrossRef]
- Gogé, F.; Joffre, R.; Jolivet, C.; Ross, I.; Ranjard, L. Optimization criteria in sample selection step of local regression for quantitative analysis of large soil NIRS database. Chemom. Intell. Lab. Syst. 2012, 110, 168–176. [Google Scholar] [CrossRef]
- Kim, S.; Okajima, R.; Kano, M.; Hasebe, S. Development of soft-sensor using locally weighted PLS with adaptive similarity measure. Chemom. Intell. Lab. Syst. 2013, 124, 43–49. [Google Scholar] [CrossRef]
- Zamora-Rojas, E.; Garrido-Varo, A.; Berg, F.V.D.; Guerrero-Ginel, J.E.; Pérez-Marín, D.C. Evaluation of a new local modelling approach for large and heterogeneous NIRS data sets. Chemom. Intell. Lab. Syst. 2010, 101, 87–94. [Google Scholar] [CrossRef]
- Cheng, C.; Chiu, M.S. A new data-based methodology for nonlinear process modeling. Chem. Eng. Sci. 2004, 59, 2801–2810. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in partial least squares regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Wu, Z.H.; Ma, Q.; Lin, Z.H.; Peng, Y.F.; Ai, L.; Shi, X.Y.; Qiao, Y.J. A novel model selection strategy using total error concept. Talanta 2013, 107, 248–254. [Google Scholar] [CrossRef] [PubMed]
- Lavine, B.K.; Moores, A.J. Genetic algorithms in analytical chemistry. Anal. Lett. 1999, 32, 433–445. [Google Scholar] [CrossRef]
- Niazi, A.; Soufi, A.; Mobarakabadi, M. Genetic algorithm applied to selection of wavelength in partial least squares for simultaneous spectrophotometric determination of nitrophenol isomers. Anal. Lett. 2006, 39, 2359–2372. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.L.; De Noord, O.E.; De Jong, S.; Vandeginste, B.M.; Sterna, C. Elimination of uninformative variables for multivariate calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.Z.; Pan, T.; Chen, J.M.; Lu, Q.P. Waveband selection for NIR spectroscopy analysis of soil organic matter based on SG smoothing and MWPLS methods. Chemom. Intell. Lab. Syst. 2011, 107, 139–146. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, F.; Kong, W.W.; He, Y. Application of Visible and Near-Infrared Hyperspectral Imaging to Determine Soluble Protein Content in Oilseed Rape Leaves. Sensors 2015, 15, 16576–16588. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.L. The control problems of grey systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Huang, J.C. Application of grey system theory in telecare. Comput. Biol. Med. 2011, 41, 302–306. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.H.; Lin, C.T.; Peng, K.H.; Huang, C.C. Applying hierarchical grey relation clustering analysis to geographical information systems—A case study of the hospitals in Taipei City. Expert. Syst. Appl. 2012, 39, 7247–7254. [Google Scholar] [CrossRef]
- Ai, X.B.; Hu, Y.Z.; Chen, G.H. A systematic approach to identify the hierarchical structure of accident factors with grey relations. Safety Sci. 2014, 63, 83–93. [Google Scholar] [CrossRef]
- Liu, S.F.; Lin, Y. Grey Systems Theory and Applications; Springer-Verlag: Berlin/Heidelberg, Germany, 2011; pp. 57–63. [Google Scholar]
- Windig, W.; Heckler, C.E.; Agblevor, F.A.; Evans, R.J. Self-modeling mixture analysis of categorized pyrolysis mass spectral data with the SIMPLISMA approach. Chemom. Intell. Lab. Syst. 1992, 14, 195–207. [Google Scholar] [CrossRef]
- Bu, D.S.; Brown, C.W. Self-modeling mixture analysis by interactive principal component analysis. Appl. Spectrosc. 2000, 54, 1214–1221. [Google Scholar] [CrossRef]
- Windig, W.; Antalek, B.; Lippert, J.L.; Batonneau, Y.; Brémard, C. Combined use of conventional and second-derivative data in the SIMPLISMA self-modeling mixture analysis approach. Anal. Chem. 2002, 74, 1371–1379. [Google Scholar] [CrossRef] [PubMed]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
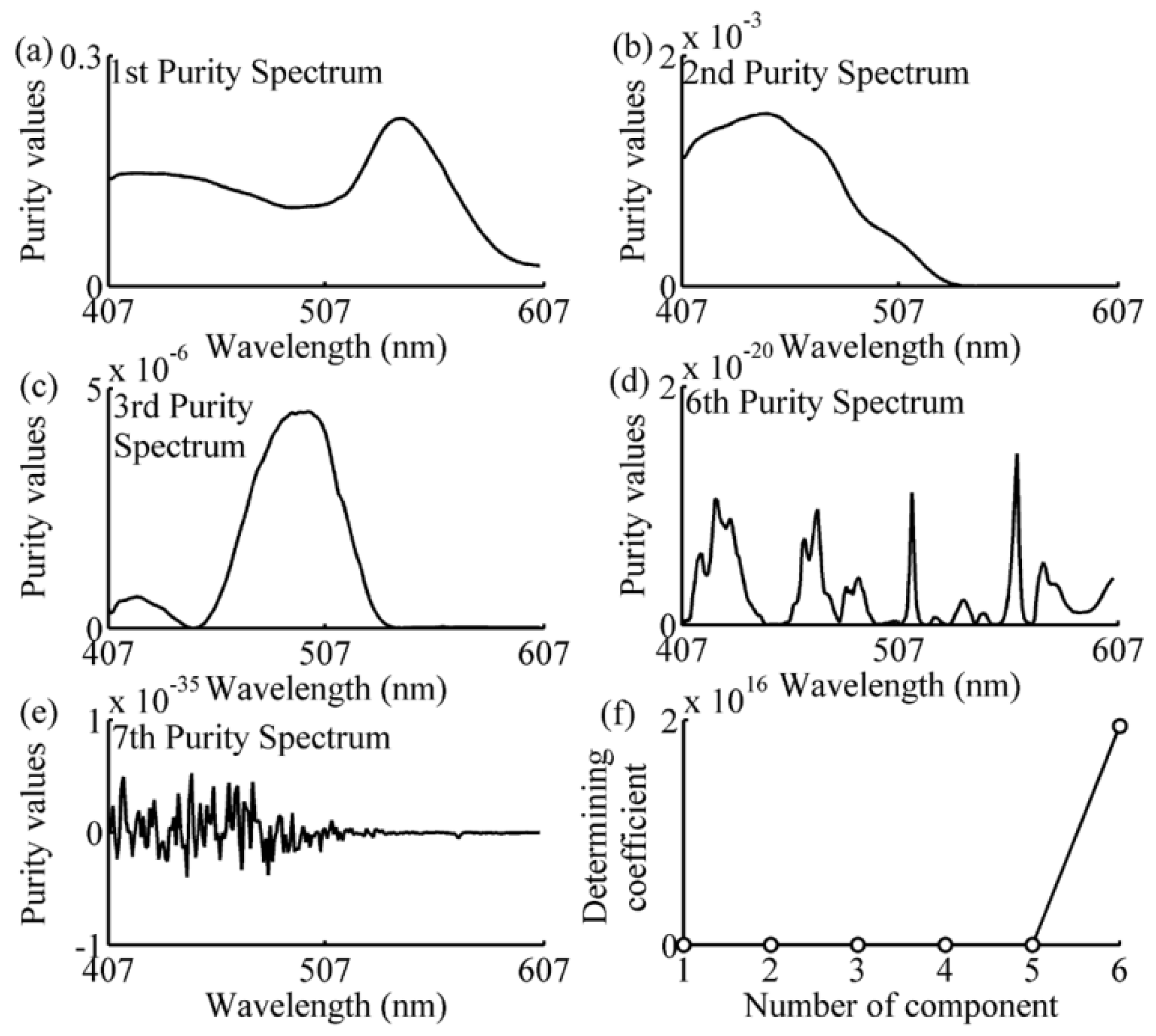
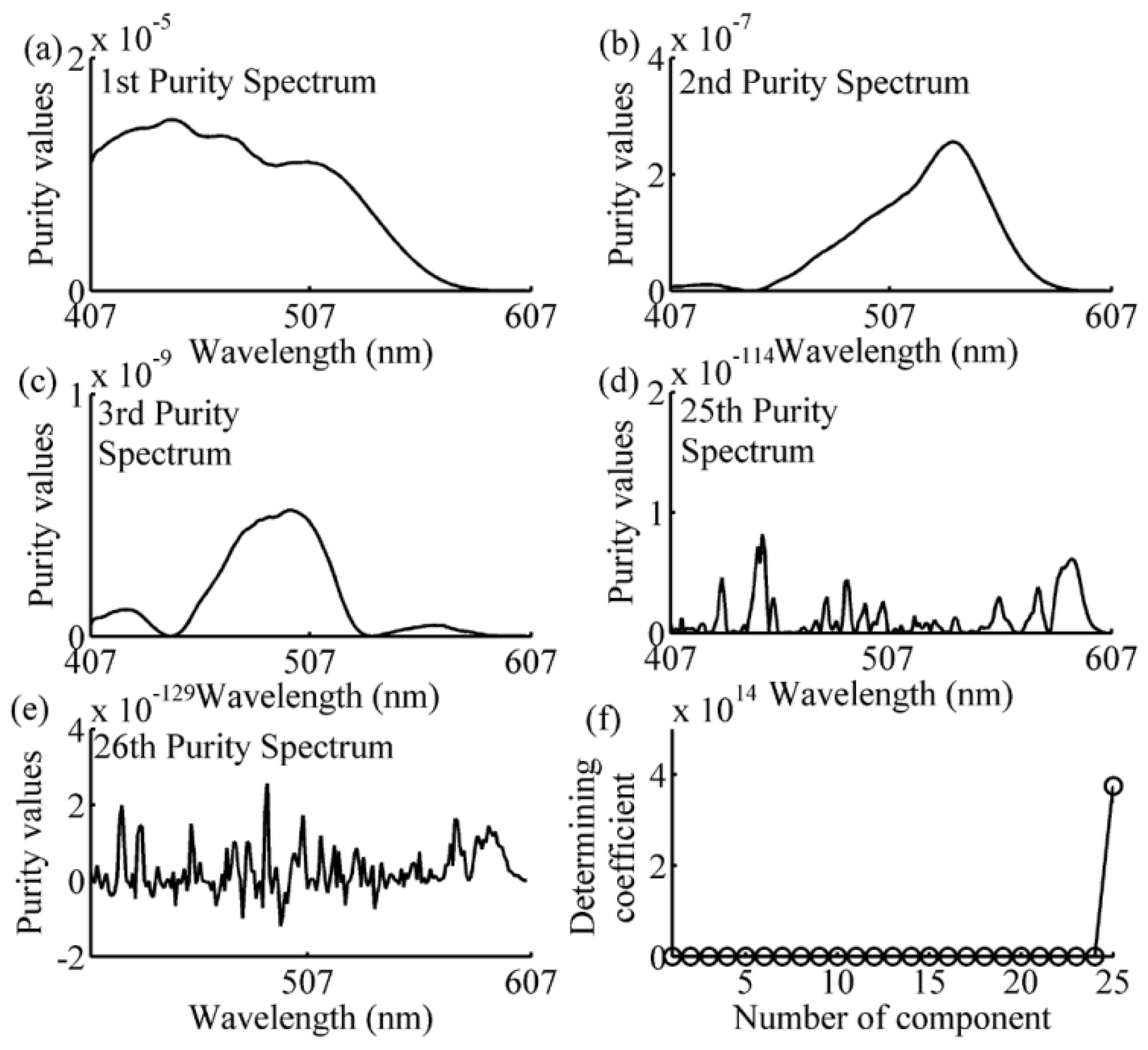
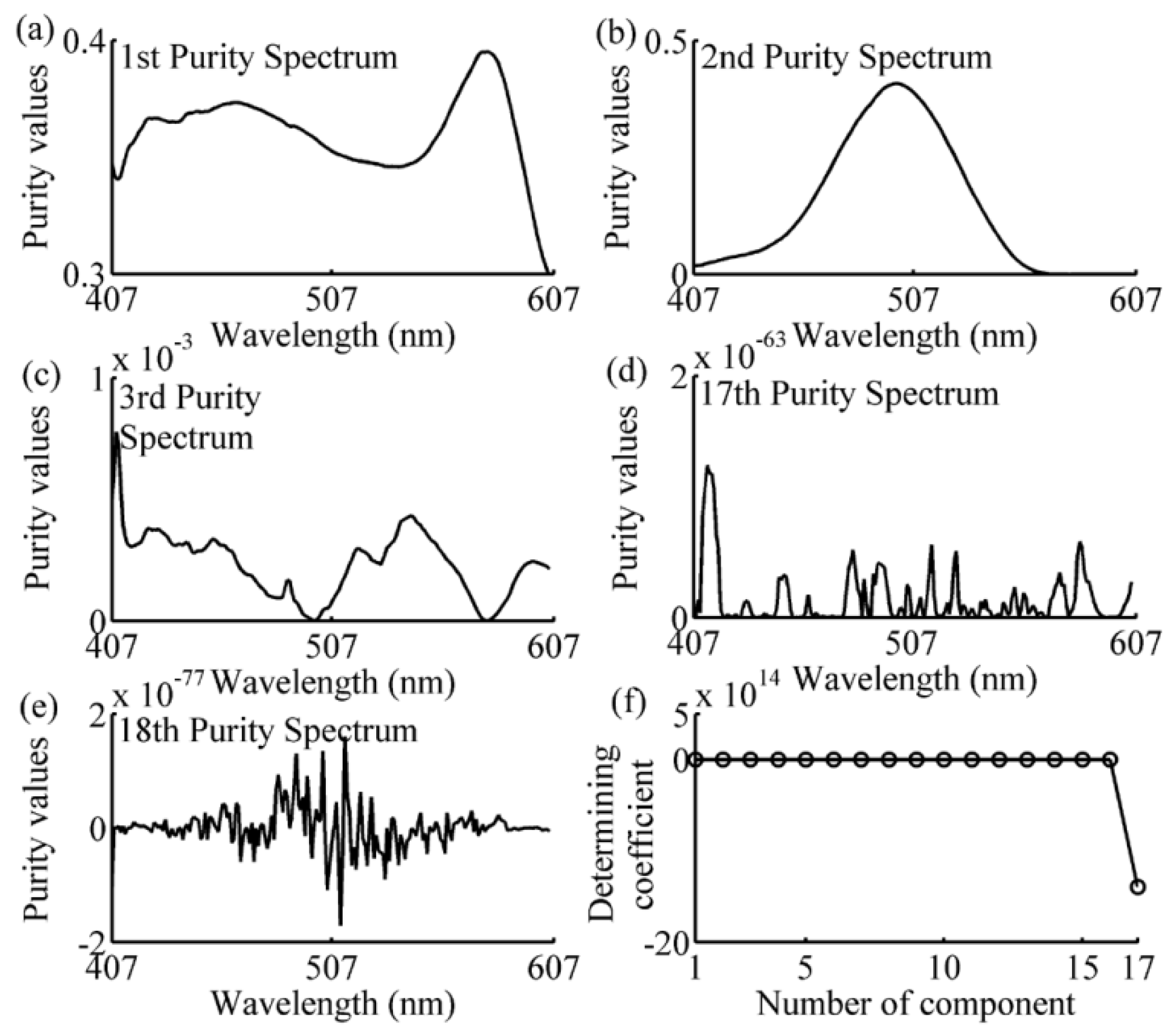
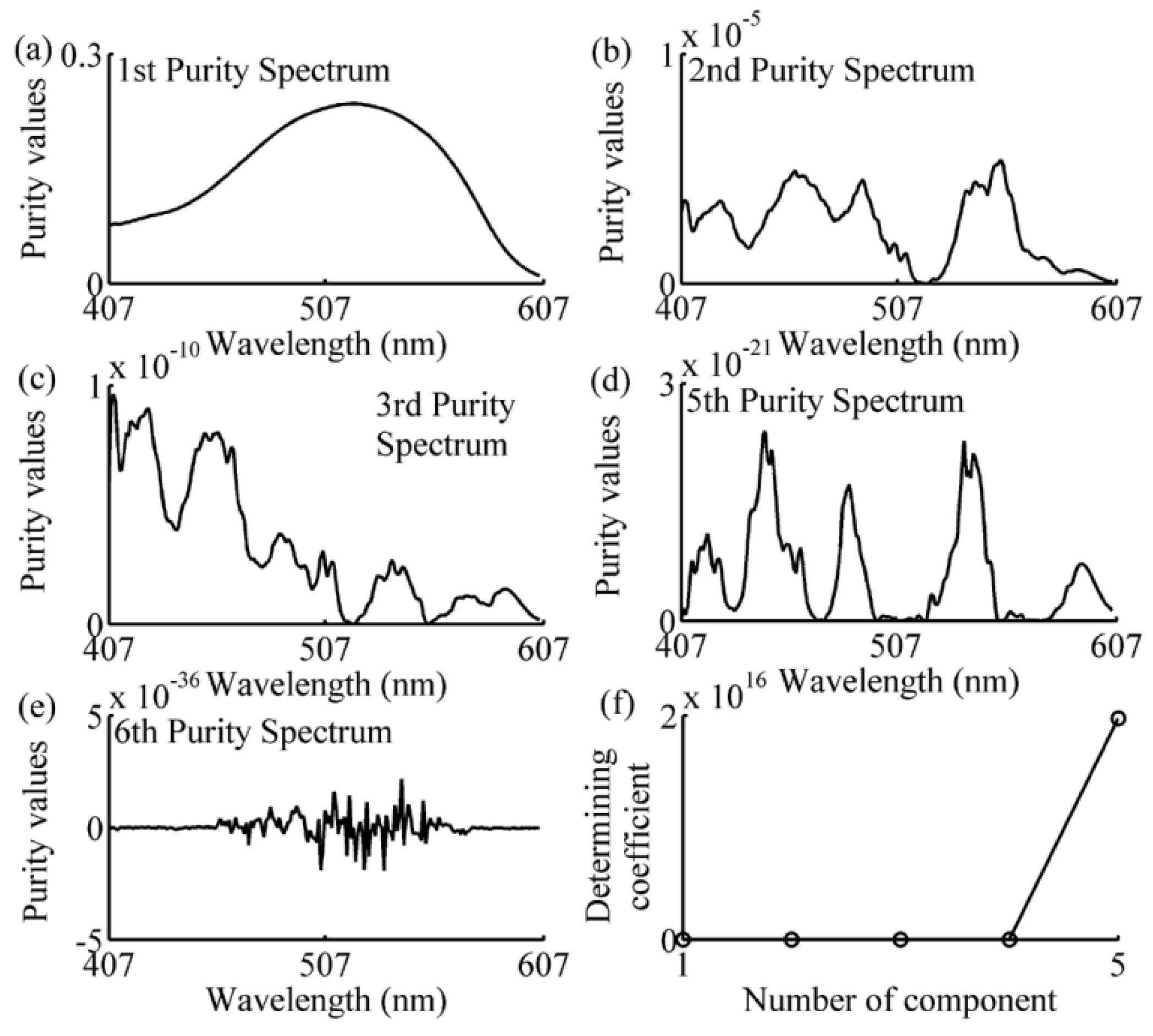
| Symbol | Representation |
|---|---|
| weight of the rates of change | |
| distinguishing coefficient | |
| synthetic degree of GRC between sequences Xi and Xj | |
| absolute degree of GRC between sequences Xi and Xj | |
| relative degree of GRC between sequences Xi and Xj | |
| n | the number of wavelengths |
| number of samples in prediction set | |
| number of samples in calibration set |
| Samples | No. | SGRC | S1 (μg/mL) | SGRC | S2 (μg/mL) | SGRC | S3 (μg/mL) | SGRC | S4 (μg/mL) |
|---|---|---|---|---|---|---|---|---|---|
| Samples of Calibration subset | 1 | 0.945 | 0-0-80-60 | 0.969 | 60-60-40-30 | 0.968 | 80-60-0-0 | 0.980 | 140-0-0-0 |
| 2 | 0.900 | 0-0-100-100 | 0.949 | 50-80-50-30 | 0.957 | 100-60-0-0 | 0.970 | 200-0-0-0 | |
| 3 | 0.899 | 0-0-80-80 | 0.949 | 60-80-50-30 | 0.930 | 100-80-0-0 | 0.970 | 120-0-0-0 | |
| 4 | 0.885 | 0-0-50-60 | 0.947 | 60-80-50-40 | 0.922 | 80-80-0-0 | 0.920 | 50-0-0-0 | |
| 5 | 0.855 | 0-0-60-80 | 0.944 | 60-60-50-40 | 0.904 | 60-50-0-0 | 0.920 | 60-0-0-0 | |
| 6 | 0.837 | 0-0-50-80 | 0.935 | 50-60-40-40 | 0.904 | 100-100-0-0 | 0.892 | 40-0-0-0 | |
| 7 | 0.726 | 0-0-80-0 | 0.930 | 60-80-40-40 | 0.900 | 80-100-0-0 | ─ | ─ | |
| … | … | … | … | … | … | … | … | ─ | |
| 12 | 0.693 | 0-0-0-80 | 0.913 | 80-60-40-40 | 0.874 | 200-0-0-0 | ─ | ─ | |
| 13 | ─ | ─ | 0.913 | 80-80-50-30 | ─ | 50-80-0-0 | ─ | ─ | |
| … | … | … | … | … | … | … | … | … | |
| 28 | ─ | ─ | 0.703 | 0-180-0-0 | 0.656 | 60-80-30-30 | ─ | ─ | |
| … | … | … | … | … | … | … | … | … | |
| 35 | ─ | ─ | 0.680 | 0-0-80-80 | ─ | ─ | ─ | ─ | |
| Predicted sample | 0-0-60-50 | 50-60-40-30 | 100-50-0-0 | 160-0-0-0 |
| Prediction Sample | Number of Samples in Calibration Subset | Number of Selected Wavelengths | Prediction Sample | Number of Samples in Calibration Subset | Number of Selected Wavelengths |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 15 | 34 | 19 |
| 2 | 35 | 25 | 16 | 7 | 3 |
| 3 | 37 | 18 | 17 | 5 | 6 |
| 4 | 13 | 12 | 18 | 6 | 5 |
| 5 | 38 | 16 | 19 | 5 | 5 |
| 6 | 7 | 8 | 20 | 4 | 5 |
| 7 | 7 | 3 | 21 | 4 | 5 |
| 8 | 5 | 6 | 22 | 28 | 17 |
| 9 | 5 | 6 | 23 | 10 | 11 |
| 10 | 4 | 4 | 24 | 13 | 12 |
| 11 | 12 | 5 | 25 | 33 | 17 |
| 12 | 34 | 18 | 26 | 38 | 16 |
| 13 | 26 | 15 | 27 | 5 | 5 |
| 14 | 34 | 18 | - | - | - |
| Model | Wavelength Selection Approach | Parameters | Size of Calibration Set | Times (s) | RMSEP (µg/mL) | |||
|---|---|---|---|---|---|---|---|---|
| A | C | T | S | |||||
| Global | ― | ― | 70 × 198 | 0.4 | 4.12 | 4.15 | 1.01 | 0.99 |
| SIMPLISMA | Rj = 2 × 10−5 | 70 × 19 | 0.4 | 3.71 | 3.72 | 0.97 | 1.08 | |
| GA | Gen = 300 | 70 × 75 | 3666.6 | 2.74 | 3.05 | 1.14 | 1.28 | |
| UVE | 70 × [100,177] | 4.2 | 4.01 | 3.92 | 0.99 | 1.07 | ||
| MWPLSR | Win = 60 | 70 × 60 | 57.1 | 3.01 | 2.17 | 1.34 | 1.12 | |
| SPA | M = 69 | 70 × 69 | 98.9 | 3.76 | 3.61 | 1.00 | 1.03 | |
| LocalS | ― | = 0.2, = 0.5 | [4,38] × 198 | 123.1 | 1.63 | 1.77 | 0.88 | 0.59 |
| LocalE | ― | ― | [4,34] × 198 | 145.4 | 3.14 | 3.97 | 0.76 | 0.80 |
| LocalM | ― | fpca = 2 | [4,32] × 198 | 152.7 | 2.15 | 1.95 | 0.63 | 0.81 |
| LocalA | ― | ― | [3,40] × 198 | 156.6 | 2.99 | 2.53 | 0.81 | 0.77 |
| LocalS | SIMPLISMA | Rj = 2 × 10−5 | [4,38] × [3,25] | 128.2 | 1.41 | 1.76 | 0.72 | 0.68 |
| UVE | [4,38] × [65,174] | 136.8 | 1.64 | 1.73 | 1.06 | 0.76 | ||
| Model | Wavelength Selection Approach | P value between Reference and Predicted Concentrations | Standard Error of Prediction Residual Error (µg/mL) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | C | T | S | A | C | T | S | ||
| Global | ― | 0.75 | 0.68 | 0.63 | 0.66 | 4.19 | 4.19 | 1.02 | 1.01 |
| SIMPLISMA | 0.77 | 0.86 | 0.53 | 0.77 | 3.78 | 3.78 | 0.98 | 1.10 | |
| GA | 0.63 | 0.68 | 0.99 | 0.35 | 2.78 | 3.02 | 1.16 | 1.29 | |
| UVE | 0.80 | 0.77 | 0.56 | 0.63 | 4.10 | 3.96 | 1.00 | 1.09 | |
| MWPLSR | 0.20 | 0.84 | 0.27 | 0.68 | 2.97 | 2.20 | 1.32 | 1.14 | |
| SPA | 0.61 | 0.93 | 0.93 | 0.97 | 3.83 | 3.68 | 1.02 | 1.05 | |
| LocalS | ― | 0.36 | 0.81 | 0.27 | 0.72 | 1.55 | 1.80 | 0.89 | 0.59 |
| LocalE | ― | 0.86 | 0.76 | 0.80 | 0.89 | 3.19 | 4.04 | 0.76 | 0.81 |
| LocalM | ― | 0.48 | 0.66 | 0.80 | 0.61 | 2.17 | 1.97 | 0.64 | 0.83 |
| LocalA | ― | 0.87 | 0.95 | 0.71 | 0.56 | 2.94 | 2.55 | 0.82 | 0.75 |
| LocalS | SIMPLISMA | 0.71 | 0.54 | 0.80 | 0.83 | 1.43 | 1.69 | 0.73 | 0.66 |
| UVE | 0.38 | 0.89 | 0.60 | 0.30 | 1.64 | 1.74 | 1.07 | 0.76 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Zhu, L.; Lou, X.; Meng, X.; Guo, Y.; Wang, Z. Local Strategy Combined with a Wavelength Selection Method for Multivariate Calibration. Sensors 2016, 16, 827. https://doi.org/10.3390/s16060827
Chang H, Zhu L, Lou X, Meng X, Guo Y, Wang Z. Local Strategy Combined with a Wavelength Selection Method for Multivariate Calibration. Sensors. 2016; 16(6):827. https://doi.org/10.3390/s16060827
Chicago/Turabian StyleChang, Haitao, Lianqing Zhu, Xiaoping Lou, Xiaochen Meng, Yangkuan Guo, and Zhongyu Wang. 2016. "Local Strategy Combined with a Wavelength Selection Method for Multivariate Calibration" Sensors 16, no. 6: 827. https://doi.org/10.3390/s16060827
APA StyleChang, H., Zhu, L., Lou, X., Meng, X., Guo, Y., & Wang, Z. (2016). Local Strategy Combined with a Wavelength Selection Method for Multivariate Calibration. Sensors, 16(6), 827. https://doi.org/10.3390/s16060827







