A Highly Sensitive Fiber-Optic Fabry–Perot Interferometer Based on Internal Reflection Mirrors for Refractive Index Measurement
Abstract
:1. Introduction
- (1)
- A new type of structure of the FFPI sensor is proposed with high sensitivity on a wide RI measurement range, including RI around that of optical fiber;
- (2)
- A small amount of the analyte is needed for the proposed FFPI sensor as an open micro-cavity, which is used to accommodate the measuring media;
- (3)
- Moderate requirements for detection setup are needed for the proposed FFPI sensor due to a clear fringe visibility of optical interference and a narrower operating wavelength range;
- (4)
- The proposed FFPI sensor has small temperature cross-sensitivity, and the effect from the temperature change can be almost eliminated by a compensated calculation method;
- (5)
- The good chemical stability characteristic of the silica fiber and gold films makes the proposed FFPI sensor suitable to be used in applications prone to chemical reaction.
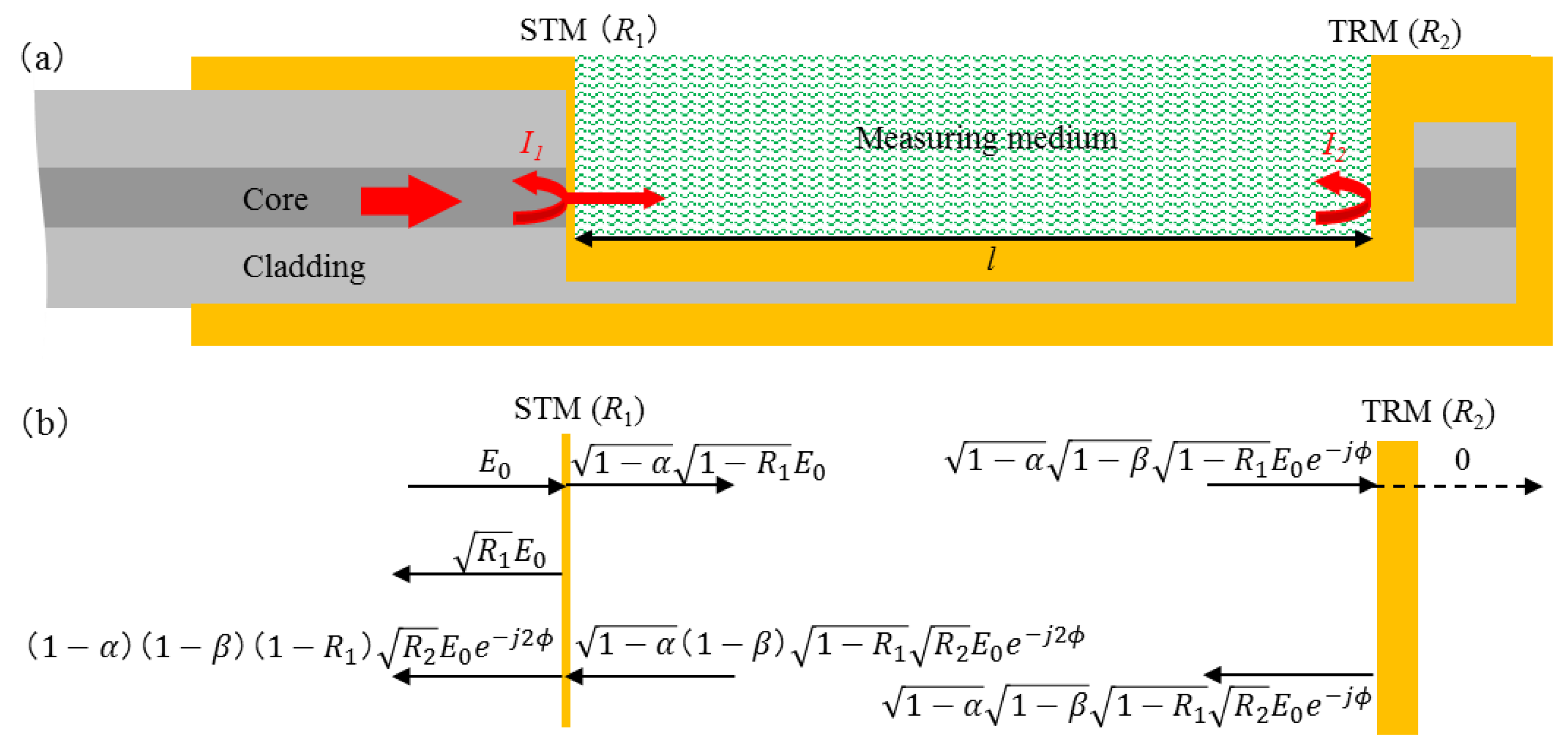
2. Design of Sensor and Principle Analysis
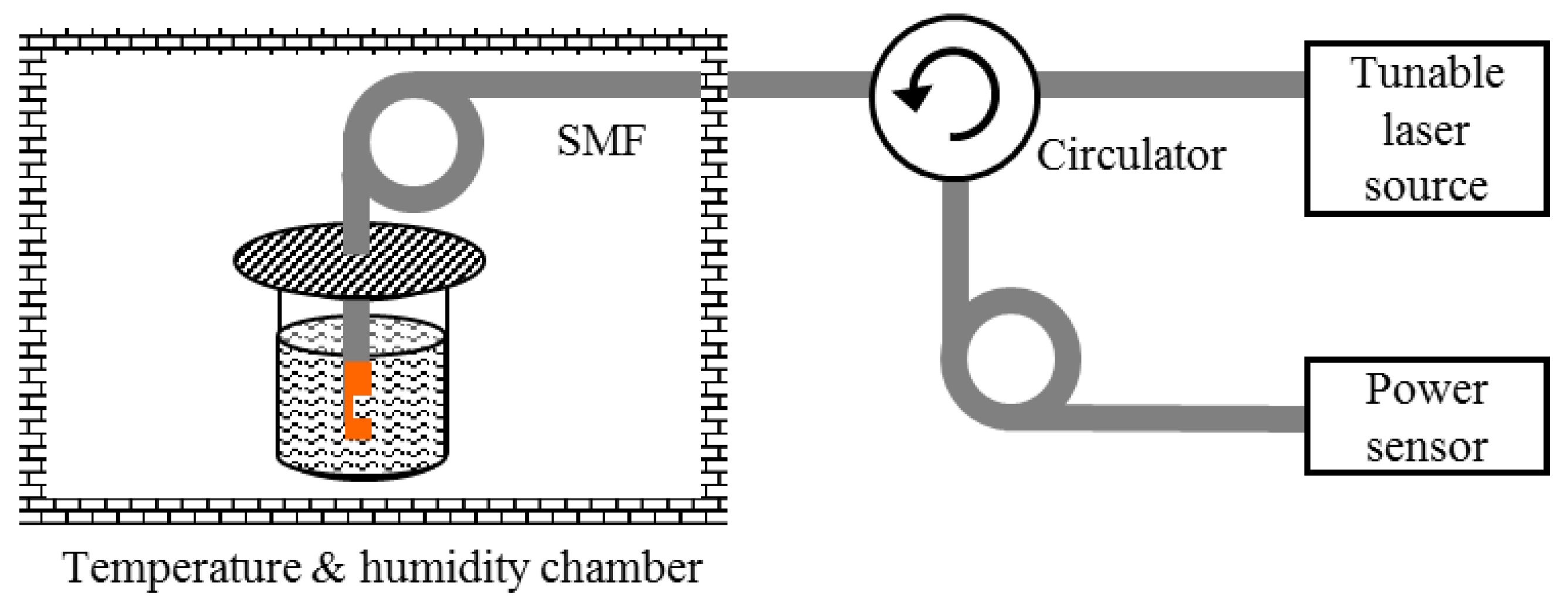
3. Experimental Verifications
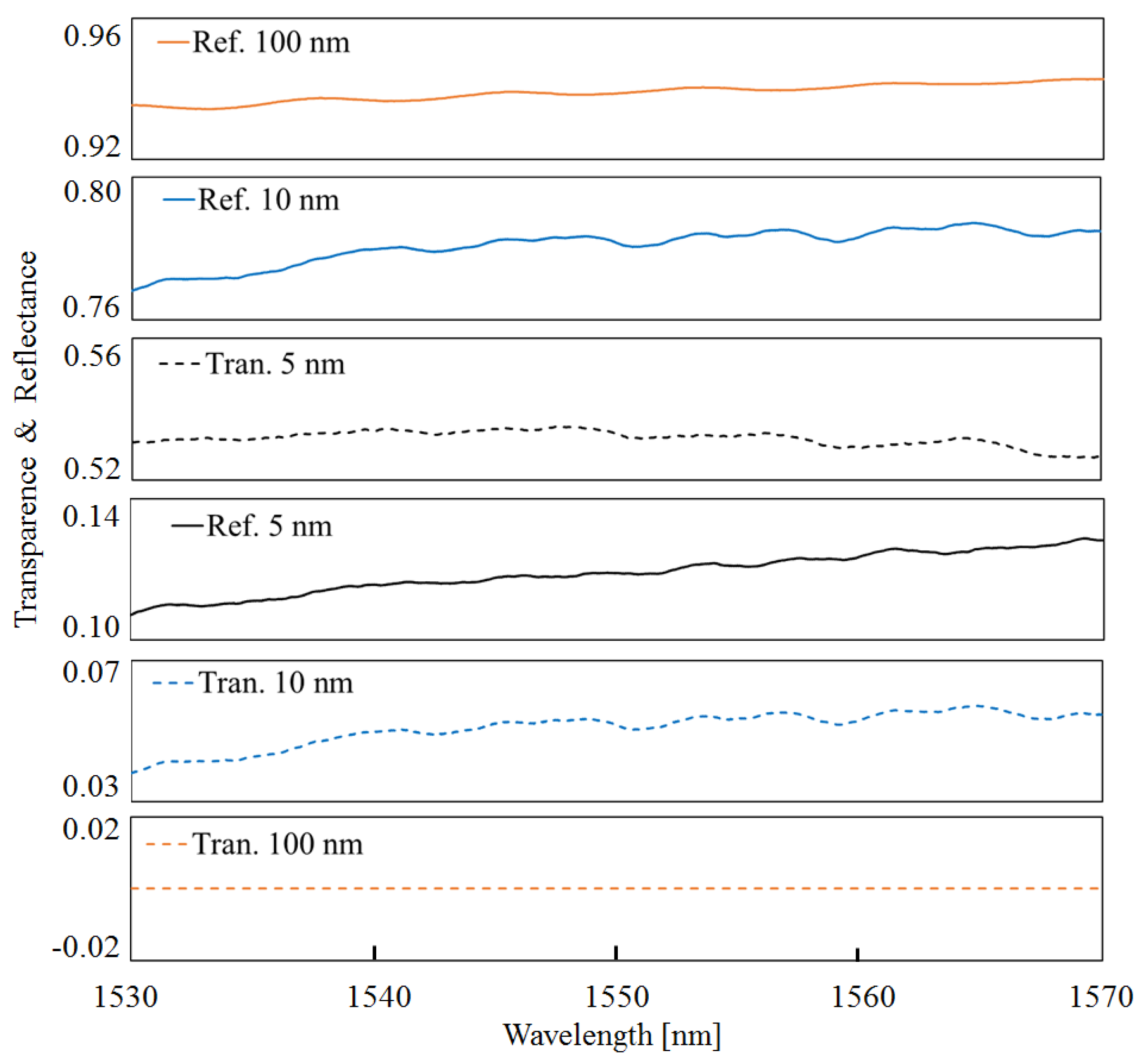
3.1. Production and Evaluation of Gold Thin Films
3.2. Fabrication of Sensor Head
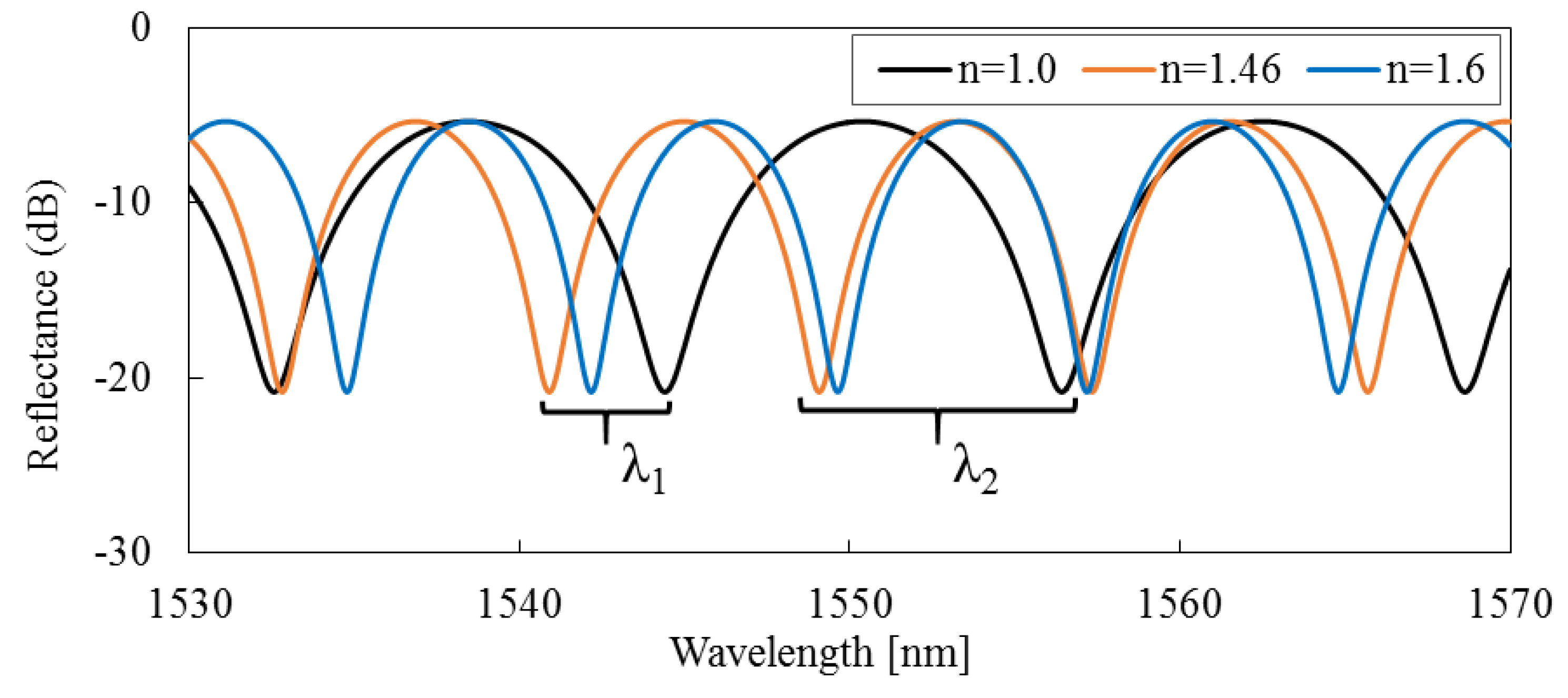
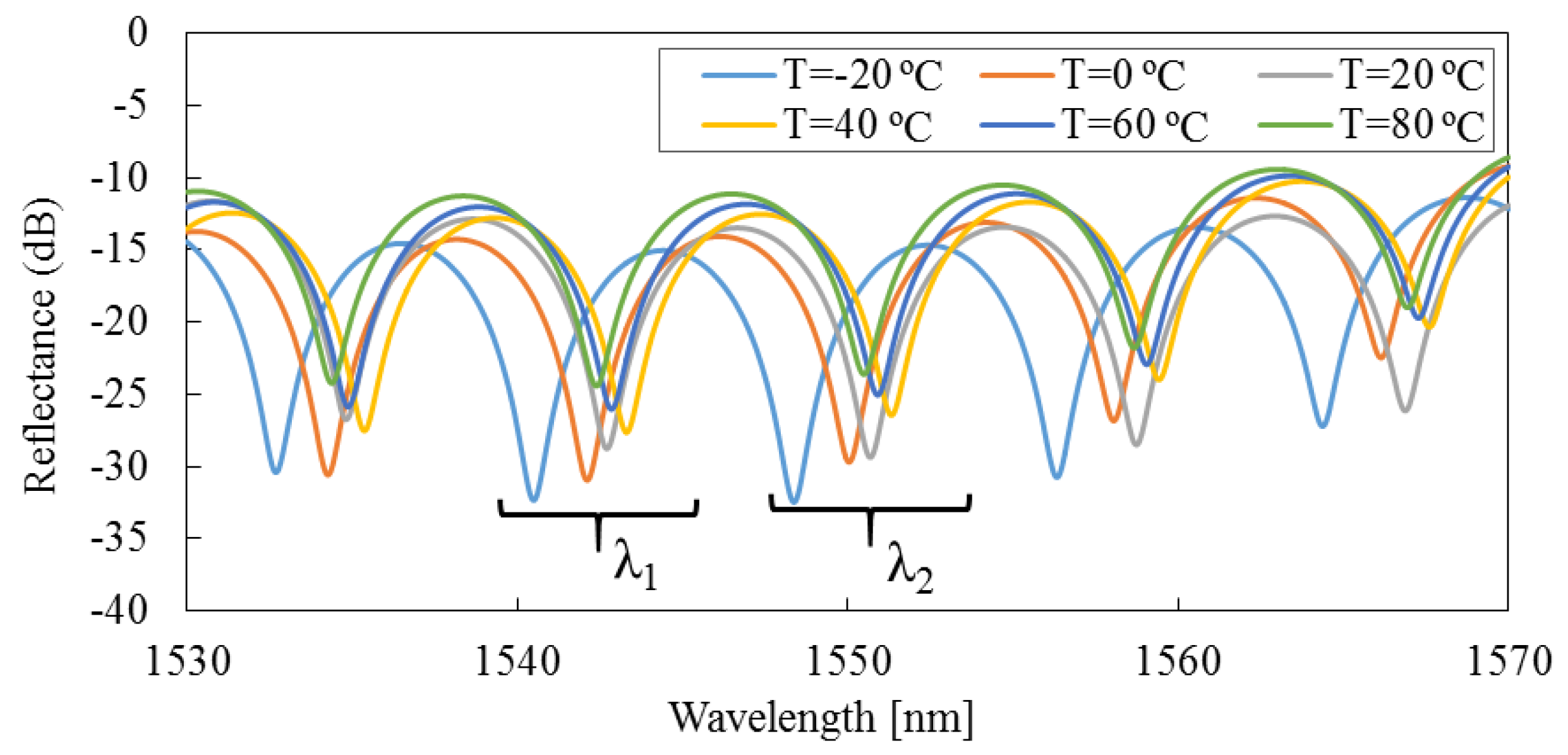
3.3. Experimental Results
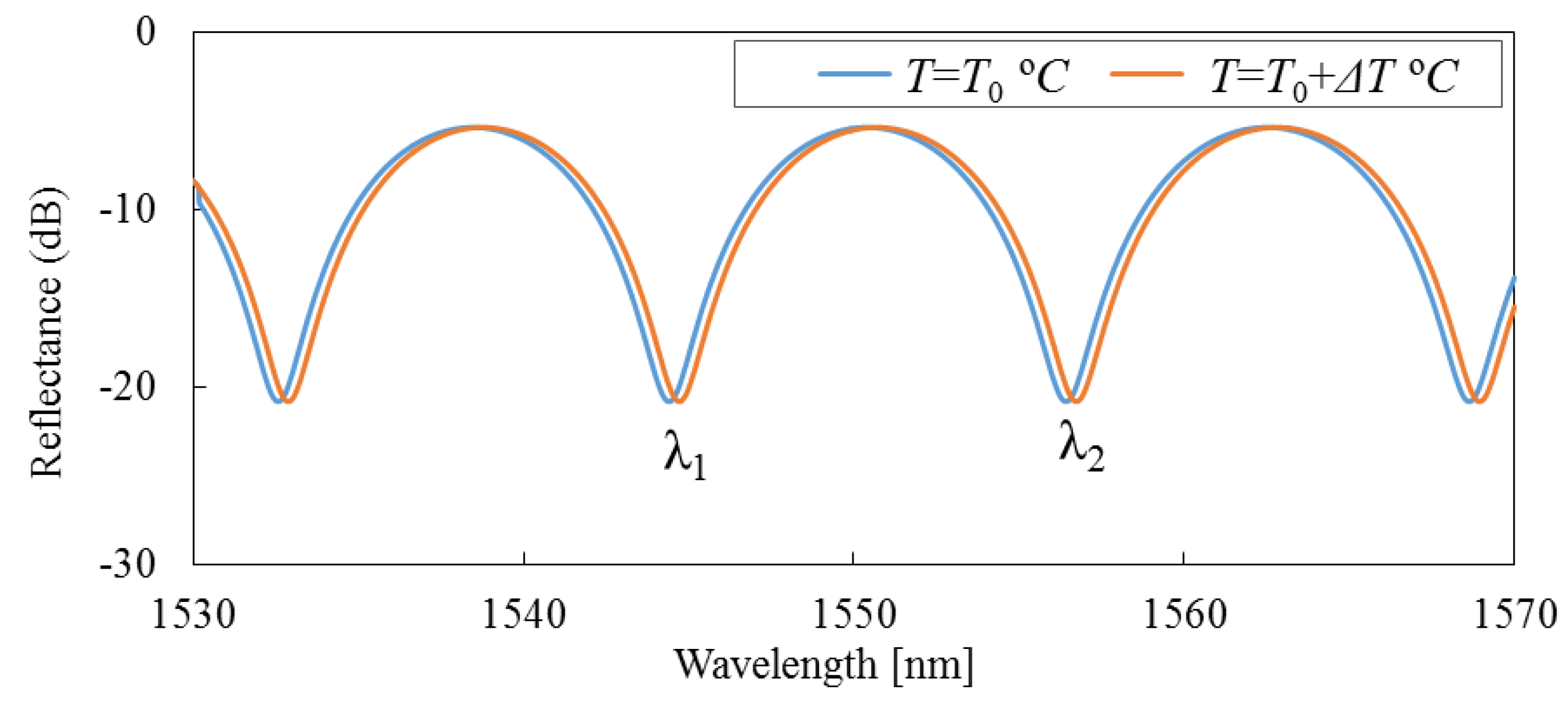
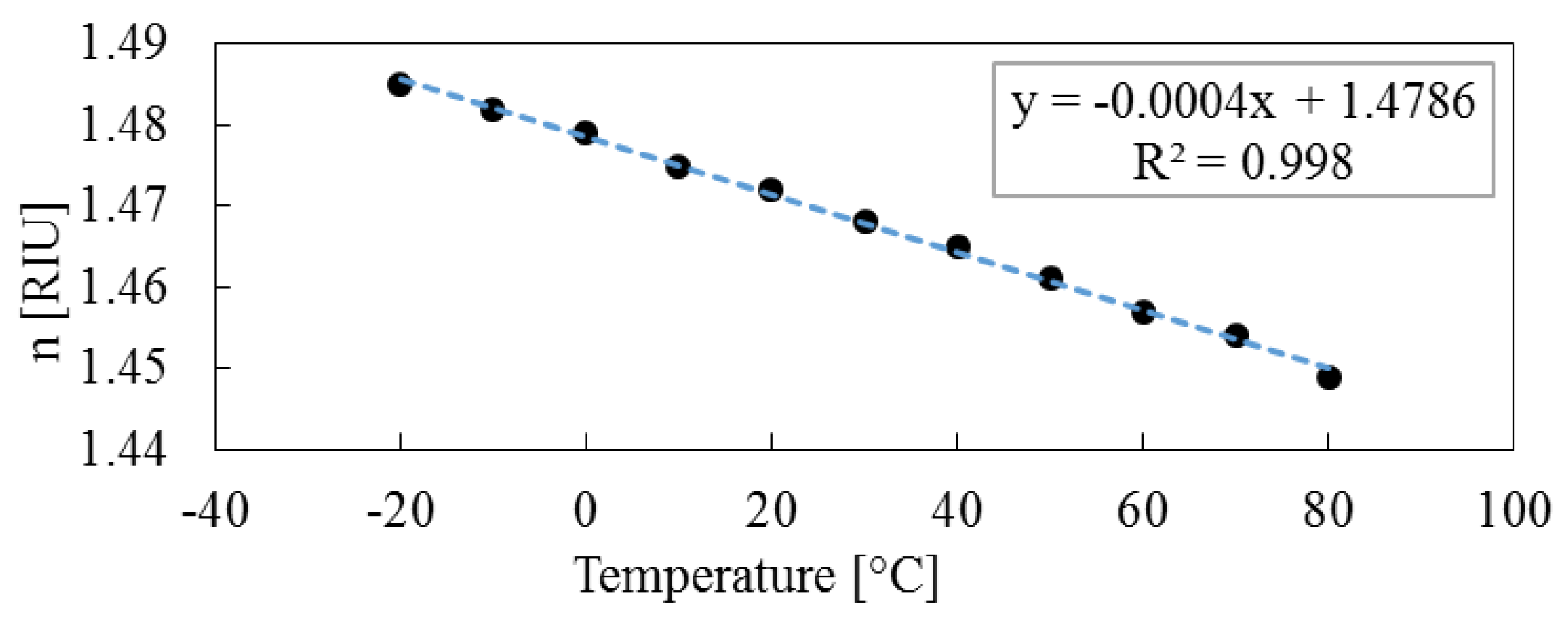
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lin, V.S.Y.; Motesharei, K.; Dancil, K.P.; Sailor, M.J.; Ghadiri, M.R. A porous silicon-based optical interferometric biosensor. Science 1997, 278, 840–843. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Simon, G. Surface plasmon resonance spectroscopy for characterisation of membrane protein–ligand interactions and its potential for drug discovery. Biochim. Biophys. Acta 2014, 1838, 43–55. [Google Scholar]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1021–1028. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Wei, T.; Han, Y.; Li, Y.; Tsai, H.L.; Xiao, H. Temperature-insensitive miniaturized fiber inline Fabry–Perot interferometer for highly sensitive refractive index measurement. Opt. Express 2008, 16, 5764–5769. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.R.; Hu, T.Y.; Wang, D.N. Optical fiber Fabry–Perot interferometer cavity fabricated by femtosecond laser micromachining and fusion splicing for refractive index sensing. Opt. Express 2012, 20, 22813–22818. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.S.; Islam, M.D.; Ali, M.M.; Lai, M.H.; Ahmad, H. Chronology of Fabry–Perot Interferometer Fiber-Optic Sensors and Their Applications: A Review. Sensors 2014, 14, 7451–7488. [Google Scholar]
- Liang, W.; Huang, Y.; Xu, Y.; Lee, R.K.; Yariv, A. Highly sensitive fiber Bragg grating refractive index sensors. Appl. Phys. Lett. 2005, 86, 151122. [Google Scholar] [CrossRef]
- Kou, J.; Qiu, S.; Xu, F.; Lu, Y. Demonstration of a compact temperature sensor based on first-order Bragg grating in a tapered fiber probe. Opt. Express 2011, 19, 18452–18457. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Zhu, Y.; Du, H. Long-period gratings inscribed in air- and water-filled photonic crystal fiber for refractometric sensing of aqueous solution. Appl. Phys. Lett. 2008, 92, 044105. [Google Scholar] [CrossRef]
- Wang, Y.P. Review of long period fiber gratings written by CO2 laser. J. Appl. Phys. 2010, 108, 081101. [Google Scholar] [CrossRef]
- Petrović, M.D.; Petrovic, J.; Daničić, A.; Vukčević, M.; Bojović, B.; Hadžievski, L.J.; Allsop, T.; Lloyd, G.; Webb, D.J. Non-invasive respiratory monitoring using long-period fiber grating sensors. Biomed. Opt. Express 2014, 5, 1136–1144. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.Y.; Huang, C.H.; Cheng, G.L.; Chen, N.K.; Chui, H.C. Tapered optical fiber sensor based on localized surface plasmon resonance. Opt. Express 2012, 20, 21693–21701. [Google Scholar] [CrossRef] [PubMed]
- Camara, A.R.; Gouvêa, P.M.P.; Dias, C.M.S.; Braga, A.M.B.; Dutra, R.F.; Araujo, R.E.; Carvalho, I.C.S. Dengue immunoassay with an LSPR fiber optic sensor. Opt. Express 2013, 21, 27023–27031. [Google Scholar] [CrossRef] [PubMed]
- Ortega-Mendoza, J.G.; Padilla-Vivanco, A.; Toxqui-Quitl, C.; Zaca-Morán, P.; Villegas-Hernández, D.; Chávez, F. Optical Fiber Sensor Based on Localized Surface Plasmon Resonance Using Silver Nanoparticles Photodeposited on the Optical Fiber End. Sensors 2014, 14, 18701–18710. [Google Scholar] [CrossRef] [PubMed]
- Ji, W.B.; Liu, H.H.; Tjin, S.C.; Chow, K.K.; Lim, A. Ultrahigh Sensitivity Refractive Index Sensor Based on Optical Microfiber. IEEE Photo. Tech. Lett. 2012, 24, 1872–1874. [Google Scholar] [CrossRef]
- May-Arrioja, D.A.; Guzmán-Sepúlveda, J.R.; Guzmán-Cabrera, R.; Torres-Cisneros, M.; Sánchez-Mondragón, J.J. A Highly Sensitive Fiber Optic Sensor Based on Two-Core Fiber for Refractive Index Measurement. Sensors 2013, 13, 14200–14213. [Google Scholar]
- Tong, L.; Lou, J.; Wang, Y. Microfiber Optical Sensors: A Review. Sensors 2014, 14, 5823–5844. [Google Scholar]
- Lu, Y.; Yang, X.; Wang, M.; Yao, J. An Exposed-Core Grapefruit Fibers Based Surface Plasmon Resonance Sensor. Sensors 2015, 15, 17106–17114. [Google Scholar]
- Rao, Y.J.; Deng, M.; Duan, D.W.; Zhu, T. In-line fiber Fabry–Perot refractive-index tip sensor based on endlessly photonic crystal fiber. Sens. Actuators A Phys. 2008, 148, 33–38. [Google Scholar] [CrossRef]
- Ran, Z.; Rao, Y.; Liu, W.; Liao, X.; Chiang, K. Laser-micromachined Fabry–Perot optical fiber tip sensor for high-resolution temperature-independent measurement of refractive index. Optics Express 2008, 16, 2252–2263. [Google Scholar] [CrossRef] [PubMed]
- Kou, J.; Feng, J.; Ye, L.; Xu, F.; Lu, Y. Miniaturized fiber taper reflective interferometer for high temperature measurement. Opt. Express 2010, 18, 14245–14250. [Google Scholar] [CrossRef] [PubMed]
- Rao, Y.J.; Deng, M.; Duan, D.W.; Yang, X.C.; Zhu, T.; Cheng, G.H. Micro Fabry–Perot interferometers in silica fibers machined by femtosecond laser. Opt. Express 2007, 15, 14123–14128. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lin, S.; Liang, J.; Oigawa, H.; Ueda, T. Fiber-Optic Temperature Sensor Based on Difference of Thermal Expansion Coefficient between Fused Silica and Metallic Materials. IEEE Photon. J. 2012, 4, 155–162. [Google Scholar]
- Li, X.; Lin, S.; Liang, J.; Zhang, Y.; Oigawa, H.; Ueda, T. High-Sensitivity Fiber-Optic Fabry–Perot Interferometer Temperature Sensor. Jpn. J. Appl. Phys. 2012, 51, 06FL10. [Google Scholar] [CrossRef]
- Xiao, G.; Adnet, A.; Zhang, Z.; Sun, F.; Grover, C.P. Monitoring changes in the refractive index of gases by means of a fiber optic Fabry–Perot interferometer sensor. Sensor Actuat. A Phys. 2005, 118, 177–182. [Google Scholar] [CrossRef]
- Wieduwilt, T.; Dellith, J.; Talkenberg, F.; Bartelt, H.; Schmidt, M.A. Reflectivity enhanced refractive index sensor based on a fiber-integrated Fabry–Perot microresonator. Opt. Express 2014, 22, 25333–25346. [Google Scholar] [CrossRef] [PubMed]
- Pevec, S.; Donlagic, D. High resolution, all-fiber, micro-machined sensor for simultaneous measurement of refractive index and temperature. Opt. Express 2014, 22, 16241–16253. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.S.R.; Reza, A. Optical and electrical properties of optimized thin gold films as top layer of MIS solar cells. Appl. Phys. A. 1992, 54, 204–207. [Google Scholar] [CrossRef]
- Liang, J.; Matsuo, T.; Kohsaka, F.; Li, X.; Kunitomo, K.; Ueda, T. Fabrication of Two-Axis Quartz MEMS-Based Capacitive Tilt Sensor. J. Inst. Electr. Eng. Jpn. 2008, 128, 85–90. [Google Scholar] [CrossRef]
- Li, X.; Liang, J.; Oigawa, H.; Ueda, T. Doubled optical path length for photonic bandgap fiber gas cell using micromirror. Jpn. J. Appl. Phys. 2011, 50, 06GM01. [Google Scholar] [CrossRef]
- Marcuse, A.D. Loss analysis of single-mode fiber splices. Bell Syst. Tech. J. 1977, 56, 703–718. [Google Scholar] [CrossRef]
- Marek, R. Loss analysis of single mode telecommunication fiber thermally-diffused core areas. Optica Applicate 2007, 27, 279–294. [Google Scholar]
- Wu, C.; Liu, Z.; Zhang, A.; Guan, B.; Tam, H. In-line open-cavity Fabry–Pérot interferometer formed by C-shaped fiber fortemperature-insensitive refractive index sensing. Opt. Express 2014, 22, 21757–21766. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Fu, H.; Qureshi, K.; Guan, B.; Tam, H. High-pressure and high-temperature characteristics of a Fabry–Perot interferometer based on photonic crystal fiber. Opt. Lett. 2011, 36, 412–414. [Google Scholar] [CrossRef] [PubMed]
- Data Sheet of Shin-Etsu Chemical Homepage. Available online: http://www.shinetsusilicone-global.com/catalog/pdf/grease_e.pdf (accessed on 10 May 2016).
- Li, X.; Liang, J.; Lin, S.; Zhang, Y.; Ueda, T. Applied Technique of Focused Ion Beam Milling Based on Microstructure of Photonic Bandgap Fiber. Int. J. Adv. Manuf. Tech. 2013, 68, 465–471. [Google Scholar] [CrossRef]
- Li, X.; Pawłat, J.; Liang, J.; Xu, G.; Ueda, T. Fabrication of photonic bandgap fiber gas cell using focused ion beam cutting. Jpn. J. Appl. Phys. 2009, 48, 06FK05. [Google Scholar] [CrossRef]



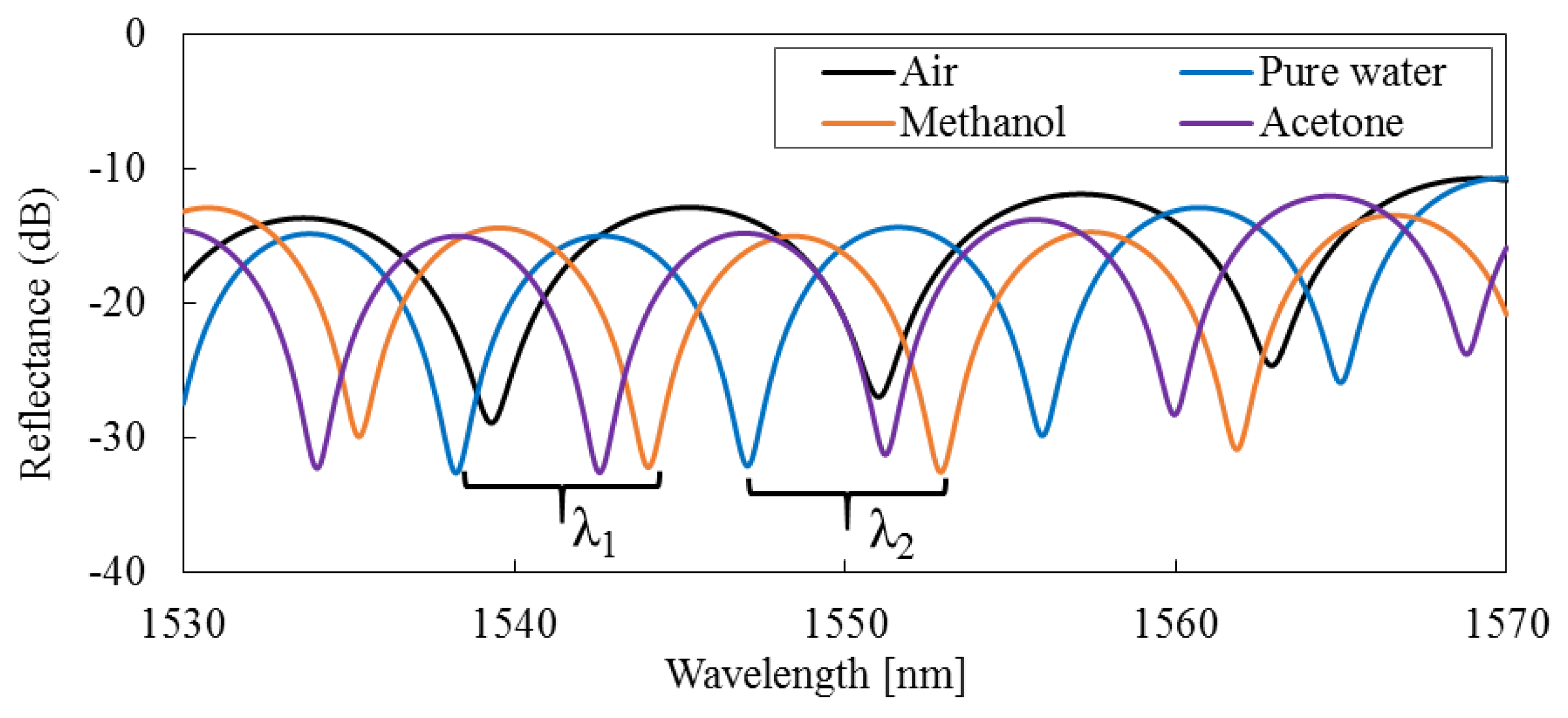
| Medium | Air | Pure Water | Methanol | Acetone |
|---|---|---|---|---|
| λ1 [nm] | 1539.327 | 1538.243 | 1544.054 | 1542.585 |
| λ2 [nm] | 1551.033 | 1547.055 | 1552.899 | 1551.224 |
| l [µm] | 101.949 | - | - | - |
| n [RIU] | - | 1.3245 | 1.3295 | 1.3585 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Shao, Y.; Yu, Y.; Zhang, Y.; Wei, S. A Highly Sensitive Fiber-Optic Fabry–Perot Interferometer Based on Internal Reflection Mirrors for Refractive Index Measurement. Sensors 2016, 16, 794. https://doi.org/10.3390/s16060794
Li X, Shao Y, Yu Y, Zhang Y, Wei S. A Highly Sensitive Fiber-Optic Fabry–Perot Interferometer Based on Internal Reflection Mirrors for Refractive Index Measurement. Sensors. 2016; 16(6):794. https://doi.org/10.3390/s16060794
Chicago/Turabian StyleLi, Xuefeng, Yujiao Shao, Yuan Yu, Yin Zhang, and Shaowen Wei. 2016. "A Highly Sensitive Fiber-Optic Fabry–Perot Interferometer Based on Internal Reflection Mirrors for Refractive Index Measurement" Sensors 16, no. 6: 794. https://doi.org/10.3390/s16060794
APA StyleLi, X., Shao, Y., Yu, Y., Zhang, Y., & Wei, S. (2016). A Highly Sensitive Fiber-Optic Fabry–Perot Interferometer Based on Internal Reflection Mirrors for Refractive Index Measurement. Sensors, 16(6), 794. https://doi.org/10.3390/s16060794





