The Real-Valued Sparse Direction of Arrival (DOA) Estimation Based on the Khatri-Rao Product
Abstract
:1. Introduction
2. Signal Model for DOA Estimation
2.1. Input Signal Model
2.2. Signal Model Based on Sparse Representation
3. The Real-Valued Sparse DOA Estimation Based on the KR Product
3.1. The Real-Valued Sparse Model for DOA Estimation
3.2. DOA Estimation Based on a SRACV
4. Simulation Experiments
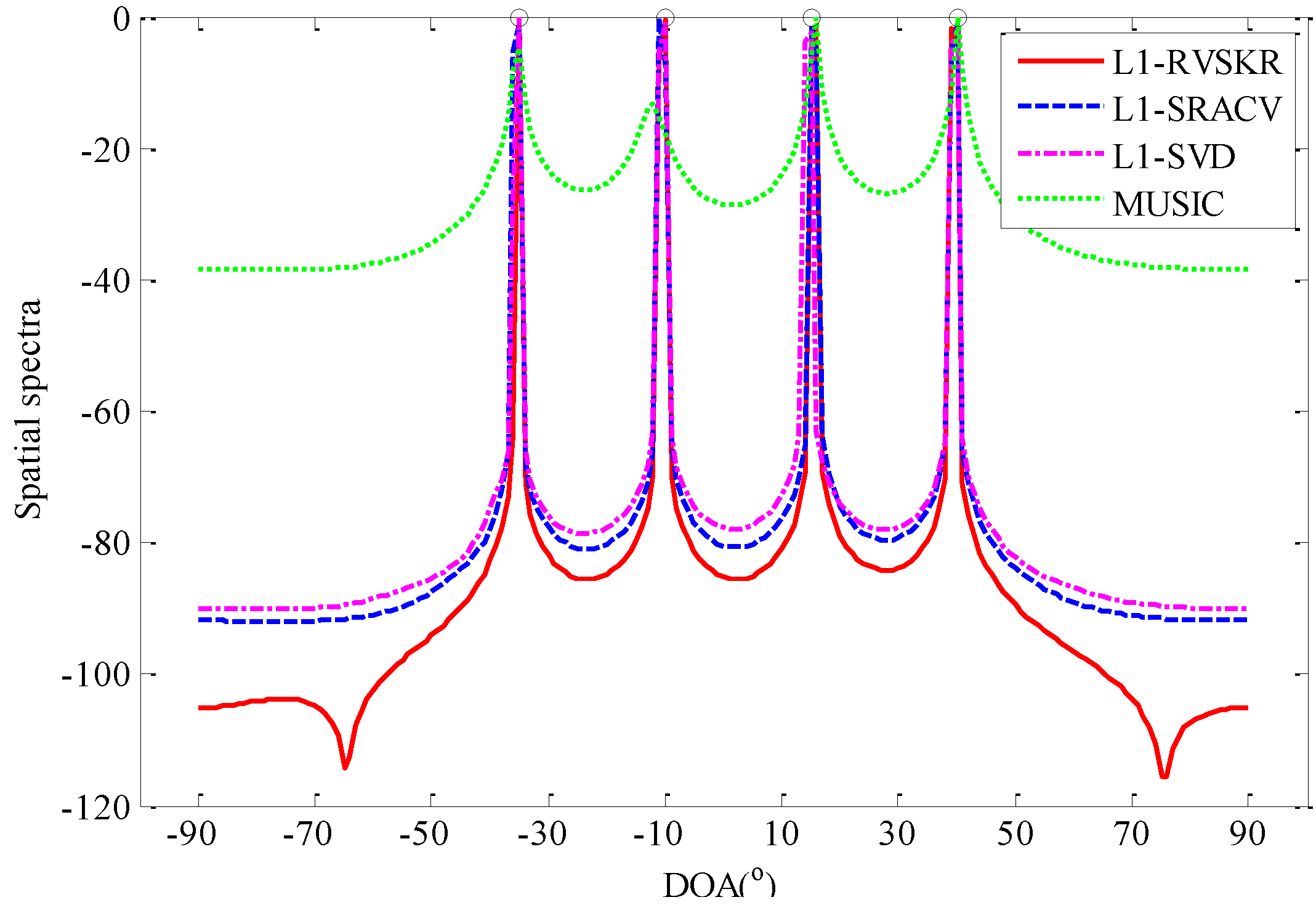
4.1. The Spatial Spectra Comparison
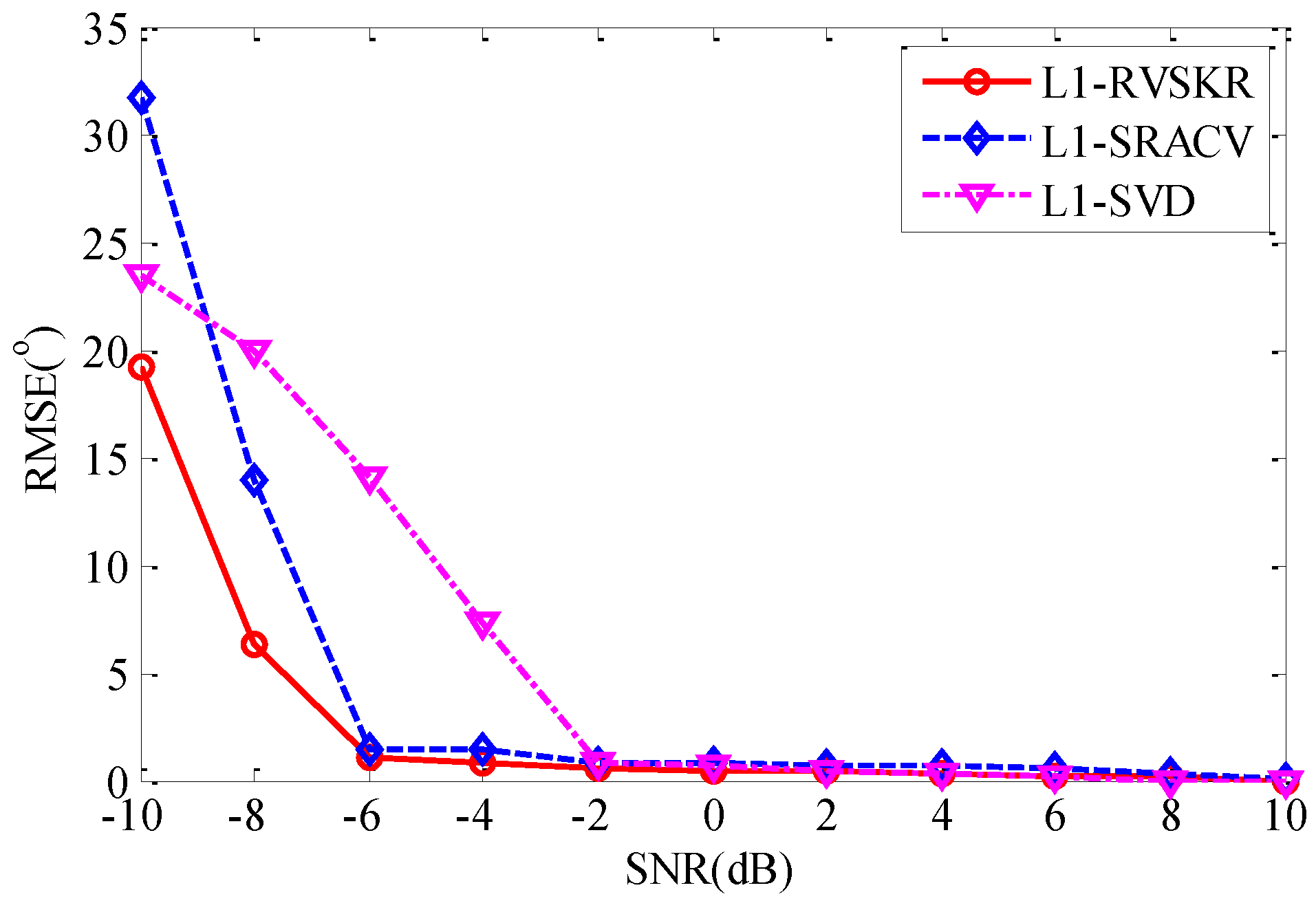
4.2. The Estimation Performance versus SNR
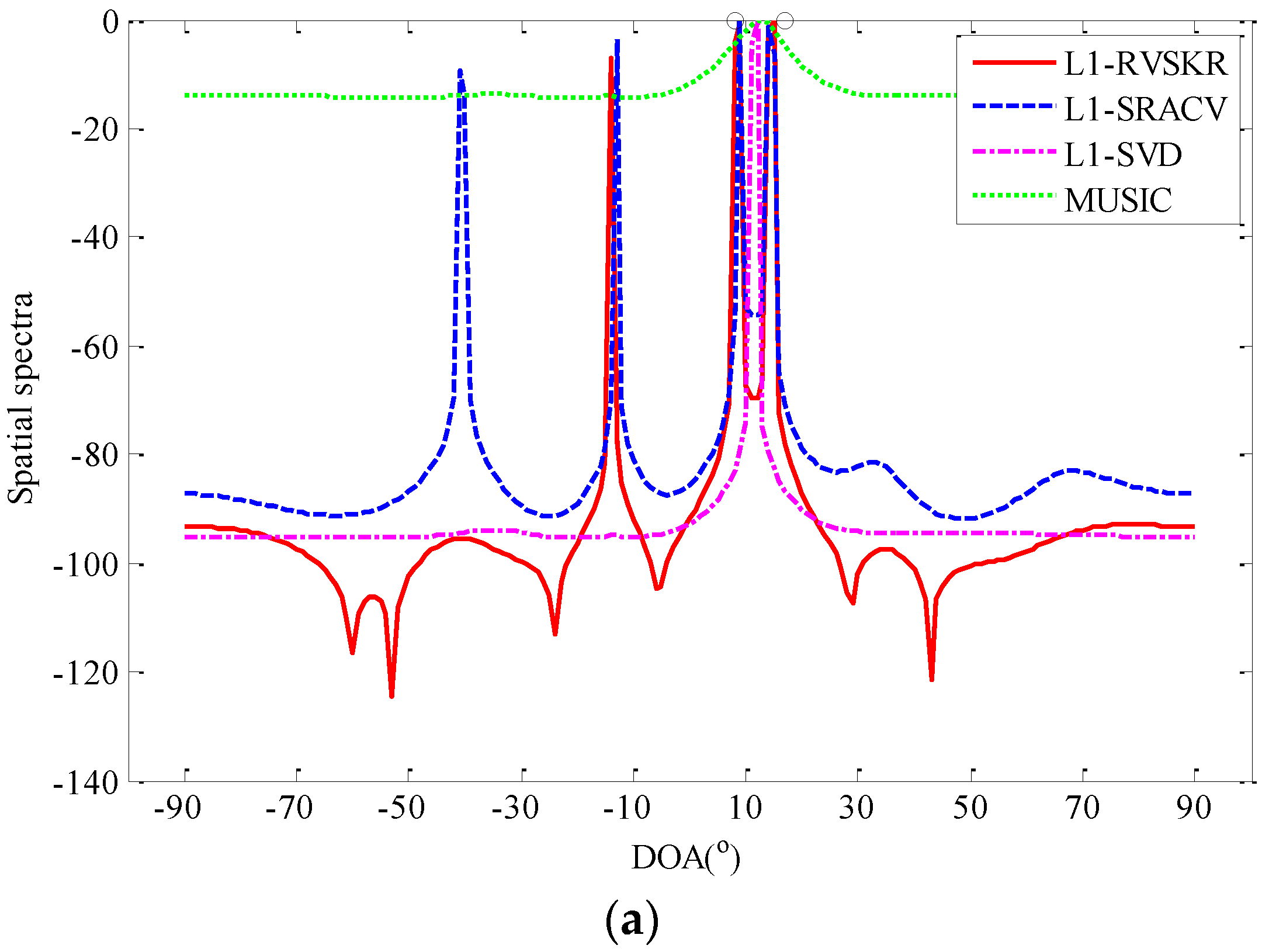
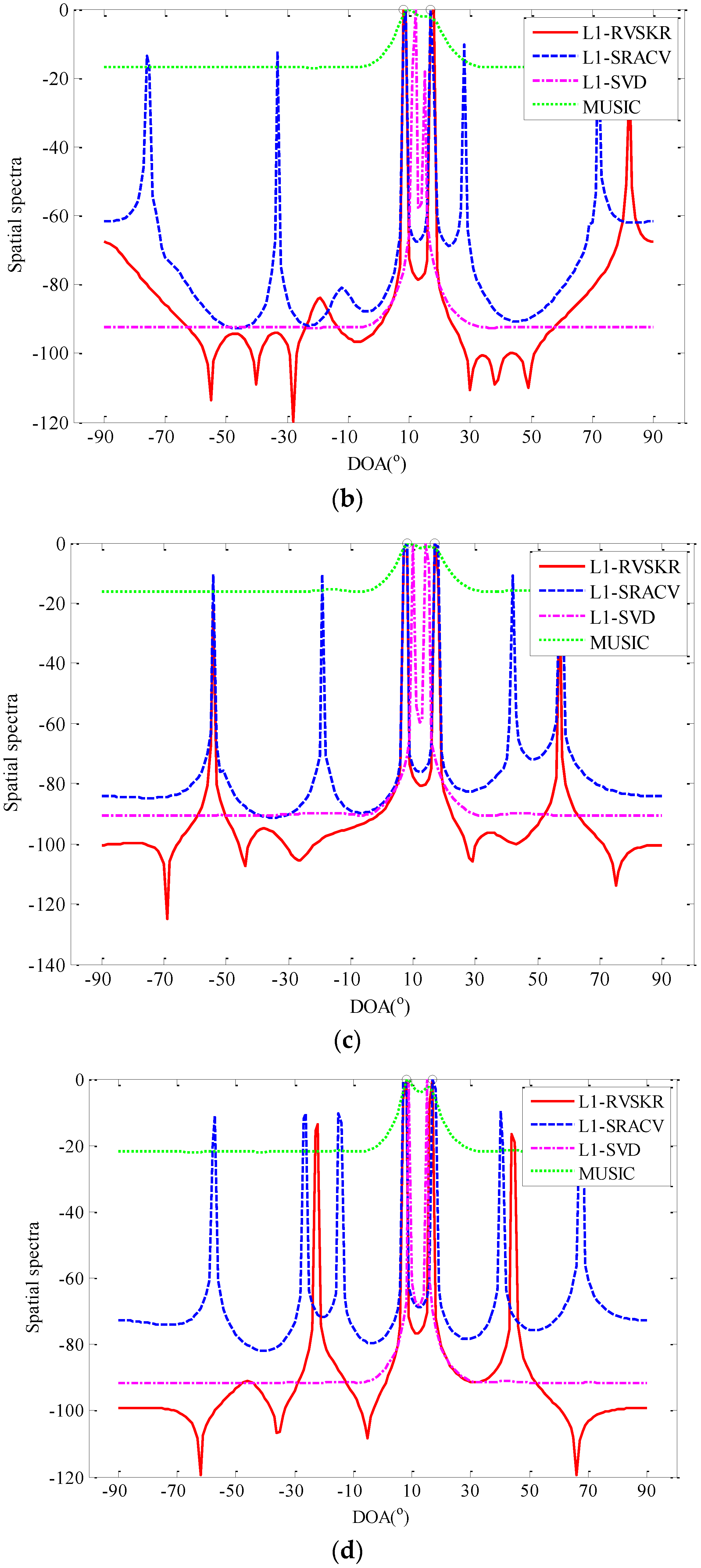
4.3. The Angle Resolution Capability
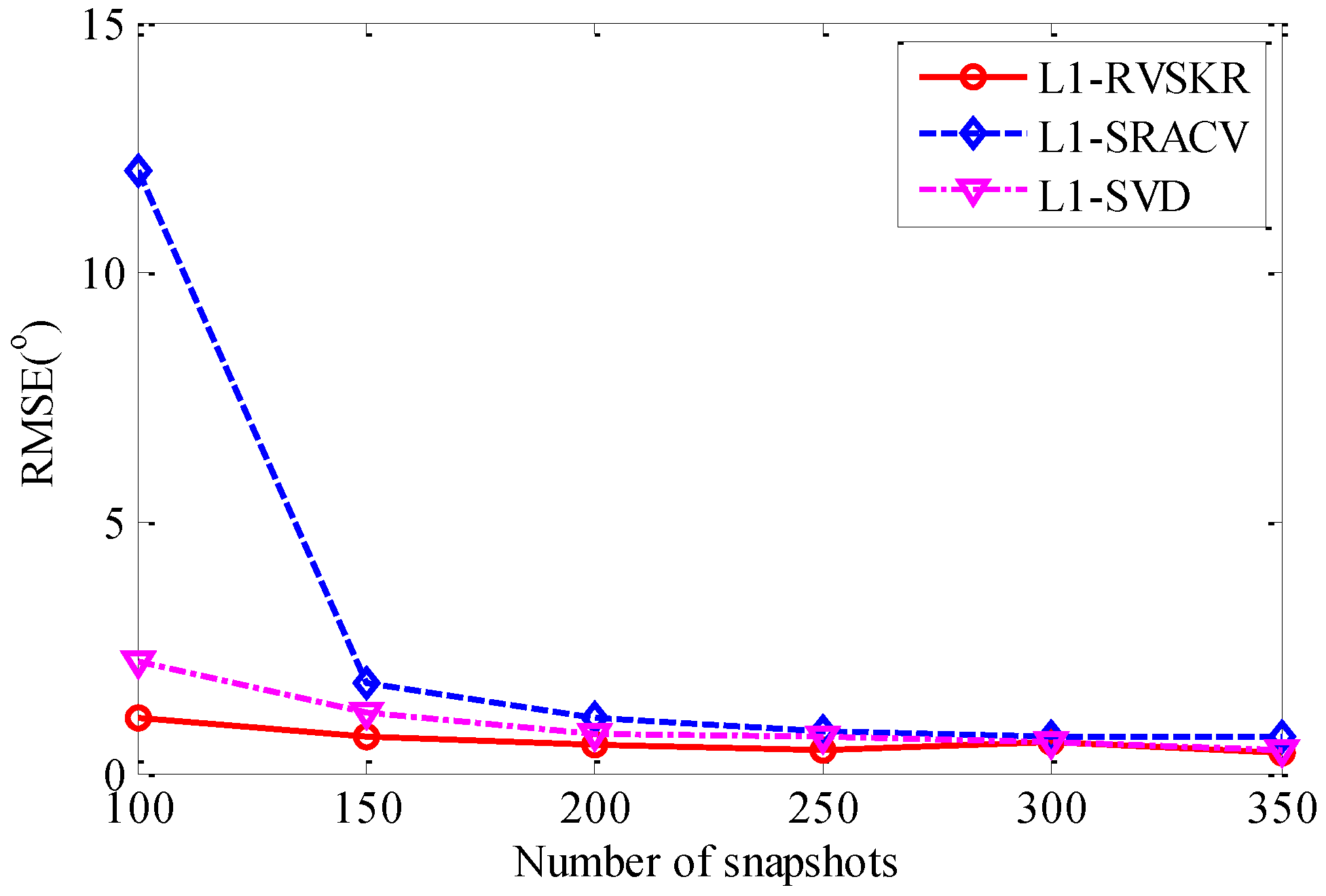
4.4. The Estimation Performance versus the Number of Snapshots
4.5. The Algorithm Complexity Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- He, Z.Q.; Shi, Z.P.; Huang, L.; So, H.C. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting. IEEE Signal Process. Lett. 2015, 22, 435–439. [Google Scholar] [CrossRef]
- Si, W.J.; Qu, X.G.; Qu, Z.Y. Off-Grid DOA Estimation Using Alternating Block Coordinate Descent in Compressed Sensing. Sensors 2015, 15, 21099–21113. [Google Scholar] [CrossRef] [PubMed]
- Pejoski, S.; Kafedziski, V. Sparse covariance fitting method for direction of arrival estimation of uncorrelated wideband signals. Telfor J. 2014, 6, 115–120. [Google Scholar] [CrossRef]
- Lin, B.; Liu, J.; Xie, M.; Zhu, J. Sparse Signal Recovery for Direction-of-Arrival Estimation Based on Source Signal Subspace. J. Appl. Math. 2014, 2014, 101–111. [Google Scholar] [CrossRef]
- Malioutov, D.; Çetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Yin, J.H.; Chen, T.Q. Direction-of-arrival estimation using a sparse representation of array covariance vectors. IEEE Trans. Signal Process. 2011, 59, 4489–4493. [Google Scholar] [CrossRef]
- He, Z.Q.; Shi, Z.P.; Huang, L. Covariance sparsity-aware DOA estimation for nonuniform noise. Digit. Signal Process. 2014, 28, 75–81. [Google Scholar] [CrossRef]
- Xie, H.; Feng, D.Z.; Yuan, M.D. DOA estimation method by utilizing sparse representation of the covariance matrix. J. Xidian Univ. 2015, 42, 35–41. [Google Scholar]
- Ma, W.K.; Hsieh, T.H.; Chi, C.Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: A Khatri-Rao subspace approach. IEEE Trans. Signal Process. 2010, 58, 2168–2180. [Google Scholar] [CrossRef]
- Liu, Q.H.; Jin, L.N.; Ouyang, S. Wideband DOA Estimation with Interpolated Focusing KR Product Matrix. Int. J. Signal Process. Image Process. Pattern Recognit. 2015, 8, 201–210. [Google Scholar] [CrossRef]
- Liu, Q.H.; Ouyang, S.; He, Z.Q. DOA estimation of quasi-stationary signals based on Khatri-Rao product using joint sparse signal representation. Syst. Eng. Electron. 2012, 34, 1753–1757. [Google Scholar]
- Huarng, K.C.; Yeh, C.C. A unitary transformation method for angle-of-arrival estimation. IEEE Trans. Signal Process. 1991, 39, 975–977. [Google Scholar] [CrossRef]
- Dai, J.S.; Wu, Z.; Tang, Z. Real-valued sparse representation method for DOA estimation with uniform linear array. In Proceedings of the 2012 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 3794–3797.
- Dai, J.J.; Xu, X.; Zhao, D.B. Direction-of-arrival estimation via real-valued sparse representation. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 376–379. [Google Scholar] [CrossRef]
- Wu, Z.; Dai, J.S.; Zhu, X.L.; Zhao, D.A. A Real-Valued Sparse Representation Method for DOA Estimation with Unknown Mutual Coupling. Acta Armamentarii 2015, 36, 294–298. [Google Scholar]
- Hu, N.; Ye, Z.F.; Xu, X.; Bao, M. DOA estimation for sparse array via sparse signal reconstruction. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 760–773. [Google Scholar] [CrossRef]
- Ottersten, B.; Stoica, P.; Roy, R. Covariance matching estimation techniques for array signal processing applications. Digit. Signal Process. 1991, 8, 185–210. [Google Scholar]
- Li, H.; Stoica, P.; Li, J. Computationally efficient maximum likelihood estimation of structured covariance matrices. IEEE Trans. Signal Process. 1999, 47, 1314–1323. [Google Scholar]
- Seber, G.A. A Matrix Handbook for Statisticians, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 427–462. [Google Scholar]
- He, Z.Q.; Liu, Q.H.; Jin, L.N.; Ouyang, S. Low complexity method for DOA estimation using array covariance matrix sparse representation. Electron. Lett. 2013, 49, 228–230. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Du, R.Y.; Liu, F.L.; Peng, L. W-L1-Sracv Algorithm for Direction-of-Arrival Estimation. Prog. Electromagn. Res. C 2013, 38, 165–176. [Google Scholar] [CrossRef]


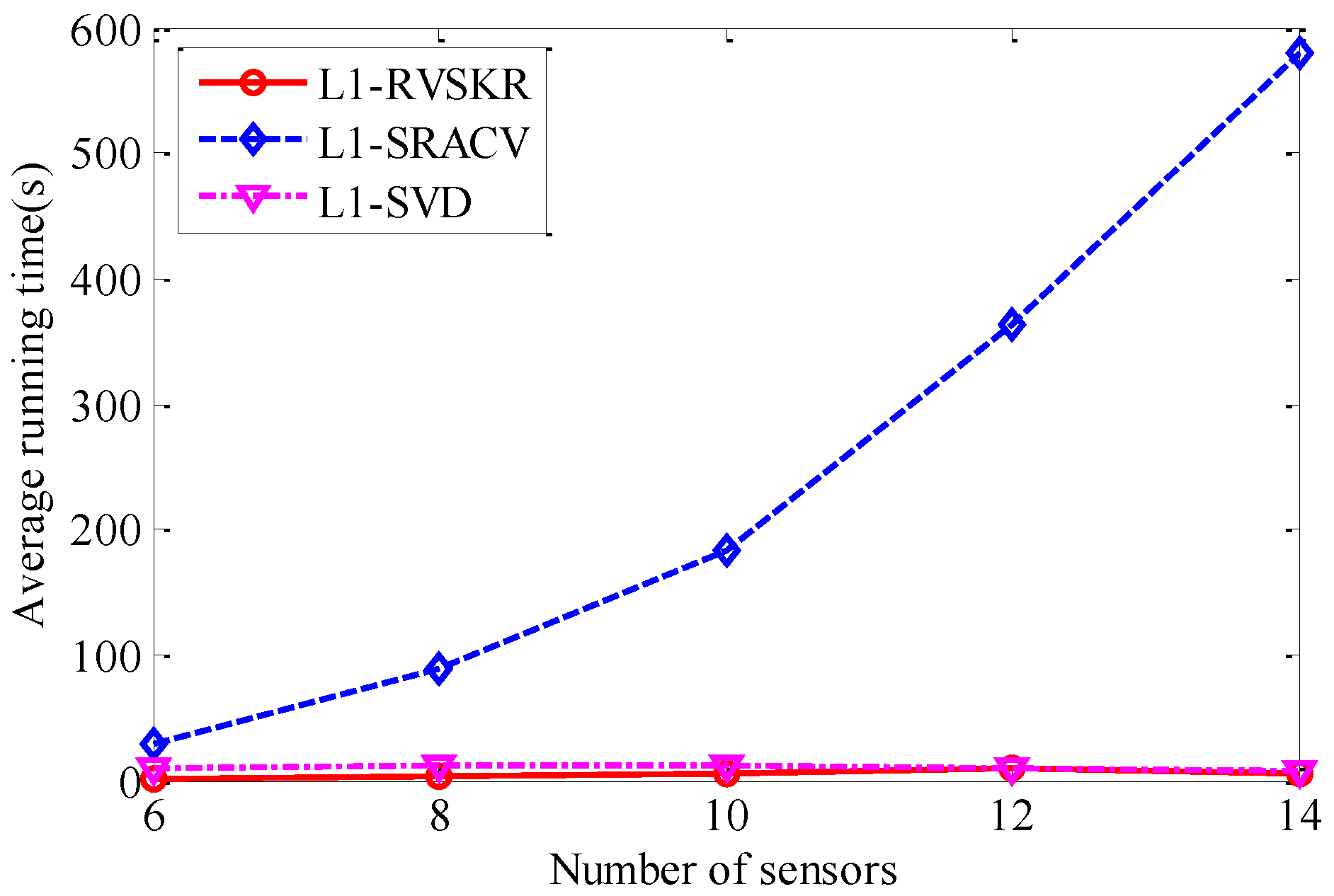
| Number of Sensors | L1-RVSKR | L1-SRACV | L1-SVD |
|---|---|---|---|
| 6 | 3.2773 s | 36.9106 s | 12.9263 s |
| 8 | 3.4291 s | 89.6315 s | 12.2859 s |
| 10 | 5.8132 s | 183.1054 s | 12.3405 s |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Wu, H.; Zhao, Z. The Real-Valued Sparse Direction of Arrival (DOA) Estimation Based on the Khatri-Rao Product. Sensors 2016, 16, 693. https://doi.org/10.3390/s16050693
Chen T, Wu H, Zhao Z. The Real-Valued Sparse Direction of Arrival (DOA) Estimation Based on the Khatri-Rao Product. Sensors. 2016; 16(5):693. https://doi.org/10.3390/s16050693
Chicago/Turabian StyleChen, Tao, Huanxin Wu, and Zhongkai Zhao. 2016. "The Real-Valued Sparse Direction of Arrival (DOA) Estimation Based on the Khatri-Rao Product" Sensors 16, no. 5: 693. https://doi.org/10.3390/s16050693
APA StyleChen, T., Wu, H., & Zhao, Z. (2016). The Real-Valued Sparse Direction of Arrival (DOA) Estimation Based on the Khatri-Rao Product. Sensors, 16(5), 693. https://doi.org/10.3390/s16050693






