The nonlinear dynamic model of the target with state
at time
k is given as follows,
where
is the state transition function, and
denotes the relationship between state and observation.
and
are the process and observation noises at time
and
k, respectively. Both
and
are assumed to be Gaussian noises with zero means, and their covariances are denoted as
and
. According to this model, the transition density
and likelihood
are subject to Gaussian distributions.
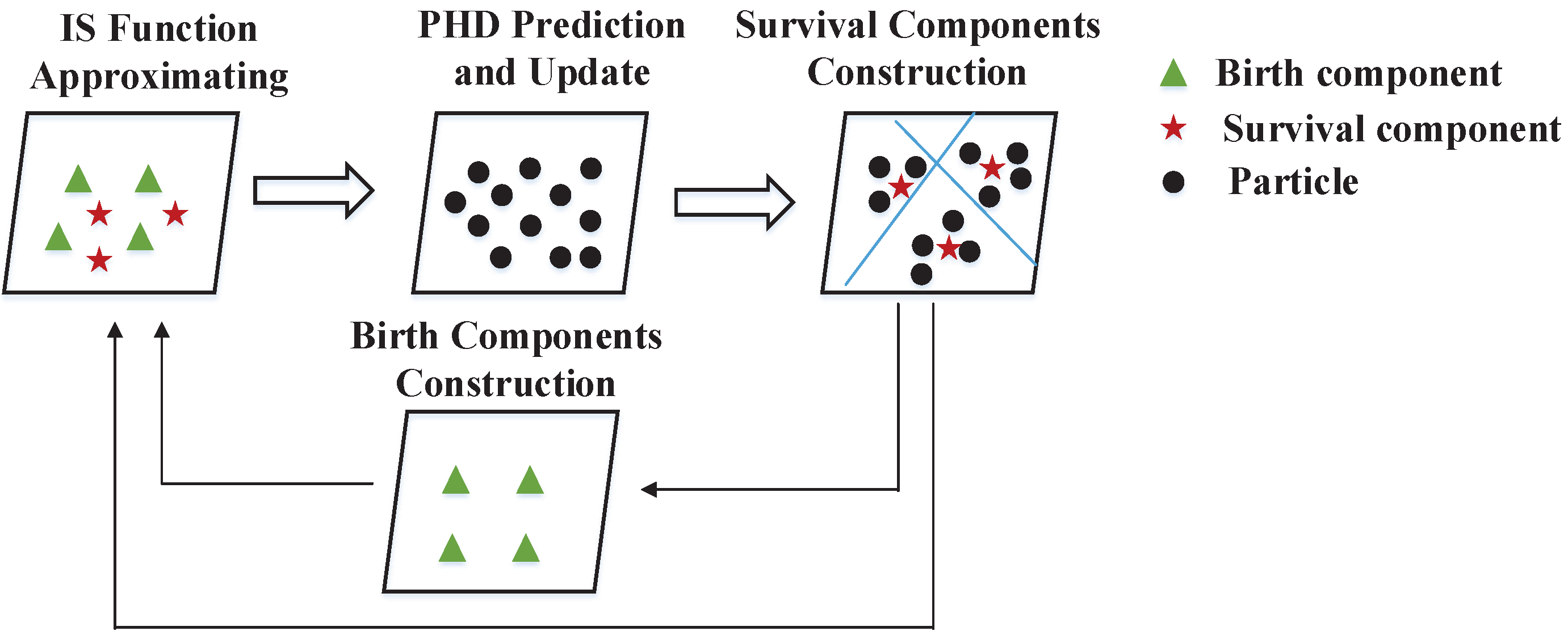
3.1. The IS Function Approximation Algorithm
As mentioned in
Section 2, most of the conventional SMC-PHD filters utilize the transition density function as the IS functions, resulting in great tracking error for targets with nonlinear dynamics. A novel IS function approximation algorithm, incorporating the CIF with a gating method, is presented to improve the tracking accuracy.
In our approach, we select the IS functions of Equations (3) and (4) as
where
and
are means of the survival and birth particles, respectively.
and
denotes the corresponding covariances of them.
Then, the problem of IS function design can be reduced to calculate and . Now, we discuss on how to calculate them. For simplicity, they are replaced by and , respectively. Here we use the CIF and gating methods to estimate them.
Before introducing the CIF method, we review the cubature rules [
27]. The cubature rules are used to approximate the Gaussian weight integral. Assuming
is a function on the n-dimension
, its Gaussian weight integral can be approximated by
where
and
is the
j-th vector of the set
According to Equation (12), the cubature rules can be used to compute the multi-dimension integrals in the prediction and update steps of the CIF method.
Prediction: In this step, we first predict the state and covariance according to cubature rules. Then, the predicted information state vector and matrix are estimated for the update step.
Let
and
be the previous state and covariance, respectively. According to Equations (12) and (13), the
j-th cubature point
can be estimated by
Then, we can calculate
and
using the following formulations:
where
is the transpose operator, and
Given Equations (15) and (16), the information forms of
and
are represented [
28] by
and
where
and
are the information state and matrix, respectively.
Update: We use the observation set to update the predicted and in the current step. In order to construct the associations between the observation set and predicted observation , a gating method is applied to extract the associated observations. With the extracted observations, we can finally obtain and covariance .
We denote
as the predicted observation, computed by
where
and
Utilizing the predicted observation
of Equation (20), the error cross covariance matrix of state and observation can be evaluated by
With the above obtained parameters, we can calculate the state contribution and its corresponding information matrix as
and
where
is the innovation of the
j-th observation
(
), expressed by
In our scenario, is a two-dimension vector, and follows a two-dimension Gaussian distribution.
In practice, the observation set may contain large clutters. The existence of these clutters cannot only degenerate the estimation accuracy, but also increase the computational complexity. Recently, several gating technologies have been proposed to remove the clutters from the observation set [
29,
30]. Inspired by [
30], we utilize the gating technology to reduce the influence of clutters.
Intuitively, observations far away from the predicted observation are subject to be generated by clutters. These observations must be removed from the observation set. With the gating technology, the left observations can be represented by
where
is the covariance matrix of the predicted observation
, and
is the matrix inversion.
is the threshold of the gate. According to Equation (27), the innovation
follows the Chi-square distribution. Thus,
can be determined by the dimension of
and association probability. Commonly, the square root of
is known as the number of Sigma. Literature [
30] proved that the number of Sigma gates ranging from 3 to 5 (corresponding to
) can guarantee the true observation lying inside the gate with “enough” probability (
), when the dimension of
is less than three. In this paper, we select the number of Sigma gates being to 4 (corresponding to
). When the dimension of
is less than three, such a selection guarantee that the association probability
.
Then, we concentrate on computing
of Equation (27). Let
be the cross covariance matrix between observation and state space. According to the linear error propagating of [
31],
can be rewritten as
where
is the linearized matrix.
Obviously,
can be approximated by
With the achieved
, according to [
32],
can be calculated by
Substituting the achieve into Equation (27), can be extracted from the current observation set .
With the extracted observation set
, the information state vector
and matrix
are represented as:
Given information state
and matrix
, posterior state
can be reconstructed based on Equation (18) :
Moreover, the posterior covariance
is recovered based on Equation (19):
If there is no observation that lies inside the gate (
), we approximate
and
in the following,
Substituting the above obtained and into Equations (10) and (11), we can approximate the IS functions of survival and birth targets for our CISMC-PHD approach.
3.2. The Birth Intensity Initialization Method
According to Equation (2), the birth intensity has large effect on the posterior intensity estimation. Targets may “born at anywhere” of the state space. In other words, birth intensity
may cover the whole state space, which is rather exhaustive [
25]. To avoid such a disadvantage, observation-driven birth intensity initiation methods were proposed [
20,
33,
34]. Inspired by these methods, an adaptive birth intensity initialization method is proposed for the CISMC-PHD approach. Instead of initializing birth intensity across the whole state space, the proposed method of CISMC-PHD approach utilizes the current observations and estimated targets to initialize the birth intensity at the next recursion. Compared with the conventional SMC-PHD filters, our method can initialize the birth intensity without knowing it as a prior.
The implementation of our method consists of two steps. First, in order to initialize the birth intensity, we remove observations generated by the estimated targets That is because the current survival targets cannot be new-born targets at the next recursion. Second, we use the remaining observations to estimate the birth target components, which can be used to calculate the birth intensity. With these two steps, the birth intensity can be initialized for the next recursion.
Step1. Remove observations generated by the estimated targets.
In the basic PHD filter, it is assumed that each target can yield at most one observation [
35]. According to this assumption, each target has one and only one corresponding observation. Influenced by the noises and clutters, the observation generated by the target may appear around the target. In other words, observations around the target has the large probability to be generated by the same target. Therefore, the birth target state set can be estimated by removing states of estimated targets from the multi-target state.
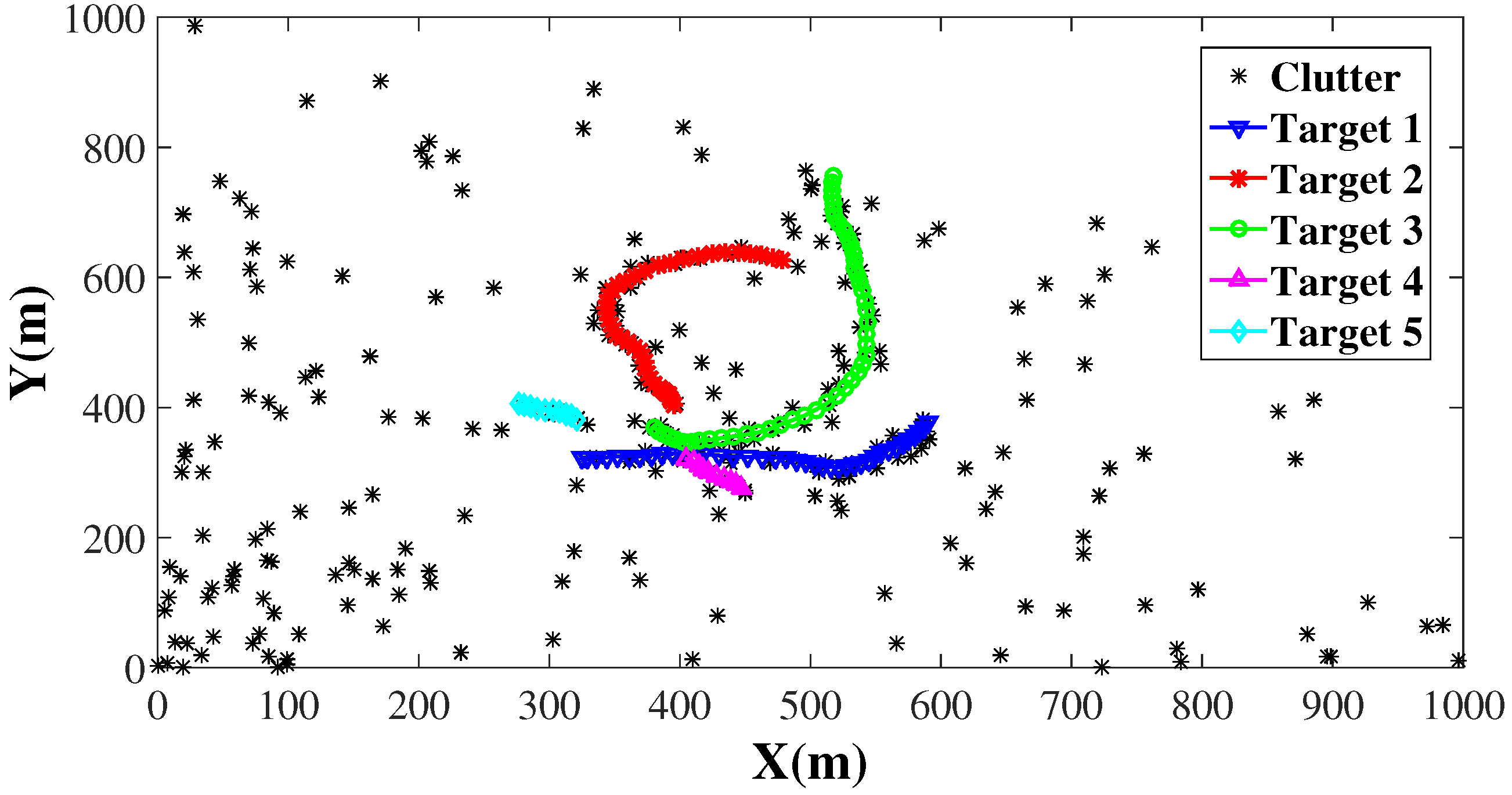
Here, we adopt the bearing and range tracking model [
36] to illustrate the birth intensity initialization method of our CISMC-PHD approach. Let
be the state of the
i-th target in the estimate state set
.
consists of position and velocity, while
(
) consists of the bearing angle and range. We define the distance between
and
(
) as
where
denotes the range-dimension element, and
is the absolution value.
We follow the way of [
30] to select the certain threshold for Equation (37),
where
is the error of the range-dimension (known as a prior).
l is the confidence level, commonly selected from
. Here, we use
, which can guarantee that the associated probability equals to 0.997.
With Equations (37) and (
38), we can remove the observations associated with the estimated targets. Let
be the observations of birth targets, the removing procedure is summarized in
Table 1.
Step2. Estimate the birth target components.
Once
is obtained, we turn to estimate the birth target components (the mean of the
i-th target state vector
and its corresponding covariance
) by the unbiased model of [
37].
Let
, we map
into state space denoted by
.
and
can be computed by
and
.
is a biased comparison factor, where
, as a prior, is the error of bearing angle
. According to [
37],
, the mean of the
i-th birth target state, can be estimated as
The covariance can be approximated by
where
, as a prior, is the standard deviation of velocity. In Equation (40), the following exists,
Finally, we can construct the new-born targets as
, where
is considered as the number of birth targets. We use Equation (11) to sample states of birth particles. The weights of these birth particles are initialized with the same values,
, where
N is the number particles for each target, and
is defined in
Section 2. On this basis, these birth particles become survival particles at time
. That is to say, the IS functions of these particles at time
can be computed by the method of
Section 3.1. Notice that the new-born target in this section may contain clutters, and these clutters can be removed in the resampling step of the CISMC-PHD approach.
The proposed initialization method may cause overestimation of targets. To overcome the issue of overestimation, some advanced methods, such as [
33,
34],
etc., may be incorporated for initialization of our approach. It is an interesting future work.
3.3. State Estimation
In multi-target tracking, it is rather important to estimate the target number and states. As for the state estimation, clustering methods, are commonly used in SMC-PHD filters [
16,
18]. However, they are subject to biased estimation [
21]. Ristic
et al. [
21] proposed an method that clusters the particles into several groups at the
update stage. In this paper, we intend to adopt the method of [
38] for state estimation, which is an improved method of [
21]. There are also several alternative methods, such as Zhao’s method [
39] and MEAP method [
40], which have better estimation performance.
According to Equation (6), the updated weight
of the
i-th particle consists of two parts,
In Equation (42),
denotes that there is no observation, and
can be computed by Equation (
7). For state estimation, we aggregate
of particle weights corresponding to observation
,
According to Equations (42) and (
43), if
is generated by the clutter, then the likelihood
may be small, leading to low value of
. However, if
is generated by the target, then
may be large due to the large value of
. Thus, setting certain threshold
for
, we can assign particles
that satisfy
to the
j-th target. In this paper, we set
, the same as [
21]. Then,
and
can be calculated in the following
Given Equations (44) and (45), the states of multi-target can be finally output. We summarize our approach at time
k in
Table 2.