Implementation Strategies for a Universal Acquisition and Tracking Channel Applied to Real GNSS Signals
Abstract
:1. Introduction
- A dual-component (AltBOC-ready) apparatus;
- An improved Dual Estimator code discriminator;
- A time-multiplexing code module;
- A secondary chip wipe-off (for longer coherent integration);
- A configurable sub-carriers and code clocks combination module derived from a single Numerically Controlled Oscillator (NCO) master clock and
- A sub-carrier time-multiplexing with weighted sub-carriers combination module.
1.1. Survey of GNSS Signals and Receiver Architectures
1.1.1. GNSS Signal Description
- is the reference chipping rate, i.e., 1.023 Mchip/s,
- is the current chipping rate, defined as,
- is the first sub-carrier rate, defined as and
- is the second sub-carrier rate, defined as ,
- is the second sub-carrier power ratio, i.e., ,
- is the second sub-carrier weight, in terms of an occurrence ratio, i.e., .
- is the detection probability (assumed at 0.995)
- is the false alarm probability, i.e., a false positive (assumed at 0.001)
- is the false alarm weight (assumed at 2)
- is the number of search cells (combining code with 0.5 chip resolution and ±5 kHz Doppler span)
- is the non-coherent integration count (assumed at 1)
- is the pre-integration time (assumed to match primary code period)
1.1.2. GNSS Signals Modulations
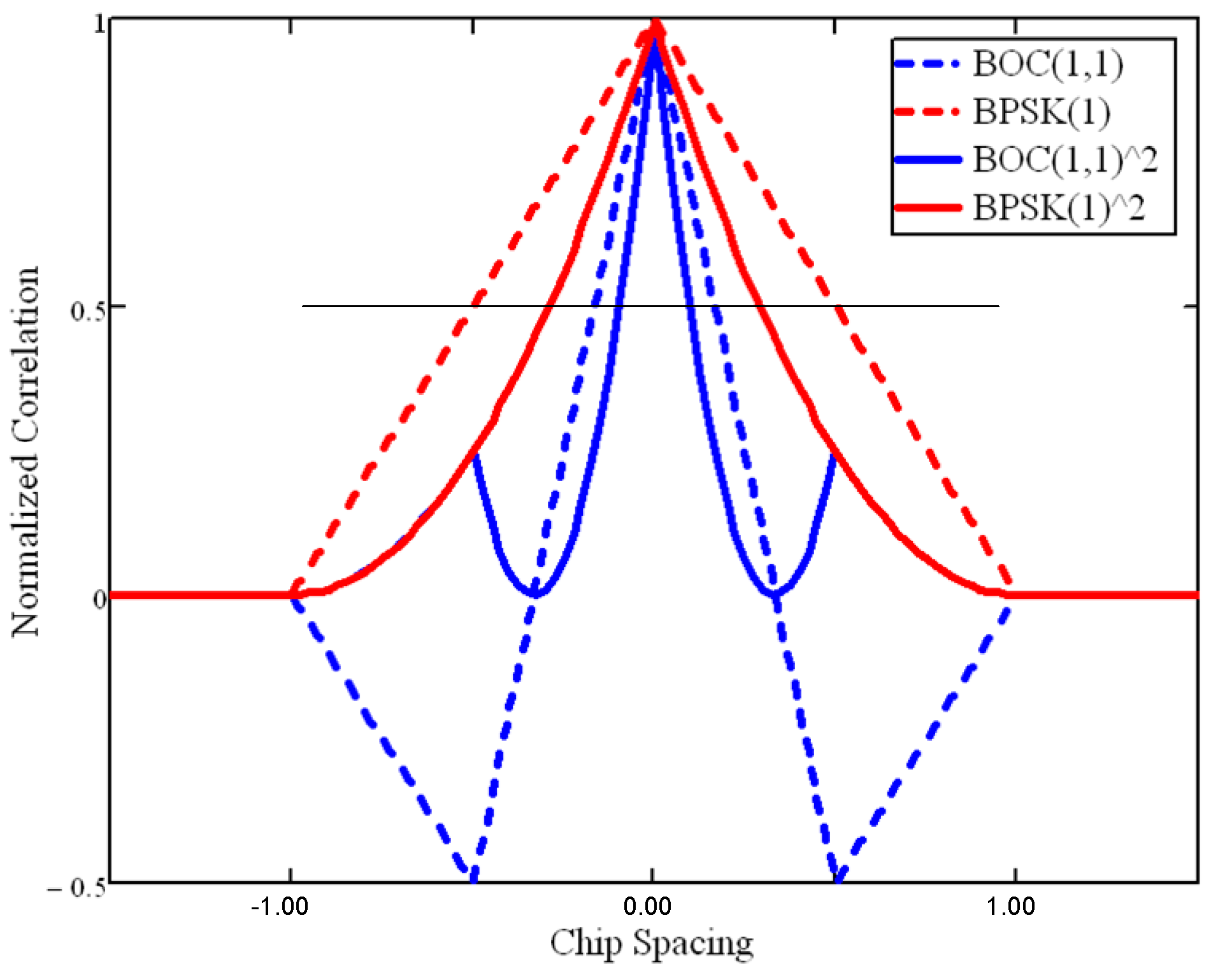
1.1.3. BOC-Ready Tracking Channels
2. Materials and Methods
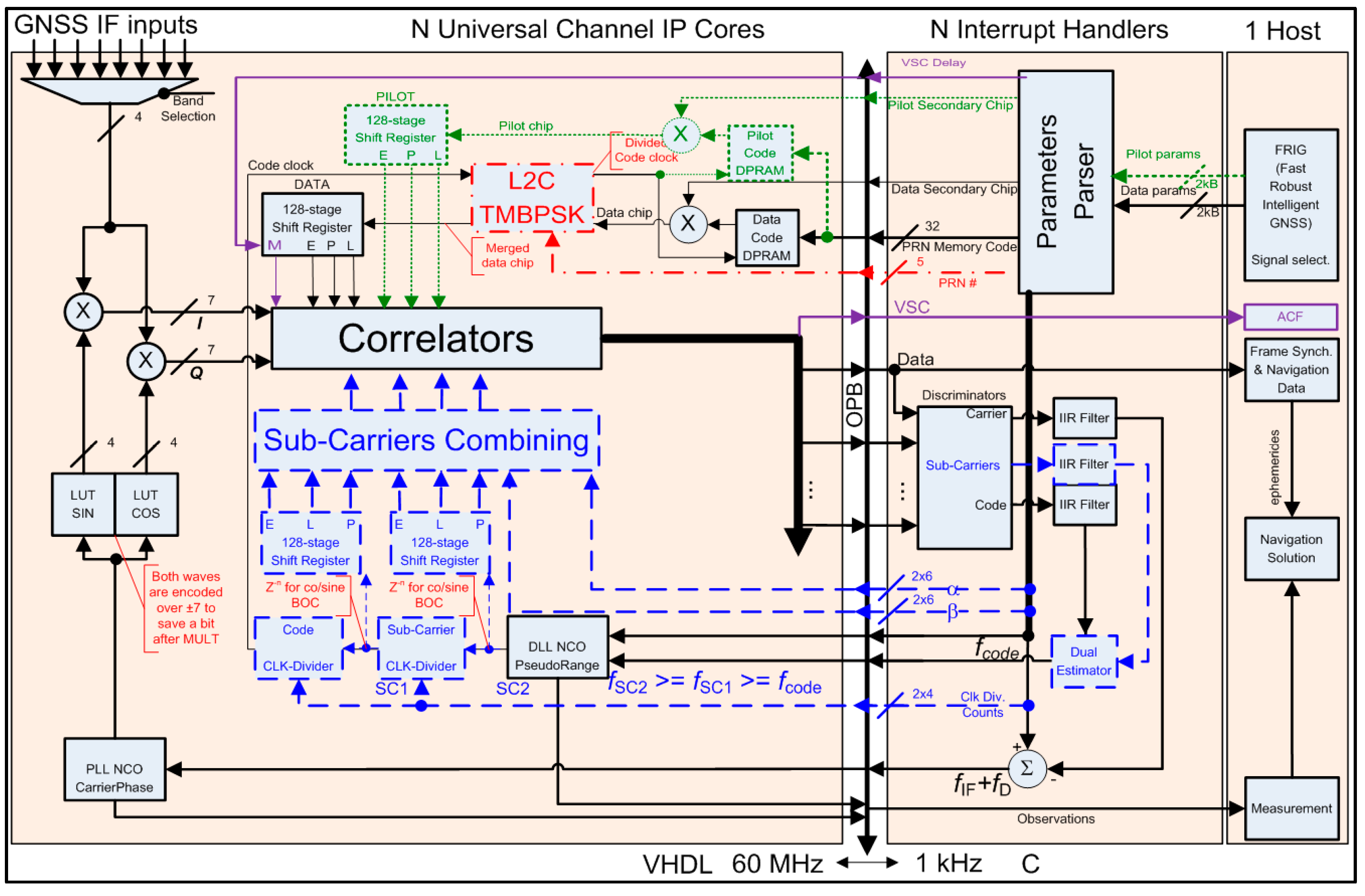
2.1. Universal GNSS Channel Design Decisions
- IF to Baseband Down-conversion and Carrier (including FDMA) Wipe-off module
- Sub-carriers and Spreading Codes Wipe-off module
- Spreading Codes (including Time Multiplexing) Generation module
- Correlation module
- Data & Pilot components merging
- Discriminator and Filters
2.1.1. Carrier
- Galileo E5B and Beidou B2-I (and eventually B2b) on 1207.14 MHz, as well as 1202.025 MHz for GLONASS L3 signals.
- Beidou B3 on 1268.52 MHz as well as Galileo (and QZSS) E6 signal on 1278.75 MHz:
- ○
- In order to preserve both signals bandwidth integrity, the RF front-end would take 1273,635 MHz down to IF. Assuming IF = 15 MHz, Beidou B3 would manage 20 MHz for its QPSK (10) signal as well as 10 MHz for the Galileo E6B/C BPSK (5) signals.
- ○
- This simplified approach could only process half of Galileo E6A BOC(10,5) and Beidou B3-Ad/Ap BOC(15,2.5) signals, considering the current 30 MHz bandwidth.
- Beidou B1-1 on 1561.098 and B1-2 on 1589.74 MHz around GPS L1 (and others) on 1575.42 MHz:
- ○
- An alternate approach would be to implement a 14.322 MHz sub-carrier, thus dealing with both Beidou signals as , just as with Galileo E1A , but with a slight sensitivity loss caused by superposing these two signals, each having their spreading code providing >20 dB isolation.
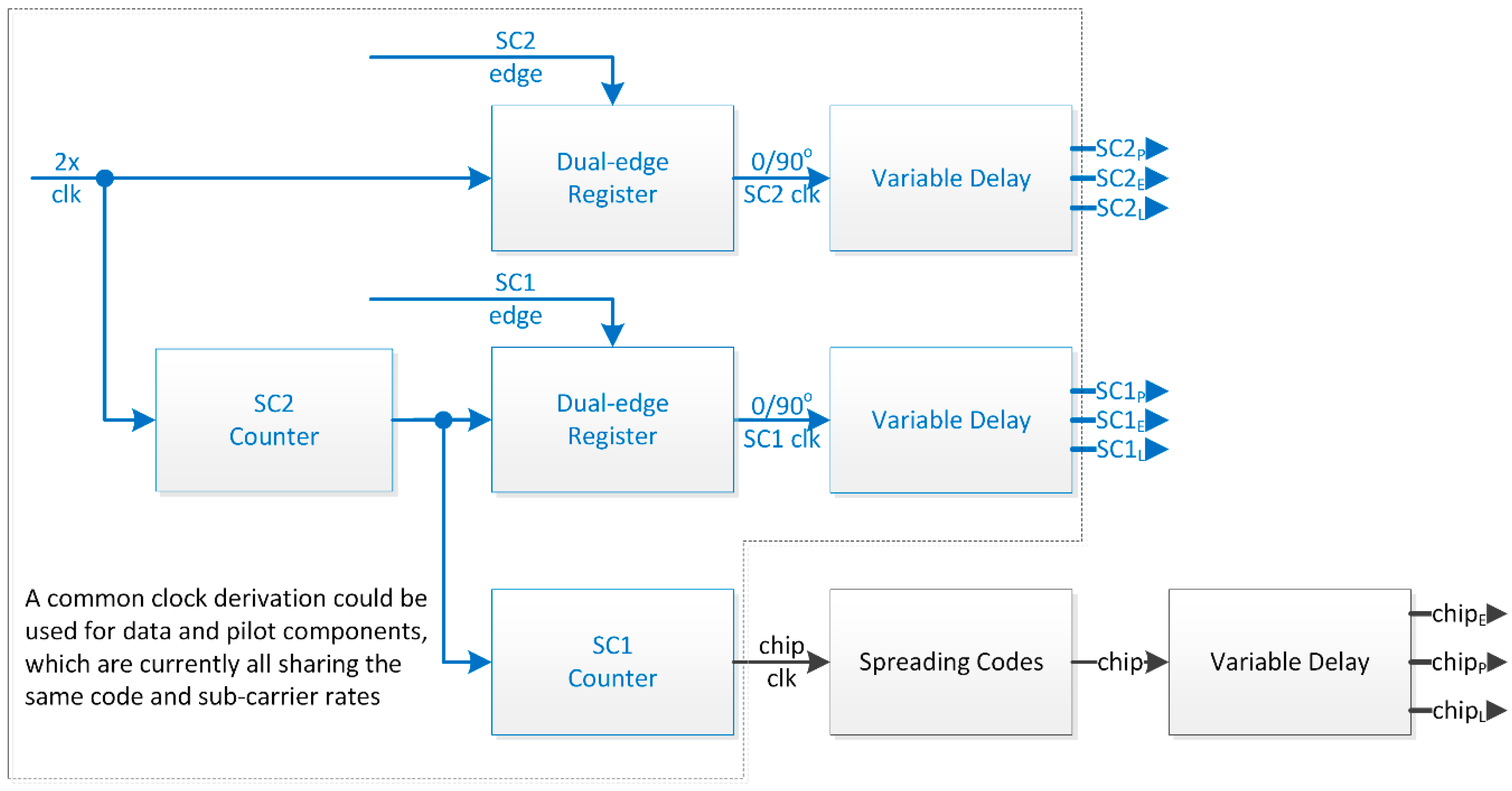
2.1.2. Sub-Carriers
- For each component, both 1-bit square sub-carriers are delayed to obtain Early (E), Prompt (P) and Late (L) replicas; the correlator spacing is set to with the fastest sub-carrier period .
- Prompt and Differential (D = E − L) are obtained on 2 bits for each sub-carrier.
- P & D replicas are scaled to their pre-defined constant weight through a mapping function or Look-Up Table (LUT).
- For each component, the two scaled sub-carriers are summed.
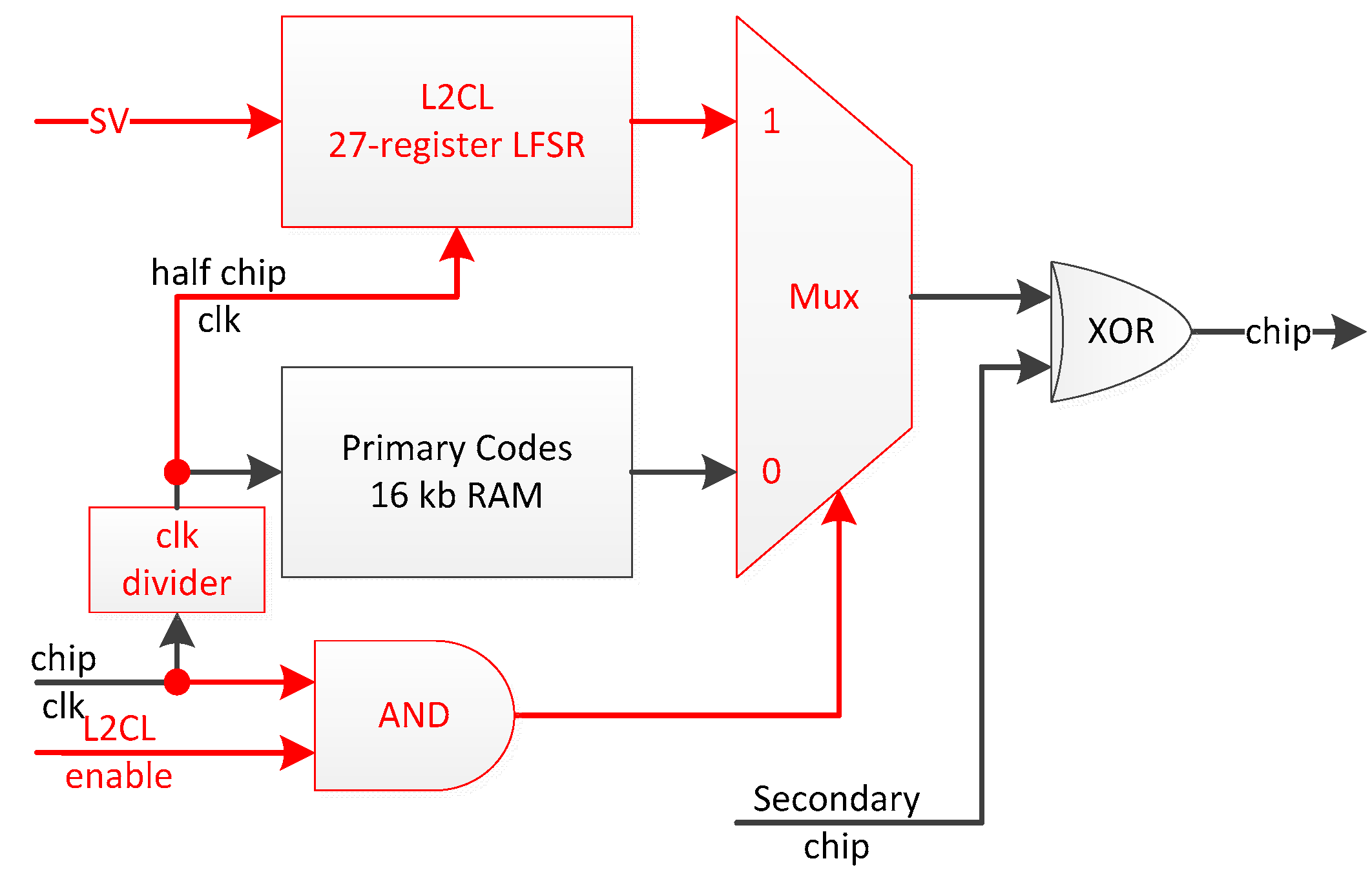
2.1.3. Spreading Codes
2.1.4. Correlation
- is the combined delay estimate;
- is the sub-carrier delay estimate;
- is the code delay estimate;
- is the sub-carrier half-period.
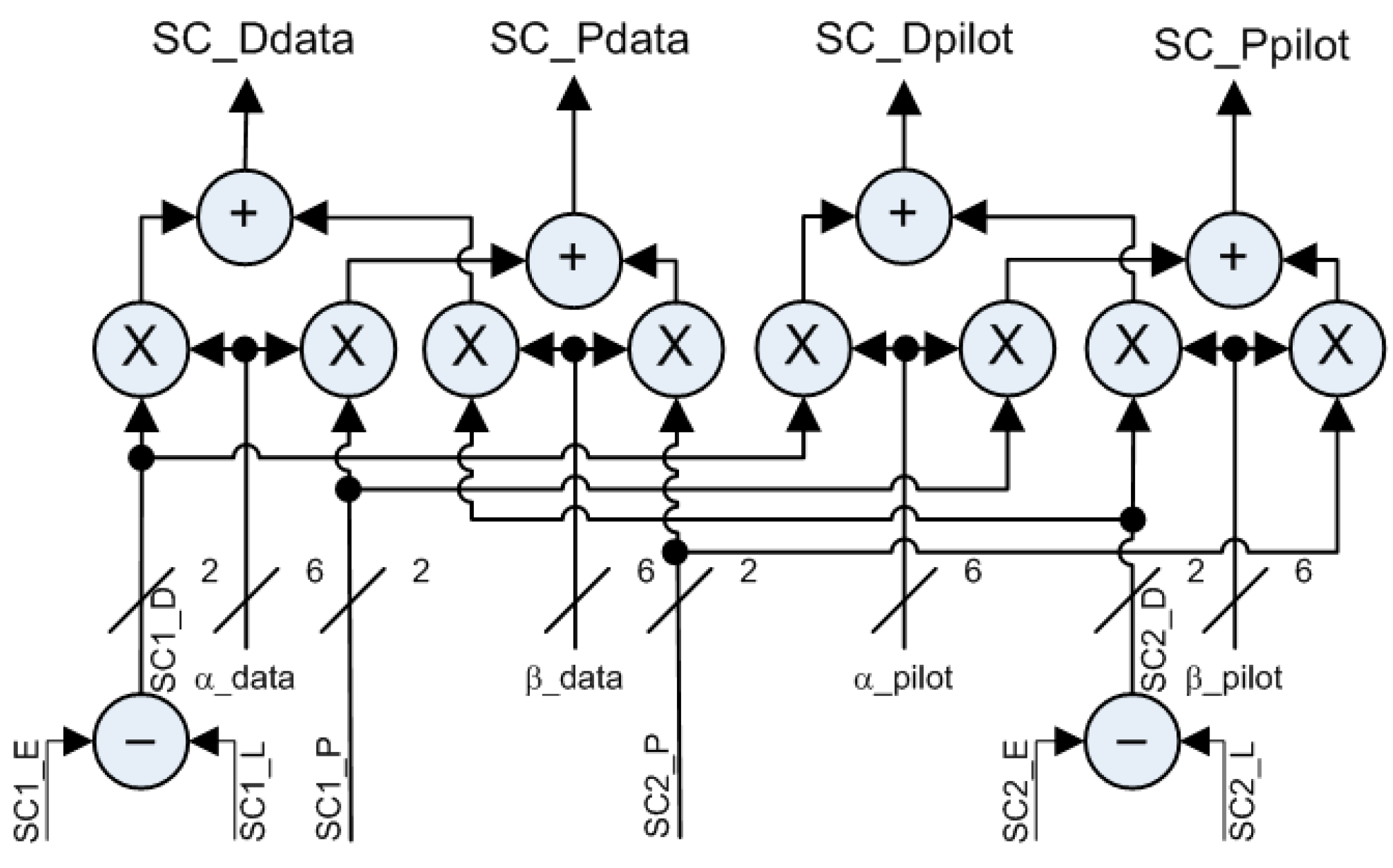
2.1.5. Data & Pilot Components Merging
- Memory codes address and control logic.
- Carrier and sub-carrier NCOs direct and derived clock signals.
- Sub-Carrier generation of Prompt (P) and Differential (D) shared by both signal components as the data and pilot chipping rates are always equal in the publically disclosed signals.
- Sine and cosine LUTs and carrier multipliers leading to the I and Q branches.
- 27-stage LFSR L2CL code generation implemented only once per dual component channel (i.e., implementing more than 32 universal channels would waste even more resources as there should not be more than 32 L2CL codes being broadcast by the current GPS constellation).
- Acquire and track the data component only, ignoring the pilot component available power.
- Acquire pilot component with a longer integration time for greater sensitivity and then transfer to data component tracking to extract the navigation message.
- Acquire and track both pilot and data components in independent channels.
- Dual-code delay search makes primary code acquisition two times faster and;
- Once synchronized onto the primary code, a dual secondary chip estimation (i.e., either the secondary chip changes or not) allows for an integration time over twice the primary code period by using the best of these two integration outputs.
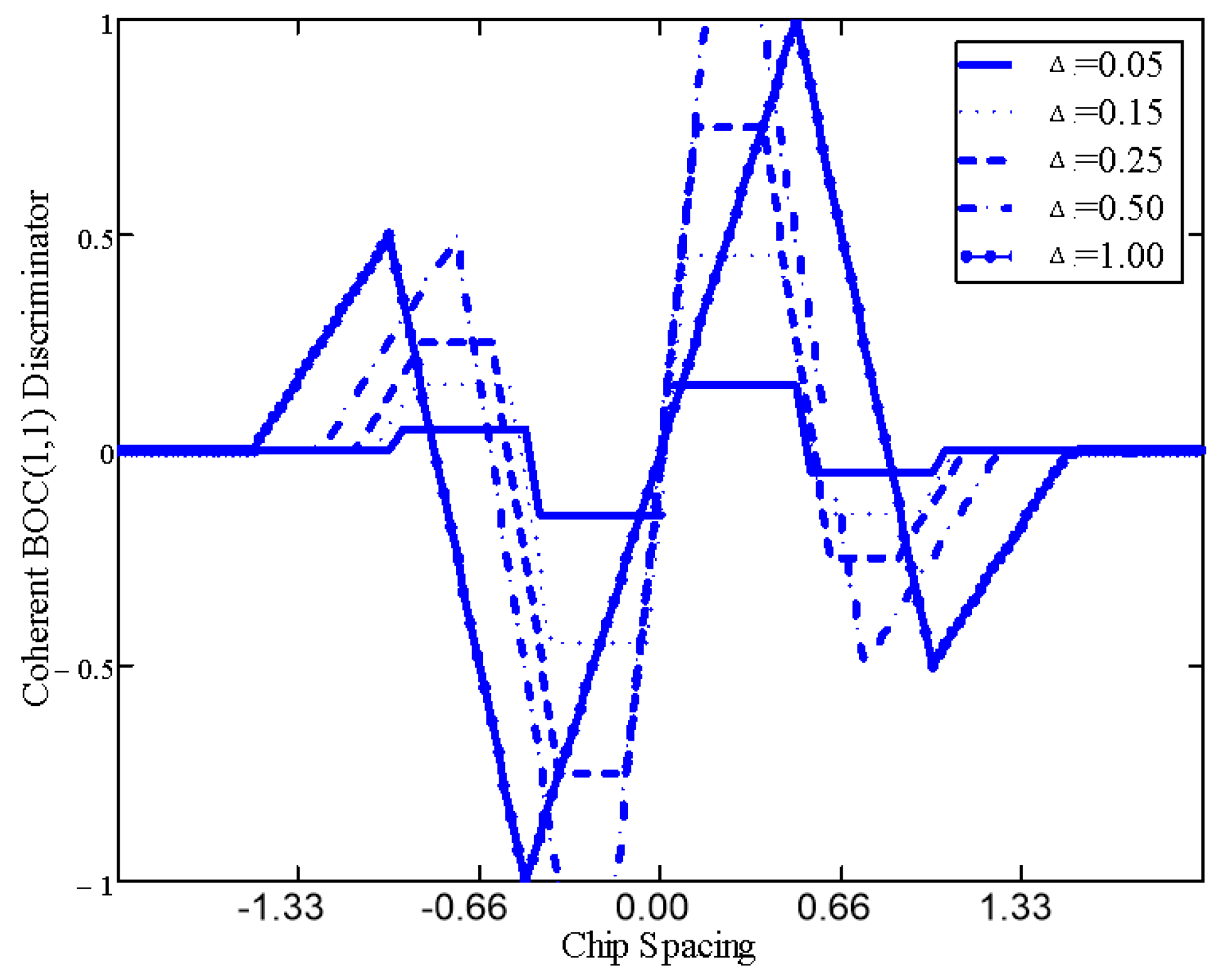
2.1.6. Discriminator and Filter
- is the speed of light (m/s);
- is the chip period, the inverse of the chipping rate ;
- is the unilateral noise equivalent bandwidth of the code tracking loop, a.k.a. one-sided equivalent rectangular bandwidth, with the time frame of interest ;
- is the pre-integration time (s);
- is the signal vs. replica misalignment (chip);
- is the early-late correlator spacing (chip), i.e, ;
- is the early to prompt and prompt to late correlator spacing (chip);
- is the Carrier power to Noise density ratio (dB-Hz);
- is the slope of the correlation function;
- is the normalized receiver front-end complex bandwidth ;
- is the ideal front-end complex bandwidth (with a brick-wall filter (Hz)).
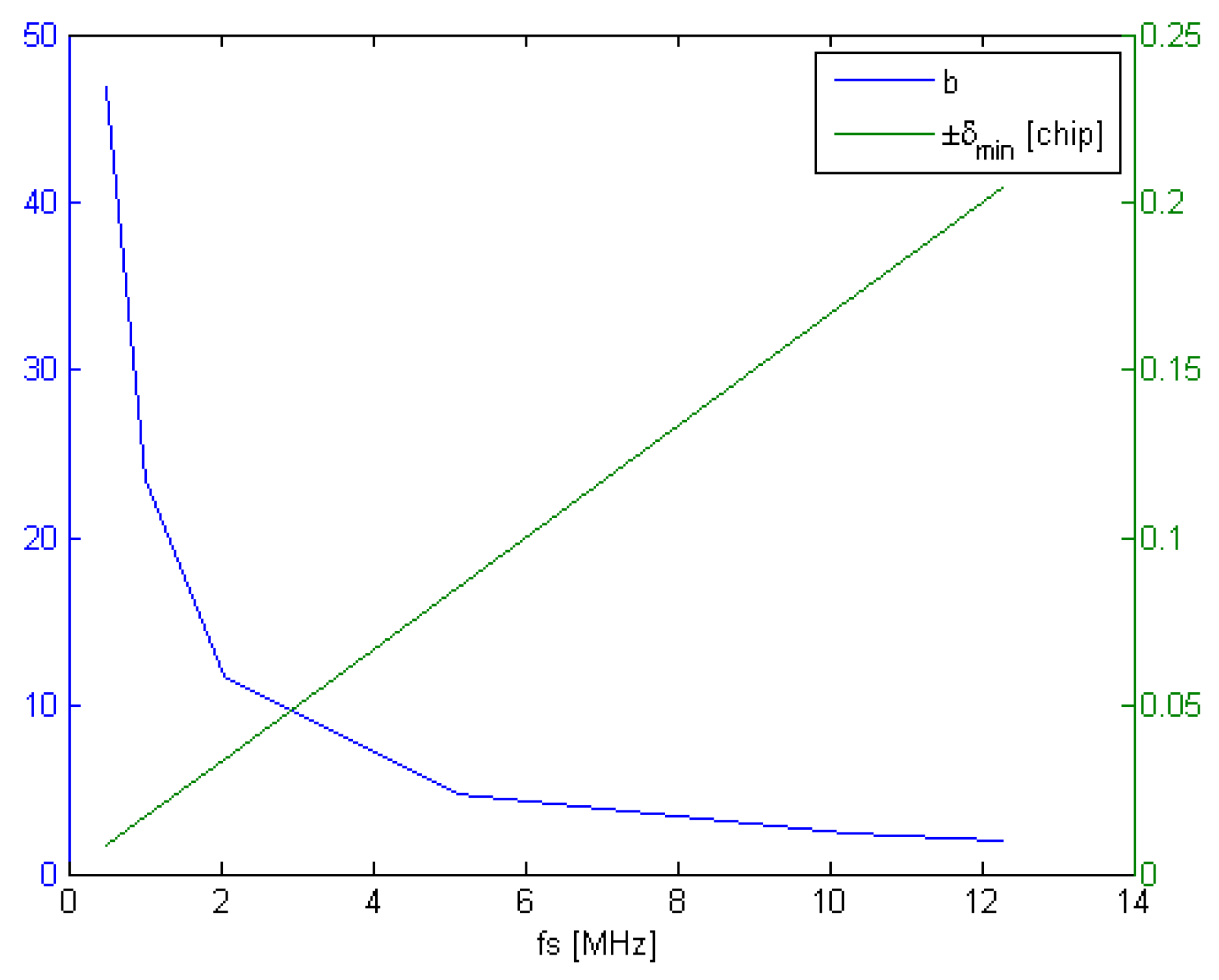
2.1.7. Power Consumption and Resource Usage
2.2. Universal GNSS Channel Validation
- red dotted and dashed lines for L2C TMBPSK of a L2CM memory code with a locally generated L2CL code,
- blue dashed lines for MBOC sub-carriers replicas generation and feedback,
- green dotted lines for dual-component overhead (extra correlators and sub-carriers combining not shown),
- purple solid lines for the optional Variable Spacing Correlator (VSC) used to plot Auto-Correlation Function (ACF) plots.
2.2.1. Constellation Compatibility
2.2.2. Frequency Bands Compatibility
2.2.3. Spreading Code Schemes Compatibility
2.2.4. Modulations Compatibility
2.2.5. GNSS Test Scenarios
Galileo E1 B&C
GPS L1C
GPS L2C
GPS L5
GLONASS L1OF
BeiDou B1-I
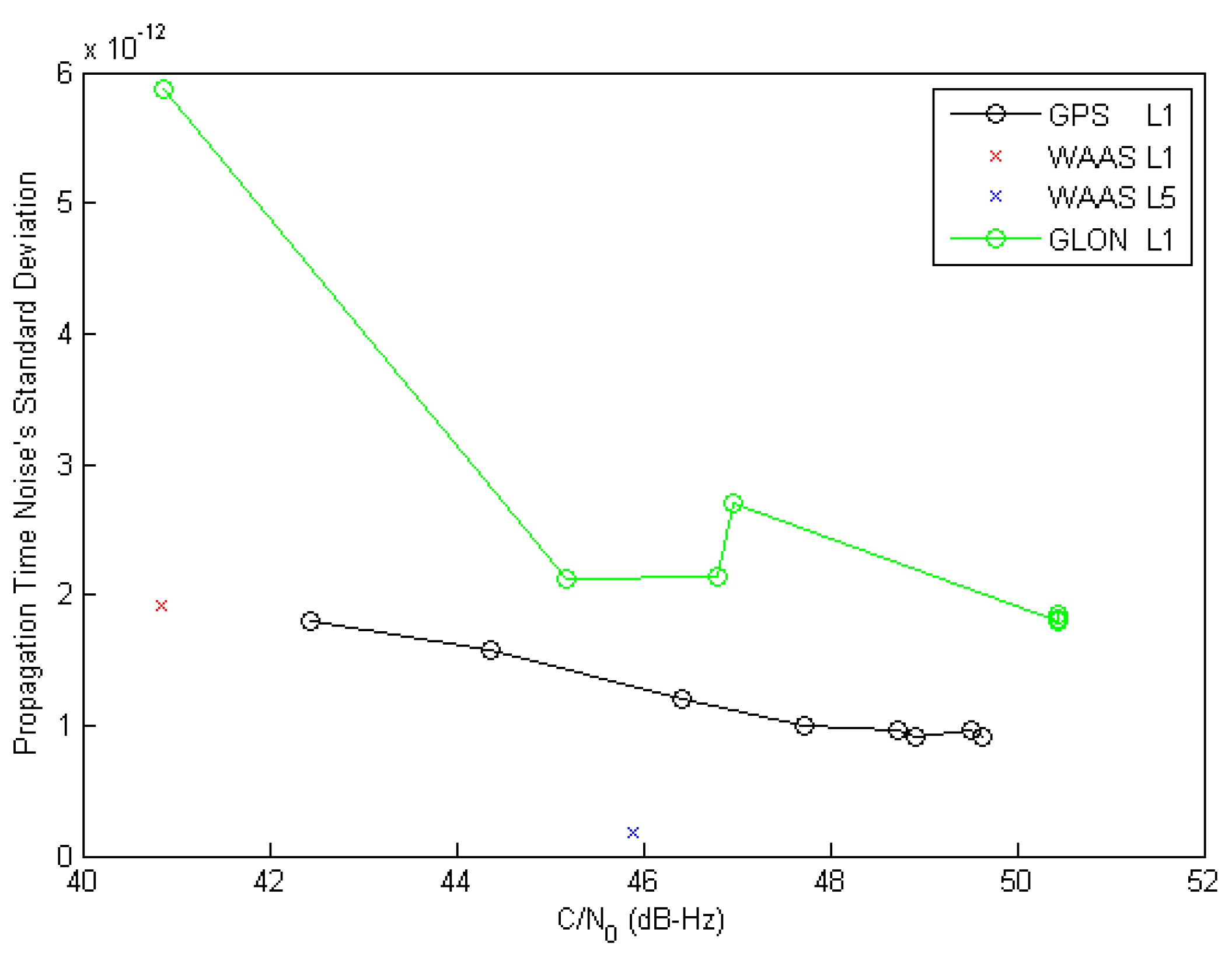
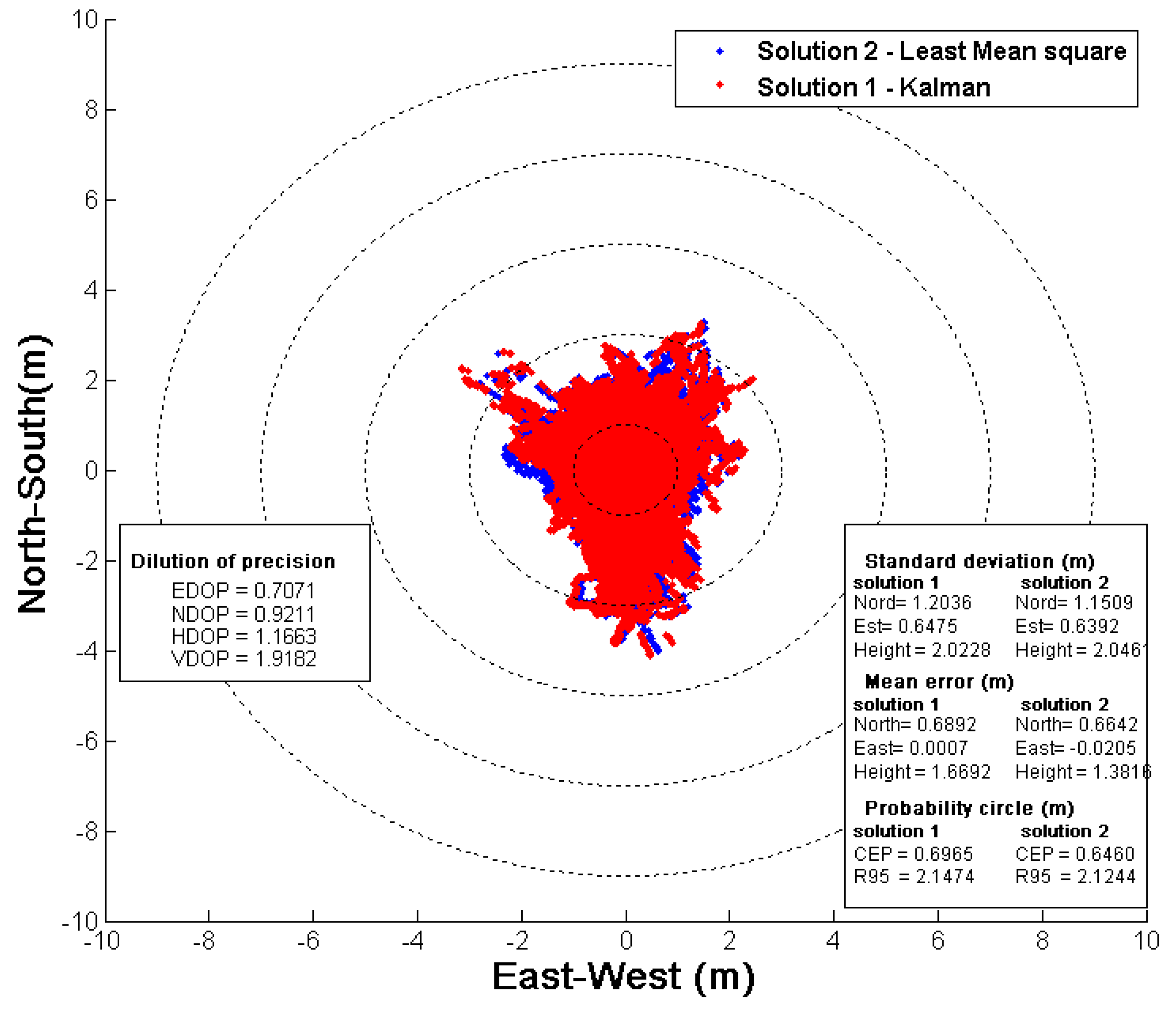
3. Results
- is the propagation time;
- is the number of complete code;
- is a complete code period;
- is the chip index of the primary code;
- is the phase of the chipping rate clock;
- is the chipping rate;
- is the pseudo-range noise.
4. Conclusions
Opening on Satellite Selection
Author Contributions
Conflicts of Interest
References
- U-blox AG. Standalone GNSS Chips. Available online: https://www.u-blox.com/en/gps-chips.html (assessed on 14 April 2014).
- Sheridan, J. Russia Sticks With Glonass Mandate. 2013. Available online: http://www.ainonline.com/aviation-news/aviation-international-news/2013-01-02/russia-sticks-glonass-mandate (assessed on 11 January 2015).
- Government Mandates Compass (Beidou) Navigation Devices on Certain Commercial Vehicles. 2013. Available online: http://www.chinaautoweb.com/2013/01/government-mandates-compass-beidou-navigation-devices-on-certain-commercial-vehicles/ (assessed on 22 May 2015).
- Hamilton, J. GPS World Receiver Survey. 2014. Available online: http://gpsworld.com/resources/gps-world-receiver-survey/ (assessed on 7 December 2014).
- Javad GNSS Inc. OEM Boards Compare. Available online: http://www.javad.com/jgnss/products/oem/compare.html (assessed on 13 Novembre 2014).
- Leveson, I. Benefits of the New GPS Civil Signal—The L2C Study. Insid. GNSS Mag. 2006, 1, 42–56. [Google Scholar]
- Thölert, S.; Erker, S.; Langley, R.; Montenbruck, O.; Meurer, M.; Temple, M.A.; Hauschild, A. A Preliminary Analysis of SVN49‘s Demonstration Signal. Available online: http://www.gpsworld.com/gnss-system/gps-modernization/innovation-l5-signal-first-light-8661 (accessed on 22 Februar 2010).
- Kaplan, E.D.; Hegarty, C. Understanding GPS Principles and Applications, 2nd ed.; Artech House: Boston, MA, USA, 2006. [Google Scholar]
- Julien, O.; Macabiau, C.; Cannon, M.E.; Lachapelle, G. ASPeCT: Unambiguous sine-BOC(n,n) acquisition/tracking technique for navigation applications. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 150–162. [Google Scholar] [CrossRef]
- European Union. European GNSS (Galileo) Open Service Signal In Space Interface Control Document; Galileo Joint Undertaking: Brussels, Belgium, 2010. [Google Scholar]
- ARINC Engineering Services. Navstar GPS Space Segment/User Segment L1C Interfaces; En ligne IS-GPS-800; ARINC Engineering Services: Panama City, FL, USA, 2006. [Google Scholar]
- Ries, L.; Lestarquit, L.; Armengou-Miret, E.; Legrand, F.; Vigneau, W.; Bourga, C.; Erhard, P.; Issler, J.L. A Software Simulation Tool for GNSS2 BOC Signals Analysis. In Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2002), Portland, OR, USA, 24–27 September 2002; pp. 2225–2239.
- Betz, J.W. Binary Offset Carrier Modulations for Radionavigation. J. Inst. Navig. 2001, 48, 227–246. [Google Scholar] [CrossRef]
- Morrissey, T.N.; Shallberg, K.W.; Townsend, B. Code tracking errors for double delta discriminators with narrow correlator spacings and bandlimited receivers. In Proceedings of the 2006 National Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 18–20 January 2006; pp. 914–926.
- Burian, A.; Lohan, E.S.; Renfors, M.K. Efficient delay tracking methods with sidelobes cancellation for BOC-modulated signals. Eurasip J. Wirel. Commun. Netw. 2007, 2007. [Google Scholar] [CrossRef]
- Sauriol, B. Mise en Oeuvre en Temps Réel d‘un Récepteur Hybride GPS-Galileo; École de Technologie Supérieurel: Montréale, QC, Canada, 2008. [Google Scholar]
- Heiries, V.; Roviras, D.; Ries, L.; Calmettes, V. Analysis of non ambiguous BOC signal acquisition performance. In Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2004), Long Beach, CA, USA, 21–24 September 2004; pp. 2611–2622.
- Martin, N.; Leblond, V.; Guillotel, G.; Heiries, V. BOC(x,y) Signal Acquisition Techniques and Performances. In Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2003; pp. 188–198.
- Fine, P.; Wilson, W. Tracking Algorithm for GPS Offset Carrier Signals. In Proceedings of the 1999 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 25–27 January 1999; pp. 671–676.
- Julien, O. Future GNSS Signal Processing I-II; GNSS Solutions Ltd: Fort Worth, TX, USA, 2007. [Google Scholar]
- Kim, S.; Yoon, S.; Kim, S.Y. A novel multipath mitigated side-peak cancellation scheme for BOC(kn, n) in GNSS. In Proceedings of the 9th International Conference on Advanced Communication Technology (ICACT 2007), Phoenix Park, Korea, 12–14 February 2007; pp. 1258–1262.
- Paonni, M.; Avila-Rodriguez, J.A.; Pany, T.; Hein, G.W.; Eissfeller, B. Looking for an Optimum S-Curve Shaping of the Different MBOC Implementations. Navigation 2008, 55, 255–266. [Google Scholar] [CrossRef]
- Avellone, G.; Frazzetto, M.; Messina, E. A new waveform family for secondary peaks rejection in code tracking discriminators for Galileo BOC(n,n) modulated signals. In Proceedings of the 2007 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 22–24 January 2007; pp. 246–251.
- Sousa, F.M.G.; Nunes, F.D.; Leitao, J.M.N. Code Correlation Reference Waveforms for Multipath Mitigation in MBOC GNSS Receivers. In Proceedings of the European Navigation Conference ENC-GNSS 2008, Toulouse, France, 23–25 April 2008; Volume 1, pp. 1–10.
- Hodgart, M.S.; Weiller, R.M.; Unwin, M. A Triple Estimating Receiver of Multiplexed Binary Offset Carrier (MBOC) Modulated Signals. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 877–886.
- Yang, C.; Miller, M. Novel GNSS receiver design based on satellite signal channel transfer function/impulse response. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 1103–1115.
- Miller, M.; Nguyen, T.; Yang, C. Symmetric Phase-Only Matched Filter (SPOMF) for frequency-domain software GNSS receivers. In Proceedings of the 2006 IEEE/ION Position, Location, And Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 187–197.
- Pany, T.; Eissfeller, B. Use of a vector delay lock loop receiver for GNSS signal power analysis in bad signal conditions. In Proceedings of the 2006 IEEE/ION Position, Location, And Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 893–903.
- Lashley, M.; Bevly, D.M. Analysis of Discriminator Based Vector Tracking Algorithms. In Proceedings of the 2007 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 22–24 January 2007; pp. 570–576.
- Macchi-Gernot, F.; Petovello, M.G.; Lachapelle, G. Combined Acquisition and Tracking Methods for GPS L1 C/A and L1C Signals. Int. J. Navig. Obs. 2010, 2010. [Google Scholar] [CrossRef]
- Fenton, P.C.; Jones, J. The theory and performance of NovAtel Inc.‘s Vision Correlator. In Proceedings of the 19 th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS-2006), Long Beach, CA, USA, 26–29 September 2006; pp. 2178–2186.
- Fortin, M.-A.; Guay, J.-C.; Landry, R.J. Development of a Universal GNSS Tracking Channel. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 259–272.
- Landry, R.J.; Fortin, M.-A.; Guay, J.-C. Universal Acquisition and Tracking Apparatus for Global Navigation Satellite System (GNSS). Canada Patent US 8401546 B2, 2010. [Google Scholar]
- Tsui, J.B.-Y. Fundamentals of Global Positioning System Receivers: A Software Approach, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- IP Processor Block RAM (BRAM) Block (v1.00a). 2011. Available online: http://www.xilinx.com/support/documentation/ip_documentation/bram_block.pdf (assessed on 3 March 2012).
- Mao, W.L.; Lin, W.H.; Tsao, H.W.; Chang, F.R.; Huang, W.H. Acquisition of GPS Software Receiver Using Split-Radix FFT. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 6, pp. 4608–4613.
- Hodgart, M.S.; Blunt, P.D.; Unwin, M. The optimal dual estimate solution for robust tracking of Binary Offset Carrier (BOC) modulation. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 1017–1027.
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Betz, J.W. Design and Performance of Code Tracking for the GPS M Code Signal. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 2140–2150.
- Betz, J.W.; Kolodziejski, K.R. Extended Theory of Early-Late Code Tracking for a Bandlimited GPS Receiver. J. Inst. Navig. 2000, 47, 211–226. [Google Scholar] [CrossRef]
- ARINC Engineering Services. Navstar GPS Space Segment/User Segment L5 Interfaces. In Interface Specification; Navstar GPS Joint Program Office: El Segundo, CA, USA, 2005.
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Signal Service; China Satellite Navigation Office: Beijing, China, 2013. [Google Scholar]
- Russian Institute of Space Device Engineering. GLONASS Interface Control Document Navigational radiosignal in Bands L1, L2; Russian Institute of Space Device Engineering: Moscow, Russia, 2008. [Google Scholar]
- Global Positioning System Wing (GPSW) Systems Engineering & Integration. Navstar GPS Space Segment/Navigation User Interfaces; Global Positioning System Wing (GPSW) Systems Engineering & Integration: El Segundo, CA, USA, 2012. [Google Scholar]
- Lockheed Martin Corporation. News Releases. 2012. Available online: http://www.lockheedmartin.com/us/news/press-releases/2012/january/0112_ss_gps.html (assessed on 28 June 2014).
- Kuon, I.; Rose, J. Measuring the gap between FPGAs and ASICs. IEEE Trans.Comput. Aided Des. Integr. Circuits Syst. 2007, 26, 203–215. [Google Scholar] [CrossRef]
- U-blox AG. UBX-G6010-ST Low-Cost u-blox 6 GPS Chip. 2011. Available online: http://u-blox.com/images/downloads/Product_Docs/UBX-G6010-ST_ProductSummary_%28GPS.G6-HW-09001%29.pdf (assessed on 2 August 2012).
- Julien, O.; Macabiau, C.; Issler, J.-L.; Nouvel, O.; Vigneau, W. Analysis and Quality Study of GNSS Monitoring Ground Stations‘ Pseudorange and Carrier-Phase Measurements. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 971–980.
- Guay, J.-C. Récepteur SBAS-GNSS Logiciel Pour des Applications Temps-Réel; École de Technologie Supérieure: Montréal, QC, Canada, 2010. [Google Scholar]
- Fortin, M.-A.; Guay, J.-C.; Landry, R., Jr. Single-Frequency WAAS L1 vs. L5 Augmenta-tion Observations on a Ground-Based GPS L1 C/A Solution. Positioning 2014, 5, 70–83. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Fortin, M.-A.; Landry, R.J. A Recursive Quasi-optimal Fast Satellite Selection Method for GNSS Receivers. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 2061–2071.




| System | # SV | Center Freq. (MHz) | Broadcast BW (MHz) | Signal Component | Modulation Type (fr = 1023 kHz) | Phase (°) | Gabor (MHz) | Code Length (chip) | Code Period (ms) | MTTA (s) | Symbol Rate (symbol/s) | Data ambiguity | Forward Error Correction | Earth Power (dBW) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Primary | Secondary | Primary | Secondary | Primary | Secondary | |||||||||||||
| GPS / WAAS | 32/24 + 3/3 | L1: 1575.42 | 24 | L1C/A | BPSK(1) | 90 | 2.046 | 1023 | 0 | 1 | 0 | 16 | 0 | 50 | 20 | none | −158.50 | |
| L1P(Y) | BPSK(10) | 0 | 20.460 | 6.187E+12 | 0 | 6.05E+08 | 0 | 3.4E+28 | 0 | 50 | 0 | none | −161.50 | |||||
| L1M | sBOC(10,5) | 90 | 30.690 | undisclosed | undisclosed | FEC(½) | −158.00 | |||||||||||
| L1C-I | sBOC(1,1) | 0 | 4.092 | 10,230 | 0 | 10 | 0 | 15634 | 0 | 100 | 1 | BCH/LDPC (½) | −163.00 | |||||
| L1C-Q | TMsBOC(6,1,4/33) | 0 | 14.322 | 10,230 | 1800 | 10 | 18000 | 15634 | 4.427E+09 | --- | --- | --- | −158.25 | |||||
| WAAS-L1 | BPSK(1) | 90 | 2.046 | 1023 | 0 | 1 | 0 | 16 | 0 | 500 | 2 | 171o; +133o | −161.00 | |||||
| L2: 1227.60 | 24 | L2CM | BPSK(½) | TMBPSK (½,½) | 90 | 2.046 | 10,230 | 0 | 20 | 0 | 62328 | 0 | 50 | 1 | 171o; +133o | −160.00 | ||
| L2CL | BPSK(½) | 90 | 767,250 | 0 | 1500 | 0 | 2.6E+10 | 0 | --- | --- | --- | |||||||
| L2P(Y) | BPSK(10) | 0 | 20.460 | 6.187E+12 | 0 | 6.05E+08 | 0 | 3E+28 | 0 | 50 | 0 | none | −161.50 | |||||
| L2M | sBOC(10,5) | 90 | 30.690 | undisclosed | undisclosed | FEC(½) | −158.00 | |||||||||||
| L5: 1176.45 | 24 | L5-I | QPSK(10) | 0 | 20.460 | 10,230 | 10 | 1 | 10 | 155 | 8 | 100 | 1 | 171o; +133o | −157.90 | |||
| L5-Q | 90 | 20.460 | 10,230 | 20 | 1 | 20 | 155 | 61 | --- | --- | --- | −157.90 | ||||||
| WAAS-L5 | BPSK(10) | 0 | 20.460 | 10,230 | 0 | 1 | 0 | 155 | 0 | 500 | 1 | 171o; +133o | −154.00 | |||||
| Galileo / EGNOS | (2+4+2)/30 + 3/3 | L1: 1575.42 | 40.92 | E1B | CsBOC(6,1,1/11,+) | 0 | 14.322 | 4092 | 0 | 4 | 0 | 1010 | 0 | 250 | 1 | 171o; −133o | −160.00 | |
| E1C | CsBOC(6,1,1/11,−) | 180 | 14.322 | 4092 | 25 | 4 | 100 | 1010 | 1899 | --- | --- | --- | −160.00 | |||||
| EGNOS | BPSK(1) | 90 | 2.046 | 1023 | 0 | 1 | 0 | 16 | 0 | 500 | 2 | 171o; +133o | −161.00 | |||||
| E1A | cBOC(15,2.5) | 35.805 | undisclosed | undisclosed | 100 | |||||||||||||
| E6: 1278.75 | 40.92 | E6A | cBOC(10,5) | 30.690 | undisclosed | undisclosed | 100 | |||||||||||
| E6B | BPSK(5) | 0 | 10.230 | 5115 | 0 | 1 | 0 | 78 | 0 | 1000 | 1 | 171o; −133o | −158.00 | |||||
| E6C | BPSK(5) | 180 | 10.230 | 5115 | 100 | 1 | 100 | 78 | 7596 | --- | --- | --- | −158.00 | |||||
| E5a:1176.45 | 20.46 | E5a-I | QPSK(10) | AltBOC(15,10) | 0 | 20.460 | 10,230 | 20 | 1 | 20 | 155 | 61 | 50 | 1 | 171o; −133o | −158.00 | ||
| E5a-Q | 90 | 20.460 | 10,230 | 100 | 1 | 100 | 155 | 7596 | --- | --- | --- | −158.00 | ||||||
| E5: 1191.795 | 92.07 | 8-PSK | 51.150 | 0 | 0 | −152.00 | ||||||||||||
| E5b:1207.14 | 20.46 | E5b-I | QPSK(10) | 0 | 20.460 | 10,230 | 4 | 1 | 4 | 155 | 0 | 250 | 1 | 171o; −133o | −158.00 | |||
| E5b-Q | 90 | 20.460 | 10,230 | 100 | 1 | 100 | 155 | 7596 | --- | --- | --- | −158.00 | ||||||
| GLONASS / SDCM | 28/24 + 2/3 | L1g: 1602.00 | 17.5275 | L1OF | BPSK(~½) - FDMA | 90 | 8.335 | 511 | 0 | 1 | 0 | 8 | 0 | 100 | 10 | none | −161.00 | |
| L1SF | BPSK(~5) - FDMA | 0 | 17.533 | undisclosed | 50 | |||||||||||||
| L1: 1575.42 | L1OC | BOC(n,n) | 0 | undisclosed | ||||||||||||||
| L1SC | undisclosed | |||||||||||||||||
| SDCM | undisclosed | −158.00 | ||||||||||||||||
| L2g: 1246.00 | 15.9075 | L2OF | BPSK(~½) - FDMA | 90 | 6.710 | 511 | 0 | 1 | 0 | 8 | 0 | 100 | 10 | none | −167.00 | |||
| L2SF | BPSK(~5) - FDMA | 0 | 15.908 | undisclosed | 250 | |||||||||||||
| L2: 1227.60 | L2OC | 13.683 | undisclosed | |||||||||||||||
| L2SC | 13.683 | undisclosed | ||||||||||||||||
| L3: 1202.025 | L3OC-D | QPSK(x) | 0 | 20.460 | 10,230 | 5 | 1 | 5 | 155 | 1 | 200 | 1 | 171o; +133o | |||||
| L3OC-P | 90 | 20.460 | 10,230 | 10 | 1 | 10 | 155 | 8 | --- | --- | ||||||||
| L3: 1208.088 | L3SC | 0 | 0 | |||||||||||||||
| L5: 1176.45 | L5OC | 0 | 16.368 | undisclosed | ||||||||||||||
| BeiDou / SNAS | (5/27 + 5/3 + 6/5) + 1/3 | B1-1: 1561.098 | 4.092 | B1-I: C/A | QPSK(2) | AltBOC(14,2) | 0 | 2.046 | 2046 | 20 | 1 | 20 | 31 | 61 | 50 | 1 | −163.00 | |
| B1-Q: military | 90 | 2.046 | >400 | |||||||||||||||
| L1: 1575.42 | 2.046 | 2046 | 0 | 1 | 0 | 31 | 0 | 500 | 2 | −163.00 | ||||||||
| B1-2: 1589.74 | 4.092 | B1-2: military | QPSK(2) | 0 | 2.046 | filed at ITU, although nothing is being broadcast | ||||||||||||
| 90 | 2.046 | |||||||||||||||||
| E5b:1207.14 | 20.46 | B2-I: C/A | BPSK(2) | 0 | 2.046 | 2046 | 20 | 1 | 20 | 31 | 61 | 50 | 1 | |||||
| B2-Q: military | BPSK(10) | 20.460 | >160 | |||||||||||||||
| B3: 1268.52 | 20.46 | B3-I: C/A | QPSK(10) | 0 | 20.460 | 10,230 | 20 | 1 | 20 | 155 | 61 | 50 | 1 | |||||
| B3-Q: military | 90 | 20.460 | >160 | |||||||||||||||
| L1: 1575.42 | B1-Cd | MBOC(6,1,1/11) | 14.322 | OS | 100 | ½ | ||||||||||||
| B1-Cp | --- | |||||||||||||||||
| B1d | sBOC(14,2) | 32.736 | AS | 100 | ½ | |||||||||||||
| B1p | --- | |||||||||||||||||
| B2: 1191.795 | B2ad | QPSK(10) | AltBOC(15,10) | 0 | 20.460 | 50 | ½ | |||||||||||
| B2ap | 90 | 20.460 | --- | |||||||||||||||
| 8-PSK | 51.150 | OS | ||||||||||||||||
| B2bd | QPSK(10) | 0 | 20.460 | 100 | ½ | |||||||||||||
| B2bp | 90 | 20.460 | --- | |||||||||||||||
| B3: 1268.52 | B3 | QPSK(10) | 0 | 20.460 | AS | 500 | none | |||||||||||
| 90 | ||||||||||||||||||
| B3-Ad | sBOC(15,2.5) | 35.805 | AS | 100 | ½ | |||||||||||||
| B3-Ap | sBOC(15,2.5) | --- | ||||||||||||||||
| Category | Main Methods | Approach |
|---|---|---|
| Narrow Correlators | Double-Delta (DD) [14]; High Resolution Correlator (HRC) [15]; BOC universel [16] | Narrow tracking once aligned with the main peak of the correlation curve. Weak performances in presence of noise and multipath. A complex combination of absolute values of correlators approaches the BPSK triangular ACF shape during initial alignment. |
| Single Lobe (~BPSK) | Single Side Lobe (SSL) [17]; Dual Sideband (DS) [18] | Independently process main lobe(s), achieving BPSK-like correlation curve. |
| Extra-Correlators | Bump and Jump (BJ) aka Very Early Very Late (VE-VL) [19] | Extra correlators allow monitoring secondary peaks of the correlation curve. Their location depends on the targeted modulation scheme. |
| Replica Spreading Code Combination | Time-Multiplexed BOC(6,1) (TM61(a)) [20]; Shaping Correlator Receiver (SCR) [21]; S-Curve Shaping [22]; Code Composite Ranging Waveform (CCRW) [23]; Strobe Correlator [24]; Autocorrelation Side-Peak Cancellation Technique (ASPeCT) [9] | Minimize secondary peaks of the correlation curve by combining different spreading codes into the local replicate signal. Despite good multipath performances, these approaches suffer from higher noise levels as they are not based on the Maximum Likelihood “Matched Filter”-like Correlator, targeting the Cramer-Rao lower bound. Furthermore, S-Curve Shaping would require a minimum sampling frequency reaching 200 MHz to track MBOC signals. ASPeCT only applies to BOC(p,p). |
| Extra-Loops | Sub Carrier Phase Cancellation (SCPC) [17]; Triple-Loop Dual-Estimator (TLDE) [25] | Tracking of sub-carrier on top of carrier and code, avoiding periodic signal integer uncertainty. |
| Frequency Response | Channel Transfer Function H(f) [26]; Symmetric Phase-Only Matched Filter (SPOMF) [27] | Frequency-domain analysis is more flexible and precise, no matter what the signal modulation is; at the extra cost (e.g., hardware resources) of direct and inverse Fourier transforms. |
| Loop filters | A shared Extended Kalman Filter (EKF) is used to compute the channels feedback [28,29]. VDLL could also be considered to distinguish main peak from secondary ones by eliminating solutions with larger positioning residues. EKF can also be used as individual tracking channel loop filter [30] | Vectorial DLL (VDLL) allows for inter-channel assistance, minimizing satellite loss and reacquisition occurrences by replacing independent loop filters by integrated EKF. Was successfully applied to BPSK tracking. Independent Extended Kalman Filtering (EKF) could also be used to compute the loop feedback in every channel. Both approaches could be adapted to BOC. |
| Time-Domain Analysis | Vision correlator [31] | Extra complex integrator measurements are taken at slightly different time offsets in order to assess the chip transition in the time-domain. This method could be applied to sub-carrier transitions as well. |
| Signal assistance | Combined Signals [30] | GPS L1 C/A combined with GPS L1C for enhanced tracking |
| Resources in xc4vsx55-10ff1148 | Available | BPSK w/FDMA | L2C | BOC | Single MBOC | Dual MBOC | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dynamic Power (mW) | 25.1 | 100% | 25.1 | 100% | 29.6 | 118% | 33.4 | 133% | 41.8 | 166% | |
| Quiescent Power (mW) | 860 | 100% | 860 | 100% | 860 | 100% | 861 | 100% | 861 | 100% | |
| Total Power (mW) | 885 | 100% | 885 | 100% | 890 | 101% | 894 | 101% | 903 | 102% | |
| Slices | 24576 | 651 | 2.6% | 765 | 3.1% | 943 | 3.8% | 1018 | 4.1% | 1410 | 5.7% |
| Slice Flip Flops | 49152 | 775 | 1.6% | 918 | 1.9% | 1118 | 2.3% | 1186 | 2.4% | 1476 | 3.0% |
| 4 input LUTs | 49152 | 908 | 1.8% | 1127 | 2.3% | 1456 | 3.0% | 1554 | 3.2% | 2123 | 4.3% |
| as logic | 894 | 1113 | 1436 | 1528 | 2091 | ||||||
| as shift registers | 14 | 14 | 20 | 26 | 32 | ||||||
| FIFO16/RAMB16s | 320 | 2 | 0.6% | 2 | 0.6% | 2 | 0.6% | 3 | 0.9% | 4 | 1.3% |
| DSP48s | 512 | 11 | 2.1% | 11 | 2.1% | 17 | 3.3% | 17 | 3.3% | 29 | 5.7% |
| Max. number of single channels | 37 | 32 | 26 | 24 | 17 | ||||||
| Max. number of dual channels | 18 | 16 | 13 | 12 | 17 | ||||||
| GNSS | RF (MHz) | Signal | Primary Code | Modulation | ± (Chip) | Particularity | |
|---|---|---|---|---|---|---|---|
| 1 | GPS | 1575.42 | L1C | 10 ms; 10,230 chips | I: sBOC(1,1); Q: TM-sBOC (6, 1, 4/33) | 0.48→0.05; 0.48→0.05 | L1 band; GPS; MBOC |
| 2 | GPS | 1227.60 | L2C | L2CM: 20 ms; 10,230 chips; L2CL: 1.5 s; 767,250 chips | TMBPSK (½, ½, ½) | 0.24→0.05; off→same as L2CM | L2 band; LFSR logic; TMBPSK |
| 3 | GPS | 1176.45 | L5 | 1 ms; 10,230 chips | QPSK (10) | 0.50→0.17; 0.50→0.17 | L5 band; QPSK; Code rate |
| 4 | Galileo | 1575.42 | E1 B&C | 4 ms; 4092 chips | CsBOC (6, 1, 1/11, ±) | 0.48→0.05; 0.48→0.05 | Galileo; MBOC; Code period |
| 5 | GLONASS | 1602.00 | L1OF | 1 ms; 511 chips | BPSK(~½) | 0.26→0.05 | Δ RF in L1; GLONASS; FDMA |
| 6 | BeiDou | 1561.098 | B1-I | 1 ms; 2046 chips | BPSK(2) | 0.48→0.03 | Δ RF in L1; BeiDou; Code length |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fortin, M.-A.; Landry, R., Jr. Implementation Strategies for a Universal Acquisition and Tracking Channel Applied to Real GNSS Signals. Sensors 2016, 16, 624. https://doi.org/10.3390/s16050624
Fortin M-A, Landry R Jr. Implementation Strategies for a Universal Acquisition and Tracking Channel Applied to Real GNSS Signals. Sensors. 2016; 16(5):624. https://doi.org/10.3390/s16050624
Chicago/Turabian StyleFortin, Marc-Antoine, and René Landry, Jr. 2016. "Implementation Strategies for a Universal Acquisition and Tracking Channel Applied to Real GNSS Signals" Sensors 16, no. 5: 624. https://doi.org/10.3390/s16050624
APA StyleFortin, M.-A., & Landry, R., Jr. (2016). Implementation Strategies for a Universal Acquisition and Tracking Channel Applied to Real GNSS Signals. Sensors, 16(5), 624. https://doi.org/10.3390/s16050624





