1. Introduction
Industrial safety inspection has recently received considerable attention in the academic community and technology companies. The accurate three-dimensional (3D) measurement provides important information on monitoring workplaces for industrial safety. Numerous techniques on 3D measurement have been studied, including Stereo-vision, Time-of-Flight, and structured light technique. Among these techniques, the phase-shifting digital fringe projection is widely recognized and studied due to its high resolution, high speed, and noncontact property [
1,
2]. In a fringe projection vision system, the projector projects light patterns with a sinusoidally changing intensity onto the detected objects, and the pattern images are deformed because of the objects
physical profile; then, a camera captures the deformed pattern images. The absolute phase map on the detected objects is derived by the phase unwrapping of the captured deformed fringe patterns. The 3D information is uniquely extracted on the basis of the mapping relationship between the image coordinates and the corresponding absolute phase value. Considering the digital projector has a large working range, the fringe projection technique can be used on large scene reconstruction for industrial safety inspection.
In contrast to the polynomial fitting method [
3,
4] and least-squares method [
5,
6,
7], the phase-to-depth transformation based on the geometrical modeling method [
8,
9,
10,
11,
12,
13] has been widely studied and used in the phase-shifting structured light technique owing to several advantages. First, no additional gauge block or precise linear z stage is needed for calibration, which simplifies the calibration process and offers more flexibility and a cost savings. Second, there can be no restriction on the camera’s and projector’s relative alignment regarding parallelism and perpendicularity. Third, it has a clear and explanatory mathematical expression for the phase to 3D coordinates transformation since it is derived from the triangulation relationship of the camera, projector, and detected object.
Although it has the advantages mentioned above, the given mathematical expression does not have sufficient accuracy because the adopted simplified geometrical model ignores the lens distortion and lens defocus of the fringe projection system. On the other hand, there are some other error sources that exist in the vision system that influence the accuracy of the 3D measurement. As a result, a large amount of work has been devoted to improving the measurement accuracy by considering the lens distortion [
5,
14], the gamma nonlinearity for phase error elimination [
15,
16], the high-order harmonics for phase extraction [
17], the ambient light for phase error compensation [
18],
etc.
The extended mathematical model proposed in this paper eliminates the uncertainty in the calibration parameters and the uncertainty in the phase extraction. In addition, it will not incur any computational burden during normal computation of the phase to depth transformation. It avoids the time-consuming iterative operation and exhibits more precision.
Experiments are carried out for a single object and multiple spatially discontinuous objects with the proposed flexible fringe projection vision system by the extended mathematical model. For spatially isolated objects, the fringe orders will be ambiguous for the phase unwrapping, which makes it difficult to retrieve the absolute phase directly for three-step phase-shifting technique. As a result, the depth difference between spatially isolated surfaces is indiscernible. Therefore, in order to obtain an accurate 3D measurement of multiple discontinuous objects, several approaches are developed to derive an accurate absolute phase map. The gray-coding plus phase-shifting technique is one of the better methods to obtain the fringe order [
19]. However, at least several more patterns are required to generate the appropriate number of codewords, which slows down the computational timing. In addition, Su [
20] generated sinusoidal fringe patterns by giving every period a certain color, and the fringe order was provided by the color information of the fringe patterns. However, the phase accuracy might be influenced by the poor color response and color crosstalk. Wang
et al. [
21] presented a phase-coding method. Instead of encoding the codeword into binary intensity images, the codeword is embedded into the phase range of phase-shifted fringe images. This technique has the advantages of less sensitivity to the surface contrast, ambient light, and camera noise. However, three more frames are necessary for the phase-coding method. In this research, in order to realize the accurate 3D measurement of multiple discontinuous objects with the abovementioned extended mathematical model, we propose a new phase-coding method to obtain the absolute phase map by only adding one additional fringe pattern.
The structure of this paper is as follows.
Section 2 reviews the principles for obtaining the 3D coordinates from the absolute phase.
Section 3 introduces the mathematical model extension with least-squares parameter estimation.
Section 4 presents the realization of the flexible fringe projection vision system for the accurate 3D measurement of a single continuous object by the extended mathematical model.
Section 5 introduces the new phase-coding method for deriving an accurate absolute phase map for spatially isolated objects. Finally, the conclusions and the plans for future work are summarized.
2. Principle on Absolute Phase to 3D Coordinates Transformation
The geometrical model of the proposed fringe projection measurement system is shown in
Figure 1. The camera and the projector are all described by a pinhole model. The camera imaging plane and the projection plane are arbitrarily arranged. The reference plane
is an imaginary plane, which is parallel to the projection plane. The projector coordinate system is denoted as
. The camera coordinate system is denoted as
. The imagined reference plane coordinate system is denoted as
denotes.
P represents an arbitrary point on the detected object.
,
,
denote the imaginary reference coordinate, the camera coordinate and the projector coordinate of the point
P, respectively. The imaging point of the point
P is indicated as the point
C. The point
D indicates the fringe point which projects at the point
P in space. The points A and B denote the lens center of the camera and the projector, respectively. Line
is one of the sinusoidal fringes which is parallel to
- axis. Line
is vertical to Line
. Line
is parallel to
Z-axis and crosses the imaginary reference plane at point
.
is the extension line of ray
and crosses the imaginary reference plane at point
.
and
are parallel to
X-axis and cross the
Y-axis at point
and
, respectively. The mathematical description of the phase to 3D coordinates transformation [
22] is as follows:
where
,
, and
. Furthermore, the coordinates
at the given pixel
are obtained by the calculated depth
as follows:
By solving Equations (1)–(3), the , , and coordinates for each point of the detected object in space are obtained from the absolute phase φ.
is the absolute phase of the center of the circle at Point B.
is principal point of the camera plane.
and
are the scale factors in the image plane along the
and
axes.
is principal point of the projector plane.
is the scale factor in the projector plane along the
x and
y axes.
and
are the rotation and translation matrixes from the projector coordinate system to the camera coordinate system. They are expressed as:
5. Experiments with Multiple Discontinuous Objects
In phase-shifted fringe projection technique, three sinusoidal fringe patterns are projected onto the object surface with phase shifts of 0,
, and
in this study. The corresponding intensity distributions are as follows:
where
is the average intensity,
is the intensity modulation, and
is the phase to be solved. By solving the above equations, the phase at each point
of the image plane is obtained as follows:
By solving Equation (10), the obtained phase is a relative value between
and
. A spatial phase-unwrapping algorithm can be used to remove the 2
π discontinuities. The obtained absolute phase is
where
is the fringe order.
Nevertheless, for spatially isolated objects, the fringe orders will be ambiguous. It is difficult to retrieve the absolute phase directly. As a result, the depth difference between spatially isolated surfaces is indiscernible. In order to reliably obtain the absolute phase map, a new phase-coding method is proposed that takes full advantage of the frequency characteristic of the sinusoidal fringe pattern.
Figure 11 shows the designed fringe pattern. It consists of the codewords that give the fringe order information of
k.
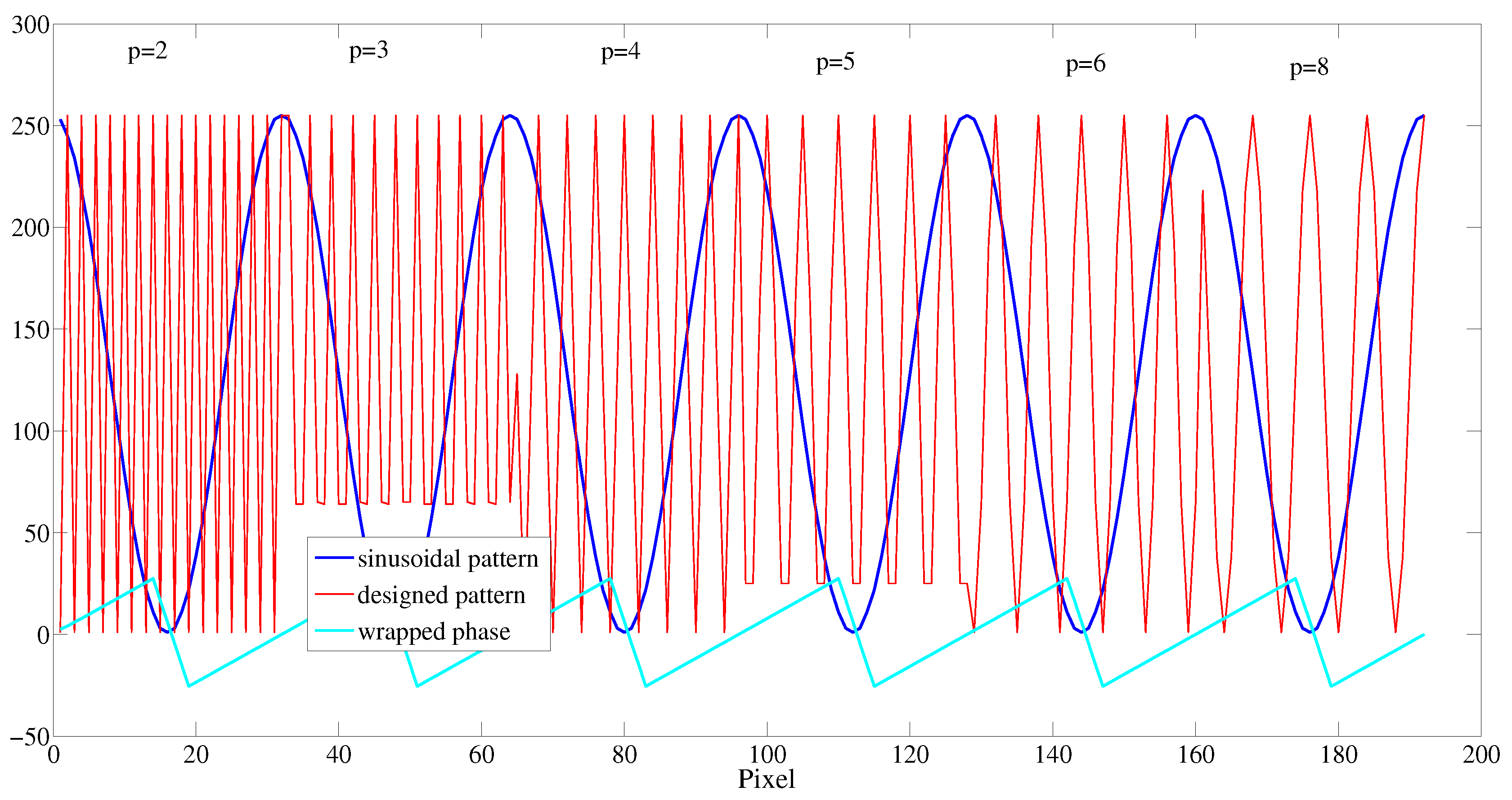
Figure 12 illustrates the relationship among the sinusoidal fringe pattern with a phase shift of zero, the wrapped phase with a relative value between
and
, and the codewords of the designed pattern. It should be mentioned that the retrieved wrapped phase is ten times the actual value in order to observe the relationship with the codewords of the designed pattern clearly. The period of the sinusoidal fringe pattern
is set to 32 pixels in this study.
is the regional period of the designed codewords. Each codeword consists of a sequence of sinusoidal fringe patterns, and the codewords change from period to period according to the
phase-change period.
equals 2, 3, 4, 5, 6, and 8 pixels separately, as shown in
Figure 12. The designed pattern shown in
Figure 11 is formed by repeating the codewords
. In addition, when in the system calibration, the projector projects the design pattern to the calibration board, and the camera captures the design pattern. The obtained design pattern is recognized as the template design pattern. It can be used for partition to the detected area to avoid the phase codewords aliasing effect. With the design pattern as shown in
Figure 11, there are three partitions at most in the practical application.
From the plot of the codewords of the designed pattern, we know that the frequency component of the codewords changes from high to low. An analysis of the sinusoidal fringe pattern of the designed codewords was carried out for the ideal projected patterns and captured patterns. The results are listed in
Table 1. It can be seen that the frequency components for various codewords do not exhibit aliasing. The fringe order
k in Equation (11) can be reliably obtained on the basis of a frequency analysis of the codewords.
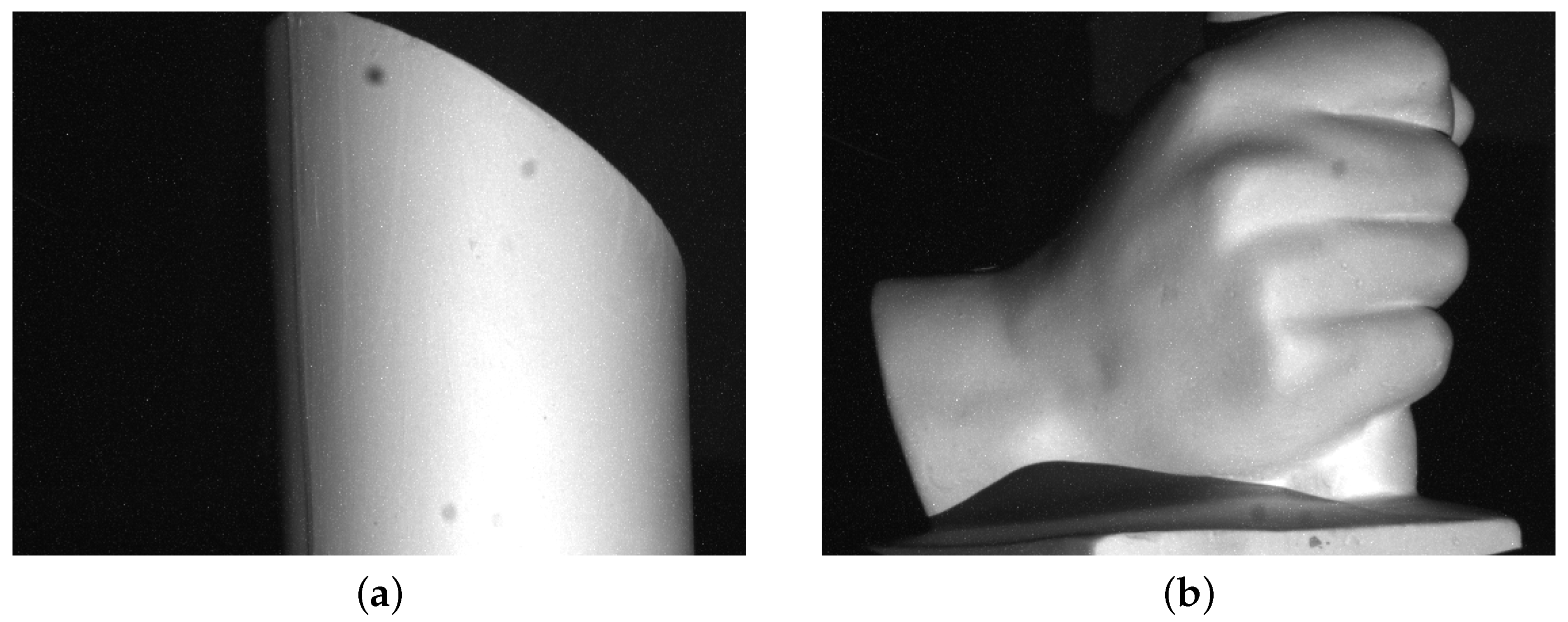
We take one example to describe the framework for obtaining the absolute phase map for multiple discontinuous objects. The detected objects include one cylinder and one cone. They are discontinuous. The designed pattern shown in
Figure 11 is projected onto the detected objects. The captured fringe pattern is shown in
Figure 13a. The left object is one cylinder. The right object is one cone. The absolute phase map retrieval of the spatially isolated objects is implemented in the following steps:
Step 1: Obtain the wrapped phase from the captured sinusoidal fringe patterns. Segment the whole image into
I various continuous regions on the basis of the branch-cut map of the wrapped phase. Set the feature point in a continuous region, such as Point A
and Point B
in
Figure 13a. The chosen feature points are better located in the middle of a
phase period as shown in
Figure 13a.
Step 2: Adopt the conventional phase-unwrapping algorithm to unwrap the phase for each region to obtain the relative phase map
. In the example shown in
Figure 13a,
denotes the relative phase map of the cylinder.
denotes the relative phase map of the cone. Here we still take the cylinder as the object of research. The absolute phase map of the cone equals its relative phase map as follows:
The absolute phase map of the cylinder is obtained as
where
k is the fringe order difference between Points B and A.
Step 3: Obtain the fringe order difference of the phase codeword of Points A and B. We take Point A as an example to explain the retrieval of the fringe order. Firstly, find the
phase period that includes Point A and locate the zero-crossing points
and
A within the
phase period, as shown in
Figure 13b. Take a Fast Fourier Transformation (FFT) of this phase period and derive the frequency component, as shown in
Figure 13c. The obtained frequency component is about 54 Hz. From
Table 1, we know that the phase codeword is p2. Similarly for Point B, the codeword is p1. The difference in the fringe order
k of Points A and B is 5.
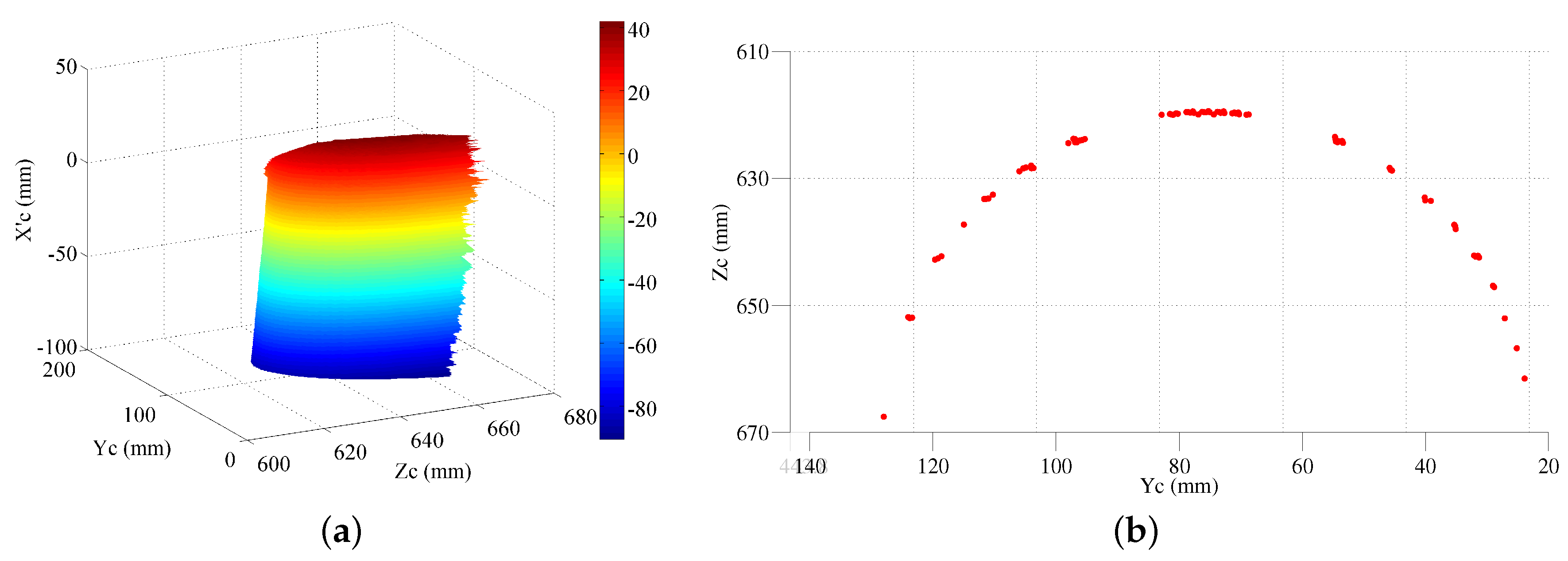
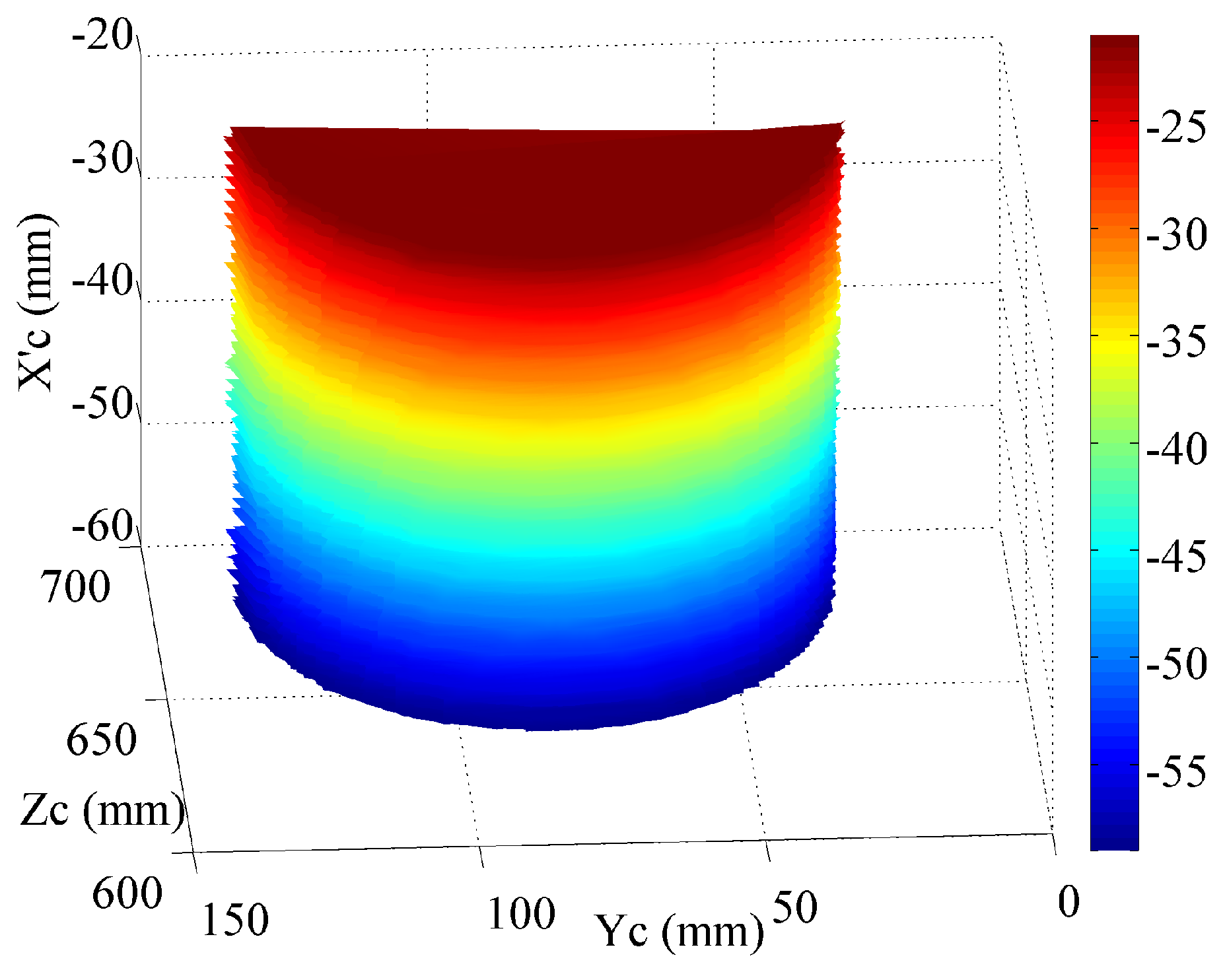
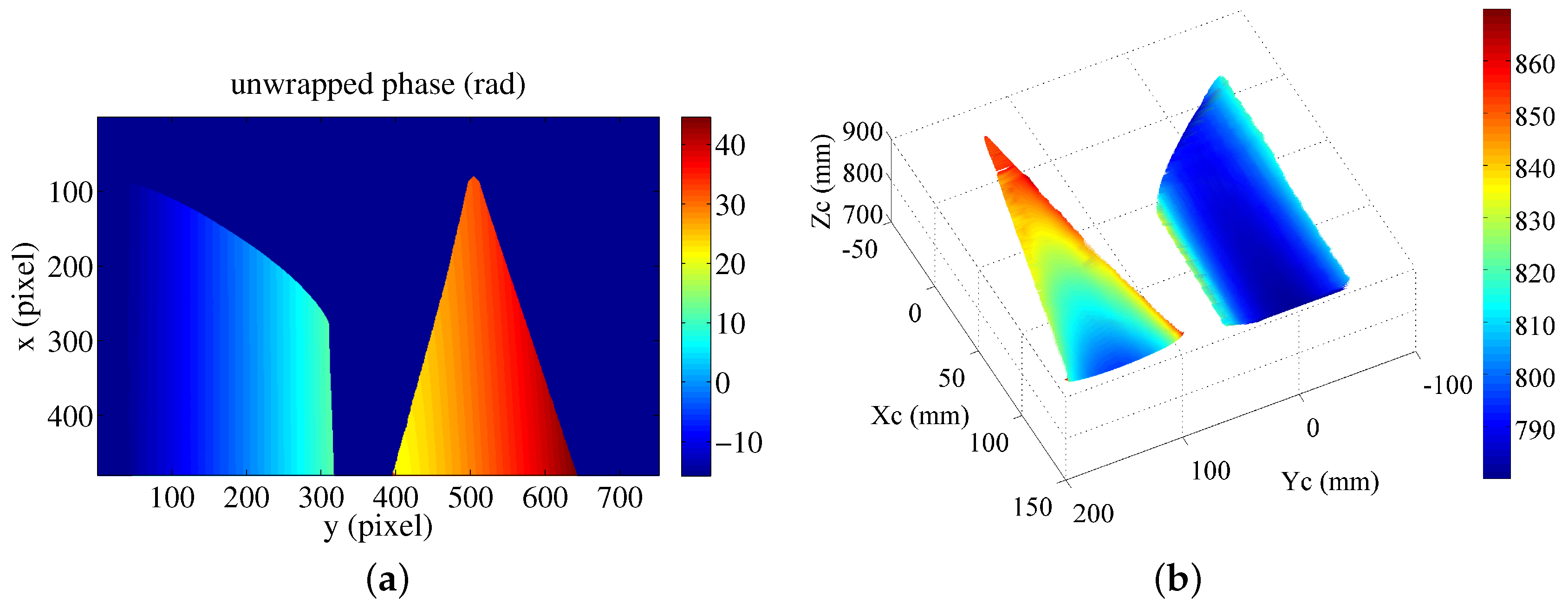
On the basis of the Equations (12)–(14), the absolute phase map of the detected objects is derived as shown in
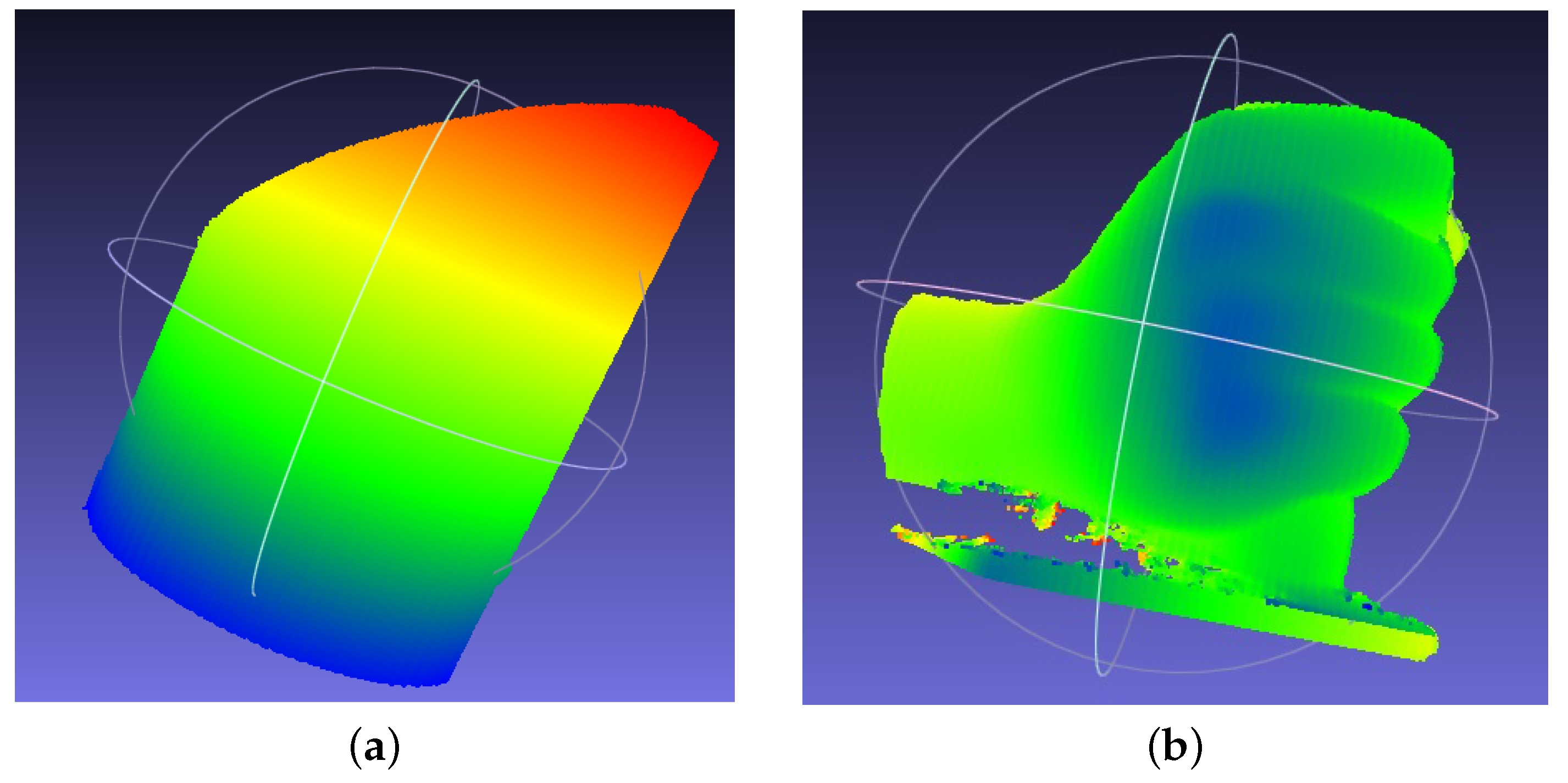
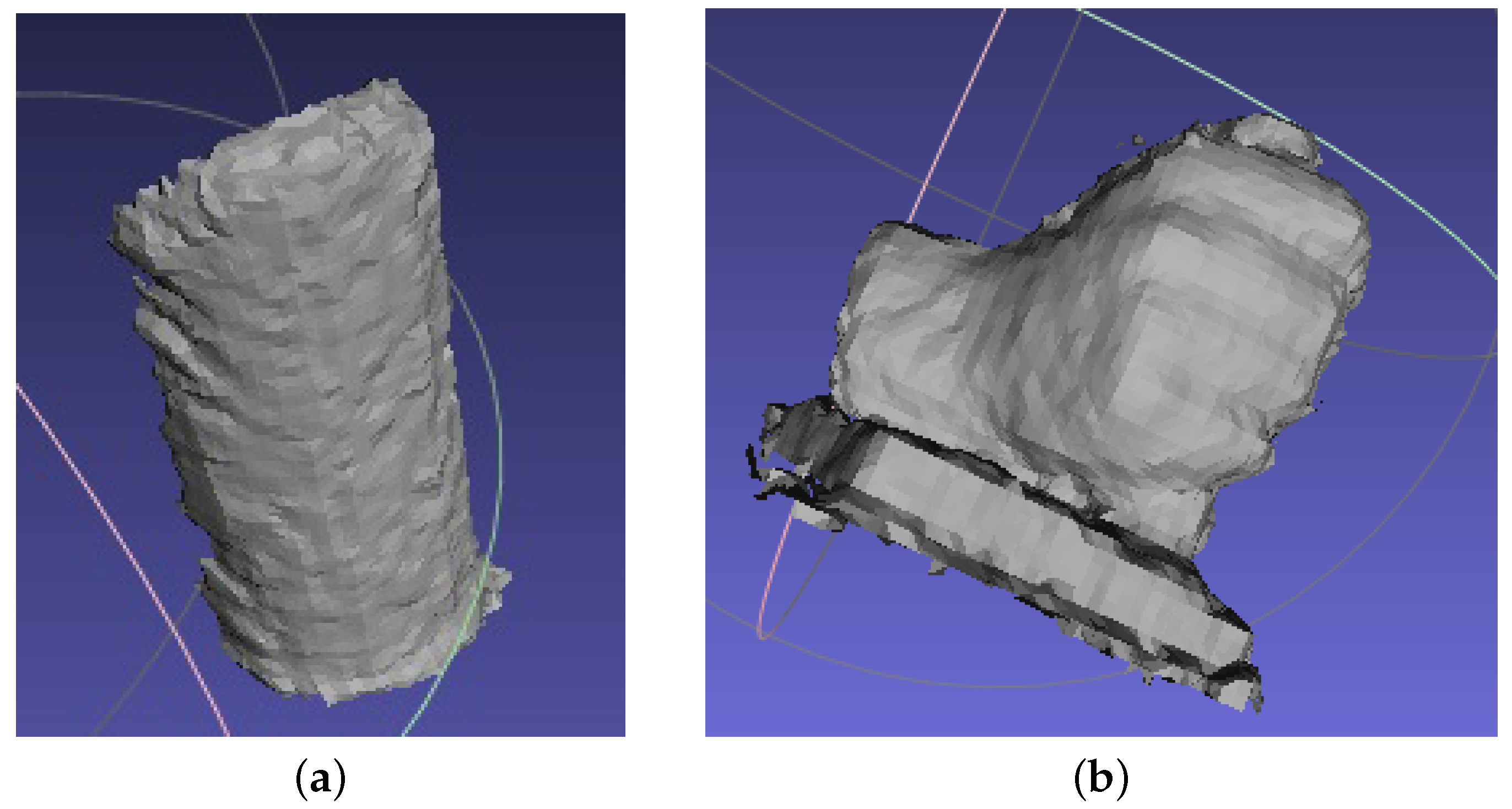
Figure 14a. Furthermore, gray-coding plus phase-shifting method is also applied to obtain the absolute phase map of the detected objects. The obtained absolute phase map is the same with the result obtained by the proposed phase-coding method. By applying the abovementioned extended mathematical model, the measured surfaces in Matlab are shown in
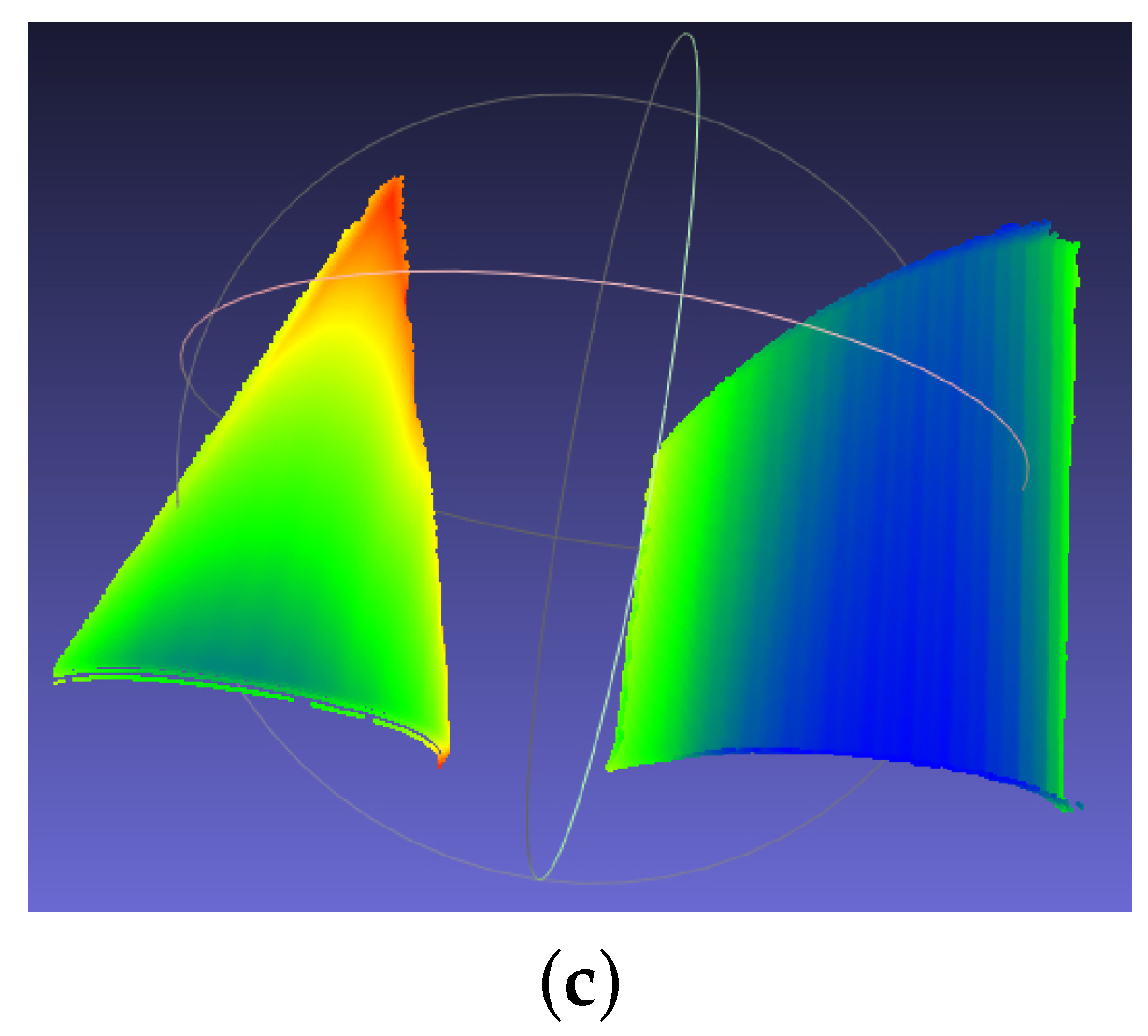
Figure 14b. The measured surfaces in Meshlab are shown in
Figure 14c. The color changes gradually on the basis of the coordinate
. The calculated radius of the cylinder is 52.56 mm. The error is 0.06 mm. The experimental results demonstrate the effectiveness of the proposed phase-coding method. However, the error is a little larger than the measured radius with single object. More effort will be made to improve the performance of the proposed fringe projection vision system on multiple spatially discontinuous objects.
6. Conclusions
In this study, a flexible fringe projection vision system is proposed that relaxes the restriction on the camera’s and projector’s relative alignment and simplifies the calibration process with more flexibility and a cost savings. The proposed flexible fringe projection vision system is designed to realize an accurate 3D measurement to large scene for industrial safety inspection. The measured range can be flexibly adjusted on the basis of the measurement requirements. Accurate 3D measurement is obtained with an extended mathematical model that avoids the complex and laborious error compensation procedures for various error sources.
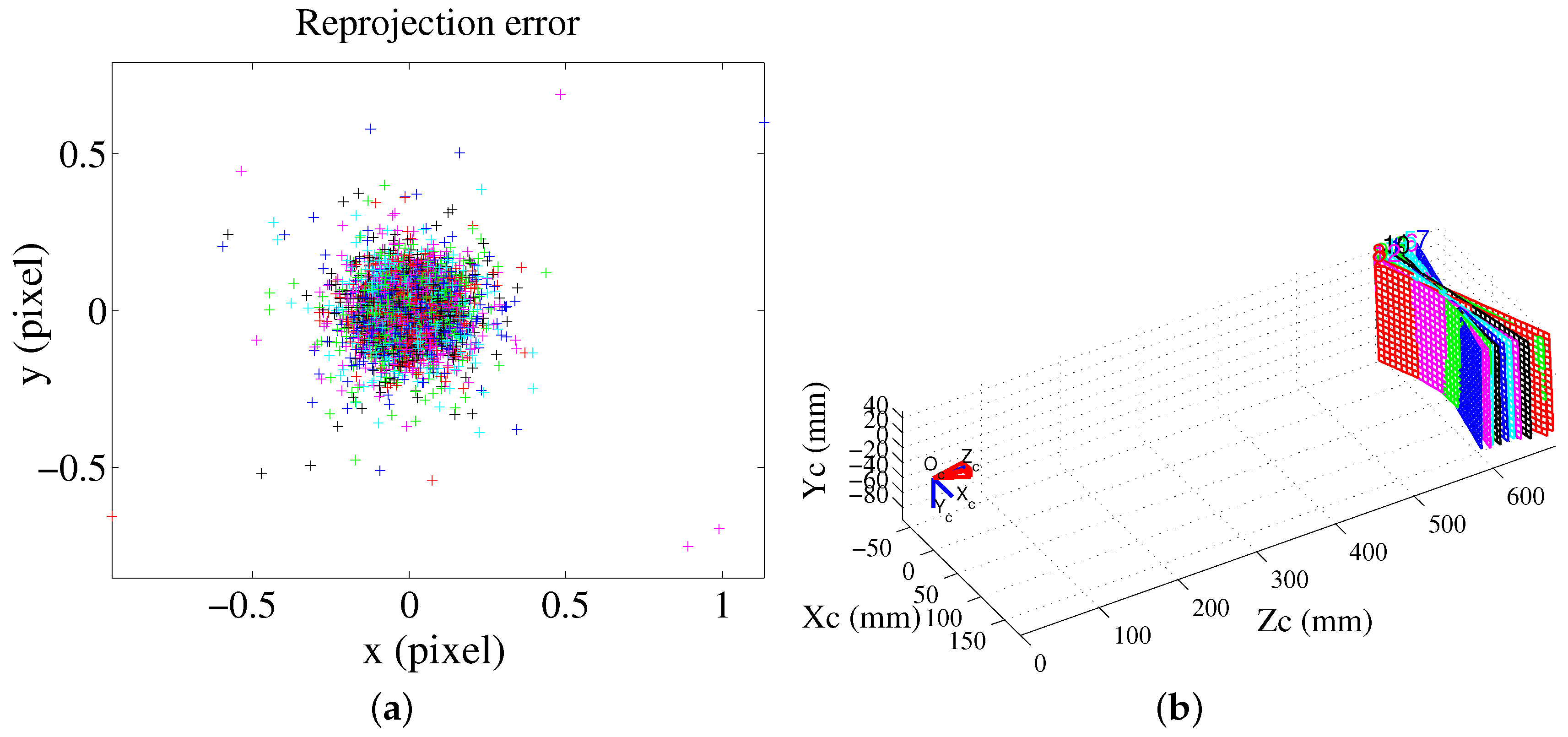
In addition, the system accuracy is only determined by the derived point clouds with a mature camera calibration technique. It is not influenced by the numerous systematic error sources. Moreover, the system accuracy can be further improved by the following ways. (1) In this paper, a low-cost printed plane is used for the calibration; if a high-accuracy planar plane is used, the calibration accuracy can be further improved, and the known geometrical information (the calibration reference plane) will provide a more accurate reference value for the following nonlinear parameter estimation; (2) A high-resolution camera is applied. For the vision system in this work, the std of the reprojection error is 0.03 mm, and it can be reduced to 0.015 mm with a camera with a two-fold higher resolution; (3) A more advanced camera calibration algorithm with highly accurate feature point extraction can be used.
Finally, a new phase-coding method is proposed to obtain the absolute phase map of spatially isolated objects. Only one additional fringe pattern is added for the proposed phase codeword method. There is no gray level or color information that is used to unwrap the phase with depth discontinuities because they are sensitive to noise. Since the proposed method takes full advantage of the frequency characteristic of the sinusoidal fringe pattern, it is insensitive to noise and object texture. However, accurate retrieval of the fringe order is dependent on the FFT of the signal of the phase period. If the signal is too short, the accuracy of the fringe order retrieval will be affected. In our future work, it will be improved by combining the FFT and a correlation technique for the phase period signal.