SHM-Based Probabilistic Fatigue Life Prediction for Bridges Based on FE Model Updating
Abstract
:1. Introduction
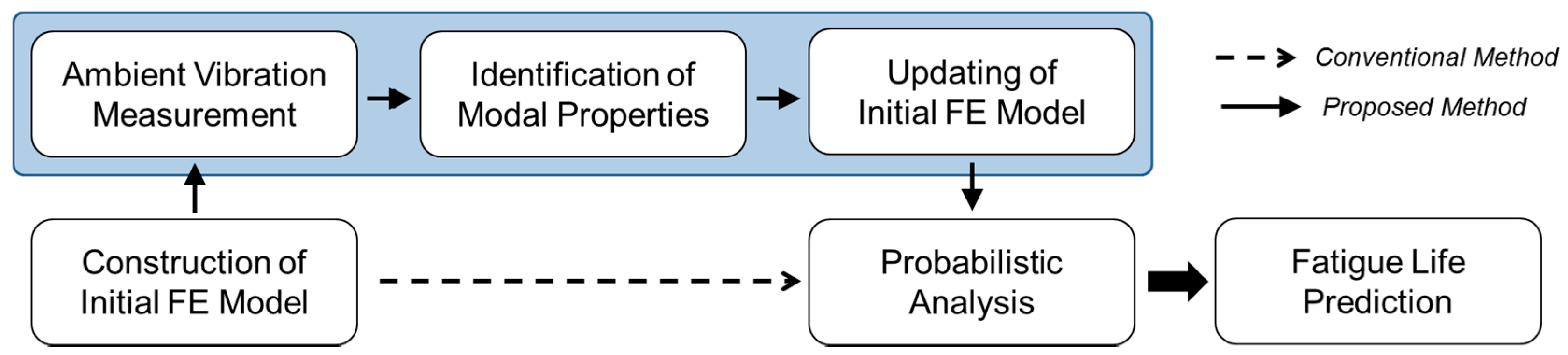
2. Probabilistic Fatigue Life Prediction Using FE Model Updating Based on SHM Data
2.1. Limit-State Function Formulations for Fatigue Failure
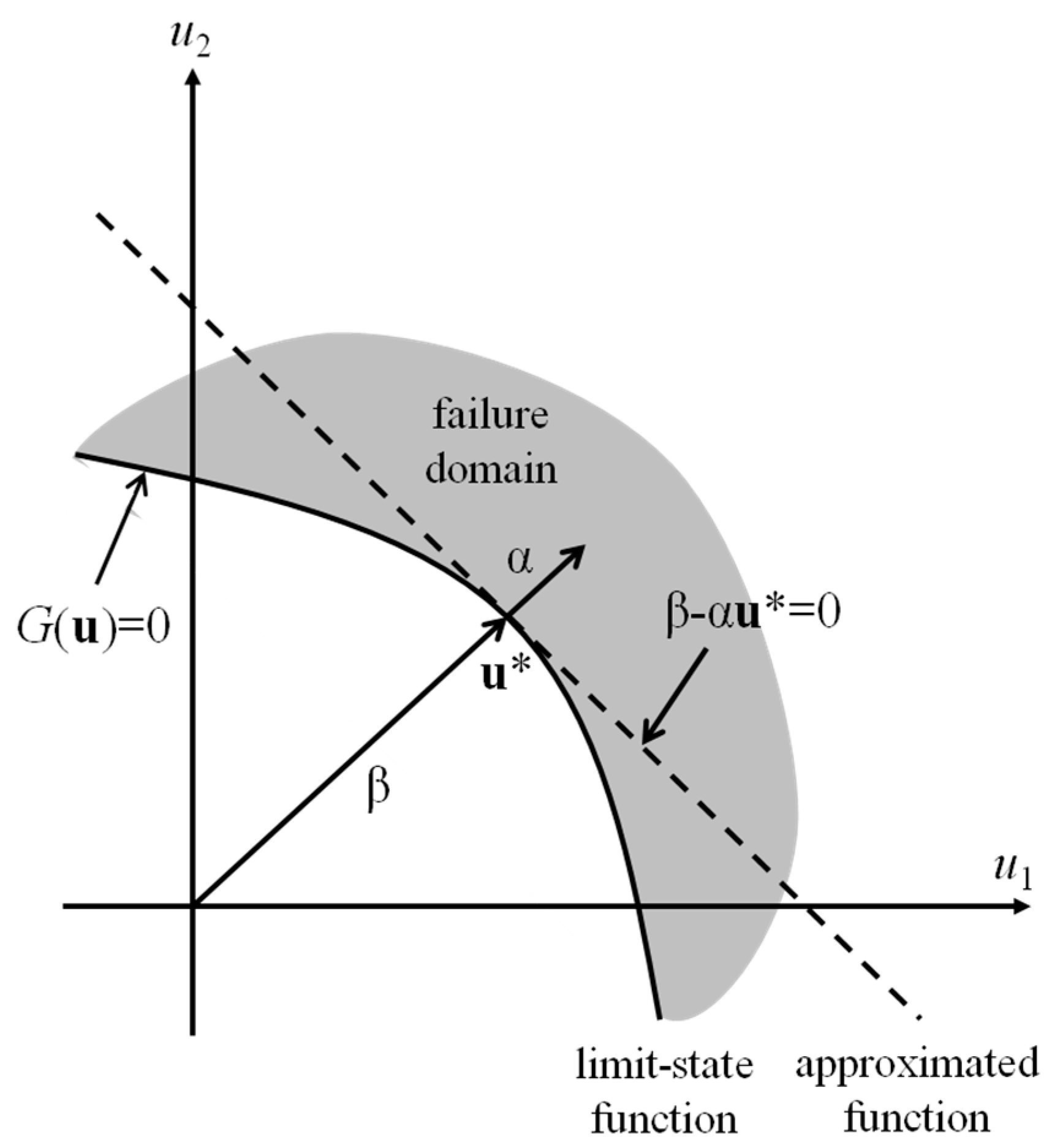
2.2. Component and System Reliability Analysis
2.3. Finite Element Model Updating Based on Structural Health Monitoring Data
3. Numerical Example
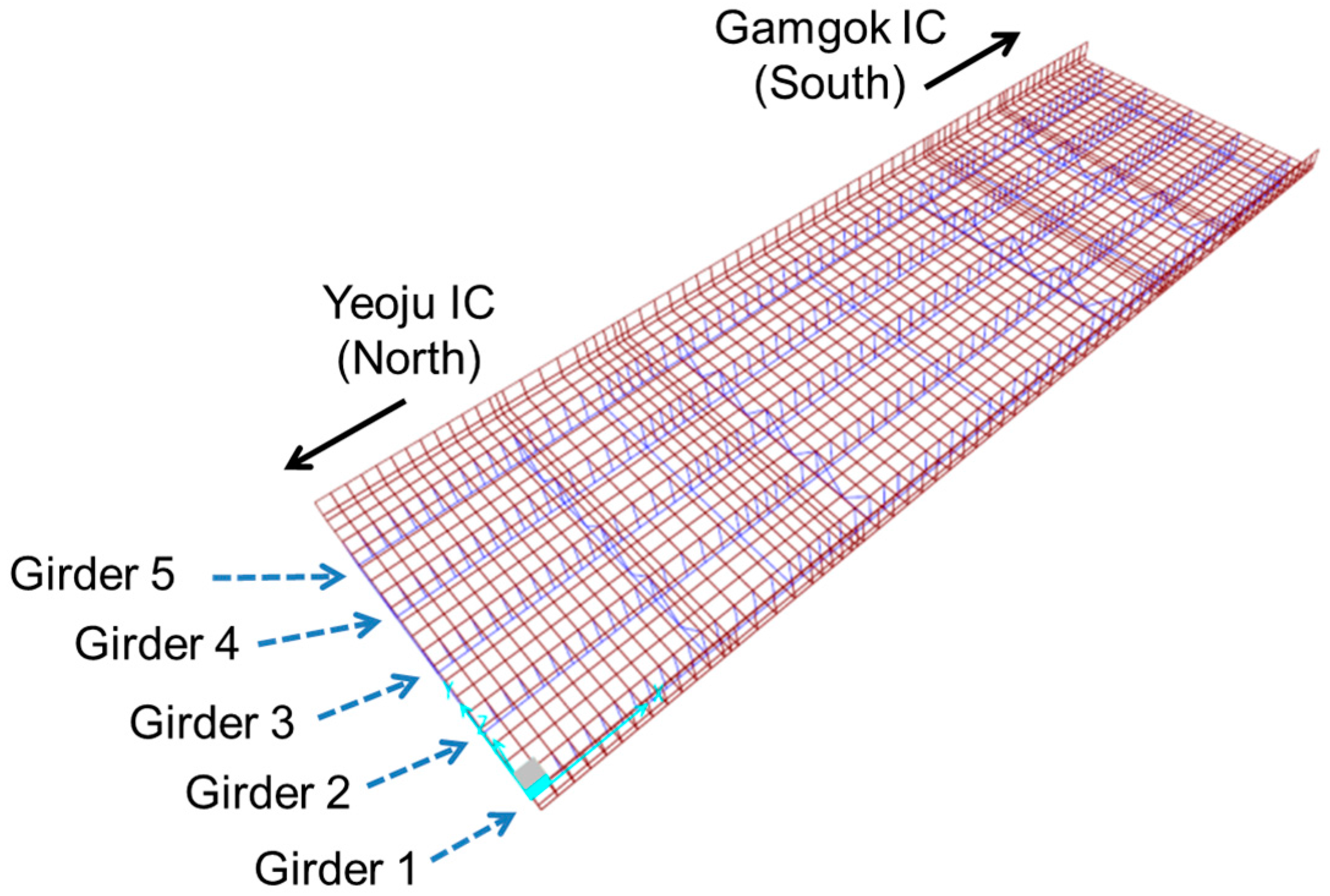
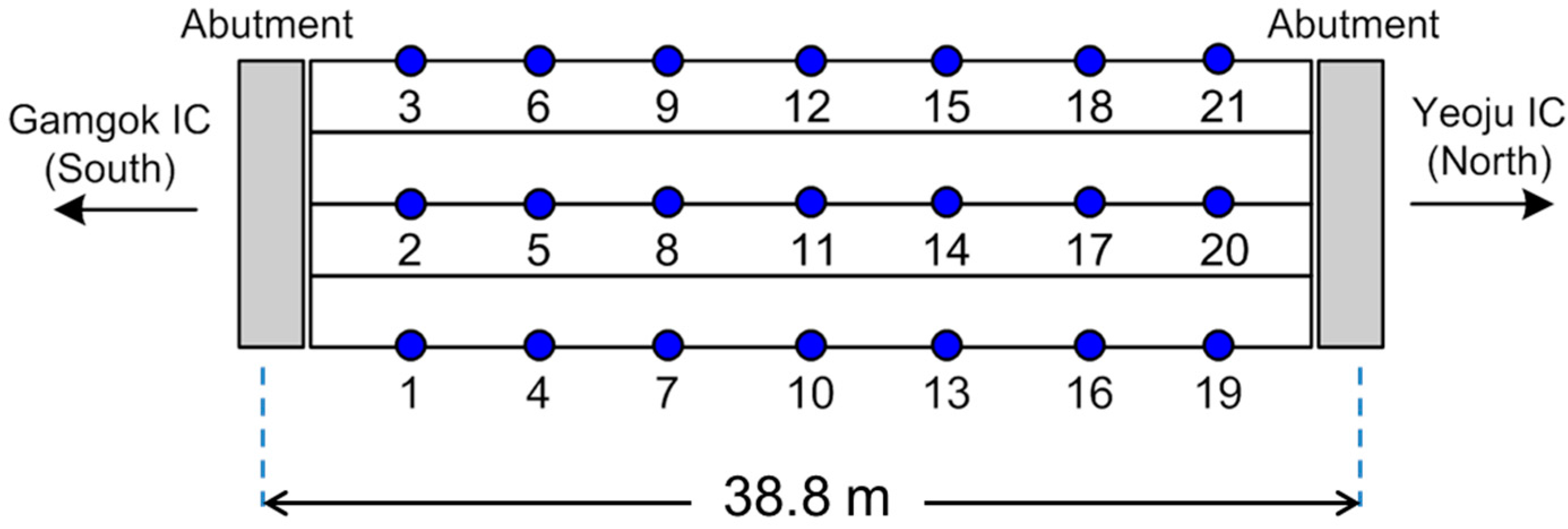
3.1. Example Bridge: Samseung Bridge
3.2. FE Model Updating
3.3. Statistical Parameters
3.4. Random Variables and Deterministic Parameters
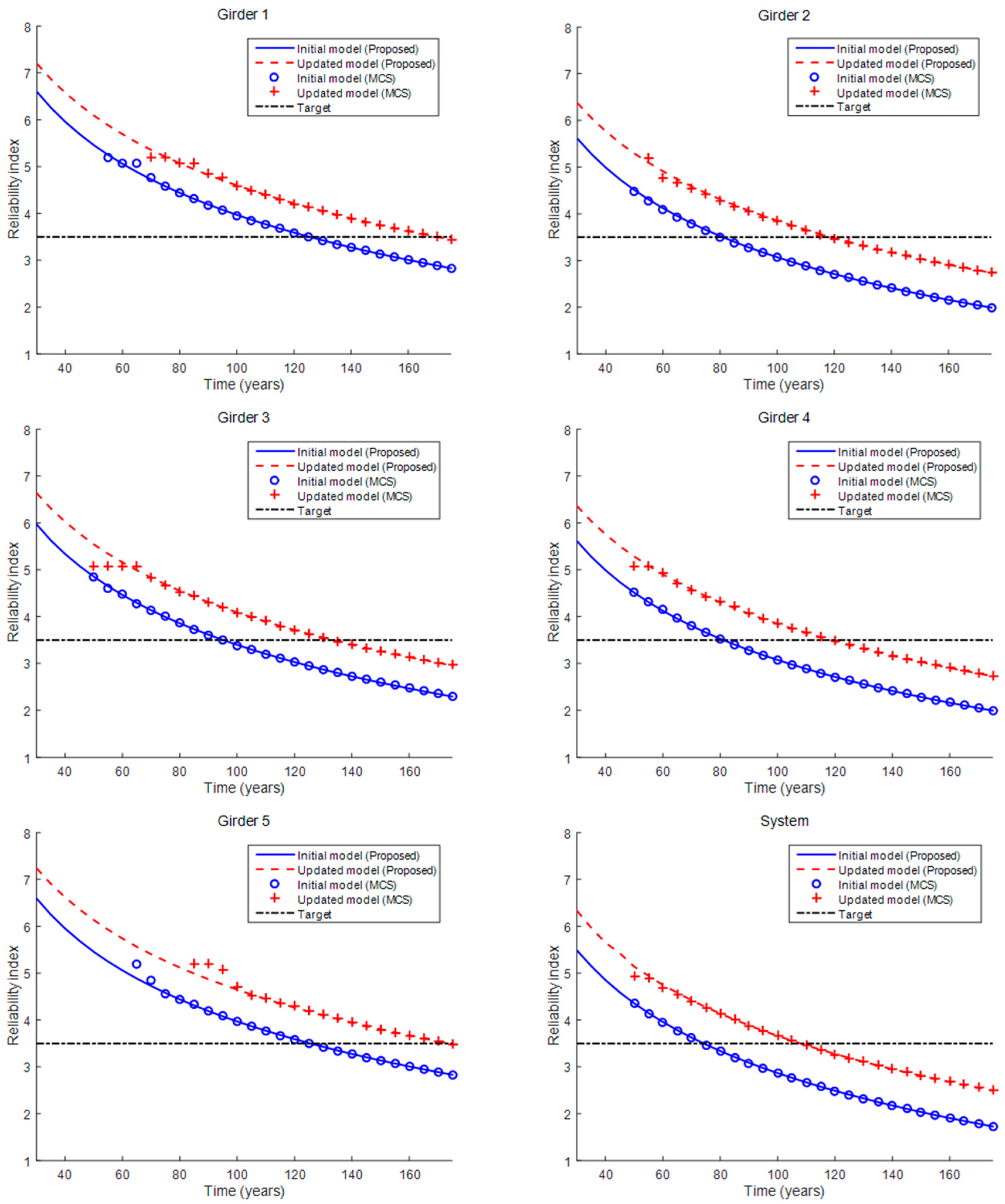
3.5. Analysis Results
4. Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Byers, W.G.; Marley, M.J.; Mohammadi, J.; Nielsen, R.J.; Sarkani, S. Fatigue reliability reassessment applications: State-of-the-art paper. J. Struct. Eng. 1997, 123, 277–285. [Google Scholar] [CrossRef]
- Karamchandani, A.; Dalane, J.I.; Bjerager, P. Systems reliability approach to fatigue of structures. Struct. Eng. 1992, 118, 684–700. [Google Scholar] [CrossRef]
- Millwater, H.R.; Wieland, D.H. Probabilistic sensitivity-based ranking of damage tolerance analysis elements. J. Aircr. 2010, 47, 161–171. [Google Scholar] [CrossRef]
- Imam, B.M.; Righiniotis, T.D.; Chryssanthopoulos, M.K. Probabilistic fatigue evaluation of riveted railway bridges. J. Bridge Eng. 2008, 13, 237–244. [Google Scholar] [CrossRef]
- Park, Y.-S.; Han, S.-Y.; Suh, B.-C. Fatigue reliability analysis of steel bridge welding member by fracture mechanics method. Struct. Eng. Mech. 2005, 19, 347–359. [Google Scholar] [CrossRef]
- Zhao, Z.; Haldar, A.; Breen, F.L. Fatigue-reliability evaluation of steel bridges. J. Struct. Eng. 1994, 120, 1608–1623. [Google Scholar] [CrossRef]
- Madsen, H.O. Probabilistic and Deterministic Models for Predicting Damage Accumulation Due to Time Varying Loading. In DIALOG 5-82; Danish Engineering Academy: Lyngby, Denmark, 1983. [Google Scholar]
- Lukić, M.; Cremona, C. Probabilistic assessment of welded joints versus fatigue and fracture. J. Struct. Eng. 2001, 127, 211–218. [Google Scholar] [CrossRef]
- Kwon, K.; Frangopol, D.M. Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data. Int. J. Fatigue 2010, 32, 1221–1232. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Ye, X.W.; Ko, J.M. Monitoring-based fatigue reliability assessment of steel bridges: Analytical model and application. J. Struct. Eng. 2010, 132, 1563–1573. [Google Scholar] [CrossRef]
- Zhao, Z.; Haldar, A. Bridge fatigue damage evaluation and updating using non-destructive inspections. Eng. Fract. Mech. 1996, 53, 775–788. [Google Scholar] [CrossRef]
- Nagayama, T.; Sim, S.H.; Miyamori, Y.; Spencer, B.F. Issues in structural health monitoring employing smart sensors. Smart Struct. Syst. 2007, 3, 299–320. [Google Scholar] [CrossRef]
- Yi, J.-H.; Cho, S.; Koo, K.-Y.; Yun, C.-B.; Kim, J.-T.; Lee, C.-G.; Lee, W.-T. Structural performance evaluation of a steel-plate girder bridge using ambient acceleration measurements. Smart Struct. Syst. 2007, 3, 281–298. [Google Scholar] [CrossRef]
- Yi, J.-H.; Kim, D.; Go, S.; Kim, J.-T.; Park, J.-H.; Feng, M.Q.; Kang, K.-S. Application of structural health monitoring system for reliable seismic performance of infrastructures. Adv. Struct. Eng. 2012, 15, 955–967. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar]
- Paris, P.C.; Erdogan, F. An effective approximation to evaluate multinormal integrals. Struct. Saf. 1963, 20, 51–67. [Google Scholar]
- Lee, Y.-J.; Song, J. Risk analysis of fatigue-induced sequential failures by branch-and-bound method employing system reliability bounds. J. Eng. Mech. 2011, 137, 807–821. [Google Scholar] [CrossRef]
- Newman, J.C.; Raju, I.S. An empirical stress intensity factor equation for the surface crack. Eng. Fract. Mech. 1981, 15, 185–192. [Google Scholar] [CrossRef]
- Melchers, R.E. Structural Reliability: Analysis and Prediction; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Der Kiureghian, A. Chapter 14. First- and Second-Order Reliability Methods. In Engineering Design Reliability Handbook; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Song, J.; Der Kiureghian, A. Bounds on system reliability by linear programming. J. Eng. Mech. 2003, 129, 627–636. [Google Scholar] [CrossRef]
- Song, J.; Kang, W.-H. System reliability and sensitivity under statistical dependence by matrix-based system reliability method. Struct. Saf. 2009, 31, 148–156. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. First-order concepts in system reliability. Struct. Saf. 1983, 1, 177–188. [Google Scholar] [CrossRef]
- Genz, A. Numerical computation of multivariate normal probabilities. J. Comput. Graph. Stat. 1992, 1, 141–149. [Google Scholar]
- Lee, Y.-J.; Song, J. Finite-element-based system reliability analysis of fatigue-induced sequential failures. Reliab. Eng. Syst. Saf. 2012, 108, 131–141. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Yi, J.H.; Yun, C.B. Comparative study on modal identification methods using output-only information. Struct. Eng. Mech. 2004, 17, 445–466. [Google Scholar] [CrossRef]
- Ministry of Construction and Transportation. Korea Highway Bridge Design Specifications; Korea Society of Civil Engineers: Seoul, Korea, 2005. [Google Scholar]
- Moan, T.; Song, R. Implications of inspection updating on system fatigue reliability of offshore structures. J. Offshore Mech. Arct. Eng. 2000, 122, 173–180. [Google Scholar] [CrossRef]
- Riahi, H.; Bressolette, P.; Chateauneuf, A.; Bouraoui, C.; Fathallah, R. Reliability analysis and inspection updating by stochastic response surface of fatigue cracks in mixed mode. Eng. Struct. 2011, 33, 3392–3401. [Google Scholar] [CrossRef]
- Zheng, R.; Ellingwood, B.R. Stochastic fatigue crack growth in steel structures subject to random loading. Struct. Saf. 1998, 20, 303–323. [Google Scholar] [CrossRef]
- Borrego, L.P.; Ferreira, J.M.; Costa, J.M. Fatigue crack growth and crack closure in an AlMgSi alloy. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 255–266. [Google Scholar] [CrossRef]
- Yarema, S.Y. Correlation of the parameters of the Paris equation and the cyclic crack resistance characteristics of materials. Strength Mater. 1980, 13, 1090–1098. [Google Scholar] [CrossRef]
- Wang, C.S.; Chen, A.R.; Chen, W.Z.; Xu, Y. Application of probabilistic fracture mechanics in evaluation of existing riveted bridges. Bridge Struct. Assess. Des. Constr. 2006, 2, 223–232. [Google Scholar] [CrossRef]

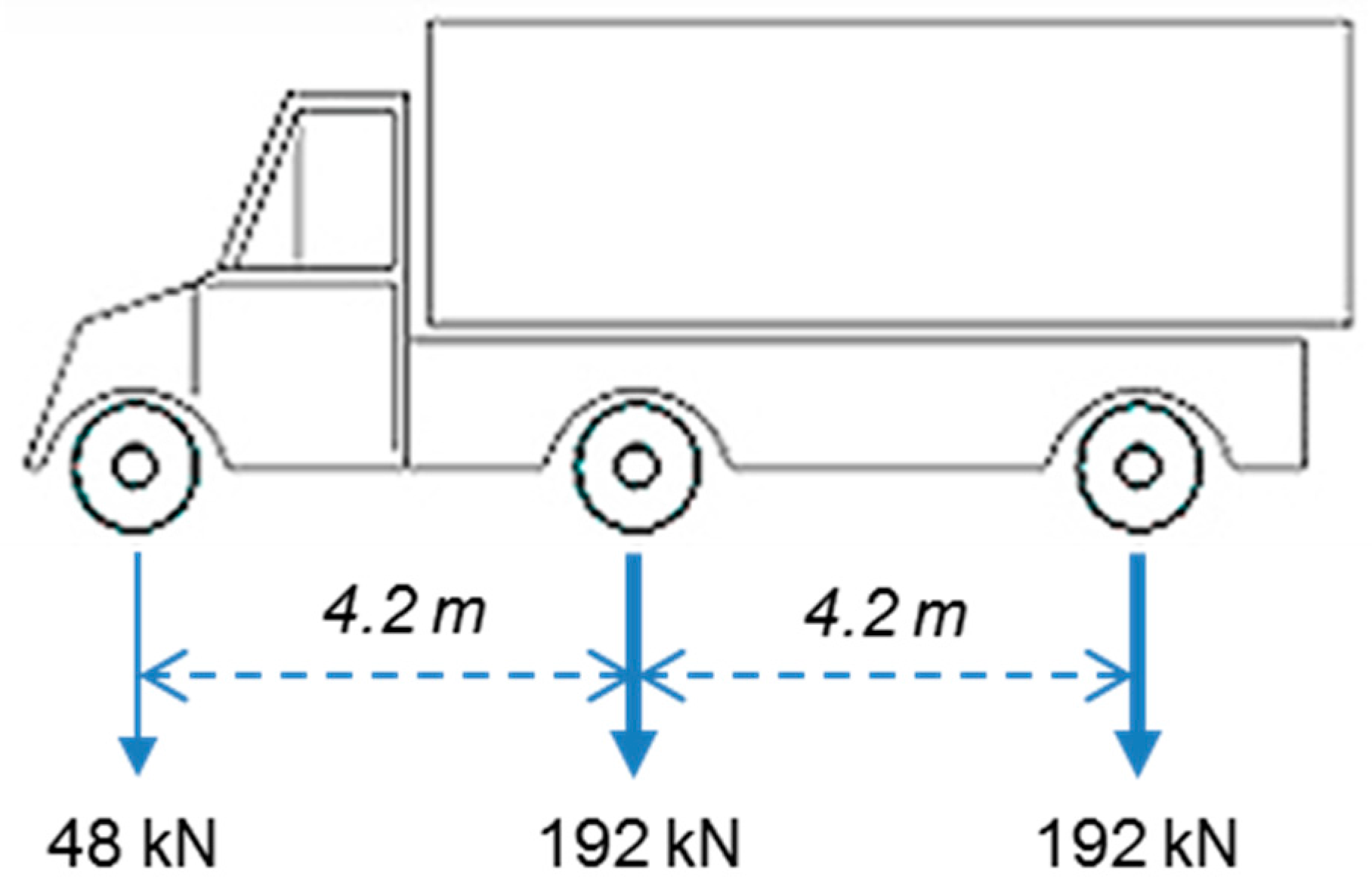
| Members | Updating Parameters | Count | |
|---|---|---|---|
| First Step | Second Step | ||
| Support | Rotational Spring Constant | 1 | 2 |
| Concrete Slab | Young’s Modulus | 1 | 1 |
| Main Girder | Second Moment of Inertia | 5 | 5 |
| Torsional Coefficient | 0 | 5 | |
| Floor Beam | Second Moment of Inertia | 1 | 9 |
| Torsional Coefficient | 1 | 9 | |
| Total | 9 | 31 | |
| Stress (MPa) | Girder 1 | Girder 2 | Girder 3 | Girder 4 | Girder 5 |
|---|---|---|---|---|---|
| Initial FE model | 18.24 | 20.77 | 20.03 | 20.77 | 18.24 |
| Updated FE model | 15.95 | 17.52 | 17.11 | 17.52 | 15.83 |
| Random Variables (RVs) | Mean | COV | Distribution Type | Number of RVs |
|---|---|---|---|---|
| Paris law parameter © | 2.18 × 10−13 (mm/cycle/(MPa·mm)m) | 0.2 | Lognormal | 5 |
| Initial crack length (a0) | 0.1 (mm) | 1.0 | Exponential | 5 |
| Live load scale factor (S) | 1 | 0.1 | Lognormal | 1 |
| Fatigue Life (Years) | Girder 1 | Girder 2 | Girder 3 | Girder 4 | Girder 5 | System |
|---|---|---|---|---|---|---|
| Initial FE model | 125.6 | 81.2 | 95 | 81.2 | 125.6 | 74.3 |
| Updated FE model | 170 | 119.4 | 133.6 | 118.3 | 175 | 108 |
| Bridge System Fatigue Life (Years) | ρ = 0.0 | ρ = 0.2 | ρ = 0.4 | ρ = 0.6 | ρ = 0.8 |
|---|---|---|---|---|---|
| Initial FE model | 73 | 73.3 | 73.7 | 74.3 | 75.7 |
| Updated FE model | 106 | 106.5 | 107 | 108 | 110 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-J.; Cho, S. SHM-Based Probabilistic Fatigue Life Prediction for Bridges Based on FE Model Updating. Sensors 2016, 16, 317. https://doi.org/10.3390/s16030317
Lee Y-J, Cho S. SHM-Based Probabilistic Fatigue Life Prediction for Bridges Based on FE Model Updating. Sensors. 2016; 16(3):317. https://doi.org/10.3390/s16030317
Chicago/Turabian StyleLee, Young-Joo, and Soojin Cho. 2016. "SHM-Based Probabilistic Fatigue Life Prediction for Bridges Based on FE Model Updating" Sensors 16, no. 3: 317. https://doi.org/10.3390/s16030317
APA StyleLee, Y.-J., & Cho, S. (2016). SHM-Based Probabilistic Fatigue Life Prediction for Bridges Based on FE Model Updating. Sensors, 16(3), 317. https://doi.org/10.3390/s16030317






