1. Introduction
With the rapid development and extensive application of wireless communication technology, limited spectrum resource and inflexible spectrum assignment policy bring about poor spectrum utilization currently. Cognitive radio technology that allows smart spectrum sharing between licensed (primary) users and unlicensed (secondary) users emerged in 1999 which is regarded as a promising technology for improving spectrum utilization [
1].
There are two kinds of spectrum sharing modes between the PU and the SU. One is spectrum sensing that the unlicensed secondary users can access the channels that are not currently occupied by the licensed primary users through spectrum sensing to avoid harmful interference on the primary user(PU) for data transmission. Another is spectrum leasing which is adopted in this paper, specifically, the PU is aware of existence of the SU and it can gain some revenue by leasing parts of spectrum to the SU. There have been many literatures about research in the lease spectrum. In [
2], the authors proposed the "cooperative cognitive radio networks" in which PUs rent a fraction of the owned spectrum to SUs in exchange for cooperative relaying and model the spectrum leasing strategies as a Stackelberg game. Similar scenario and model take place in [
3], where a primary link has the possibility to lease the licensed spectrum to an ad hoc network of secondary users in return for assistance in the form of distributed space-time coding. The authors in [
4] investigated multi-access protocols allowing simultaneous transmission of relaying and secondary database on dirty-paper coding (DPC) with considering cooperation between PUs and SUs, which introduces a trade-off between PU and SU performance combining with opportunistic relay selection. In [
5], the authors studied an overlay spectrum sharing scheme where the SU leases half of the time-slot from the PU at the cost of relaying the PU’s data transmission, they proposed the SU’s antenna combining weights as well as power allocation scheme to encounter a certain error or rate design standard for both PU and SU. In [
6], considered the problem of two wireless networks operating on the same frequency band. Pairs within a given network cooperate to schedule transmissions, but between networks there is competition for spectrum.
In recent years, the problem about energy consumption has become increasingly severe; this urgently calls for solutions to improve energy efficiency [
7]. Apart from energy-efficient wireless communication technologies, energy harvesting communication systems powered either largely or exclusively by renewable sources are regarded as another useful alternative that can efficiently relieve energy-deficiency and have become more attractive [
8]. Compared to traditional battery-powered communication systems, energy harvesting could potentially provide infinite energy supply from the environment in a much easier and safer way for conventional energy-constrained wireless communication systems, such as wireless sensor networks (WSNs). Pappas
et al. studied the maximum stable throughput region for a simple cognitive radio network when the primary transmitter harvests ambient energy but the secondary transmitter is plugged into a reliable power supply [
9]. Lee
et al. analyzed the transmission probability of secondary transmitters and the resulting spatial throughput of the secondary network when the secondary transmitters harvest ambient RF energy from transmissions by nearby active primary transmitters, while opportunistically accessing the spectrum licensed to the primary network [
10]. Energy harvesting is also regarded as a promising approach for powering relay node [
11,
12,
13,
14,
15]. In [
11], the authors derived the optimal switching rule between the information decoding mode and the energy harvesting mode to minimize the outage probability. In [
12], the authors formulated the optimal sensing and access policies as a Markov decision process and derived the optimal policy by the probability of PU’s presence and the amount of stored energy. In [
13], the authors considered a cognitive radio sensor network powered by RF energy harvesting and formulated the optimal mode selection (“access” or “harvest”) policy as a partially observable Markov decision process (POMDP). In [
15], spatial spectrum reused in CR networks with energy harvesting was investigated based on a stochastic-geometry model where the primary and secondary transmitters are modeled as independent homogeneous Poisson point processes (HPPPs). In [
14], the authors provided an optimal spectrum sensing policy for an energy-harvesting CR that can maximize the expected total throughput under energy causality and collision constraints.
In [
16], a multi-antenna model was proposed where the receiver can only harvest energy from the transmitter by wireless energy transfer to serve for its data transmission. In [
17], the authors discussed an efficient resource-allocation strategy for a multiuser multiple-input-multiple-output rate less coded cognitive radio network with quality-of-service provisioning. The authors of [
18] designed an efficient MAC protocol with selective grouping and cooperative sensing in CR networks. Generally, due to the dynamic and random feature of energy in natural circumstance, we consider merely a scenario that wireless communication device collects energy from ambient wireless signal. Compared with these works, the salient feature of this paper is that, by considering the aforementioned trade-offs between energy harvesting and secondary transmission, we investigate the optimal secondary transmission duration time that maximizes the SU’s achievable throughput and further present energy efficiency ratio of the entire network based on the optimal closed-form solutions.
Besides, we introduce an important concept: utility. In economics, utility is a measure of preference over some set of goods and services. The concept is an important underpinning of rational choice theory in economics and game theory, because it represents consumers’ satisfaction. A good is something that satisfies human wants. Since one cannot directly measure benefit, satisfaction or happiness from a good or service, economists have devised ways of representing and measuring utility in terms of economic choices that can be measured. Economists have attempted to improve highly-abstract methods of comparing utilities by observing and calculating economic choices. In the simplest sense, economists consider utility to be revealed by people’s willingness to pay different amounts of money for different goods. There are some papers which discussed utility-based resource allocation in wireless networks. In [
19], the authors presented a time-aware admission control and resource allocation scheme in wireless networks in the context of a future generation cellular network. In [
20], the authors studied utility-based resource allocation for soft QoS traffic in infrastructure-based wireless networks.
To achieve the access chance, the SU should make a payment for the PU, which is proportional to the access time. For the PU, the target is to maximize its utility which depends on both its transmission capacity and revenue obtained from the SU. For the SU, the target is to decide how much it should pay for the PU so as to achieve its maximal transmission capacity.
In a word, this paper proposes a spectrum leasing scheme in cognitive radio network with energy harvesting. The SU has equipment which can collect energy from the ambient environment. We assume the SU is powered by harvesting energy and exhausts all the harvesting energy in each time slot for the sake of transmitting data at the highest power. In order to obtain higher energy efficiency of the entire network, the PU prefers to allocate a portion of its spectrum resource to the SU. We derive the optimal spectrum leasing ratio in the following sections. To the best of our knowledge, this work is the first to explore the optimal spectrum leasing ratio in cognitive radio network with energy harvesting, aiming at maximize energy efficiency ratio of the entire network.
The main contributions of this paper are summarized as follows:
By proving the concavity of the achievable throughput maximization problem in our proposed spectrum leasing model, we derive the closed-form solution.
We get an improved energy efficiency scheme. Despite reduction of the throughput, the PU can lease its spectrum to SU and allow it to utilize the harvest energy rationally, so as to improve the energy efficiency of the whole system.
We numerically analyze the impact of various system parameters. The numerical results are consistent with the theoretical analysis.
The rest of the paper is organized as follows. In
Section 2, we give a detailed description of the system model and assumptions. Problem formulations are presented in
Section 3. We discuss throughput analysis and EER of the model in
Section 4. In
Section 5, we present and analyze the numerical results. Finally, the conclusion is in
Section 6.
2. System Model and Assumptions
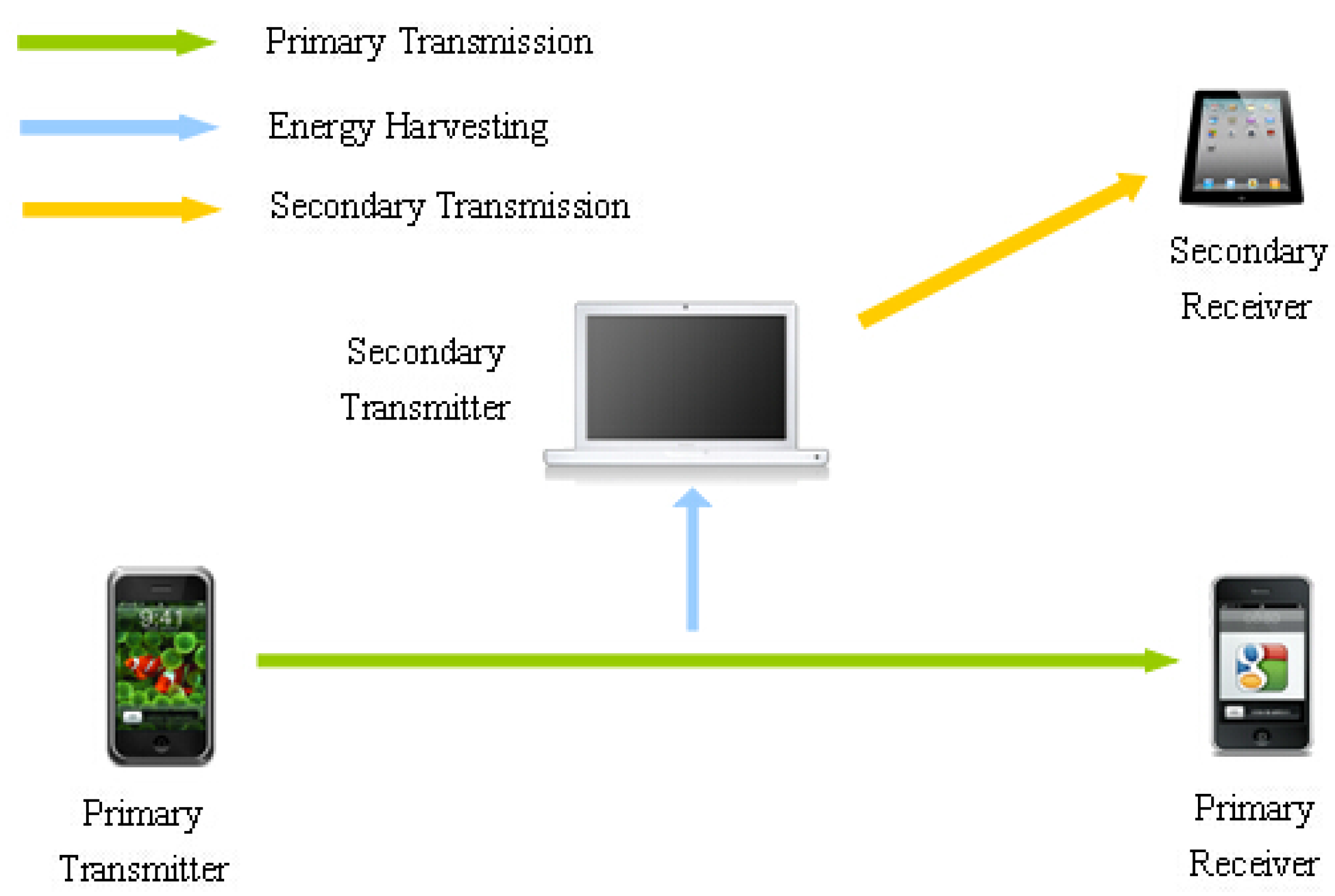
We assume an energy harvesting cognitive radio network which consists of a PU link pair and a SU link pair as the
Figure 1 depicts. Both of them operate in time-slotted mode, as shown in
Figure 2. The PU would like to lease a portion of its timeslot to the SU for some revenue only when its utility can be guaranteed.
PU has the priority of using licensed channel and transmits data to its receiver whenever it has data to send. PU has a certain number of data stored in its buffer. In each time-slot, PU uses licensed channel to transmit its data. After the transmission of all the PU’s data, PU turns to be silent and the channel is vacated.
By comparison, SU has no licensed spectrum, to avoid interference on PU ,it has to transmit its data only when the licensed channel is unused by PU. Besides, we assume a self-powered cognitive radio network with a single SU working in slotted mode, the SU has no fixed power supplies (e.g., batteries) and gets power from the ambient radio signal by energy harvester. We consider that SU works in a saving-transmitting way because of the duplex-constrained hardware [
8,
13]. In each time-slot, the PU uses a fraction of time-slot to transmit data, at the same time, the SU harvests energy exclusively. The rest fraction is used for SU’s data transmission, but SU must pay some remuneration as dividend to the PU.
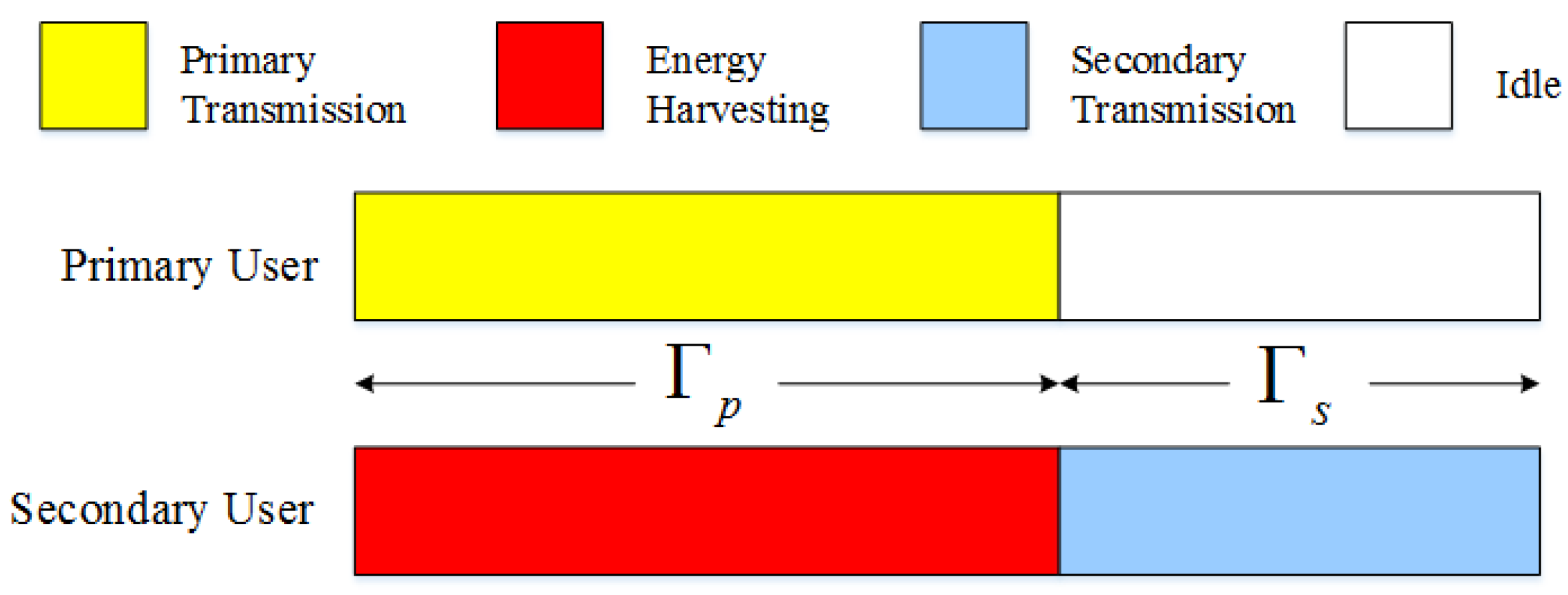
In such a cognitive radio network, the SU can transmit its data only when the licensed channel is unused by PU so as to avoid interference on the primary receiver. The saving-transmitting structure is shown in
Figure 2. In this section, we elaborate the time-slot structure.
The data transmissions are divided into frames with duration of one unit time, and each frame is further partitioned into two fractions for primary usage and secondary usage. The primary user data transmission period, with the duration of
,
, is dedicated for the data transmission of primary users. The secondary data transmission period, with the duration of
, is dedicated for the data transmission of secondary users, as shown in
Figure 2. Which can be detailed as follows:
(1) During time interval , primary user accesses channel to transmit its data, in the meantime, the SU harvests energy from ambient signal. SU’s harvested energy amounts to , where X denotes SU’s energy harvesting rate (average energy harvested in unit time). Meanwhile, the PU completes data transmitting, where .
(2) During time interval , PU’s transmission is finished and the licensed channel is vacated, then the PU leases the vacated channel to SU which can transmit in the remaining time. In return, the SU gives some remuneration to the PU. Then SU starts to transmit its own data. The PU keeps silent and of energy harvests for secondary transmission. The SU’s signal to noise ratio(SNR) is given as follows, where is the power of additive white Gaussian noise, h denotes the channel gain. The channel model is the foundation for the calculation of transmission rate.
4. Throughput Analysis and Energy Efficiency Ratio
In this section, we analyze achievable throughput of the SU and then we aim at calculating optimal accessing time () to maximize achievable throughput of the SU.
Lemma 1. is concave while .
Proof. Obviously, is a continuous function when . Thus, we discuss the second derivative of SU’s achievable throughput to demonstrate its concavity.
The first derivative of
with respect to
can be expressed as
Then the second derivative of
with respect to
can be further obtained
Thus, for
and
, we have
which proves the concavity of SU’s achievable throughput for
.
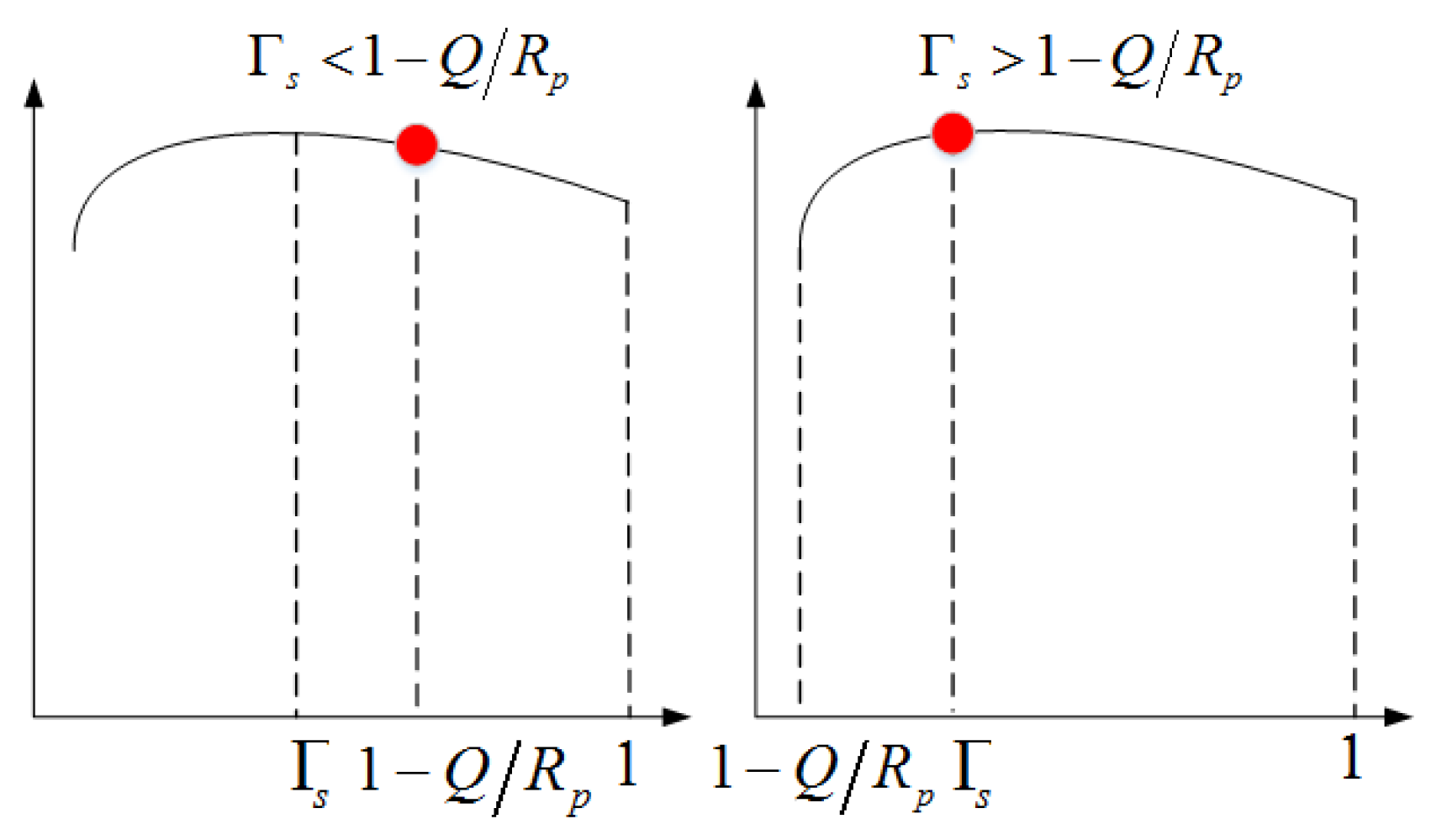
Theorem 1. reaches the global optimality atwhere W(·) refers to the Lambert W function.
Proof. We denote the stationary point of SU’s achievable throughput by
and consequently we have
From Lemma 1, It can be inferred that reaches the global optimality at for .
Then
can be derived as follows:
Since
is bounded within
, in which
is concave according to Lemma 1, the optimal accessing time
of SU can be derived as
which is graphically illuminated by
Figure 5 (where the red dot represents the optimal leasing time).
According to solving the optimal
, we can calculate the achievable throughput of the primary user
as follows,
where
is signal noise ratio
and
is the power of PU transmitter and
is additive white gaussian noise.
Based on the above analysis, we can obtain energy efficiency ratio
η of the whole network, which is the ratio between the achievable utility and the consumption of energy, as follows:
5. Numerical Results and Analysis
In this section, numerical simulations are conducted to evaluate the performance of the proposed framework. We consider the energy harvesting based spectrum leasing scheme in cognitive radio network with one PU and one SU. The PU could lease a part of spectrum to the SU. Additional white gaussian noise = −60 dbm, channel gain h equals to 0.75, the equivalent revenue per unit satisfactory is set to 1.5, payment of unit time c is 1.1, satisfactory factor of the PU α = 0.8, satisfactory factor of the SU b is set to 0.6, the min traffic data requirement of PU Q is 30 bit.
In
Figure 6, we evaluate the optimal access time
versus the energy harvesting rate
X with different
. It can be observed in this figure that the the optimal access time
increases as
X does. But it can not exceed the value
. This is because the energy can only be harvested from signal of the PU and the frame is constant. With the increasing of
, there is less time left for the energy harvesting, and the transmission power of SU will decrease while its transmission time increases. On the contrary, a small
will result in a greater transmission power and longer transmission time of SU. Therefore, we should find out the optimal access time to maximize utility of the entire network.
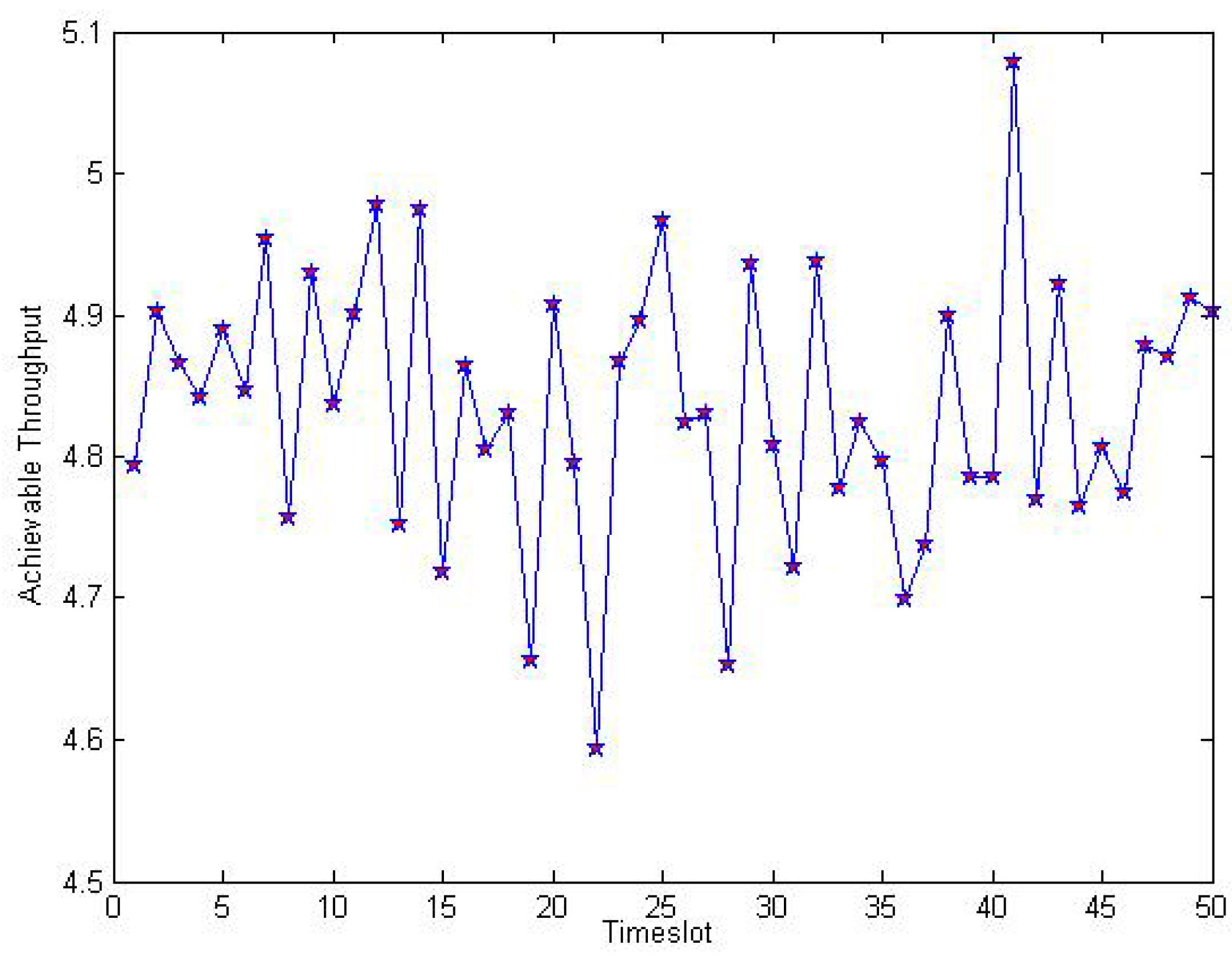
Figure 7 illustrates achievable throughput trace with
with respect to the different timeslot in the dynamic spectrum leasing scheme. Due to the randomness of energy harvesting rate, it has a great impact on
, so the achievable throughput fluctuates randomly, but its value keeps within a level around constant value 4.8.
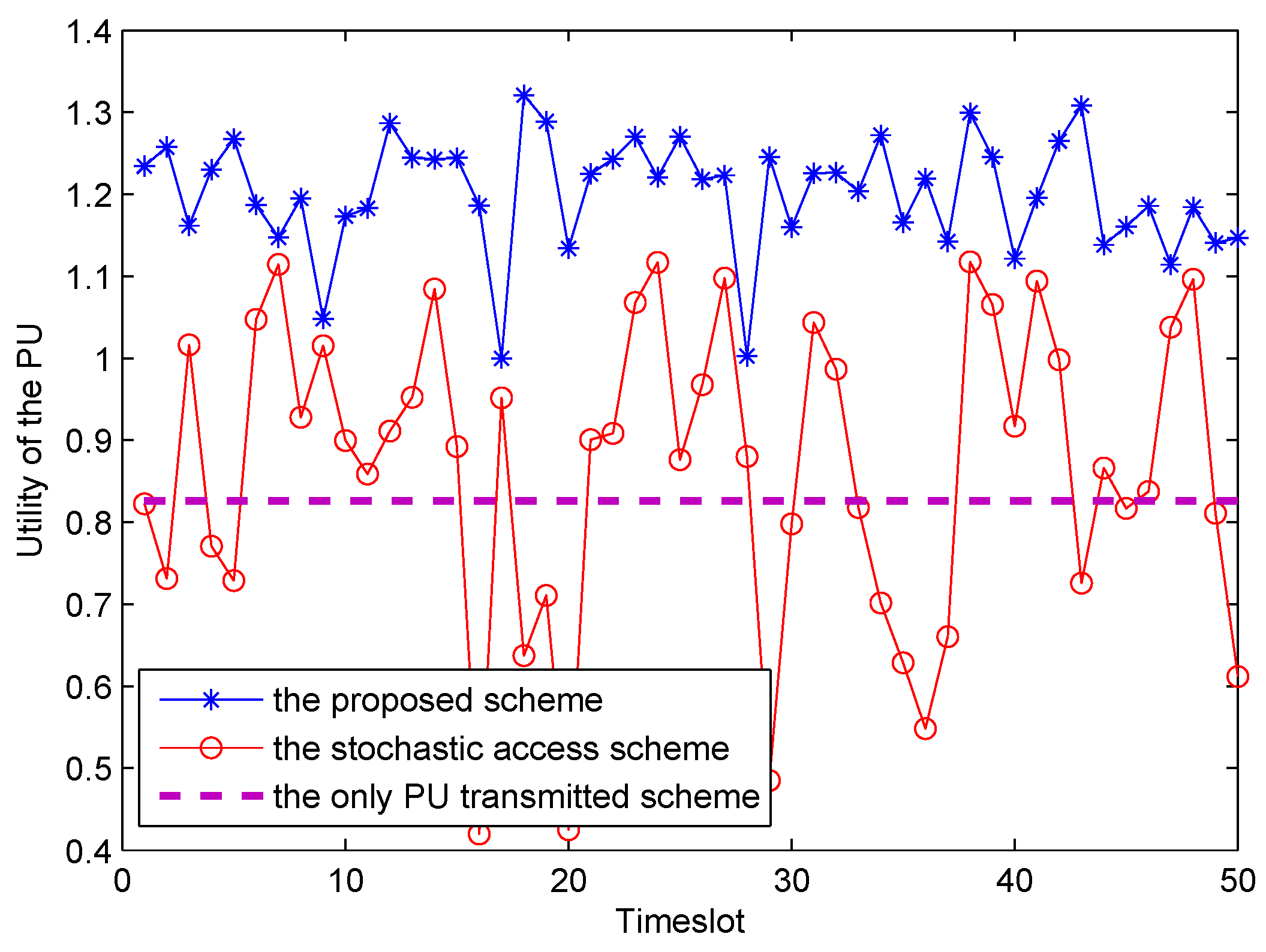
Figure 8 shows the utility of the PU with respect to different
X in the corresponding time-slot for different access schemes. As shown in
Figure 8, it is obvious that utility of our proposed spectrum leasing scheme outperforms that of the stochastic access scheme to a large extent. In the stochastic access scheme, the
follows a Poisson distribution. Due to the monopolizing on the entire frame by PU in the only PU transmitted scheme, the energy harvesting ratio is not relevant to utility of the PU. Therefore, the utility of PU is identically equals to 0.826. In conclusion, this is the reason why the PU is willing to rent a fraction of time slot to the SU.
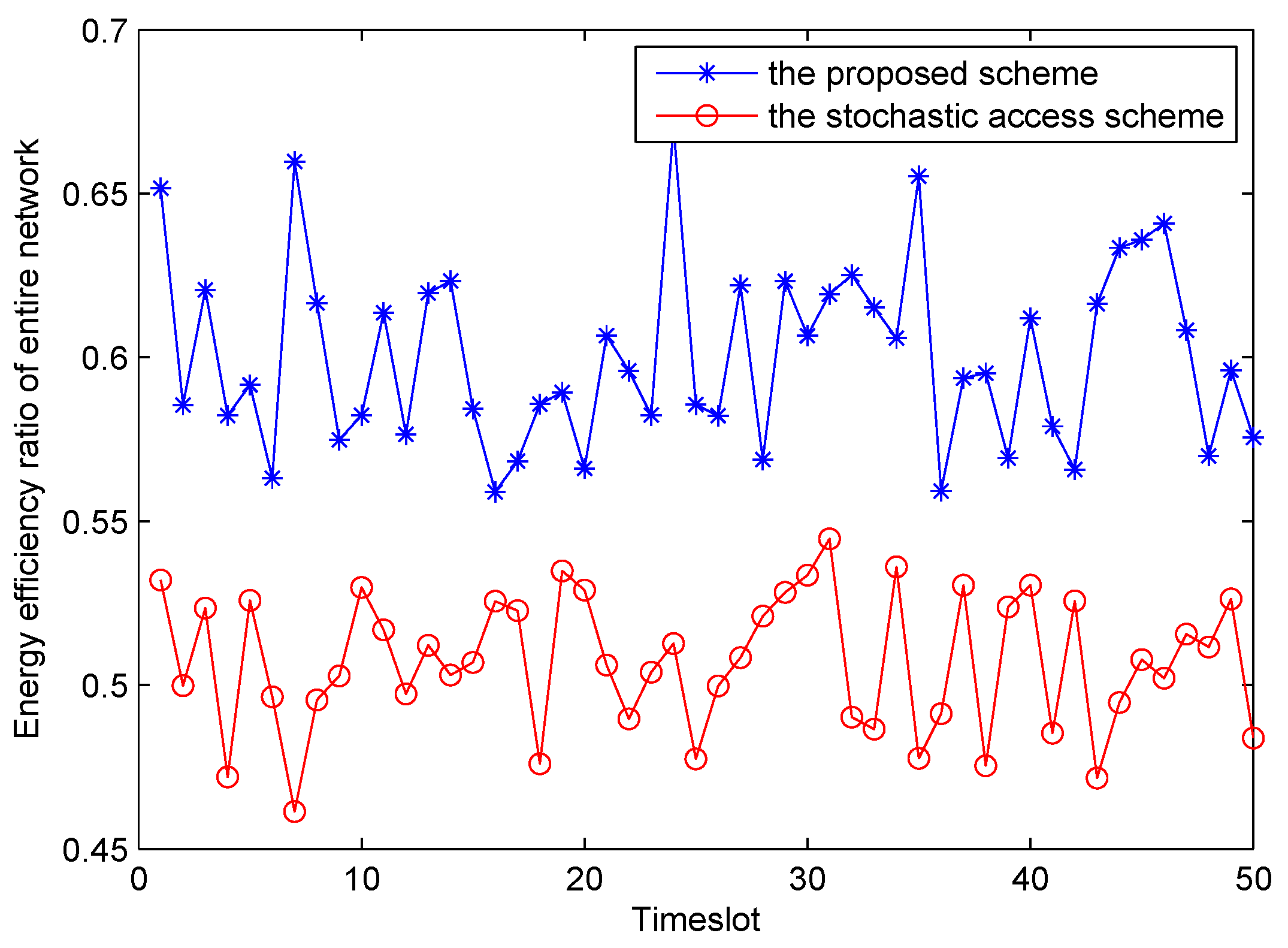
We also compared the energy efficiency ratio of our proposed energy harvesting mode based on optimal leasing time with that of stochastic access. The simulation results (50 time-slot energy efficiency ratio traces) with different probability distributions of energy harvesting ratio
X are depicted in
Figure 9, apparently, it can be seen that energy utilization rate of our proposed scheme is higher than that of stochastic scheme. Overall, obvious superiority and viability of the proposed scheme in this paper have been confirmed.