Accelerometry-Based Activity Recognition and Assessment in Rheumatic and Musculoskeletal Diseases
Abstract
:1. Introduction
1.1. Activity Detection and Recognition
1.2. Activity Assessment
2. Experimental Section
2.1. Data Acquisition
2.2. Activity Recognition: Fusing Patterns and Signal Features
2.2.1. Dynamic Region Detection
- (1)
- Rough segmentation: The first phase provides a rough per-channel segmentation. The signals are divided in windows of one second, with 50% overlap. The standard deviation and range are then compared to empirical thresholds. The regions for which both thresholds are exceeded are marked as ‘dynamic’.
- (2)
- Refining: Then, the initial segmentation is refined based on the variance of the static regions (regions between two dynamic segments). Shrinking and extending with a quarter of a second are considered. The decision is based on the difference in variance between half-second regions. The initial and final half second of a static region serve as baselines. For the start of the static segment, extending is accepted if the half second starting at a quarter second before the current start has a variance that is maximally 10% higher than the baseline. This tries to grow the static regions avoiding incorporating too much movement. Shrinking is accepted if the variance of the half second starting at a quarter second later than the current start is at least 10% lower. This tries to eliminate movement at the start of the region. For the end of the region, the procedure is identical. The value of 10% was chosen empirically as an acceptable difference.
- (3)
- Merging: After refinement of the segmentation, the channels are joined. A region is considered dynamic if one of its channel regions is dynamic. Furthermore, if regions are less than half a second apart and their mean is similar, they are joined. Finally, dynamic segments of less than one second are discarded.
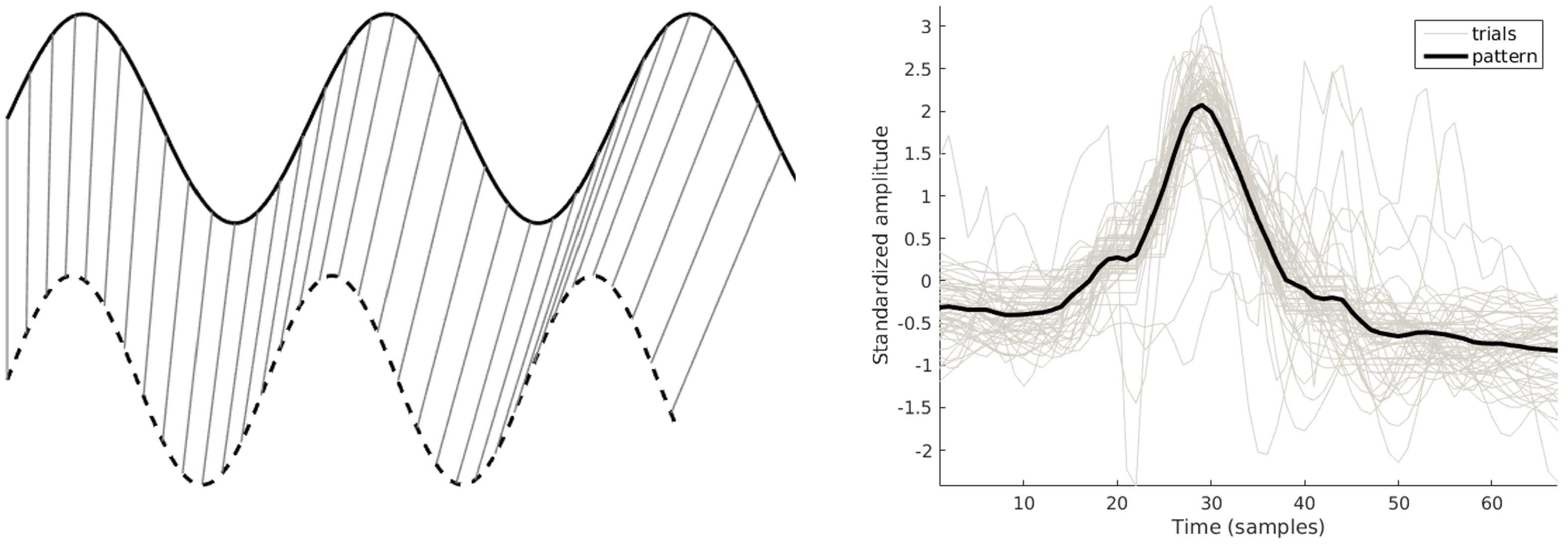
2.2.2. Pattern and Feature Extraction
Pattern-Based Features
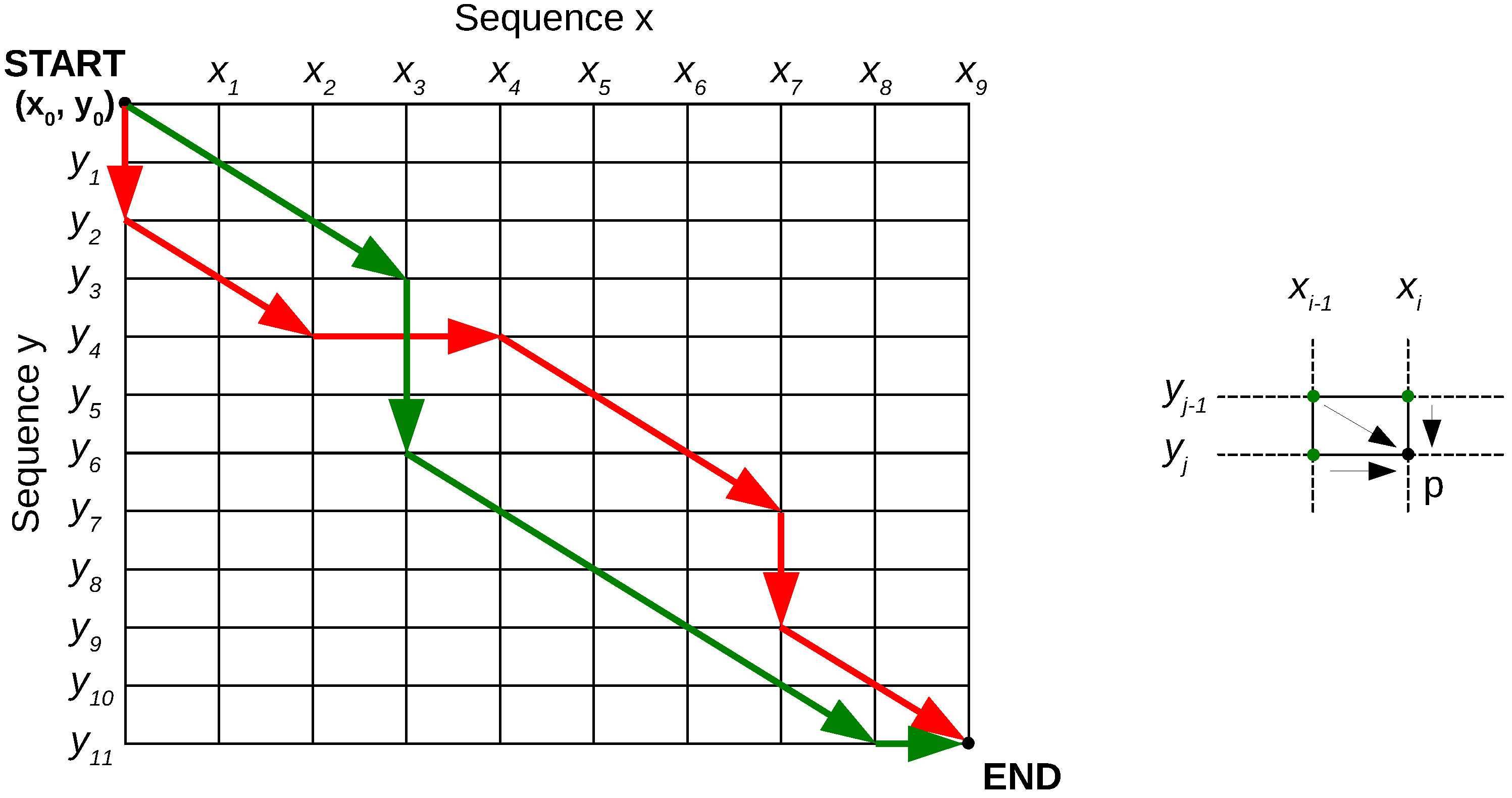
- (1)
- Calculate the costs of the paths to the top row or leftmost column points in the warping grid in Figure 3.
- (2)
- Calculate the rest of the grid point costs using Equation (1), row-by-row or column-by-column.
- (3)
- Once the end is reached, the final optimal cost is known. Backtrack through the grid using the costs to find the optimal path.
Window Features
- The duration of the activity is already used in several studies as an important marker (1). It is defined as , with the sample frequency of 32 Hz.
- The means of and give among others information about the orientation of the sensor due to the gravity component (2).
- We divide the segment S in three uniform bins (indices 1…N/3, N/3+1…2N/3 and 2N/3+1…N, rounded to integer values) for a coarse approximation. For each bin, we compute the two channel means, e.g., , , etc. This yields 6 features (6).
- We also calculate the standard deviation (2), power (2) and range (2) of and . They characterize the intensity of the activity.
- Line length (2) and spectral entropy (2) provide insight in the complexity of each channel’s acceleration. The following definitions were used:with . is the normalized power spectrum of the channel , and ‘log’ is Briggs’ logarithm.
- Finally, the average of the autocorrelation function for N/7 lags (rounded to the nearest integer), each 1/ apart, of each channel (2) relates to the repetitive nature of some activities. The length-dependent number of lags was estimated empirically.
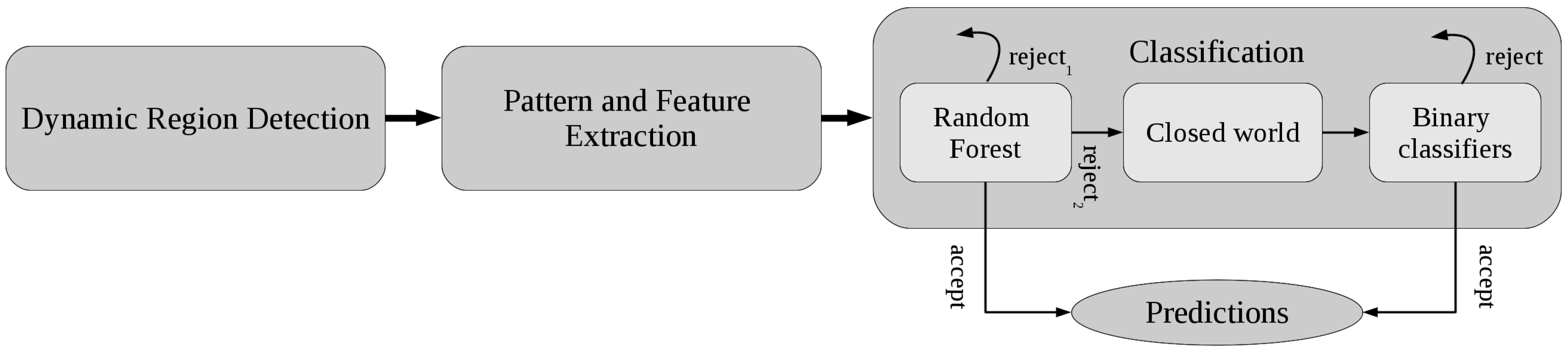
2.2.3. Classification
Stage 1. Random Forest with Rejection
Stage 2. A Closed World Assumption
Stage 3. Activity-Specific Binary Classifiers
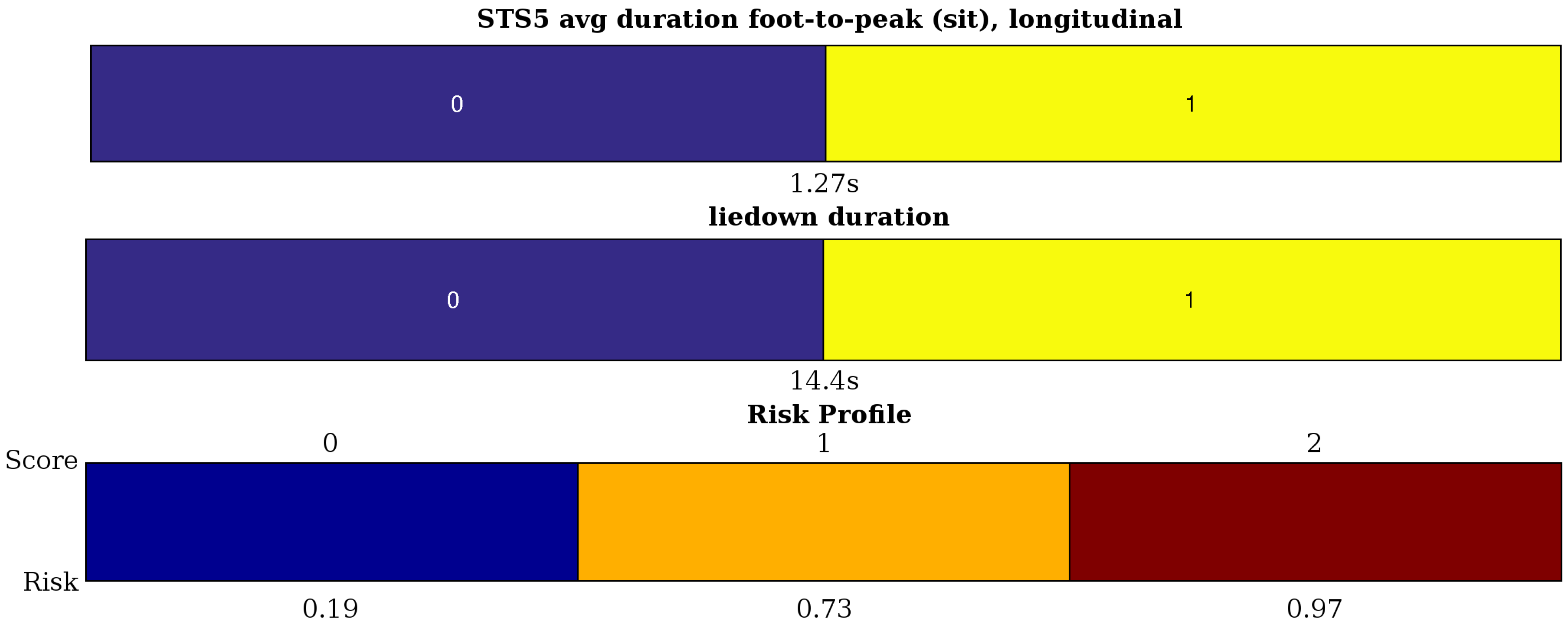
2.3. Activity Assessment: Interval Coded Scoring
Usage for Activity Assessment
- The duration of each activity (6).
- For getup, liedown and maxreach, we define the maximum acceleration (1), the slope of a linear approximation of the signal (1) and the variance around this slope (1) for the longitudinal channel and the variance of the sagittal channel (1).
- pen5 and reach5 contain local maxima in the acceleration signals. As features, we take the average peak values (1) and the average (1) and standard deviation (1) of the peak-to-peak duration. This captures their acceleration capability, as well as the variability in the execution of the repetitive activities. Furthermore, this is quantified even further by also looking at the average foot-to-peak duration (1) and the average slopes of these subsegments (1). This is all measured on the longitudinal channel. For reach5, the peaks in the sagittal channel are clear, as well, hence, the average peak value is yet another feature (1).
- STS5 (sit-to-stand) has a more complicated acceleration pattern in both channels with two kinds of local peaks: the locally-maximal acceleration towards sitting and towards standing. Therefore, on both channels, we define the average ‘sit peak’ (2) and ‘stand peak’ value (2). We can also define the mean foot-to-peak durations for sit and stand (4). Finally, the non-smoothness of the movement is measured by the variance of the channels (2) filtered with a high-pass fourth order Butterworth filter (cutoff at 2.4 Hz).
| Algorithm 1 Activity assessment |
|
3. Results
3.1. Evaluating Recognition
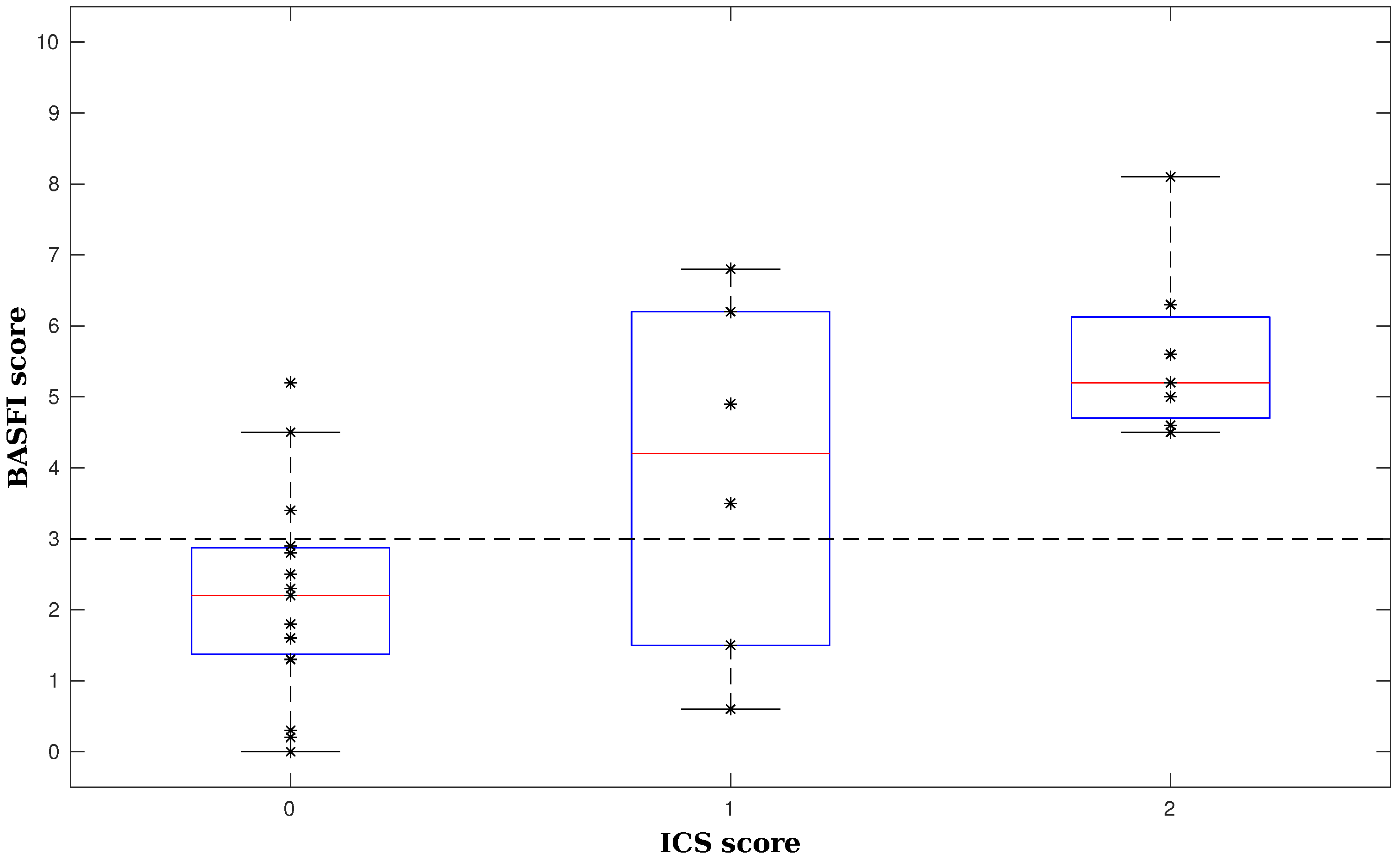
3.2. Evaluating Assessment of the Activity Capacity
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- European Musculoskeletal Conditions Surveillance and Information Network (eumusc.net). Musculoskeletal Health in Europe Report v5.0. Available online: http://eumusc.net/myUploadData/files/MusculoskeletalHealthinEuropeReportv5.pdf (accessed on 14 December 2016).
- Sieper, J.; Braun, J. Clinician’s Manual on Axial Spondyloarthritis; Springer Healthcare Ltd.: London, UK, 2014. [Google Scholar]
- Van Weely, S.F.; van Denderen, J.C.; Steultjens, M.P.; van der Leeden, M.; Nurmohamed, M.T.; Dekker, J.; Dijkmans, B.A.; van der Horst-Bruinsma, I.E. Moving instead of asking? Performance-based tests and BASFI-questionnaire measure different aspects of physical function in ankylosing spondylitis. Arthritis Res. Ther. 2012, 14, R52. [Google Scholar] [CrossRef] [PubMed]
- Calin, A.; Garrett, S.; Whitelock, H.; Kennedy, L.G.; O’Hea, J.; Mallorie, P.; Jenkinson, T. A new approach to defining functional ability in ankylosing spondylitis: The development of the Bath Ankylosing Spondylitis Functional Index. Rheumatology 1994, 21, 2281–2285. [Google Scholar]
- Jette, A.M.; Haley, S.M.; Kooyoomjian, J.T. Are the ICF Activity and Participation dimensions distinct? J. Rehabil. Med. 2003, 35, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Brionez, T.F.; Assassi, S.; Reveille, J.D.; Learch, T.J.; Diekman, L.; Ward, M.M.; Davis, J.C.; Weisman, M.H.; Nicassio, P. Psychological correlates of self-reported functional limitation in patients with ankylosing spondylitis. Arthritis Res. Ther. 2009, 11, R182. [Google Scholar] [CrossRef] [PubMed]
- Swinnen, T.W.; Milosevic, M.; Van Huffel, S.; Dankaerts, W.; Westhovens, R.; de Vlam, K. Instrumented BASFI (iBASFI) Shows Promising Reliability and Validity in the Assessment of Activity Limitations in Axial Spondyloarthritis. J. Rheumatol. 2016, 43, 1532–1540. [Google Scholar] [CrossRef] [PubMed]
- Alberts, J.; Hirsch, J.; Koop, M.; Schindler, D.; Kana, D.; Linder, S.; Campbell, S.; Thota, A. Using Accelerometer and Gyroscopic Measures to Quantify Postural Stability. J. Athl. Train. 2015, 50, 578–588. [Google Scholar] [CrossRef] [PubMed]
- Reichert, M.; Lutz, A.; Deuschle, M.; Gilles, M.; Hill, H.; Limberger, M.F.; Ebner-Priemer, U.W. Improving Motor Activity Assessment in Depression: Which Sensor Placement, Analytic Strategy and Diurnal Time Frame are Most Powerful in Distinguishing Patients from Controls and Monitoring Treatment Effects. PLoS ONE 2015, 10, e0124231. [Google Scholar] [CrossRef] [PubMed]
- Taraldsen, K.; Chastin, S.F.M.; Riphagen, I.I.; Vereijken, B.; Helbostad, J.L. Physical activity monitoring by use of accelerometer-based body-worn sensors in older adults: A systematic literature review of current knowledge and applications. Maturitas 2012, 71, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Bourke, A.; O’Brien, J.; Lyons, G. Evaluation of a threshold-based tri-axial accelerometer fall detection algorithm. Gait Posture 2007, 26, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Altini, M.; Penders, J.; Vullers, R.; Amft, O. Estimating Energy Expenditure Using Body-Worn Accelerometers: A Comparison of Methods, Sensors Number and Positioning. IEEE J. Biomed. Health 2015, 19, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Semanik, P.A.; Lee, J.; Song, J.; Chang, R.W.; Sohn, M.W.; Ehrlich-Jones, L.; Ainsworth, B.E.; Nevitt, M.M.; Kwoh, C.K.; Dunlop, D.D. Accelerometer-monitored sedentary behavior and observed physical function loss. Am. J. Public Health 2015, 105, 560–566. [Google Scholar] [CrossRef] [PubMed]
- Attal, F.; Mohammed, S.; Dedabrishvili, M.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. Physical Human Activity Recognition Using Wearable Sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef] [PubMed]
- Avci, A.; Bosch, S.; Marin-Perianu, M.; Marin-Perianu, R.; Havinga, P. Activity Recognition Using Inertial Sensing for Healthcare, Wellbeing and Sports Applications: A Survey. In Proceedings of the Architecture of Computing Systems (ARCS’10), Hannover, Germany, 22–25 February 2010; pp. 1–10.
- Preece, S.; Goulermas, J.; Kenney, L.; Howard, D.; Meijer, K.; Crompton, R. Activity identification using body-mounted sensors—A review of classification techniques. Physiol. Meas. 2009, 30, R1. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Dallas, T. Feature Selection and Activity Recognition System Using a Single Triaxial Accelerometer. IEEE Trans. Biomed. Eng. 2014, 61, 1780–1786. [Google Scholar] [CrossRef] [PubMed]
- Huisinga, J.M.; Mancini, M.; St. George, R.J.; Horak, F.B. Accelerometry Reveals Differences in Gait Variability between Patients with Multiple Sclerosis and Healthy Controls. Ann. Biomed. Eng. 2012, 41, 1670–1679. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Sawchuk, A.A. Motion Primitive-Based Human Activity Recognition Using a Bag-of-Features Approach. In Proceedings of the SIGHIT International Health Informatics Symposium (SIGHIT IHI’12), Miami, FL, USA, 28–30 January 2012; pp. 631–640.
- Kale, N.; Lee, J.; Lotfian, R.; Jafari, R. Impact of Sensor Misplacement on Dynamic Time Warping Based Human Activity Recognition Using Wearable Computers. In Proceedings of the Wireless Health (WH’12), La Jolla, CA, USA, 22–25 October 2012.
- Ganea, R.; Paraschiv-lonescu, A.; Aminian, K. Detection and Classification of Postural Transitions in Real-World Conditions. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 688–696. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer Science&Business Media: New York, NY, USA, 2006. [Google Scholar]
- Alvarado, A. A practical score for the early diagnosis of acute appendicitis. Ann. Emerg. Med. 1986, 15, 557–564. [Google Scholar] [CrossRef]
- Camm, A.J.; Lip, G.Y.; De Caterina, R.; Savelieva, I.; Atar, D.; Hohnloser, S.H.; Hindricks, G.; Kirchhof, P.; Bax, J.J.; Baumgartner, H.; et al. 2012 focused update of the ESC Guidelines for the management of atrial fibrillation. Eur. Heart J. 2012, 33, 2719–2747. [Google Scholar] [CrossRef] [PubMed]
- Mounzer, R.; Langmead, C.J.; Wu, B.U.; Evans, A.C.; Bishehsari, F.; Muddana, V.; Singh, V.K.; Slivka, A.; Whitcomb, D.C.; Yadav, D.; et al. Comparison of Existing Clinical Scoring Systems to Predict Persistent Organ Failure in Patients With Acute Pancreatitis. Gastroenterology 2012, 142, 1476–1482. [Google Scholar] [CrossRef] [PubMed]
- Lukas, C.; Landewé, R.; Sieper, J.; Dougados, M.; Davis, J.; Braun, J.; van der Linden, S.; van der Heijde, D. Development of an ASAS-endorsed disease activity score (ASDAS) in patients with ankylosing spondylitis. Ann. Rheum. Dis. 2009, 68, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Rish, I.; Grabarnik, G. Sparse Modeling: Theory, Algorithms, and Applications, 1st ed.; CRC Press Inc.: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ustun, B.; Rudin, C. Supersparse Linear Integer Models for Optimized Medical Scoring Systems. Comput. Res. Repos. 2015, 1502, 04269. [Google Scholar] [CrossRef]
- McRoberts. Movetest: Unobtrusive Assessment of Physical Performance under Supervised Conditions. Available online: www.mcroberts.nl/products/movetest (accessed on 15 October 2016).
- Sieper, J.; van der Heijde, D.; Landewe, R.; Brandt, J.; Burgos-Vagas, R.; Collantes-Estevez, E.; Dijkmans, B.; Dougados, M.; Khan, M.; Leirisalo-Repo, M.; et al. New criteria for inflammatory back pain in patients with chronic back pain: A real patient exercise by experts from the Assessment of Spondyloarthritis international Society (ASAS). Ann. Rheum. Dis. 2009, 68, 784–788. [Google Scholar] [CrossRef] [PubMed]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef]
- Long, X. On the Analysis and Classification of Sleep Stages from Cardiorespiratory Activity. Ph.D. Thesis, TU Eindhoven, Eindhoven, The Netherlands, June 2015. [Google Scholar]
- Zhou, F.; la Torre, F.D. Generalized time warping for multi-modal alignment of human motion. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR’12), Providence, RI, USA, 16–21 June 2012; pp. 1282–1289.
- Billiet, L.; Swinnen, T.; Westhovens, R.; de Vlam, K.; Van Huffel, S. Activity Recognition for Physical Therapy: Fusing Signal Processing Features and Movement Patterns. In Proceedings of the 3rd International Workshop on Sensor-Based Activity Recognition and Interaction (iWOAR’16), Rostock, Germany, 23–24 June 2016.
- Homenda, W.; Luckner, M.; Pedrycz, W. Classification with Rejection: Concepts and Evaluations. In Knowledge, Information and Creativity Support Systems; Skulimowski, A.M., Kacprzyk, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 413–425. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Van Belle, V.M.C.A.; Van Calster, B.; Timmerman, D.; Bourne, T.; Bottomley, C.; Valentin, L.; Neven, P.; Van Huffel, S.; Suykens, J.A.K.; Boyd, S. A Mathematical Model for Interpretable Clinical Decision Support with Applications in Gynecology. PLoS ONE 2012, 7, e34312. [Google Scholar] [CrossRef] [PubMed]
- Billiet, L.; Van Huffel, S.; Van Belle, V. Interval Coded Scoring Index with Interaction Effects: A Sensitivity Study. In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM’16), Rome, Italy, 24–26 February 2016; pp. 33–40.
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Sørensen, T. A Method of Establishing Groups of Equal Amplitude in Plant Sociology Based on Similarity of Species Content and Its Application to Analyses of the Vegetation on Danish Commons. Biol. Skr. 1948, 5, 1–34. [Google Scholar]
- Miller, R.A.; Masarie, F.E. The demise of the “Greek Oracle” model for medical diagnostic systems. Methods Inf. Med. 1990, 29, 1–2. [Google Scholar] [PubMed]
- Akay, M.F. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 36, 3240–3247. [Google Scholar] [CrossRef]
- Lai, D.T.H.; Levinger, P.; Begg, R.K.; Gilleard, W.L.; Palaniswami, M. Automatic Recognition of Gait Patterns Exhibiting Patellofemoral Pain Syndrome Using a Support Vector Machine Approach. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 810–817. [Google Scholar] [CrossRef] [PubMed]
- Mourcou, Q.; Fleury, A.; Franco, C.; Klopcic, F.; Vuillerme, N. Performance Evaluation of Smartphone Inertial Sensors Measurement for Range of Motion. Sensors 2015, 15, 23168–23187. [Google Scholar] [CrossRef] [PubMed]
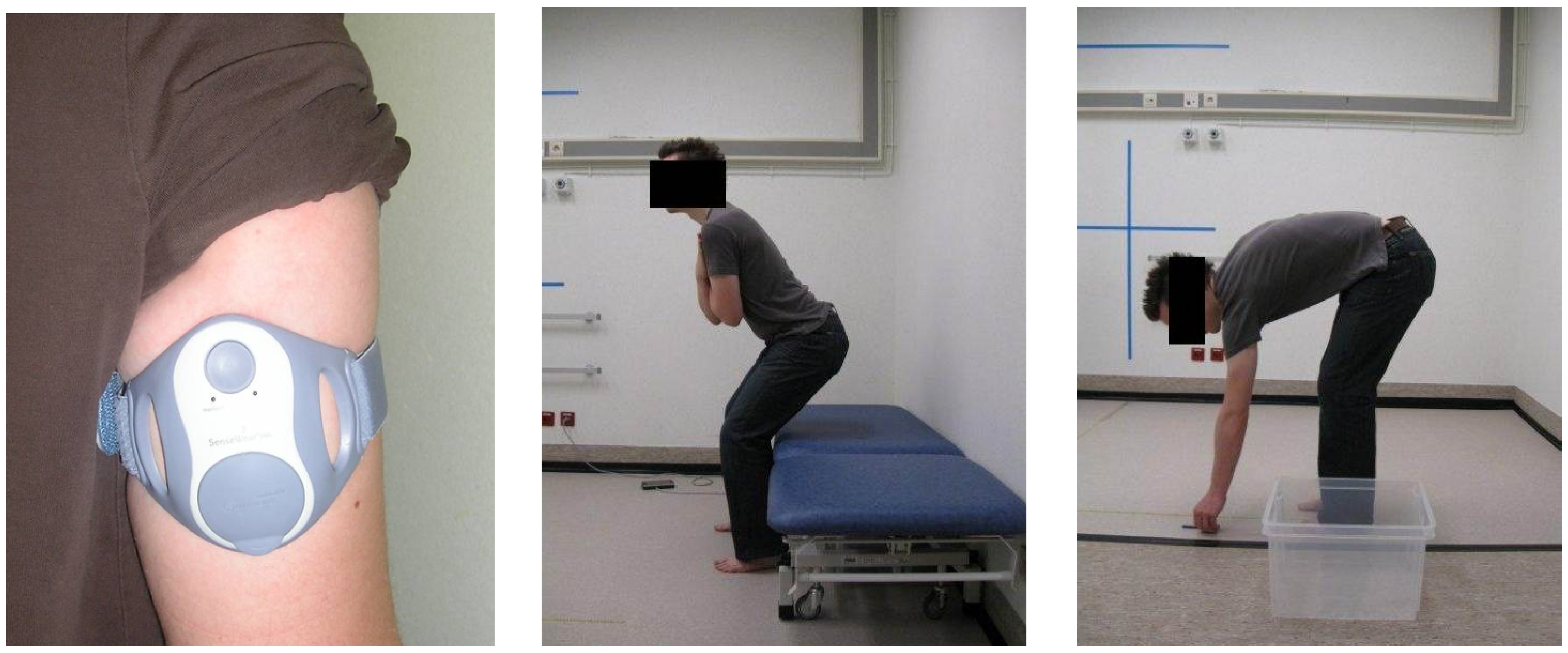
| Abbreviation | Description |
|---|---|
| getup | getting up starting from lying down |
| liedown | lying down starting from stance |
| maxreach | reaching up as far as possible |
| pen5 | picking up a pen from the ground five times, as quickly as possible |
| reach5 | touching a mark five times, as quickly as possible |
| STS5 | performing a sit-to-stand movement five times, as quickly as possible |
| Pattern Features | Number of Features |
|---|---|
| Matching cost to each activity pattern | 6 |
| Pearson’s correlation of aligned first channel | 6 |
| Pearson’s correlation of aligned second channel | 6 |
| Window Features | Number of Features |
| Duration of the activity segment | 1 |
| Mean of each channel | 2 |
| Means of three uniform time bins | 6 |
| Standard deviation for each channel | 2 |
| Power of each channel | 2 |
| Range of each channel | 2 |
| Line length of each channel | 2 |
| Spectral entropy of each channel | 2 |
| Average autocorrelation of each channel | 2 |
| nrFD | DTPR | avgSDC | stdSDC | ACC | ACC | |
|---|---|---|---|---|---|---|
| Patient 1 | 1 | 100% | 0.94 | 0.05 | 100% | 92.3% |
| Patient 2 | 0 | 91.7% | 0.93 | 0.09 | 100% | 91.7% |
| Patient 3 | 1 | 100% | 0.94 | 0.04 | 100% | 92.3% |
| Patient 4 | 1 | 100% | 0.95 | 0.03 | 91.7% | 84.6% |
| Patient 5 | 0 | 100% | 0.93 | 0.09 | 100% | 100% |
| Patient 6 | 1 | 100% | 0.95 | 0.03 | 100% | 92.3% |
| Patient 7 | 1 | 100% | 0.92 | 0.05 | 100% | 92.3% |
| Patient 8 | 0 | 100% | 0.84 | 0.11 | 100% | 100% |
| Patient 9 | 0 | 100% | 0.93 | 0.05 | 100% | 100% |
| Patient 10 | 1 | 100% | 0.91 | 0.08 | 100% | 92.3% |
| Patient 11 | 3 | 100% | 0.92 | 0.07 | 100% | 80.0% |
| Patient 12 | 1 | 100% | 0.92 | 0.06 | 100% | 92.3% |
| Patient 13 | 0 | 100% | 0.92 | 0.08 | 100% | 100% |
| Patient 14 | 0 | 100% | 0.95 | 0.03 | 100% | 100% |
| Patient 15 | 1 | 100% | 0.91 | 0.08 | 100% | 92.3% |
| Patient 16 | 0 | 100% | 0.87 | 0.08 | 100% | 100% |
| Patient 17 | 0 | 91.7% | 0.93 | 0.04 | 100% | 91.7% |
| Patient 18 | 0 | 100% | 0.91 | 0.06 | 100% | 100% |
| Patient 19 | 2 | 100% | 0.91 | 0.08 | 100% | 85.7% |
| Patient 20 | 0 | 100% | 0.96 | 0.04 | 100% | 100% |
| Patient 21 | 0 | 100% | 0.93 | 0.06 | 100% | 100% |
| Patient 22 | 1 | 100% | 0.90 | 0.10 | 100% | 92.3% |
| Patient 23 | 0 | 100% | 0.93 | 0.04 | 100% | 100% |
| Patient 24 | 0 | 100% | 0.92 | 0.08 | 100% | 100% |
| Patient 25 | 1 | 100% | 0.90 | 0.12 | 100% | 92.3% |
| Patient 26 | 1 | 75% | 0.90 | 0.09 | 100% | 69.2% |
| Patient 27 | 1 | 100% | 0.93 | 0.05 | 100% | 92.3% |
| Patient 28 | 0 | 100% | 0.88 | 0.08 | 91.7% | 91.7% |
| Average | 0.6 | 98.5% | 0.92 | – | 99.4% | 93.5% |
| Activity | nrFD | DTPR | avgSDC | stdSDC |
|---|---|---|---|---|
| getup | 6 | 98.2% | 0.92 | 0.07 |
| liedown | 0 | 96.4% | 0.89 | 0.10 |
| maxreach | 6 | 100% | 0.87 | 0.06 |
| pen5 | 5 | 96.4% | 0.95 | 0.06 |
| reach5 | 0 | 100% | 0.94 | 0.04 |
| STS5 | 0 | 100% | 0.95 | 0.05 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billiet, L.; Swinnen, T.W.; Westhovens, R.; De Vlam, K.; Van Huffel, S. Accelerometry-Based Activity Recognition and Assessment in Rheumatic and Musculoskeletal Diseases. Sensors 2016, 16, 2151. https://doi.org/10.3390/s16122151
Billiet L, Swinnen TW, Westhovens R, De Vlam K, Van Huffel S. Accelerometry-Based Activity Recognition and Assessment in Rheumatic and Musculoskeletal Diseases. Sensors. 2016; 16(12):2151. https://doi.org/10.3390/s16122151
Chicago/Turabian StyleBilliet, Lieven, Thijs Willem Swinnen, Rene Westhovens, Kurt De Vlam, and Sabine Van Huffel. 2016. "Accelerometry-Based Activity Recognition and Assessment in Rheumatic and Musculoskeletal Diseases" Sensors 16, no. 12: 2151. https://doi.org/10.3390/s16122151
APA StyleBilliet, L., Swinnen, T. W., Westhovens, R., De Vlam, K., & Van Huffel, S. (2016). Accelerometry-Based Activity Recognition and Assessment in Rheumatic and Musculoskeletal Diseases. Sensors, 16(12), 2151. https://doi.org/10.3390/s16122151






