Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays
Abstract
:1. Introduction
- (1)
- The k-nearest neighbour rule is introduced to solve the fault detection problem of gas sensor arrays for the first time. Based on this, the reliable detection of slight faults can be achieved because kNN naturally handles the possible non-linearity of the data samples.
- (2)
- The clustering-kNN rule is proposed to improve the efficiency of the kNN rule by reducing the number of training samples involved in the detection process of each test sample. The landmark-based spectral clustering (LSC) algorithm is employed to divide the entire training sample set into several clusters, and the kNN rule is only performed in the cluster that is nearest to the test sample.
- (3)
- The clustering-kNN rule is proposed to improve the efficiency of the kNN rule by reducing the number of training samples involved in the detection process of each test sample. The landmark-based spectral clustering (LSC) algorithm is employed to divide the entire training sample set into several clusters, and the kNN rule is only performed in the cluster that is nearest to the test sample.
- (4)
- A real experimental system for gas sensor arrays is realized to perform a series of experiments, and the results show that the proposed clustering-kNN rule can greatly enhance both the accuracy and efficiency of fault detection methods.
2. Methodology
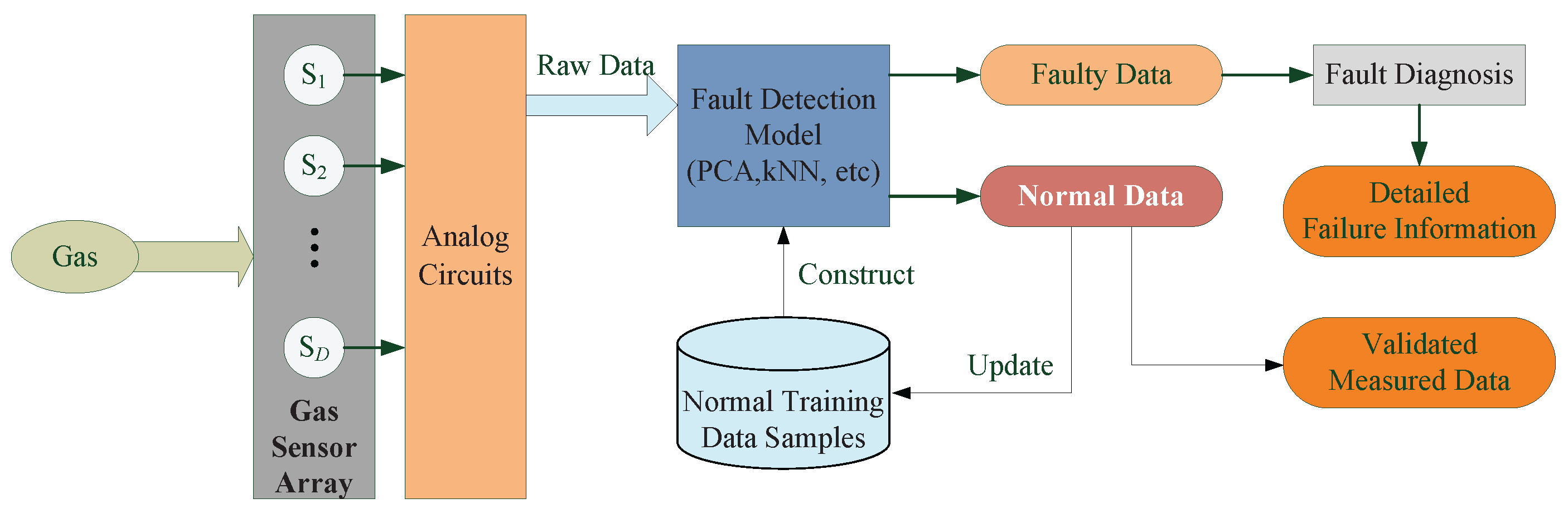
2.1. Overview
2.2. Off-Line Model Construction
2.2.1. The Landmark-Based Spectral Clustering
| Algorithm 1 Landmark-based Spectral Clustering |
| Input: Training samples , clustering number M Output: M clusters, clusters centers ,,..., 1: Produce P landmark samples using random selection or k-means methods; 2: Construct a sparse affinity matrix Z between training data samples and landmarks, with the affinity matrix calculated based on Equation (1); 3: Calculate the first M eigenvectors of , denoted by ; 4: Calculate based on Equation (5); 5: Each row of V is a sample and k-means is adopted to achieve the clusters and cluster centers. |
2.2.2. The Statistic of the Clustering-kNN-Based Fault Detection Model
2.2.3. The Threshold of the Statistic
2.3. On-Line Fault Detection
| Algorithm 2 Fault Detection based on the Clustering-kNN rule |
| Input: M clusters, clusters centers ,,...,, new test sample , the threshold of the statistic Output: Fault detection result 1: Calculate the distance between the new test sample and each cluster center, denoted by , ; 2: Computer the nearest cluster center to according to , ; 3: Adopt the cluster of as the calculation subset of the new test sample ; 4: Apply the kNN algorithm to the calculation subset of , and achieve the value of the statistic; 5: If the value of statistic is larger than the threshold , output the faulty work condition; otherwise, output the normal work condition. |
3. Simulations
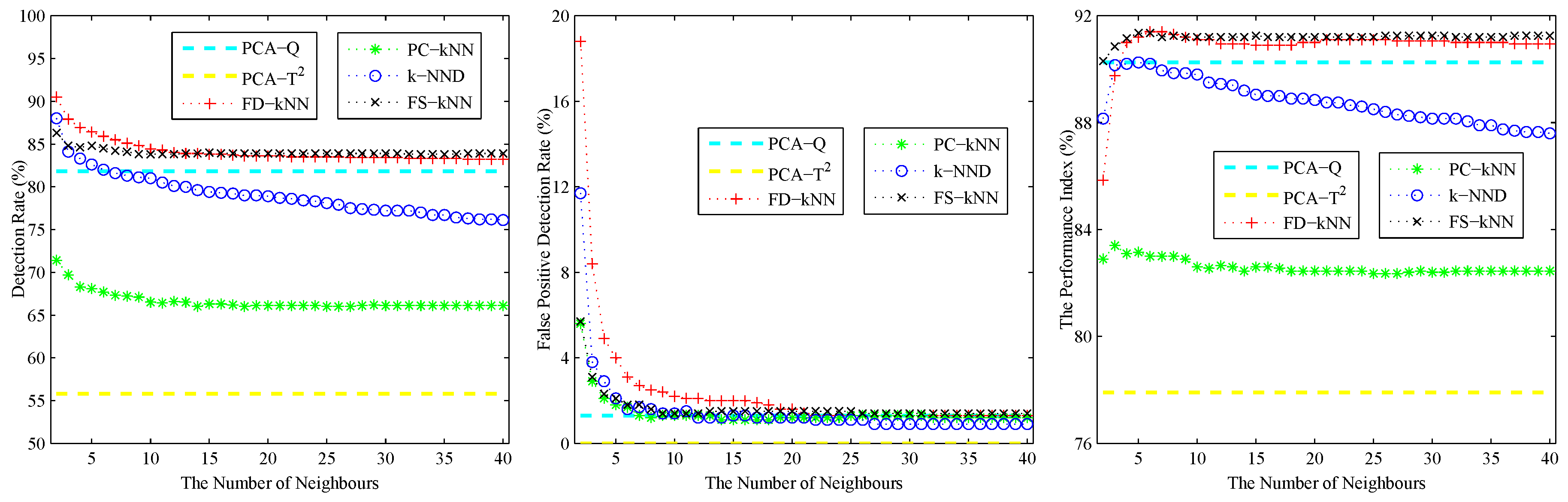
3.1. Linear Model
3.2. Non-Linear Model
4. Experiments and Results
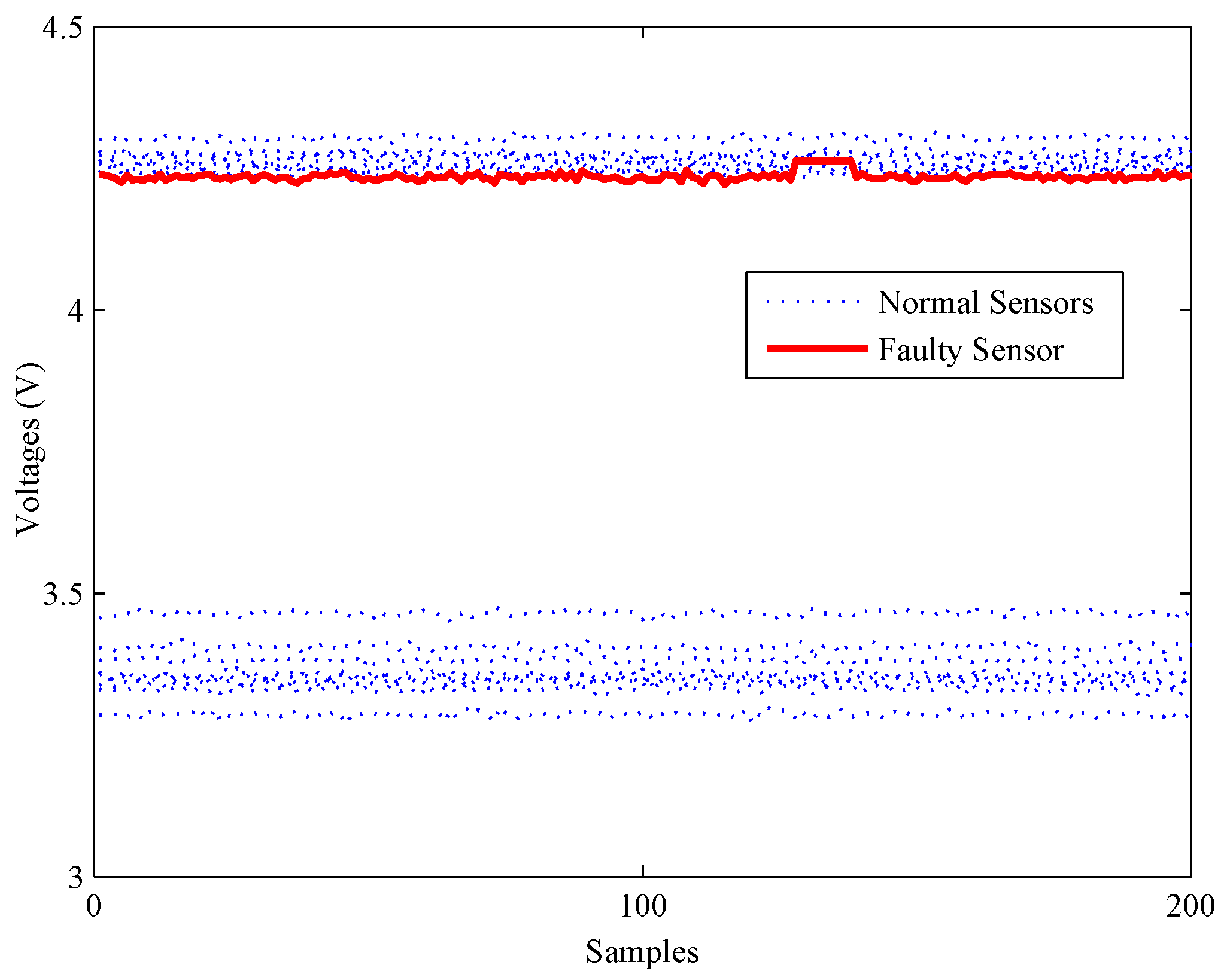
4.1. Experimental Setup
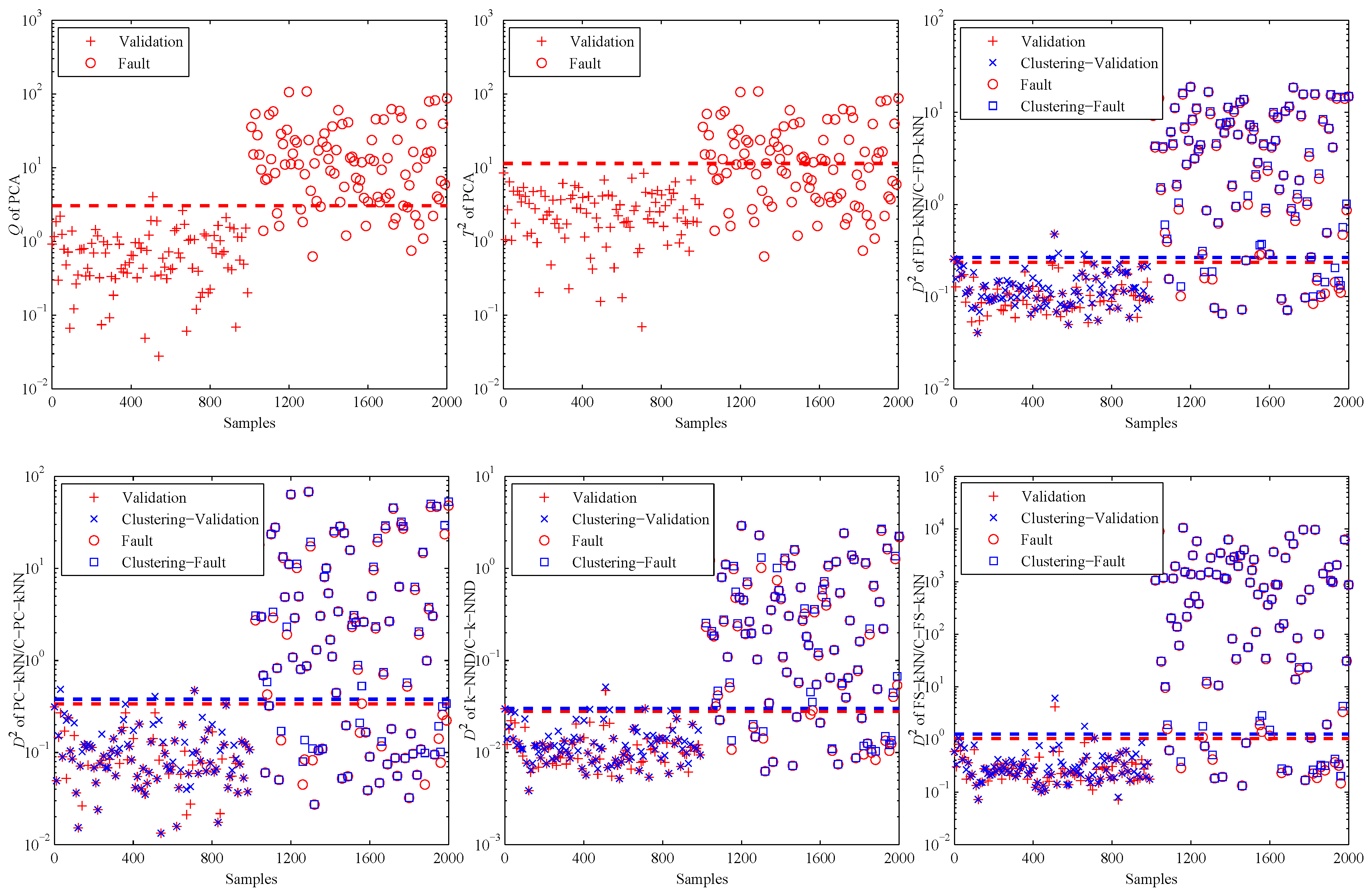
4.2. Model Construction
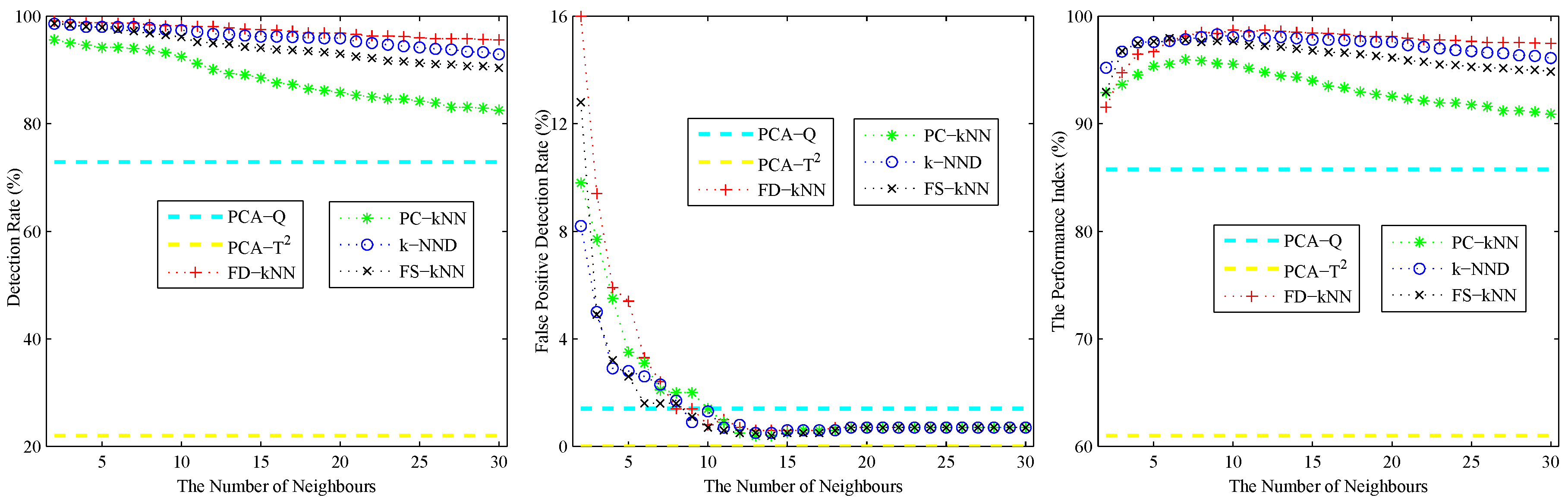
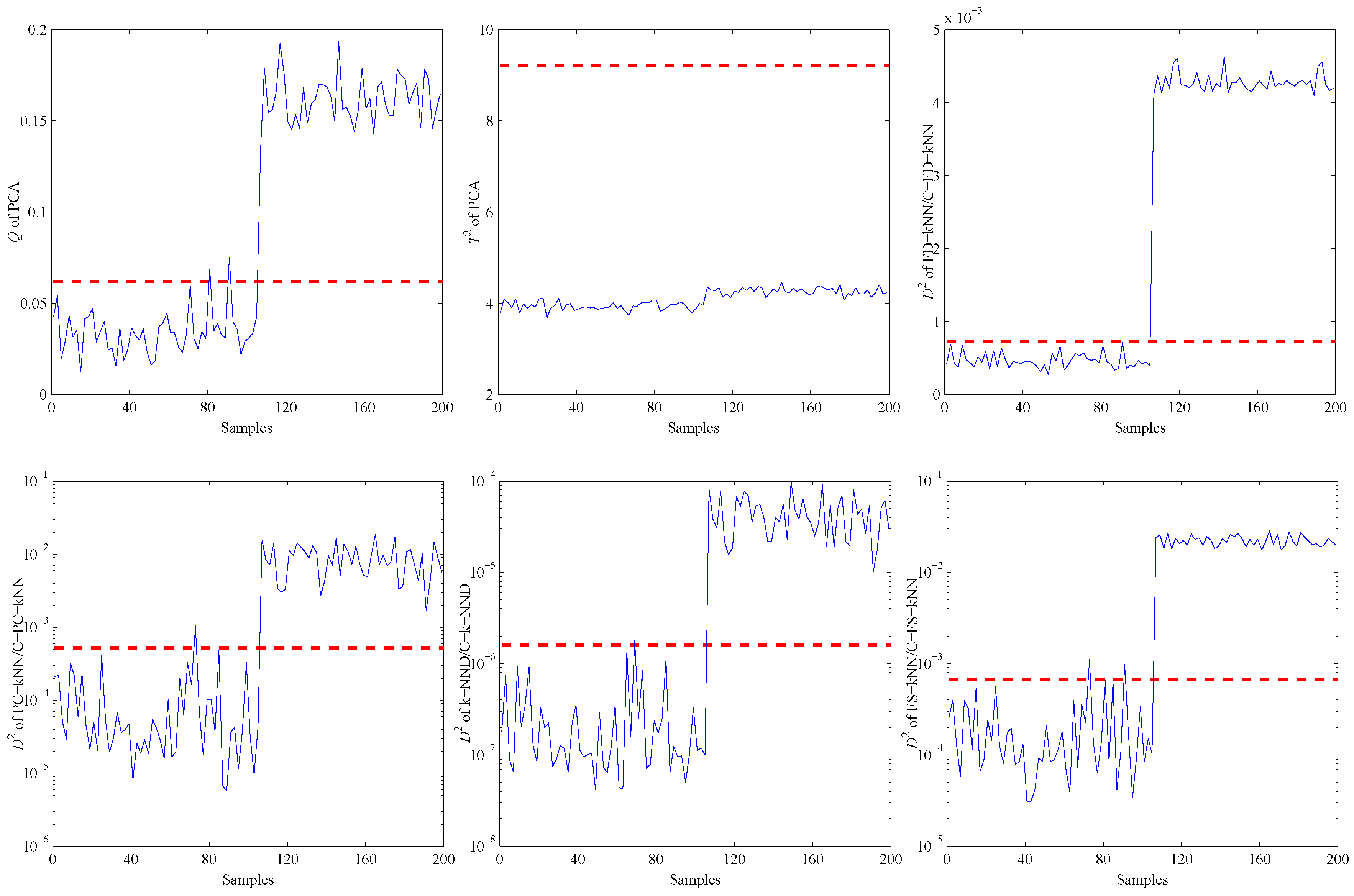
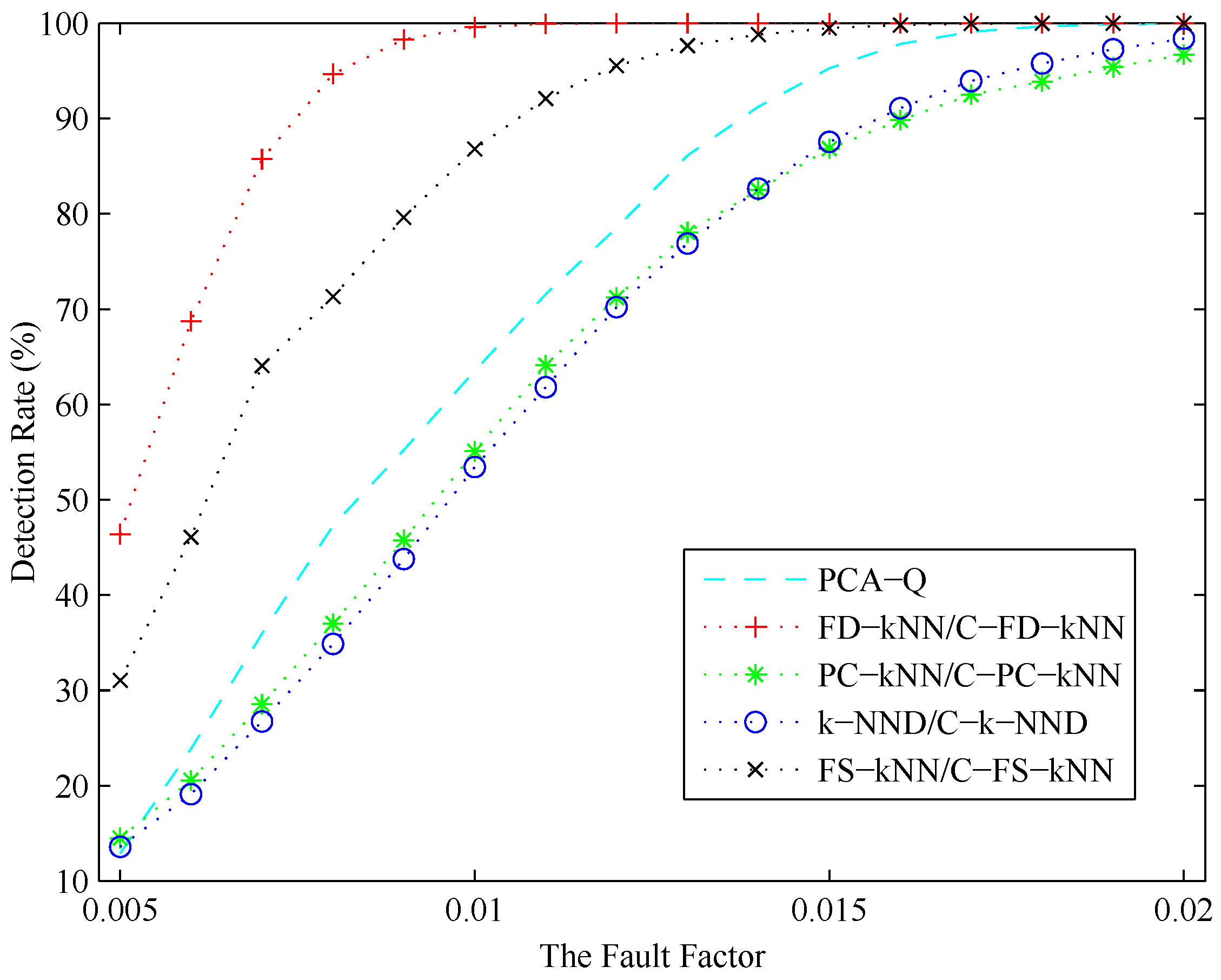
4.3. Fault Detection
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Persaud, K.; Dodd, G.H. Analysis of discrimination mechanisms of the mammalian olfactory system using a model nose. Nature 1982, 299, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Gardner, J.W.; Bartlett, P.N. A brief history of electronic noses. Sens. Actuators B Chem. 1994, 18, 210–211. [Google Scholar] [CrossRef]
- Marquis, B.T.; Vetelino, J.F. A semiconducting metal oxide sensor array for the detection of NOx and NH3. Sens. Actuators B Chem. 2001, 77, 100–110. [Google Scholar] [CrossRef]
- Hannon, A.; Lu, Y.; Li, J.; Meyyappan, M. A sensor array for the detection and discrimination of methane and other environmental pollutant gases. Sensors 2016, 16, 1163. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Li, J.; Dai, Q.; Li, D.; Ma, X.; Lv, Y. Temperature compensation and data fusion based on a multifunctional gas detector. IEEE Trans. Instrum. Meas. 2015, 64, 204–211. [Google Scholar] [CrossRef]
- Qian, X.; Yan, Y. Flow measurement of biomass and blended biomass fuels in pneumatic conveying pipelines using electrostatic sensor-arrays. IEEE Trans. Instrum. Meas. 2012, 61, 1343–1352. [Google Scholar] [CrossRef]
- Fonollosa, J.; Vergara, A. Algorithmic mitigation of sensor failure: Is sensor replacement really necessary? Sens. Actuators B Chem. 2013, 183, 211–221. [Google Scholar] [CrossRef]
- Fernandez, L.; Marco, S. Robustness to sensor damage of a highly redundant gas sensor array. Sens. Actuators B Chem. 2015, 218, 296–302. [Google Scholar] [CrossRef]
- Padilla, M.; Perera, A.; Montoliu, I.; Chaudry, A.; Persaud, K.; Marco, S. Fault Detection, Identification, and Reconstruction of Faulty Chemical Gas Sensors under Drift Conditions, Using Principal Component Analysis and Multiscale-PCA. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–7.
- Pardo, M.; Faglia, G.; Sberveglieri, G.; Corte, M.; Masulli, F.; Riani, M. Monitoring reliability of sensors in an array by neural networks. Sens. Actuators B Chem. 2000, 67, 128–133. [Google Scholar] [CrossRef]
- Yin, S.; Wang, G.; Karimi, H.R. Data-driven design of robust fault detection system for wind turbines. Mechatronics 2014, 24, 298–306. [Google Scholar] [CrossRef]
- Heredia, G.; Ollero, A. Virtual sensor for failure detection, identification and recovery in the transition phase of a morphing aircraft. Sensors 2011, 11, 2188–2201. [Google Scholar] [CrossRef] [PubMed]
- Zarei, J.; Tajeddini, M.A.; Karimi, H.R. Vibration analysis for bearing fault detection and classification using an intelligent filter. Mechatronics 2014, 24, 151–157. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Zhu, D.Q.; Bai, J.; Yang, S.X. A multi-fault diagnosis method for sensor systems based on principle component analysis. Sensors 2010, 10, 241–253. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Qin, S.; Lee, I. Fault detection and diagnosis based on modified independent component analysis. AIChE J. 2006, 52, 3501–3514. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Zhang, L.; Sun, Z. Fault detection, isolation, and diagnosis of self-validating multifunctional sensors. Rev. Sci. Instrum. 2016, 87, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Wang, Q. Failure detection, isolation and recovery of multifunctional self-validating sensor. IEEE Trans. Instrum. Meas. 2012, 61, 3351–3362. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y.; Yang, J.; Shi, Z.; Jiang, S.; Wang, Q. Fault detection, isolation, and diagnosis of status self-validating gas sensor arrays. Rev. Sci. Instrum. 2016, 87, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Scholkopf, B.; Muller, A. Nonlinear component analysis as kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1399. [Google Scholar] [CrossRef]
- Lee, J.; Yoo, C.; Lee, I. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Glowacz, A. DC motor fault analysis with the use of acoustic signals, coiflet wavelet transform, and k-nearest neighbour classifier. Arch. Acoust. 2015, 40, 321–327. [Google Scholar] [CrossRef]
- Liao, Y.; Vemuri, V.R. Use of k-nearest neighbour classifier for intrusion detection. Comput. Secur. 2002, 21, 439–448. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, Z. Diagnostics of stator faults of the single-phase induction motor using thermal images, MoASoS and selected classifiers. Measurement 2016, 93, 86–93. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Fault detection using the k-nearest neighbour rule for semiconductor manufacturing processes. IEEE Trans. Semicond. Manuf. 2007, 20, 345–354. [Google Scholar] [CrossRef]
- Zhou, Z.; Wen, C.; Yang, C. Fault isolation based on k-nearest neighbour rule for industrial processes. IEEE Trans. Ind. Electron. 2016, 63, 2578–2586. [Google Scholar]
- He, Q.P.; Wang, J. Large-scale semiconductor process fault detection using a fast pattern recognition-based method. IEEE Trans. Semicond. Manuf. 2010, 23, 194–200. [Google Scholar] [CrossRef]
- Zhou, Z.; Wen, C.; Yang, C. Fault isolation using random projections and k-nearest neighbour rule for semiconductor. IEEE Trans. Semicond. Manuf. 2016, 28, 70–79. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, J.; Li, Y. Feature space k nearest neighbour based batch process monitoring. Acta Autom. Sin. 2014, 40, 135–142. [Google Scholar]
- Verdier, G.; Ferreira, A. Adaptive mahalanobis distance and k-nearest neighbour rule for fault detection in semiconductor manufacturing. IEEE Trans. Semicond. Manuf. 2011, 24, 59–68. [Google Scholar] [CrossRef]
- Glowacz, A. Recognition of acoustic signals of synchronous motors with the use of MoFS and selected classifiers. Meas. Sci. Rev. 2015, 15, 167–175. [Google Scholar] [CrossRef]
- Zhu, X.; Suk, H.-I.; Shen, D. A novel matrix-similarity based loss function for joint regression and classification in ad diagnosis. Neuroimage 2014, 100, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Cai, D. Large Scale Spectral Clustering with Landmark-Based Representation. In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–11 August 2011; pp. 313–318.
- Zdravko, I.B.; Dirk, P.K. The generalized cross entropy method, with applications to probability density estimation. Methodol. Comput. Appl. Probab. 2011, 13, 1–27. [Google Scholar]
- Zdravko, I.B.; Dirk, P.K. Non-asymptotic bandwidth selection for density estimation of discrete data. Methodol. Comput. Appl. Probab. 2008, 10, 435–451. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: New York, NY, USA, 2012; Chapter 4. [Google Scholar]
- Aouaouda, S.; Chadli, M.; Shi, P.; Karimi, H.R. Discrete-time H−/H∞ sensor fault detection observer design for nonlinear systems with parameter uncertainty. Int. J. Robust Nonlinear Control 2015, 25, 339–361. [Google Scholar] [CrossRef]
- Yigit, H. ABC-based distance-weighted kNN algorithm. J. Exp. Theor. Artif. Intell. 2015, 27, 189–198. [Google Scholar] [CrossRef]
- Zuo, W.; Zhang, D.; Wang, K. On kernel difference-weighted k-nearest neighbour classification. Pattern Anal. Appl. 2008, 11, 247–257. [Google Scholar] [CrossRef]
- Karimi, H.R.; Zapateiro, M.; Luo, N. A linear matrix inequality approach to robust fault detection filter design of linear systems with mixed time-varying delays and nonlinear perturbations. J. Franklin Inst. 2010, 347, 957–973. [Google Scholar] [CrossRef]

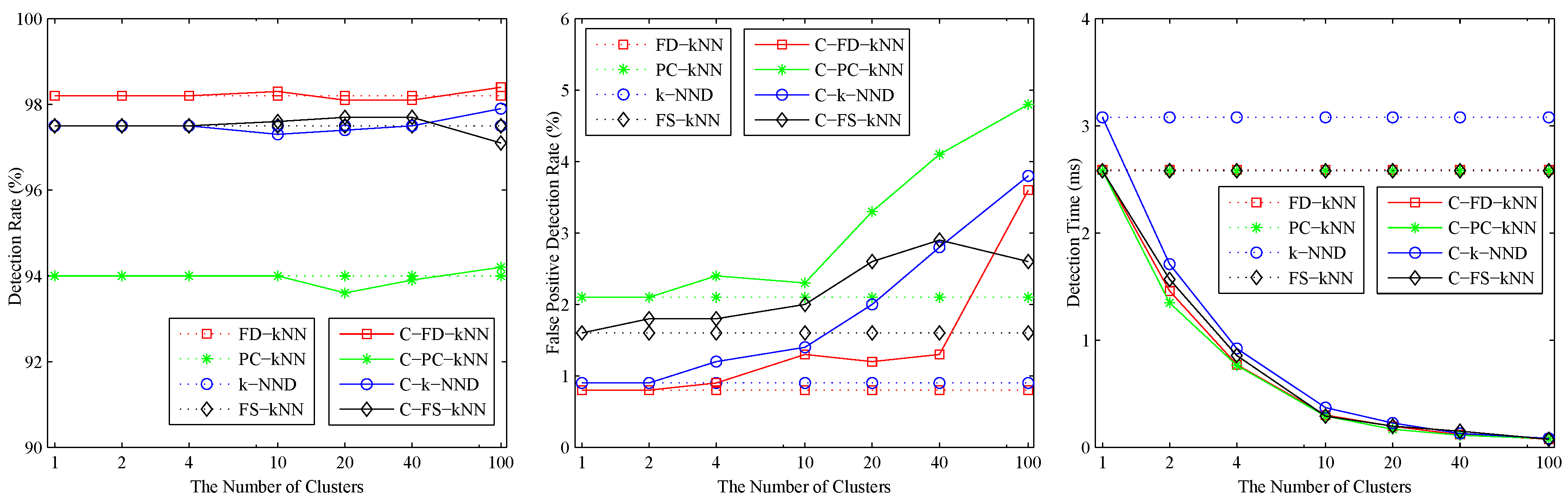
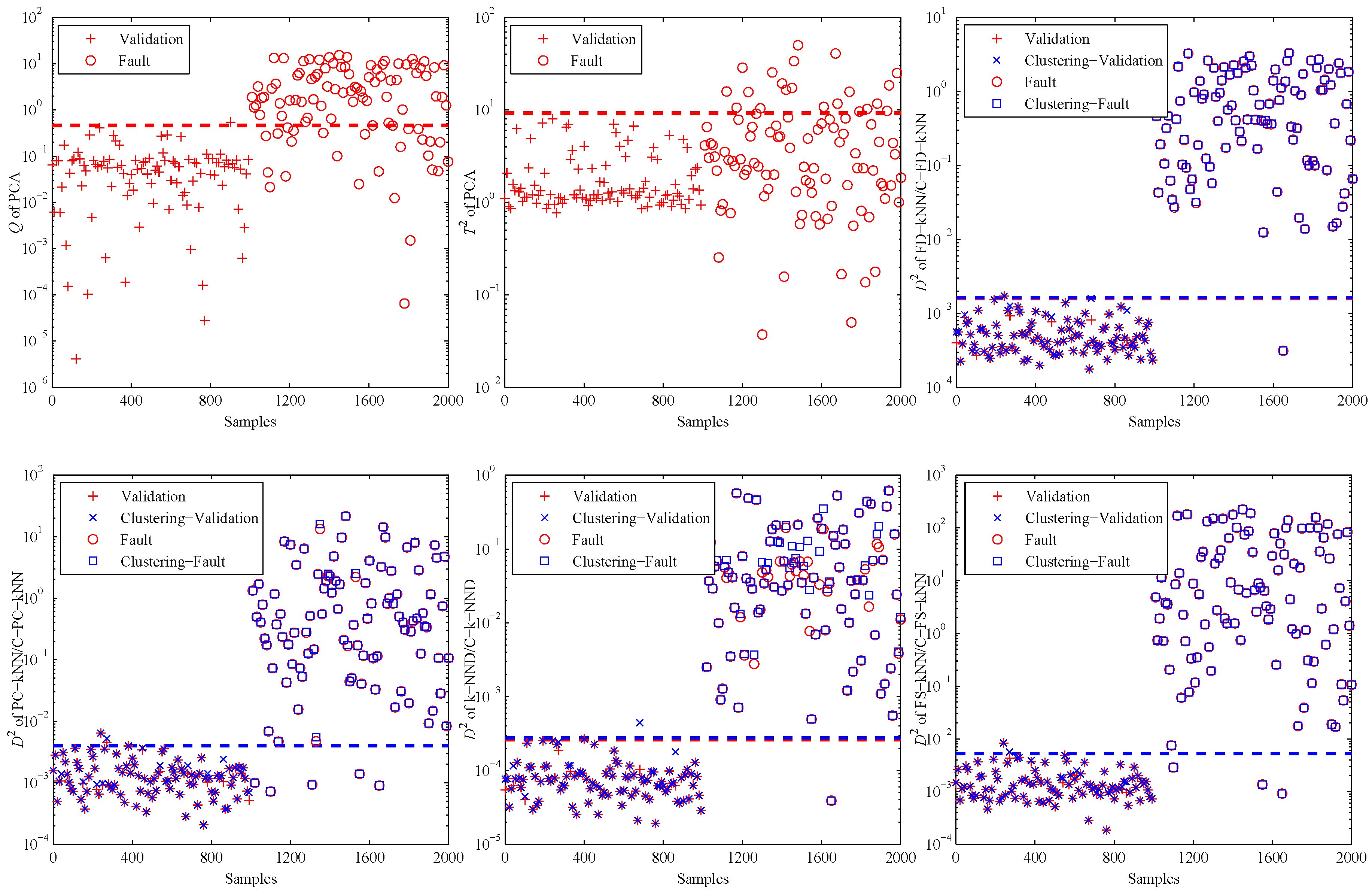

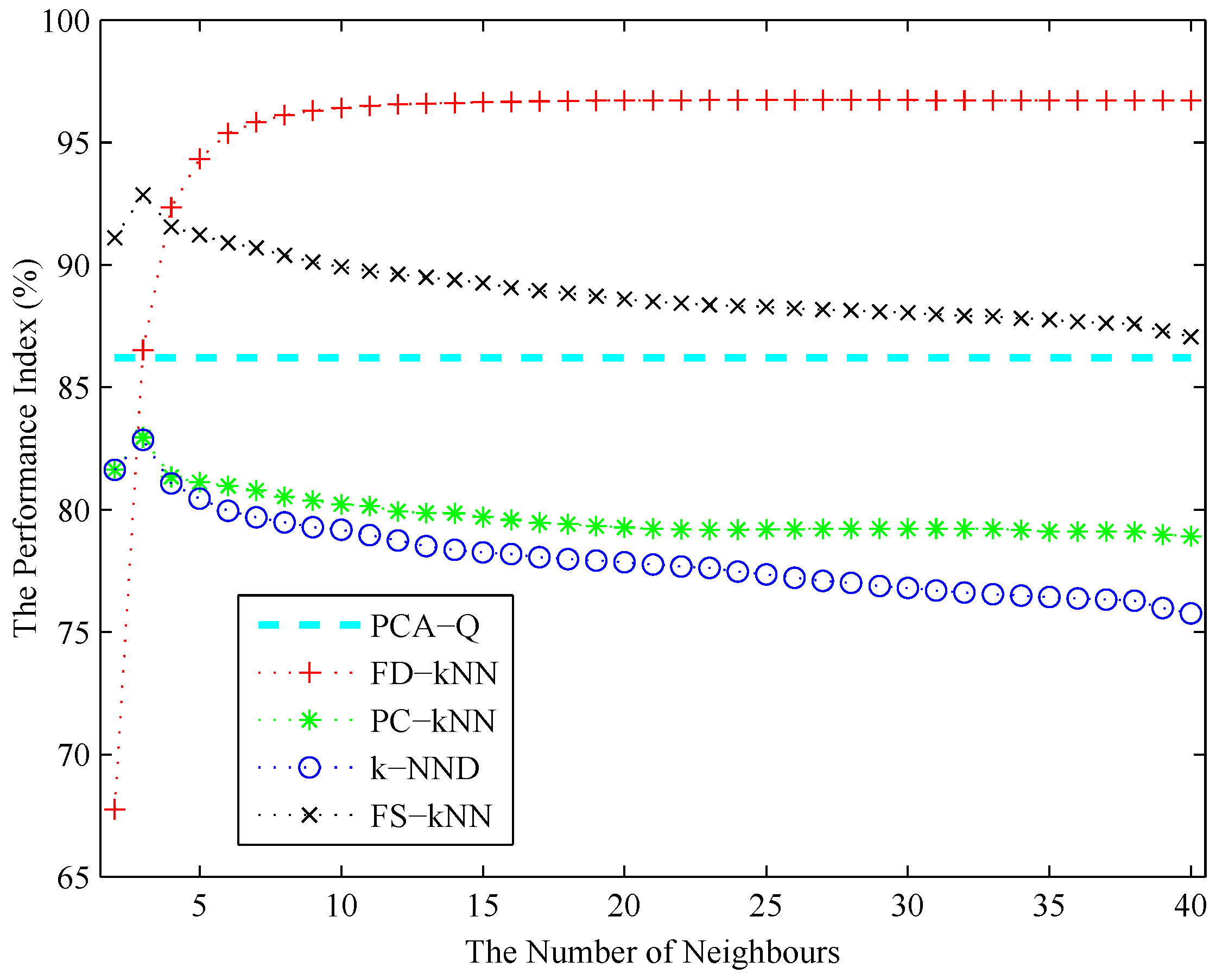
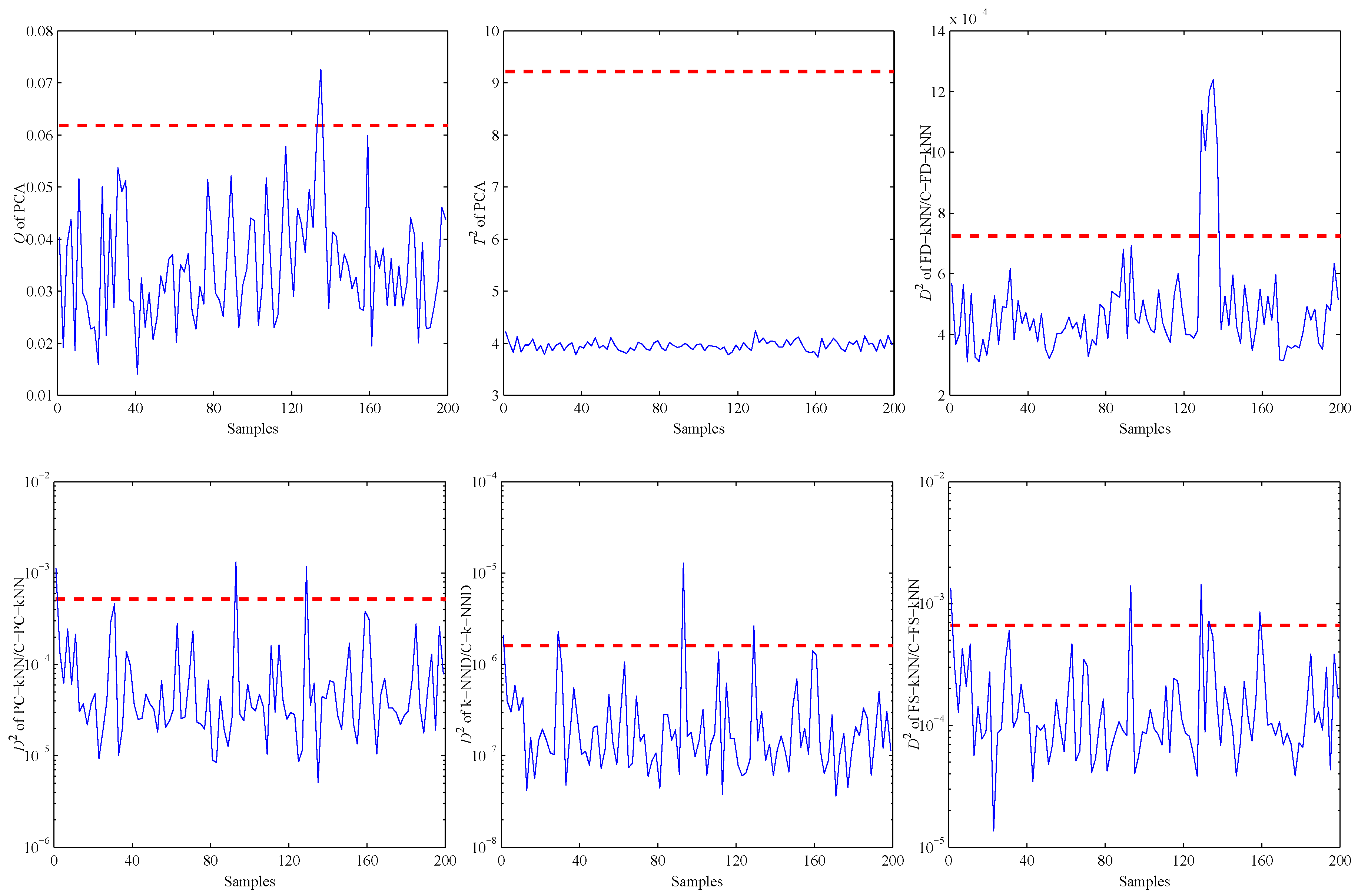
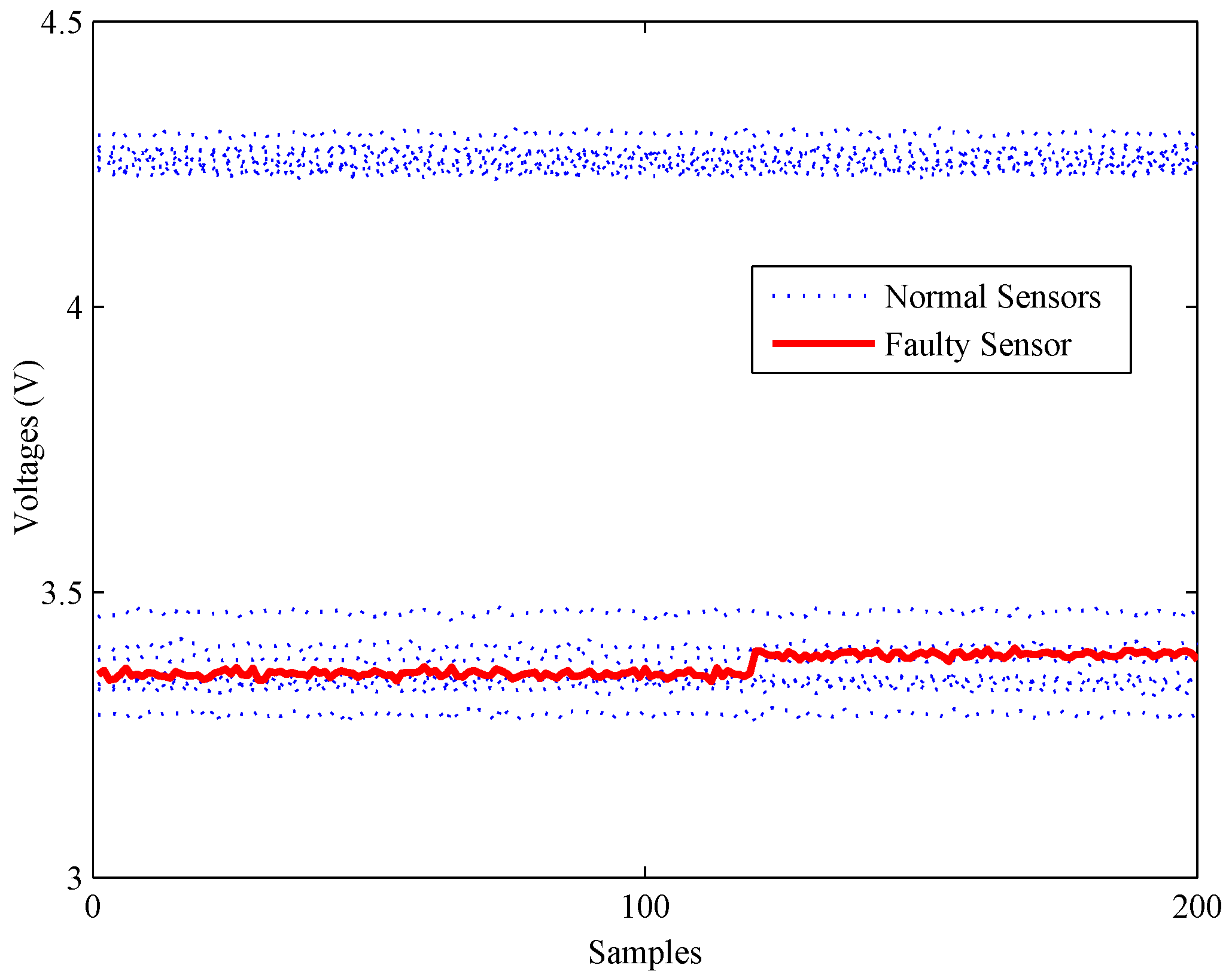
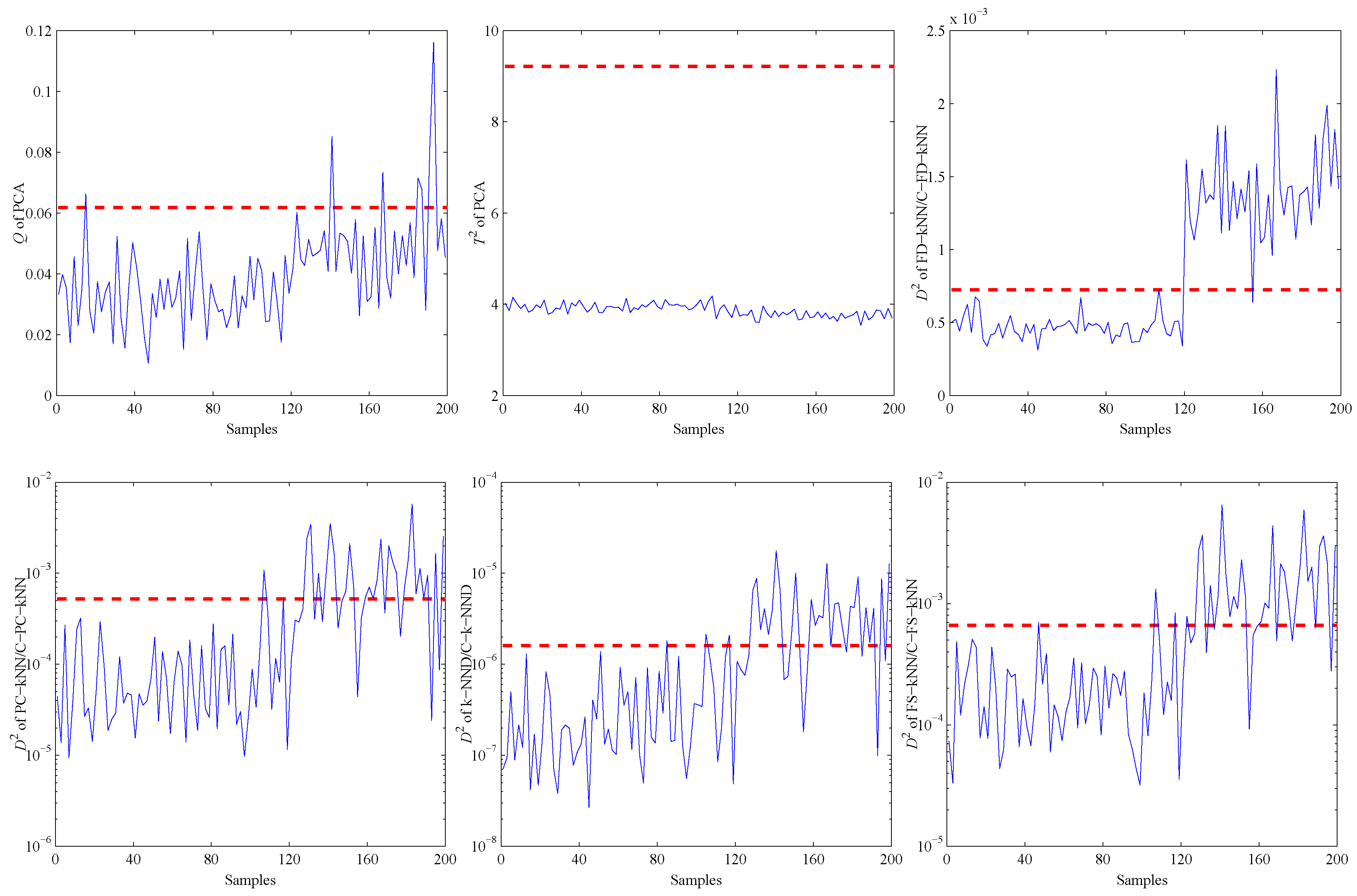
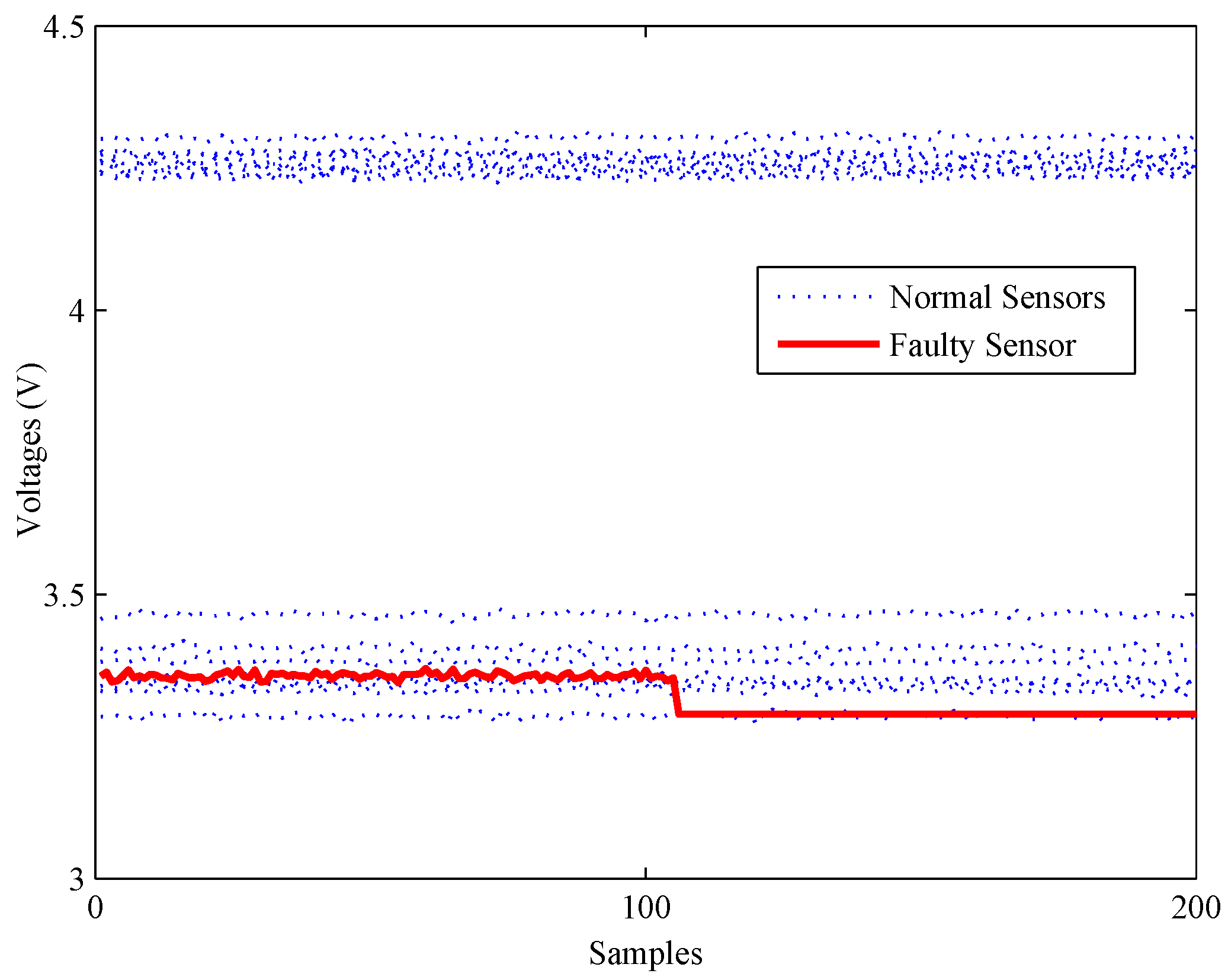
| Metrics | FD-kNN | C-FD-kNN | PC-kNN | C-PC-kNN | k-NND | C-k-NND | FS-kNN | C-FS-kNN |
|---|---|---|---|---|---|---|---|---|
| (s) | 10.41 | 0.73 | 10.36 | 0.66 | 12.63 | 0.85 | 10.31 | 0.77 |
| (ms) | 5.20 | 0.29 | 5.20 | 0.30 | 6.34 | 0.34 | 5.19 | 0.22 |
| DR (%) | 85.9 | 85.5 | 69.7 | 69.9 | 82.6 | 82.5 | 84.8 | 84.2 |
| FPR (%) | 3.1 | 2.9 | 2.9 | 3.1 | 2.1 | 2.5 | 2.1 | 2.3 |
| Metrics | FD-kNN | C-FD-kNN | PC-kNN | C-PC-kNN | k-NND | C-k-NND | FS-kNN | C-FS-kNN |
|---|---|---|---|---|---|---|---|---|
| (s) | 2.57 | 0.31 | 2.56 | 0.33 | 3.09 | 0.37 | 2.57 | 0.33 |
| (ms) | 2.59 | 0.30 | 2.58 | 0.29 | 3.08 | 0.37 | 2.58 | 0.29 |
| DR (%) | 98.2 | 98.3 | 94.0 | 94.0 | 97.5 | 97.3 | 97.5 | 97.6 |
| FPR (%) | 0.8 | 1.3 | 2.1 | 2.3 | 0.9 | 1.4 | 1.6 | 2.0 |
| Methods | PCA-Q | FD-kNN/C-FD-kNN | PC-kNN/C-PC-kNN | k-NND/C-k-NND | FS-kNN/C-FS-kNN |
|---|---|---|---|---|---|
| FPR (%) | 1.6 | 1.8 | 2.9 | 3.5 | 3.9 |
| Metrics | FD-kNN | C-FD-kNN | PC-kNN | C-PC-kNN | k-NND | C-k-NND | FS-kNN | C-FS-kNN |
|---|---|---|---|---|---|---|---|---|
| (s) | 160.82 | 5.13 | 157.20 | 4.47 | 200.15 | 5.70 | 157.13 | 4.48 |
| (ms) | 4.01 | 0.12 | 3.95 | 0.11 | 5.00 | 0.14 | 3.96 | 0.12 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Sun, Z.; Chen, Y. Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays. Sensors 2016, 16, 2069. https://doi.org/10.3390/s16122069
Yang J, Sun Z, Chen Y. Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays. Sensors. 2016; 16(12):2069. https://doi.org/10.3390/s16122069
Chicago/Turabian StyleYang, Jingli, Zhen Sun, and Yinsheng Chen. 2016. "Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays" Sensors 16, no. 12: 2069. https://doi.org/10.3390/s16122069
APA StyleYang, J., Sun, Z., & Chen, Y. (2016). Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays. Sensors, 16(12), 2069. https://doi.org/10.3390/s16122069






