1. Introduction
It is inevitable that human beings will face the exhaustion of fossil energy sources. Finding an alternative energy source that can satisfy global demand for energy is one of the most crucial and critical challenges that today’s society faces. The structures of the solar panels can be identified by the fixed structure and solar tracking structure. The solar tracking structure is not essential for the operation of a solar panel, but without it, the performance is reduced. Experiments show that photovoltaic (PV) panels with sun-tracking structures are able to generate 20%~50% more electricity than those with a fixed structure [
1,
2,
3]. Solar tracking can be implemented by using one-axis, or for greater accuracy, two-axis sun-tracking systems. High-concentration photovoltaic (HCPV) systems can only accept direct solar light, and the acceptance angle deviation from the Sun will lead to a significant decrease in energy conversion efficiency. Therefore, a highly accurate and stable solar tracker is especially important to obtain maximum power for an HCPV system [
4]. However, if the solar trackers can increase energy efficiency of PV arrays, some problems, such as cost, reliability, energy consumption, weather and maintenance may arise and counteract the benefits of the solar tracker.
Basically, solar-tracking systems are classified into two categories: passive (mechanical) and active (electrical) trackers [
1]. Passive solar-tracking systems are based on the thermal expansion of chemicals (usually Freon) or on shape memory alloys. This kind of solar-tracking system is usually composed of a couple of actuators which work against each other. Under equal illumination, the solar-tracking system will be balanced. If the actuators are illuminated under different conditions, unbalanced forces will be generated to rotate the panel perpendicular to the point where the sun is located for realizing new equal illumination.
Traditionally, active trackers can be classified as microprocessor and electro-optical sensor-based, PC-controlled date and time-based, auxiliary bifacial solar cell-based and a combination of these three systems. Nevertheless, from the viewpoint of control, the active solar-tracking systems can be realized as open loop or closed loop control systems [
5,
6]. Regarding an open loop control system, the trajectories of sun movement relative to the Earth can be precisely predetermined. Thus, there is no need for feedback to the tracking system. However, such systems need electronic and mechanical systems with high-precision, and lack the mechanism to automatically modify tracking errors [
7,
8,
9]. Thus, if a solar power system is constructed on a mobile platform like vehicles and ships, the open loop control system will not be appropriate for satisfying the need for continuing modification of tracking parameters in such systems. With respect to the closed loop system, it usually uses photo sensors, such as light-dependent resistors or photodiodes, as feedback signals, and then sends these signals to control circuits to establish the approximate position of the sun [
10,
11,
12]. The main disadvantage of using this type of sensor is the high sensitivity to temperature, humidity, and irradiation [
13]. Additionally, cloudy days may severely affect the performance of the tracking system.
Recently, the use of low cost webcams as sensing elements for active solar tracking systems has been investigated [
14,
15,
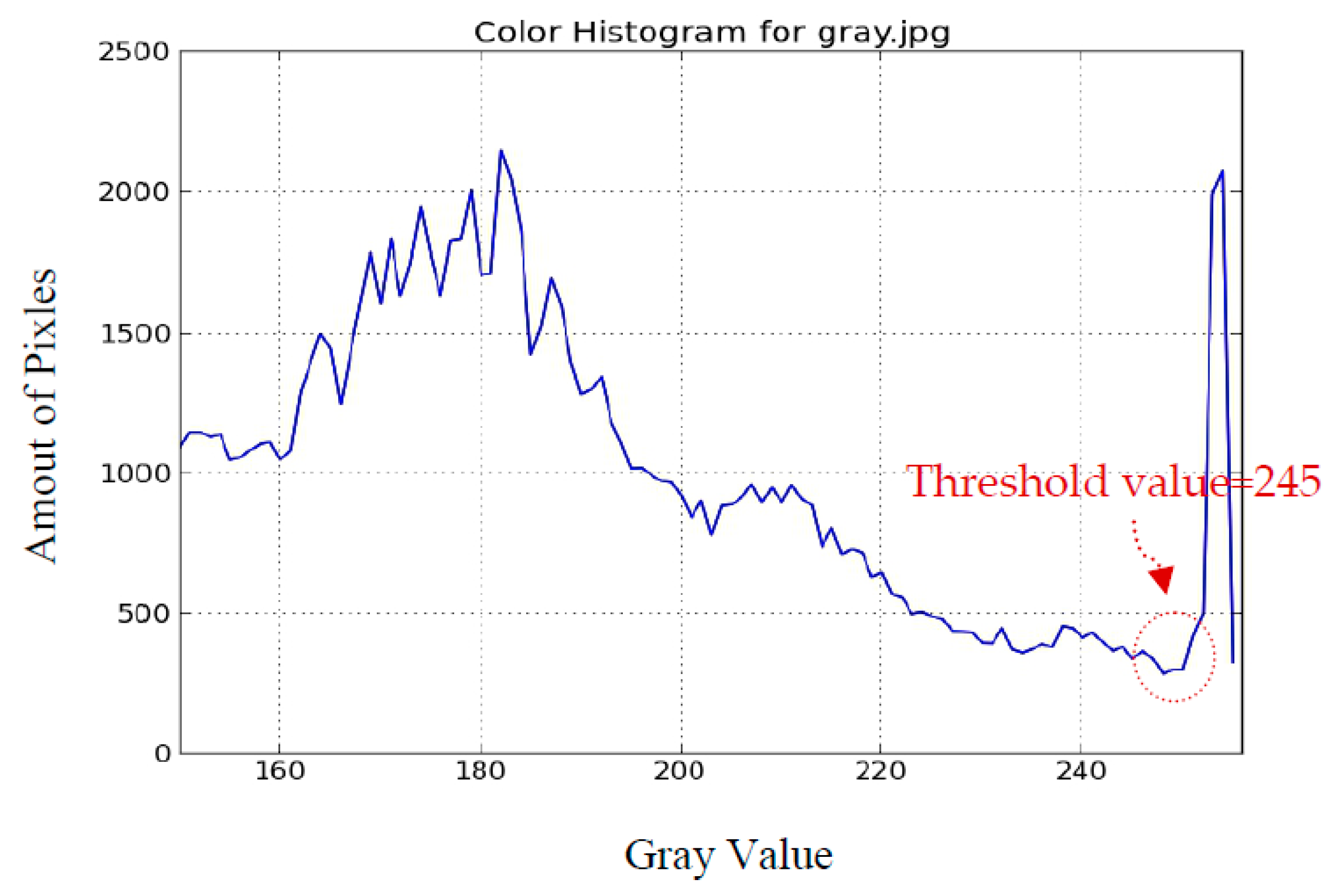
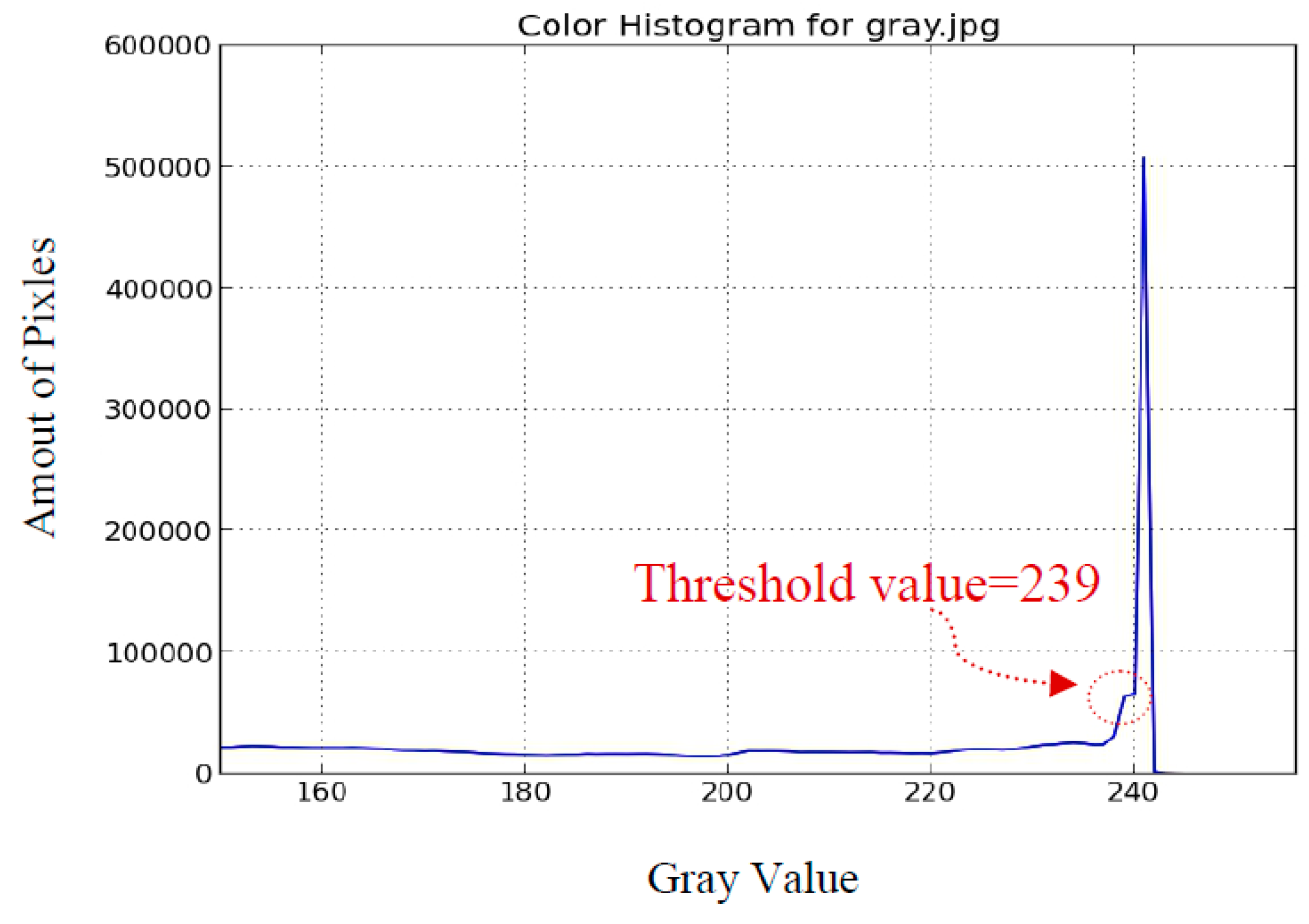
16]. Due to the mature technology of webcams and image processing, they can be easily adopted in practical solar tracking systems. Such tracking systems have also shown high efficiency in studies. Nevertheless, most of the image methods unavoidably used binary images to find the shape and position of the sun. The problem of finding the threshold value to generate the binary image arises. Different choices of the threshold value will lead to entirely different results. Many complex methods used to find the threshold value are presented, such as histogram shape, measurement space, clustering, entropy, object attributes, spatial correlation, and local gray-level surface [
17]. Actually, to get the proper threshold value is complex and energy-consuming. Especially on cloudy days, the accuracy is low. Hence, the solar tracking system using such image methods are not suited to practical application. This study proposes an innovative image method to identify and evaluate the sun’s location. Eventually, we compare our method with that of using the Hough transform to find the sun.
3. Experiment and Results
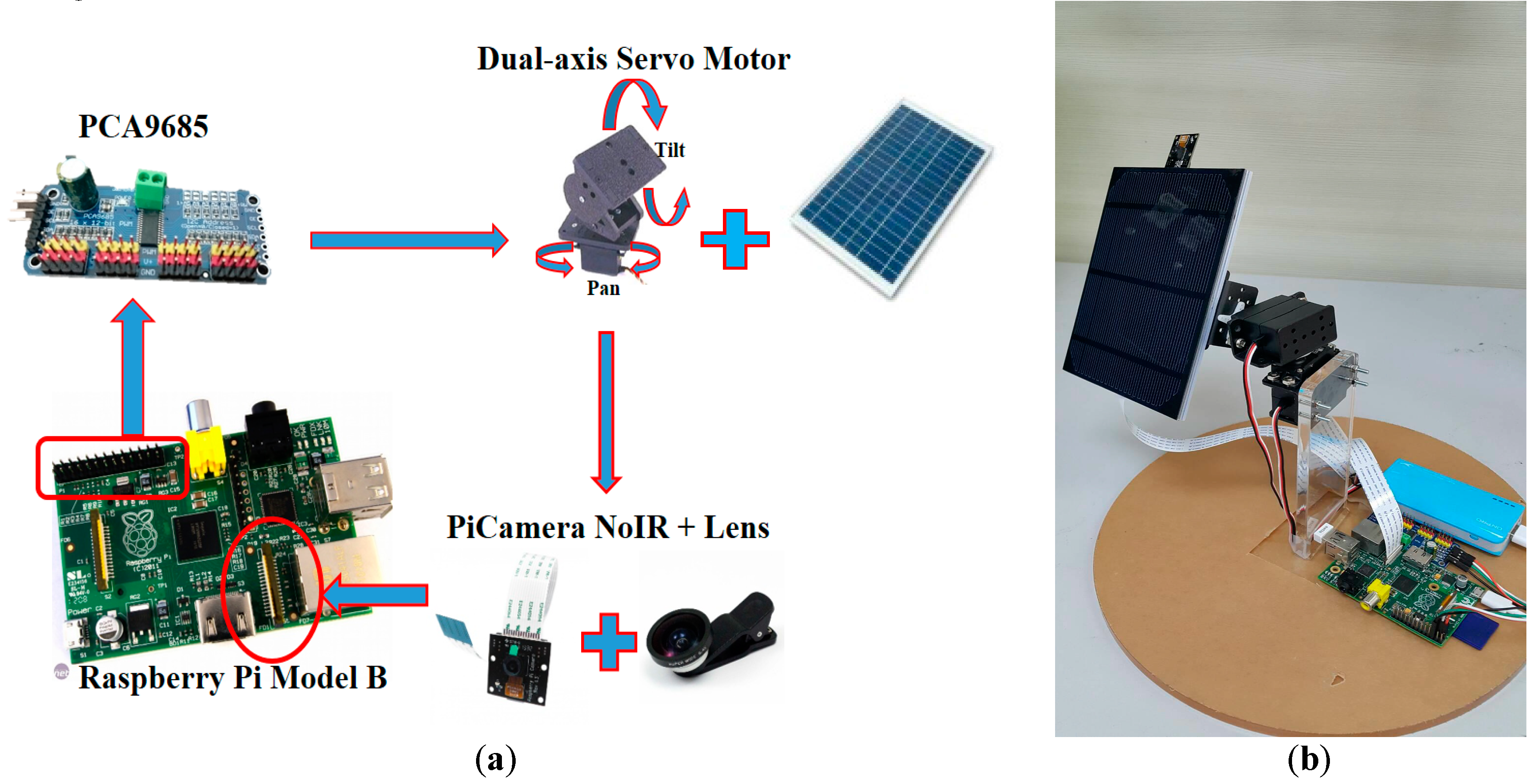
The practical solar tracking system herein is composed of an embedded processor (Raspberry Pi) (RS Components, Corby, UK), a dual-axis servo motor, a pulse width modulation (PWM) servo driver (PCA 9685), a camera for the Pi ($20), and a small solar panel, as illustrated in
Figure 11a. The camera board attaches to the Raspberry Pi via a 15-way ribbon cable. We need to get the cable the right way round, or the camera will not work. No optical filters, like ND (Neutral Density) filters, polarizing filters, or others were used on the camera of the Raspberry Pi. The major computer language in the system is Python, which is a widely used high-level, general-purpose, interpreted, dynamic programming language. Regarding the software of digital image processing, we used OpenCV (Open Source Computer Vision), which is a library of programming functions mainly aimed at real-time computer vision. The PWM signal used for controlling the motor can be generated by the GPIO (general-purpose input/output) pins of Raspberry Pi. The driver circuit (PCA 9685) can provide enough current for motors and acts as a bridge between the Raspberry Pi and the motors.
Figure 11b shows the completed system, which is used to preliminarily verify our proposed method. The camera lens is vertically placed on the surface of the solar panel. In other words, if the evaluated sun center is located at the center of the picture, it means that the normal direction on the solar panel is aligned with that of the evaluated sun center. The original digital image of the RGB mode was captured by the camera of Raspberry Pi with a wide-angle lens. The camera size is around 25 × 24 × 9 mm
3. Hence, it can be easily integrated into this solar power system. The still image resolution is 5 megapixels. Sensor resolution is 2592 × 1944 pixels. The image was captured on the top floor at Chaoyang University of Technology in Taiwan.
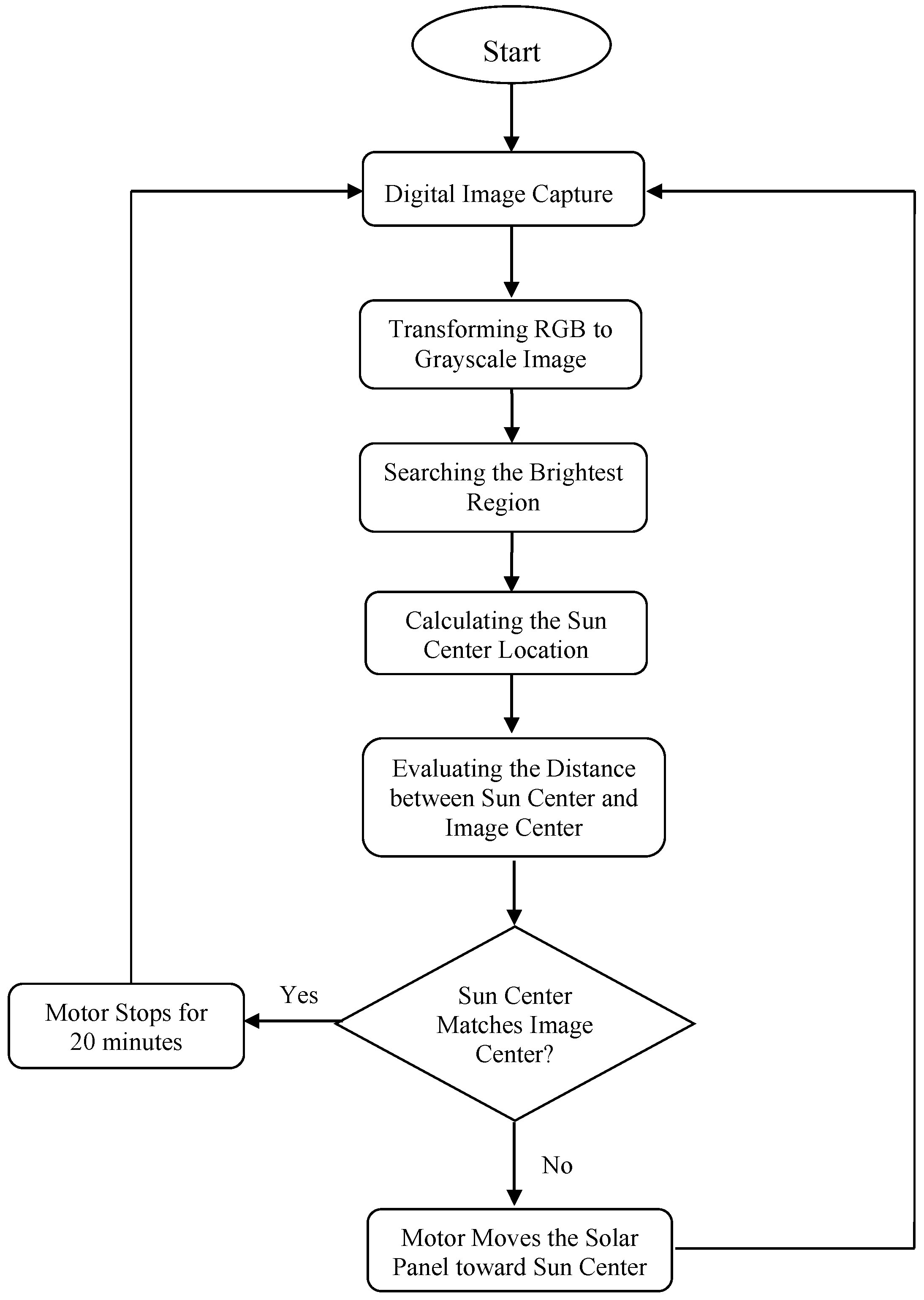
The operation flow of the solar tracking system is demonstrated in
Figure 12. If the evaluated sun center does not match the center of the picture, the tracking system will restart the image capture and identification procedure until the sun is located at the center of the picture. Hence, the tracking system possesses closed-loop feedback. If the evaluated sun center is located at the picture center, the motor will stop for twenty minutes before starting the next routine.
The captured images under various weather conditions, such as no clouds, few clouds, or some clouds, are recorded and discussed. In
Figure 13a, the sky is clear, and the evaluated sun center approaches the real sun center well; the center is marked with a red point. The brightest region is marked with blue points. The handrail and surrounding buildings are also seen in the figure for reference position. Since the sun moves, the camera on the solar panel keeps tracking to move with the sun. Thus, the sun is always in the center of the picture; the handrail and surrounding buildings look like they are moving in the continuous pictures. In
Figure 13b, the sky is clear most of the time, but sometimes there are clouds. We can find less deviation in the pictures with some clouds. In
Figure 13c, the sky is cloudy most times. We can, thus, find some deviations from the real sun center in the pictures. Nevertheless, generally speaking, the system keeps good tracking of the sun.
4. Discussion
We have a single sun in the sky, and no other possible strong light source periodically appears in the sky. Therefore, the region where the sun is located signifies the brightest region in the sky and it is reasonable to find the sun’s position by identifying that region. Regarding the traditional image method to find the sun’s position, researchers focused on how to recognize the circular object in the sky, i.e., the sun. The key procedure in such a method is determining the optimum threshold value to generate the binary image. Sometimes it is difficult and complex to obtain the optimum threshold value by an automatic method, and should be done by a manual method; hence, it cannot be applied in a practical application. Even under some interference, there is no optimum value to generate a circular object in a binary image, and great deviations from the real sun center are observed.
Regarding our brightest region method, it obviously precludes the threshold value problem. From the results we can know it is easy to obtain the accurate position of the sun in a clear sky. Under some slight interference resulting from less cloud, only a small deviation from the real sun center occurs. The evaluated sun center is always approximately within the sun region, and will not go out of control. However, when a large and thick cloud interferes, the bright side of the cloud will appear and the evaluated sun center is possible to be far from the real sun center. The problem under this situation still needs to be improved. The camera of the Raspberry Pi can not only be used in a solar tracking system, but can also be used in monitoring the weather conditions; it is important in managing and maintaining the solar energy system. In addition, the low cost and real-time operation are the advantages of our method. In summary, this novel image method provides a new way to overcome the disadvantages of the traditional image method for solar tracking, and makes the image method possible in real applications. However, we still face some challenges. For example, the clouds behave like space noises. Determining how to remove the noises by using a space filter and making the system more robust are worthy future endeavors.