Ex-Vivo Characterization of Bioimpedance Spectroscopy of Normal, Ischemic and Hemorrhagic Rabbit Brain Tissue at Frequencies from 10 Hz to 1 MHz
Abstract
:1. Introduction
2. Materials and Methods
2.1. Animal Preparation
2.2. Surgery
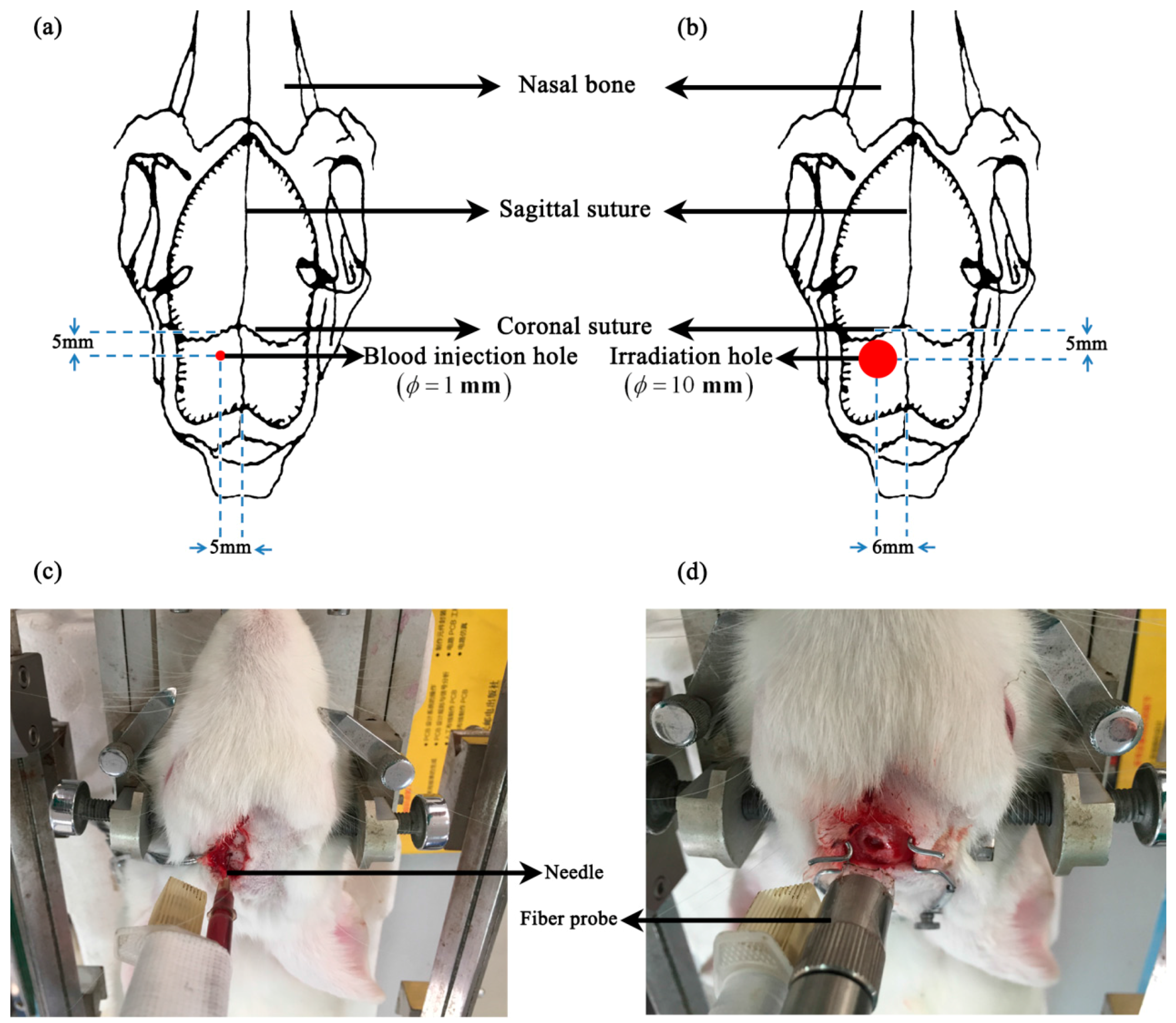
2.2.1. Intracerebral Hemorrhage Model
2.2.2. Ischemic Model
2.3. Tissue Impedance Spectra and Electrical Property Analysis
2.3.1. Measurement of Tissue Impedance Spectra
2.3.2. Saline Solution Control
2.3.3. Properties of Tissue Impedance Spectra
2.4. Histopathology
2.5. Data Analysis
3. Results
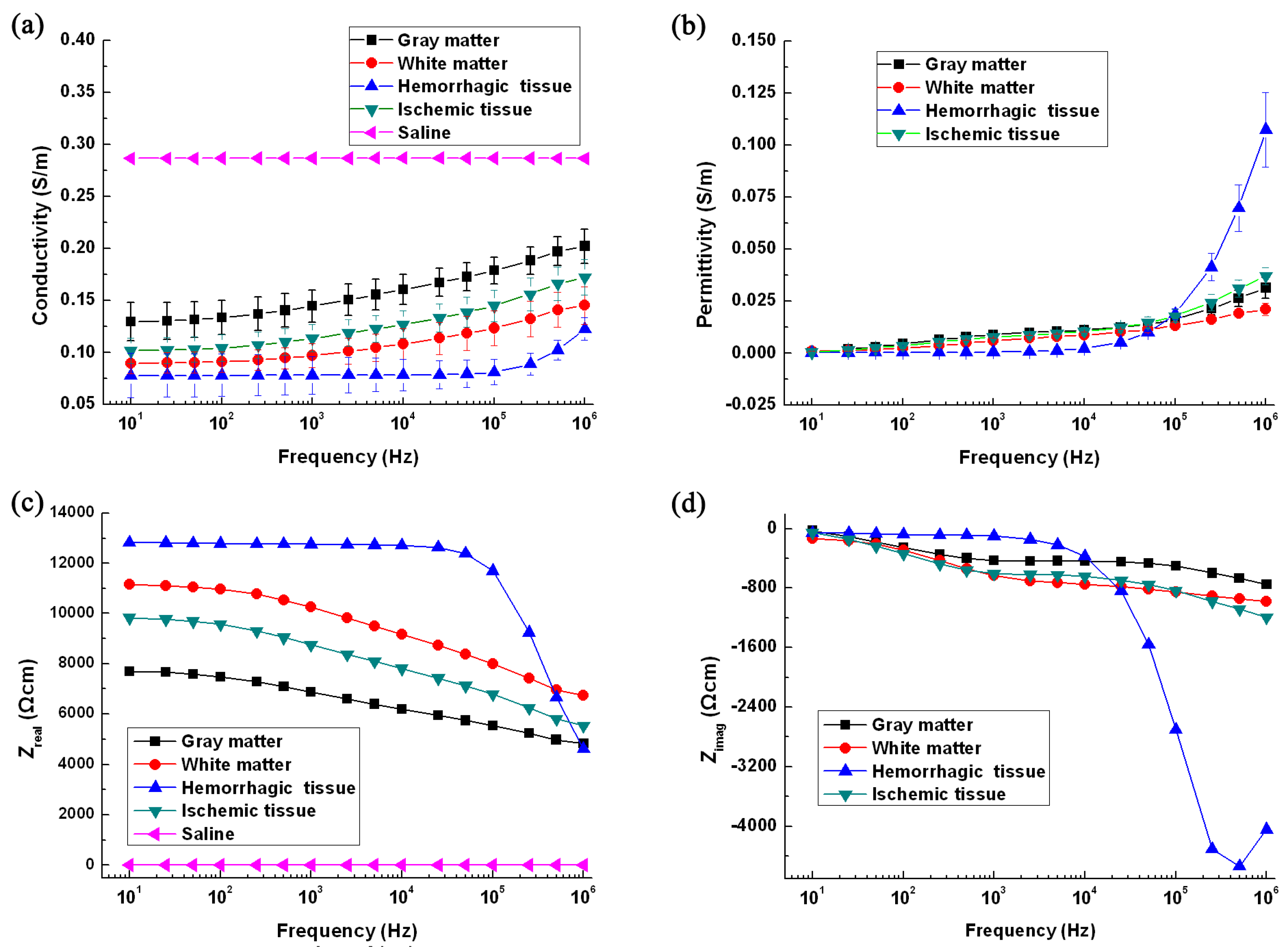
3.1. Measurement of the Impedance Spectra of Normal Brain Tissue and Stroke Lesions
3.2. Difference in Impedance Spectra between Normal Brain Tissue and Stroke Lesions
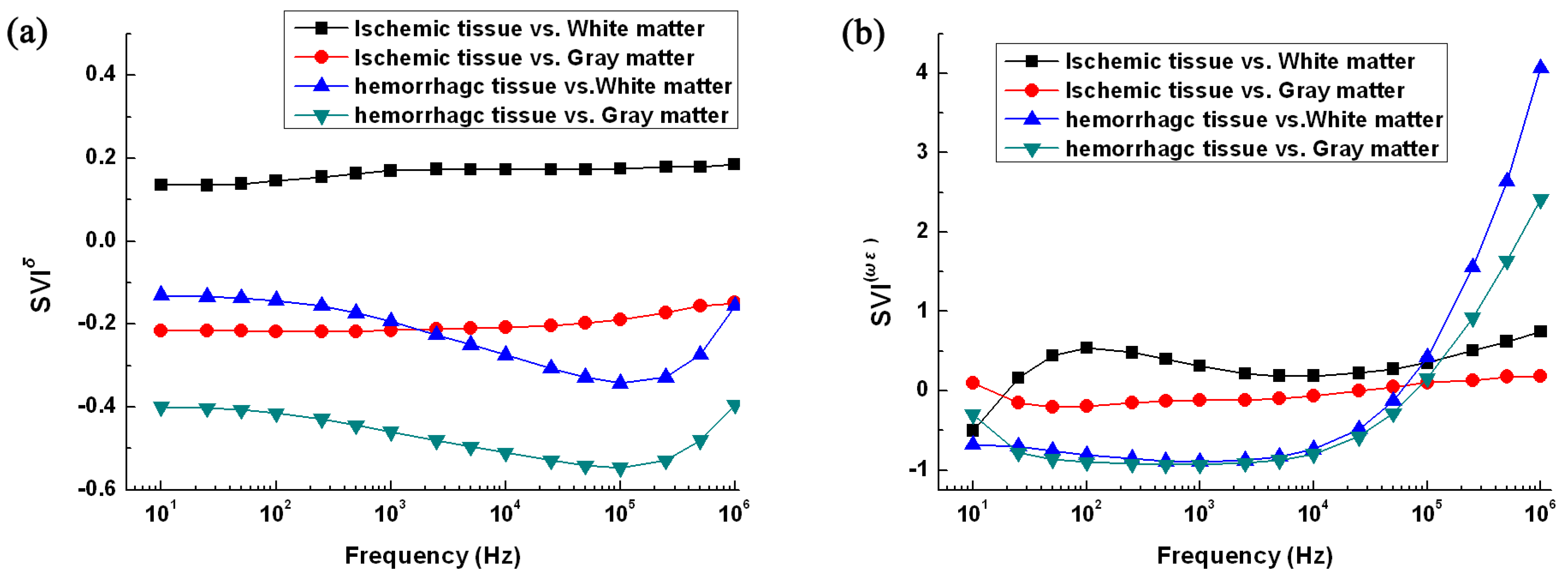
3.3. Difference in the Ratio of Change in Impedance with Frequency between Ischemic and Hemorrhagic Tissue
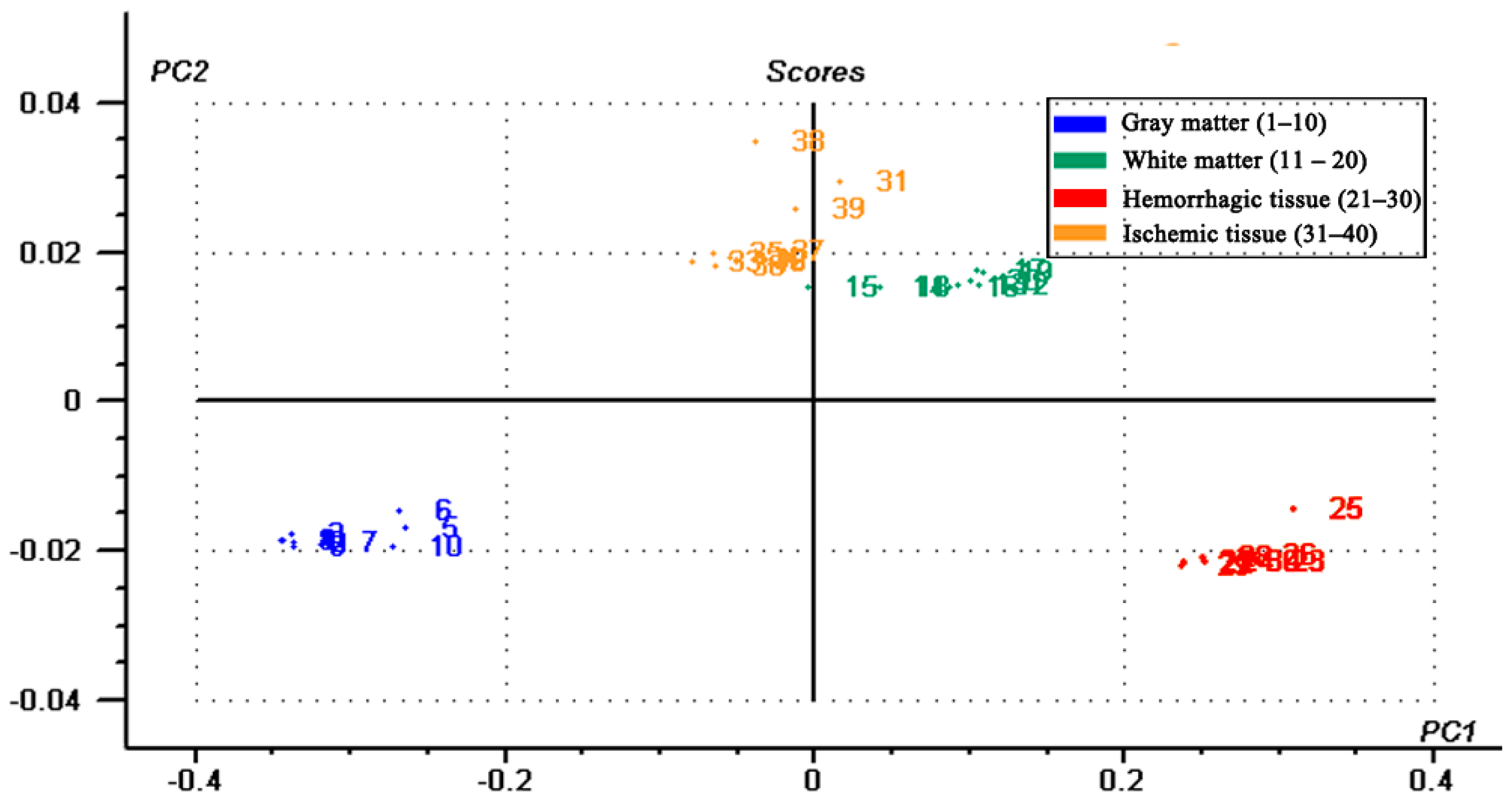
3.4. Using Impedance Spectra to Discriminate Tissue Type
3.5. Histopathology
4. Discussion
4.1. Summary of Experimental Results and Comparison with Previous Studies
4.2. Helpful Information on Stroke Detection with MFEIT
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donnan, G.A.; Fisher, M.; Macleod, M.; Davis, S.M. Stroke. Lancet 2008, 371, 1612–1623. [Google Scholar] [CrossRef]
- Mozaffarian, D.; Benjamin, E.J.; Go, A.S.; Arnett, D.K.; Blaha, M.J.; Cushman, M.; de Ferranti, S.; Despres, J.P.; Fullerton, H.J.; Howard, V.J.; et al. Executive summary: Heart disease and stroke statistics-2015 update a report from the american heart association. Circulation 2015, 131, 434–441. [Google Scholar] [CrossRef]
- Zoppo, D. Expansion of the time window for treatment of acute ischemic stroke with intravenous tissue plasminogen activator: A science advisory from the american heart association/american stroke association. Stroke 2010, 41, e562. [Google Scholar]
- Saver, J.L.; Fonarow, G.C.; Smith, E.E.; Reeves, M.J.; Grau-Sepulveda, M.V.; Pan, W.; Olson, D.M.; Hernandez, A.F.; Peterson, E.D.; Schwamm, L.H. Time to treatment with intravenous tissue plasminogen activator and outcome from acute ischemic stroke. JAMA 2013, 309, 2480–2488. [Google Scholar] [CrossRef] [PubMed]
- Khalil, S.F.; Mohktar, M.S.; Ibrahim, F. The theory and fundamentals of bioimpedance analysis in clinical status monitoring and diagnosis of diseases. Sensors 2014, 14, 10895–10928. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, C.; Peyman, A.; Grant, E.H. Electrical conductivity of tissue at frequencies below 1 MHz. Phys. Med. Biol. 2009, 54, 4863–4878. [Google Scholar] [CrossRef] [PubMed]
- Atefi, S.R.; Seoane, F.; Thorlin, T.; Lindecrantz, K. Stroke damage detection using classification trees on electrical bioimpedance cerebral spectroscopy measurements. Sensors 2013, 13, 10074–10086. [Google Scholar] [CrossRef] [PubMed]
- Seoane, F.; Lu, M.; Persson, M.; Lindecrantz, K. Electrical bioimpedance cerebral monitoring. A study of the current density distribution and impedance sensitivity maps on a 3D realistic head model. In Proceedings of the 2007 3rd International IEEE/EMBS Conference on Neural Engineering, Kohala Coast, HI, USA, 2–5 May 2007; pp. 256–260.
- Seoane, F.; Lindecrantz, K. Electrical bioimpedance cerebral monitoring. In Encyclopedia of Healthcare Information Systems; IGI Global: Hershey, PA, USA, 2008; pp. 480–486. [Google Scholar]
- Seoane, F. Electrical Bioimpedance Cerebral Monitoring: Fundamental Steps towards Clinical Application; Department of Signals and Systems: Gothenburg, Sweden, 2007. [Google Scholar]
- Schuier, F.J.; Hossmann, K.A. Experimental brain infarcts in cats. II. Ischemic brain edema. Stroke 1980, 11, 593–601. [Google Scholar] [CrossRef] [PubMed]
- Lingwood, B.E.; Dunster, K.R.; Healy, G.N.; Ward, L.C.; Colditz, P.B. Cerebral impedance and neurological outcome following a mild or severe hypoxic/ischemic episode in neonatal piglets. Brain Res. 2003, 969, 160–167. [Google Scholar] [CrossRef]
- Holder, D.S. Detection of cerebral ischaemia in the anaesthetised rat by impedance measurement with scalp electrodes: Implications for non-invasive imaging of stroke by electrical impedance tomography. Clin. Phys. Physiol. Meas. 1992, 13, 63. [Google Scholar] [CrossRef] [PubMed]
- Seoane, F.; Lindecrantz, K.; Olsson, T.; Kjellmer, I.; Flisberg, A.; Bågenholm, R. Spectroscopy study of the dynamics of the transencephalic electrical impedance in the perinatal brain during hypoxia. Physiol. Meas. 2005, 26, 849. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.K.; Lee, J.; Kim, S.W.; Zribi, H.; Woo, E.J. Frequency-difference electrical impedance tomography (fdEIT): Algorithm development and feasibility study. Physiol. Meas. 2008, 29, 929–944. [Google Scholar] [CrossRef] [PubMed]
- Seoane, F.; Atefi, S.R.; Tomner, J.; Kostulas, K.; Lindecrantz, K. Electrical bioimpedance spectroscopy on acute unilateral stroke patients: Initial observations regarding differences between sides. Biomed. Res. Int. 2015, 2015, 613247. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Xu, C.; Dai, M.; You, F.; Shi, X.; Dong, X.; Fu, F. Exploratory study on the methodology of fast imaging of unilateral stroke lesions by electrical impedance asymmetry in human heads. Sci. World J. 2014, 2014, 534012. [Google Scholar] [CrossRef] [PubMed]
- Bonmassar, G.; Iwaki, S. The shape of electrical impedance spectroscopy (EIS) is altered in stroke patients. Eng. Med. Biol. Soc. 2004, 5, 3443–3446. [Google Scholar]
- Atefi, S.R.; Seoane, F.; Lindecrantz, K. Electrical bioimpedance cerebral monitoring. Preliminary results from measurements on stroke patients. Eng. Med. Biol. Soc. 2012, 2012, 126–129. [Google Scholar]
- Jehl, M.; Holder, D. Correction of electrode modelling errors in multi-frequency eit imaging. Physiol. Meas. 2016, 37, 893–903. [Google Scholar] [CrossRef] [PubMed]
- Packham, B.; Koo, H.; Romsauerova, A.; Ahn, S.; McEwan, A.; Jun, S.C.; Holder, D.S. Comparison of frequency difference reconstruction algorithms for the detection of acute stroke using eit in a realistic head-shaped tank. Physiol. Meas. 2012, 33, 767–786. [Google Scholar] [CrossRef] [PubMed]
- Malone, E.; dos Santos, G.S.; Holder, D.; Arridge, S. Multifrequency electrical impedance tomography using spectral constraints. IEEE Trans. Med. Imaging 2014, 33, 340–350. [Google Scholar] [CrossRef] [PubMed]
- Surowiec, A.; Stuchly, S.S.; Swarup, A. Postmortem changes of the dielectric properties of bovine brain tissues at low radiofrequencies. Bioelectromagnetics 1986, 7, 31–43. [Google Scholar] [CrossRef] [PubMed]
- Stoy, R.D.; Foster, K.R.; Schwan, H.P. Dielectric properties of mammalian tissues from 0.1 to 100 MHZ: A summary of recent data. Phys. Med. Biol. 1982, 27, 501–513. [Google Scholar] [CrossRef] [PubMed]
- Ranck, J.B., Jr. Analysis of specific impedance of rabbit cerebral cortex. Exp. Neurol. 1963, 7, 153–174. [Google Scholar] [CrossRef]
- Latikka, J.; Kuurne, T.; Eskola, H. Conductivity of living intracranial tissues. Phys. Med. Biol. 2001, 46, 1611–1616. [Google Scholar] [CrossRef] [PubMed]
- Romsauerova, A.; McEwan, A.; Horesh, L.; Yerworth, R.; Bayford, R.H.; Holder, D.S. Multi-frequency electrical impedance tomography (EIT) of the adult human head: Initial findings in brain tumours, arteriovenous malformations and chronic stroke, development of an analysis method and calibration. Physiol. Meas. 2006, 27, S147. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; He, Y.; Yan, Q.G.; You, F.S.; Fu, F.; Dong, X.Z.; Shi, X.T.; Yang, M. Correlation between the dielectric properties and biological activities of human ex vivo hepatic tissue. Phys. Med. Biol. 2015, 60, 2603–2617. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Dong, X.; Qin, M.; Fu, F.; Wang, Y.; You, F.; Xiang, H.; Liu, R.; Shi, X. The in vitro measurement of the rabbit brain complex impedance frequency response and the equivalent circuit model. Chin. J. Biomed. Eng. 2003, 22, 228–234. [Google Scholar]
- Wu, X.; Dong, X.; Qin, M.; Fu, F.; Wang, Y.; You, F.; Xiang, H.; Liu, R.; Shi, X. In vivo measurement of rabbits brain impedance frequency response and the elementary imaging of EIT. J. Bio. Eng. 2003, 20, 49–51. [Google Scholar]
- Ur, A. Changes in the electrical impedance of blood during coagulation. Nature 1970, 226, 269–270. [Google Scholar] [CrossRef] [PubMed]
- Lei, K.F.; Chen, K.H.; Tsui, P.H.; Tsang, N.M. Real-time electrical impedimetric monitoring of blood coagulation process under temperature and hematocrit variations conducted in a microfluidic chip. PLoS ONE 2013, 8, e76243. [Google Scholar] [CrossRef] [PubMed]
- Dowrick, T.; Blochet, C.; Holder, D. In vivo bioimpedance measurement of healthy and ischaemic rat brain: Implications for stroke imaging using electrical impedance tomography. Physiol. Meas. 2015, 36, 1273–1282. [Google Scholar] [CrossRef] [PubMed]
- Simsek, F.G.; Ulgen, Y. Electrical impedance of human blood with and without anticoagulants in the β-dispersion region. Eng. Med. Biol. Soc. 2012, 2012, 3262–3264. [Google Scholar]
- Yang, B.; Shi, X.T.; Dai, M.; Xu, C.H.; You, F.S.; Fu, F.; Liu, R.G.; Dong, X.Z. Real-time imaging of cerebral infarction in rabbits using electrical impedance tomography. J. Int. Med. Res. 2014, 42, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Schwan, H.P.; Ferris, C.D. Four-electrode null techniques for impedance measurement with high resolution. Rev. Sci. Instrum. 1968, 39, 481–485. [Google Scholar] [CrossRef]
- Peyman, A.; Gabriel, C.; Grant, E.H. Complex permittivity of sodium chloride solutions at microwave frequencies. Bioelectromagnetics 2007, 28, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Kalvoy, H.; Frich, L.; Grimnes, S.; Martinsen, O.G.; Hol, P.K.; Stubhaug, A. Impedance-based tissue discrimination for needle guidance. Physiol. Meas. 2009, 30, 129–140. [Google Scholar] [CrossRef] [PubMed]
- Lizhi, H.; Toyoda, K.; Ihara, I. Discrimination of olive oil adulterated with vegetable oils using dielectric spectroscopy. J. Food Eng. 2010, 96, 167–171. [Google Scholar] [CrossRef]
- Chen, T.H.; Zhu, Y.P.; Wang, P.; Han, M.Y.; Wei, R.; Xu, X.L.; Zhou, G.H. The use of the impedance measurements to distinguish between fresh and frozen-thawed chicken breast muscle. Meat Sci. 2016, 116, 151–157. [Google Scholar] [CrossRef] [PubMed]
- Botelho, B.G.; Reis, N.; Oliveira, L.S.; Sena, M.M. Development and analytical validation of a screening method for simultaneous detection of five adulterants in raw milk using mid-infrared spectroscopy and PLS-DA. Food Chem. 2015, 181, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Schwan, H.P. Electrical properties of tissue and cell suspensions. In Advances in Biological and Medical Physics; John, H.L., Cornelius, A.T., Eds.; Elsevier: Amsterdam, The Netherlands, 1957; Volume 5, pp. 147–209. [Google Scholar]
- Horesh, L. Some Novel Approaches in Modelling and Image Reconstruction for Multi-Frequency Electrical Impedance Tomography of the Human Brain. Ph.D. Thesis, University of London, London, UK, 2006. [Google Scholar]
- Ur, A. Detection of clot retraction through changes of the electrical impedance of blood during coagulation. Am. J. Clin. Pathol. 1971, 56, 713–718. [Google Scholar] [CrossRef] [PubMed]
- Burger, H.C.; van Dongen, R. Specific electric resistance of body tissues. Phys. Med. Biol. 1961, 5, 431–447. [Google Scholar] [CrossRef] [PubMed]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhang, G.; Song, J.; Dai, M.; Xu, C.; Dong, X.; Fu, F. Ex-Vivo Characterization of Bioimpedance Spectroscopy of Normal, Ischemic and Hemorrhagic Rabbit Brain Tissue at Frequencies from 10 Hz to 1 MHz. Sensors 2016, 16, 1942. https://doi.org/10.3390/s16111942
Yang L, Zhang G, Song J, Dai M, Xu C, Dong X, Fu F. Ex-Vivo Characterization of Bioimpedance Spectroscopy of Normal, Ischemic and Hemorrhagic Rabbit Brain Tissue at Frequencies from 10 Hz to 1 MHz. Sensors. 2016; 16(11):1942. https://doi.org/10.3390/s16111942
Chicago/Turabian StyleYang, Lin, Ge Zhang, Jiali Song, Meng Dai, Canhua Xu, Xiuzhen Dong, and Feng Fu. 2016. "Ex-Vivo Characterization of Bioimpedance Spectroscopy of Normal, Ischemic and Hemorrhagic Rabbit Brain Tissue at Frequencies from 10 Hz to 1 MHz" Sensors 16, no. 11: 1942. https://doi.org/10.3390/s16111942
APA StyleYang, L., Zhang, G., Song, J., Dai, M., Xu, C., Dong, X., & Fu, F. (2016). Ex-Vivo Characterization of Bioimpedance Spectroscopy of Normal, Ischemic and Hemorrhagic Rabbit Brain Tissue at Frequencies from 10 Hz to 1 MHz. Sensors, 16(11), 1942. https://doi.org/10.3390/s16111942






