A Node Localization Algorithm Based on Multi-Granularity Regional Division and the Lagrange Multiplier Method in Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Works
3. Multi-Granularity Region Partition Based on RSSI
3.1. Ranging Method Based on RSSI
3.2. RSSI Data Processing Method
3.2.1. Experimental Data Acquisition
3.2.2. Experimental Data Acquisition
3.2.3. Wireless Signal Transmission Loss Model
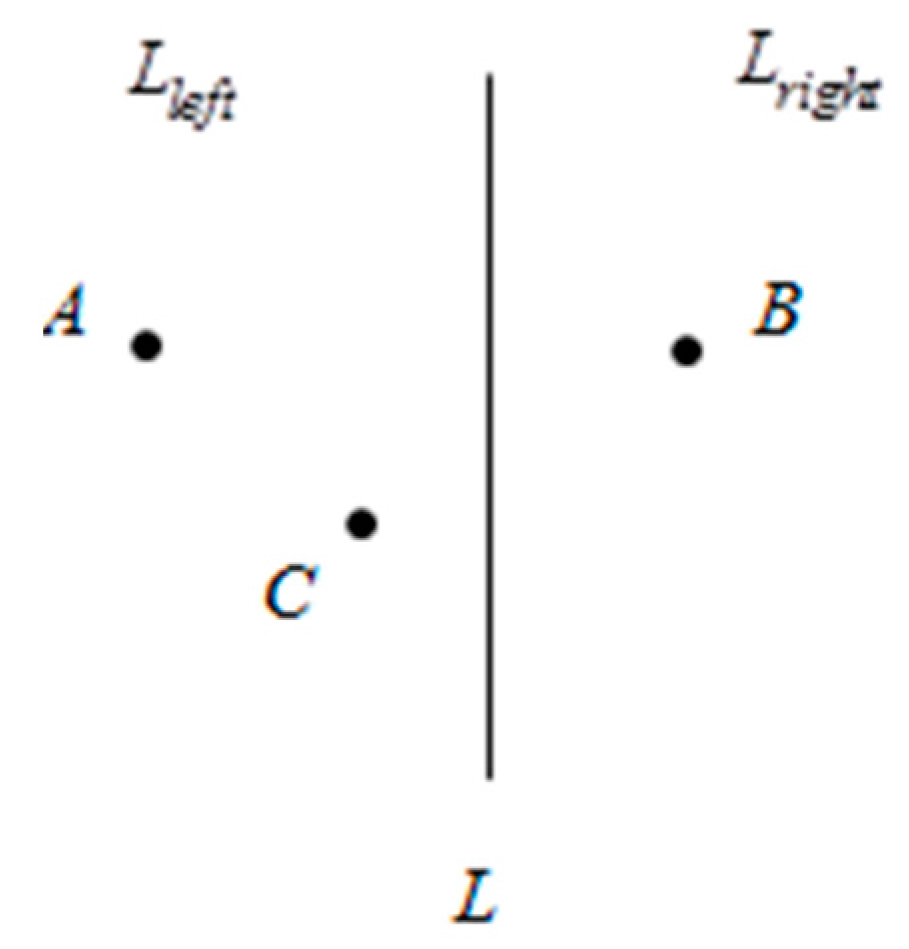
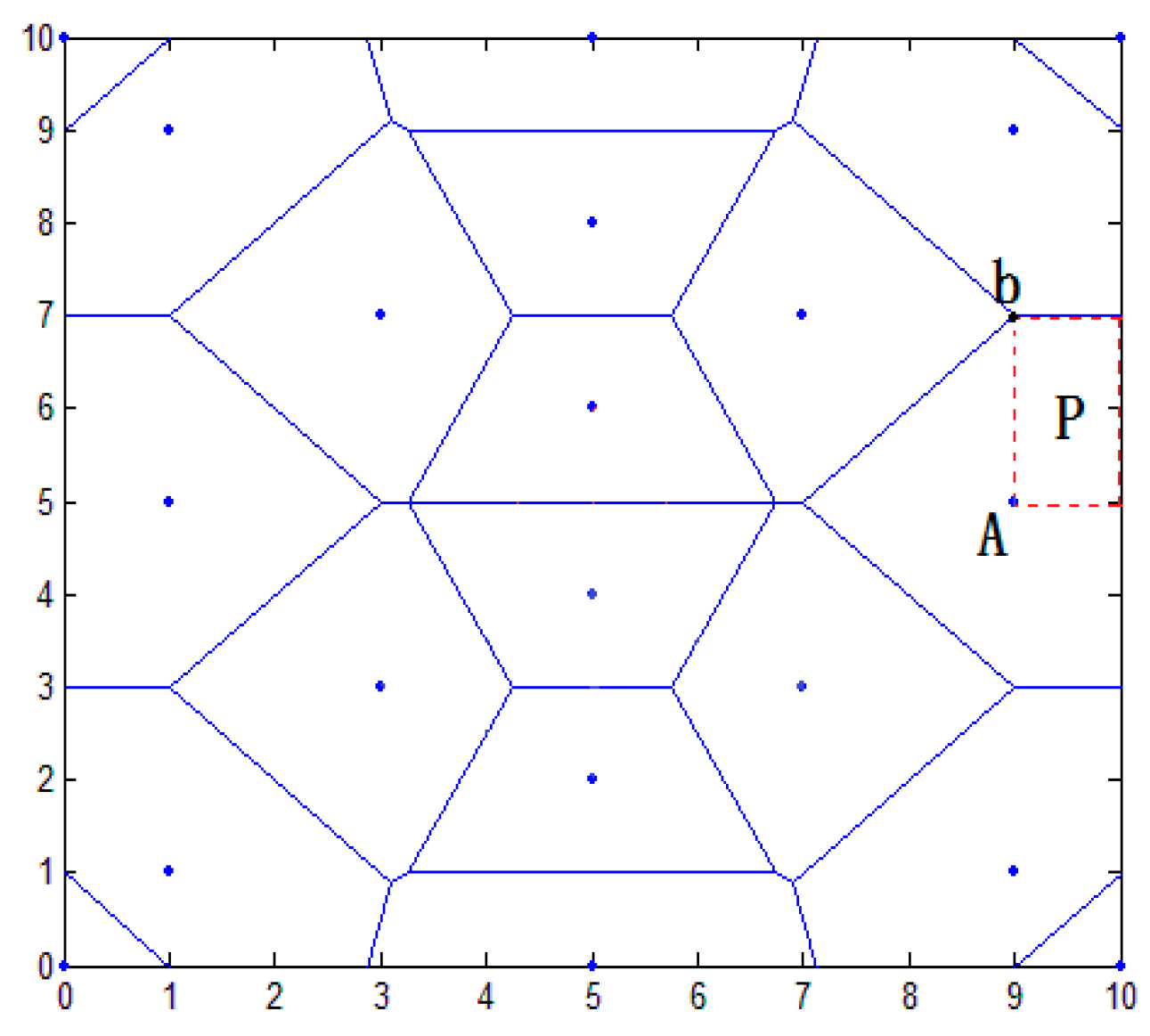
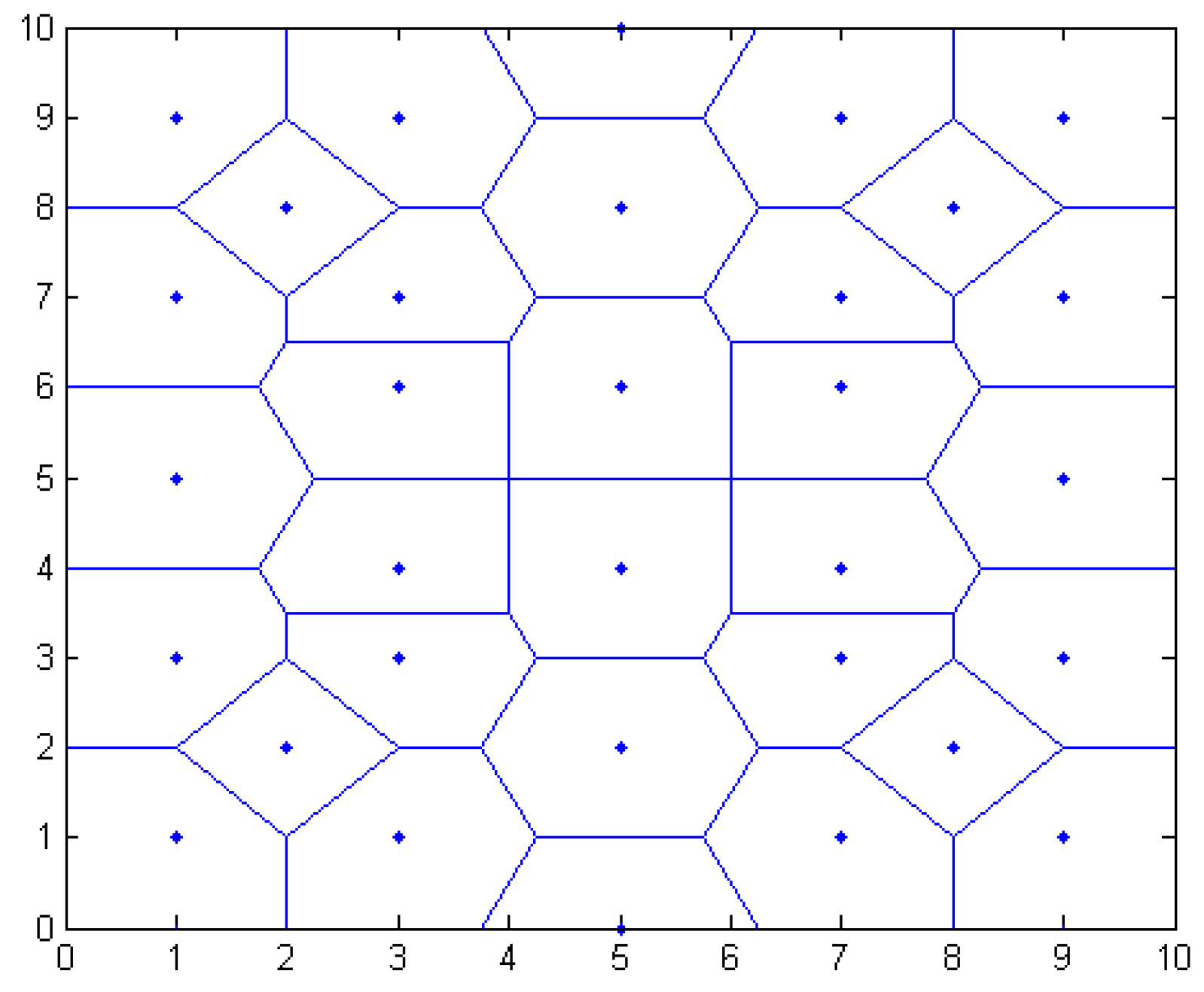
3.3. Region Division Method
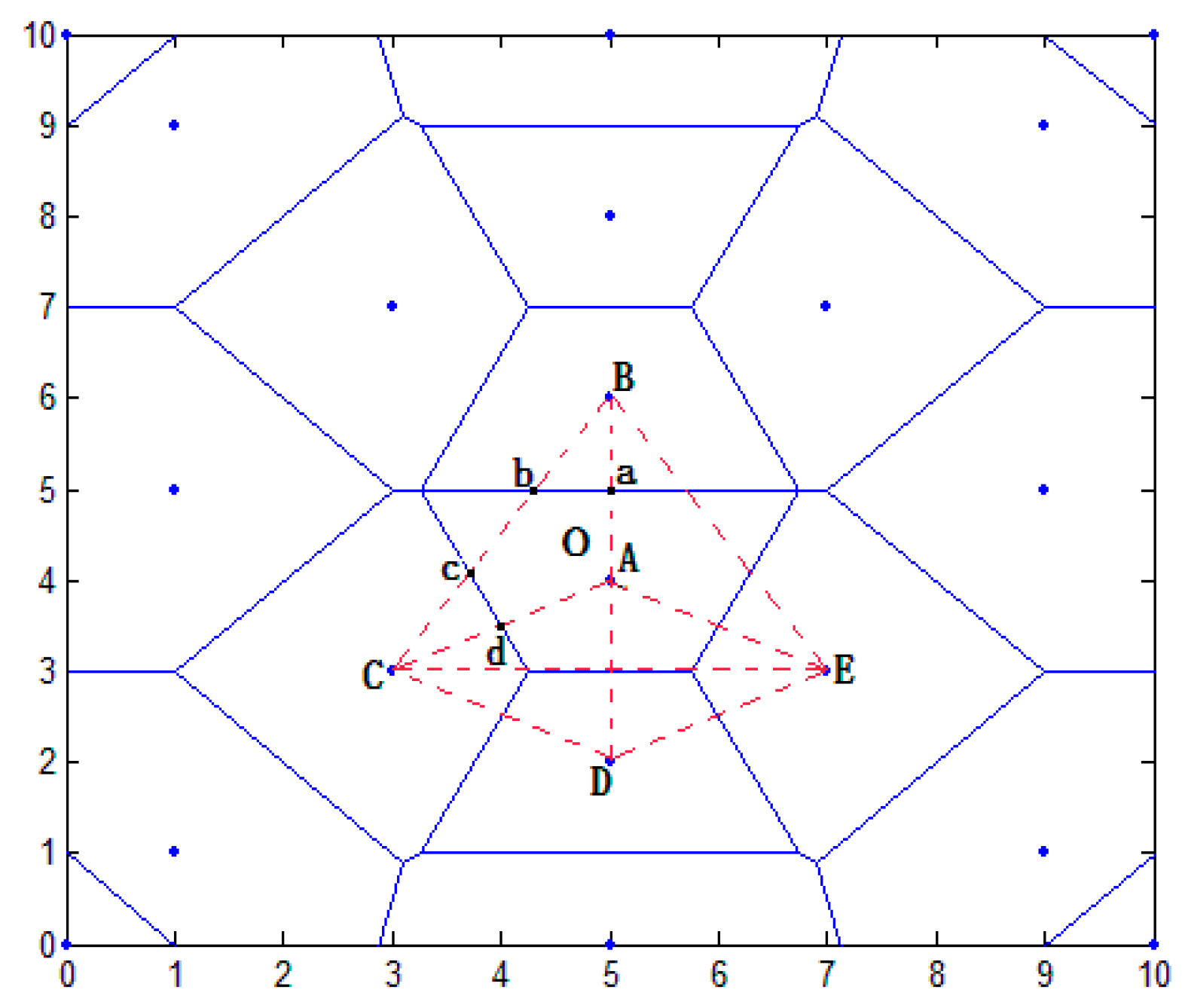
3.3.1. Regional Primary Division
3.3.2. Region Dividing Based on Second Division
3.3.3. Analysis of Regional Division Method
| Algorithm 1: LocationRegional(N) |
| Input: A set of all anchor nodes: unknown nodes evenly distributed in the location region; Output: Localization algorithm for unknown node 1. A set of anchor nodes marked serial number for anchor nodes 2. FOR (i = 1 to j) 3. RUN , obtaining the strength vector set between N and P . 4. , obtaining the strength vector set between N and P 5. , sorting in ascending order 6. , taking the first anchor node O 7. FOR (i = 1 to n-1) 8. RUN , obtaining the strength vector set between O and the other anchor node, . 9. , obtaining the distance vector set between O and the other anchor node, . 10. , sorting in ascending order 11. , taking the top six anchor nodes A, B, C, D, E, and F, using the vertical line with the O midline forming a closed polygon area . 12. IF , judge whether the distance between P and O is less than the other adjacent anchor nodes, O, B, C, D, E, and F. 13. RUN the neighboring anchor nodes A, B, C, D, E, and F following the order of forming a number of triangles . 14. IF , 15. RUN InternMethod, selecting internal unit positioning algorithm 16. ESLE RUN ExternMethod, selecting external unit positioning algorithm 17. ENDIF 18. ENDFOR 19. ENDFOR |
4. Node Localization Algorithm Based on Lagrange Multiplication and Taylor Formula
4.1. Node Location Method in Positioning Unit
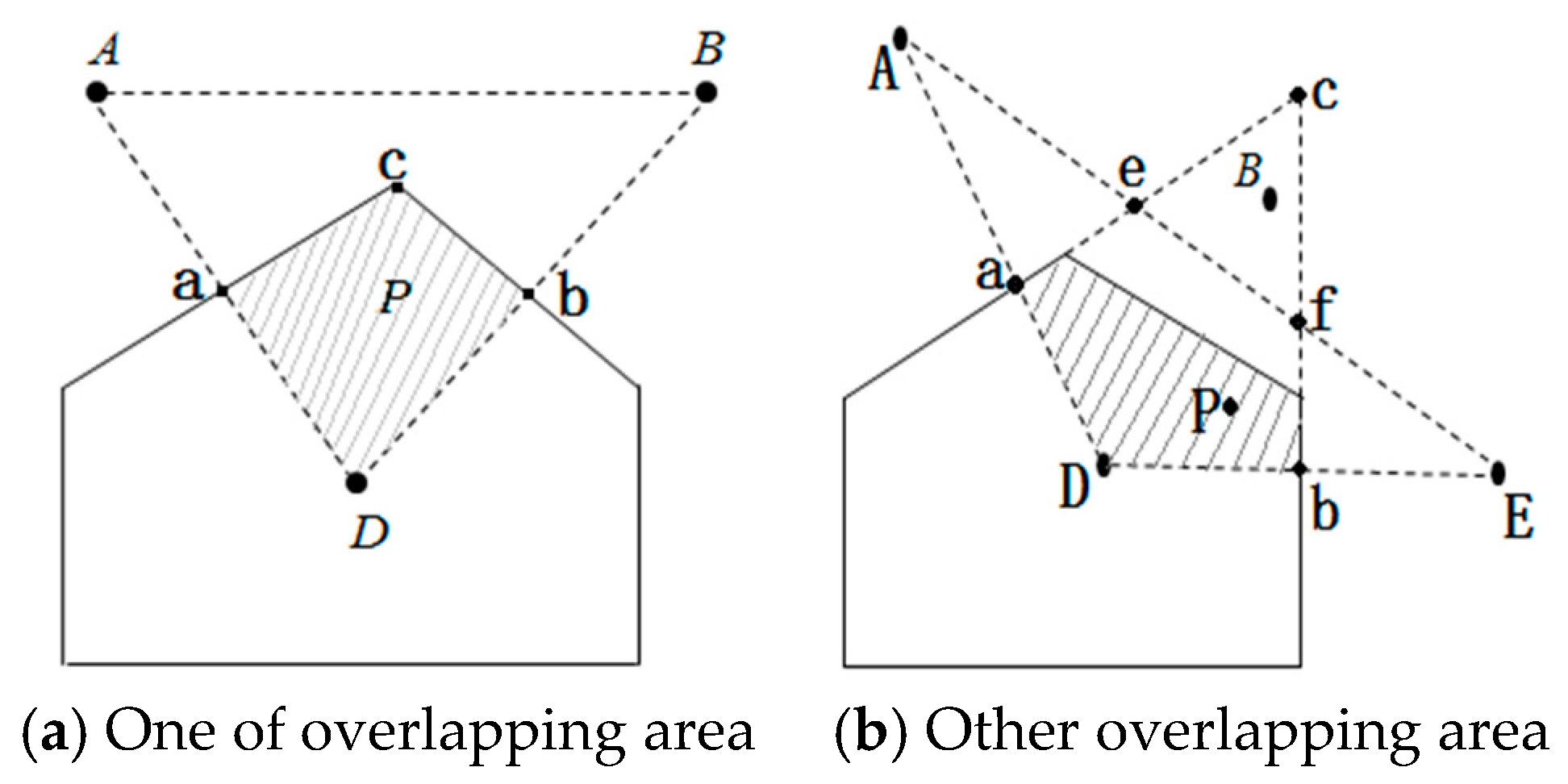
4.2. Node Location Method outside Positioning Unit
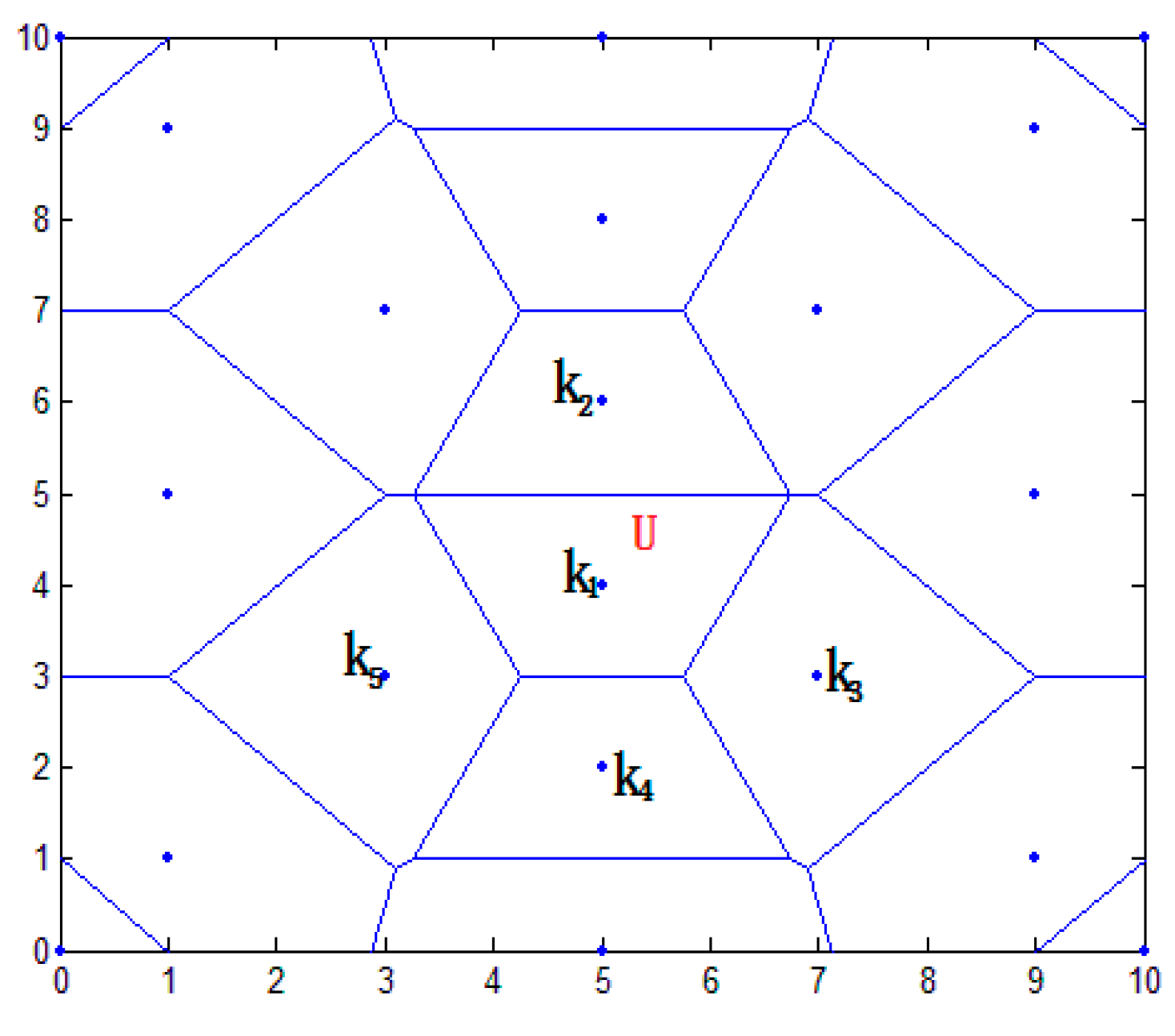
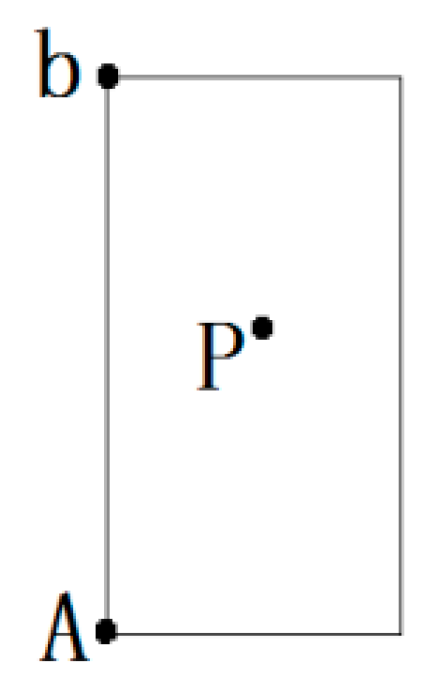
4.2.1. Determining the Location Area of Node
4.2.2. Selecting Virtual Reference Node
4.2.3. Determining the Range of Node Coordinates
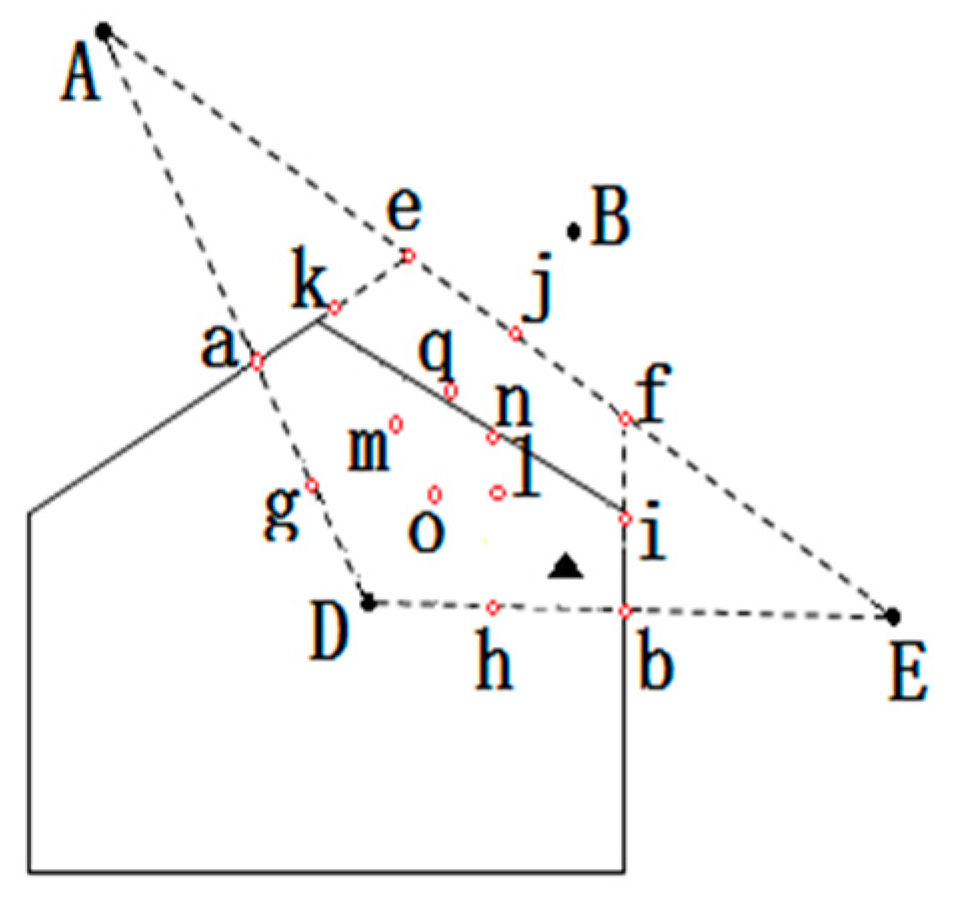
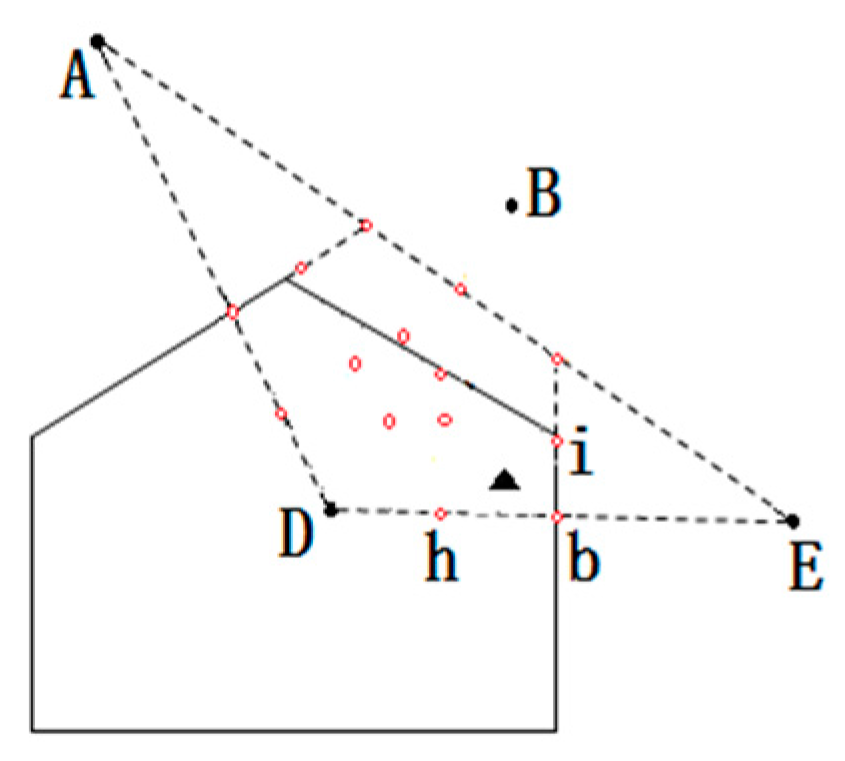
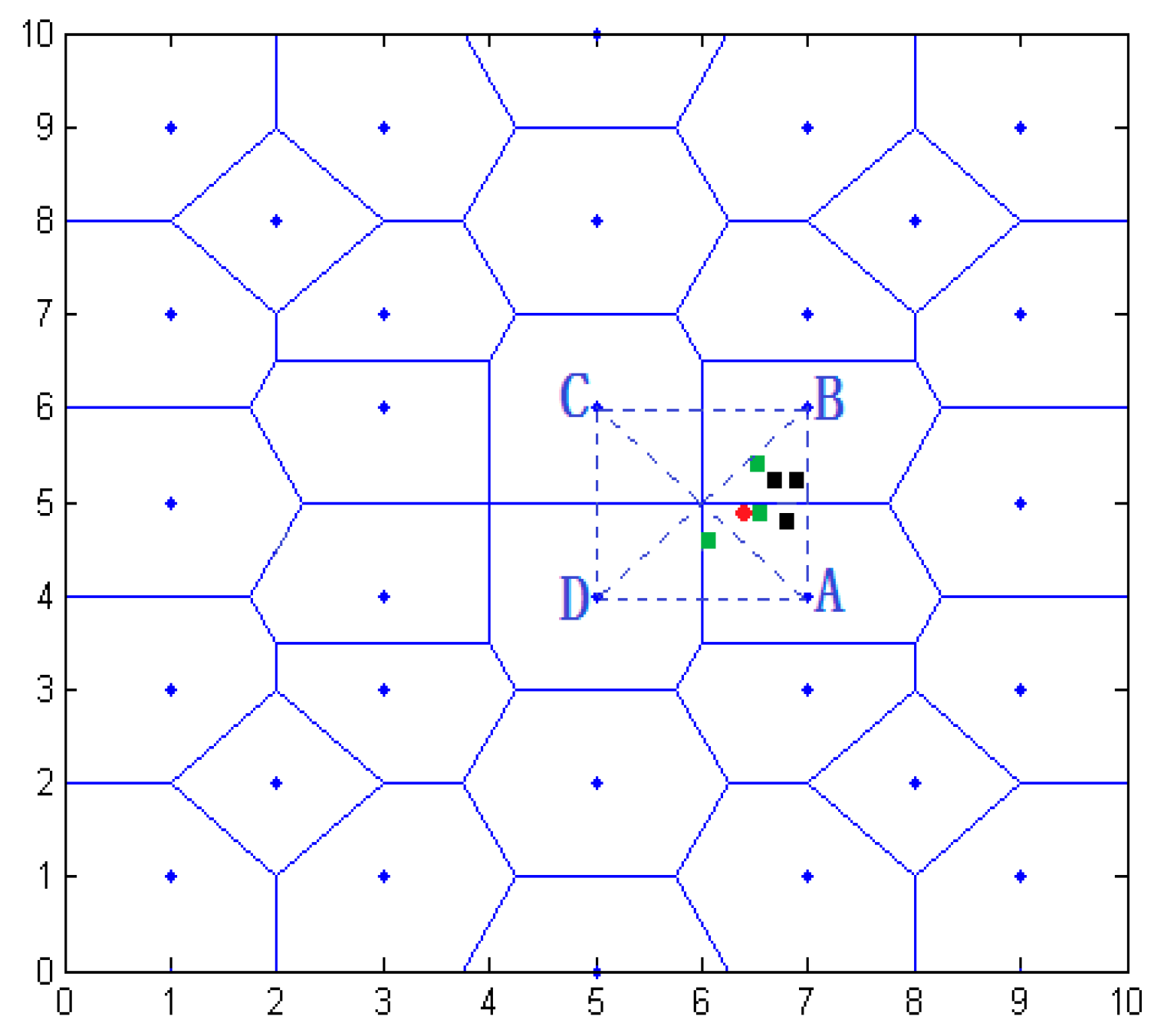
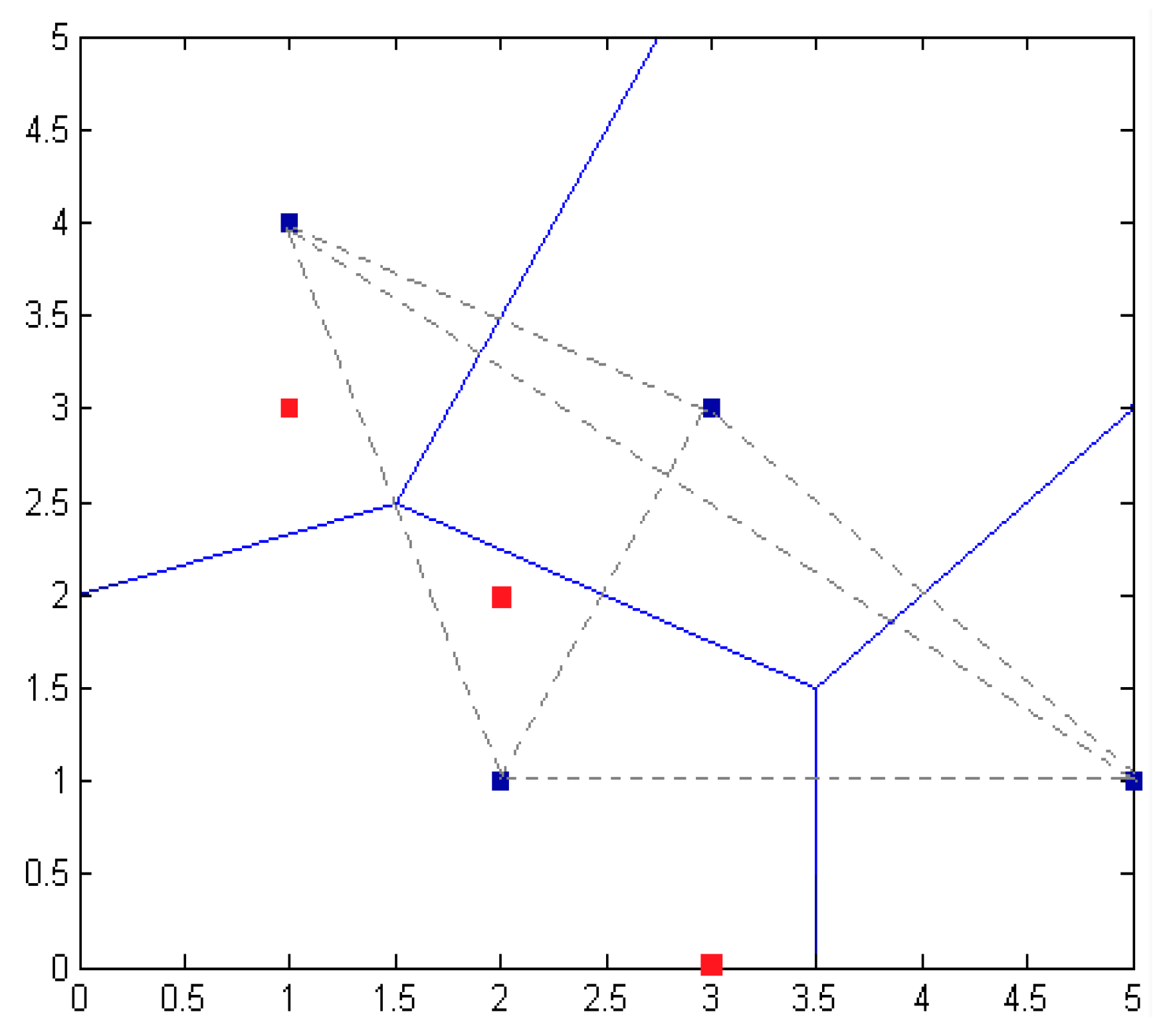
- Step 1.
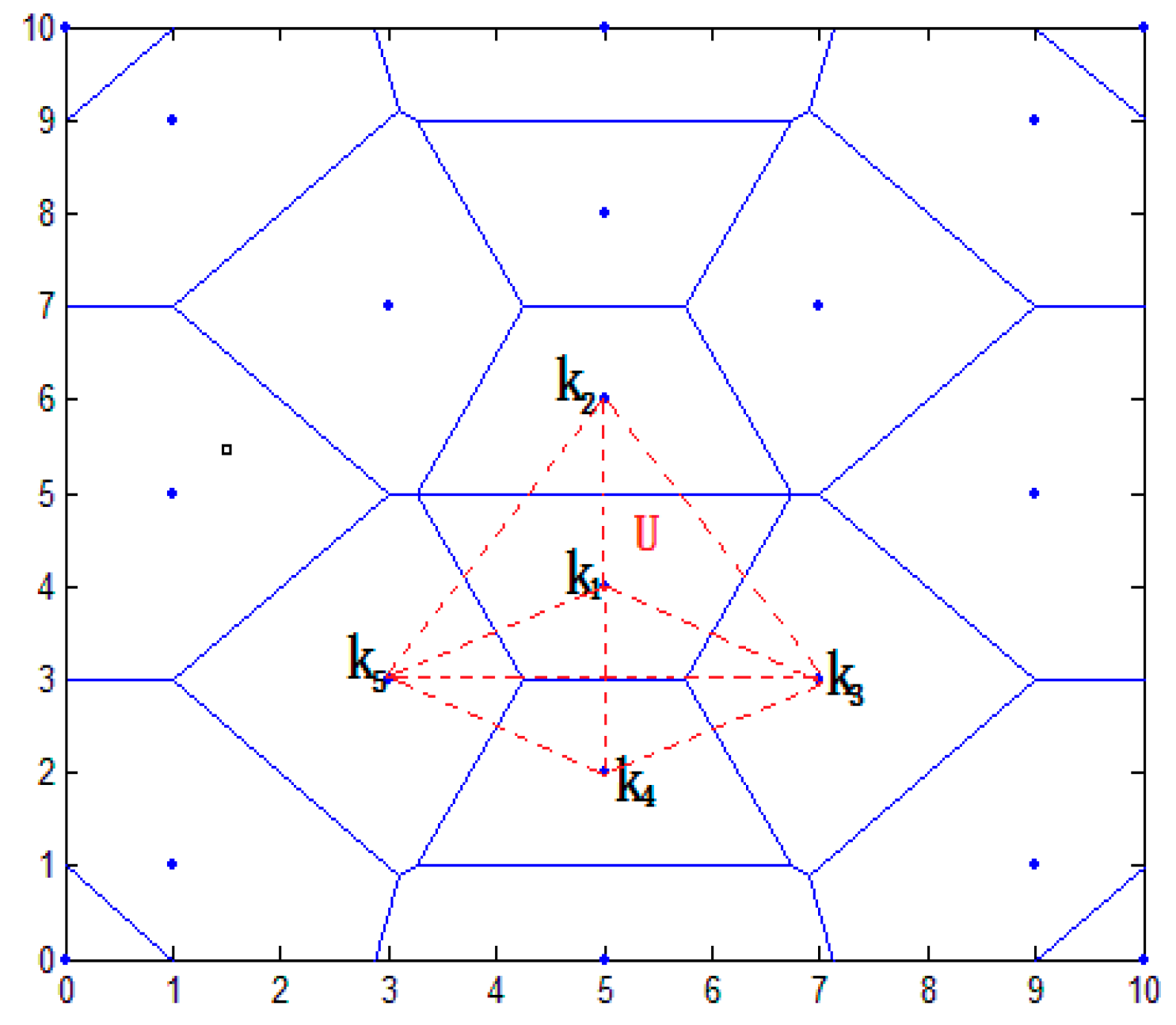
- According to the scope of the regional positioning, the boundary equation is acquired, as well as the computing distance from the center of the polygon region to the boundary. As in Figure 11, the boundary of location area are and , respectively, and we can calculate the distance from to and in ascending rank order.
- Step 2.
- By choosing the distance value, we can get the distance of the corresponding boundary equations, and the value of this equation is considered as one of the candidate coordinates. For example, the minimum distance value , which represents the distance between A and . Then will be considered as a candidate.
- Step 3.
- Taking A and B coordinate values and selecting candidate values using the above step, all values are compared, such as , , . There are three coordinates being compared, i.e., . The comparative value of are two, i.e., . The number of comparative value is determined by candidate value.
- Step 4.
- Given the comparative values of , and the , the final coordinates are determined, that is, .
4.2.4. Regional Primary Division
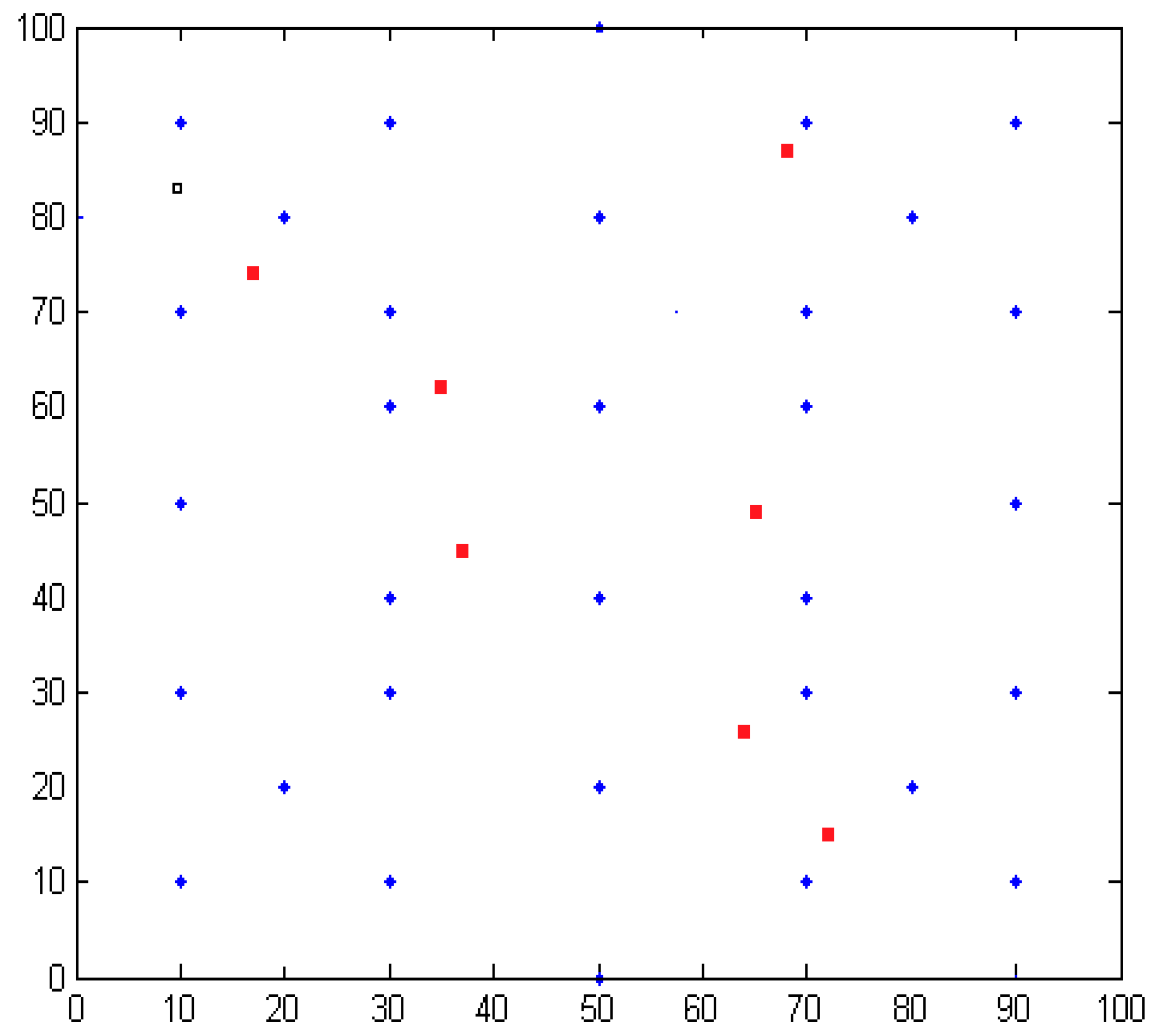
5. Localization Algorithm Simulation and Experiment
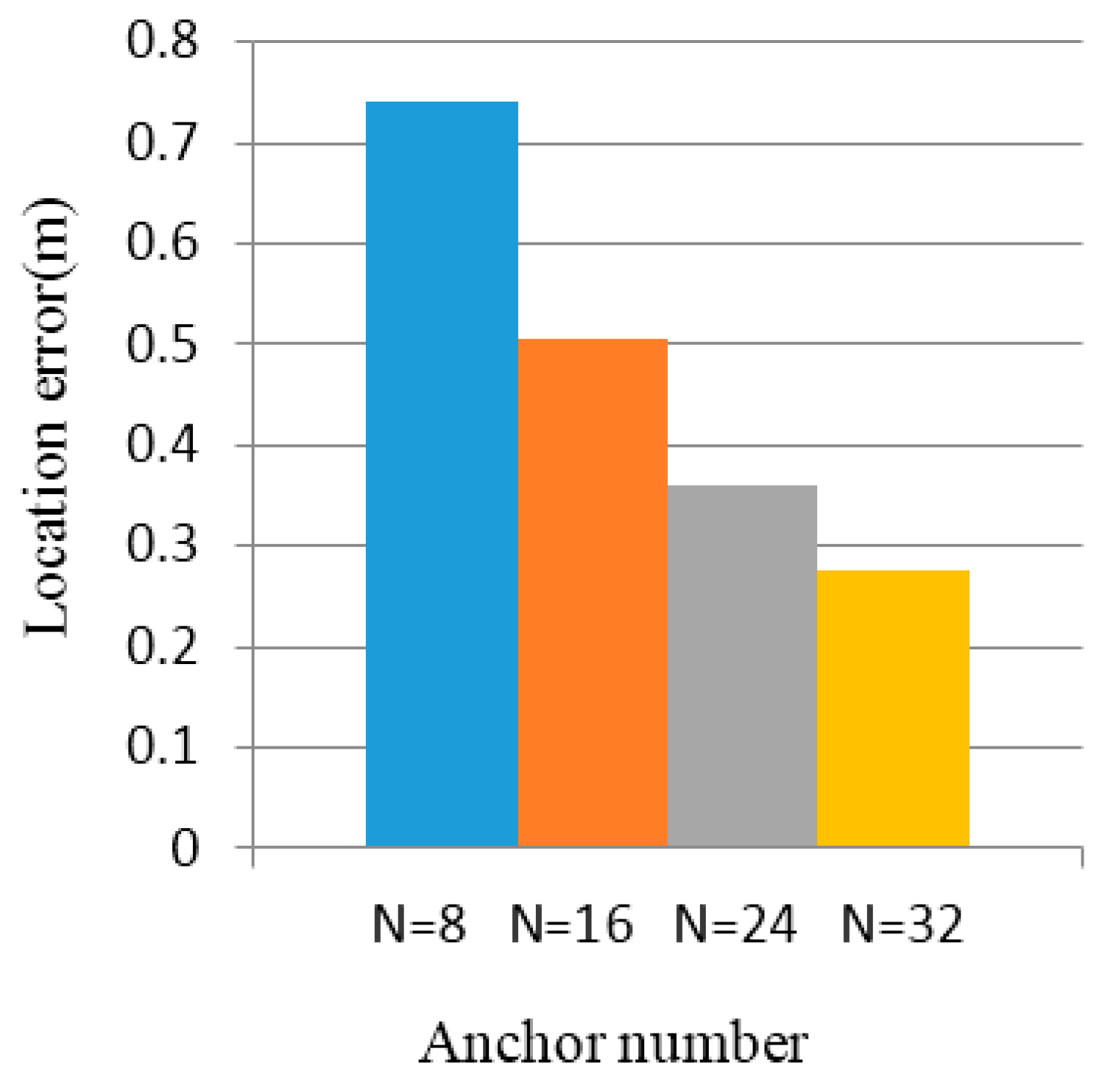
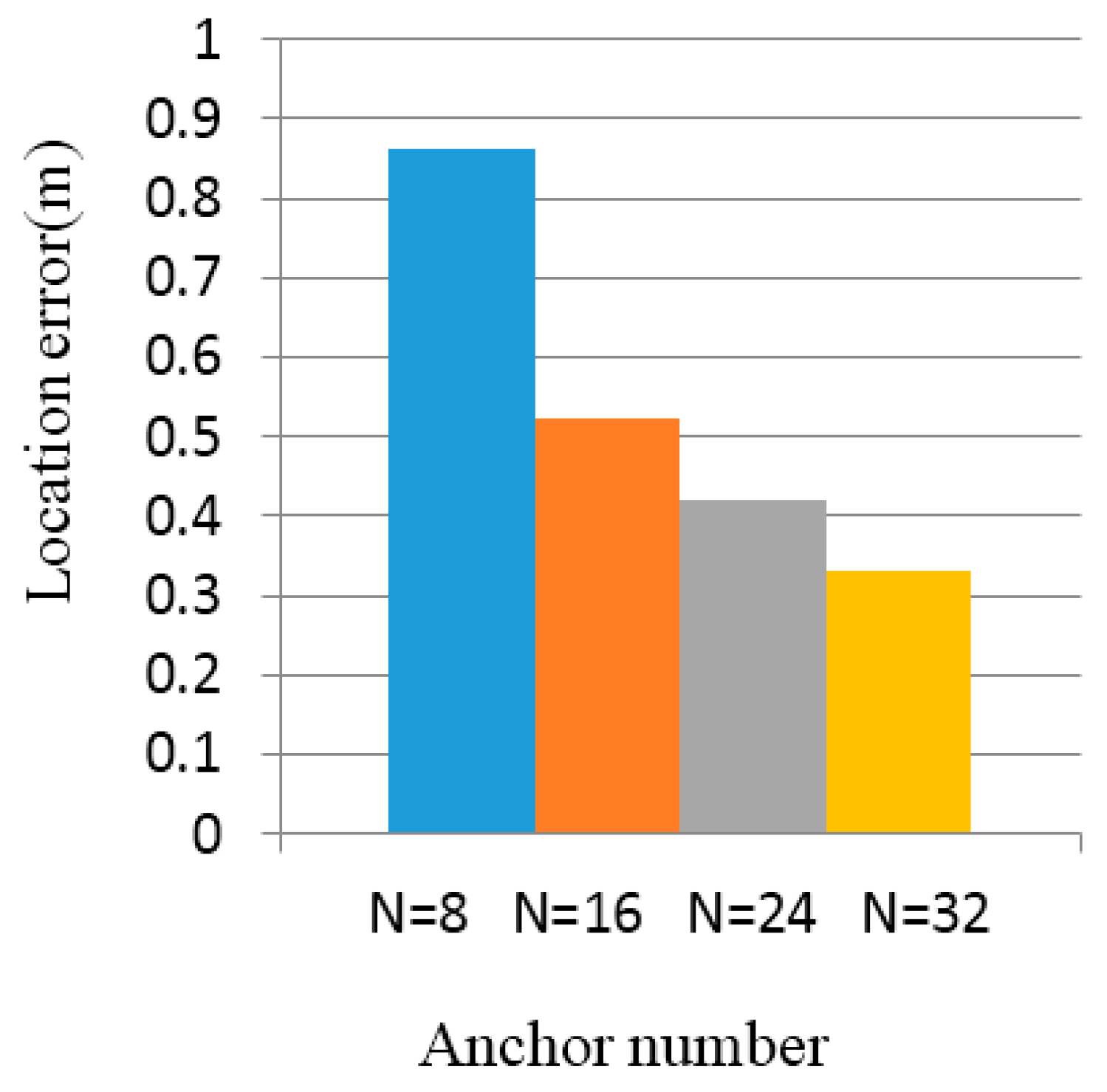
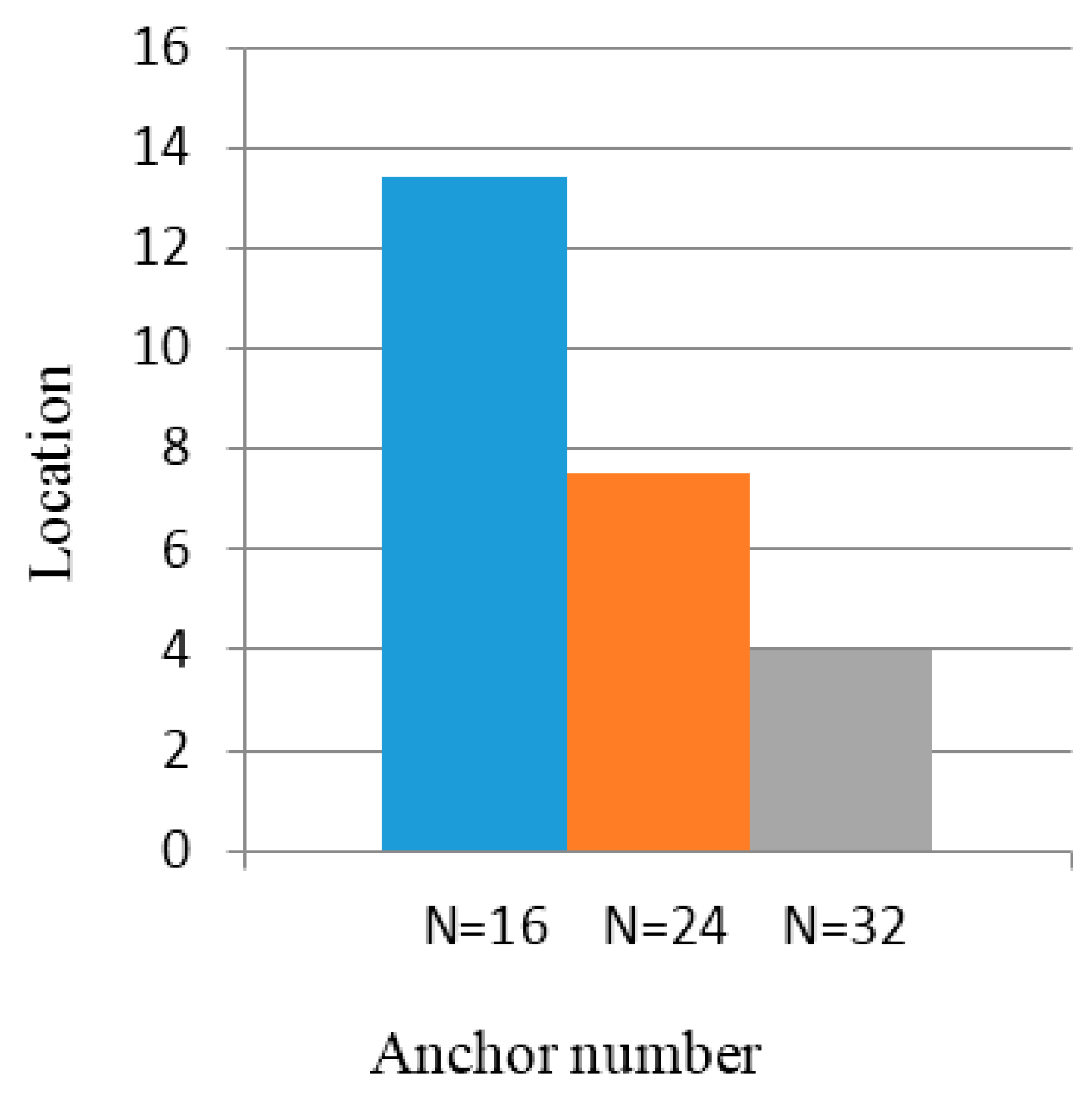
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhu, H.; Yang, L.; Yu, Q. Investigation of technical thought and application strategy for the internet of things. Chin. J. Commun. 2010, 31, 2–9. [Google Scholar]
- Qian, Z.; Wang, Y. IoT Technology and Application. Chin. J. Acta Electron. Sin. 2012, 40, 1023–1029. [Google Scholar]
- Ning, H.; Xu, Q. Research on Global Internet of Things’ Developments and it’s Lonstruction in China. Chin. J. Acta Electron. Sin. 2010, 38, 2590–2599. [Google Scholar]
- Harris, P.; Philip, R.; Robinson, S.; Wang, L. Monitoring Anthropogenic Ocean Sound from Shipping Using an Acoustic Sensor Network and a Compressive Sensing Approach. Sensors 2016, 16, 415. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jin, Q.; Ma, J. Integration of Range-Based and Range-Free Localization Algorithms in Wireless Sensor Networks for Mobile Clouds. In Proceedings of the 2013 International Conference on Internet of Things (iThings/CPSCom), Beijing, China, 20–23 August 2013; IEEE Press: Piscataway, NJ, USA, 2013; pp. 957–961. [Google Scholar]
- Jung, J.; Myung, H. Range-Based Indoor User Localization Using Reflected Signal Path Model. In Proceedings of the 2011 5th IEEE International Conference on Digital Ecosystems and Technologies Conference (DEST), Daejeon, Korea, 31 May–3 June 2011; IEEE Press: Piscataway, NJ, USA, 2011; pp. 251–256. [Google Scholar]
- Zhao, Q.; Liu, S.; Zhang, Z.; Zhang, W.; Wang, H. Analysis and Improvement for a Range Free Localization Algorithm. Chin. J. Sens. Actuators 2010, 23, 1004–1699. [Google Scholar]
- Hu, D.; Qian, S. RSSI-Based Adaptive Wireless Positioning Algorithm. Chin. J. Comput. Appl. Softw. 2014, 9, 139–141. [Google Scholar]
- Zhu, G.; Feng, D.; Xiang, P.; Zhou, Y. Linear-correction TOA localization algorithm with sensor location errors. Chin. J. Syst. Eng. Electron. 2015, 2, 498–502. [Google Scholar]
- Qiao, L.; Wang, W. Research on Improved Arithmetic of TDOA Location Based on Neural Network. Chin. J. Henan Norm. Univ. (Nat. Sci. Ed.) 2014, 4, 139–143. [Google Scholar]
- Yang, H.; Zhou, J.; Meng, Q. A Hybrid Three-dimensional Location Algorithm Based on TDOA and AOA. Chin. J. Nanjing Univ. Posts Telecommun. (Nat. Sci.) 2012, 6, 31–36. [Google Scholar]
- Wu, W.; Liu, J.; Li, H.; Kong, B. An improved weighted trilateration localization algorithm. Chin. J. Zhengzhou Univ. Light Ind. (Nat. Sci.) 2012, 3, 83–85. [Google Scholar]
- Han, J.; Zhu, M.; Ma, X.; Liu, H. Hybrid localization algorithm of maximum likelihood and weighted centroid based on RSSI. Chin. J. Electron. Meas. Instrum. 2013, 10, 937–943. [Google Scholar]
- Haiqing, C.; Huakui, W.; Hua, W. Research on Centroid Localization Algorithm that Uses Modified Weight in WSN. In Proceedings of the International Conference on Network Computing and Information Security, Guilin, China, 14–15 May 2011; pp. 287–291.
- Wang, L.; Zhao, J. Improved DV-Hop algorithm based on error compensation. Chin. J. Comput. Eng. Appl. 2014, 50, 109–113. [Google Scholar]
- Jizeng, W. Improvement on APIT Localization Algorithms for Wireless Sensor Networks. In Proceedings of the International Conference on Network Security, Wireless Communications and Trusted Computing, Wuhan, China, 25–26 April 2009; pp. 719–723.
- Joshi, S. Sensor Selection via Convex Optimization. IEEE Trans. Signal Process. 2009, 57, 451–462. [Google Scholar] [CrossRef]
- Yedavalli, K.; Krishnamachari, B. Sequence-based localization in wireless sensor networks. IEEE Trans. Mob. Comput. 2008, 17, 81–94. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.; Chen, X. A New Algorithm Research of Sequence-Based Localization Technology in Wireless Sensor Networks. Chin. J. Acta Electron. Sin. 2010, 7, 1552–1556. [Google Scholar]
- Pei, Z.; Deng, Z.; Xu, S.; Xu, X. A New Localization Method for Wireless Sensor Network Nodes Based on N-best Rank Sequence. Chin. J. Acta Autom. Sin. 2010, 2, 192–207. [Google Scholar]
- Yang, X.; Liu, J.; Yan, F. Rank Sequence Localization Algorithm in WSN Based on Voronoi Diagram. Chin. J. Comput. Eng. 2014, 7, 43–46. [Google Scholar]
- Wang, G.; Zhang, Q.; Hu, J. An overview of granular computing. Chin. J. CAAI Trans. Intell. Syst. 2007, 2, 8–26. [Google Scholar]
- Song, L.; Liping, Z.; Peng, L.; Deyun, C. New Methods for the Construction of Voronoi Diagram and the Nearest Neighbor Query. In Proceedings of the 9th International Forum on Strategic Technology (IFOST), Cox’s Bazar, Bangladesh, 21–23 October 2014; pp. 255–258.
- Liu, X.; Yao, Y.; Ma, K.; Zhao, H.; He, F. Spacecraft Angular Rates Estimation with Gyrowheel Based on Extended High Gain Observer. Sensors 2016, 16, 537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Shi, X.; Deng, G.; Gao, X.; Ren, M. Research on Indoor Location Technology Based on Back Propagation Neural Network and Taylor Series. Chin. J. Acta Electron. Sin. 2012, 9, 1876–1879. [Google Scholar]
- Chen, D.; Shen, Y.; Xie, B.; Ma, Y. A Measure Model of Similarity for Finding the Best Coach. Chin. J. Northeast. Univ. (Nat. Sci.) 2014, 35, 1697–1700. [Google Scholar]

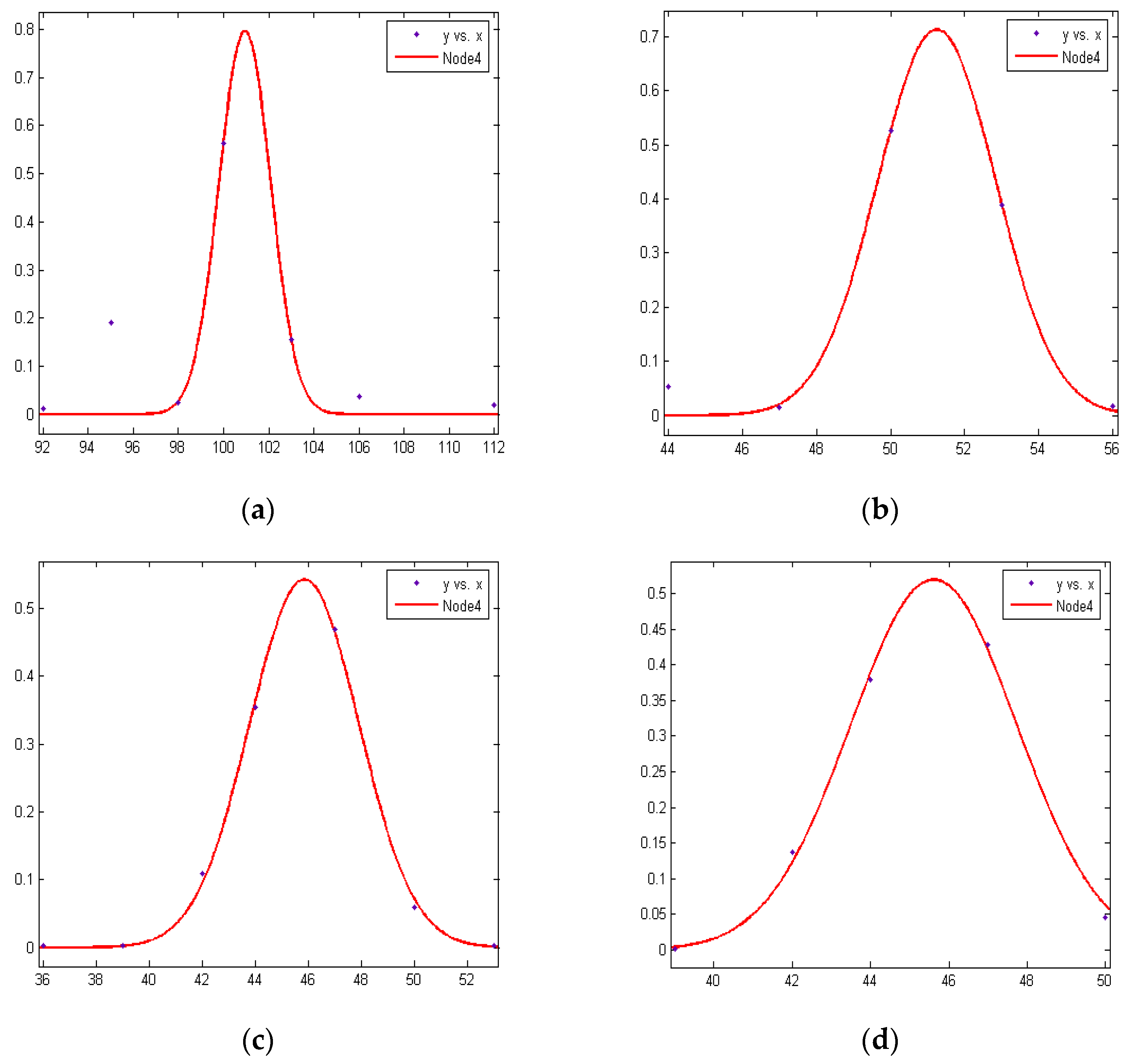





| Distance (m) | Node 1 | Node 2 | Node 3 | Node 4 |
|---|---|---|---|---|
| 1 | 89~100 | 106~109 | 64~89 | 92~112 |
| 1.4 | 72~75 | 75~81 | 56~58 | 72~78 |
| 2 | 72~78 | 50~58 | 61~64 | 44~56 |
| 2.2 | 56~64 | 64~70 | 42~47 | 36~44 |
| 3 | 28~47 | 58~64 | 44~64 | 36~53 |
| 3.2 | 14~33 | 72~75 | 64 | 22~33 |
| 4 | 72 | 75~81 | 67~72 | 39~50 |
| 4.5 | 50~64 | 0~50 | 44~61 | 75~78 |
| Node | 1.4 m | 2.2 m | 3.2 m | 4.5 m |
|---|---|---|---|---|
| Node 1 | 14.501 | 10.613 | 12.968 | 5.248 |
| Node 2 | 19.545 | 11.544 | 6.731 | 11.973 |
| Node 3 | 10.758 | 8.402 | 1.726 | 2.919 |
| Node 4 | 18.053 | 17.262 | 15.003 | 3.735 |
| Polygon Area Estimated | Actual V Area | Actual Triangle | Calculation Results of Coordinate |
|---|---|---|---|
| (7.0, 4.0) | (7.0, 6.0) | (7.0, 4.0) (7.0, 6.0) (5.0, 6.0) | (6.706, 5.226) |
| (6.929, 5.254) | |||
| (7.0, 4.0) | (6.833, 4.833) |
| Polygon Area Estimated | Actual V Area | Actual Triangle | Calculation Results of Coordinate |
|---|---|---|---|
| (7.0, 4.0) | (7.0, 4.0) | (7.0, 4.0) (7.0, 6.0) (5.0, 6.0) | (6.617, 4.967) |
| (6.676, 5.314) | |||
| (7.0 6.0) | (7.0, 4.0) (7.0, 6.0) (5.0, 4.0) | (6.061, 4.648) |
| Unknown Node Original Coordinates | The Calculated Coordinates of Intensity Fluctuation 5% | The Calculated Coordinates of Intensity Fluctuation 10% |
|---|---|---|
| (17, 74) | (21.903, 78.461) | (22.146, 73.352) |
| (37, 45) | (41.734, 25.467) | (41.888, 25.011) |
| (35, 62) | (26.790, 53.509) | (26.953, 52.599) |
| (64, 26) | (63.704, 23.186) | (63.796, 23.389) |
| (65, 49) | (58.850, 30.633) | (62.795, 43.769) |
| (68, 87) | (45.102, 76.509) | (45.103, 76.643) |
| (72, 15) | (67.238, 16.454) | (66.812, 16.079) |
| (17, 74) | (21.903, 78.461) | (22.146, 73.352) |
| Unknown Node Original Coordinates | The Calculated Coordinates of Intensity Fluctuation 5% | The Calculated Coordinates of Intensity Fluctuation 10% |
|---|---|---|
| (17, 74) | (21.58, 83.852) | (21.427, 83.947) |
| (37, 45) | (41.654, 25.246) | (41.847, 25.386) |
| (35, 62) | (39.206, 71.190) | (39.206, 71.190) |
| (64, 26) | (62.280, 23.889) | (65.416, 25.714) |
| (65, 49) | (62.899, 43.868) | (62.782, 43.935) |
| (68, 87) | (67.083, 85.833) | (68.333, 87.500) |
| (72, 15) | (66.746, 15.119) | (66.746, 15.119) |
| (17, 74) | (21.58, 83.852) | (21.427, 83.947) |
| Unknown Node Original Coordinates | The Calculated Coordinates of Intensity Fluctuation 5% | The Calculated Coordinates of Intensity Fluctuation 10% |
|---|---|---|
| (17, 74) | (14.699, 78.637) | (14.136, 78.586) |
| (37, 45) | (22.849, 42.435) | (36.666, 43.333) |
| (35, 62) | (33.333, 63.333) | (25.617, 59.021) |
| (64, 26) | (65.079, 25.714) | (61.220, 23.773) |
| (65, 49) | (63.333, 48.333) | (66.666, 48.333) |
| (68, 87) | (67.916, 86.666) | (67.222, 85.833) |
| (72, 15) | (72.500, 14.166) | (71.666, 13.333) |
| (17, 74) | (14.699, 78.637) | (14.136, 78.586) |
| RSSI of Node 1 Measurement | RSSI Probability of Node 1 | RSSI of Node 4 Measurement | RSSI Probability of Node 4 |
|---|---|---|---|
| 47 | 0.1511 | 53 | 0.0022 |
| 44 | 0.2733 | 50 | 0.0589 |
| 42 | 0.3544 | 47 | 0.4689 |
| 39 | 0.0711 | 44 | 0.3544 |
| 33 | 0.0333 | 42 | 0.1100 |
| 30 | 0.0778 | 39 | 0.0033 |
| 28 | 0.0056 | 36 | 0.0022 |
| Anchor Node Coordinates | Actual Distance (m) | Measuring Intensity | Estimating (m) |
|---|---|---|---|
| (5, 2) | 4.12 | 60.41 | 2.505 |
| (3, 3) | 2.0 | 53.68 | 2.998 |
| (1, 4) | 1.0 | 72.72 | 1.801 |
| (2, 1) | 2.23 | 41.79 | 4.125 |
| Original Coordinates | Calculating Coordinate | Location Error | MLE Coordinate | Location Error |
|---|---|---|---|---|
| (1, 3) | (1.3844, 2.7378) | 0.465 | (0.5507, 2.9138) | 0.4151 |
| (2, 2) | (0.2140, 0.4107) | 2.391 | (3.2102, 1.5525) | 1.291 |
| (3, 0) | (1.9509, 0.4104) | 1.127 | (4.1510, 1.4900) | 1.882 |
| (3, 2) | (2.9304, 2.3687) | 0.463 | (5.0829, 2.5232) | 2.876 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, F.; Jiang, Y.; Xiong, A.; Su, W.; He, L. A Node Localization Algorithm Based on Multi-Granularity Regional Division and the Lagrange Multiplier Method in Wireless Sensor Networks. Sensors 2016, 16, 1934. https://doi.org/10.3390/s16111934
Shang F, Jiang Y, Xiong A, Su W, He L. A Node Localization Algorithm Based on Multi-Granularity Regional Division and the Lagrange Multiplier Method in Wireless Sensor Networks. Sensors. 2016; 16(11):1934. https://doi.org/10.3390/s16111934
Chicago/Turabian StyleShang, Fengjun, Yi Jiang, Anping Xiong, Wen Su, and Li He. 2016. "A Node Localization Algorithm Based on Multi-Granularity Regional Division and the Lagrange Multiplier Method in Wireless Sensor Networks" Sensors 16, no. 11: 1934. https://doi.org/10.3390/s16111934
APA StyleShang, F., Jiang, Y., Xiong, A., Su, W., & He, L. (2016). A Node Localization Algorithm Based on Multi-Granularity Regional Division and the Lagrange Multiplier Method in Wireless Sensor Networks. Sensors, 16(11), 1934. https://doi.org/10.3390/s16111934





