High Quality Plasmonic Sensors Based on Fano Resonances Created through Cascading Double Asymmetric Cavities
Abstract
:1. Introduction
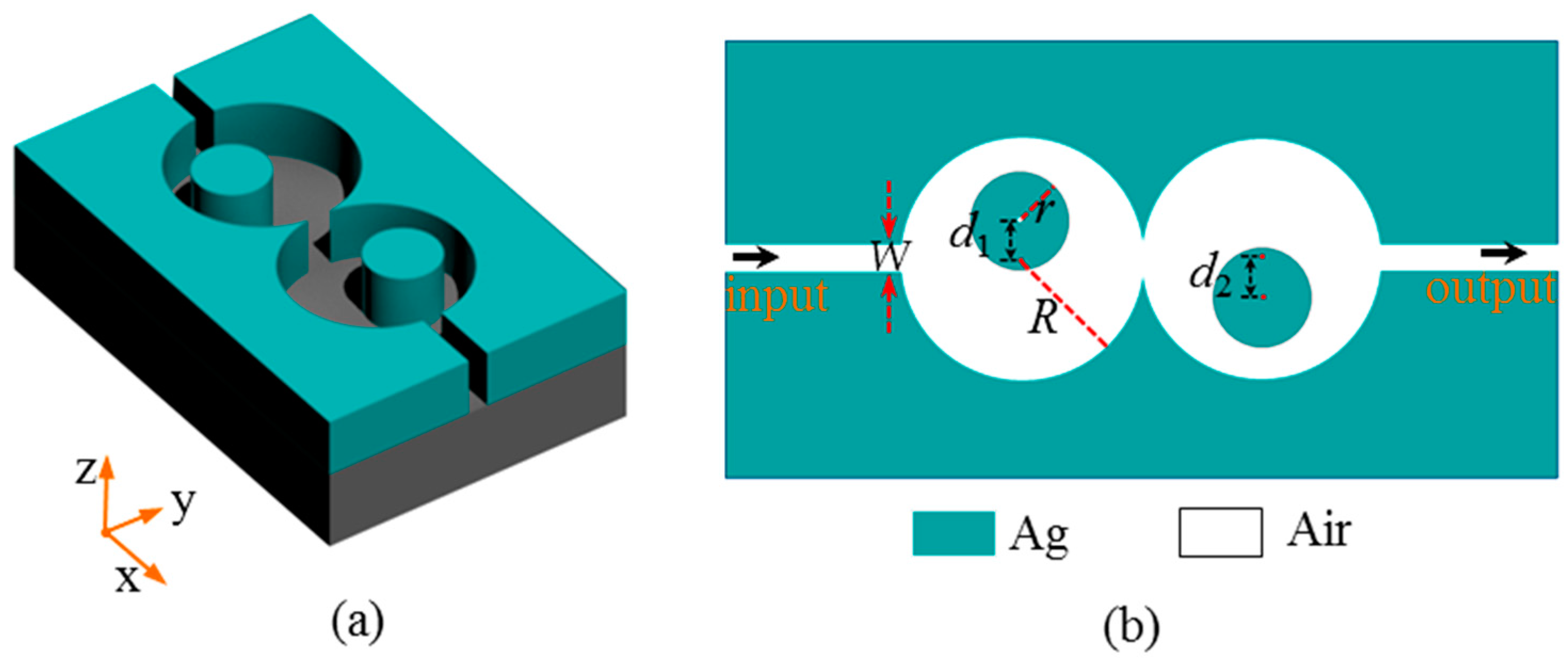
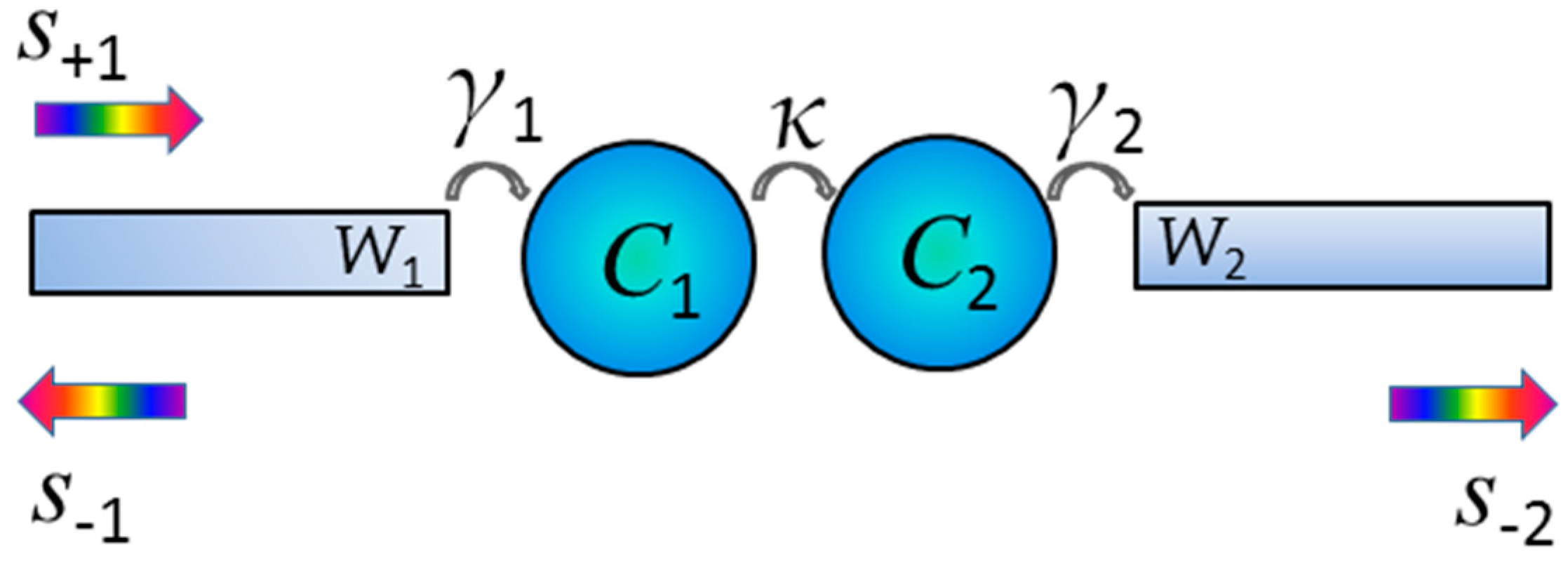
2. Structure Descriptions and Theory Analysis
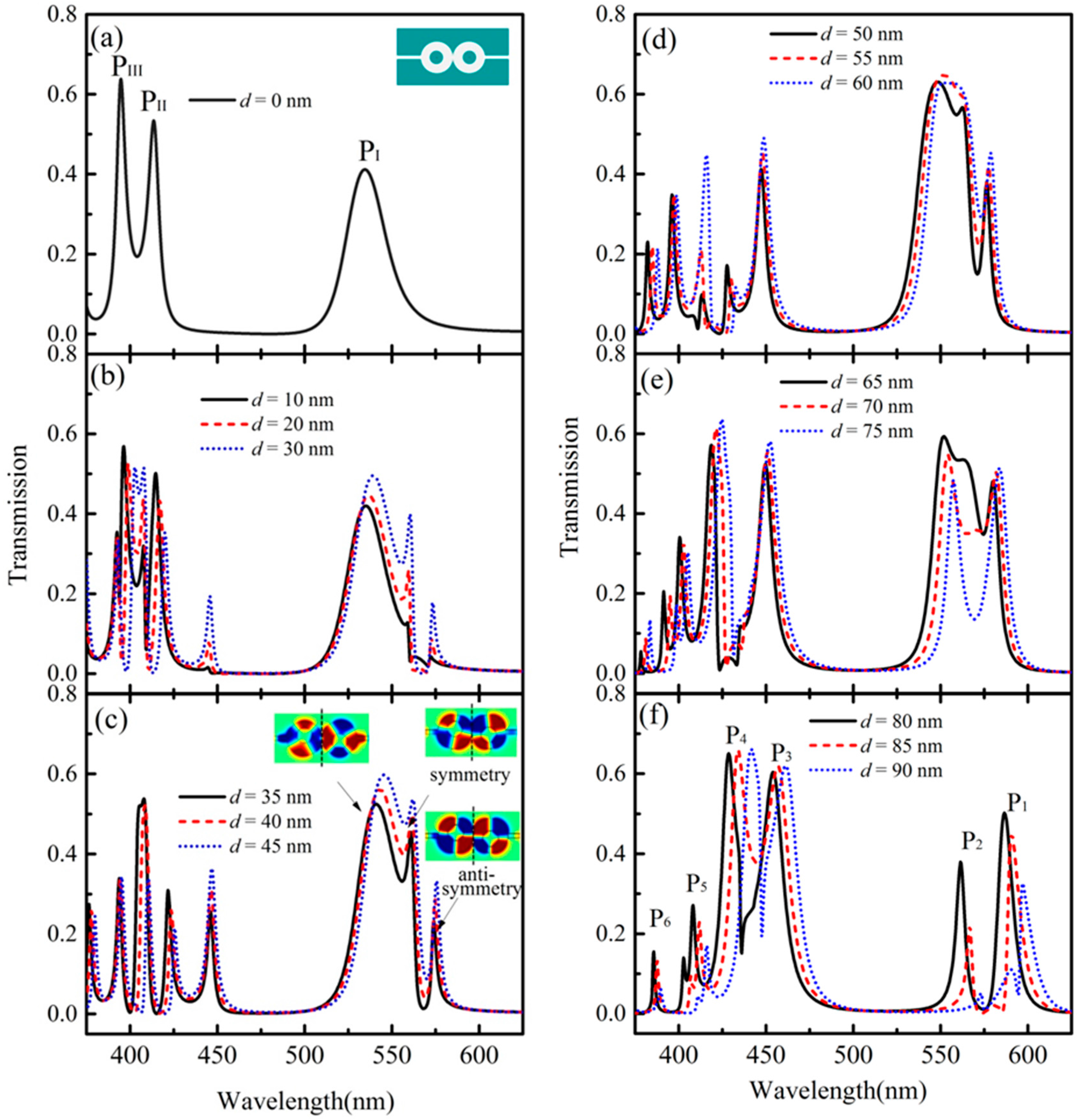
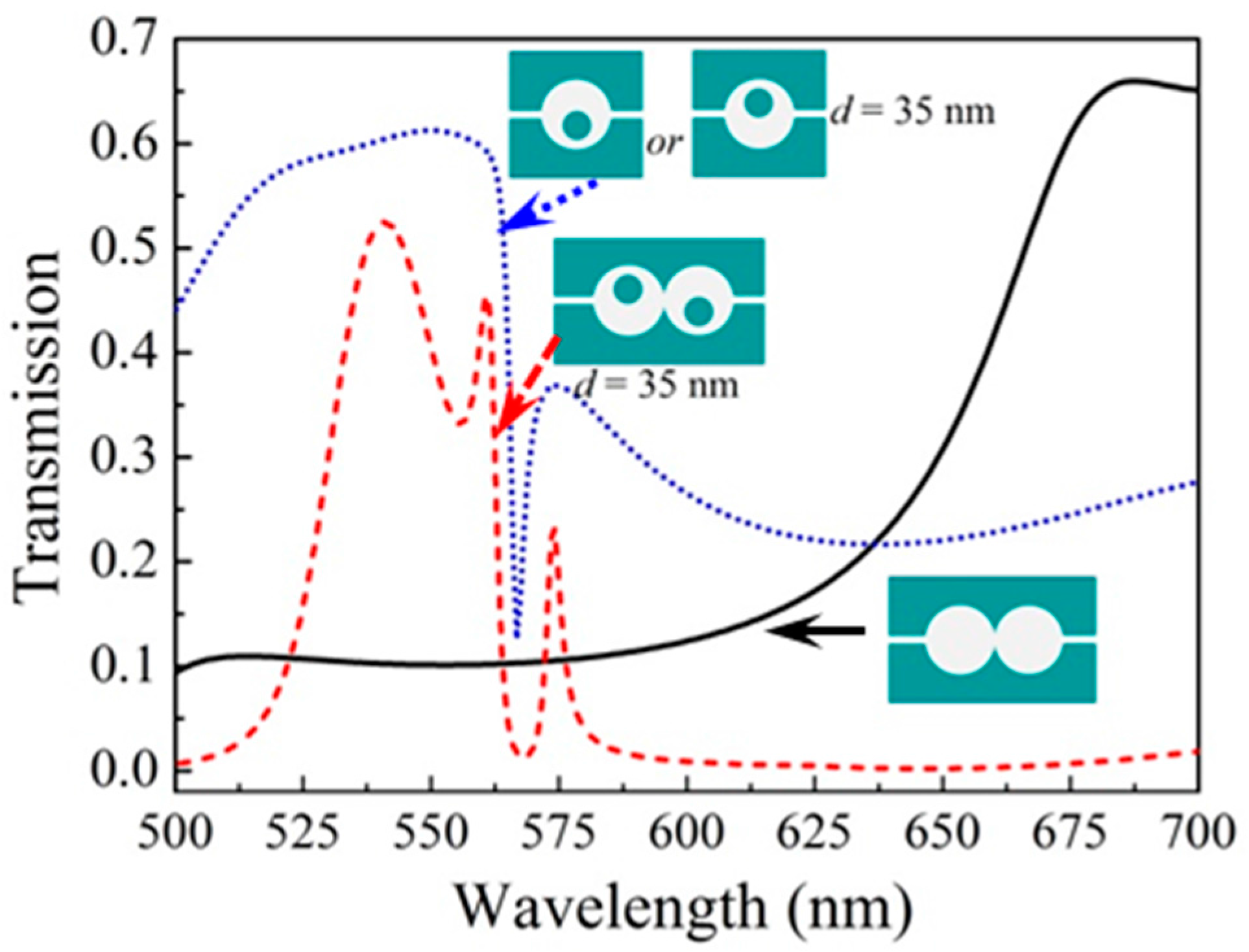
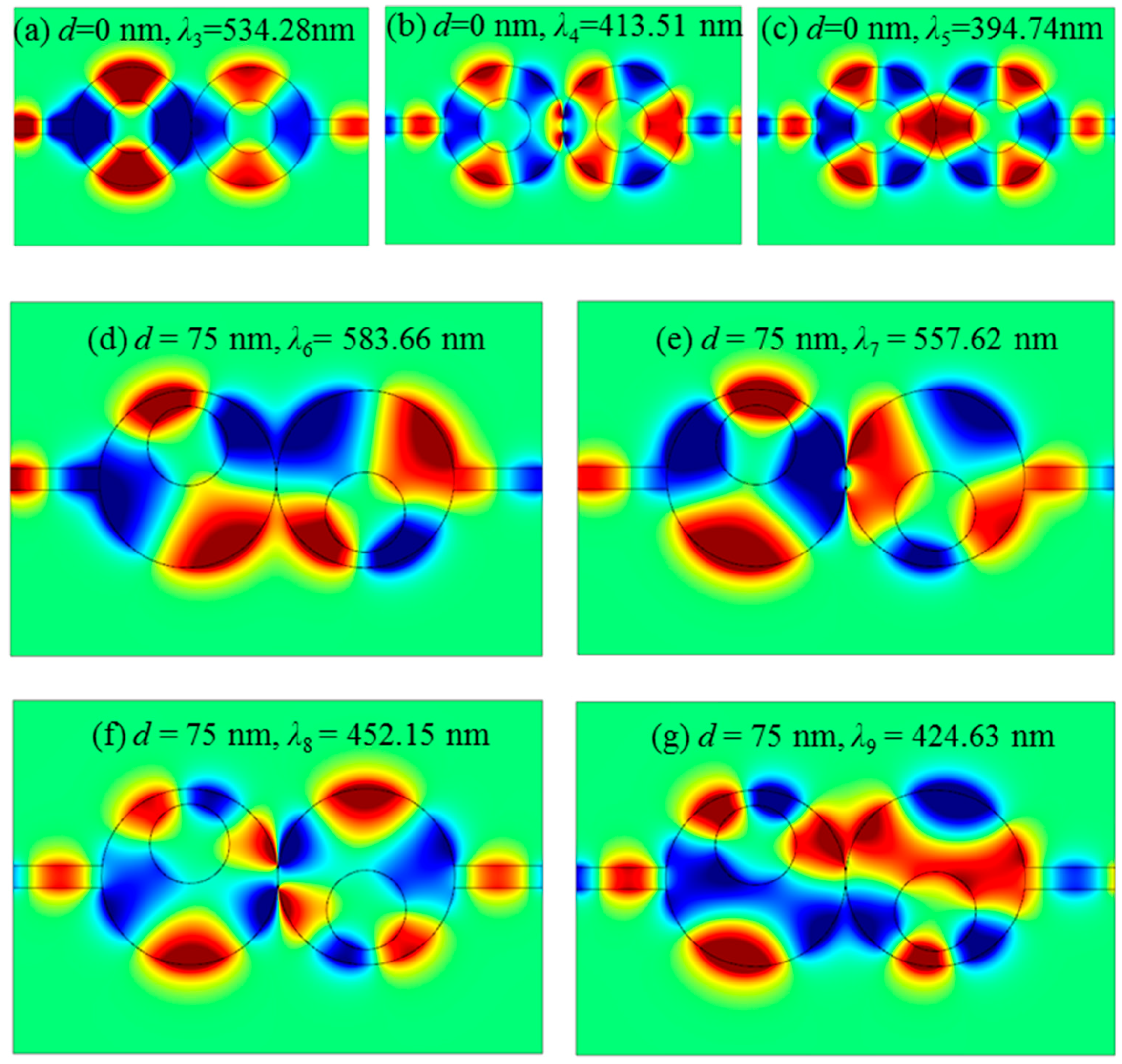
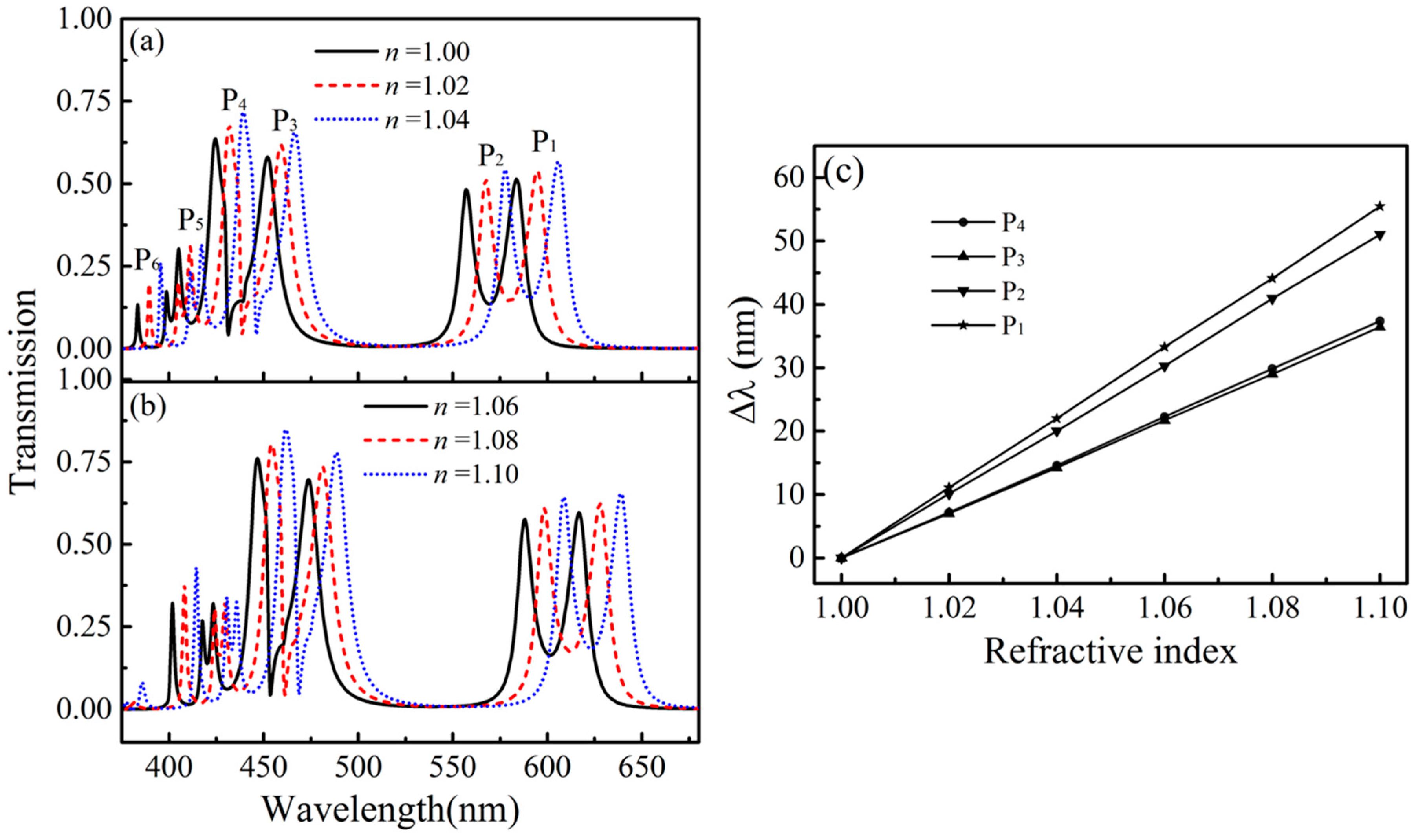
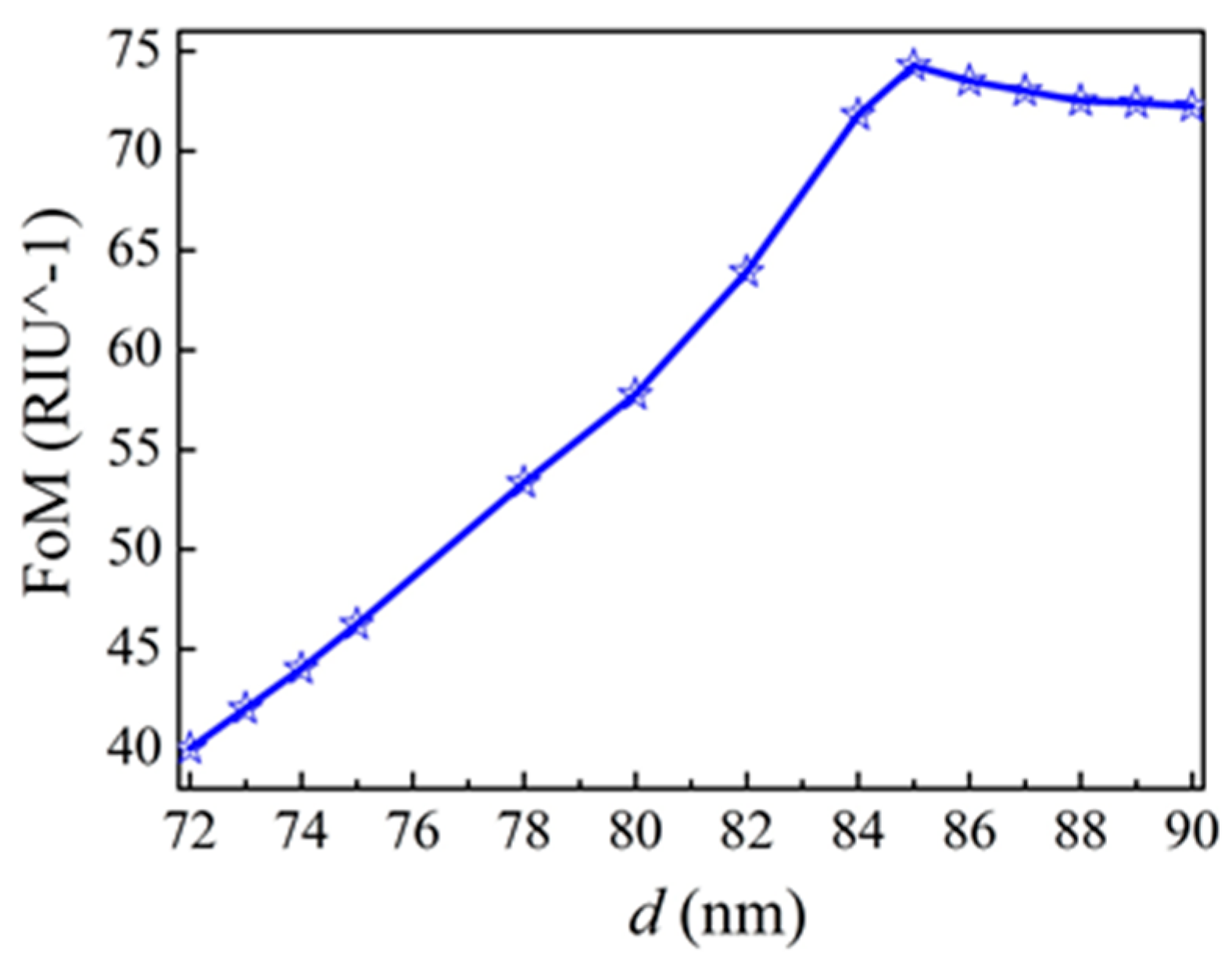
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shen, X.; Cui, T.J. Ultrathin plasmonic metamaterial for spoof localized surface plasmons. Laser Photonics Rev. 2014, 8, 137–145. [Google Scholar] [CrossRef]
- Huidobro, P.A.; Shen, X.; Cuerda, J.; Moreno, E.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Pendry, J.B. Magnetic localized surface plasmons. Phys. Rev. X 2014, 4, 340–342. [Google Scholar]
- Liao, Z.; Luo, Y.; Fernández-Domínguez, A.I.; Shen, X.; Maier, S.A.; Cui, T.J. High-order localized spoof surface plasmon resonances and experimental verifications. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Shen, X.; Pan, B.C.; Zhao, J.; Luo, Y.; Cui, T.J. Combined system for efficient excitation and capture of LSP resonances and flexible control of SPP transmissions. ACS Photonics 2015, 2, 738–743. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Thomas, B.A.; Han, Z.H.; Sergey, I.B. Compact on-chip temperature sensors based on dielectric-loaded plasmonic waveguide-ring resonators. Sensors 2011, 11, 1992–2000. [Google Scholar]
- Mark, S.A. Nonplasmonic surface enhanced Raman spectroscopy using silica microspheres. Appl. Phys. Lett. 2010, 97, 131116. [Google Scholar]
- Kashif, M.; Bakar, A.A.; Arsad, N.; Shaari, S. Development of phase detection schemes based on surface plasmon resonance using interferometry. Sensors 2014, 14, 15914–15938. [Google Scholar] [CrossRef] [PubMed]
- Brolo, A.G. Plasmonics for future biosensors. Nat. Photonics 2012, 6, 709–713. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, H.Y.; Wang, H.; Gao, B.R.; Hao, Y.W.; Jin, Y.; Chen, Q.D.; Sun, H.B. Surface plasmon enhanced fluorescence of dye molecules on metal grating films. J. Phys. Chem. C 2011, 115, 12636–12642. [Google Scholar] [CrossRef]
- Huo, Y.Y.; Jia, T.Q.; Zhang, Y.; Zhao, H.; Zhang, S.A.; Feng, D.H.; Sun, Z.R. Narrow and deep Fano resonances in a rod and concentric square ring-disk nanostructures. Sensors 2013, 13, 11350–11361. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Wang, Z.; Li, K.; Xu, A. A plasmonic triple-wavelength demultiplexing structure based on MIM waveguide with side-coupled nanodisk cavities. IEEE Trans. Nanotechnol. 2013, 12, 1185–1189. [Google Scholar] [CrossRef]
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; Lei, L.; Guo, Z. Design of an optical power and wavelength splitter based on subwavelength waveguides. J. Lightw. Technol. 2014, 32, 3020–3026. [Google Scholar] [CrossRef]
- Yin, Y.; Qiu, T.; Li, J.; Chu, P.K. Plasmonic nano-lasers. Nano Energy 2012, 1, 25–41. [Google Scholar] [CrossRef]
- Lu, X.Y.; Wan, R.G.; Zhang, T.Y. Metal-dielectric-metal based narrow band absorber for sensing applications. Opt. Express 2015, 23, 29842–29847. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, H.; Lee, B. High order plasmonic Bragg reflection in the metal-insulator-metal waveguide Bragg grating. Opt. Express 2008, 16, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, A.; Massoud, Y. A low-loss metal-insulatormetal plasmonic Bragg reflector. Opt. Express 2006, 14, 11318–11323. [Google Scholar] [CrossRef]
- Dolatabady, A.; Granpayeh, N. All optical logic gates based on two dimensional plasmonic waveguides with nanodisk resonators. J. Opt. Soc. Korea 2012, 16, 432–442. [Google Scholar] [CrossRef]
- Bian, Y.; Gong, Q. Compact all-optical interferometric logic gates based on one-dimensional metal-insulator-metal structures. Opt. Commun. 2013, 313, 27–35. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, L. Multiple Fano resonances based on different waveguide modes in a symmetry breaking plasmonic system. IEEE Photonics J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Wang, H.Y.; Zhang, Z.Y. Fano resonance in a gear-shaped nanocavity of themetal-insulator-metal waveguide. Plasmonics 2012, 8, 797–801. [Google Scholar] [CrossRef]
- Rahmani, M.; Luk’yanchuk, B.; Hong, M. Fano resonance in novel plasmonic nanostructures. Laser Photonics Rev. 2013, 7, 329–349. [Google Scholar] [CrossRef]
- Hayashi, S.; Nesterenko, D.V.; Sekkat, Z. Waveguide-coupled surface plasmon resonance sensor structures: Fano lineshape engineering for ultrahigh-resolution sensing. J. Phys. D Appl. Phys. 2015, 48, 325303. [Google Scholar] [CrossRef]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef] [PubMed]
- Saeed, G.; Arash, A.; Nezih, P. Fano resonances in nanoshell clusters deposited on a multilayer substrate of β-SiC/SiO2/Si to design high-quality plasmonic sensors. J. Lightw. Technol. 2015, 13, 2817–2823. [Google Scholar]
- Zhang, J.; Zayats, A. Multiple Fano resonances in single-layer nonconcentric core-shell nanostructures. Opt. Express 2013, 21, 8426–8436. [Google Scholar] [CrossRef] [PubMed]
- Zia, R.; Selker, D.M.; Catrysse, P.B.; Brongrsma, M.L. Geometries and materials for subwavelength surface plasmon modes. J. Opt. Soc. Am. 2004, 21, 2442–2446. [Google Scholar] [CrossRef]
- Wang, T.B.; Wen, X.W.; Yin, C.P.; Wang, H.Z. The transmission characteristics of surface plasmon polaritons in ring resonator. Opt. Express 2009, 17, 24096–24101. [Google Scholar] [CrossRef] [PubMed]
- Qu, S.N.; Song, C.; Xia, X.S.; Liang, X.Y.; Tang, B.J.; Hu, Z.D.; Wang, J.C. Detuned plasmonic Bragg grating sensor based on a defect metal-insulator-metal waveguide. Sensors 2016, 16, 784. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Bozhevolnyi, S.I. Plasmon-induced transparency with detuned ultracompact Fabry-Perot resonators in integrated plasmonic devices. Opt. Express 2011, 19, 3251–3257. [Google Scholar] [CrossRef] [PubMed]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice-Hall: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Haus, H.A.; Huang, W.P. Coupled-mode theory. IEEE Proc. 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Piao, X.; Yu, S.; Koo, S.; Lee, K.; Park, N. Fano-type spectral asymmetry and its control for plasmonic metal-insulator-metal stub structures. Opt. Express 2011, 19, 10907–10912. [Google Scholar] [CrossRef] [PubMed]
- Zhan, S.; Peng, Y.; He, Z.; Li, B.; Chen, Z.; Xu, H.; Li, H. Tunable nanoplasmonic sensor based on the asymmetric degree of Fano resonance in MDM waveguide. Sci. Rep. 2016, 6, 22428. [Google Scholar] [CrossRef] [PubMed]
- Yun, B.; Hu, G.; Zhang, R.; Cui, Y. Fano resonances in a plasmonic waveguide system composed of stub coupled with a squarecavity resonator. J. Opt. 2016, 18, 055002. [Google Scholar]
- Ahmadivand, A.; Pala, N. Localization, hybridization, and coupling of plasmon resonances in an aluminum nanomatryushka. Plasmonics 2015, 10, 809–817. [Google Scholar] [CrossRef]
- Luo, X.; Poon, A.W. Coupled spiral-shaped microdisk resonators with non-evanescent asymmetric inter-cavity coupling. Opt. Express 2007, 15, 17313–17322. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Shao, M.; Zeng, X. High Quality Plasmonic Sensors Based on Fano Resonances Created through Cascading Double Asymmetric Cavities. Sensors 2016, 16, 1730. https://doi.org/10.3390/s16101730
Zhang X, Shao M, Zeng X. High Quality Plasmonic Sensors Based on Fano Resonances Created through Cascading Double Asymmetric Cavities. Sensors. 2016; 16(10):1730. https://doi.org/10.3390/s16101730
Chicago/Turabian StyleZhang, Xiangao, Mingzhen Shao, and Xiaoqi Zeng. 2016. "High Quality Plasmonic Sensors Based on Fano Resonances Created through Cascading Double Asymmetric Cavities" Sensors 16, no. 10: 1730. https://doi.org/10.3390/s16101730
APA StyleZhang, X., Shao, M., & Zeng, X. (2016). High Quality Plasmonic Sensors Based on Fano Resonances Created through Cascading Double Asymmetric Cavities. Sensors, 16(10), 1730. https://doi.org/10.3390/s16101730




