Fault-Tolerant Algorithms for Connectivity Restoration in Wireless Sensor Networks
Abstract
:1. Introduction
1.1. Our Contributions
- (1)
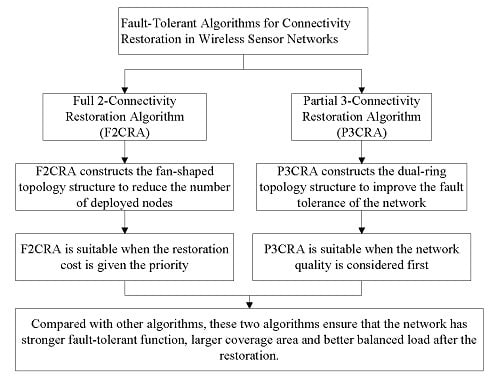
- Full 2-Connectivity Restoration Algorithm (F2CRA) provides two vertex-disjoint paths between every pair of network nodes. This algorithm is suitable when the cost is considered first.
- (2)
- Partial 3-Connectivity Restoration Algorithm (P3CRA) provides three vertex-disjoint paths between every pair of segments and at least two vertex-disjoint paths between every pair of relay nodes. This algorithm is suitable when the fault tolerance, network coverage and topology quality are considered first.
1.2. Paper Organization
2. Related Work
| Algorithms | k | Deployment Locations | Fault-Tolerance | Network Types |
|---|---|---|---|---|
| Lloyd [9] | k = 1 | Unconstrained | No | Homogeneous |
| Li [10] | k = 1 | Unconstrained | No | Heterogeneous |
| Bhattacharya [13] | k = 1 | Constrained | No | Homogeneous |
| Yang [11] | k = 1, 2 | Constrained | Full | Hierarchical |
| Hao [2] | k > 1 | Unconstrained | Partial | Hierarchical |
| Zhang [3] | k = 2 | Unconstrained | Full | Hierarchical |
| Han [4] | k > 1 | Unconstrained | Full, Partial | Heterogeneous |
| Senel [5] | k = 2 | Unconstrained | Full | Homogeneous |
| Our algorithms | k = 2, 3 | Unconstrained | Full, Partial | Homogeneous |
3. System Model and Preliminaries
3.1. System Model
3.2. Preliminaries

| Notation | Description |
|---|---|
| OCH | Outer Convex Hull |
| ICH | Inner convex hull |
| CP | Corner point |
| Center of OCH | |
| Radius of relay node | |
| Set of relay nodes | |
| Set of segments, . The corresponding coordinate set of these segments is . |
4. Algorithms
4.1. Full 2-Connectivity Restoration Algorithm
| Algorithms 1 F2CRA |
| INPUT: , and . is null. |
| OUTPUT: A set of relay nodes . |
| Step 1. Find OCH. |
| (1) Adopt the Graham scan algorithm to find OCH in . |
| Suppose that CPs set of OCH is and their corresponding coordinate is . The remaining segments set inside OCH is . |
| (2) Calculate the coordinate of . |
| (3) Calculate each side length of OCH. |
| for to do |
| if then |
| end if |
| end for |
| Then the set of the side lengths of OCH is . |
| Step 2. Find ICH. |
| (1) Line each CP with , respectively, and calculate the length of each line: |
| for to do |
| Then the set of these lines is |
| (2) Calculate the angle between two adjacent lines: |
| for to do |
| if then |
| end if |
| Calculate the number of relay nodes to be deployed in each line: |
| , |
| Start with a CP of OCH , and deploy relay nodes towards with one relay node every distance , then get the corresponding deployment position of nodes. Add these nodes into the set of and set the last node , the coordinate . |
| end for |
| Then the CPs set of ICH is . |
| (3) Deploy the nodes along with the edge of ICH. |
| for to do |
| if then |
| end if |
| Deploy relay nodes between and , and add these nodes into the set of . |
| end for |
| Step 3. Establish 2-connectivity for the segments on OCH. |
| if then |
| Select non-adjacent sides of shortest total length from the side set , deploy relay nodes along with these sides, and add these nodes into the set of . |
| else |
| There will be a vertex not forming 2-connectivity. At this time, find a node on ICH that is closest to but not collinear with , deploy the nodes uniformly between and , and add these nodes into the set of . |
| end if |
| Step 4. Establish 2-connectivity for the isolated segments on the plane |
| for to do |
| Find the nearest two nodes and for , . Deploy relay nodes uniformly in and , and , and add these nodes into set . |
| end for |

4.2. Partial 3-Connectivity Restoration Algorithm

| Algorithms 2 P3CRA |
| INPUT: , and . is null. |
| OUTPUT: A set of relay nodes . |
| Step 1 and Step 2 are the same with F2CRA’s. |
| Step 3. Establish 3-connectivity for the segments on OCH. |
| for to do |
| Deploy relay nodes between and .(if , then ) |
| end for |
| Step 4. Establish 3-connectivity for the isolated segments on the plane. |
| for to do |
| Find the nearest three nodes , and for . (, , are not on the same line) |
| Deploy nodes uniformly in and , and , and . |
| end for |
5. Algorithm Analysis

6. Algorithm Comparison and Simulation Analysis
6.1. Algorithm Comparison
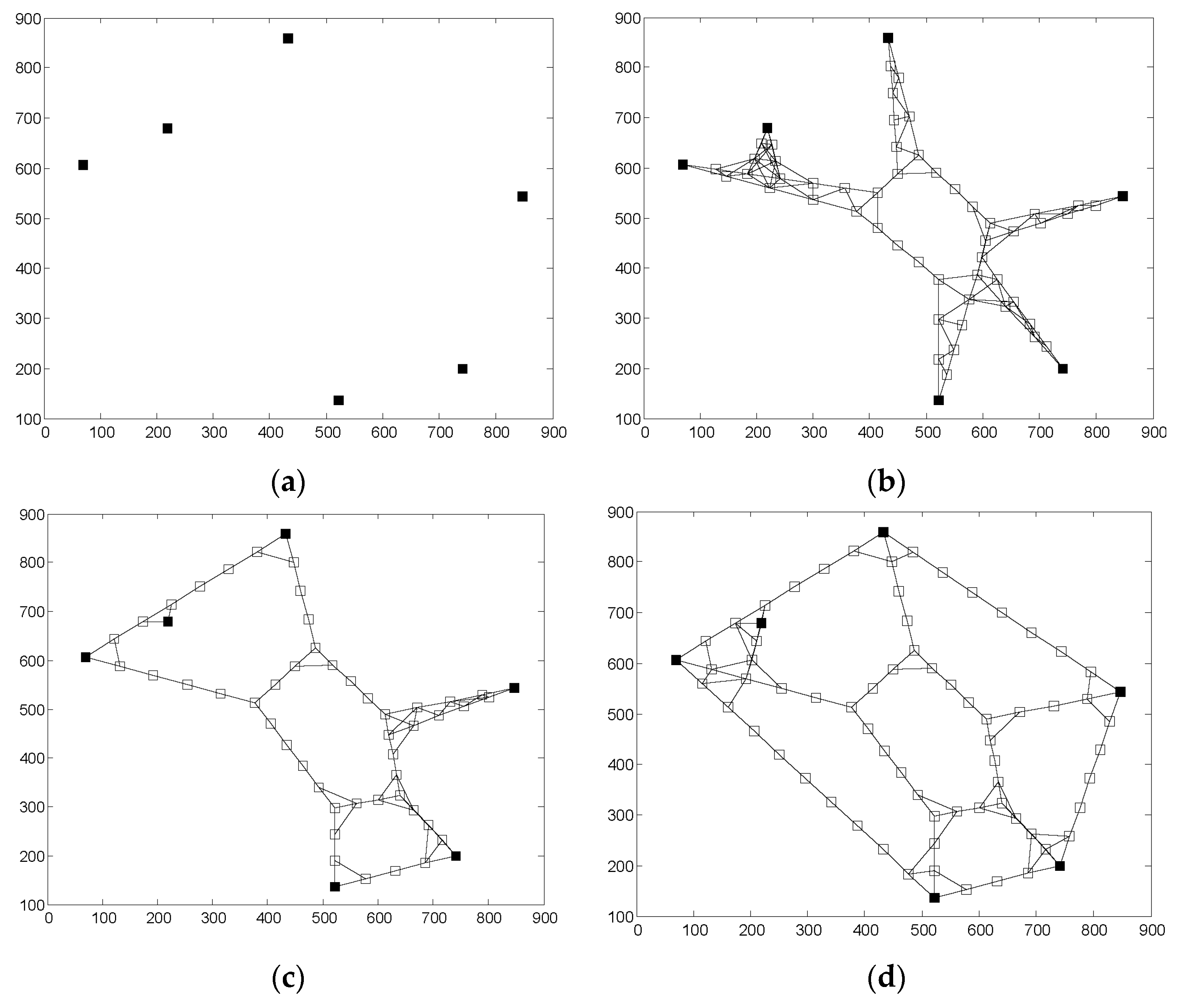
6.2. Simulation Analysis
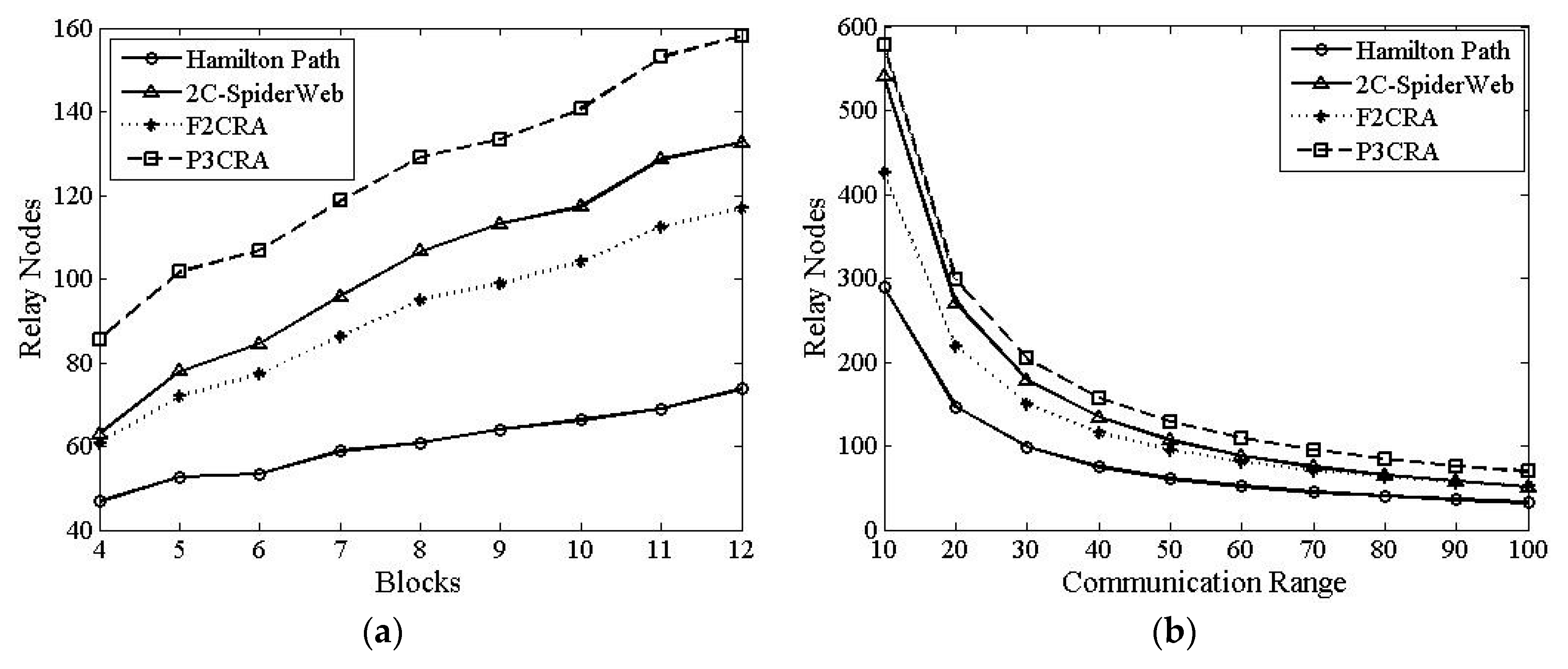
6.2.1. The Number of Relay Nodes
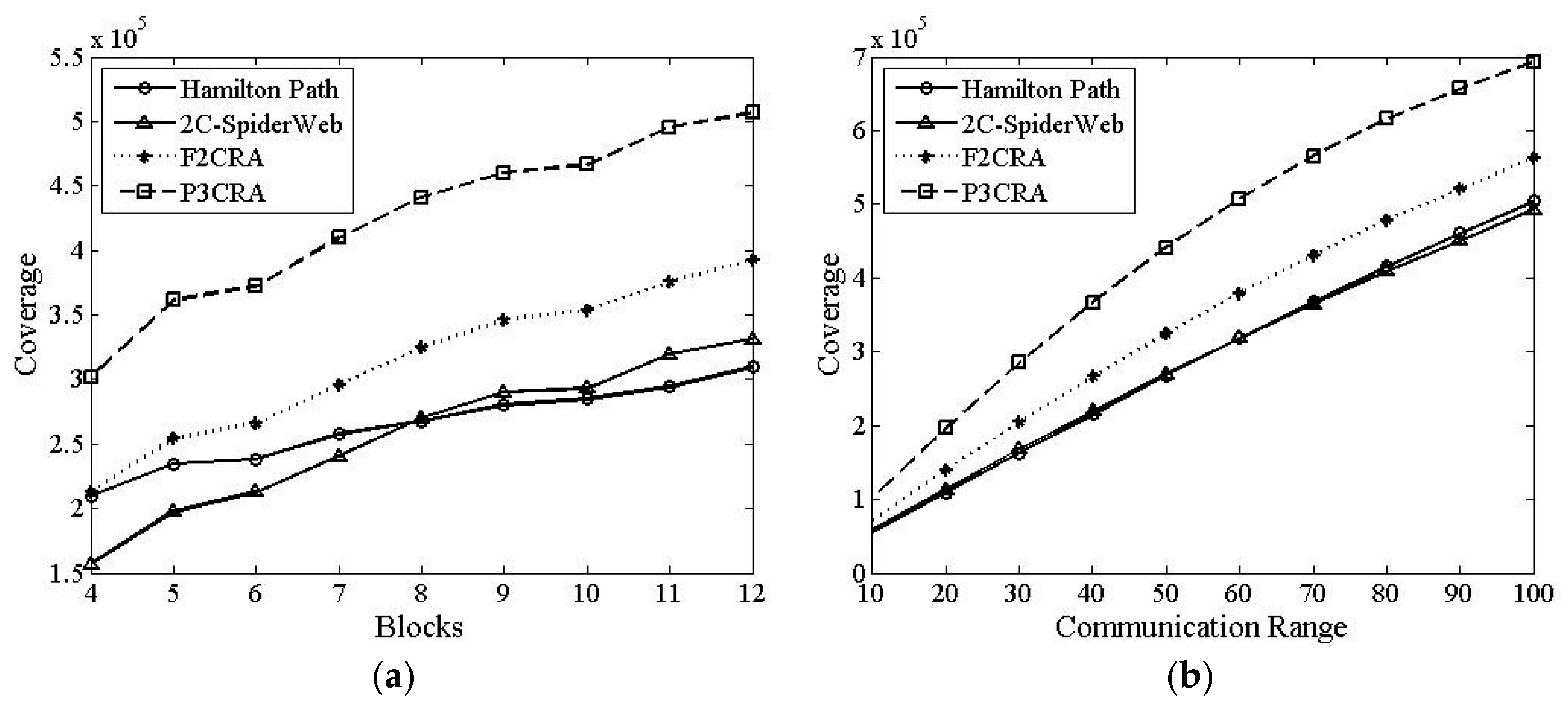
6.2.2. Total Coverage
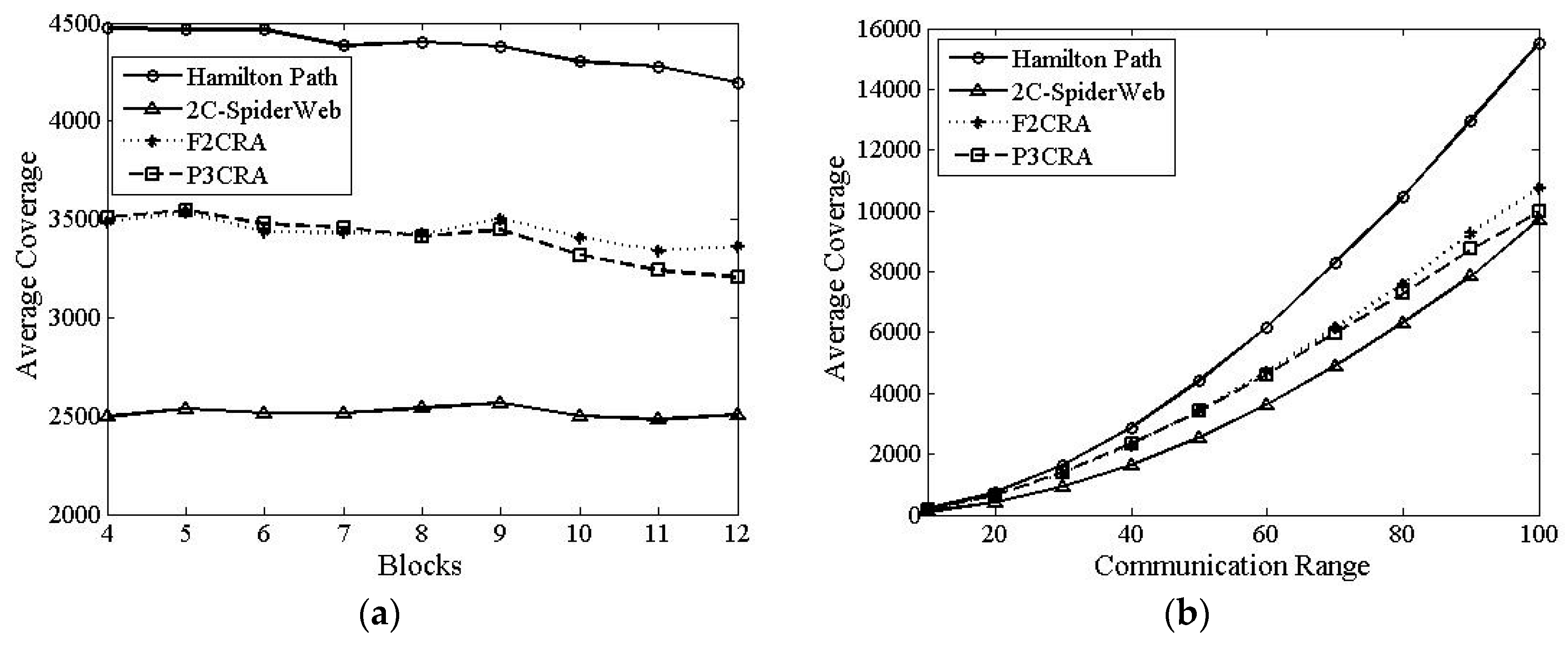
6.2.3. Average Coverage
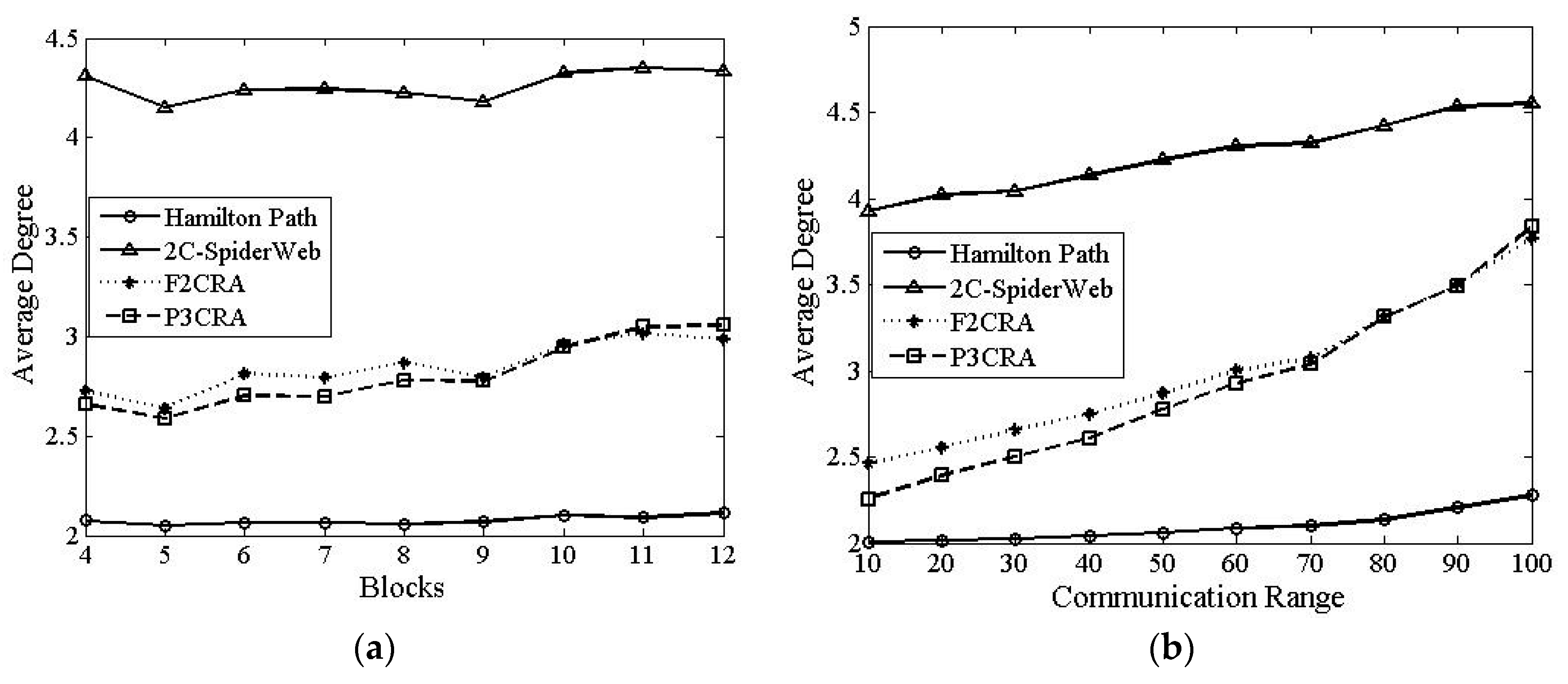
6.2.4. Average Degree
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
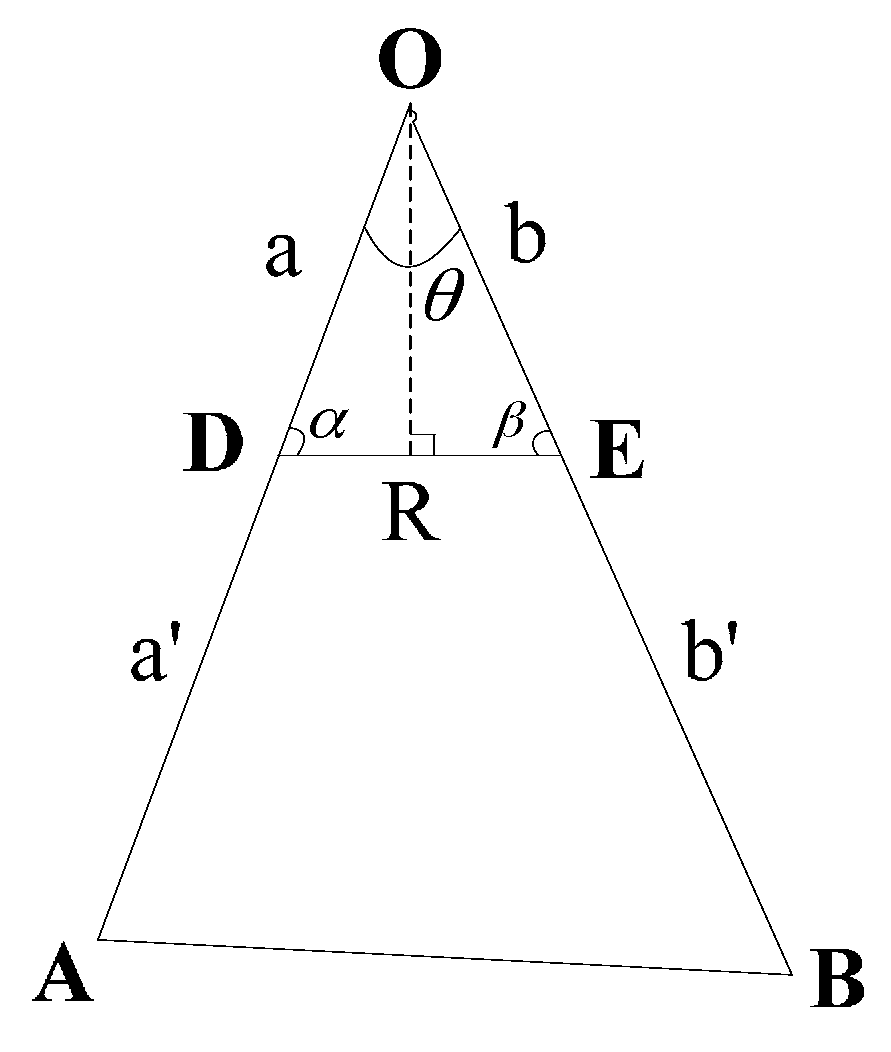
Appendix
References
- Malaver, A.; Motta, N.; Corke, P.; Gonzalez, F. Development and integration of a solar powered unmanned aerial vehicle and a wireless sensor network to monitor greenhouse gases. Sensors 2015, 15, 4072–4096. [Google Scholar] [CrossRef] [PubMed]
- Hao, B.; Tang, J.; Xue, G. Fault-Tolerant Relay Node Placement in Wireless Sensor Networks: Formulation and Approximation. In Proceedings of the International Conference on High Performance Switching and Routing, Phoenix, AZ, USA, 19–21 April 2004; pp. 246–250.
- Zhang, W.; Xue, G.; Misra, S. Fault-Tolerant relay Node Placement in Wireless Sensor Networks: Problems and Algorithms. In Proceedings of the IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 1649–1657.
- Han, X.; Cao, X.; Lloyd, E.L.; Shen, C. Fault-tolerant relay node placement in heterogeneous wireless sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 643–656. [Google Scholar]
- Senel, F.; Younis, M.F.; Akkaya, K. Bio-inspired relay node placement heuristics for repairing damaged wireless sensor networks. IEEE Trans. Veh. Technol. 2011, 60, 1835–1848. [Google Scholar] [CrossRef]
- Sitanayah, L.; Brown, K.N.; Sreenan, C.J. A fault-tolerant relay placement algorithm for ensuring k vertex-disjoint shortest paths in wireless sensor networks. Ad Hoc Netw. 2014, 23, 145–162. [Google Scholar] [CrossRef]
- Lin, G.H.; Xue, G. Steiner tree problem with minimum number of Steiner points and bounded edge-length. Inf. Process. Lett. 1999, 69, 53–57. [Google Scholar] [CrossRef]
- Chen, D.; Du, D.Z.; Hu, X.D.; Lin, G.; Wang, L.S.; Xue, G.L. Approximations for Steiner trees with minimum number of Steiner points. J. Glob. Optim. 2000, 18, 17–33. [Google Scholar] [CrossRef]
- Lloyd, E.L.; Xue, G. Relay node placement in wireless sensor networks. IEEE Trans. Comput. 2007, 56, 134–138. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Ding, W. Relay Node Placement in Heterogeneous Wireless Sensor Networks with Basestations. In Proceedings of the International Conference on Communications and Mobile Computing, Kunming, China, 6–8 January 2009; pp. 573–577.
- Yang, D.; Misra, S.; Fang, X.; Xue, G.; Zhang, J. Two-tiered constrained relay node placement in wireless sensor networks: Computational complexity and efficient approximations. IEEE Trans. Mob. Comput. 2012, 11, 1399–1411. [Google Scholar] [CrossRef]
- Senel, F.; Younis, M. Relay node placement in structurally damaged wireless sensor networks via triangular Steiner tree approximation. Comput. Commun. 2011, 34, 1932–1941. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Kumar, A. A shortest path tree based algorithm for relay placement in a wireless sensor network and its performance analysis. Comput. Netw. 2014, 71, 48–62. [Google Scholar] [CrossRef]
- Tang, J.; Hao, B.; Sen, A. Relay node placement in large scale wireless sensor networks. Comput. Commun. 2006, 29, 490–501. [Google Scholar] [CrossRef]
- Misra, S.; Hong, S.D.; Xue, G.; Tang, J. Constrained Relay Node Placement in Wireless Sensor Networks to Meet Connectivity and Survivability Requirements. In Proceedings of the IEEE International Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 281–285.
- Kashyap, A.; Khuller, S.; Shayman, M.A. Relay Placement for Higher Order Connectivity in Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006; p. 12.
- Bredin, J.; Demaine, E.D.; Hajiaghayi, M.T.; Rus, D. Deploying Sensor Networks with Guaranteed Capacity and Fault Tolerance. In Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Cologne, Germany, 28 August–2 September 2005; pp. 309–319.
- Lee, S.; Younis, M.; Lee, M. Connectivity restoration in a partitioned wireless sensor network with assured fault tolerance. Ad Hoc Netw. 2015, 24, 1–19. [Google Scholar] [CrossRef]
- Pu, J.; Xiong, Z.; Lu, X. Fault-tolerant deployment with k-connectivity and partial k-connectivity in sensor networks. Wirel. Commun. Mob. Comput. 2009, 9, 909–919. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Xu, L.; Chen, Z. Fault-Tolerant Algorithms for Connectivity Restoration in Wireless Sensor Networks. Sensors 2016, 16, 3. https://doi.org/10.3390/s16010003
Zeng Y, Xu L, Chen Z. Fault-Tolerant Algorithms for Connectivity Restoration in Wireless Sensor Networks. Sensors. 2016; 16(1):3. https://doi.org/10.3390/s16010003
Chicago/Turabian StyleZeng, Yali, Li Xu, and Zhide Chen. 2016. "Fault-Tolerant Algorithms for Connectivity Restoration in Wireless Sensor Networks" Sensors 16, no. 1: 3. https://doi.org/10.3390/s16010003
APA StyleZeng, Y., Xu, L., & Chen, Z. (2016). Fault-Tolerant Algorithms for Connectivity Restoration in Wireless Sensor Networks. Sensors, 16(1), 3. https://doi.org/10.3390/s16010003