1. Introduction
The health monitoring of aging structures and infrastructures [
1,
2,
3,
4] is nowadays becoming more and more important, and can exploit devices and methodologies developed within the field of embedded or inclusive smart technologies [
5,
6,
7]. The envisioned structural health monitoring (SHM) systems have to sense in real-time the changing environment, so as to send out early warnings if dangerous situations are approached. Such feature would also be appealing if structures have to be monitored in regions where environmental and geological risks are of concern [
8].
To provide some data highlighting the timeliness of smart SHM technologies, it is worth noting that a high percentage of civil structures and infrastructures in the developed and industrialized nations was built in the first half of the twentieth century: over 50% of the bridges in the USA were built prior to 1940 [
9]; furthermore, over 42% of all the aforementioned bridges are structurally deficient, as reported in [
10]. In Canada, over 40% of the bridges were built earlier than 1970, and a majority of them demands prompt rehabilitation, strengthening or replacement [
11].
The aim of this paper is the development of an online damage identification method, or SHM strategy based on recursive Bayesian filters [
12]. Such filters have been already successfully applied to the (grey-box) identification of shear-type buildings: in [
13], unscented Kalman and particle filters were adopted for the online parametric identification of nonlinear hysteretic models with uncertainties; in [
14], an efficient extended Kalman-particle filter scheme was adopted for the online identification of a structural model featuring a softening inter-story behavior. Recently, the attention has also been drawn to input-state estimation so that the obtained structural response can be used for the fatigue damage assessment, via vibration measurements, of structures subject to cyclic loadings [
15,
16].
The focus of the present study is on the design of a SHM strategy featuring fast, robust and unbiased estimations of damage indexes, obtained thanks to partial observations of the structural response. Within this frame, the aforementioned local damage indexes quantify the reduction of the stiffness properties of the structure. A similar approach can be adopted to also estimate the local reduction of the materials strength properties, although this topic is out of the scope of the current work and will be investigated in future activities. We therefore assume that the structure behaves piece-wise linearly, within any time window between subsequent observations of the structural response; accordingly, only the time-varying elastic properties of the system need to be identified. The goal of fast and accurate monitoring of these systems is here attained by introducing an effective model order reduction technique, to guarantee low computational costs, and by optimizing the deployment of a limited number of (inertial) sensors, collecting the observations of the system response.
The model order reduction is achieved through a Galerkin projection of the original full structural model onto a sub-space spanned by the so-called proper orthogonal modes (POMs), computed via proper orthogonal decomposition (POD) in its snapshot version [
17,
18,
19]. The simultaneous, dual estimation of the reduced-order structural state and of the mentioned damage indexes is obtained with a particle filter, enhanced through the use of an extended Kalman filter before the resampling stage [
14,
19]. The analysis of such dual estimation procedure, featuring an augmented state vector that gathers both the state of the system and the parameters to be tuned, can be traced back to [
20] and, somehow, to the seminal paper [
21]. In recent years, nonlinear dual estimation problems related to structural dynamics have been tackled with the use of the extended Kalman filter (see [
22,
23] among others), of the unscented Kalman filter [
24], of particle filters [
25,
26], and of hybrid particle-Kalman filters [
19,
27]. Hence, in this work we do not focus on the development of a new filtering technique but we instead show how a hybrid particle-Kalman filter can be adopted to identify on-the-fly the time-dependent properties of a reduced-order model of the structural system.
It is known that, as number of parameters to be identified increases, the accuracy of identification tends to decrease: this issue can be linked to the so-called curse of dimensionality. When dealing with the identification of structural systems featuring a large number of degrees-of-freedom (DOFs), methods like component mode synthesis were developed for reducing the number of unknown system parameters in procedures for model updating; with this approach, modal properties are identified offline. In this study, the goal is the online and real-time estimation of the damage parameters of the system, so the POMs are directly obtained from the response of the system in the initial training phase. As the inception and growth of damage modify the structural properties and, thereby, the relevant response to the external actions, the sub-space spanned by the POMs needs to be continuously updated during the filtering process; such update is here obtained thanks to a further Kalman filter. The resulting intricate formulation allows tracking the time evolution of the damage parameters as well as of the state of the partially observed system.
To assess the capability of the proposed SHM procedure, a thin plate subject to bending-dominated deformations and (possibly) time evolving damage is considered. It is shown that the filter is able to identify the spatial distribution of damage even if an extremely low number of POMs (on the order of 1 to 4) is adopted. This strongly reduced-order of the model handled by the filter is not strictly related to the kind of excitation considered; it takes instead advantage of the filter adopted to track the evolution of the POMs, which beneficially affects the overall accuracy of the procedure. Concerning observations, it has been assumed that a network of inertial sensors is surface-mounted on the plate, according to what proposed in [
28,
29]. To investigate the computational advantage of the proposed method, the computational complexity and the CPU time have been considered: it is demonstrated that the proposed method can speed-up the analyses up to hundreds of times in comparison to the full finite element model.
Methods similar to the one adopted herein for dual estimation and sub-space update, were recently developed and successfully applied to shear-type buildings in [
18,
19]. The current study represents an evolution of previous works, as it proves to be able to locate and estimate a structural damage via a few vibration measurements only.
The remainder of this paper is organized as follows. In
Section 2 the proposed SHM strategy is described: first, the model order reduction approach is detailed; next, the intricate filtering strategy, developed to simultaneously track the damage evolution and the response of the structure in the reduced-order space, is reported. In
Section 3, results are shown for the SHM of a thin square plate displaying a reduction of its stiffness properties. Some closing remarks and suggestions for future developments are gathered in
Section 4. Finally,
Appendix A collects some major algorithmic details of the proposed procedure.
3. Results and Discussion
We consider in this Section a benchmark test represented by a thin plate subject to bending. We provide first the geometrical features of the plate and the mechanical properties of the material considered, along with loading/boundary conditions. We next discuss possible effects on the health monitoring capabilities of the major parameters of the proposed approach, namely: the number of the POMs retained in the reduced-order model; the process noise; the measurement noise. We provide outcomes at varying damage level in one region of plate only, and also at a varying spreading of the damage over the plate. Finally, data are reported considering the speed-up provided by the reduced-order modeling, at varying space discretization adopted for the initial full-order finite element model.
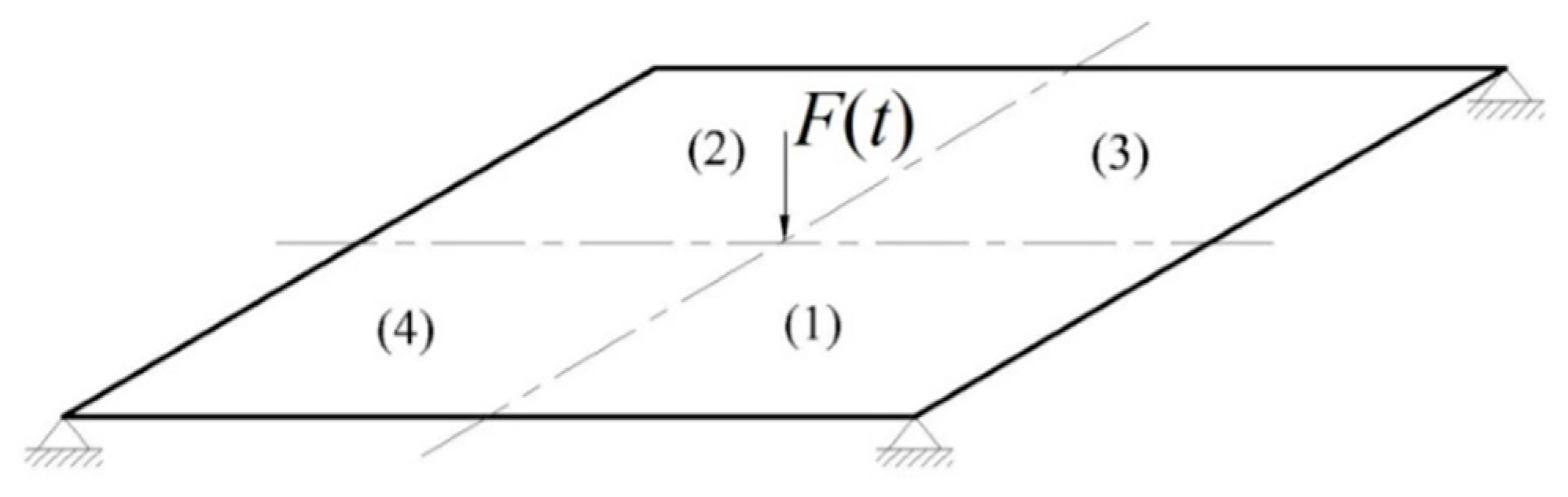
As shown in
Figure 1, the structure to be monitored is a thin square plate, with side length
mm and thickness
mm. The plate is assumed to be made of aluminum (6061-T6), whose relevant mechanical properties (in the virgin state) are: Young’s modulus
GPa, Poisson’s ratio
, and density
kg/m
3.
Figure 1.
Benchmark plate test: boundary and loading conditions, and zone numbering.
Figure 1.
Benchmark plate test: boundary and loading conditions, and zone numbering.
The plate has been modeled with the commercial finite element code Abaqus, using the S4R general-purpose, conventional shell elements which take into account also transverse shear deformations [
43]. The kinematics of this element type is fully characterized by six DOFs per node, that are the three displacements along the axes of any orthonormal reference frame (typically with two of them belonging to the mid-plane of the plate and one pointing perpendicularly to such mid-plane) and the three rotations about the same axes.
The plate is simply supported at the four corners, and subject to a sinusoidally varying force
at its center (
Figure 1). The maximum value of the force
N has been set to avoid damage development in the plate caused by it; the plate is therefore considered already damaged during the test, and to possibly suffer damage growth due to external causes. The frequency of the load has been instead set to
Hz, which is smaller than the fundamental frequency of vibrations of the aluminum plate, which amounts to
Hz for the undamaged case, and
Hz for the reference damage case described in what follows.
The structure is decomposed into four regions, each of them associated with the relevant target damage index
, with
. If not stated otherwise, in the examples to follow the structure is supposed to be damaged only in zone 2 (see
Figure 1), where the Young’s modulus is reduced to one half of its virgin value: therefore,
is the target damage value to be estimated.
In a pseudo-experimental test frame, finite element analyses have been adopted to first obtain the mass matrix
of the whole system and the (undamaged) stiffness submatrices
(see Equation (6)) of the mentioned
regions. Next, for each damage scenario here considered, the same code has been used to run the full-order analysis (although it can be run independently, once the mass and stiffness matrices have been obtained); accordingly, the snapshots are collected for the considered loading/boundary conditions, and POMs in
are obtained. As for measurements, results of the simulations have been corrupted with a Gaussian noise of known variance according to Equation (7). For the plate bending model considered in this paper, rotations about the in-plane reference axes, at the mid-point of each plate edge are handled as observations; this is in line with the optimal spatial distribution of measurements gathered through a network of surface-mounted inertial sensors, proposed in [
28,
29] to achieve sensitivity to damage independently of its location and amount.
The uncertainty and noise levels in the model are quantified for the structural system by the time-independent matrices
and
(
Section 2.2). As for the process noise, which takes into account the uncertainties introduced by the model (due to the spatial and temporal discretization and to the order reduction procedure), its covariance
is scaled by a dimensionless factor
, having the role of a standard deviation for the DOFs in the reduced-order model, according to:
where
is an identity matrix of appropriate size.
The measurement noise takes instead into account what related to the physical medium of communication between the sensors and the acquisition system, the random electrical noise due to the sensors and the electrical circuits, the quality of the measurement devices and also the environmental noise. Similar to the process noise, the measurement covariance
is scaled by a dimensionless factor
, playing the role of the standard deviation of the collected rotation angles, according to:
where now
. So, all the measurements are assumed uncorrelated. It is well-known that the performance of Bayesian filters rests on a proper choice of the above covariance matrices. By tuning the values of the process and measurement noise variances, the level of confidence in the model and measurements equations can be set; for instance, in case the measurements are deemed more reliable than the model, a low measurement noise variance
should be assigned, when compared with the process one
. In practice, measurement noise variance is known for the used sensors; tuning of the process noise variance is in general more intricate, and is normally achieved by a trial and error procedures offline. The optimal estimation of noise parameters in an online fashion has recently gained attention; reader are referred to [
36,
37,
44] for further details.
In this study, the number of samples in particle filtering has been always assumed . Moreover, to build the initial POMs, a number of snapshots always led to convergence of those retained in the analyses.
Moving to the results, let us first investigate the effects of the number
of POMs taken in the reduced-order model, on the accuracy of the estimations obtained. In
Figure 2, it is possible to see that such accuracy grows as the number of POMs gets higher. If the plate is coarsely meshed using only one finite element for each single region, the resulting structural DOFs turn out to amount to
, once the constraints at plate corners are taken into account. Although both the geometry and the loading condition are two-fold symmetric, such symmetry has not been exploited in the analyses, as damage in only one region breaks it. A remarkable result reported in
Figure 2d is the proof that, for this benchmark, it is possible to reduce the number of DOFs to only
and get an estimation error smaller than 10%.
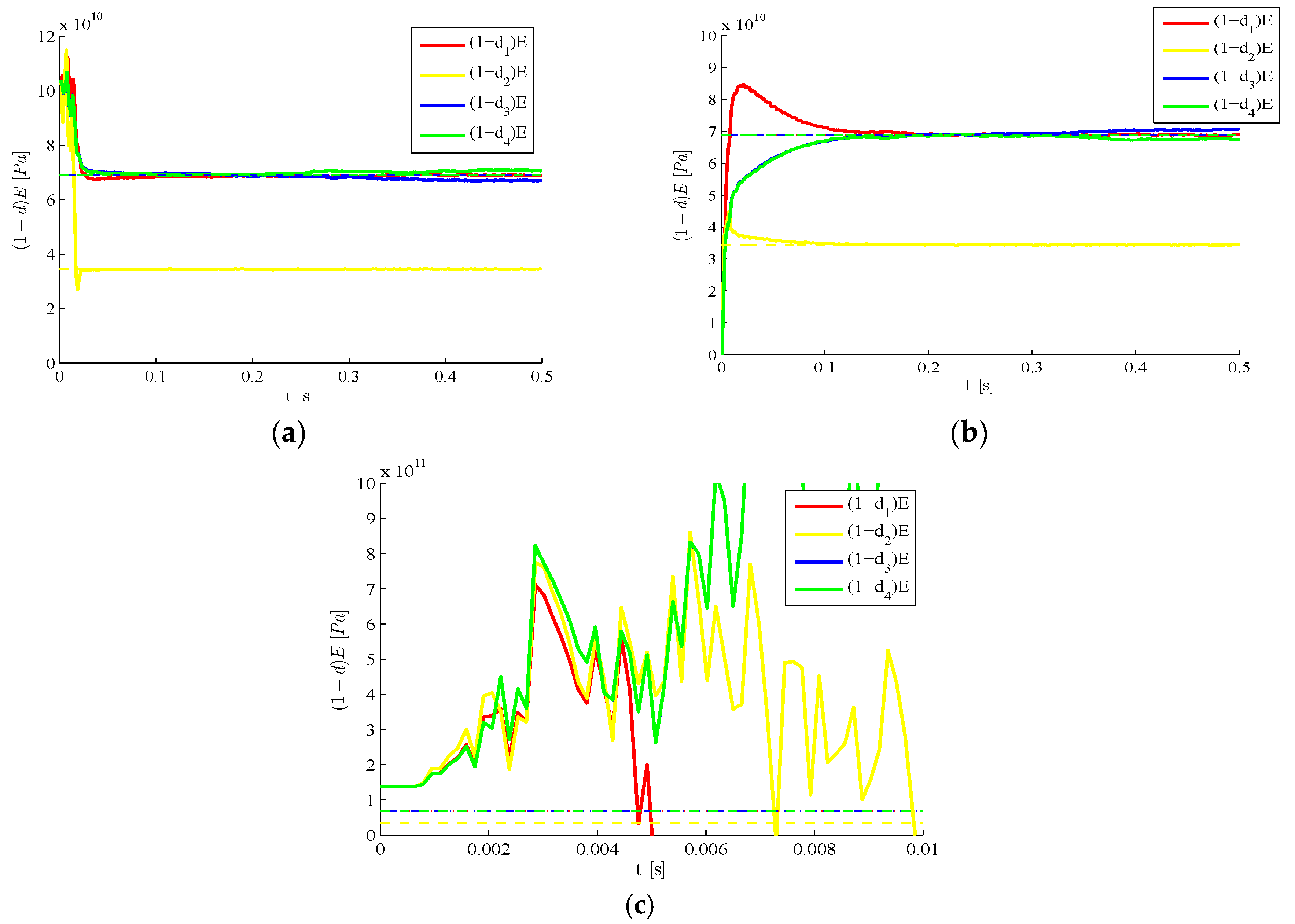
To assess the influence on the results of the initialization of the filter in terms of the damage state
,
Figure 3 shows for
that estimates are stable whenever the initial guess is close enough to the target one. Such performance test guarantees a wide range of applicability of the method, since the undamaged state
and also an underestimation by 50% of the initial elastic moduli allow to assure stability. The other way around, an initial guess too far from the target solution (
Figure 3c) is shown to insert instabilities or biases in the estimations.
Figure 2.
Time-invariant target damage state, : time evolution of estimations of the damage indexes , identified with (a) ; (b) ; (c) ; and (d) relative error in the damage indexes, at varying order of the reduced-order model.
Figure 2.
Time-invariant target damage state, : time evolution of estimations of the damage indexes , identified with (a) ; (b) ; (c) ; and (d) relative error in the damage indexes, at varying order of the reduced-order model.
Figure 3.
Time-invariant target damage state, : time evolution of estimations of the scaled elastic moduli (and, therefore, of the damage indexes ), identified with initial values (a) , ; (b) ; and (c) .
Figure 3.
Time-invariant target damage state, : time evolution of estimations of the scaled elastic moduli (and, therefore, of the damage indexes ), identified with initial values (a) , ; (b) ; and (c) .
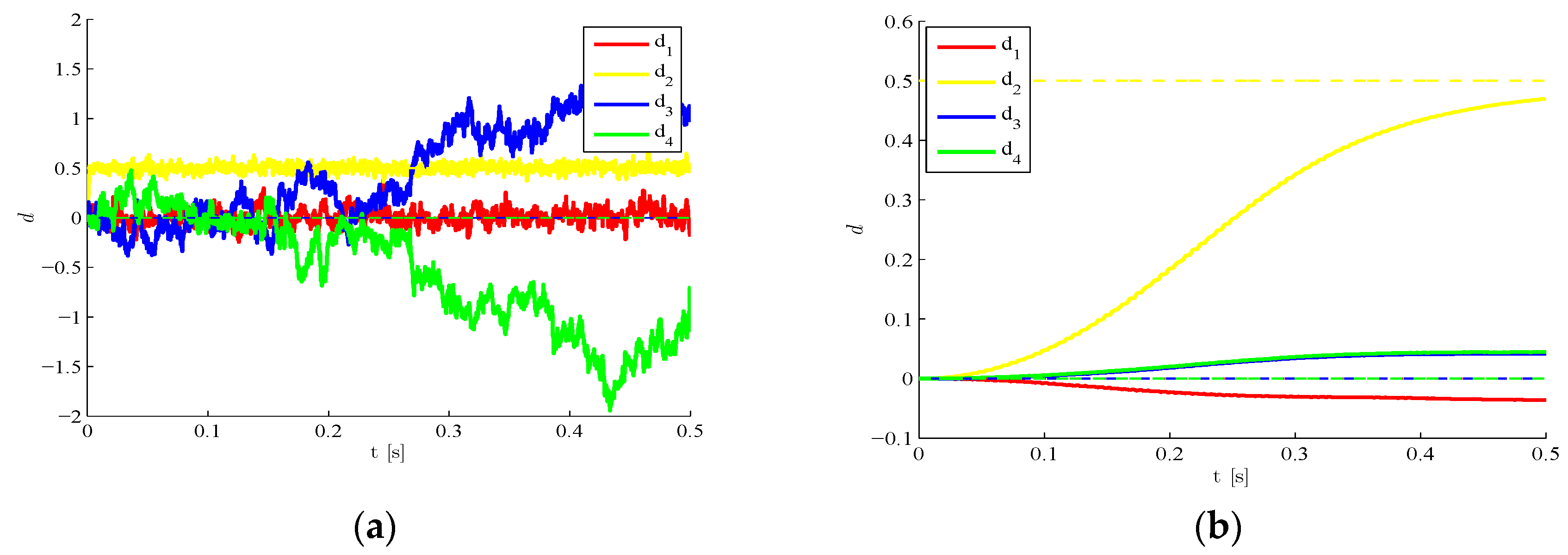
If we consider the effects of the process noise, some exemplary results are gathered in
Figure 4. As expected, a high noise level amounting to
(
Figure 4a), can incept large variations of the estimates over each time interval, and therefore gives rise to possible biases or even divergence in the final solution. On the other hand, if the process noise is lowered to
(
Figure 4b), wild oscillations do not show up any longer and the estimation evolutions become smooth.
Figure 4.
Time-invariant target damage state, : time evolution of estimations of the damage indexes , identified with a process noise (a) and (b) .
Figure 4.
Time-invariant target damage state, : time evolution of estimations of the damage indexes , identified with a process noise (a) and (b) .
In the analyses so far, the measurement noise level was kept low through
,
i.e., (even if not explicitly shown) smaller than 10% of the maximum amplitude of the structural response under the considered loading.
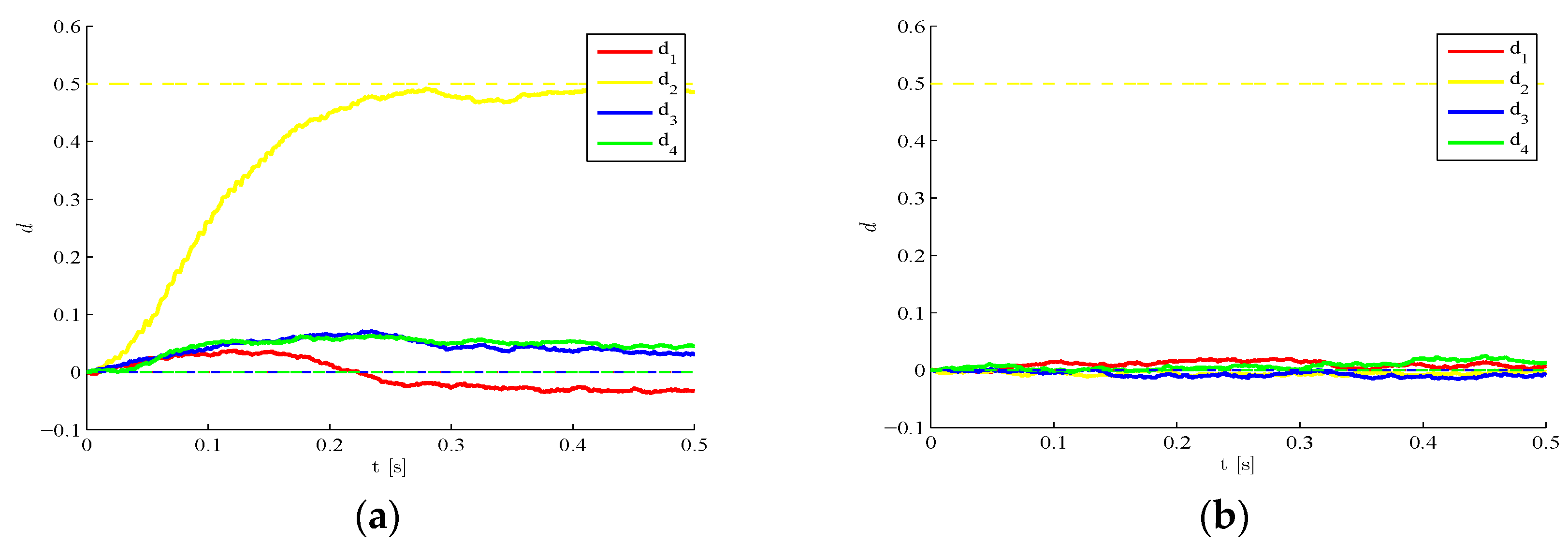
Figure 5 testifies that, as the measurement noise gets bigger (up to
), the ability of the procedure to estimate the damage indexes drops; as results are here shown for
, they can be compared to the plots already reported in
Figure 2a for
. The trend shown by the accuracy of the estimates and by the readiness to approach the target values is basically due to the fact that the structural response gets hidden by the noise if
becomes bigger, and the filter is not able to extract significant information from measurements. Overall, by increasing
the transitory stage in the time evolution of the damage indexes lasts more and more (
Figure 5a), or the SHM procedure can even lose the ability to estimate the damage in a region (
Figure 5b). This response has been checked to vary monotonically and smoothly when
changes; moreover, plots in
Figure 5 are reported for a null initialization of damage parameters, namely for
, but similar results can be obtained for any other initial guess guaranteeing the stability of estimations.
Figure 5.
Time-invariant target damage state, : time evolution of estimations of the damage indexes , identified with a measurement noise featuring (a) and (b) .
Figure 5.
Time-invariant target damage state, : time evolution of estimations of the damage indexes , identified with a measurement noise featuring (a) and (b) .
We next investigate the method performance at a varying value of the target damage index
, with
and still keeping the noise factors
adopted in
Figure 3.
Figure 6 shows the results in terms of time evolutions of the estimate of
for the four target cases
. Such evolutions are obtained along with those relevant to the other damage indexes (all zero valued); since the trend shown by these latter ones is basically the same reported in
Figure 3b, we focus on the initial transient stage of the estimations of
starting from the initial guess
. Such transient stage is reported to last less than
s; after that, estimates are affected by small fluctuations only. It also appears that target values are promptly matched if damage values are large. This is somehow expected, as small target values of
provide small drifts from the response of the healthy structure, and so the sensitivity to damage of the monitoring system in the noisy environment gets detrimentally affected.
Figure 6.
Time-invariant target damage state, : time evolution of estimations of the damage index at varying target value.
Figure 6.
Time-invariant target damage state, : time evolution of estimations of the damage index at varying target value.
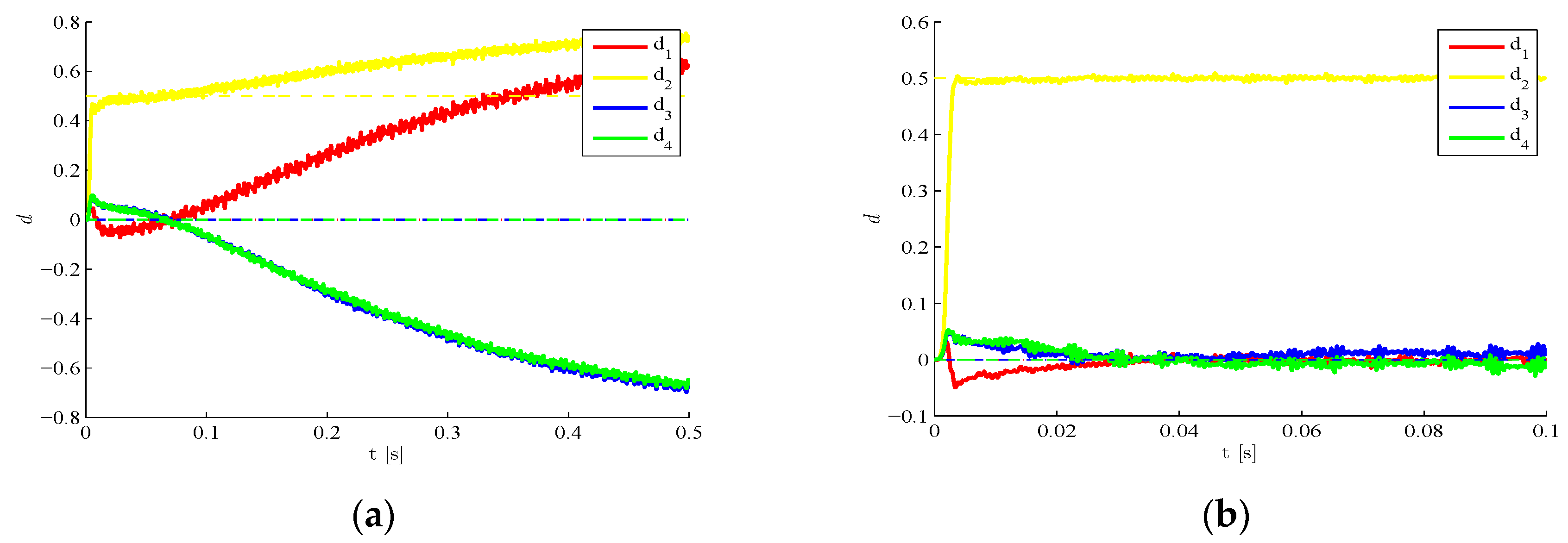
The proposed methodology also features the same accuracy level if all the plate regions are damaged.
Figure 7 provides the time evolutions of the estimates, in the exemplary case characterized by target values
,
,
and
. For two different initialization sets, it is shown that estimates converge fast towards the target values, and small oscillations around them are next linked to the hybrid filtering methodology adopted. Comparing these results with those reported in
Figure 6, it can be seen once again that smaller values of the damage indexes (and, so bigger values of the residual stiffness reported in the graphs) are connected to a delayed convergence of the filter estimates. Indeed, the provided steady-state solutions always perfectly match the target one.
Figure 7.
Time-invariant target damage state, four plate regions damaged, : time evolution of estimations of the scaled elastic moduli, identified with initial values (a) and (b) .
Figure 7.
Time-invariant target damage state, four plate regions damaged, : time evolution of estimations of the scaled elastic moduli, identified with initial values (a) and (b) .
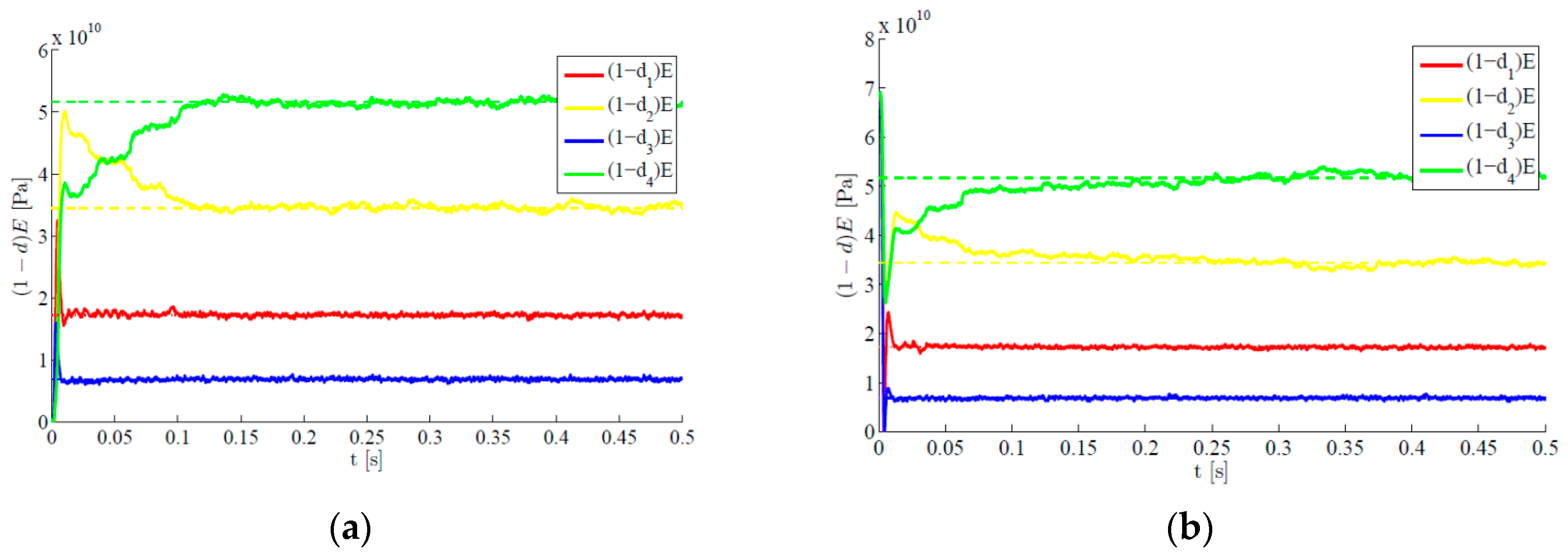
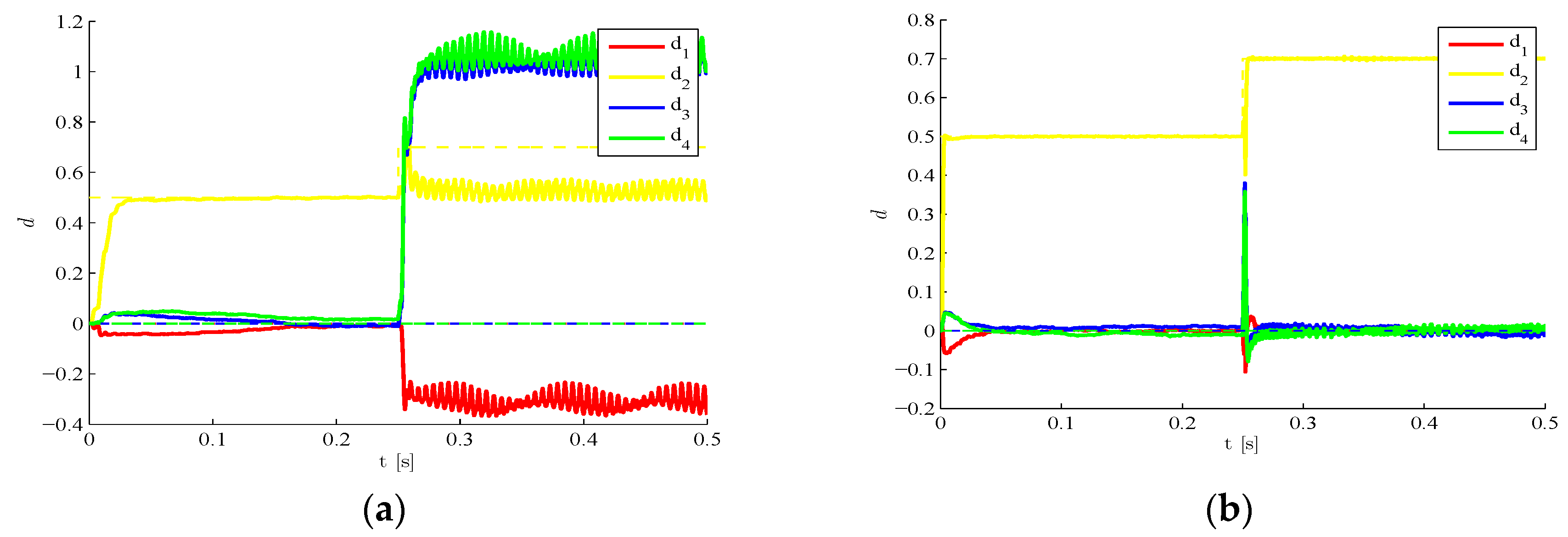
We move now to a case characterized by a time evolving damage state. The structure is still assumed to be initially damaged with
, but such damage is suddenly increased to
around
s due to a further event, possibly linked in real-life situations to unexpected or extreme loadings. In
Figure 8 results are provided concerning the estimated time evolution of the damage indexes, by either disregarding (
Figure 8a) or allowing for (
Figure 8b) the sub-space update. Such update, according to the setting defined in
Section 2, is automatically driven by the filtering procedure as soon as the structural observations display a drift away from the response expected on the basis of the current damage state. POMs update is obviously compulsory to keep a similar degree of accuracy of the reduced-order model when the damage state is altered. If such update is not performed, the reduced-order model (that has been trained with the initial damage state) does not match the current structural health, and the damage estimates diverge or are affected by unacceptable biases.
Figure 8.
Time-varying target damage state, : time evolution of estimations of the damage indexes , identified (a) without update of POMs and (b) with POMs update.
Figure 8.
Time-varying target damage state, : time evolution of estimations of the damage indexes , identified (a) without update of POMs and (b) with POMs update.
Some additional results are provided in
Figure 9 in relation to a finer mesh adopted to build the full-order model; in this case, the free DOFs of the initial finite element model amount to
. Compared to the former case linked to the coarsest possible mesh, a slightly higher number of POMs would be necessary to attain a high level of accuracy of the reduced-order model, if the proposed filtering procedure were not adopted. However, as stated in
Section 2, the intricate formulation consisting in three filters processing the data, allows also to increase the accuracy of the reduced-order model, so that only two POMs prove enough to achieve an unbiased estimation of the damage state in a short time, see
Figure 9b.
Figure 9.
Time-invariant target damage state, fine space discretization, : time evolution of estimations of the damage indexes , identified with (a) and (b) .
Figure 9.
Time-invariant target damage state, fine space discretization, : time evolution of estimations of the damage indexes , identified with (a) and (b) .
Results in the figures have shown that each damage index, although theoretically constrained to belong to the [0–1) interval, may be estimated out of the bounds on such interval. If damage becomes negative, then the stiffness properties of the structure results to be enhanced, hence greater than in the virgin state; that is obviously of no practical interest, and should be considered as a wrong outcome of filtering procedure. Anyhow, this kind of results does not violate the thermodynamic requirement to always have a positive reduced Young's modulus (see [34]). The other way around, damage can become greater than one, and so the reduced stiffness turns out to be negative. Although negative tangent stiffness values can be encountered at the structural level when local failure phenomena take place, in our case those values are to be considered wrong outcomes of the filtering procedure. Nonetheless, values of the damage indexes have not been constrained in our procedure, so that a standard particle-Kalman filter can be adopted. Alternatively, implementations centered on the so-called constrained Kalman filters were offered [
45,
46,
47]; such possible alternative implementations have not been considered in our work since, as clearly depicted in the graphs of this Section, estimates of the damage indexes largely exceed the bounds only when the solution becomes unstable. In all the analyses providing reliable results, it usually happens that only some indexes slightly move below the zero value threshold.
Finally, concerning the analysis speed-up, relevant outcomes are reported in
Table 2 at varying mesh and order
of the model, in terms of both CPU time and floating-point operation metrics. These data have been obtained by running the procedure implemented in Matlab (release 2014a) on a personal computer featuring an Intel Xeon E3-1270 V2 @ 3.50 GHz processor, with 8.00 Gb of RAM and Windows 7 64-bit as OS. It can be seen that the finer the full-order space discretization, the higher the speed-up; on the basis of a minimum reported speed-up value exceeding
for the coarse mesh, this joint use of intricate filtering schemes and reduced-order modeling can prove successful in the design of real-time SHM procedures.
Table 2 also shows that the speed-up computed through the algorithmic complexity discussed in
Section 2.2, actually represents an upper bound on the real one given by the CPU time. It decreases at a smaller rate than that linked to CPU time when the number
of retained POMs is increased, but it converges to unitary values when
tends to the number
of total DOFs of the full-order model (actually it converges to values slightly less than one, as POM update is not carried out with the full-order model).
Table 2.
Analysis speed-up provided by CPU time and flops, at varying mesh and order of the reduced-order model.
Table 2.
Analysis speed-up provided by CPU time and flops, at varying mesh and order of the reduced-order model.
| Coarse Mesh | Fine Mesh |
|---|
| CPU Time | Flops | CPU Time | Flops |
|---|
| 1 | 41.8 | 100 | 1319.5 | 1812 |
| 2 | 37.2 | 89 | 701.7 | 1810 |
| 3 | 33.3 | 79 | 611.7 | 1809 |