Multi-Stage Feature Selection by Using Genetic Algorithms for Fault Diagnosis in Gearboxes Based on Vibration Signal
Abstract
:1. Introduction
2. Experimental Section
2.1. Theoretical Background
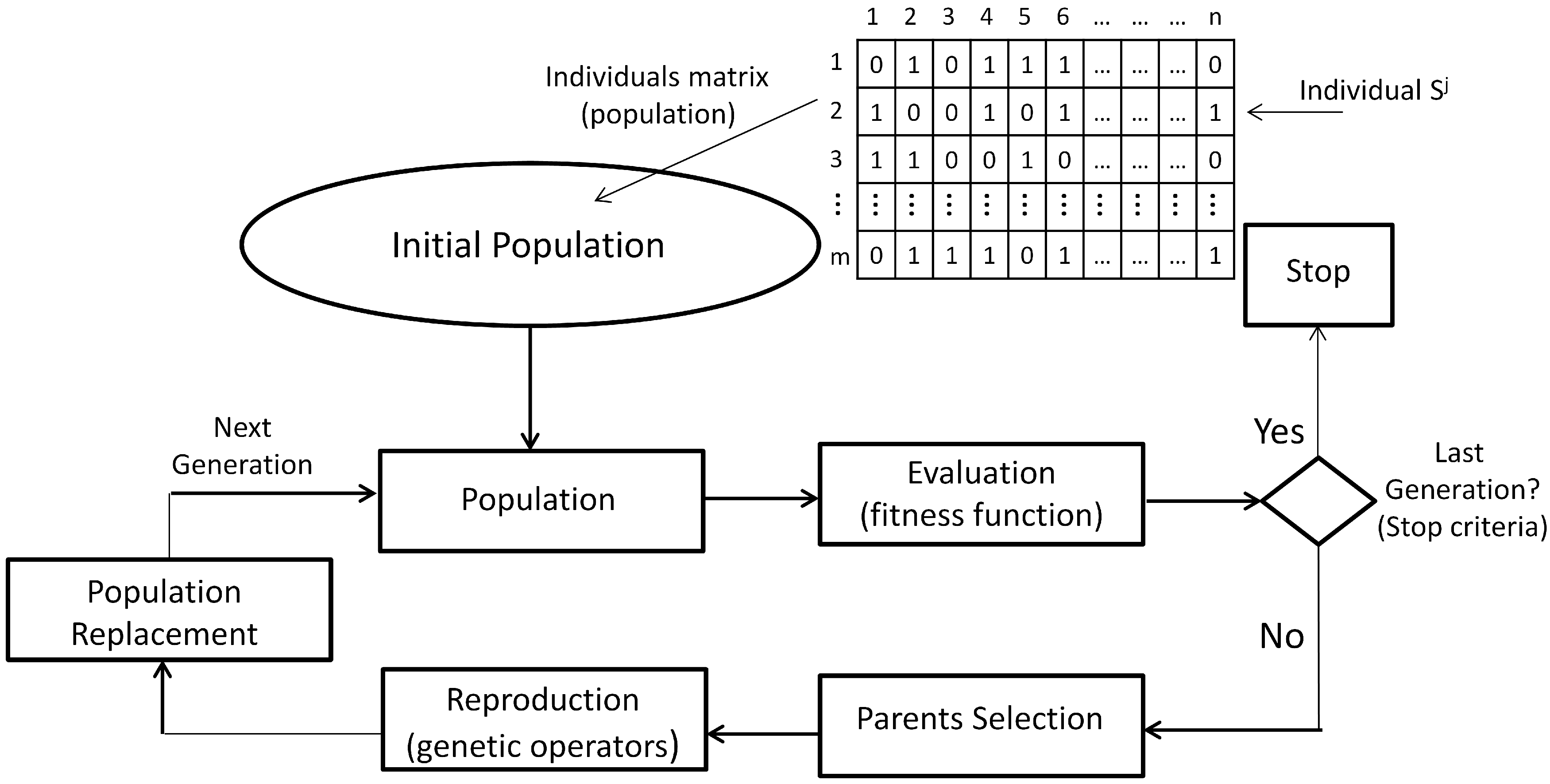
2.1.1. Genetic Algorithms
- (1)
- Individual encoding: In the GA technique, each individual is associated with a structure and a content. The structure refers to the format, and the content refers to the information provided by the individual in each component of its structure. In general, an individual is encoded as a binary string of length n, where each binary element is called a gene. However, individual encoding can be adapted to the nature of the solutions for the particular problem.
- (2)
- Initial population: This is composed of individuals of the first generation of possible parents. In this way, the initial population P is the set , , which can be seen as a binary matrix, where each row is one individual and each column is the value of the corresponding gene.
- (3)
- Fitness function: The value of the fitness function f, or the evaluation function, is a measure of each individual performance in the GA. In general, the fitness function f is a mapping , which assigns to each individual a real value according to its performance for solving the optimization problem. A fitness scaling is performed sometimes to avoid the dispersion of the function values.
- (4)
- Parent selection: The process for selecting the best individuals for the next generation should be guided, based on the values of the fitness function. There are different selection mechanisms, most of them based on the relative probability of the selection of an individual .
- (5)
- Genetic operators and reproduction: The reproduction is achieved by applying genetic operators to produce new individuals with improved genetic material. Usually, the crossover and mutation operators are applied; however, other operators also exist, and they can be more appropriate in specific problems.
- (6)
- Population replacement: Replacement strategies should aim to maintain diversity in the population, as well as to improve the evaluation of the fitness function of the individuals of the new population. Once new individuals have been generated, they replace only a part of the parents for the new generation. Other replacement strategies are the direct replacement, where the children replace the parents in the next generation, and the elitist replacement, where a fraction of the best individuals goes directly to the next generation.
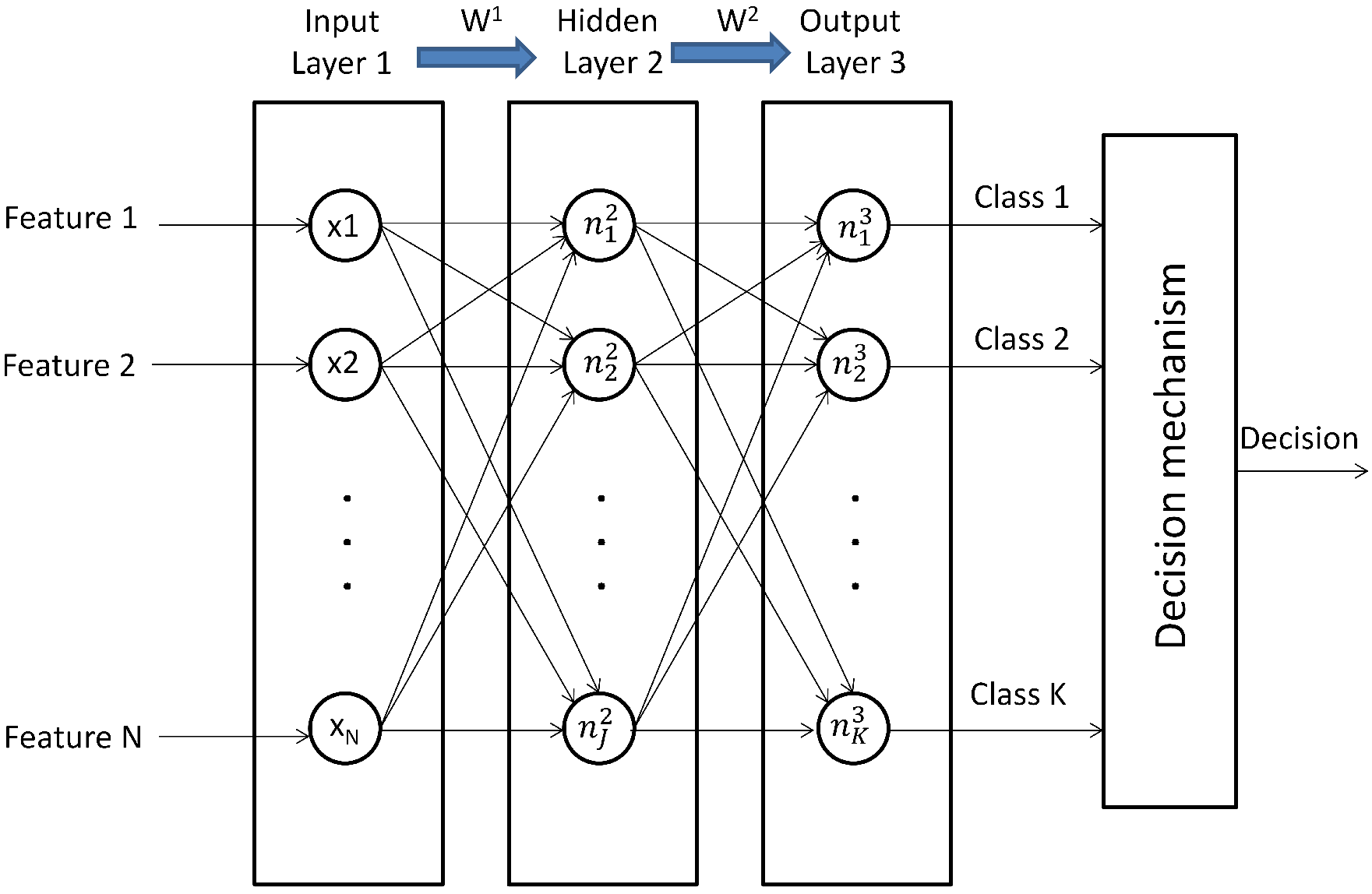
2.1.2. Artificial Neural Networks
- (1)
- Randomly initialize the weights of each layer , , where is the weight from the neuron to the neuron .
- (2)
- Compute the feedforward propagation to obtain .
- (3)
- Compute the cost function .
- (4)
- Run the backpropagation algorithm to compute .
- (5)
- Use the gradient descent method for adjusting the weights according to the equation .
2.2. Measurement Procedure and Feature Extraction

| Label | Description |
|---|---|
| f0 | Normal |
| f1 | Gear crack 0.5 mm |
| f2 | Gear tooth breakage 10% |
| f3 | Pinion pitting |
| f4 | Pinion with face wear 0.5 mm |
| f5 | Gear misalignment |
| f6 | Gear tooth breakage 50% |
| f7 | Gear tooth breakage 100% |
| Image | Description |
|---|---|
 | Gear crack 0.5 mm |
 | Gear tooth breakage 10% |
 | Pinion pitting |
 | Pinion with face wear 0.5 mm |
 | Gear misalignment |
 | Gear tooth breakage 50% |
 | Gear tooth breakage 100% |
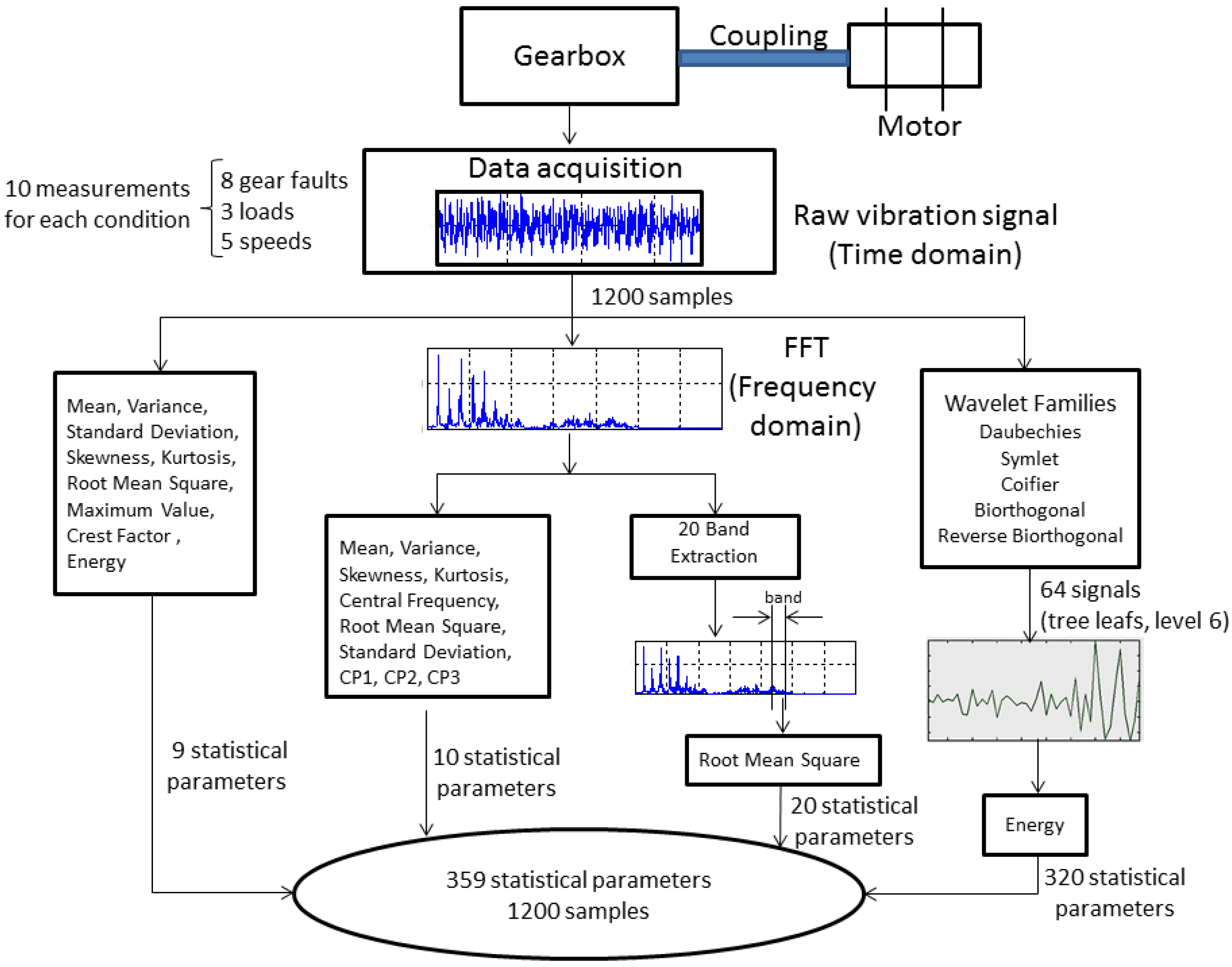
2.2.1. Condition Parameters on the Time and Frequency Domains
2.2.2. Condition Parameters on the Time-Frequency Domain
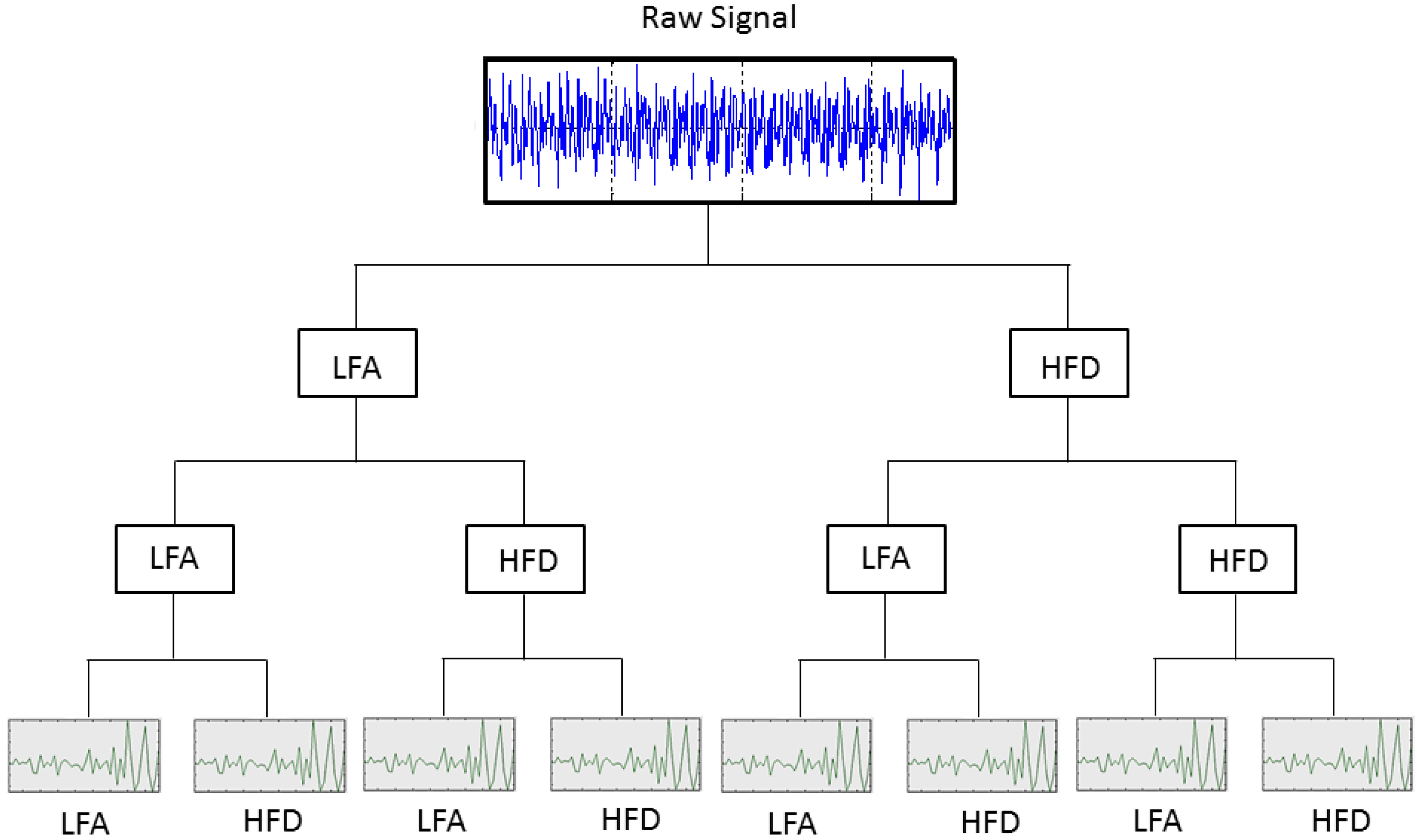
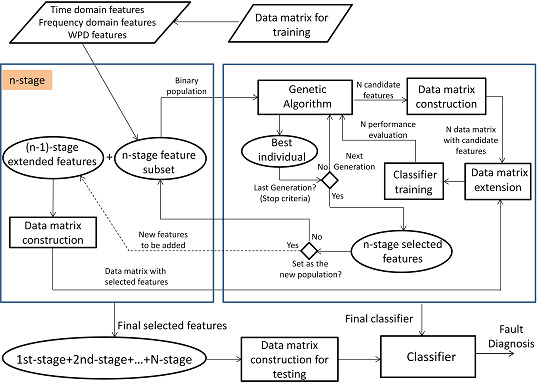
2.3. Multi-Stage Feature Selection Based on GA with NN Classifiers

2.3.1. GA Design
- (1)
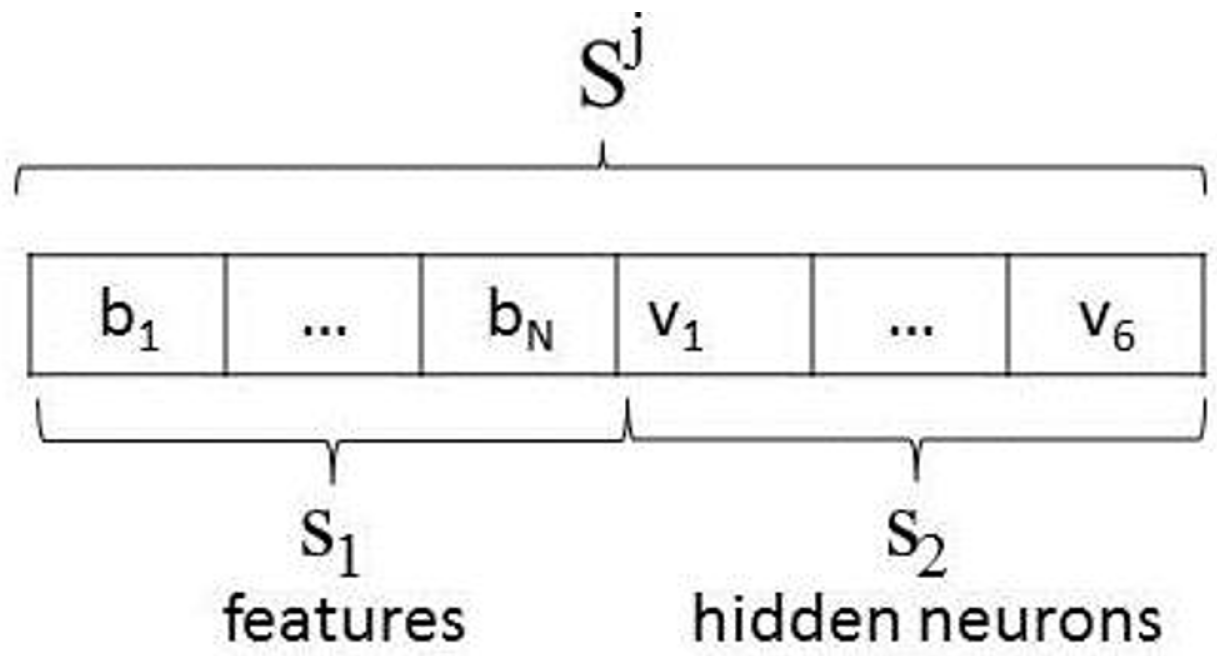
- Individual encoding: Two partial solutions are encoded in this approach: the features to be selected and the number of hidden neurons in the NN. Figure 7 shows the encoding for only one hidden layer. In this way, every possible solution is a vector with the first chain of bits encoding the condition parameters in the subset , where the bit , , can be , which indicates the selection of the condition parameter , or otherwise. The second chain of bits is composed of six bits , 0 or 1, encoding the binary number to propose 63 hidden neurons at most.
- (2)
- Initial population: At each stage, a population P from the set is generated with random selection of 0 or 1 for each bit and .
- (3)
- Fitness function: The performance of the classifier in the training and test phases is based on the mean square error value that is defined in Beleitesa et al. [41].
- (4)
- Parent selection: Firstly, fitness scaling based on rank was used for defining the raw fitness value over a suitable range [42]. According to this scaling, an individual with a lower value of raw fitness is assigned to a higher value of scaling fitness; consequently, the individual has a higher probability to be chosen as a parent by the selection function. The rank is a function , which sorts individuals from 1 to N based on the best fitness value (lower value of the fitness function). Once the individuals are ranked, their new fitness is recalculated according to Equation (6):where r is the rank of the individual, p is the desired selective pressure and is the population size. The selective pressure is the probability that the best individual is selected regarding the average selection probability of the remaining individuals. The rank-based fitness scaling allows a selective pressure between about . The uniform stochastic selection method was applied in this approach:
- (a)
- Determine the cumulative probabilities based on the value of each individual, as follows:
- (b)
- Select K parents, in the following manner:
- (5)
- Genetics operators: Crossover and mutation operators were applied. The crossover fraction was set at 80%, that is the number of children that will be obtained from crossover. The crossover point selection was performed by applying a random scattered selection, as follows:
- (a)
- Select Father 1
- (b)
- Select Father 2
- (c)
- Generate a random binary vector v of N bits, that is or
- (d)
- If ,
- Gene i of Parent 1 is preserved,otherwise,
- Replace the gene i of Parent 1 with the gene i of Parent 2.
- (6)
- Parent replacement: A direct replacement mechanism was used; 10% of the current population was selected by elitism, and they will be part of the next generation. The remaining individuals are replaced according to the fraction of children obtained by crossover and mutation.
- (7)
- Stop criteria: The maximum number of generations, the cycles of GA in each stage, was selected as the stop criteria.
3. Results and Discussion
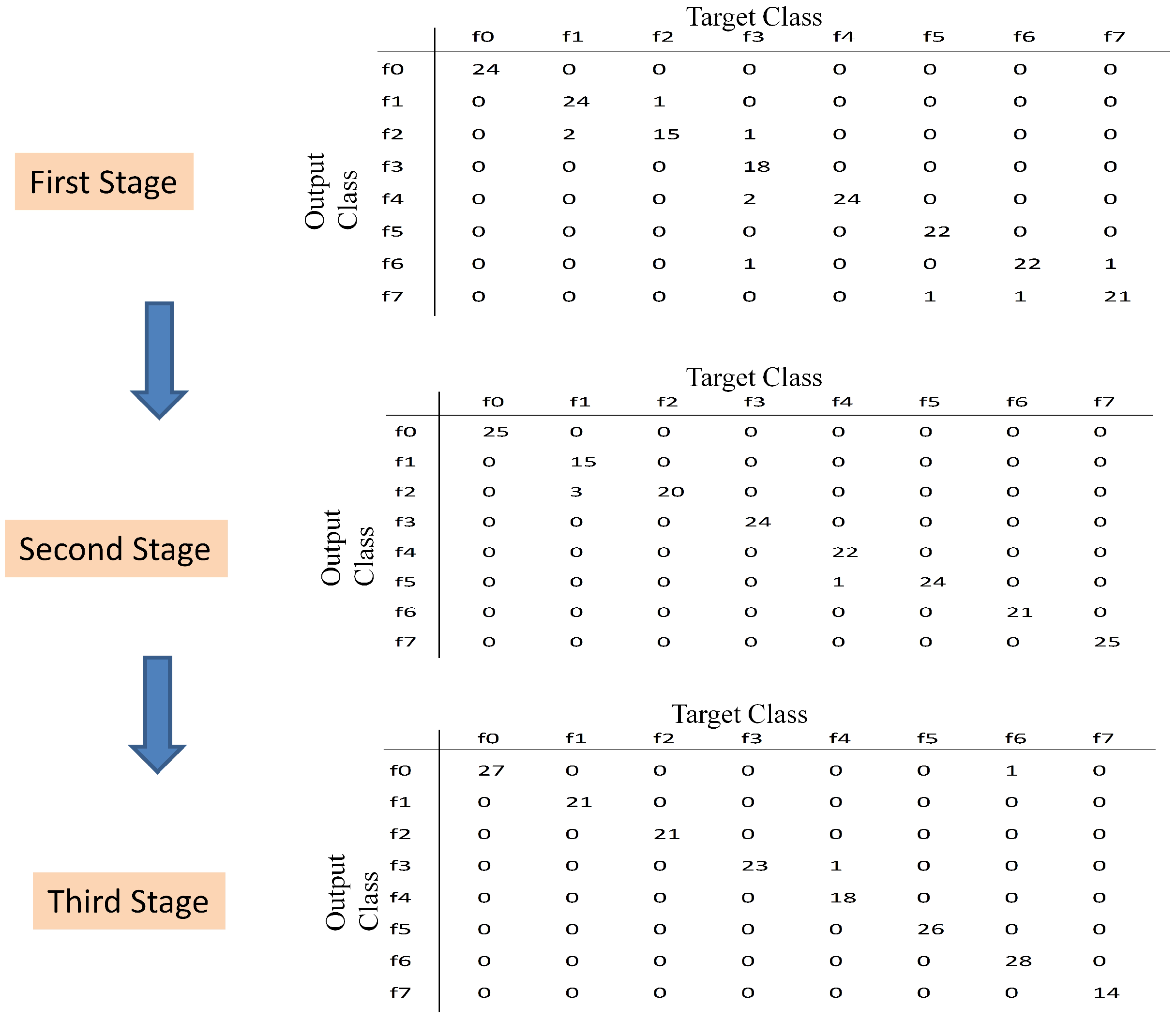
- (1)
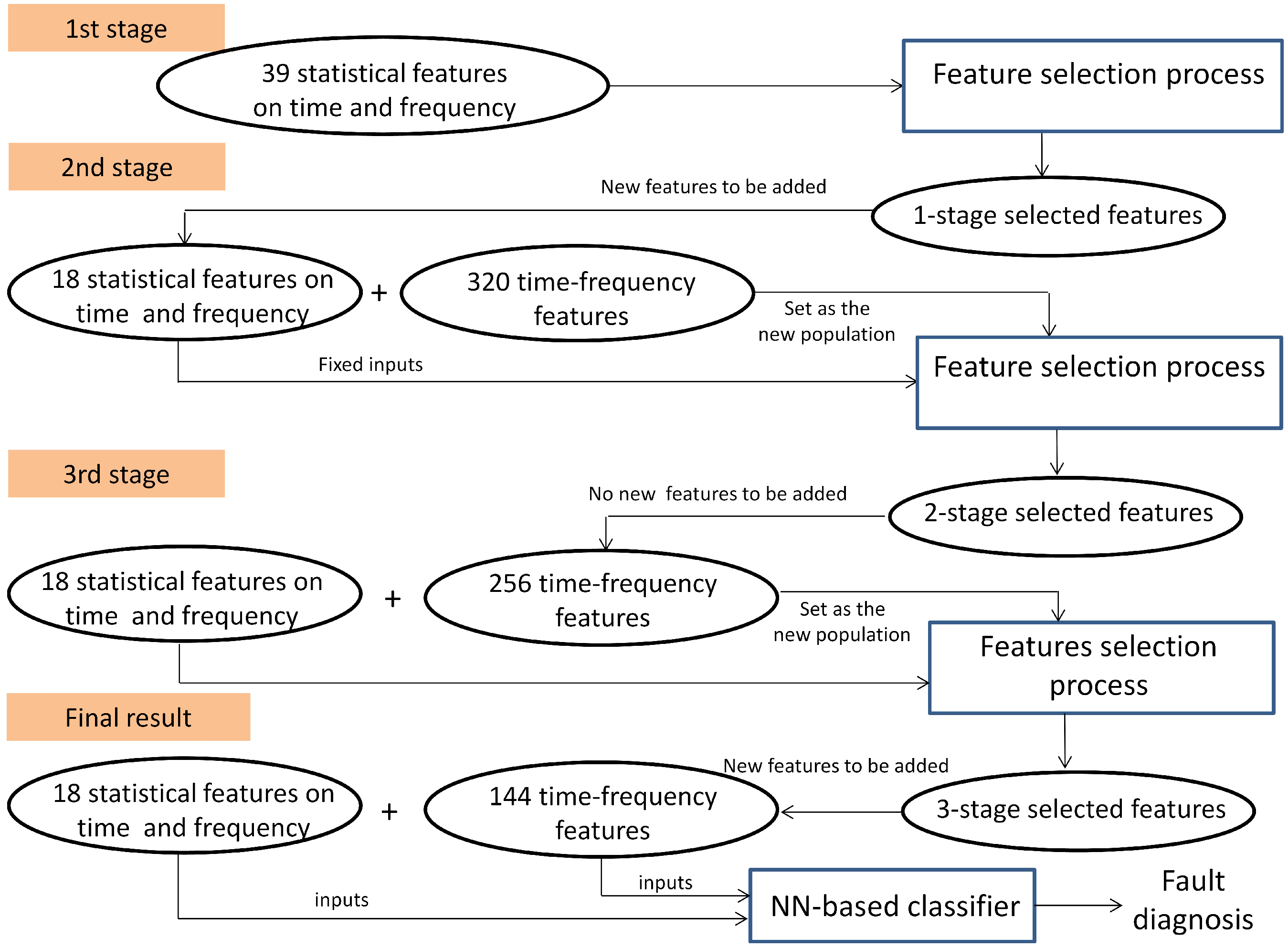
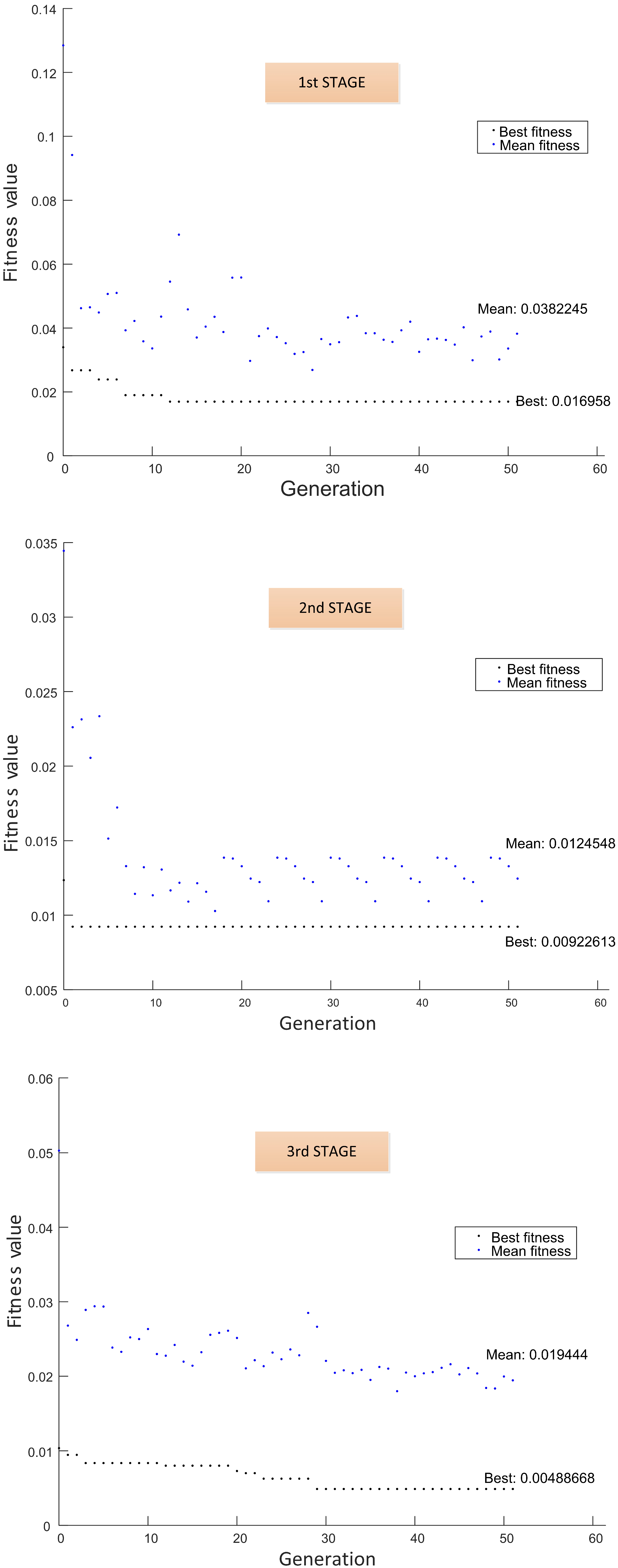
- First stage: The subset was processed at first, (see Table 3). The initial population was 20 individuals; then, a binary matrix with 20 rows and 45 columns is defined, and 20 data matrices for training and validation are created for each individual. After the selection process by using GA, 18 features are selected with 43 hidden neurons. These features are fixed inputs for the NN-based classifier in the second stage.
- (2)
- Second stage: The subset was processed at this stage, (see Table 3). At this stage, the selection process is addressed for detecting the relevance of the condition parameters from each wavelet family. In this sense, the partial solution related to the input features is encoded as a binary sequence of five bits, where indicates that all of the energy parameters from wavelet family coefficients are selected as inputs, and indicates that all parameters are excluded. The initial population was 20 individuals; then, a binary matrix with 20 rows and 11 columns is defined, and the corresponding data matrices for training and validation are created for each individual. The selection process only runs on the partial inputs to the NN that are being optimized. Finally, all parameters from wavelet family rbior6.8 are discarded, and 30 hidden neurons are selected. At this stage, according to the decision of the user, the selected condition parameters are not taken for extending the previous fixed inputs (18 features in the first stage), and a new subset containing parameters from the remaining wavelet families is created. This subset will be treated in the third stage.
- (3)
- Third stage: The subset was processed at this stage, (see Table 3). The initial population was 100 individuals; then, a binary matrix with 100 rows and 262 columns is defined, and the corresponding data matrices for training and validation are created for each individual. The selection process runs on the partial inputs to the NN. As a result of the selection process, 144 parameters are selected and accepted to extend the previous 18 fixed inputs. The proposed number of hidden neurons was 36. All subsets have been processed, and the multi-stage process is completed.
| Number of Stages | Number of Features | Condition Parameters |
|---|---|---|
| 1 | 39 | 20 RMS values from frequency bands + 10 from the frequency domain |
| + 9 from the time-domain | ||
| 2 | 320 | energy from wavelets coefficients (db7 + sym3 + coif4 + bior6.8 + rbior6.8) |
| 3 | 256 | energy from wavelets coefficients (db7 + sym3 + coif4 + bior6.8) |
| Parameters | Total Number | Description |
|---|---|---|
| RMS from frequency bands | 12 | −183 Hz (1st band) |
| 733 Hz to 915 Hz (5th band) | ||
| 915 Hz to 1098 Hz (6th band) | ||
| 1281 Hz to 2702 Hz (8th band to 14th band) | ||
| 2745 Hz to 3111 Hz (16th band to 17th band) | ||
| Frequency | 2 | Standard deviation |
| Skewness | ||
| Time | 4 | Mean |
| Standard deviation | ||
| Root Mean Square | ||
| Crest Factor | ||
| Energy from Wavelets | 144 | 36 coefficients from db7 |
| coefficients | 37 coefficients from sym3 | |
| 35 coefficients from coif4 | ||
| 36 coefficients from bior6.8 |
| Number of Stages | Number of Fixed Features | Number of Available Initial Features | Number of Final Features | Number of Hidden Neurons | -Score |
|---|---|---|---|---|---|
| 1 | 0 | 39 | 18 | 43 | 0.9444 |
| 2 | 18 | 320 | 274 | 30 | 0.9778 |
| 3 | 18 | 256 | 162 | 36 | 0.9889 |
| Number of
Initial Features | Number of
Final Features | Number of
Hidden Neurons | Precision | Sensibility | -Score |
|---|---|---|---|---|---|
| 320 | 156 | 63 | 0.9611 | 0.9611 | 0.9611 |
| 359 | 193 | 50 | 0.9778 | 0.9778 | 0.9778 |
| Number of Features | Precision with 40 Hidden Nodes | Precision with 60 Hidden Nodes |
|---|---|---|
| 6 | 0.5000 | 0.5185 |
| 31 | 0.8278 | 0.8284 |
| 88 | 0.9037 | 0.9111 |
| 162 | 0.9389 | 0.9593 |
| 193 | 0.9481 | 0.9585 |
| 359 | 0.9481 | 0.9593 |
| Parameters | Total Number | Description | Number of Coincident Parameters |
|---|---|---|---|
| RMS from frequency bands | 12 | 2nd band | 0 |
| 5th band to 7th band | 2 | ||
| 9th band | 1 | ||
| 11th band to 17th band | 5 | ||
| Frequency | 1 | Standard deviation | 1 |
| Time | 0 | ——– | 0 |
| Energy from Wavelets | 149 | 39 coefficients from db7 | 22 |
| coefficients | 39 coefficients from sym3 | 22 | |
| 24 coefficients from coif4 | 22 | ||
| 24 coefficients from bior6.8 | 22 | ||
| 23 coefficients from rbior6.8 | 0 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Randall, R.B. Vibration-Based Condition Monitoring; John Wiley & Sons, Ltd: West Sussex, UK, 2011. [Google Scholar]
- Moumene, I.; Ouelaa, N. Gears and bearings combined faults detection using hilbert transform and wavelet multiresolution analysis. In Condition Monitoring of Machinery in Non-Stationary Operations; Fakhfakh, T., Bartelmus, W., Chaari, F., Zimroz, R., Haddar, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 319–328. [Google Scholar]
- Kanneg, D. A Wavelet Spectrum Technique for Machinery Fault Diagnosis. J. Signal Inf. Process. 2011, 2, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way; Elsevier Academic Press: Burlington, USA, 2009. [Google Scholar]
- Wang, K.; Heyns, P. Application of computed order tracking, Vold-Kalman filtering and EMD in rotating machine vibration. Mech. Syst. Signal Process. 2011, 25, 416–430. [Google Scholar] [CrossRef]
- Pan, H.; Yuan, J. A fault diagnosis method under varying rotate speed conditions based on auxiliary particle filter. In Neural Information Processing; Lee, M., Hirose, A., Hou, Z.G., Kil, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8228, pp. 425–432. [Google Scholar]
- Yuan, J.; He, Z.; Zi, Y.; Liu, H. Gearbox fault diagnosis of rolling mills using multiwavelet sliding window neighboring coefficient denoising and optimal blind deconvolution. Sci. China Ser. E-Technol. Sci. 2009, 52, 2801–2809. [Google Scholar] [CrossRef]
- Li, C.; Liang, M. Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform. Mech. Syst. Signal Process. 2012, 26, 205–217. [Google Scholar] [CrossRef]
- Ng, S.S.Y.; Tse, P.W.; Tsui, K.L. A One-Versus-All Class Binarization Strategy for Bearing Diagnostics of Concurrent Defects. Sensors 2014, 14, 1295–1321. [Google Scholar] [CrossRef] [PubMed]
- Hajnayeb, A.; Ghasemloonia, A.; Khadem, S.; Moradi, M. Application and comparison of an ANN-based feature selection method and the genetic algorithm in gearbox fault diagnosis. Expert Syst. Appl. 2011, 30, 10205–10209. [Google Scholar] [CrossRef]
- Marichal, G.; Artés, M.; Prada, J.G.; Casanova, O. Extraction of rules for faulty bearing classification by a Neuro-Fuzzy approach. Mech. Syst. Signal Process. 2011, 25, 2073–2082. [Google Scholar] [CrossRef]
- Saravanan, N.; Siddabattuni, V.K.; Ramachandran, K. Fault diagnosis of spur bevel gear box using artificial neural network (ANN), and proximal support vector machine (PSVM). Appl. Soft Comput. 2010, 10, 344–360. [Google Scholar] [CrossRef]
- Saravanan, N.; Siddabattuni, V.K.; Ramachandran, K. Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN). Expert Syst. Appl. 2010, 37, 4168–4181. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Zheng, H. Gear fault detection and diagnosis under speed-up condition based on order cepstrum and radial basis function neural network. J. Mech. Sci. Technol. 2009, 23, 2780–2789. [Google Scholar] [CrossRef]
- Rafiee, J.; Arvania, F.; Harifib, A.; Sadeghic, M. Intelligent condition monitoring of a gearbox using artificial neural network. Mech. Syst. Signal Process. 2007, 21, 1746–1754. [Google Scholar] [CrossRef]
- Kang, Y.; Wang, C.; Chang, Y. Gear fault diagnosis by using wavelet neural networks. In Advances in Neural Networks ISNN 2007; Liu, D., Fei, S., Hou, Z., Zhang, H., Sun, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4493, pp. 580–588. [Google Scholar]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Van der Maaten, L.J.; Postma, E.O.; van den Herik, H.J. Dimensionality reduction: A comparative review. J. Mach. Learn. Res. 2009, 10, 66–71. [Google Scholar]
- Bartkowiak, A.; Zimroz, R. Dimensionality reduction via variables selection. Linear and nonlinear approaches with application to vibration-based condition monitoring of planetary gearbox. Appl. Acoust. 2014, 77, 169–177. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Raymer, M.; Punch, W.; Goodman, E.; Kuhn, L.; Jain, A. Dimensionality reduction using genetic algorithms. IEEE Trans. Evolut. Comput. 2000, 4, 164–171. [Google Scholar] [CrossRef]
- Samanta, B. Gear fault detection using artificial neural networks and support vector machines with genetic algorithms. Mech. Syst. Signal Process. 2004, 18, 625–644. [Google Scholar] [CrossRef]
- Samanta, B. Artificial neural networks and genetic algorithms for gear fault detection. Mech. Syst. Signal Process. 2004, 18, 1273–1282. [Google Scholar] [CrossRef]
- Samanta, B.; Al-Balushi, K.; Al-Araimi, S. Artificial neural networks and support vector machines with genetic algorithm for bearing fault detection. Eng. Appl. Artif. Intell. 2003, 16, 657–665. [Google Scholar] [CrossRef]
- Karabadji, N.E.I.; Seridi, H.; Khelf, I.; Azizi, N.; Boulkroune, R. Improved decision tree construction based on attribute selection and data sampling for fault diagnosis in rotating machines. Eng. Appl. Artif. Intell. 2014, 35, 71–83. [Google Scholar] [CrossRef]
- Rajeswari, C.; Sathiyabhama, B.; Devendiran, S.; Manivannan, K. A Gear Fault Identification using Wavelet Transform, Rough set Based GA, ANN and C4.5 Algorithm. Procedia Eng. 2014, 97, 1831–1841. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Scarf, P.; Ball, A. Feature selection for high-dimensional machinery fault diagnosis data using multiple models and Radial Basis Function networks. Neurocomputing 2011, 74, 2941–2952. [Google Scholar] [CrossRef]
- Li, B.; Zhang, P.L.; Tian, H.; Mi, S.S.; Liu, D.S.; Ren, G.Q. A new feature extraction and selection scheme for hybrid fault diagnosis of gearbox. Expert Syst. Appl. 2011, 38, 10000–10009. [Google Scholar] [CrossRef]
- Yang, P.; Liu, W.; Zhou, B.; Chawla, S.; Zomaya, A. Ensemble-based wrapper methods for feature selection and class imbalance learning. In Advances in Knowledge Discovery and Data Mining; Pei, J., Tseng, V., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7818, pp. 544–555. [Google Scholar]
- Yang, Y.; Liao, L.; Meng, G.; Lee, J. A hybrid feature selection scheme for unsupervised learning and its application in bearing fault diagnosis. Expert Syst. Appl. 2011, 38, 11311–11320. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L. Genetic algorithms: A survey. Computer 1994, 27, 17–26. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ripley, B. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Reed, R.; Markssi, R. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; The MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J.; He, Z.; Zi, Y. A multidimensional hybrid intelligent method for gear fault diagnosis. Expert Syst. Appl. 2010, 37, 1419–1430. [Google Scholar] [CrossRef]
- Gargour, C.; Gabrea, M.; Ramachandran, V.; Lina, J. A short introduction to wavelets and their applications. IEEE Circuits Syst. Mag. 2009, 9, 57–68. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Li, C.; Sanchez, R.V.; Zurita, G.; Cerrada, M.; Cabrera, D.; Vásquez, R.E. Multimodal deep support vector classification with homologous features and its application to gearbox fault diagnosis. Neurocomputing 2015, 168, 119–127. [Google Scholar] [CrossRef]
- Mitra, S. Digital Signal Processing: A Computer-Based Approach; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Beleitesa, C.; Salzerc, R.; Sergoa, V. Validation of Soft Classification Models using Partial Class Memberships: An Extended Concept of Sensitivity & Co. applied to the Grading of Astrocytoma Tissues. Chemom. Intell. Lab. Syst. 2013, 122, 12–22. [Google Scholar]
- Sadjadi, F. Comparison of fitness scaling functions in genetic algorithms with applications to optical processing. Proc. SPIE 2004, 5557, 356–364. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; TuleauMalot, C. Variable selection using Random Forests. Pattern Recognit. Lett. 2010, 14, 2225–2236. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerrada, M.; Sánchez, R.V.; Cabrera, D.; Zurita, G.; Li, C. Multi-Stage Feature Selection by Using Genetic Algorithms for Fault Diagnosis in Gearboxes Based on Vibration Signal. Sensors 2015, 15, 23903-23926. https://doi.org/10.3390/s150923903
Cerrada M, Sánchez RV, Cabrera D, Zurita G, Li C. Multi-Stage Feature Selection by Using Genetic Algorithms for Fault Diagnosis in Gearboxes Based on Vibration Signal. Sensors. 2015; 15(9):23903-23926. https://doi.org/10.3390/s150923903
Chicago/Turabian StyleCerrada, Mariela, René Vinicio Sánchez, Diego Cabrera, Grover Zurita, and Chuan Li. 2015. "Multi-Stage Feature Selection by Using Genetic Algorithms for Fault Diagnosis in Gearboxes Based on Vibration Signal" Sensors 15, no. 9: 23903-23926. https://doi.org/10.3390/s150923903
APA StyleCerrada, M., Sánchez, R. V., Cabrera, D., Zurita, G., & Li, C. (2015). Multi-Stage Feature Selection by Using Genetic Algorithms for Fault Diagnosis in Gearboxes Based on Vibration Signal. Sensors, 15(9), 23903-23926. https://doi.org/10.3390/s150923903