Modeling of Acoustic Emission Signal Propagation in Waveguides
Abstract
:1. Introduction
2. Simulation Methodology
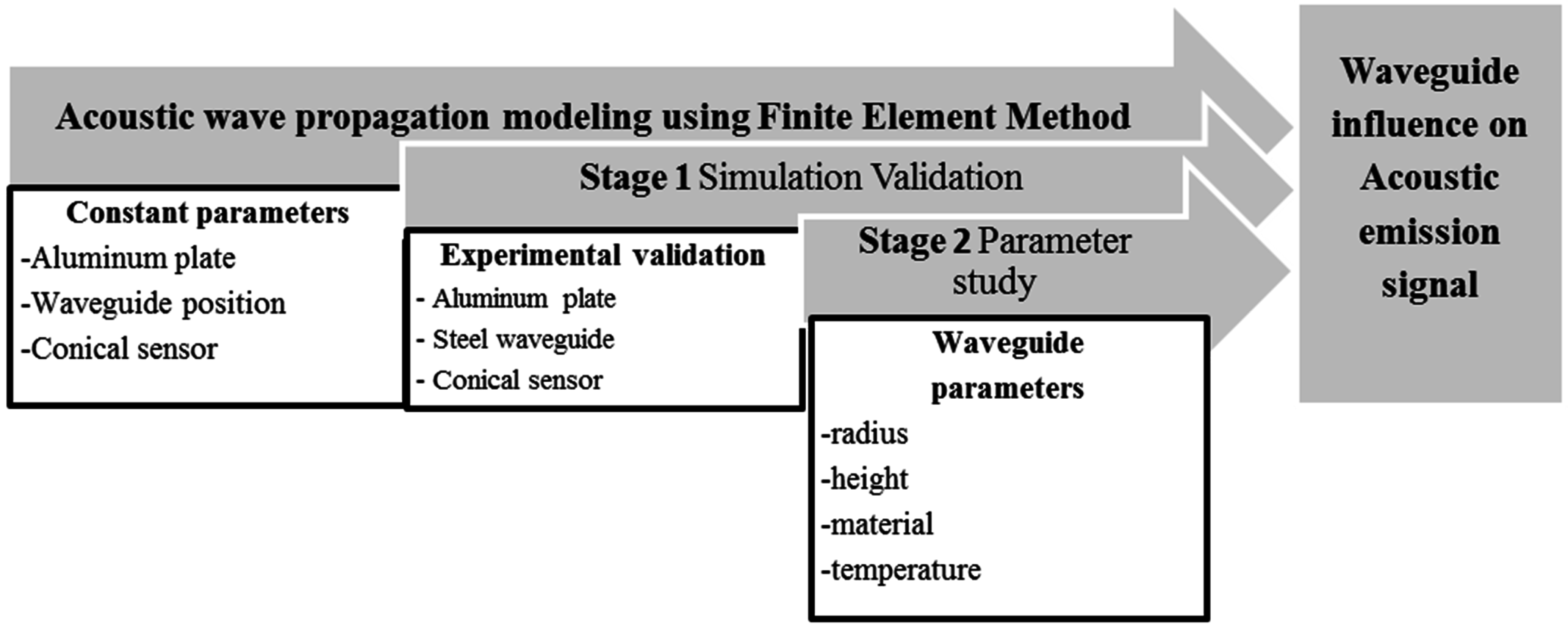
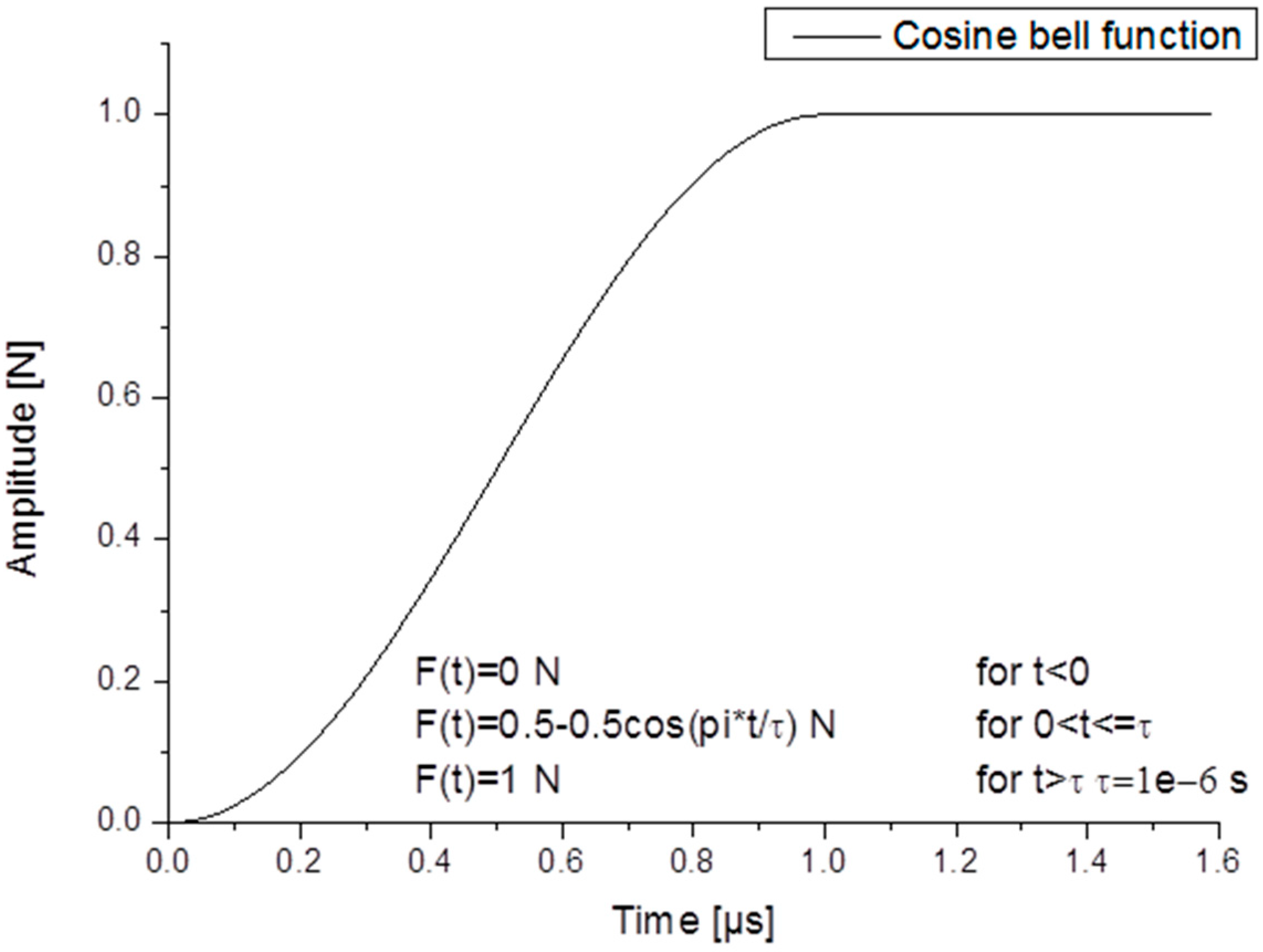
2.1. Acoustic Emission Test Source
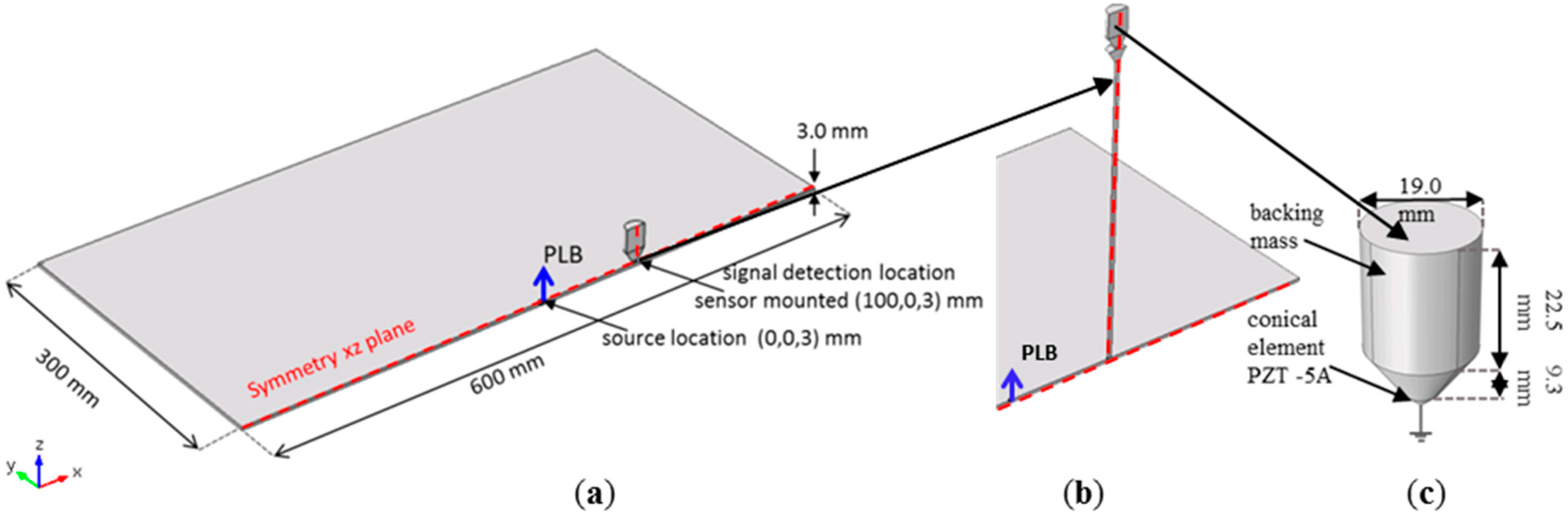
2.2. Geometry Setup
3. Validation of Simulation
3.1. Experimental Setup


3.2. Simulation Details
| Property | AlMg3 | Steel | PZT-5A | Brass UNS C2600 | Alumina |
|---|---|---|---|---|---|
| Density [kg/m3] | 2660 | 7850 | 7750 | 8627.6 | 3900 |
| Elastic modulus [GPa] | 70 | 200 | C11 = C22 = 120.3; C12 = 75.2; C13 = C23 = 75.1; C44 = C55 = 21.1; C66 = 22.6 | 113.3 | 300 |
| Poisson ratio | 0.33 | 0.33 | - | 0.34 | 0.222 |
| Rod sound velocity [m/s] | 5129.89 | 5047.54 | - | 3623.84 | 8770.5 |
| Piezoelectric constants [C/m2] | - | - | S31 = S32 = −5.4 S33 = 15.8 S24 = S15 = 12.3 | - | - |
| Electrical permittivity | - | - | χ11 = 919.1 χ22 = 919.1 χ33 = 826.6 | - | - |
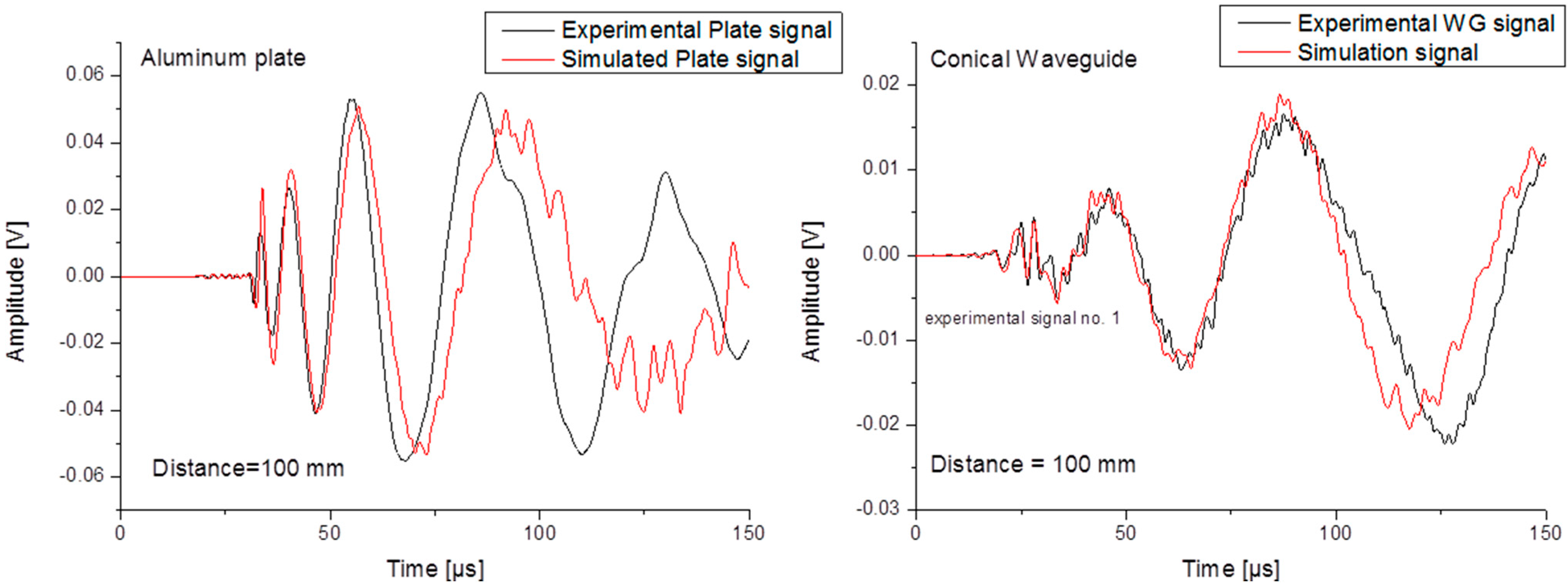
3.3. Comparison of Simulation vs. Experiment
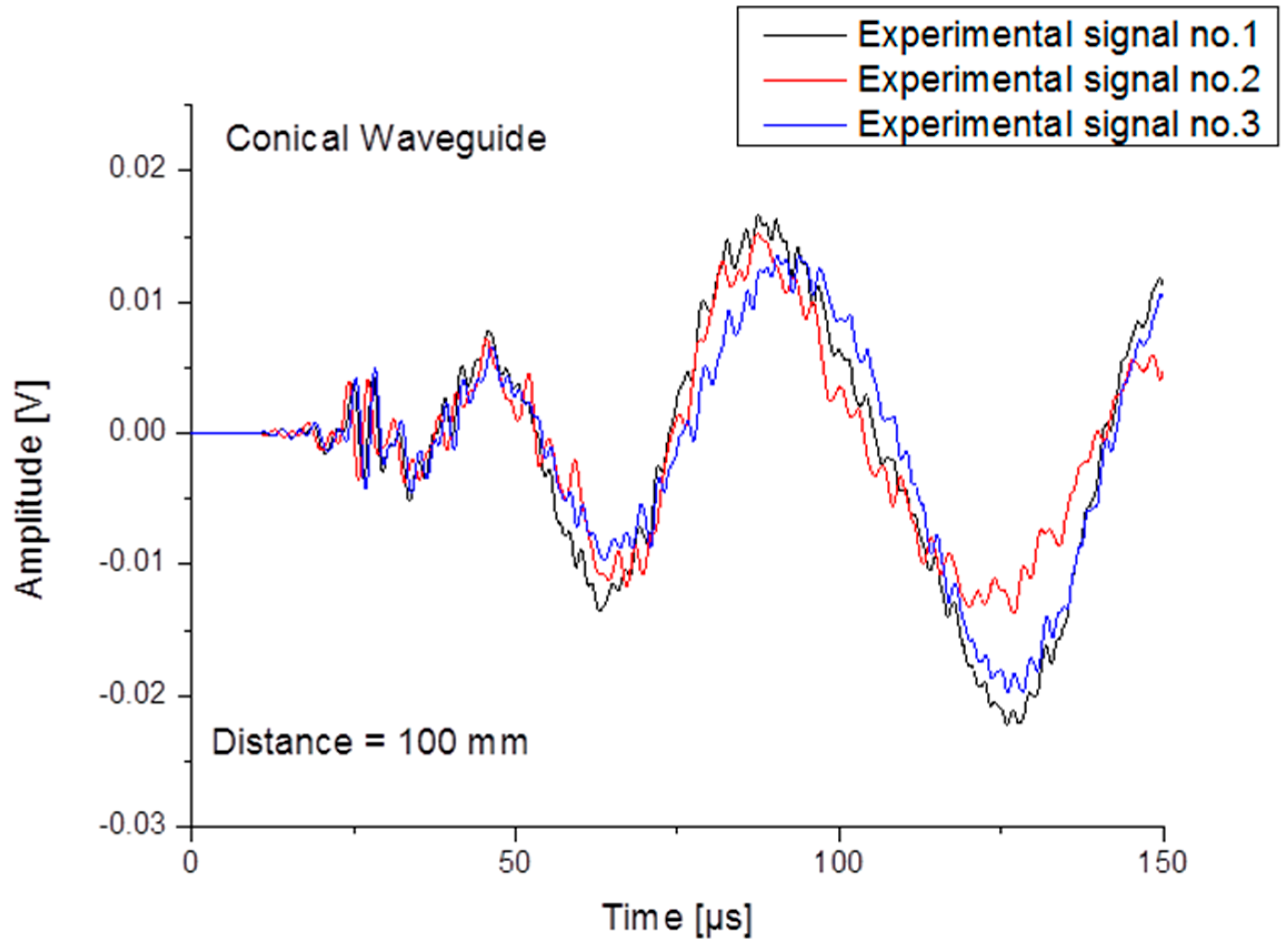
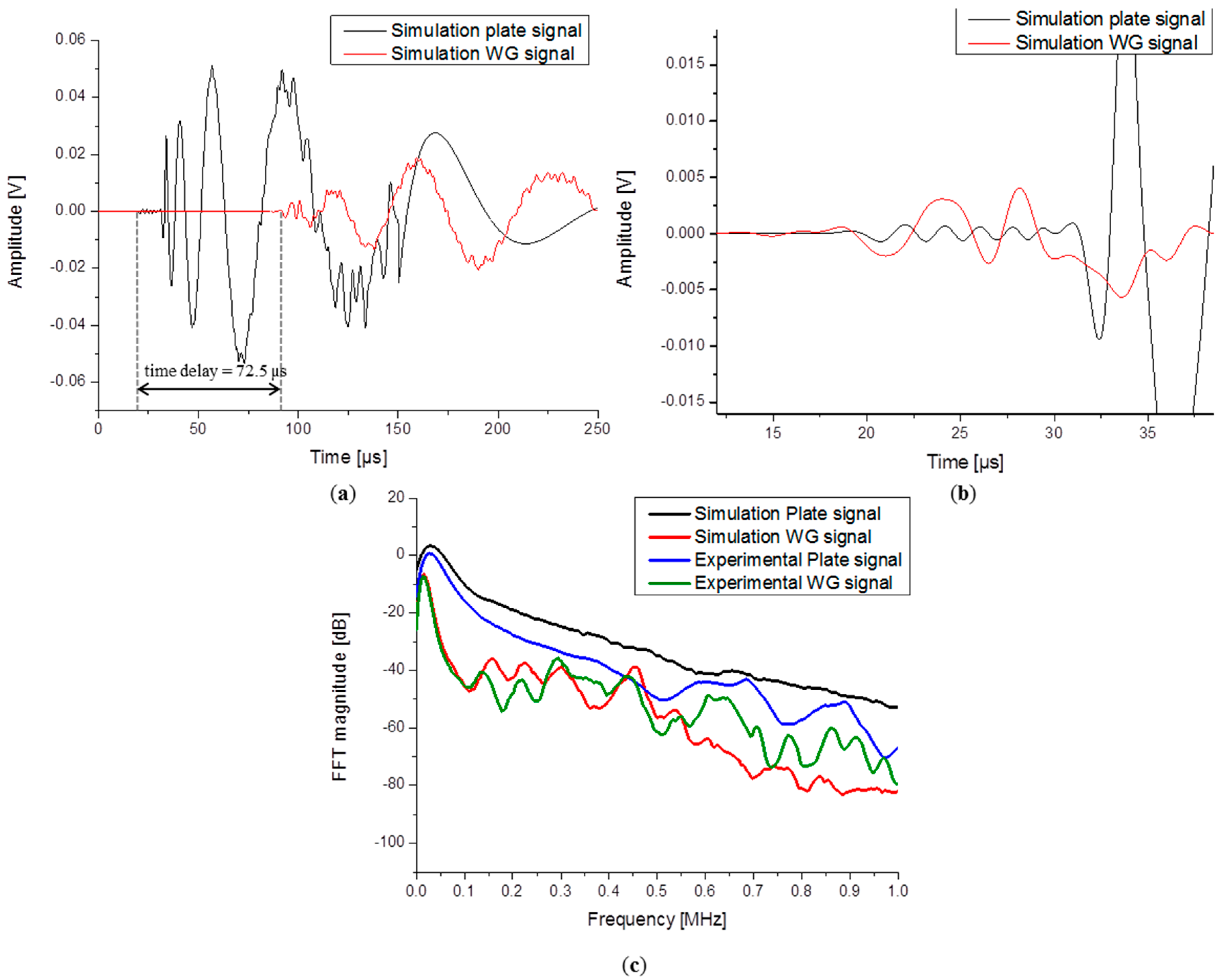
4. Parameter Study
4.1. Influence of Waveguide Geometry and Material
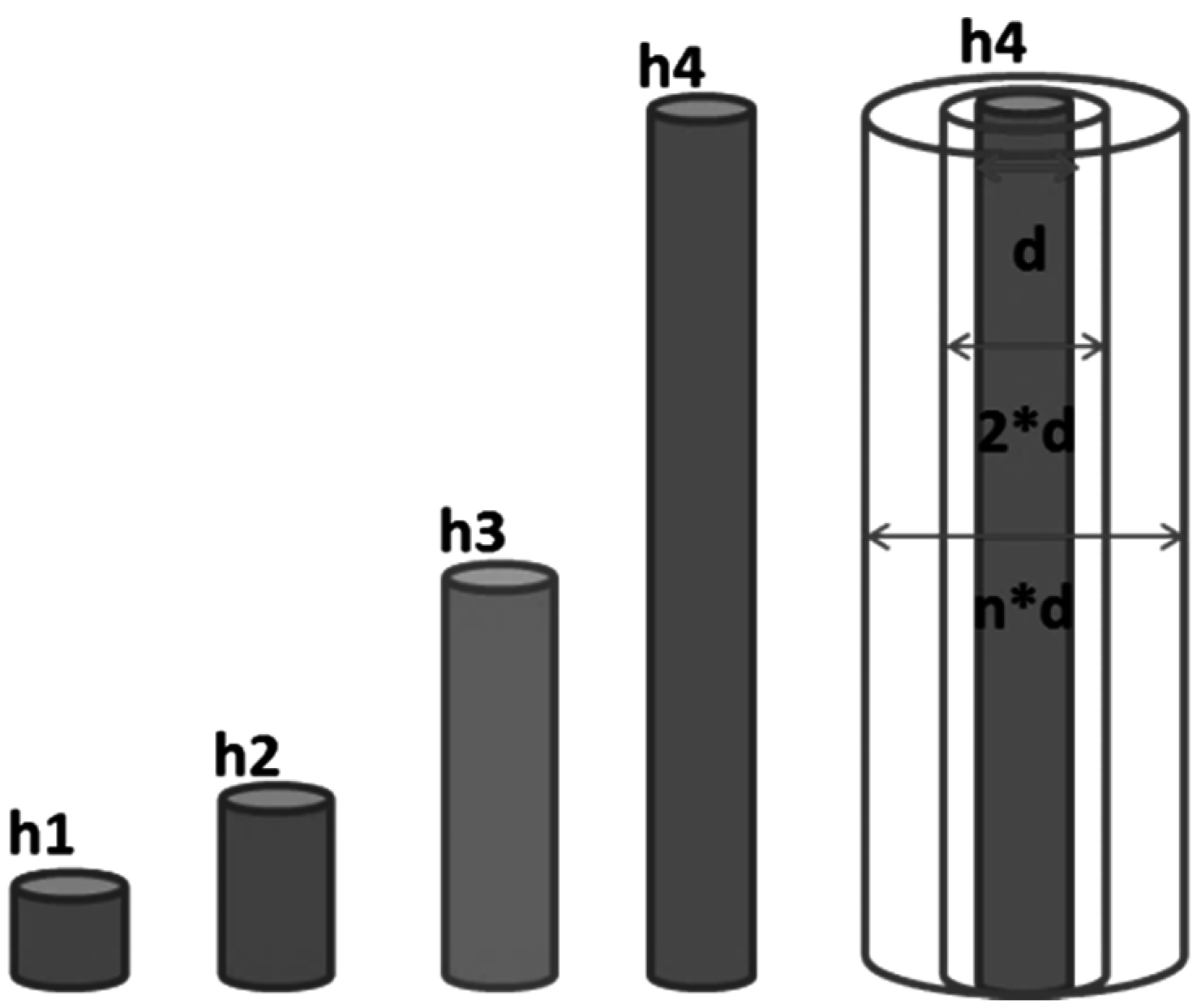
| Parameters | Constant Values | Varied Values | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Length variation [mm] | Diameter = 1.59 | 76.57 | 153.15 | 229.71 | 306.3 | ||||
| Diameter variation [mm] | Length = 306.3 | 0.79 | 1.59 | 2.38 | 3.18 | 3.97 | 4.77 | 5.56 | 7.9 |
| Material variation | Diameter = 1.59 Length = 306.3 | Aluminum | Steel | Alumina | Brass | ||||
- The WG signal was shifted forward in time to superimpose
- All signals were terminated at a convenient zero
- All signals were extended with 0 values to a total length of 2048 points
- The Fast Fourier Transformation (FFT) was calculated with a square window function
- The resulting FFTs were smoothed by a 30 point Savitzky-Golay (5th polynomial) method
- The FFTs magnitudes were compared from 0 to 100 kHz.
4.1.1. Influence of WG Diameter
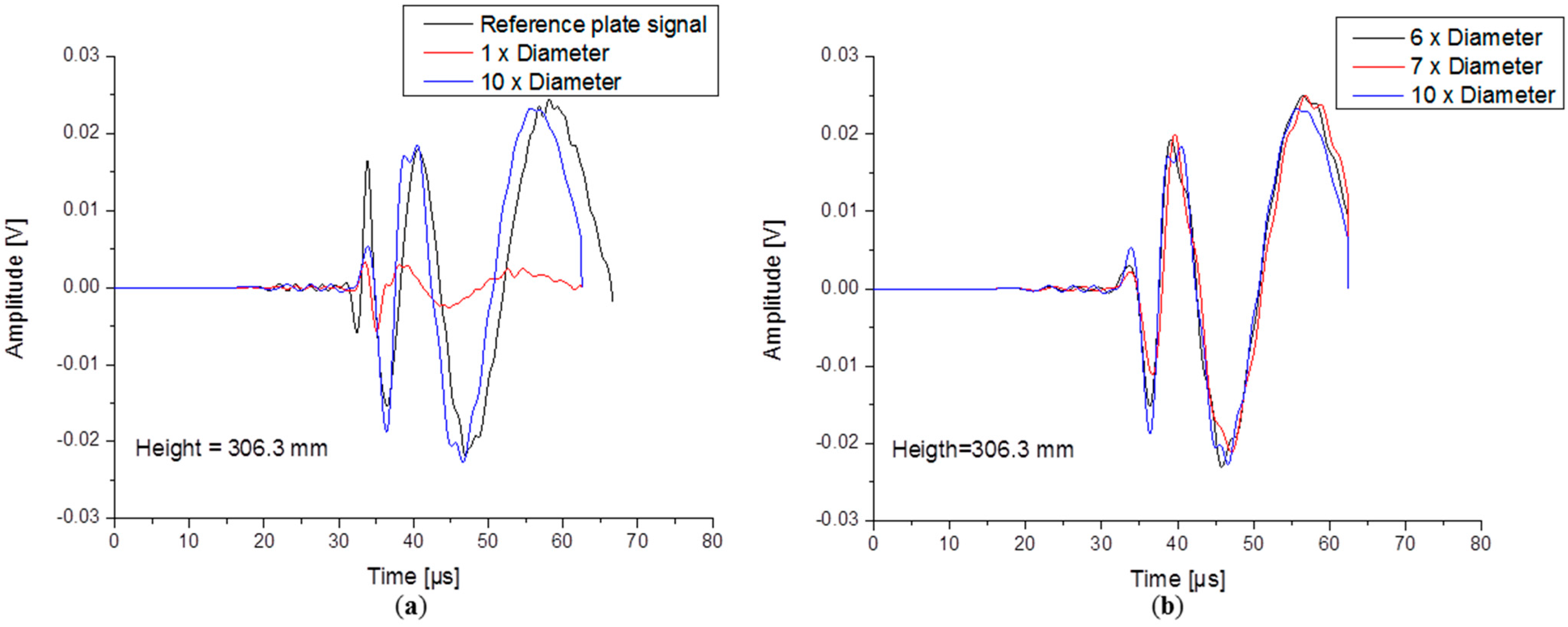
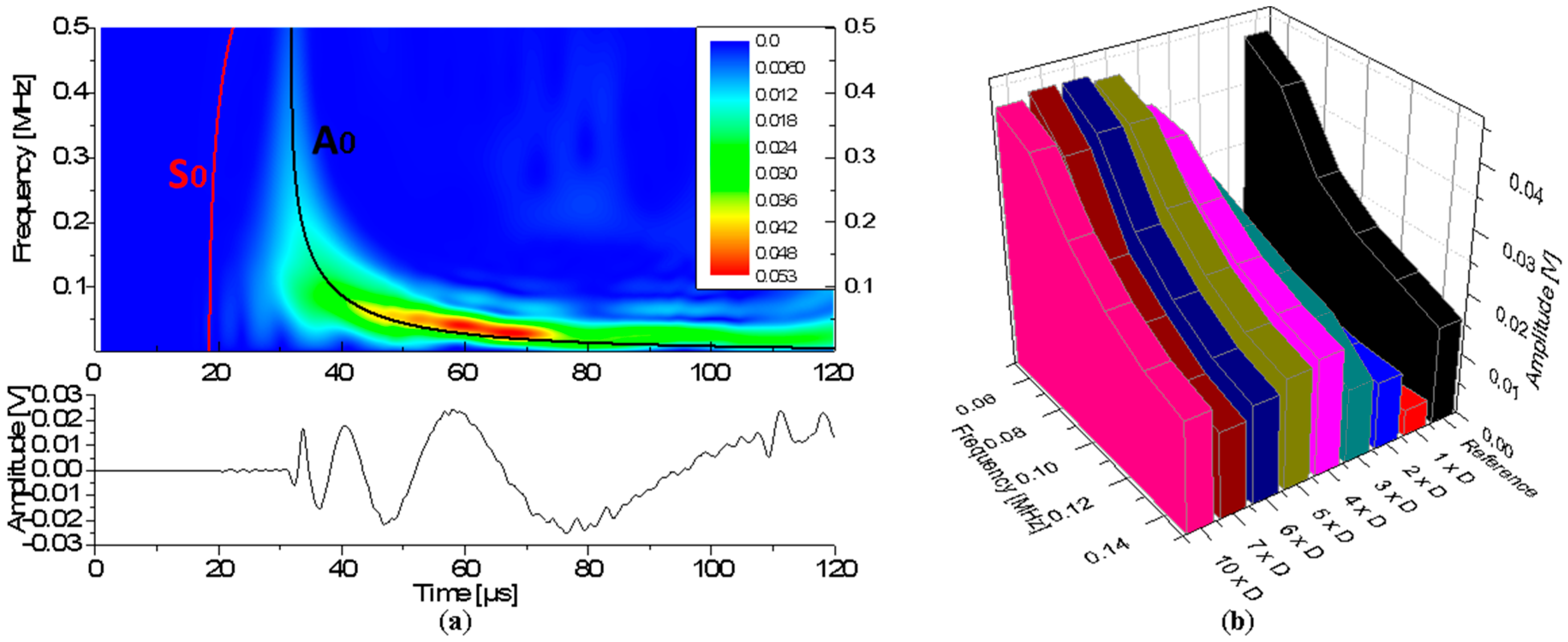
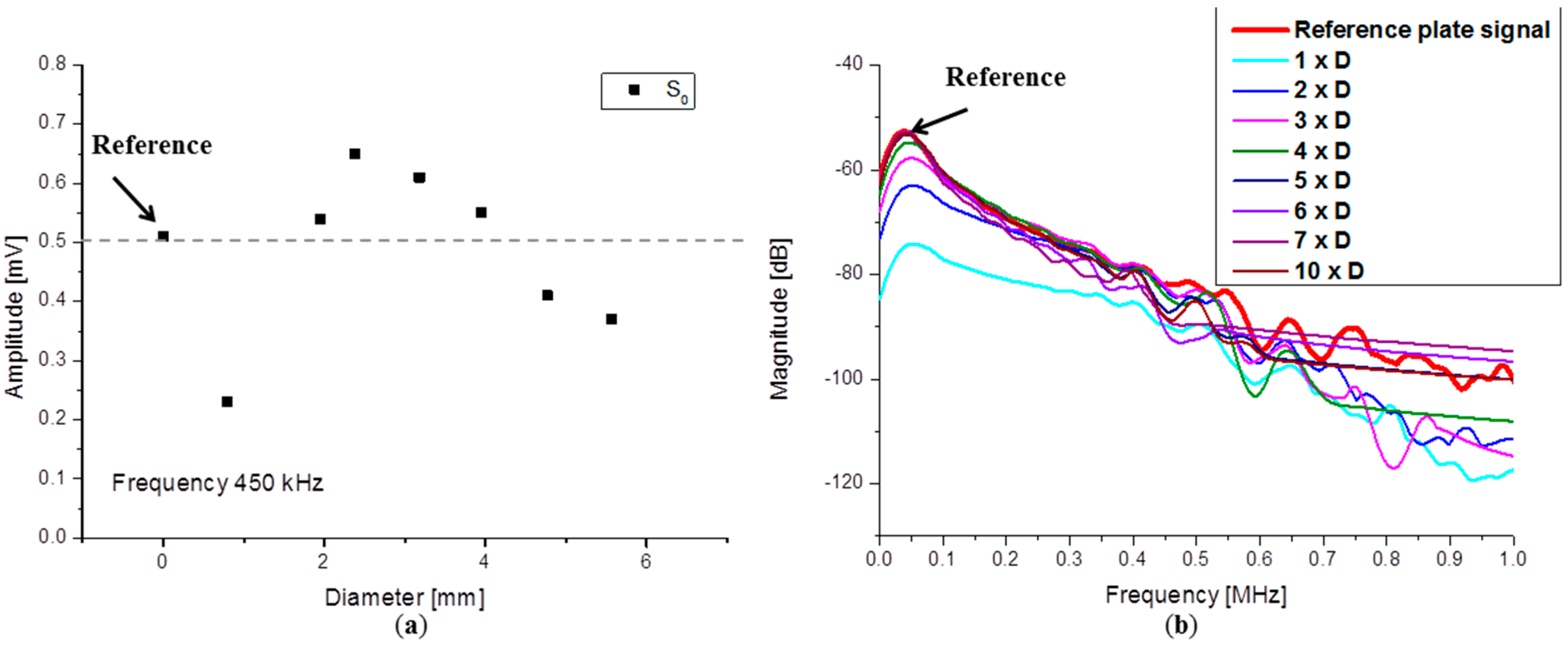
4.1.2. Influence of Waveguide Length
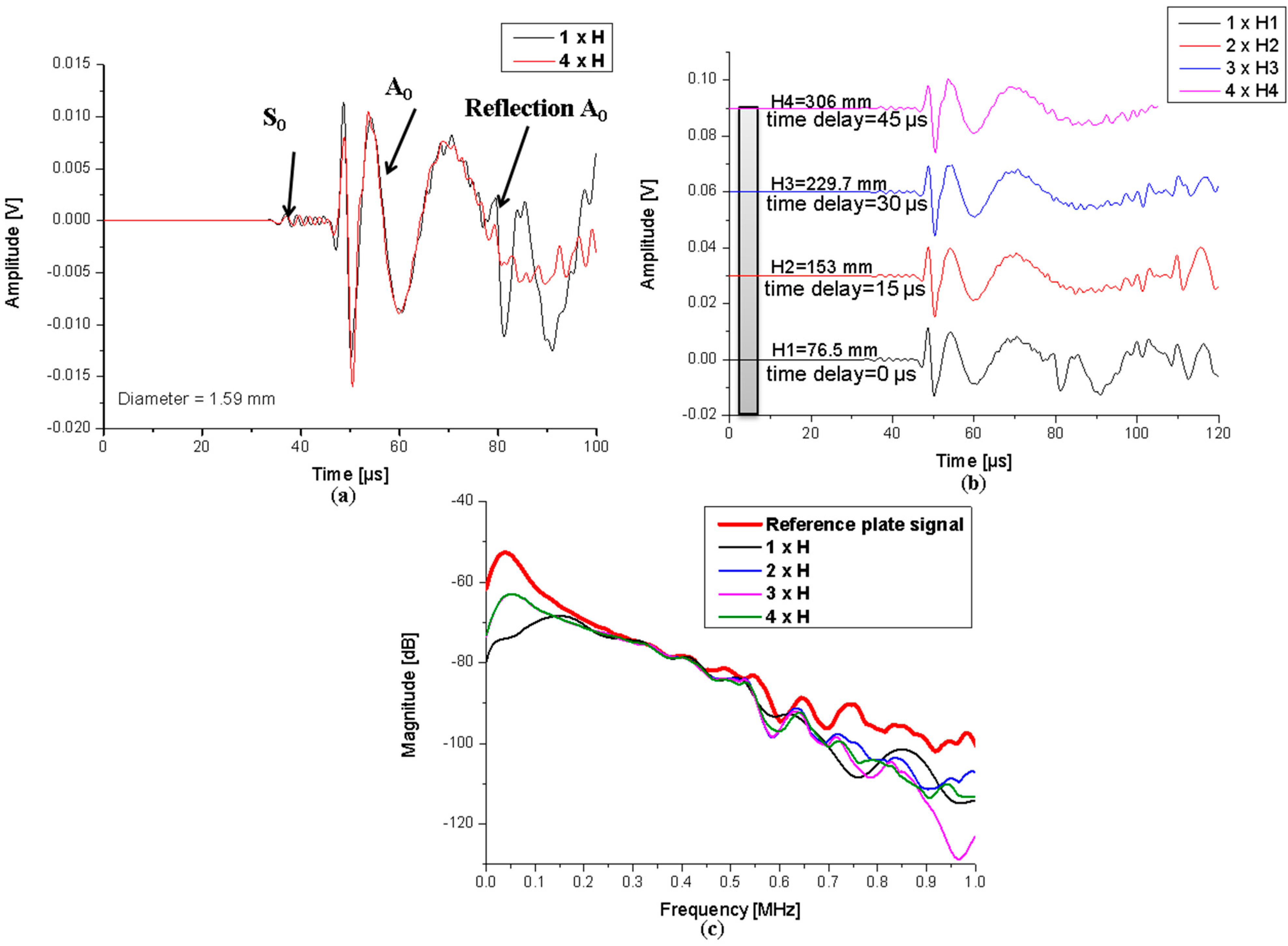
4.1.3. Influence of Waveguide Material
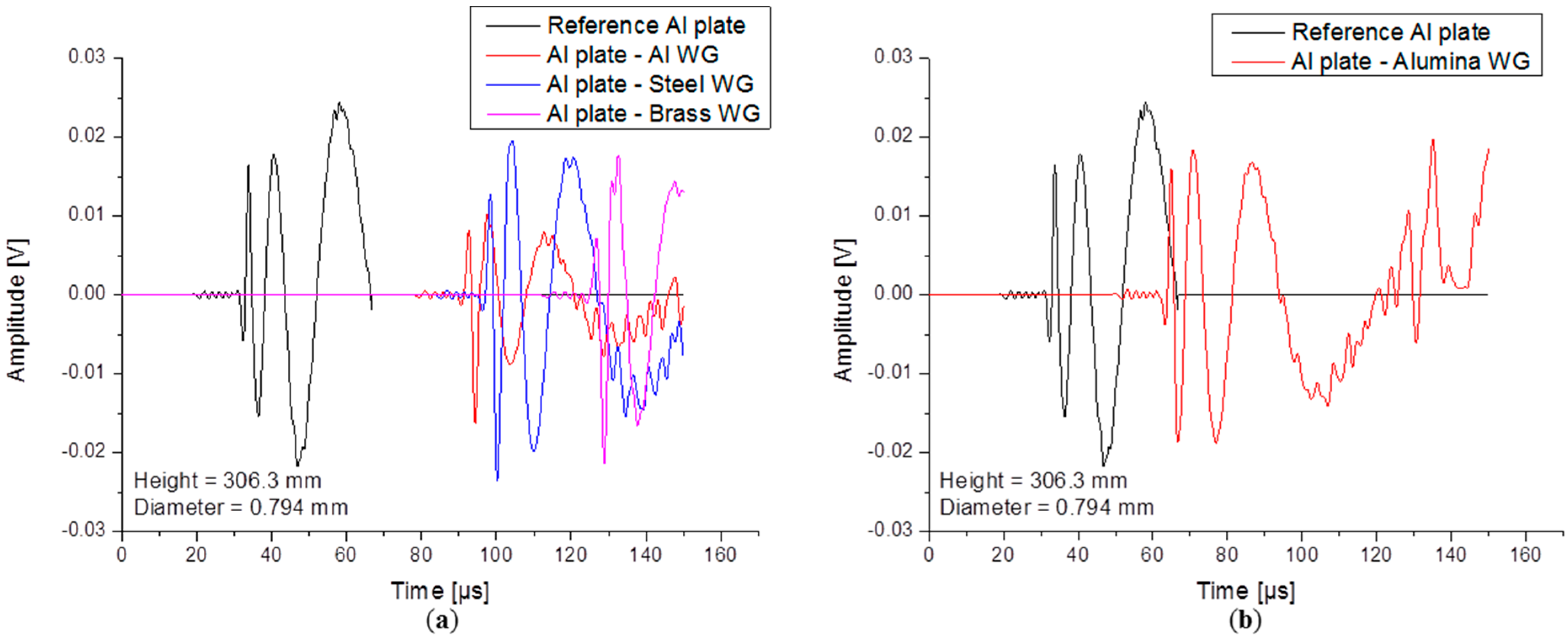

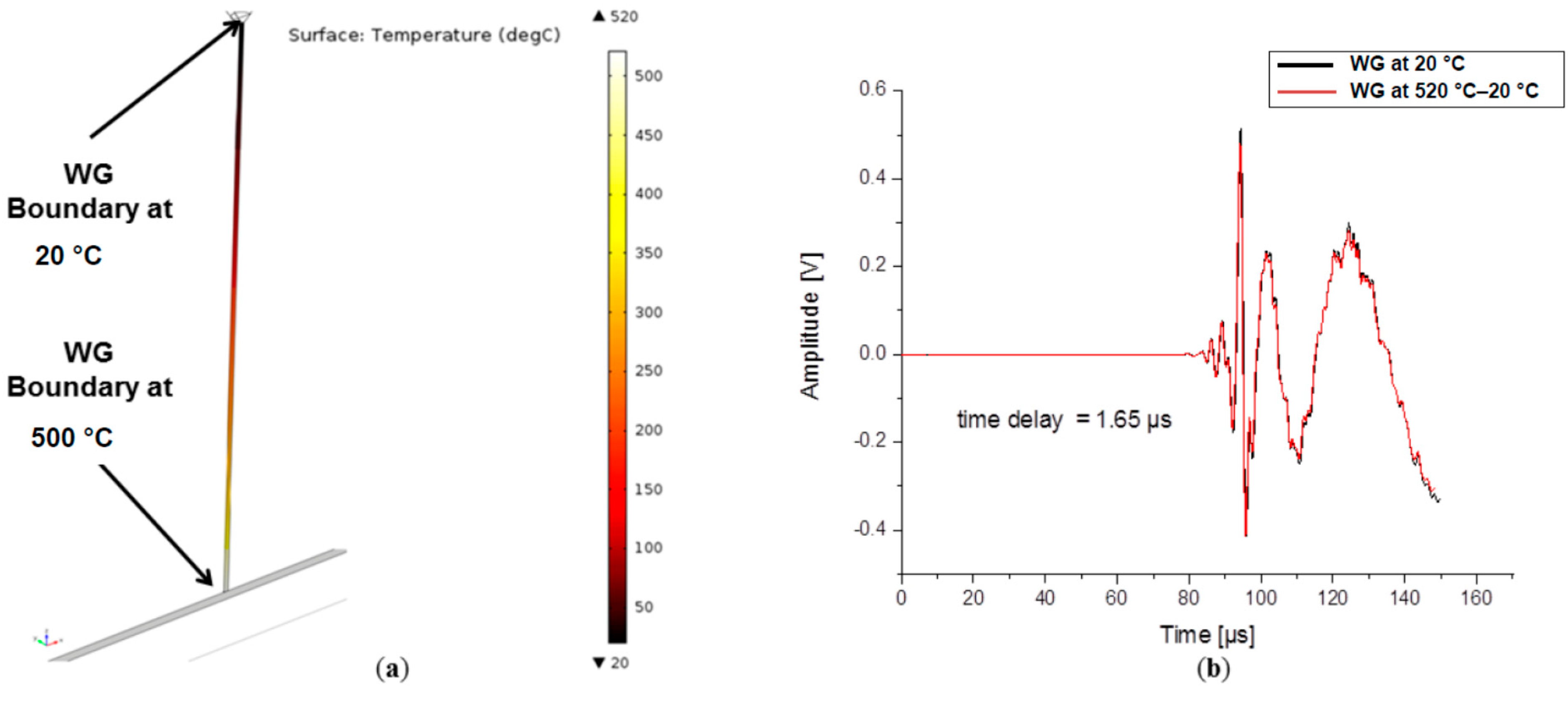
4.2. Influence of Waveguide Temperature
| Property | UNS K12211 |
|---|---|
| Density [kg/m3] | |
| Elastic modulus [GPa] | |
| Poisson ratio | |
| Thermal conductivity [W/m*K] | |
| Heat capacity at constant pressure [J/kg*K] |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Woodward, B.; Stephens, R.W.B. Some aspects of boiling noise detection in sodium reactors by means of a mechanical waveguide. Ultrasonics 1971, 9, 21–25. [Google Scholar] [CrossRef]
- Lynnworth, L.; Liu, Y.; Umina, J. Extensional Bundle Waveguide Techniques for Measuring Flow of Hot Fluids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 42, 538–544. [Google Scholar] [CrossRef]
- Peterson, M.L. A signal processing technique for measurement of multi-mode waveguide signals: An application to monitoring of reaction bonding in silicon nitride. Res. Nondestr. Eval. 1994, 5, 239–256. [Google Scholar] [CrossRef]
- Jen, C.-K.; Cao, B.; Nguyen, K.T.; Loong, C.A.; Legoux, J.-G. On-line ultrasonic monitoring of a diecasting process using buffer rods. Ultrasonics 1997, 35, 335–344. [Google Scholar] [CrossRef]
- Hamstad, M.A. Small Diameter Waveguide for Wideband Acoustic Emission. J. Acoust. Emiss. 2006, 24, 234–247. [Google Scholar]
- Prosser, W.H.; Hamstad, M.A.; Gary, J.; Gallagher, A.O. Finite element and plate theory modeling of acoustic emission waveforms. J. Nondestruct. Eval. 1999, 18, 83–90. [Google Scholar] [CrossRef]
- Sause, M.G.R.; Hamstad, M.A.; Horn, S. Finite element modeling of conical acoustic emission sensors and corresponding experiments. Sens. Actuators 2012, 184, 64–71. [Google Scholar] [CrossRef]
- Sause, M.G.R.; Hamstad, M.A.; Horn, S. Finite element modeling of lamb wave propagation in anisotropic hybrid materials. Compos. Part B Eng. 2013, 53, 249–257. [Google Scholar] [CrossRef]
- Sause, M.G.R.; Horn, S. Simulation of acoustic emission in planar carbon fiber reinforced plastic specimens. J. Nondestruct. Eval. 2010, 29, 123–142. [Google Scholar] [CrossRef]
- Vivar-Perez, J.M.; Willberg, C.; Gabbert, U. Simulation of Piezoeletric Induced Lamb Waves in Plates. PAMM 2009, 9, 503–504. [Google Scholar] [CrossRef]
- Castaings, M.; Predoi, M.V.; Hosten, B. Ultrasound propagation in Viscoelastic Material Guide. In Proceedings of the COMSOL Multiphysics User’s Conference, Paris, France, 15 November 2005.
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Elsevier, Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Lamb, H. On Waves in an Elastic Plate. Proc. Royal Soc. London Ser. A Math. Phys. Charact. 1917, 93, 114–128. [Google Scholar] [CrossRef]
- Hosten, B.; Castaings, M. Finite elements methods for modeling the guided waves propagation in structures with weak interfaces. J. Acoust. Soc. Am. 2005, 117, 1108–1113. [Google Scholar] [CrossRef]
- Predoi, M.V.; Castaings, M.; Moreau, L. Influence of Material viscoelasticity on the scattering of guided waves by defects. J. Acoust. Soc. Am. 2008, 124, 2883–2894. [Google Scholar] [CrossRef] [PubMed]
- Sause, M.G.R. Identification of Failure Mechanisms in Hybrid Materials Utilizing Pattern Recognition Techniques Applied to Acoustic Emission Analysis. Ph.D. Thesis, University of Augsburg, mbv-Verlag, Berlin, Germany, 2010. [Google Scholar]
- Zelenyak, A.-M; Hamstad, M.A.; Sause, M.G.R. Finite Element Modeling of Acoustic Emission Signal Propagation with Various Shaped Waveguides. In Proceedings of the 31st Conference of the European Working Group on Acoustic Emission (EWGAE), Dresden, Germany, 3–5 September 2014.
- Hsu, N.N.; Breckenridge, F.R. Characterization and calibration of acoustic emission sensors. Mater. Eval. 1981, 39, 60–68. [Google Scholar]
- Nielsen, A. Acoustic Emission Source based on Pencil Lead Breaking; The Danish Welding Institute Publication: Copenhagen, Danmark, 1980; pp. 15–18. [Google Scholar]
- Delaunay, B. Sur la sphere vide. A la memoire de Georges Voronoi. Bull. Acad. Sci. USSR (VII) Classe Sci. Mat. 1934, 7, 793–800. (In French) [Google Scholar]
- Sause, M.G.R. Investigation of pencil-lead breaks as acoustic emission sources. J. Acoust. Emiss. 2013, 29, 184–196. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zelenyak, A.-M.; Hamstad, M.A.; Sause, M.G.R. Modeling of Acoustic Emission Signal Propagation in Waveguides. Sensors 2015, 15, 11805-11822. https://doi.org/10.3390/s150511805
Zelenyak A-M, Hamstad MA, Sause MGR. Modeling of Acoustic Emission Signal Propagation in Waveguides. Sensors. 2015; 15(5):11805-11822. https://doi.org/10.3390/s150511805
Chicago/Turabian StyleZelenyak, Andreea-Manuela, Marvin A. Hamstad, and Markus G. R. Sause. 2015. "Modeling of Acoustic Emission Signal Propagation in Waveguides" Sensors 15, no. 5: 11805-11822. https://doi.org/10.3390/s150511805
APA StyleZelenyak, A.-M., Hamstad, M. A., & Sause, M. G. R. (2015). Modeling of Acoustic Emission Signal Propagation in Waveguides. Sensors, 15(5), 11805-11822. https://doi.org/10.3390/s150511805





