A Simulation Environment for Benchmarking Sensor Fusion-Based Pose Estimators
Abstract
:1. Introduction
2. Methods
2.1. Simulation Framework
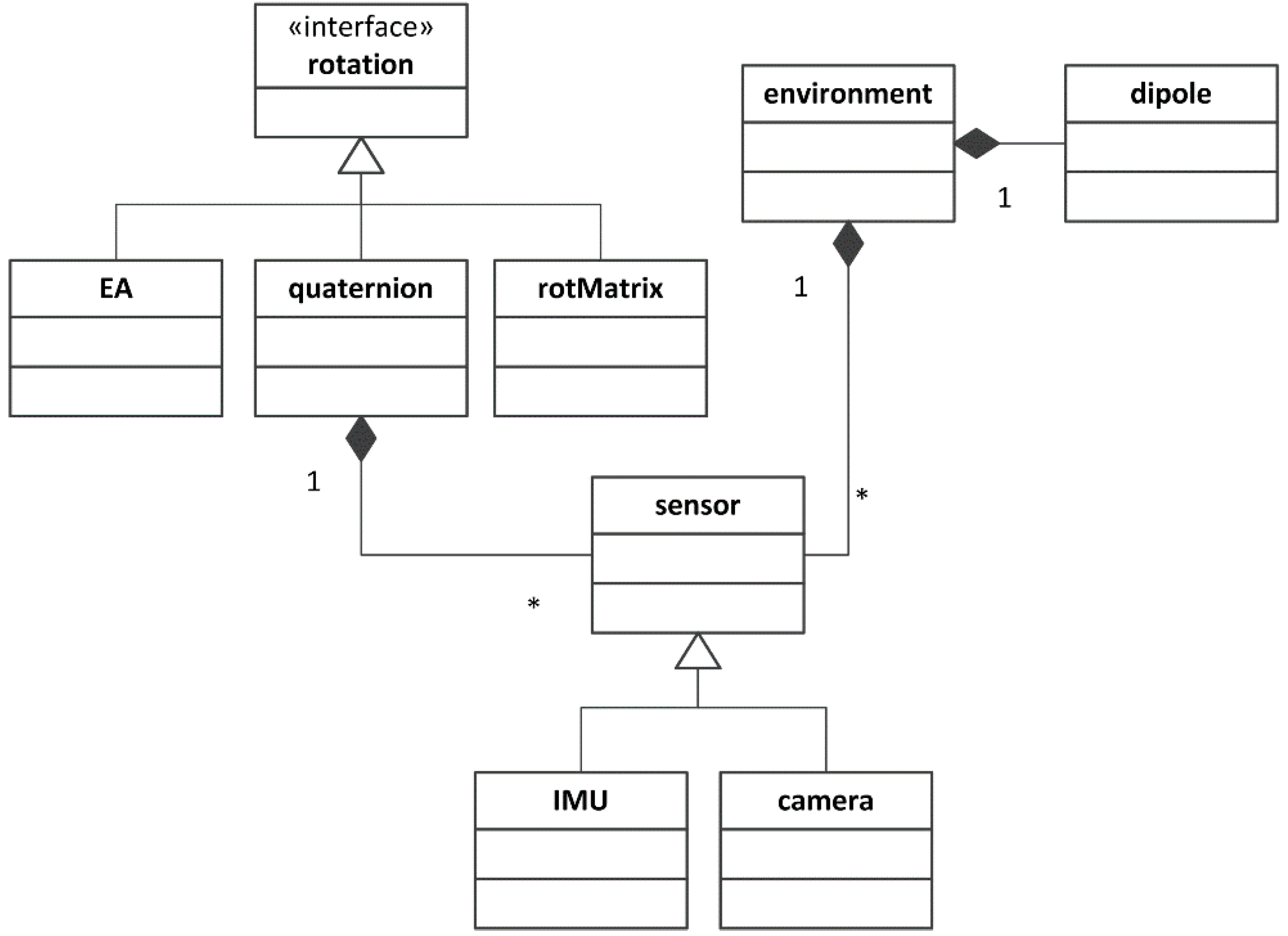
2.1.1. Rotation Classes
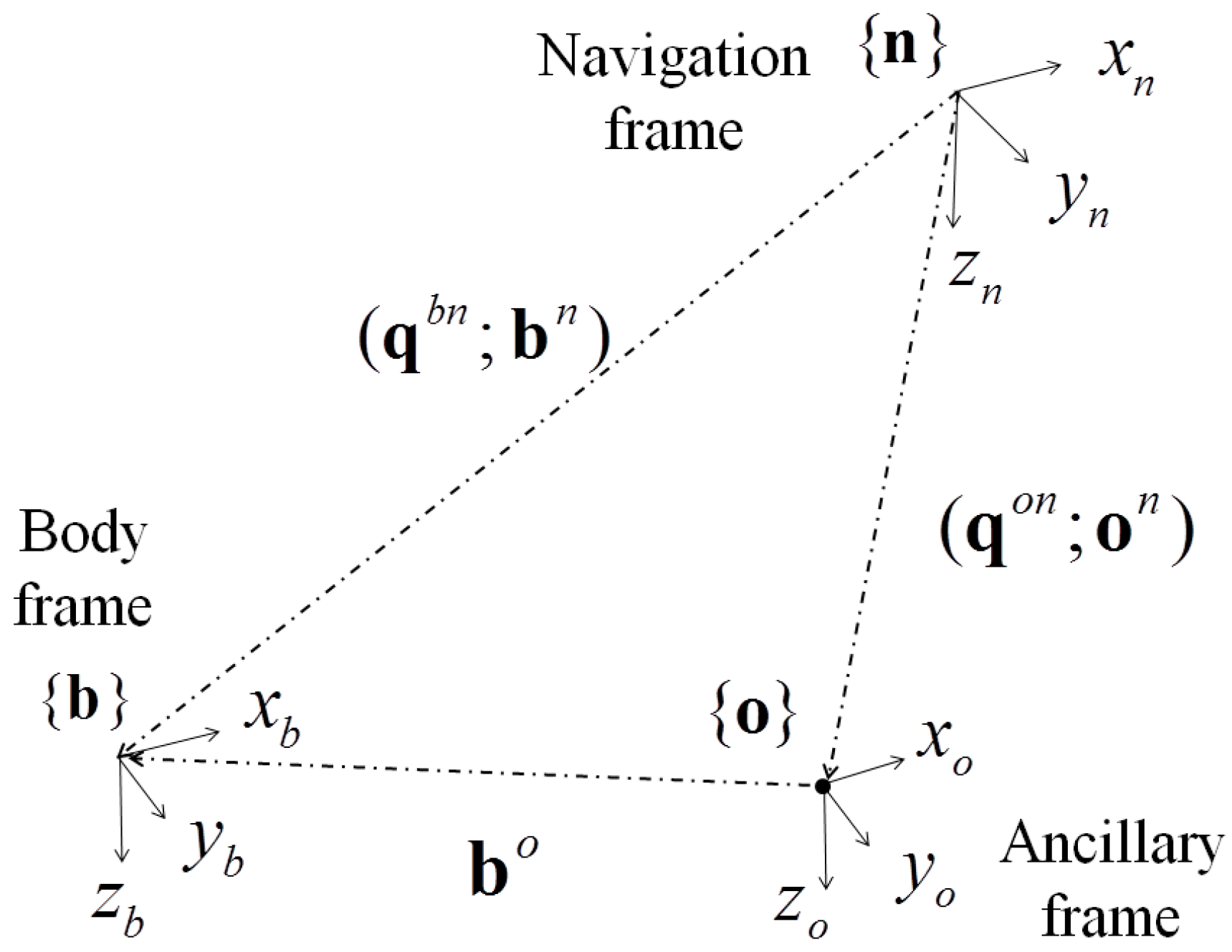
2.1.2. Environment Class
- The environment class collects the contextual information of interest to the classes named IMU and camera. Specifically, the contextual information concerns:
- The expression of the Earth’s magnetic and gravity vector fields resolved in
- The scene, namely the coordinates of the 3D points in that have to be projected onto the image plane (see Section 2.1.6);
- The reference to an array of dipole instances (see Section 2.1.3) that are intended to model local magnetic disturbances.
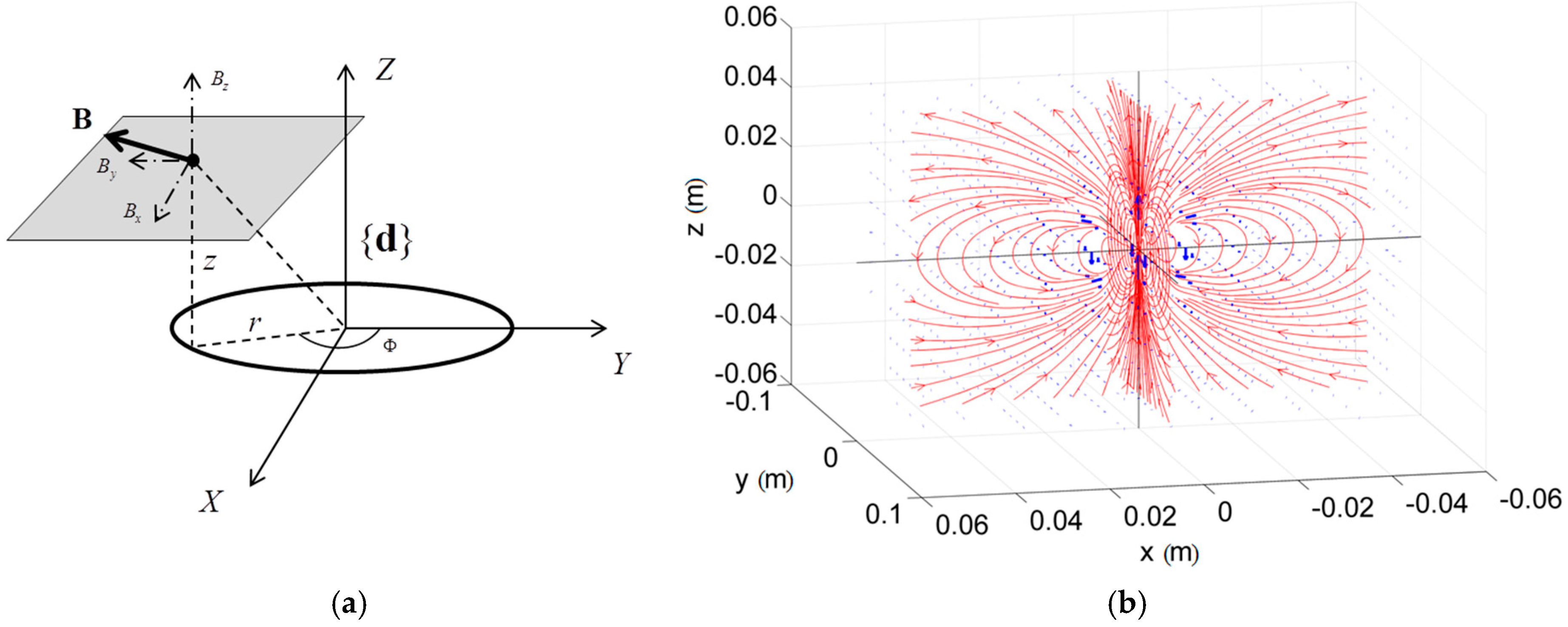
2.1.3. Dipole Class
2.1.4. Sensor Class
2.1.5. IMU Class
2.1.6. Camera Class
2.2. Case Study
2.3. Experimental Validation

| fx (pixel) | fy (pixel) | α (°) | ccx (pixel) | ccy (pixel) |
|---|---|---|---|---|
| 670.24 | 665.54 | 0.00 | 332.95 | 237.40 |
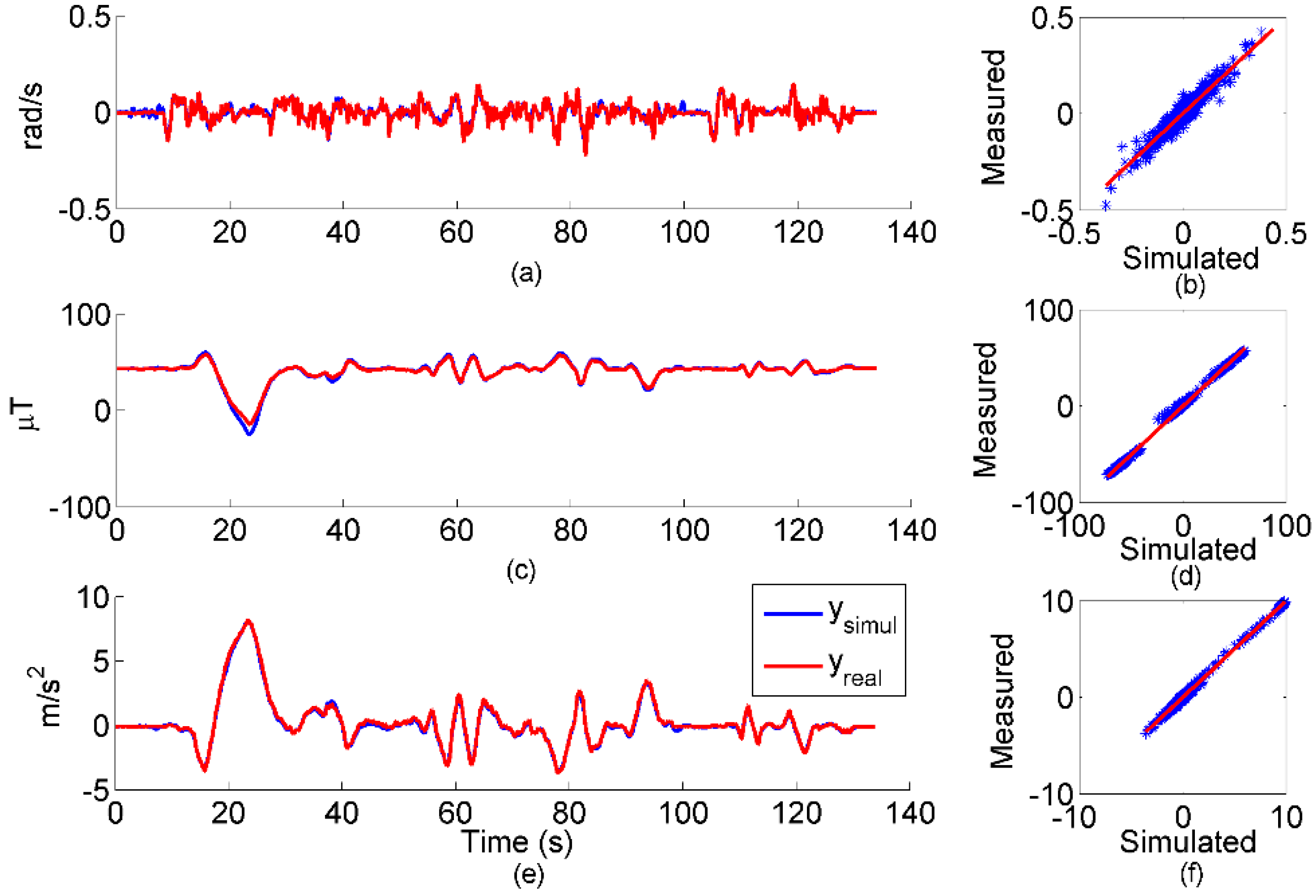
2.3.1. Simulation Environment Validation
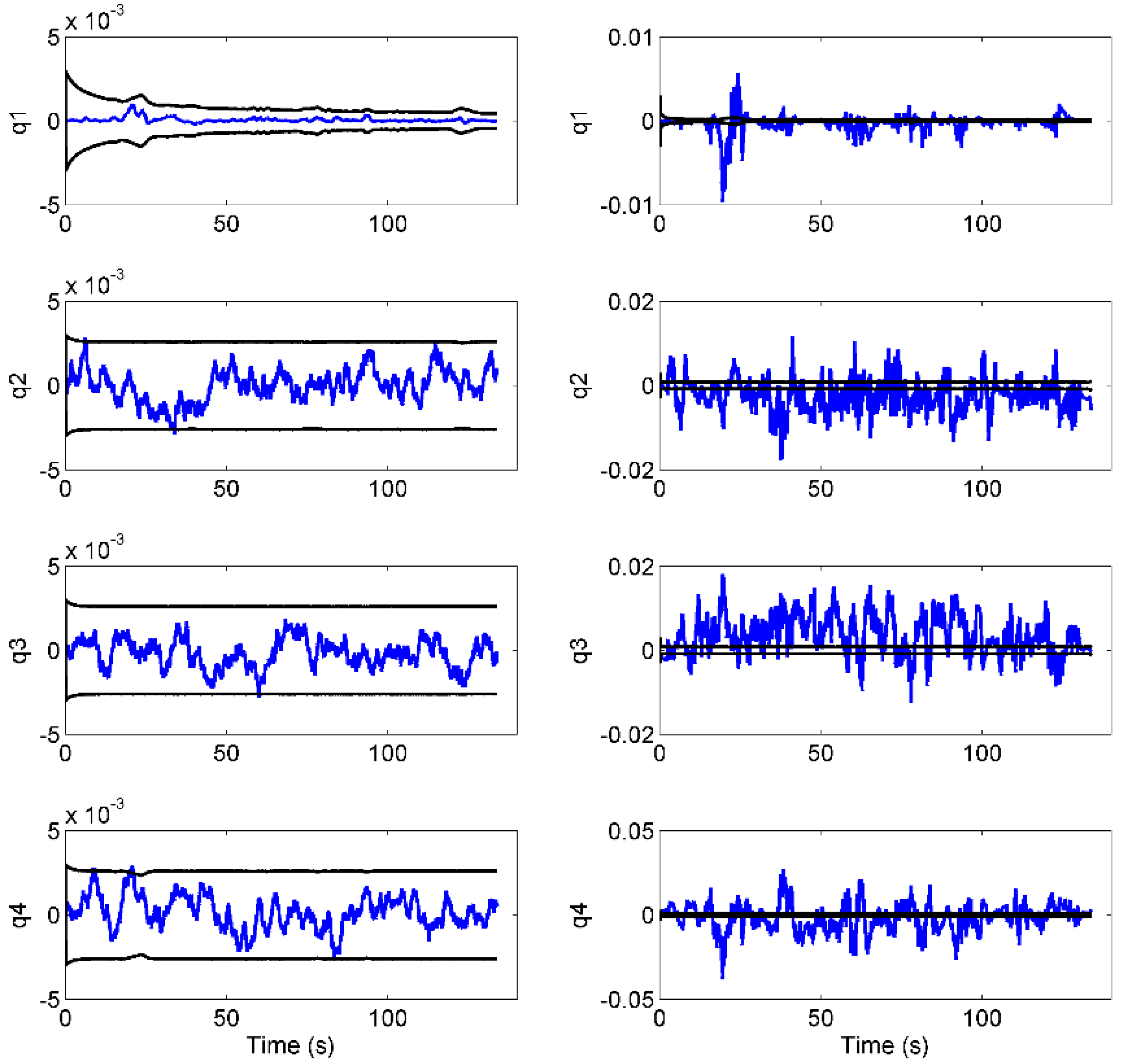
2.3.2. Case Study: EKF Consistency
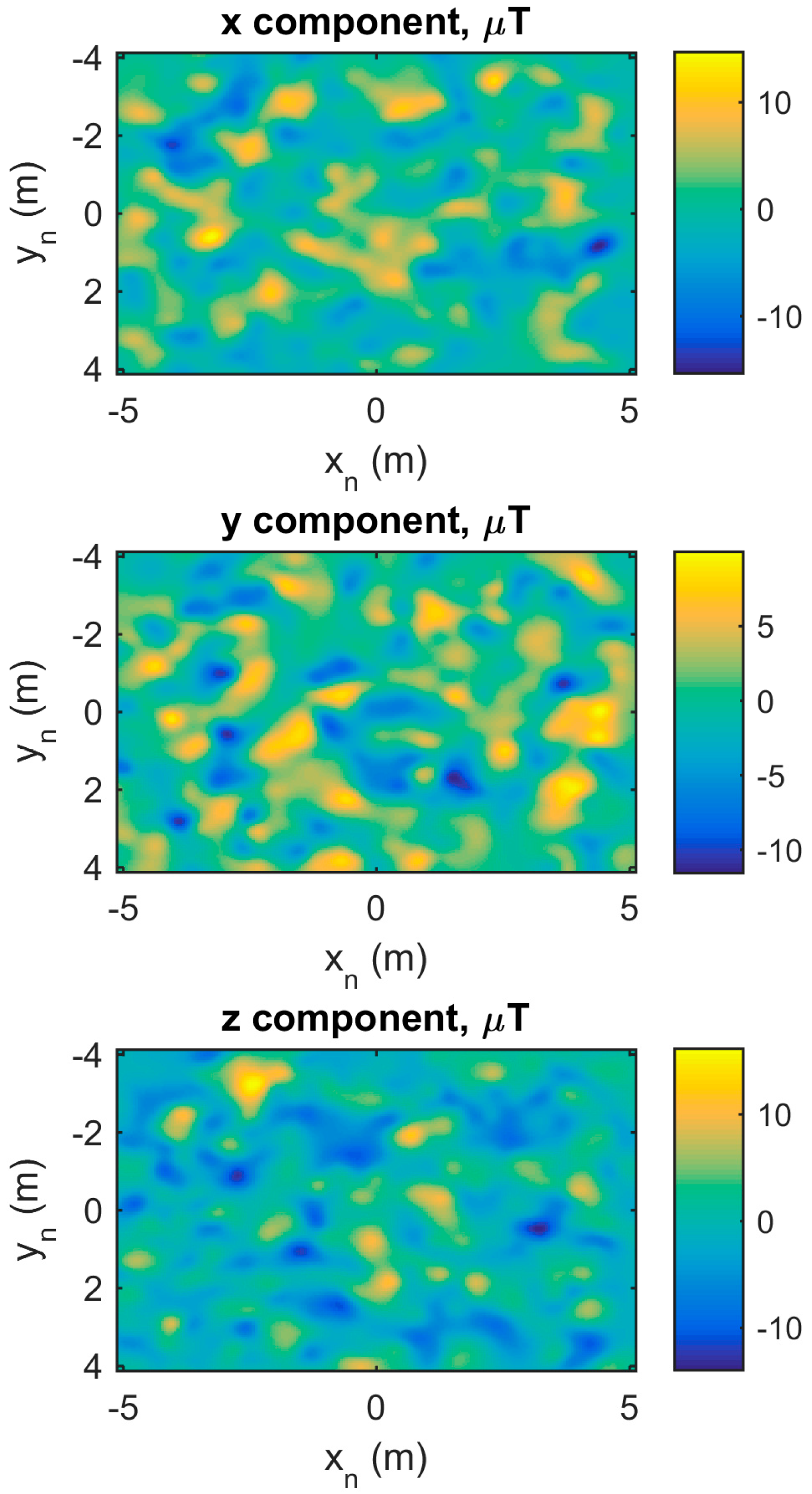
2.3.3. Simulated Distribution of Magnetic Disturbances
3. Results
3.1. Simulation Results
| Gyroscope | |||
|---|---|---|---|
| x | y | z | |
| RMSE (rad/s) | 0.03 | 0.02 | 0.02 |
| R | 0.97 | 0.90 | 0.97 |
| Magnetic Sensor | |||
| RMSE (µT) | 1.74 | 2.00 | 1.10 |
| R | 0.98 | 0.99 | 0.99 |
| Accelerometer | |||
| RMSE (m/s2) | 0.15 | 0.15 | 0.15 |
| R | 0.98 | 0.99 | 0.99 |
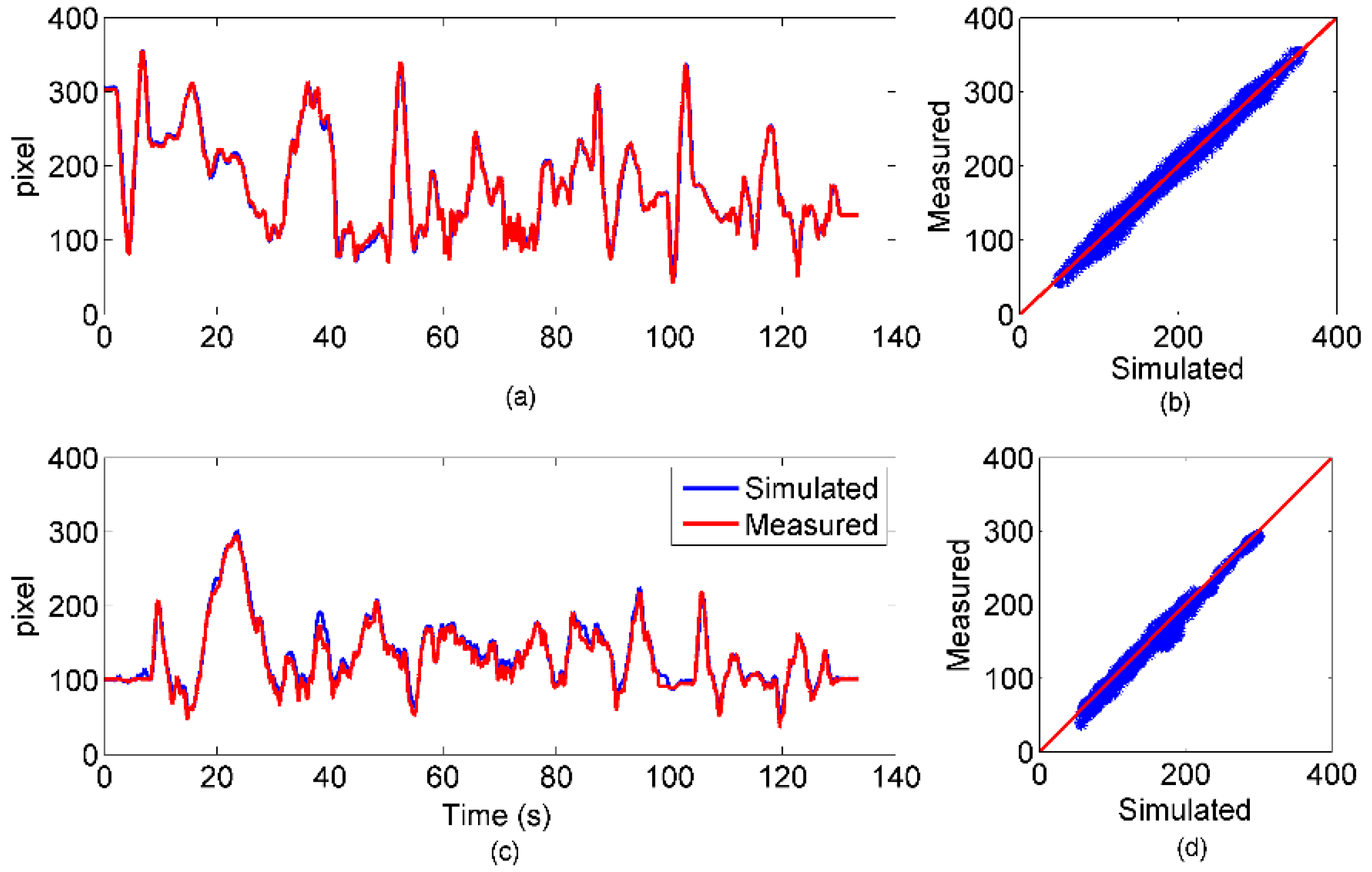
| x | y | |
|---|---|---|
| RMSE (pixel) | 7.62 (0.70) | 9.27 (0.99) |
| R | 0.99 (0.00) | 0.98 (0.00) |
3.2. EKF Results: Orientation Estimation and Filter Consistency
| RMSE Yaw (°) | RMSE Pitch (°) | RMSE Roll (°) | |
|---|---|---|---|
| Simulation | 0.11 | 0.10 | 0.12 |
| Real data | 0.53 | 0.63 | 0.96 |
3.3. Indoor Magnetic Disturbance Simulation
4. Discussions
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Camera-IMU-based localization: Observability analysis and consistency improvement. Int. J. Robot. Res. 2014, 33, 182–201. [Google Scholar] [CrossRef]
- Kelly, J.; Sukhatme, G.S. Visual-inertial sensor fusion: Localization, mapping and sensor-to-sensor self-calibration. Int. J. Robot. Res. 2011, 30, 56–79. [Google Scholar] [CrossRef]
- Himberg, H.; Motai, Y. Head orientation prediction: Delta quaternions versus quaternions. IEEE Trans. Syst. Man Cybern. B Cybern. 2009, 39, 1382–1392. [Google Scholar] [CrossRef] [PubMed]
- LaViola, J.J. A testbed for studying and choosing predictive tracking algorithms in virtual environments. In Proceedings of the Workshop on Virtual environments, Zurich, Switzerland, 22–23 May 2003; pp. 189–198.
- LaViola, J.J., Jr. A comparison of unscented and extended Kalman filtering for estimating quaternion motion. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 2435–2440.
- Parés, M.; Rosales, J.; Colomina, I. Yet another IMU simulator: Validation and applications. In Proceedings of the Eurocow, Castelldefels, Spain, 30 January–1 February 2008.
- Zampella, F.J.; Jiménez, A.R.; Seco, F.; Prieto, J.C.; Guevara, J.I. Simulation of foot-mounted IMU signals for the evaluation of PDR algorithms. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Guimaraes, Portugal, 21–23 September 2011; pp. 1–7.
- Young, A.D.; Ling, M.J.; Arvind, D.K. IMUSim: A simulation environment for inertial sensing algorithm design and evaluation. In Proceedings of the 2011 10th International Conference on Information Processing in Sensor Networks (IPSN), Chicago, IL, USA, 12–14 April 2011; pp. 199–210.
- Brunner, T.; Lauffenburger, J.-P.; Changey, S.; Basset, M. Magnetometer-Augmented IMU Simulator: In-Depth Elaboration. Sensors 2015, 15, 5293–5310. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, USA, 24–28 August 1981; pp. 674–679.
- Motai, Y.; Kosaka, A. Hand-eye calibration applied to viewpoint selection for robotic vision. IEEE Trans. Ind. Electron. 2008, 55, 3731–3741. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Eddins, S.L. Automated software testing for matlab. Comput. Sci. Eng. 2009, 11, 48–55. [Google Scholar] [CrossRef]
- Shuster, M.D. A survey of attitude representations. J. Astronaut. Sci. 1993, 41, 439–517. [Google Scholar]
- Gamma, E.; Helm, R.; Johnson, R.; Vlissides, J. Design Patterns: Elements of Reusable Object-Oriented Software; Pearson Education: New York, NY, USA, 1994. [Google Scholar]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Multi-magnetometer based perturbation mitigation for indoor orientation estimation. Navigation 2012, 58, 279–292. [Google Scholar] [CrossRef]
- Woodman, O.J. An Introduction to Inertial Navigation; Technical Report UCAMCL-TR-696; University of Cambridge, Computer Laboratory: Cambridge, UK, 2007; Volume 14, p. 15. [Google Scholar]
- Gebre-Egziabher, D.; Elkaim, G.; Powell, J.D.; Parkinson, B. A non-linear, two-step estimation algorithm for calibrating solid-state strapdown magnetometers. In Proceedings of the 8th International St. Petersburg Conference on Navigation Systems (IEEE/AIAA), St. Petersburg, Russia, 27–31 May 2001.
- Quinchia, A.G.; Falco, G.; Falletti, E.; Dovis, F.; Ferrer, C. A comparison between different error modeling of MEMS applied to GPS/INS integrated systems. Sensors 2013, 13, 9549–9588. [Google Scholar] [CrossRef] [PubMed]
- Bouguet, J.-Y. Camera Calibration Toolbox for Matlab. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 17 December 2015).
- Brown, D.C. Decentering distortion of lenses. Photom. Eng. 1966, 32, 444–462. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Sabatini, A.M. Estimating three-dimensional orientation of human body parts by inertial/magnetic sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Sabatini, A.M. Extended Kalman filter-based methods for pose estimation using visual, inertial and magnetic sensors: Comparative analysis and performance evaluation. Sensors 2013, 13, 1919–1941. [Google Scholar] [CrossRef] [PubMed]
- Lobo, J.; Dias, J. Relative pose calibration between visual and inertial sensors. Int. J. Robot. Res. 2007, 26, 561–575. [Google Scholar] [CrossRef]
- Bouguet, J.-Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker; Intel Corporation, Microprocessor Research Labs: Stanford, CA, USA, 2000. [Google Scholar]
- Frassl, M.; Angermann, M.; Lichtenstern, M.; Robertson, P.; Julian, B.J.; Doniec, M. Magnetic maps of indoor environments for precise localization of legged and non-legged locomotion. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 913–920.
- Angermann, M.; Frassl, M.; Doniec, M.; Julian, B.J.; Robertson, P. Characterization of the indoor magnetic field for applications in localization and mapping. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 2012; pp. 1–9.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ligorio, G.; Sabatini, A.M. A Simulation Environment for Benchmarking Sensor Fusion-Based Pose Estimators. Sensors 2015, 15, 32031-32044. https://doi.org/10.3390/s151229903
Ligorio G, Sabatini AM. A Simulation Environment for Benchmarking Sensor Fusion-Based Pose Estimators. Sensors. 2015; 15(12):32031-32044. https://doi.org/10.3390/s151229903
Chicago/Turabian StyleLigorio, Gabriele, and Angelo Maria Sabatini. 2015. "A Simulation Environment for Benchmarking Sensor Fusion-Based Pose Estimators" Sensors 15, no. 12: 32031-32044. https://doi.org/10.3390/s151229903
APA StyleLigorio, G., & Sabatini, A. M. (2015). A Simulation Environment for Benchmarking Sensor Fusion-Based Pose Estimators. Sensors, 15(12), 32031-32044. https://doi.org/10.3390/s151229903







