Multidirectional Image Sensing for Microscopy Based on a Rotatable Robot
Abstract
:1. Introduction
2. Experimental Section
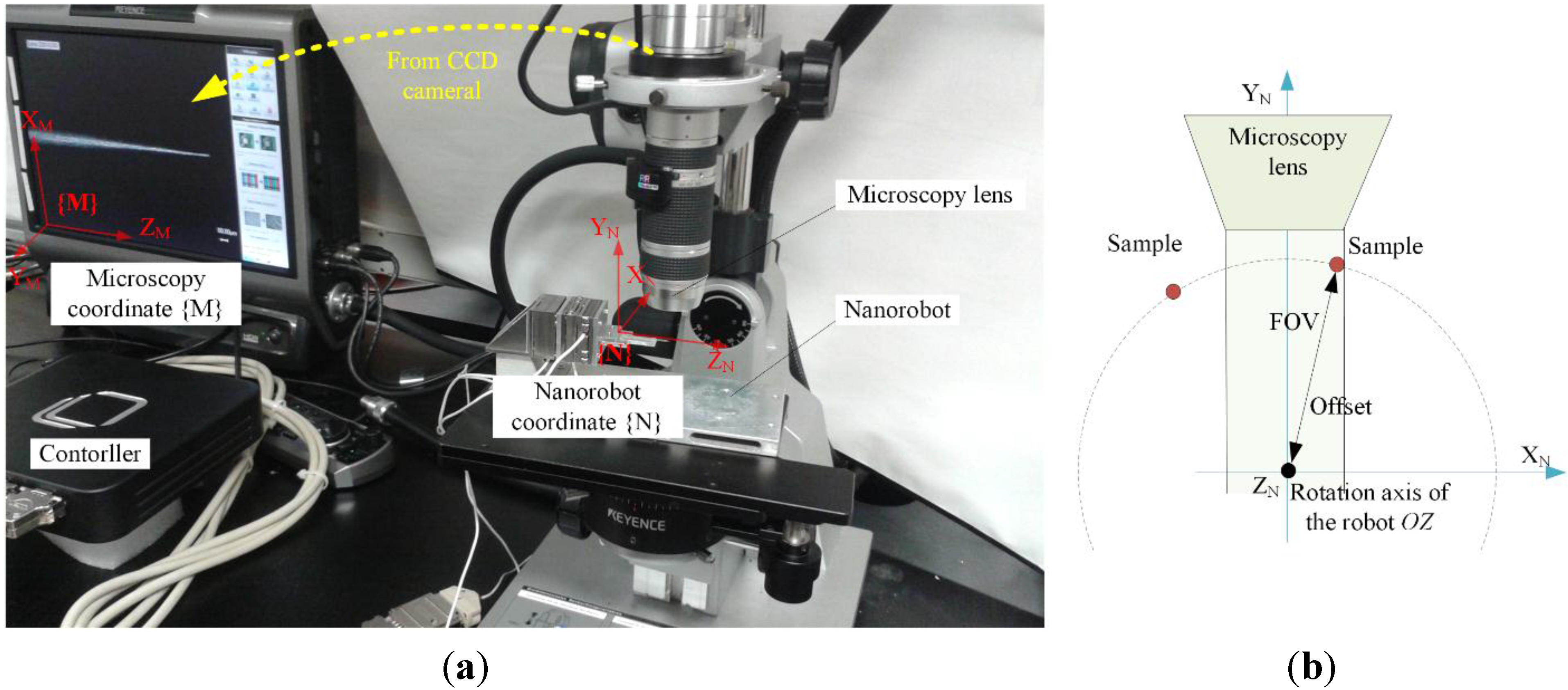
2.1. Robotic System

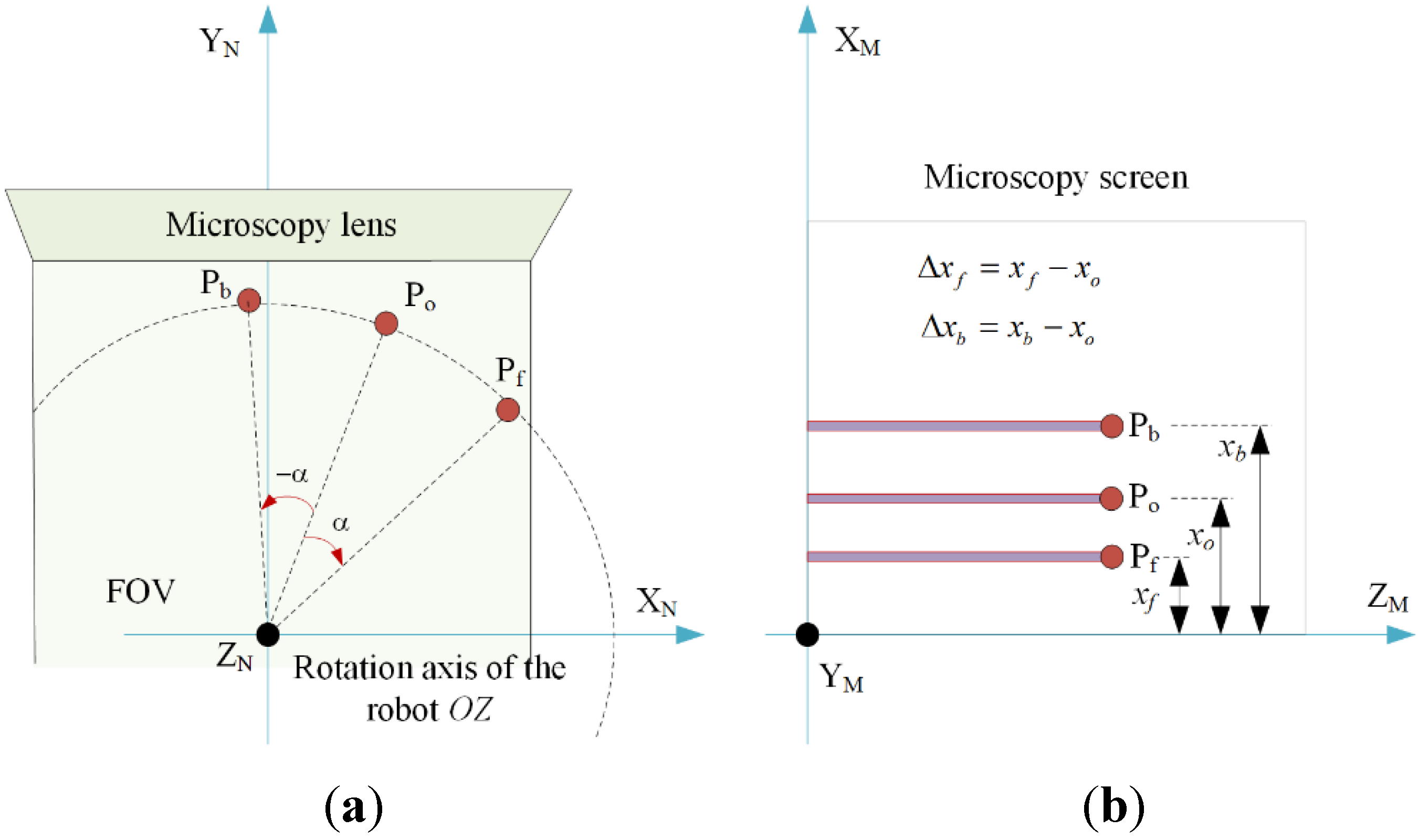
2.2. Sample Alignment
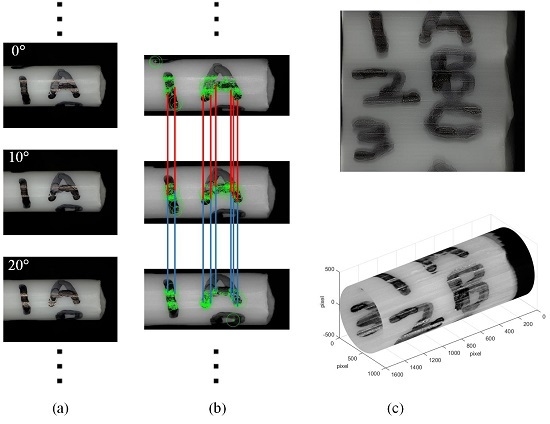
2.3. Multidirectional Imaging
2.3.1. Feature Matching
2.3.2. Image Matching
2.3.3. Bundle Adjustment
3. Result Display and Discussion
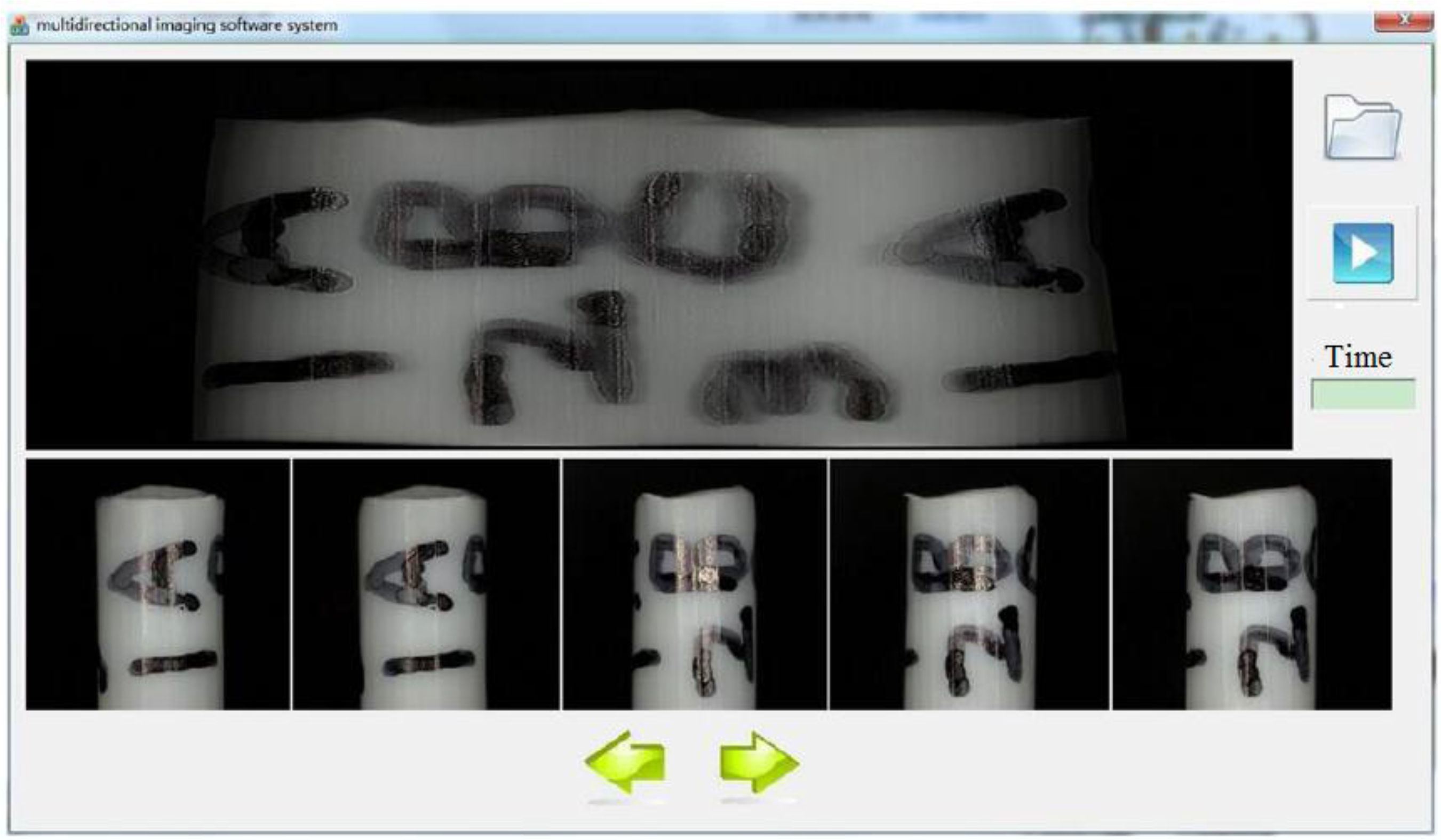
3.1. Multi-Directional Image Sensing Under an Optical Microscope
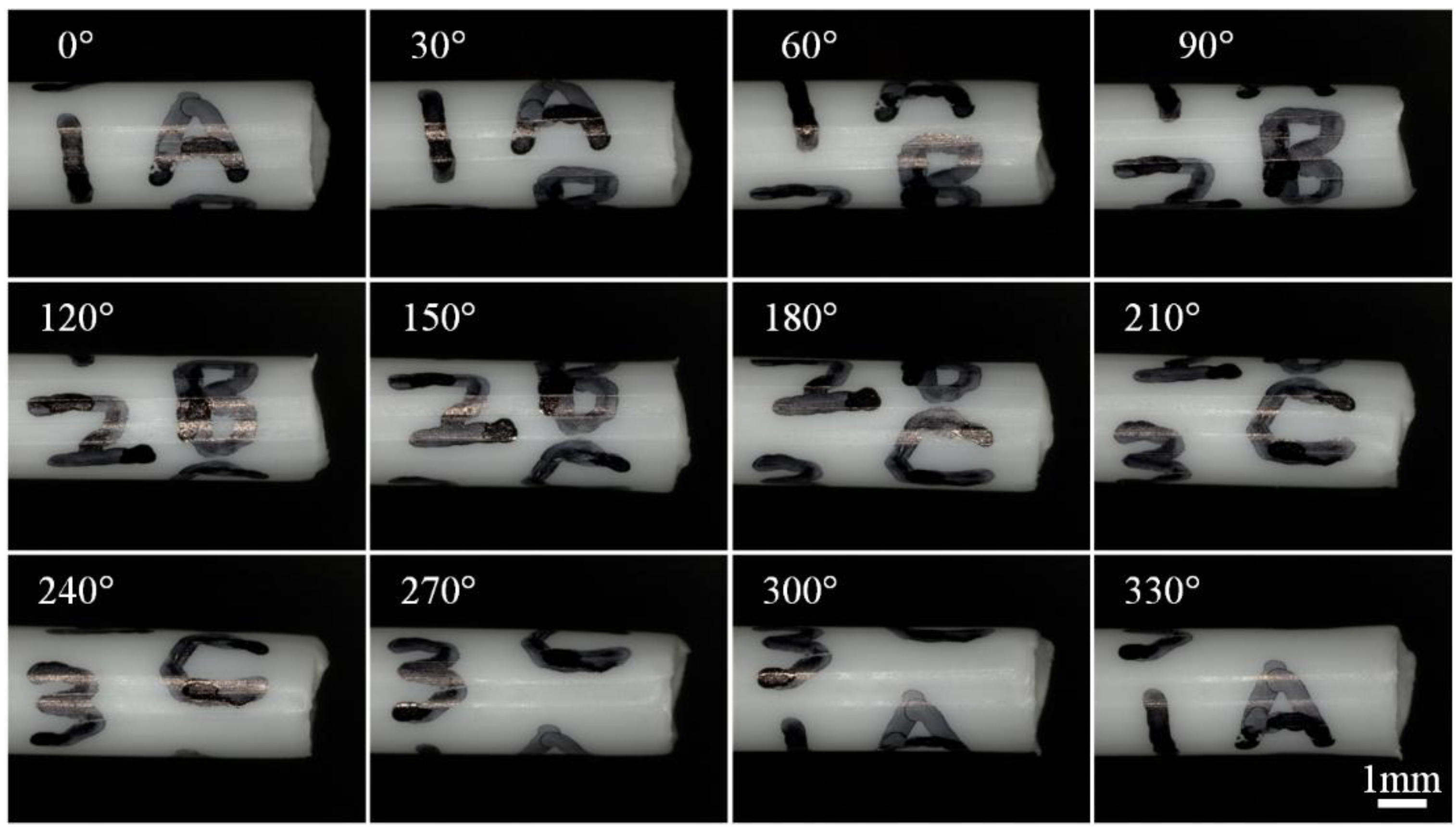
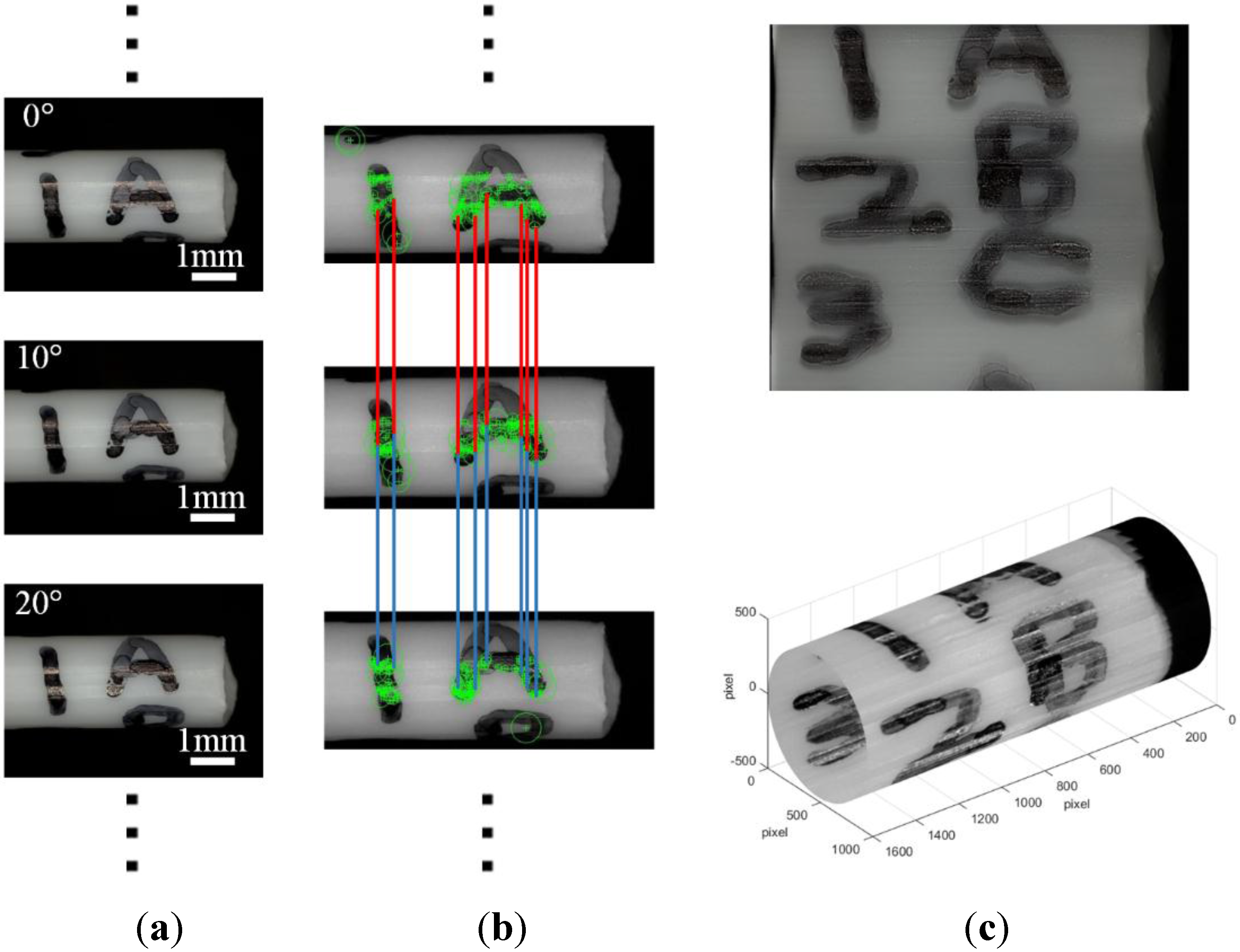
3.2. Multi-Directional Image Sensing under a Scanning Electron Microscope




3.3. Discussion
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Amano, T.; Terasawa, T.; Watanabe, H.; Toyoda, M.; Harada, T.; Watanabe, T.; Kinoshita, H. Observation of phase defect on extreme ultraviolet mask using an extreme ultraviolet microscope. J. Micro Nanolith. MEMS MOEMS 2014, 13. [Google Scholar] [CrossRef]
- Zhukov, A.; Shuvaeva, E.; Kaloshkin, S.; Churyukanova, M.; Kostitcyna, E.; Talaat, A.; Ipatov, M.; Gonzalez, J.; Zhukova, V. Studies of the defects influence on magnetic properties of glass-coated microwires. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Choi, S.; Kim, S.-K.; Lee, G.-J.; Park, H.-K. Paper-based 3D microfluidic device for multiple bioassays. Sens. Actuators B Chem. 2015, 219, 245–250. [Google Scholar] [CrossRef]
- Li, X.; Cheah, C.C. Robotic cell manipulation using optical tweezers with unknown trapping stiffness and limited fov. IEEE ASME Trans. Mechatron. 2015, 20, 1624–1632. [Google Scholar] [CrossRef]
- Saraee, M.B.; Korayem, M.H. Dynamic simulation and modeling of the motion modes produced during the 3D controlled manipulation of biological micro/nanoparticles based on the afm. J. Theor. Biol. 2015, 378, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Ocakoglu, K.; Mansour, S.A.; Yildirimcan, S.; Al-Ghamdi, A.A.; El-Tantawy, F.; Yakuphanoglu, F. Microwave-assisted hydrothermal synthesis and characterization of zno nanorods. Spectrochim Acta Part A Mol. Biomol. Spectrosc. 2015, 148, 362–368. [Google Scholar] [CrossRef] [PubMed]
- Pretzl, M.; Neubauer, M.; Tekaat, M.; Kunert, C.; Kuttner, C.; Leon, G.; Berthier, D.; Erni, P.; Ouali, L.; Fery, A. Formation and mechanical characterization of aminoplast core/shell microcapsules. ACS Appl. Mater. Inter. 2012, 4, 2940–2948. [Google Scholar] [CrossRef] [PubMed]
- Huisman, A.; Ploeger, L.S.; Dullens, H.F.J.; Poulin, N.; Grizzle, W.E.; van Diest, P.J. Development of 3D chromatin texture analysis using confocal laser scanning microscopy. Cell. Oncol. 2005, 27, 335–345. [Google Scholar] [PubMed]
- Roselli, L.; Paparella, F.; Stanca, E.; Basset, A. New data-driven method from 3D confocal microscopy for calculating phytoplankton cell biovolume. J. Microsc. 2015, 258, 200–211. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.J.; McCarron, T. Three-dimensional textural and chemical characterization of polyphase inclusions in spodumene using a dual focused ion beam-scanning electron microscope (FIB-SEM). Can. Mineral. 2011, 49, 541–553. [Google Scholar] [CrossRef]
- Heymann, J.A.W.; Hayles, M.; Gestmann, I.; Giannuzzi, L.A.; Lich, B.; Subramaniam, S. Site-specific 3D imaging of cells and tissues with a dual beam microscope. J. Struct. Biol. 2006, 155, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Lasker, K.; Dror, O.; Shatsky, M.; Nussinov, R.; Wolfson, H.J. Ematch: Discovery of high resolution structural homologues of protein domains in intermediate resolution cryo-em maps. IEEE ACM Trans. Comput. Biol. Bioinform. 2007, 4, 28–39. [Google Scholar] [CrossRef] [PubMed]
- Vonesch, C.; Wang, L.; Shkolnisky, Y.; Singer, A.; IEEE. Fast wavelet-based single-particle reconstruction in Cryo-EM. In Proceedings of the 2011 8th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; pp. 1950–1953.
- Loewke, K.; Camarillo, D.; Piyawattanametha, W.; Breeden, D.; Salisbury, K. Real-time image mosaicing with a hand-held dual-axes confocal microscope. Proc. SPIE 2008, 6851. [Google Scholar] [CrossRef]
- Iwabuchi, S.; Koh, J.-Y.; Wardenburg, M.; Johnson, J.D.; Harata, N.C. Light-microscope specimen holder with 3-axis rotation and small-angle control. J. Neurosci. Methods 2014, 221, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Shaw, P.J.; Agard, D.A.; Hiraoka, Y.; Sedat, J.W. Tilted view reconstruction in optical microscopy. Three-dimensional reconstruction of drosophila melanogaster embryo nuclei. Biophys. J. 1989, 55, 101–110. [Google Scholar] [CrossRef]
- Gavrilenko, V.P.; Karabanov, D.A.; Kuzin, A.Y.; Mityukhlyaev, V.B.; Mikhutkin, A.A.; Todua, P.A.; Filippov, M.N.; Baimukhametov, T.N.; Vasil’ev, A.L. Three-dimensional reconstruction of the surfaces of relief structures from stereoscopic images obtained in a scanning electron microscope. Meas. Tech. 2015, 58, 256–260. [Google Scholar] [CrossRef]
- Lockwood, W.D.; Reynolds, A.P. Use and verification of digital image correlation for automated 3-D surface characterization in the scanning electron microscope. Mater. Charact. 1999, 42, 123–134. [Google Scholar] [CrossRef]
- Bals, S.; Goris, B.; Liz-Marzán, L.M.; van Tendeloo, G. Three-dimensional characterization of noble-metal nanoparticles and their assemblies by electron tomography. Angew. Chem. Int. Ed. 2014, 53, 10600–10610. [Google Scholar] [CrossRef] [PubMed]
- Koster, A.J.; Ziese, U.; Verkleij, A.J.; Janssen, A.H.; de Jong, K.P. Three-dimensional transmission electron microscopy: A novel imaging and characterization technique with nanometer scale resolution for materials science. J. Phys. Chem. B 2000, 104, 9368–9370. [Google Scholar] [CrossRef]
- Bruns, T.; Schickinger, S.; Schneckenburger, H. Sample holder for axial rotation of specimens in 3D microscopy. J. Microsc. 2015, 260, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.X.; Zhang, L.; Kratochvil, B.E.; Shou, K.Y.; Nelson, B.J. Dual-chirality helical nanobelts: A novel linear-to-rotary motion converter. In Proceedings of MEMS 2008: 21st IEEE International Conference on Micro Electro Mechanical Systems, Technical Digest, Tucson, AZ, USA, 13–17 January 2008; pp. 148–151.
- Kratochvil, B.E.; Dong, L.X.; Zhang, L.; Nelson, B.J. Image-based 3D reconstruction using helical nanobelts for localized rotations. J. Microsc. Oxf. 2010, 237, 122–135. [Google Scholar] [CrossRef] [PubMed]
- Carlson, K.; Andersen, K.N.; Eichhorn, V.; Petersen, D.H.; Mølhave, K.; Bu, I.Y.Y.; Teo, K.B.K.; Milne, W.I.; Fatikow, S.; Bøggild, P. A carbon nanofibre scanning probe assembled using an electrothermal microgripper. Nanotechnology 2007, 18. [Google Scholar] [CrossRef]
- Changhai, R.; Yong, Z.; Yu, S.; Yu, Z.; Xueliang, S.; Hoyle, D.; Cotton, I. Automated four-point probe measurement of nanowires inside a scanning electron microscope. IEEE Trans. Nanotechnol. 2011, 10, 674–681. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, B.K.; Liu, J.; Zhou, C.; Anchel, D.; Li, X.; Ge, J.; Bazett-Jones, D.P.; Sun, Y. Fluorescence and SEM correlative microscopy for nanomanipulation of subcellular structures. Light Sci. Appl. 2014, 3. [Google Scholar] [CrossRef]
- Shen, Y.; Nakajima, M.; Yang, Z.; Kojima, S.; Homma, M.; Fukuda, T. Design and characterization of nanoknife with buffering beam for in situ single-cell cutting. Nanotechnology 2011, 22. [Google Scholar] [CrossRef] [PubMed]
- Murray, G. Rotation about an Arbitrary Axis in 3 Dimensions. Available online: http://inside.mines.edu/fs_home/gmurray/ArbitraryAxisRotation/ (accessed on 10 December 2015).
- Brown, M.; Lowe, D.G. Automatic panoramic image stitching using invariant features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Beis, J.S.; Lowe, D.G. Shape indexing using approximate nearest-neighbour search in high-dimensional spaces. In Proceedings of the 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, 17–19 June 1997; pp. 1000–1006.
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Triggs, B.; Zisserman, A.; Szeliski, R. Vision Algorithms: Theory and Practice: International Workshop on Vision Algorithms Corfu, Greece, September 21–22, 1999; Springer: Berlin, Germany, 2003. [Google Scholar]
- Fisheye Projections from Spherical Maps. Available online: http://paulbourke.Net/dome/2fish/ (accessed on 10 December 2015).
- Mai, W.; Zhang, L.; Gu, Y.; Huang, S.; Zhang, Z.; Lao, C.; Yang, P.; Qiang, P.; Chen, Z. Mechanical and electrical characterization of semiconducting zno nanorings by direct nano-manipulation. Appl. Phys. Lett. 2012, 101. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, S.; Deng, D.; Deng, S.; Chen, J.; Xu, N. Growth direction manipulation of few-layer graphene in the vertical plane with parallel arrangement. Carbon 2013, 56, 103–108. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Wan, W.; Zhang, L.; Yong, L.; Lu, H.; Ding, W. Multidirectional Image Sensing for Microscopy Based on a Rotatable Robot. Sensors 2015, 15, 31566-31580. https://doi.org/10.3390/s151229872
Shen Y, Wan W, Zhang L, Yong L, Lu H, Ding W. Multidirectional Image Sensing for Microscopy Based on a Rotatable Robot. Sensors. 2015; 15(12):31566-31580. https://doi.org/10.3390/s151229872
Chicago/Turabian StyleShen, Yajing, Wenfeng Wan, Lijun Zhang, Li Yong, Haojian Lu, and Weili Ding. 2015. "Multidirectional Image Sensing for Microscopy Based on a Rotatable Robot" Sensors 15, no. 12: 31566-31580. https://doi.org/10.3390/s151229872
APA StyleShen, Y., Wan, W., Zhang, L., Yong, L., Lu, H., & Ding, W. (2015). Multidirectional Image Sensing for Microscopy Based on a Rotatable Robot. Sensors, 15(12), 31566-31580. https://doi.org/10.3390/s151229872