UAVs Task and Motion Planning in the Presence of Obstacles and Prioritized Targets
Abstract
:1. Introduction
2. Problem Formulation
2.1. Example Scenario
2.2. Vehicles
- Vehicle kinematics:
- Turn rate constraint (given a minimum turn radius):
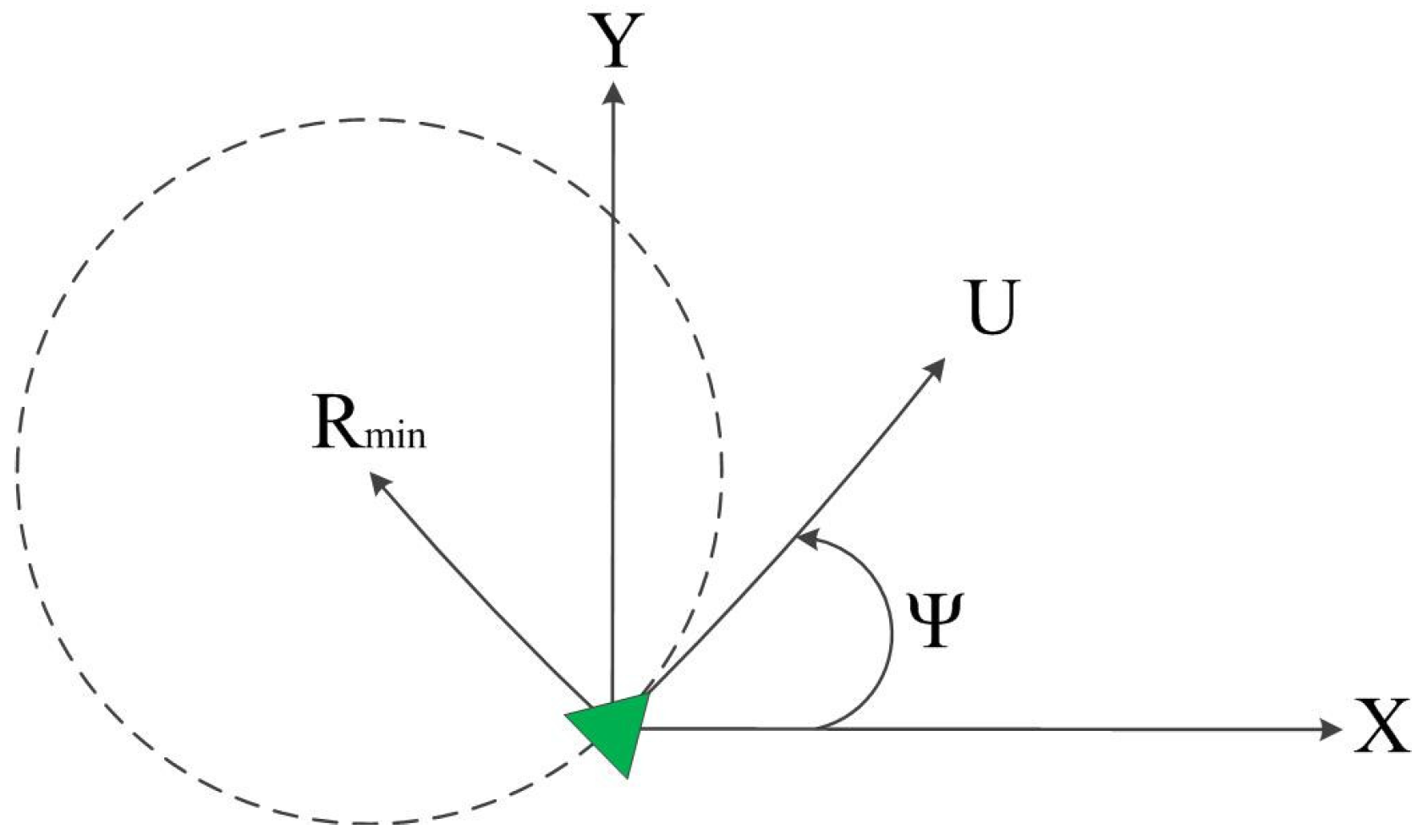
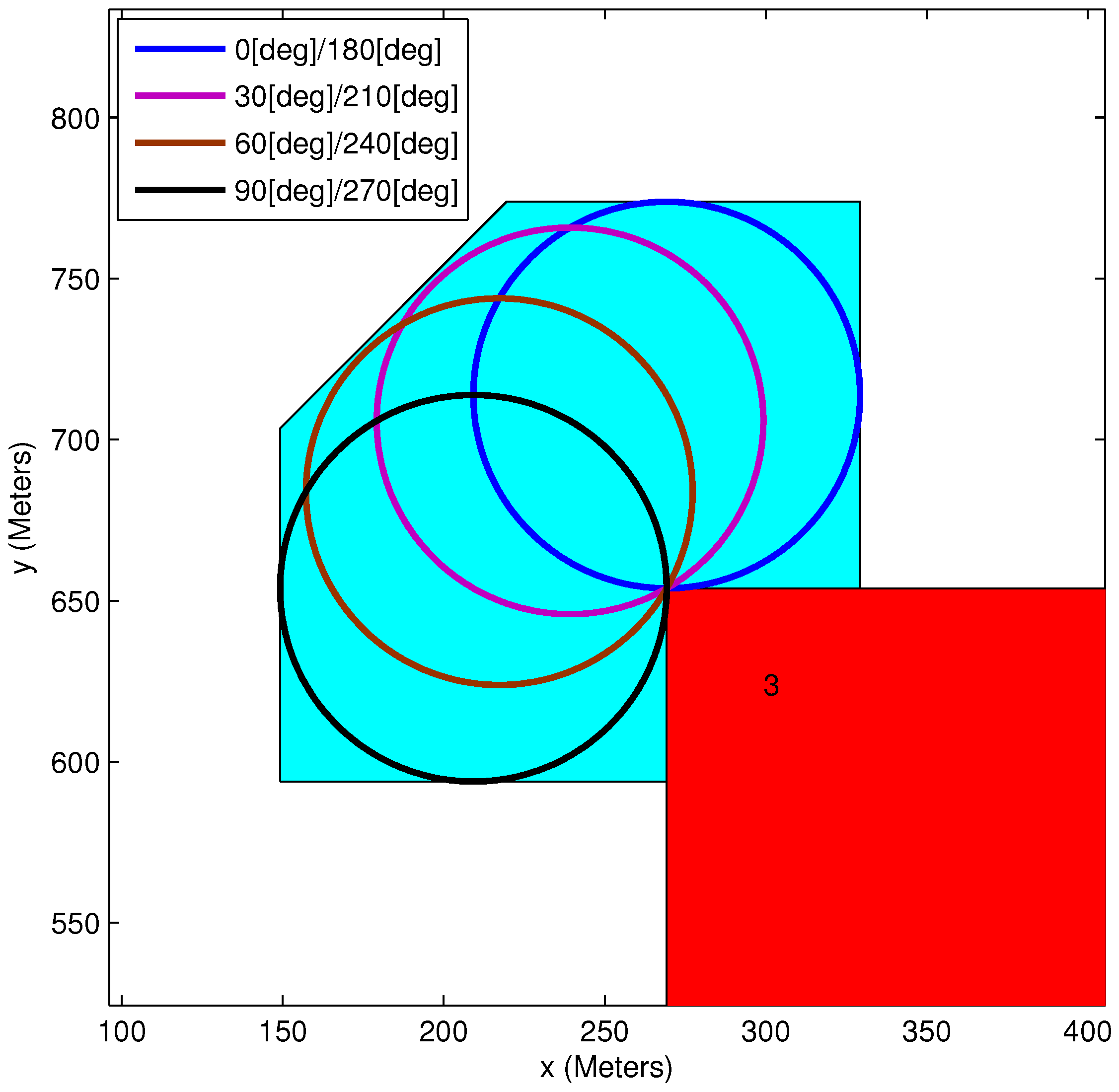
2.3. Body-Fixed Sensors
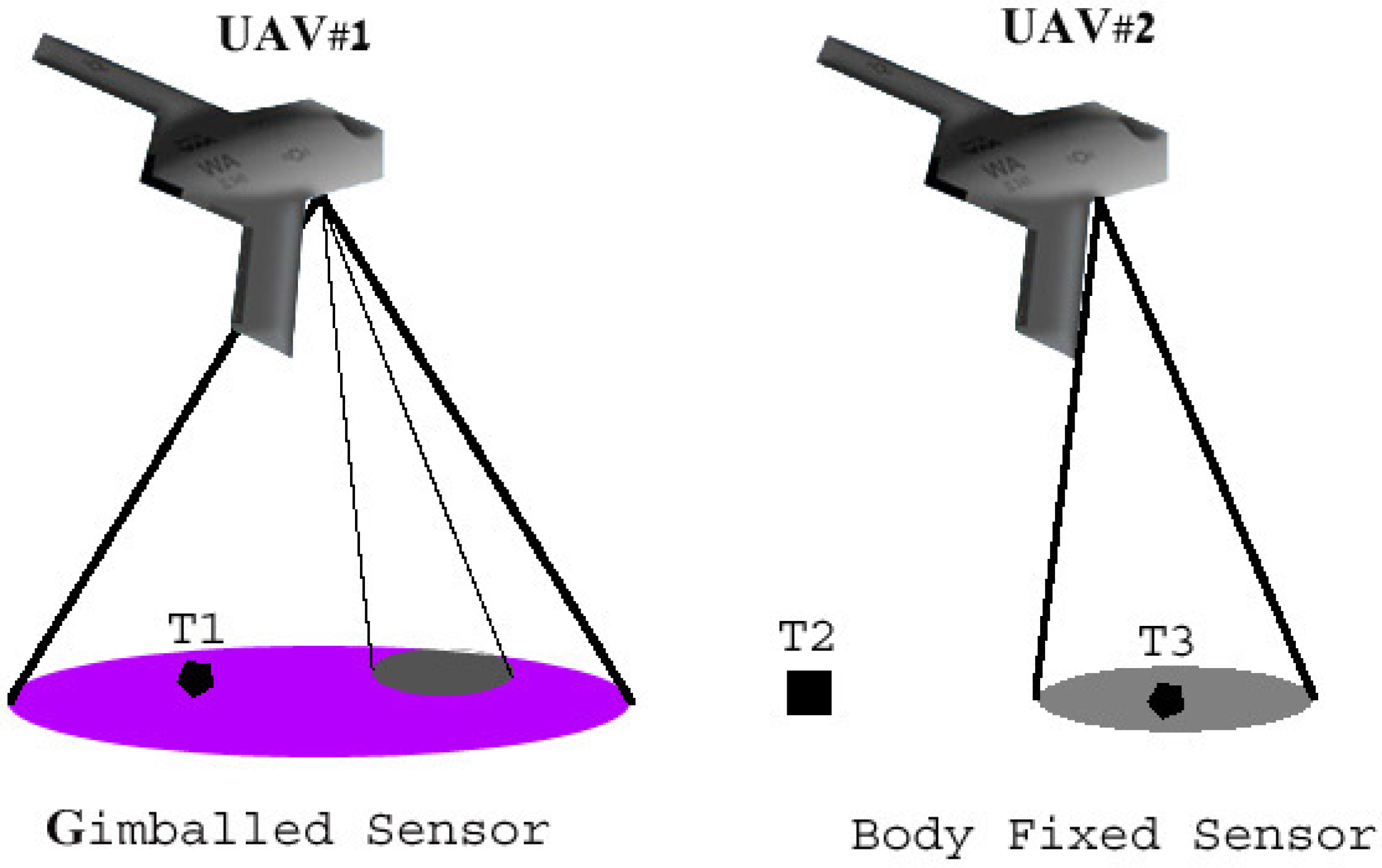
2.4. Obstacles
2.5. Targets and Benefits
2.6. Cost Function
3. Motion Planning
3.1. Tree Formulation
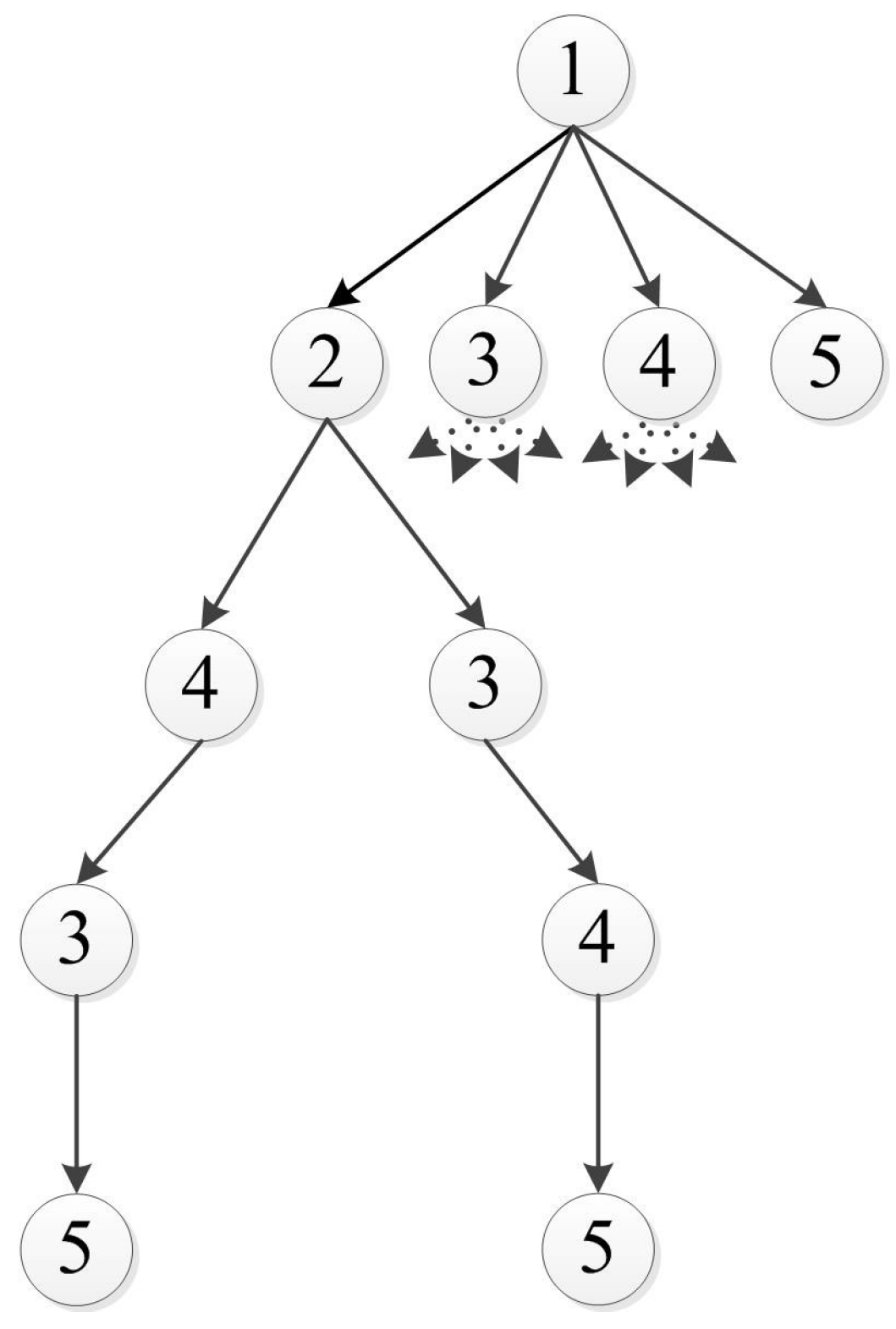
3.2. Path Elongation Algorithm
| Algorithm 1 Path elongation algorithm amidst obstacles. | |
| Input: Initial position and orientation of vehicle; vehicle speed; obstacle information; target position; path nodes position and orientation; path length; time constraint; | |
| Output: Vehicle trajectory (visit order and elongation circles node if needed) | |
| 1: | EvList ← generate a list of all elongation vertices in the environment |
| 2: | DpList ← Construct a sorted list of direct Dubins path vertices list |
| 3: | if EvList ∩ pathNodes ≠ then |
| 4: | elongationVertex ← EvList ∩ pathNodes |
| 5: | elongationNode ← elongationVertex |
| 6: | loiterCirclesNumber ←⌈(timeConstraint-(pathLength/VehicleSpeed))/2π⌉ |
| 7: | newVisitOrder ← path nodes |
| 8: | return newVisitOrder, elongationNode, loiterCirclesNumber |
| 9: | end if |
| 10: | for iPathNodes = 1 to nPathNodes do |
| 11: | intersectionCounter← checkCirclesIntersection[iPathNodes, obstaclesInfo] |
| 12: | if intersectionCounter ≠ then |
| 13: | elongationNode ← pathNodes |
| 14: | loiterCirclesNumber ←⌈(timeConstraint-(pathLength/VehicleSpeed))/2π⌉ |
| 15: | newVisitOrder ← path nodes |
| 16: | return newVisitOrder, elongationNode, loiterCirclesNumber |
| 17: | end if |
| 18: | end for |
| 19: | if DpList ∩ EvList ≠ then |
| 20: | newDplist=DpList ∩ EvList |
| 21: | for i = 1 to newDplistLength do |
| 22: | [newVisitOrder, newPathLength, newPathNodesAngles, intersectionCounter] ← |
| motionPlanningAlgo[vehicleConfiguration, newDplist, target, obstaclesInfo] | |
| 23: | if intersectionCounter= then |
| 24: | elongationNode ← newDplist |
| 25: | if timeConstraint > newPathLength/VehicleSpeed then |
| 26: | loiterCirclesNumber ←⌈(timeConstraint-(newPathLength/VehicleSpeed))/2π⌉ |
| 27: | end if |
| 28: | return newVisitOrder, elongationNode, loiterCirclesNumber |
| 29: | end if |
| 30: | end for |
| 31: | end if |
| 32: | sortedEvList ← euclideanSort[EvList] |
| 33: | for i = 1 to sortedEvListLength do |
| 34: | [newVisitOrder, newPathLength, newPathNodesAngles, intersectionCounter] ← |
| motionPlanningAlgo[vehicleConfiguration, sortedEvList, target, obstaclesInfo] | |
| 35: | if intersectionCounter= then |
| 36: | elongationNode ← sortedEvList |
| 37: | if timeConstraint > newPathLength then |
| 38: | loiterCirclesNumber ←⌈(timeConstraint-(newPathLength/VehicleSpeed))/2π⌉ |
| 39: | end if |
| 40: | return newVisitOrder, elongationNode, loiterCirclesNumber |
| 41: | end if |
| 42: | end for |


4. Task Assignment
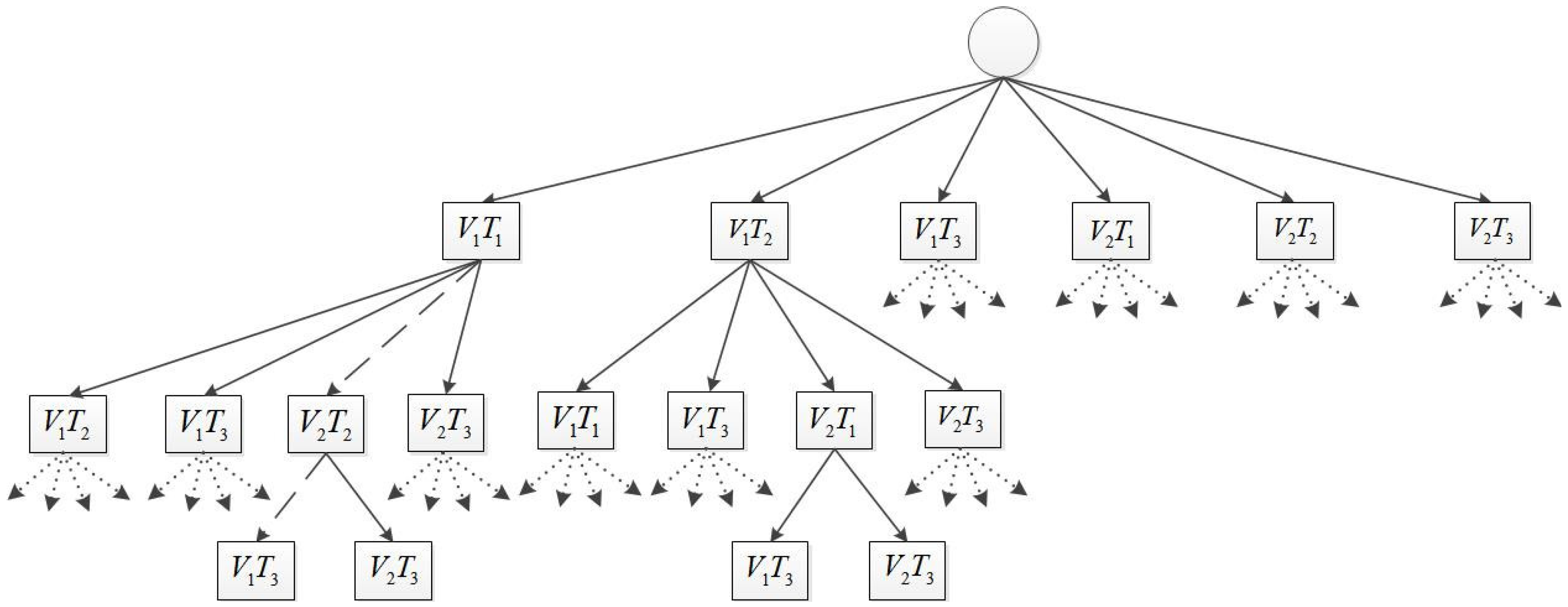
4.1. Exhaustive Task Assignment Algorithm
| Algorithm 2 Task assignment exhaustive search algorithm. | |
| Input: Vehicles’ initial configuration (V) and constant speed, targets’ position and their visit requirements (T), obstacle vertices’ positions, targets’ time constraints () | |
| Output: Assignment for each vehicle and the order in which the assigned targets needs to be visited | |
| 1: | UpperBound ← greedy task assignment algorithm solution |
| 2: | TargetsList ← } |
| 3: | TimeConstraint ← } |
| 4: | vehicleTargetList(i) ← [ ], |
| 5: | OpenSet ← [ ] |
| 6: | for do |
| 7: | for targetsToVisit do |
| 8: | node.vehiclePath(k) ← 0 , node.vehicleTargetsList ← [ ], |
| 9: | node.vehicle ← |
| 10: | node.vehicleTargetsList ← |
| 11: | node.vehiclePath=PathLength |
| 12: | if TimeConstraint < (node.vehiclePath/VehicleSpeed) then |
| 13: | node.vehiclePath=PathElongation |
| 14: | end if |
| 15: | node.cost ← lostBenefitFunction(PathLength) |
| 16: | node.targetsList ← targetsList |
| 17: | if node.targetsList then |
| 18: | if Cost(node) ≤ UpperBound then |
| 19: | UpperBound ← Cost(node.cost) |
| 20: | vehicleTargetsList(i) ← node.vehicleTargetsList |
| 21: | end if |
| 22: | else |
| 23: | OpenSet ← OpenSet ∪ node |
| 24: | end if |
| 25: | end for |
| 26: | end for |
| 27: | while OpenSet do |
| 28: | parentNode ← OpenSet(last entered node) – depth-first search |
| 29: | for parentNode.vehicle do |
| 30: | for targetsToVisit do |
| 31: | childNode.cost(k) ← parentNode.cost(k), |
| childNode.vehicleTargetsList ← parentNode.vehicleTargetsList, | |
| childNode.vehiclePath ← parentNode.vehiclePath, | |
| 32: | if TimeConstraint < (childNode.vehiclePath |
| +PathLength)/VehicleSpeed then | |
| 33: | PathLength=PathElongation |
| 34: | end if |
| 35: | childNode.vehiclePath=childNode.vehiclePath + PathElongation |
| 36: | childNode.cost(i) ← lostBenefitFunction(childNode.vehiclePath) |
| 37: | if Cost(childNode) ≤ UpperBound then |
| 38: | childNode.vehicle ← |
| 39: | childNode.vehicleTargetsList ← [childNode.vehicleTargetsList |
| 40: | childNode.targetsList ← parentNode.targetsList |
| 41: | if childNode.targetsList then |
| 42: | UpperBound ← Cost(childNode.cost) |
| 43: | vehicleTargetsList(i) ← childNode.vehicleTargetsList |
| 44: | else |
| 45: | OpenSet ← OpenSet ∪ childNode |
| 46: | end if |
| 47: | end if |
| 48: | end for |
| 49: | end for |
| 50: | OpenSet ← OpenSet ∖ parentNode |
| 51: | end while |
| 52: | return vehicleTargetsList |
4.2. Greedy Task Assignment Algorithm
| Algorithm 3 The heuristic greedy algorithm for task assignment. | |
| Input: Vehicles’ initial configuration (V) and constant speed, targets’ position and their visit requirements (T), obstacle vertices; positions, targets’ time constraint () | |
| Output: Vehicle target list - the targets assigned to each vehicle and the required visitation order. | |
| 1: | TargetsList ← | has a visit requirement} |
| 2: | TimeConstraint ← } |
| 3: | vehicleTargetsList(i) ← 0, |
| 4: | vehicleTotalBenefit(i) ← 0, |
| 5: | accumulatedPathLength(i) ← 0, |
| 6: | while TargetsList do |
| 7: | VehiclePath=PathLength, |
| 8: | if TimeConstraint < (VehiclePath+accumulatedPathLength)/VehicleSpeed then |
| 9: | PathLength=PathElongation |
| 10: | end if |
| 11: | VehicleBenefit ← BenefitFunction(PathLength+accumulatedPathLength), |
| 12: | VehicleBenefit |
| subject to: targetsList & vehicleTargetsList(i) | |
| 13: | vehicleTargetsList() ← [vehicleTargetsList() ] |
| 14: | VehiclePosition() ← VehiclePosition() |
| 15: | accumulatedPathLength ← accumulatedPathLength + PathLength |
| 16: | vehicleTotalBenefit ← vehicleTotalBenefit + VehicleBenefit |
| 17: | TargetsList ← TargetsList |
| 18: | end while |
| 19: | return vehicleTargetsList |
5. Simulation Results
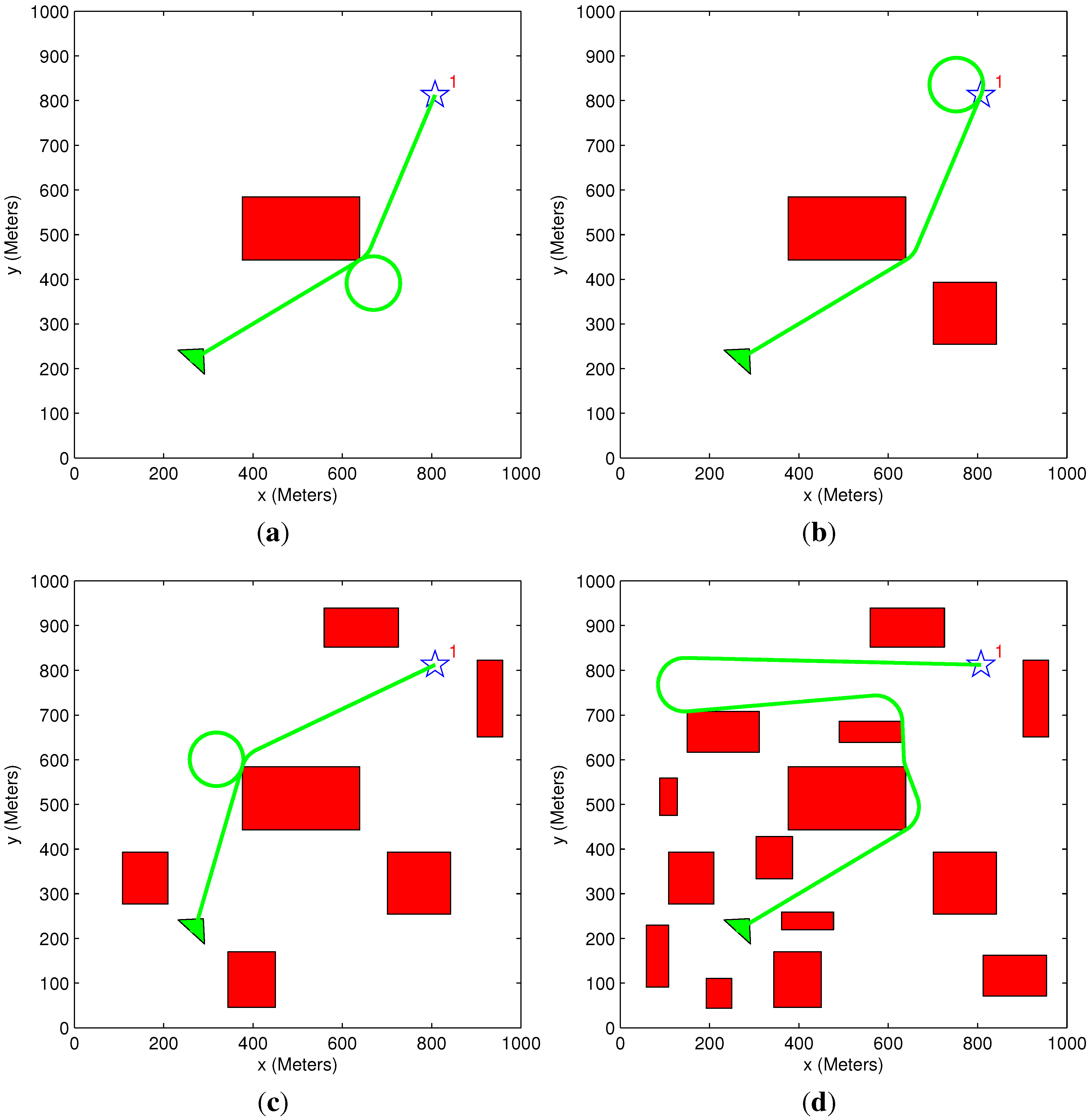
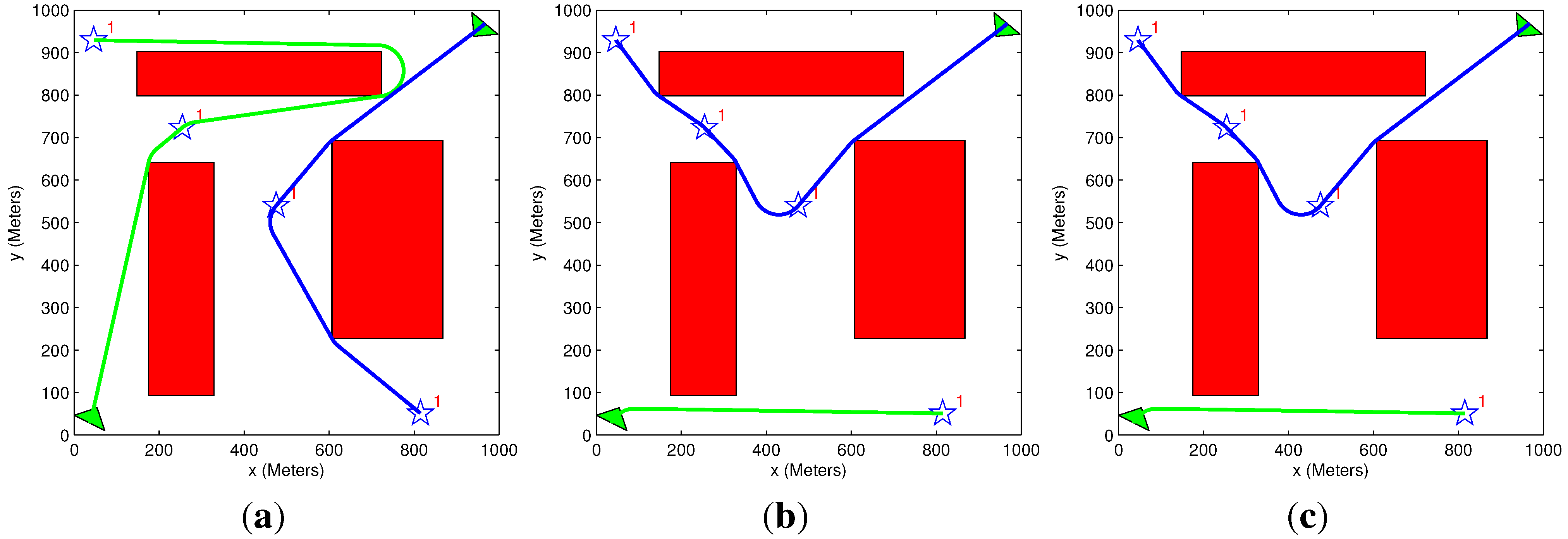
5.1. Path Elongation Algorithm Demonstration
| Figure # | Step # | Time Constraint (s) | Vehicle Trajectory Time (s) | Number of Cycles | Solution Time (s) |
|---|---|---|---|---|---|
| 9a | Step #1 | 2000 | 2357 | 4 | |
| 9b | Step #2 | 2000 | 2357 | 4 | |
| 9c | Step #3 | 2000 | 2011 | 3 | 0.45 |
| 9d | Step #4 | 2000 | 2072 | 0 | 4 |
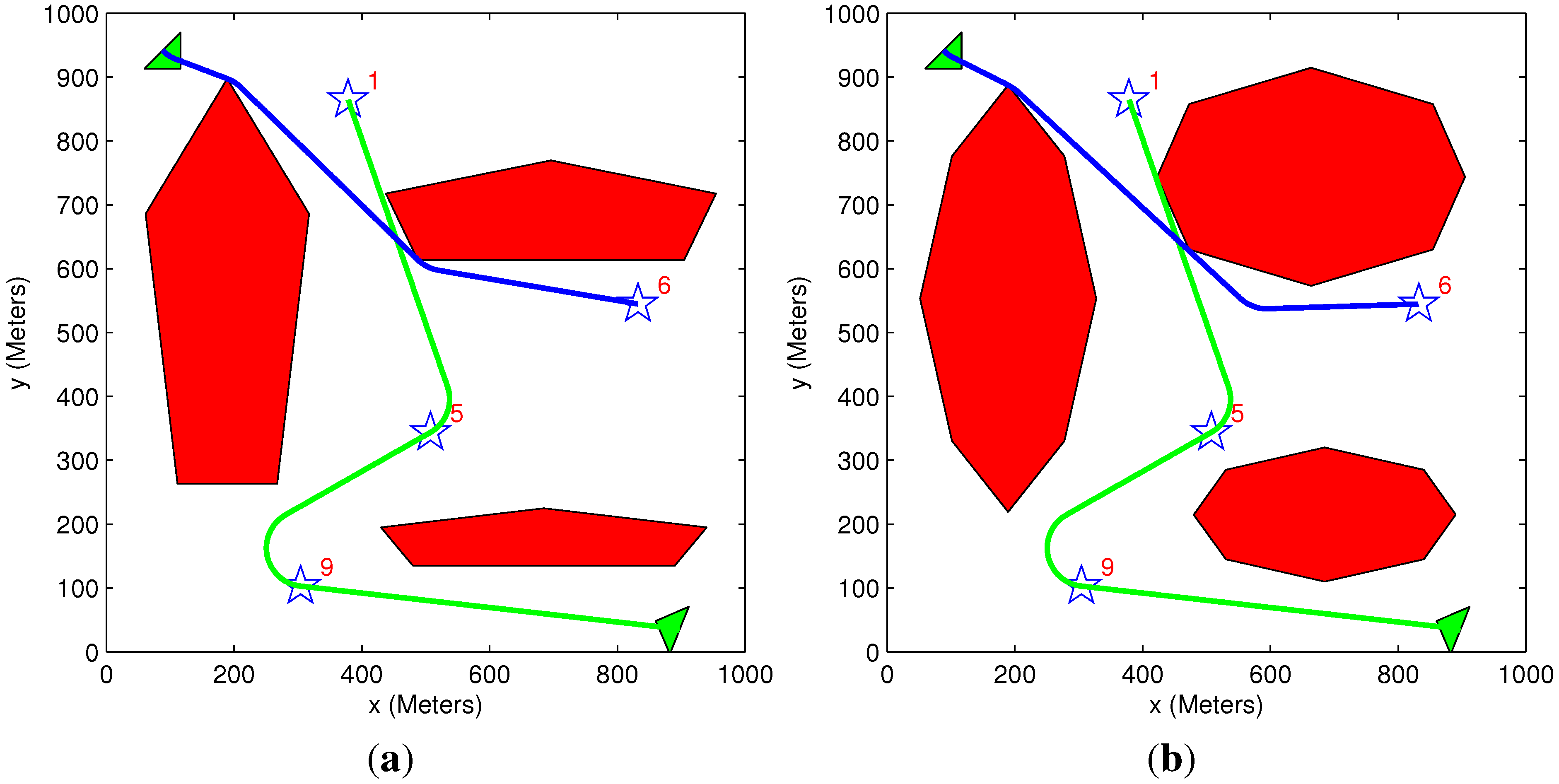
5.2. General Scenario
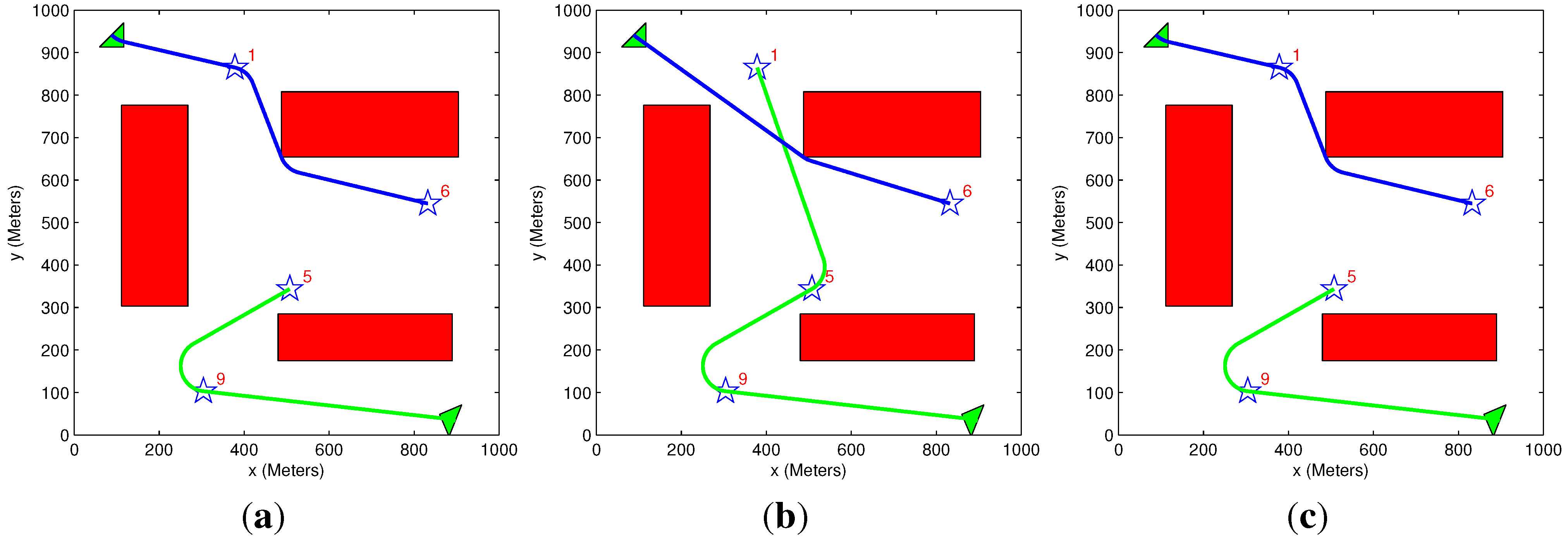
| Figure # | Algorithms Used | Initial Benefit | Acquired Benefit | Lost Benefit | Overall Distance | Solution Time (s) |
|---|---|---|---|---|---|---|
| 10a | Exhaustive TAExhaustive MP | 21,000 | 9918 | 11,082 | 1925 | 58.1 |
| 10b | Greedy TA Heuristic MP | 21,000 | 9537 | 11,463 | 2423 | 1.05 |
| 10c | Exhaustive TA Heuristic MP | 21,000 | 9918 | 11,082 | 1925 | 17.3 |
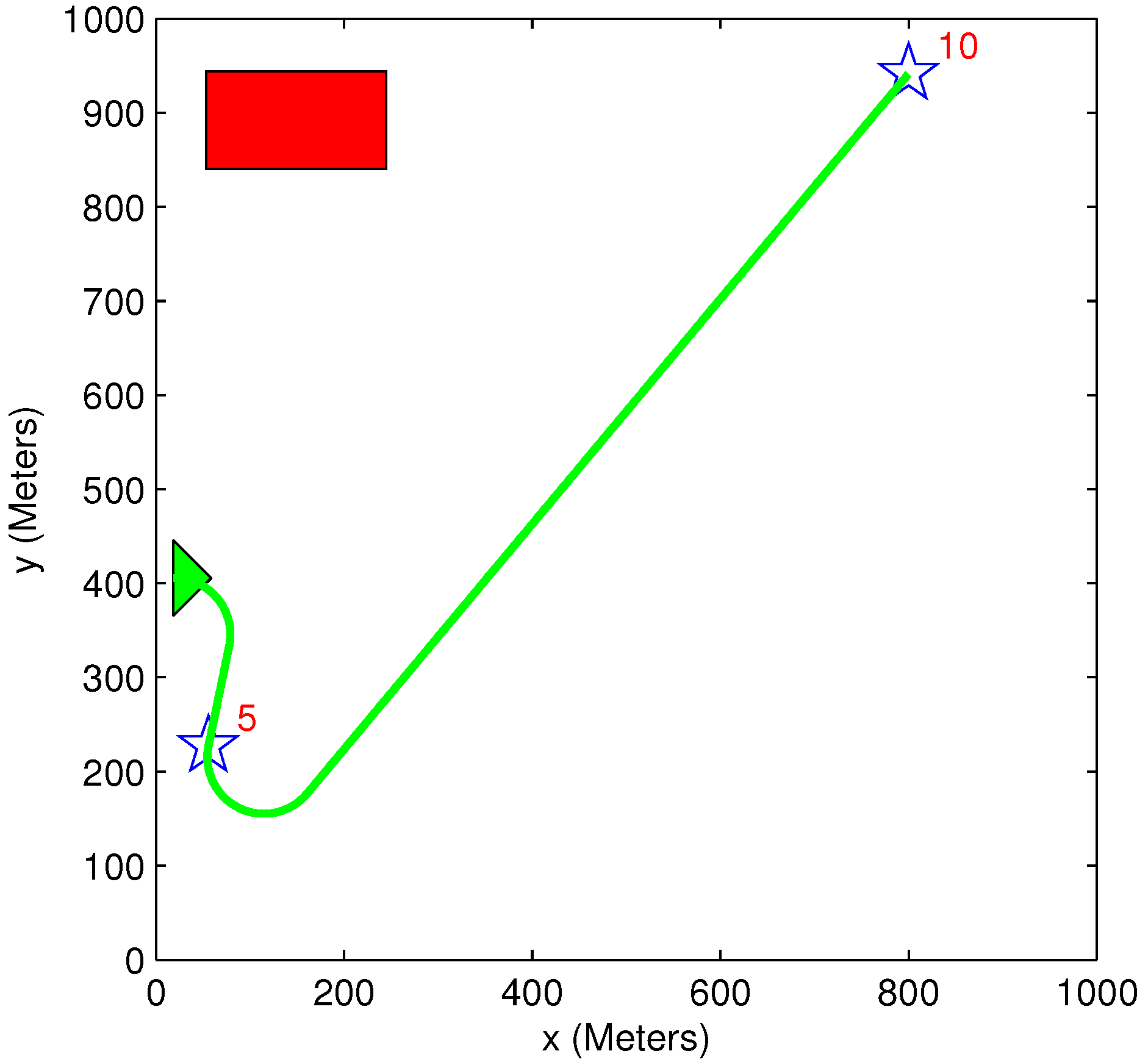
5.3. Equal Benefit Scenario
| Figure # | Algorithms Used | Initial Benefit | Acquired Benefit | Lost Benefit | Overall Distance | Solution Time (s) |
|---|---|---|---|---|---|---|
| 12a | Greedy TA Heuristic MP | 4000 | 1399 | 2601 | 3353 | 1.3 |
| 12b | Exhaustive TA Heuristic MP | 4000 | 1623 | 2377 | 2075 | 40.5 |
| 12c | Exhaustive TA Heuristic MP (Sum of path length cost function-Equation Equation (12)) | 4000 | 1623 | 2377 | 2075 | 40.5 |
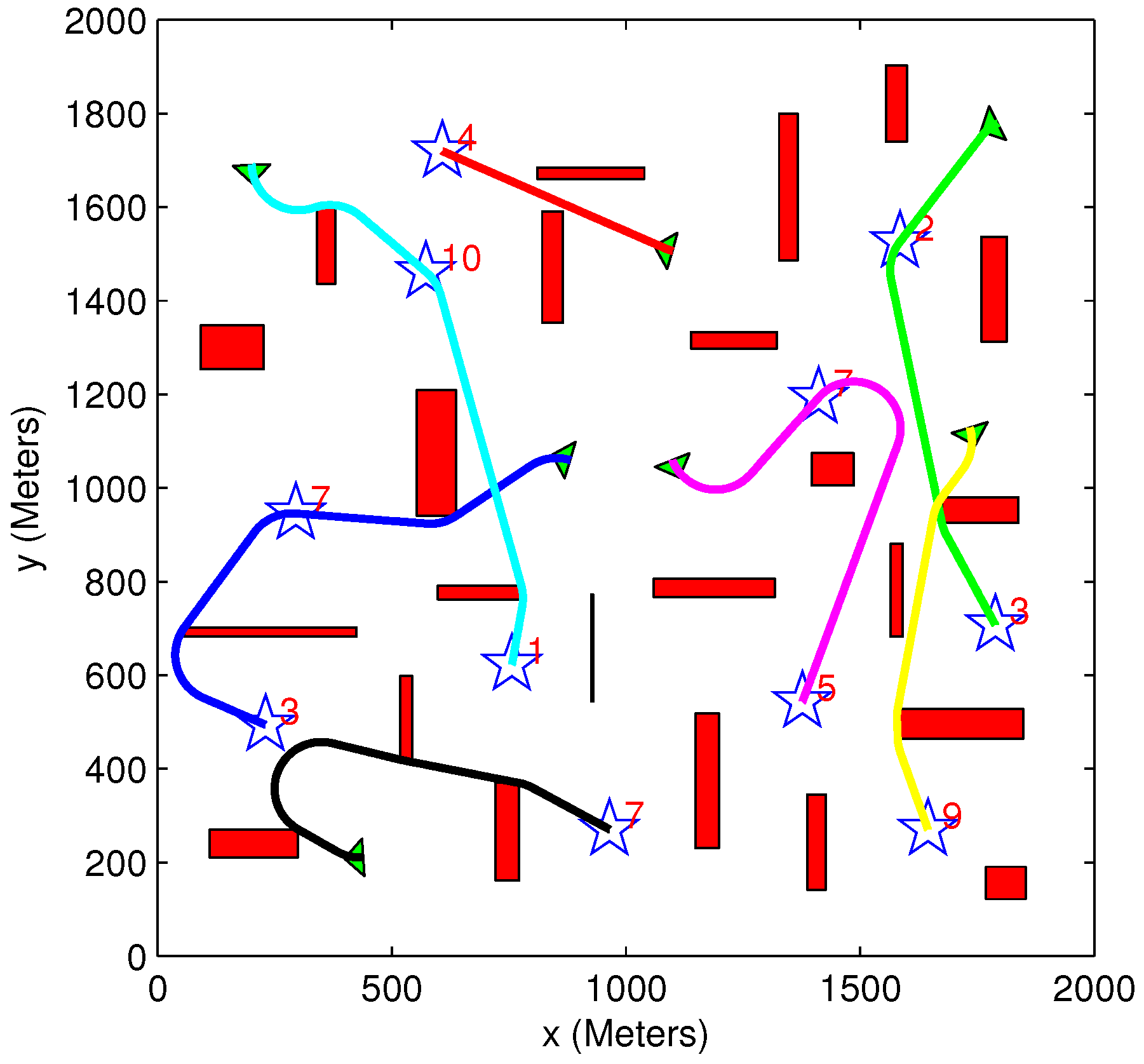
5.4. Comparing Exhaustive and Greedy Task Assignment Algorithms

| Figure # | Algorithms Used | Initial Benefit | Acquired Benefit | Lost Benefit | Overall Distance | Solution Time (s) |
|---|---|---|---|---|---|---|
| 13a | Greedy TA Heuristic MP | 29,000 | 20,120 | 8880 | 5340 | 5 |
| 13b | Exhaustive TA Heuristic MP | 29,000 | 18,050 | 10,950 | 3520 | 150 |
| Figure # | Algorithms Used | Initial Benefit | Acquired Benefit | Lost Benefit | Overall Distance | Solution Time (s) |
|---|---|---|---|---|---|---|
| 15 | Exhaustive TA Exhaustive MP | 15,000 | 6571 | 8529 | 1371 | 0.06 |
| 15 | Greedy TA Heuristic MP | 15,000 | 6571 | 8529 | 1371 | 0.016 |
| 16 | Exhaustive TA Exhaustive MP | 15,000 | 6634 | 8366 | 1333 | 0.06 |
| 16 | Greedy TA Heuristic MP | 15,000 | 6634 | 8366 | 1333 | 0.015 |
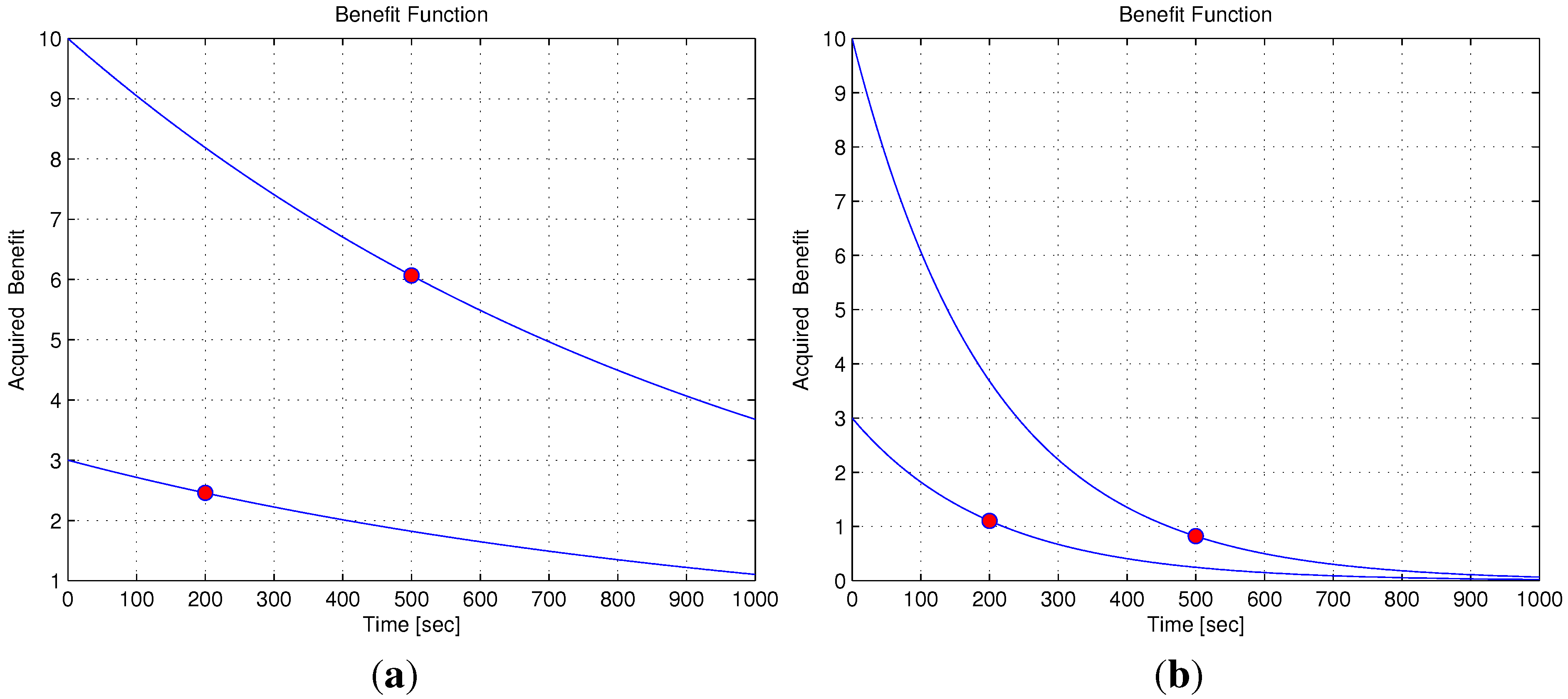
5.5. Benefit Time Dependency
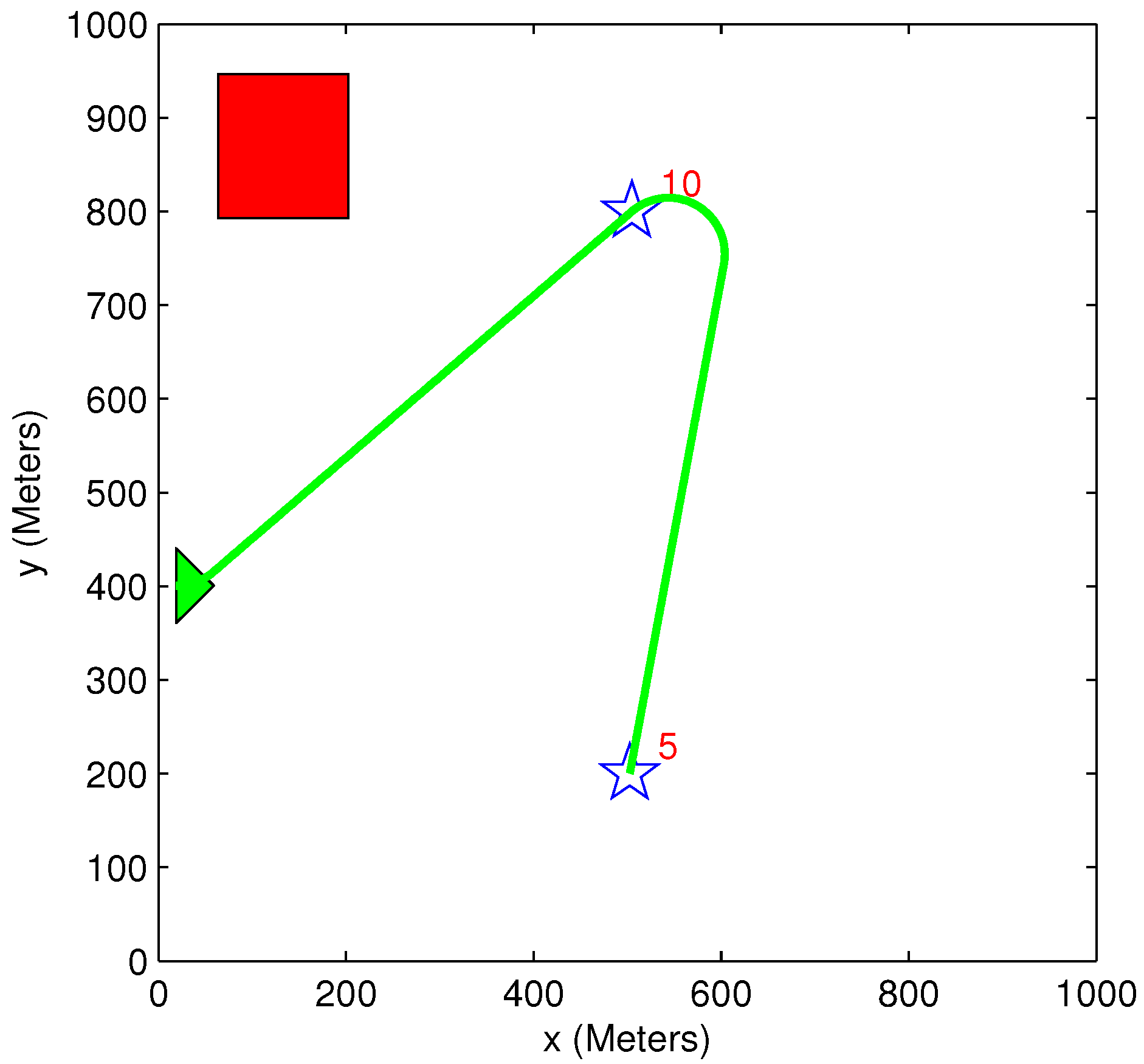
5.6. Benefit Descent Rate
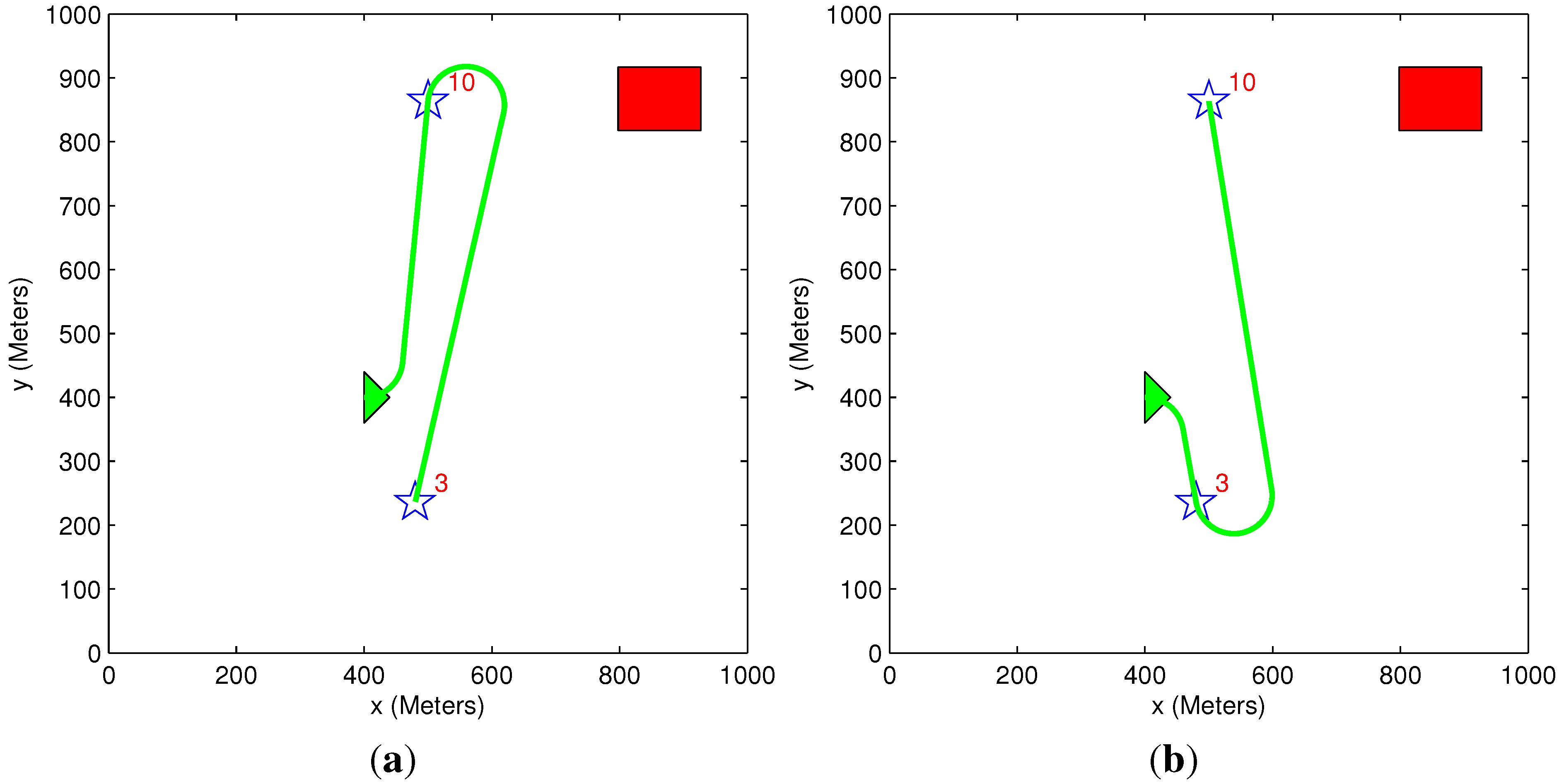
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A. Heuristic Motion Planning Algorithm
- The vehicle is assumed to be located and oriented according to the initial configuration. A visit order list is initialized to null set (Line 1).
- The following Steps 3–7 are repeated until the entire targets’ set is visited (Line 2).
- The next point of the visit is chosen as until an obstacle-free relaxed path is found from the current point to the next target in the ordered targets’ set (Line 4).
- is the node with the following property: the sum of the relaxed path length (connecting the vehicle’s current configuration and ) and the shortest Euclidean distance (connecting and the current target) is minimum (Line 5).
- The node is added to the visit order list (Line 6).
- The vehicle is assumed to be located at node (Line 7).
- The current orientation angle becomes the arrival angle at of the relaxed path from the previous point to (Line 8).
| Algorithm A1 Heuristic algorithm for motion planning of a Dubins vehicle amidst obstacles and multiple targets. | |
| Input: Initial position and orientation of vehicle; obstacle information; ordered targets | |
| Output: Vehicle trajectory (visit order) | |
| 1: | Initialize: currentPosition ← startPosition; currentOrientation ← startOrientation; visitOrderList ← [ ] |
| 2: | for iTarget = 1 to nTargets do |
| 3: | ← currentPosition |
| 4: | while do |
| 5: | ← (RelaxedPath(currentPosition,currentOrientation,n) + |
| ShortestEuclideanDistance(n,iTarget)) | |
| subject to: relaxed path from currentPosition to n is obstacle free | |
| 6: | visitOrderList ← [visitOrderList ] |
| 7: | currentPosition ← |
| 8: | currentOrientation ← final angle of relaxed path from currentPosition to |
| 9: | end while |
| 10: | end for |
B. Exhaustive Motion Planning Algorithm
- Calculate the initial upper bound, using the heuristic algorithm (Line 1).
- An OPEN list is generated to store the nodes that will be examined as the next node to visit.
- The initial configuration is entered to OPEN as a node (Line 3).
- The node with the lowest cost in OPEN (minimum relaxed path connecting the initial configuration and the node) is selected as the current node (Line 5).
- The neighbors of the current node that can come after it in the visit order are examined (Line 7). Their estimated distance is defined as the sum of the following (Line 8):
- (a)
- Cost of the selected node.
- (b)
- Relaxed path length connecting the selected node and the neighbor.
- (c)
- Euclidean distance between the neighbor and the current target to visit.
- (d)
- The total Euclidean distance that connects the current target and the remaining targets to visit in the targets’ set in the required order.
- The neighbors with an estimated distance that is lower than the current upper bound are added to OPEN as new nodes (Lines 9–10).
- All of the new nodes added to OPEN are examined.
- (a)
- In the case a new node is the next target to visit, the target is marked as visited in the current explored branch (Line 12).
- (b)
- In the case a new node is the last target to visit and the entire targets’ set is visited in the required order, a leaf node of the branch is reached, and the entire branch is explored (Line 13).
- The upper bound is updated to the relaxed path total length described by the nodes in the branch, and the visit order of the nodes is stored (Lines 14–15).
- The current node is removed from OPEN, since all of the neighbors have been evaluated (Line 23).
- This process is repeated until the OPEN list is empty.
| Algorithm B1 An exhaustive search algorithm for the motion planning of a Dubins/Reeds–Shepp vehicle amidst obstacles. | |
| Input: Initial position and orientation of vehicle, obstacle information and ordered waypoints | |
| Output: Minimum length vehicle trajectory (visit order) and its length | |
| 1: | UPPER ← upper bound on the path length obtained from heuristic |
| 2: | initialNode.{position ← initial position, angle ← initial orientation, vertex ← 0, |
| targetsVisited ← 0, visitOrder ← [ ], cost ← 0} | |
| 3: | OPEN ← initialNode |
| 4: | while notEmpty(OPEN) do |
| 5: | currNode ← OPEN.cost |
| 6: | nextTarget ← currNode.targetsVisited+1 |
| 7: | for iNode = [nextTarget obstacleVertices] do |
| 8: | pathLengthEstimate ← currNode.cost |
| + relaxedLength(currNode.{position,angle},iNode) | |
| + EuclideanDistance(iNode,nextTarget) | |
| + EuclideanDistanceCostToGo(nextTarget) | |
| 9: | if pathLengthEstimate < UPPER then |
| 10: | newNode.{position ← position(iNode), |
| angle ← arrival angle of relaxed path at iNode, | |
| vertex ← iNode, visitOrder ← [currNode.visitOrder iNode], | |
| cost ← currNode.cost | |
| + relaxedLength(currNode.{position,angle},iNode)} | |
| 11: | if iNode = nextTarget then |
| 12: | newNode.targetsVisited ← nextTarget |
| 13: | if iNode = lastTarget then |
| 14: | UPPER ← newNode.cost |
| 15: | visitOrder ← newNode.visitOrder |
| 16: | end if |
| 17: | else |
| 18: | newNode.targetsVisited ← currNode.targetsVisited |
| 19: | end if |
| 20: | OPEN ← OPEN ∪ newNode |
| 21: | end if |
| 22: | end for |
| 23: | OPEN ← OPEN ∖ currNode |
| 24: | end while |
References
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- LaValle, M.S. Planning Algorithms; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Shima, T.; Rasmussen, J. UAV Cooperative Decision and Control: Challenges and Practical Approaches; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Enright, J.; Savla, K.; Frazzoli, E.; Bullo, F. Stochastic and Dynamic Routing Problems for Multiple Uninhabited Aerial Vehicles. AIAA J. Guid. Control Dyn. 2009, 32, 1152–1166. [Google Scholar] [CrossRef]
- Shanmugavel, M.; Tsourdos, A.; Zbikowski, R.; White, B. Path Planning of Multiple UAVs Using Dubins Sets. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Francisco, CA, USA, 15–17 August 2005.
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Chitsaz, H.; LaValle, S.M. Time-optimal paths for a Dubins airplane. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2379–2384.
- Agarwal, P.K.; Wang, H. Approximation algorithms for curvature-constrained shortest paths. SIAM J. Comput. 2001, 30, 1739–1772. [Google Scholar] [CrossRef]
- Backer, J.; Kirkpatrick, D. A Complete approximation algorithm for shortest bounded-curvature paths. In Proceedings of the 19th International Symposium on Algorithms and Computation, Gold Coast, Australia, 15–17 December 2008; pp. 628–643.
- Jacobs, P.; Canny, J. Planning smooth paths for mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989. [CrossRef]
- Laumond, J.P.; Jacobs, P.; Taix, M.; Murray, R. A motion planner for nonholonomic mobile robots. IEEE Trans. Robot. Autom. 1994, 10, 577–593. [Google Scholar] [CrossRef]
- Gottlieb, Y.; Manathara, J.G.; Shima, T. Multi-Target Motion Planning Amidst Obstacles for Aerial and Ground Vehicles. Robot. Auton. Syst. 2015. submitted. [Google Scholar]
- Snape, J.; Manocha, D. Navigating multiple simple-airplanes in 3D workspace. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010; pp. 3974–3980.
- Yang, K.; Sukkarieh, S. Real-time continuous curvature path planning of UAVS in cluttered environments. In Proceedings of the 5th International Symposium on Mechatronics and its Applications, Amman, Jordan, 27–29 May 2008.
- Yang, K.; Sukkarieh, S. An Analytical Continuous-Curvature Path-Smoothing Algorithm. IEEE Trans. Robot. 2010, 26, 561–568. [Google Scholar] [CrossRef]
- Shima, T.; Rasmussen, S.; Sparks, A.; Passino, K. Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2006, 33, 3252–3269. [Google Scholar] [CrossRef]
- Richards, A.; Bellingham, J.; Tillerson, M.; How, J.P. Coordination and Control of Multiple UAVs. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, AIAA Paper 2002-4588, Monterey, CA, USA, 5–8 August 2002.
- Schumacher, C.; Chandler, P.R.; Pachter, M.; Pachter, L.S. Optimization of air vehicles operations using mixed-integer linear programming. J. Oper. Res. Soc. 2007, 58, 516–527. [Google Scholar] [CrossRef]
- Chandler, P.R.; Pachter, M.; Rasmussen, S.J.; Schumacher, C. Multiple task assignment for a UAV team. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Monterey, CA, USA, 5–8 August 2002.
- Schumacher, C.J.; Chandler, P.R.; Rasmussen, S.J. Task allocation for wide area search munitions. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 1917–1922.
- Edison, E.; Shima, T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Rasmussen, S.J.; Shima, T. Tree search algorithm for assigning cooperating UAVs to multiple tasks. Int. J. Robust Nonlinear Control 2008, 18, 135–153. [Google Scholar] [CrossRef]
- Shima, T.; Rasmussen, S.; Gross, D. Assigning micro UAVs to task tours in an urban terrain. IEEE Trans. Control Syst. Technol. 2007, 15, 601–612. [Google Scholar] [CrossRef]
- Schumacher, C.; Chandler, P.; Pachter, M.; Pachter, L. UAV Task Assignment with Timing Constraints; Defense Technical Information Center: Fort Belvoir, VA, USA, 2003. [Google Scholar]
- Schumacher, C.; Chandler, P.R.; Rasmussen, S.J.; Walker, D. Path Elongation for UAV Task Assignment; Defense Technical Information Center: Fort Belvoir, VA, USA, 2003. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Donald, B.; Xavier, P.; Canny, J.; Reif, J. Kinodynamic motion planning. J. ACM (JACM) 1993, 40, 1048–1066. [Google Scholar] [CrossRef]
- Delle Fave, F.; Rogers, A.; Xu, Z.; Sukkarieh, S.; Jennings, N. Deploying the max-sum algorithm for decentralised coordination and task allocation of unmanned aerial vehicles for live aerial imagery collection. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 469–476.
- Jiang, L.; Zhang, R. An autonomous task allocation for multi-robot system. J. Comput. Inf. Syst. 2011, 7, 3747–3753. [Google Scholar]
- Shetty, V.; Sudit, M.; Nagi, R. Priority-based assignment and routing of a fleet of unmanned combat aerial vehicles. Comput. Oper. Res. 2008, 35, 1813–1828. [Google Scholar] [CrossRef]
- Krishnamoorthy, K.; Casbeer, D.; Chandler, P.; Pachter, M.; Darbha, S. UAV search and capture of a moving ground target under delayed information. In Proceedings of the 2012 IEEE 51st Annual Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3092–3097.
- Shaferman, V.; Shima, T. Unmanned aerial vehicles cooperative tracking of moving ground target in urban environments. AIAA J. Guid. Control Dyn. 2008, 31, 1360–1371. [Google Scholar] [CrossRef]
- Boissonnat, J.D.; Bui, X.N. Accessibility Region for a Car That Only Move Forward along Optimal Paths; Research Report INRIA 2181; INRIA Sophia-Antipolis: Valbonne, France, 1994. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gottlieb, Y.; Shima, T. UAVs Task and Motion Planning in the Presence of Obstacles and Prioritized Targets. Sensors 2015, 15, 29734-29764. https://doi.org/10.3390/s151129734
Gottlieb Y, Shima T. UAVs Task and Motion Planning in the Presence of Obstacles and Prioritized Targets. Sensors. 2015; 15(11):29734-29764. https://doi.org/10.3390/s151129734
Chicago/Turabian StyleGottlieb, Yoav, and Tal Shima. 2015. "UAVs Task and Motion Planning in the Presence of Obstacles and Prioritized Targets" Sensors 15, no. 11: 29734-29764. https://doi.org/10.3390/s151129734
APA StyleGottlieb, Y., & Shima, T. (2015). UAVs Task and Motion Planning in the Presence of Obstacles and Prioritized Targets. Sensors, 15(11), 29734-29764. https://doi.org/10.3390/s151129734





