This paper introduced polynomial-based methods and their fixed-point implementation for the calibration and correction of log CMOS image sensors. The theory involved provable mathematical deductions. Nevertheless, experimental results presented here illustrate how the theory is applied in practice. More importantly, the results also validate unproved assumptions of the theory.
4.1. FPN and Photometric Calibration
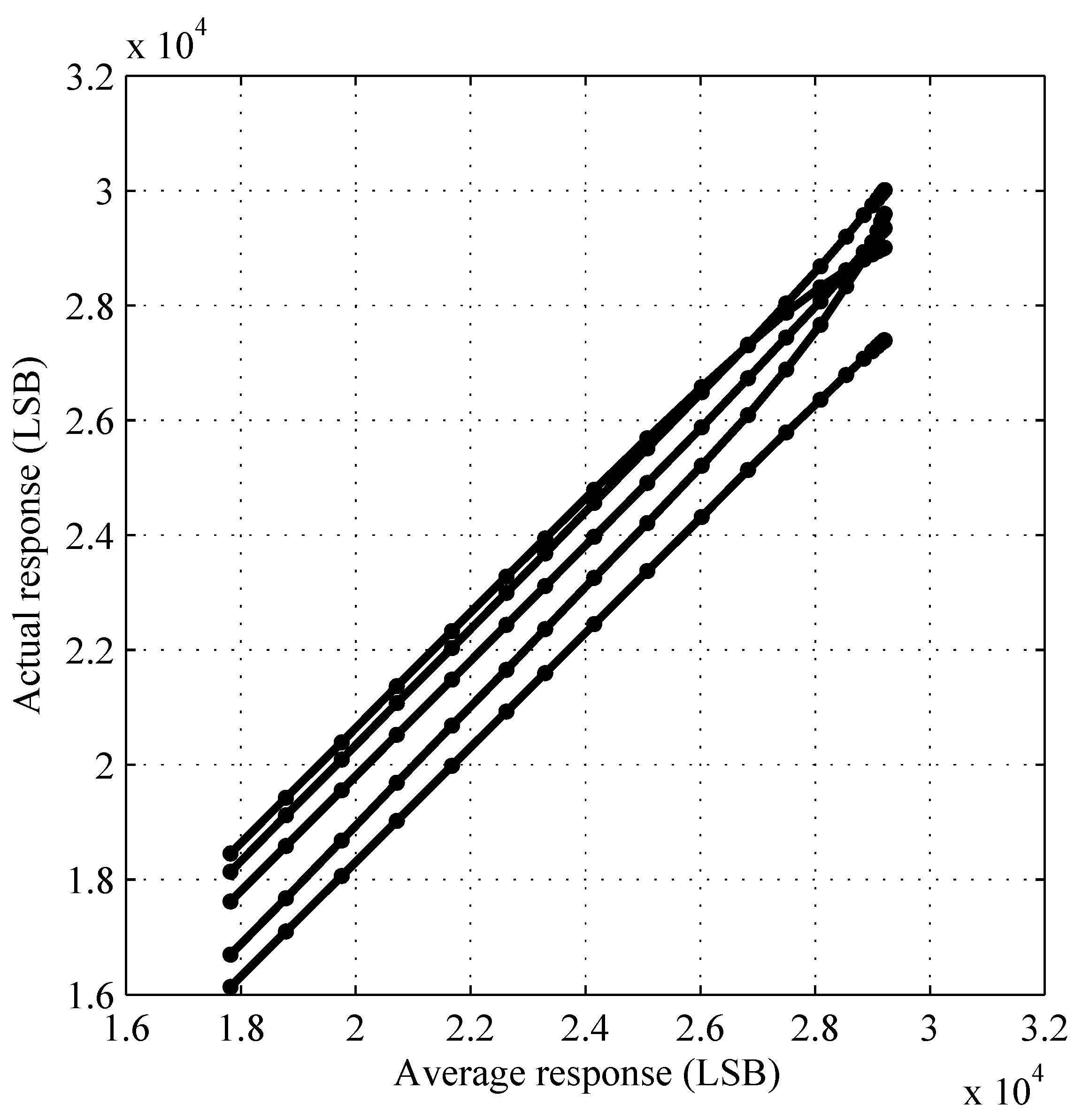
Figure 3 validates that actual responses are approximate linear functions of the average response, despite the highly nonlinear dependence of response on luminance, over a wide DR, as shown in
Figure 1. In the absence of FPN, the actual response of any pixel equals the average response of all pixels.
Figure 3.
Actual response versus average response. Because of mismatch variation, which causes FPN, the actual response of any pixel—five are shown—varies relative to the average response of all pixels. The average response is considered to be an ideal response.
Figure 3.
Actual response versus average response. Because of mismatch variation, which causes FPN, the actual response of any pixel—five are shown—varies relative to the average response of all pixels. The average response is considered to be an ideal response.
The PR and IPR methods, also called PR(
p) and IPR(
q) methods in this section, use degree
p and degree
q polynomial models, respectively, having
and
parameters per pixel (
ppp). Considering
Figure 3 as an example, the PR method models actual responses as polynomial functions of average responses, whereas the IPR method does the opposite. One of the reasons the latter proves more useful is because the purpose of FPN correction, when divorced from photometric correction, is to take non-ideal,
i.e., actual, responses as inputs and give ideal, e.g., average, responses as outputs.
An FPN, or relative, calibration involves the estimation of parameters, per pixel, for an imaging model that captures pixel-to-pixel variations. A photometric, or absolute, calibration involves the estimation of parameters, per imager, for an imaging model that captures imager-to-imager variations. Although joint FPN-photometric calibration and correction is possible, as discussed below for literature methods, the common practice with linear imagers is to separate them. In this paper, a separate approach is likewise taken for monotonic nonlinear imagers, in particular for a log CMOS image sensor.
Otim
et al. [
14] have presented three related models, founded upon circuit analysis, which could be used for joint FPN-photometric calibration and correction of log CMOS image sensors. For these models, an equivalent algebraic representation, more suitable for this discussion, is as follows:
In Equation (
50), the first two cases, called the offset-gain (OG) and offset-gain-bias (OGB) models, follow from earlier work by Joseph and Collins [
10]. We name the third case the offset-gain-bias-knee (OGBK) model. In the OGBK model,
and
are luminances at which the response function bends due to dark current and strong inversion effects, respectively. When luminances of interest are not bright enough for the strong inversion effects, the model simplifies to the OGB model. Dark current effects may also be ignored, resulting in the OG model. Parameters
(or
),
(or
),
, and
are called the offset, gain, bias, and knee, respectively. Two are functions of the others, as follows:
Section 2 explained the PR and IPR calibrations, both of which entail general linear regression. Calibration of the OGB and OGBK models requires nonlinear regression. Linearized regression may be used with the OG model, by taking
as the independent variable. For each method, the overall RMS residual FPN,
, and the RMS residual FPN per luminance,
, are computed as follows:
where complexities,
l, and residual FPN,
, are given in
Table 1. As residual FPN is a form of spatial distortion in corrected images, a superscript
is used, in contrast to
for temporal noise.
Table 1.
Summary of FPN calibration methods. For each method, the complexity is the number of parameters per pixel (ppp) required for FPN correction, and the residual FPN is the (weighted) error, at each luminance and pixel j, of the fitted response.
Table 1.
Summary of FPN calibration methods. For each method, the complexity is the number of parameters per pixel (ppp) required for FPN correction, and the residual FPN is the (weighted) error, at each luminance and pixel j, of the fitted response.
| Method | Complexity (l) | Residual FPN () |
|---|
| PR(p) | | |
| IPR(q) | | |
| OG | 2 | |
| OGB | 3 | |
| OGBK | 4 | |
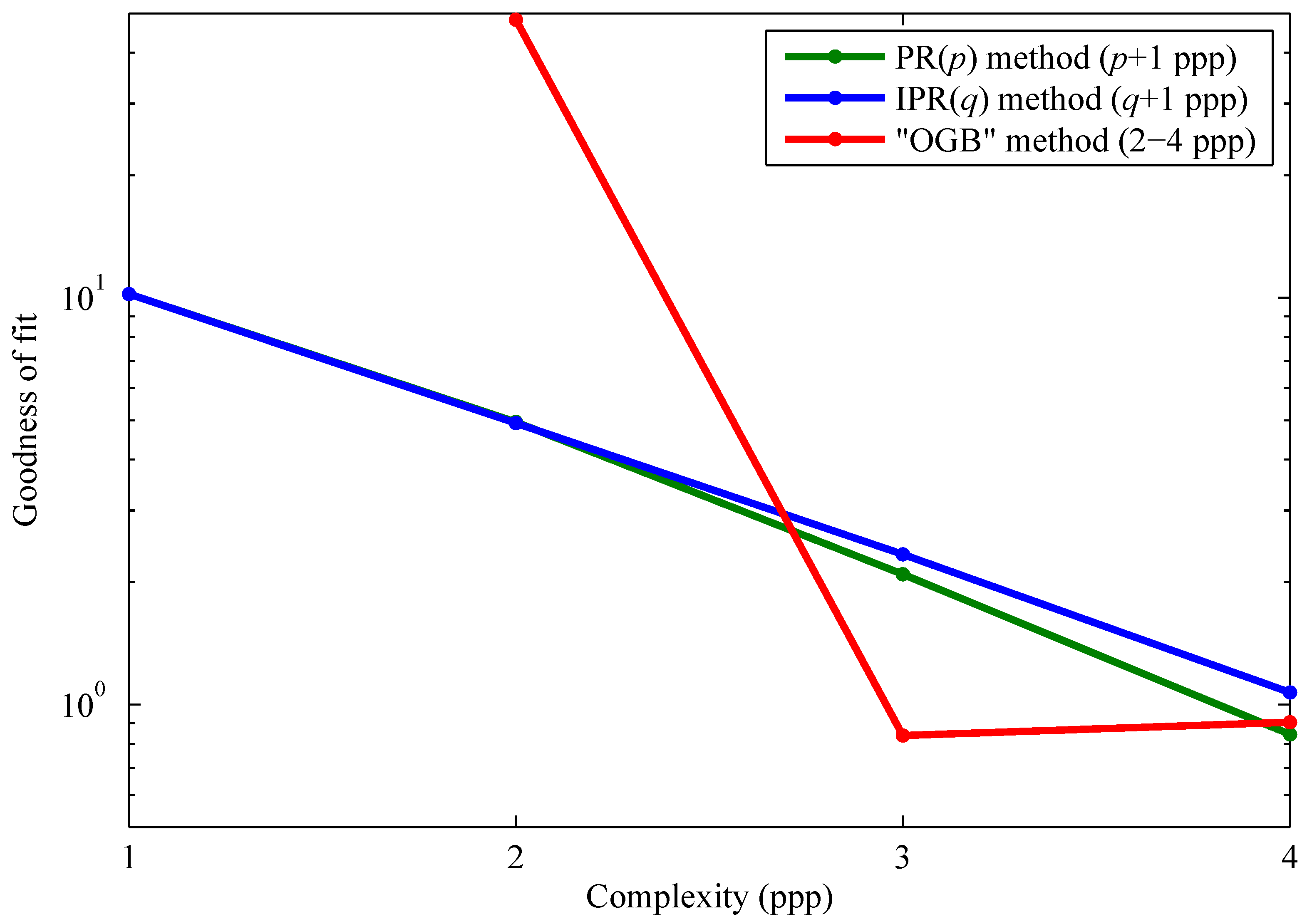
Figure 4 gives the overall goodness of fit, defined as
, for all calibration methods summarized in
Table 1. When this ratio is less than or equal to about one (or
), it means that FPN is effectively calibrated. Thus, FPN is effectively calibrated by the PR(3), IPR(3), OGB, and OGBK methods.
Figure 4.
Comparison of FPN calibration methods. The overall goodness of fit is the ratio of overall RMS residual FPN to overall RMS temporal noise. This paper introduced the polynomial regression (PR) and inverse polynomial regression (IPR) methods, whereas the offset-gain-bias (OGB) and related methods are taken from the literature.
Figure 4.
Comparison of FPN calibration methods. The overall goodness of fit is the ratio of overall RMS residual FPN to overall RMS temporal noise. This paper introduced the polynomial regression (PR) and inverse polynomial regression (IPR) methods, whereas the offset-gain-bias (OGB) and related methods are taken from the literature.
The overall goodness of fit of the PR and IPR calibrations are comparable for quadratic and cubic polynomial models, as shown in
Figure 4. However, with the PR method, it would be difficult and very difficult to perform FPN correction using quadratic and cubic polynomials, respectively, because all roots must be computed, for each pixel, and the correct root must be selected, also for each pixel. Thus, the IPR method is much preferred for these polynomial degrees. Note that overall goodnesses of fit are identical for lower degrees,
i.e.,
and
. This is expected mathematically.
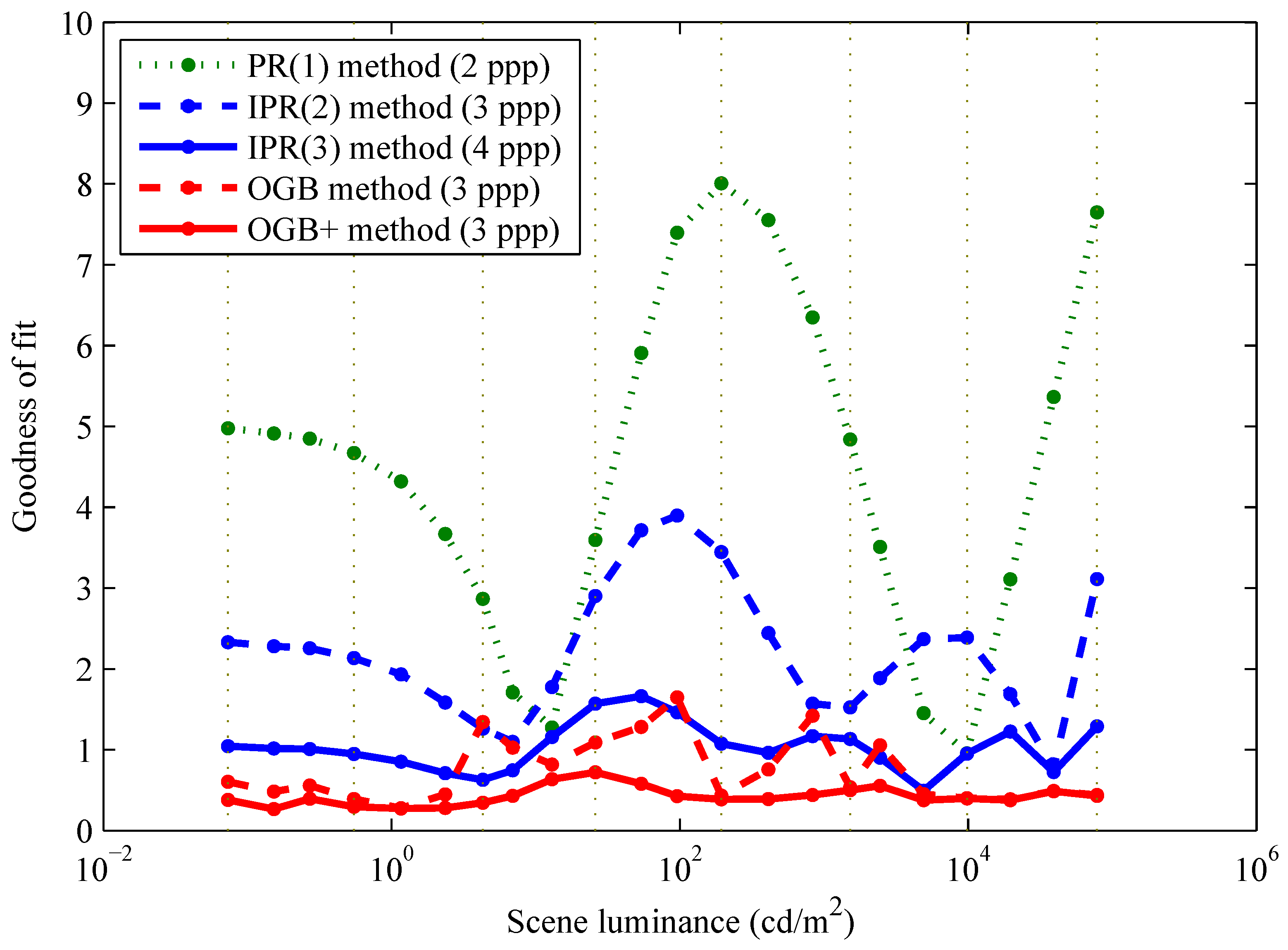
Figure 5 shows the goodness of fit per luminance, defined as
, versus luminance,
, for the linear PR, quadratic IPR, cubic IPR, OGB, and OGB+ (see below) calibrations. As shown in
Figure 4, the OGBK method, at the cost of increased complexity, provided no benefit over the OGB method.
Figure 5.
Comparing goodness of fit per luminance. This ratio divides RMS residual FPN per luminance by overall RMS temporal noise. Unlike the OGB method, the OGB+ method, also taken from the literature, corrects for luminance errors. However, unlike both OGB methods, the IPR method requires only arithmetic operations for FPN correction.
Figure 5.
Comparing goodness of fit per luminance. This ratio divides RMS residual FPN per luminance by overall RMS temporal noise. Unlike the OGB method, the OGB+ method, also taken from the literature, corrects for luminance errors. However, unlike both OGB methods, the IPR method requires only arithmetic operations for FPN correction.
In theory, a good FPN calibration should be equally good at all luminances of interest. In practice, OGB+ method aside, all calibrations exhibit dependence of goodness on luminance, which is worst for the linear PR and quadratic IPR calibrations. The cubic IPR and OGB calibrations exhibit goodnesses that are relatively independent of luminance. For both calibrations, goodnesses are approximately one, which means residual FPN is comparable to temporal noise at each luminance over the wide DR.
Luminance dependence of the OGB method, which entails a joint FPN-photometric calibration, may be attributed to measurement errors in luminances
. The OGB+ method [
10] is a complex approach, used for our prior publication [
3], that factors these out. As explained in
Section 1, the objective of this paper, as with other published papers, is to simplify correction even at some expense of accuracy. The IPR(3) method is almost as accurate as the OGB method but requires only arithmetic operations.
FPN calibration using the IPR method enables mapping of the actual response of each pixel (ordinate in
Figure 3) to an ideal response (abscissa in
Figure 3). Photometric calibration using the ISI method enables mapping of this ideal response (ordinate in
Figure 1) to scene luminance (abscissa in
Figure 1). ISI calibration is done by constructing a cubic Hermite spline, which guarantees monotonicity, to map from
to
using the 22 data points
shown in
Figure 1. The result, called an inverse spline because it represents an inverse function, is plotted in
Figure 1 (solid cyan line).
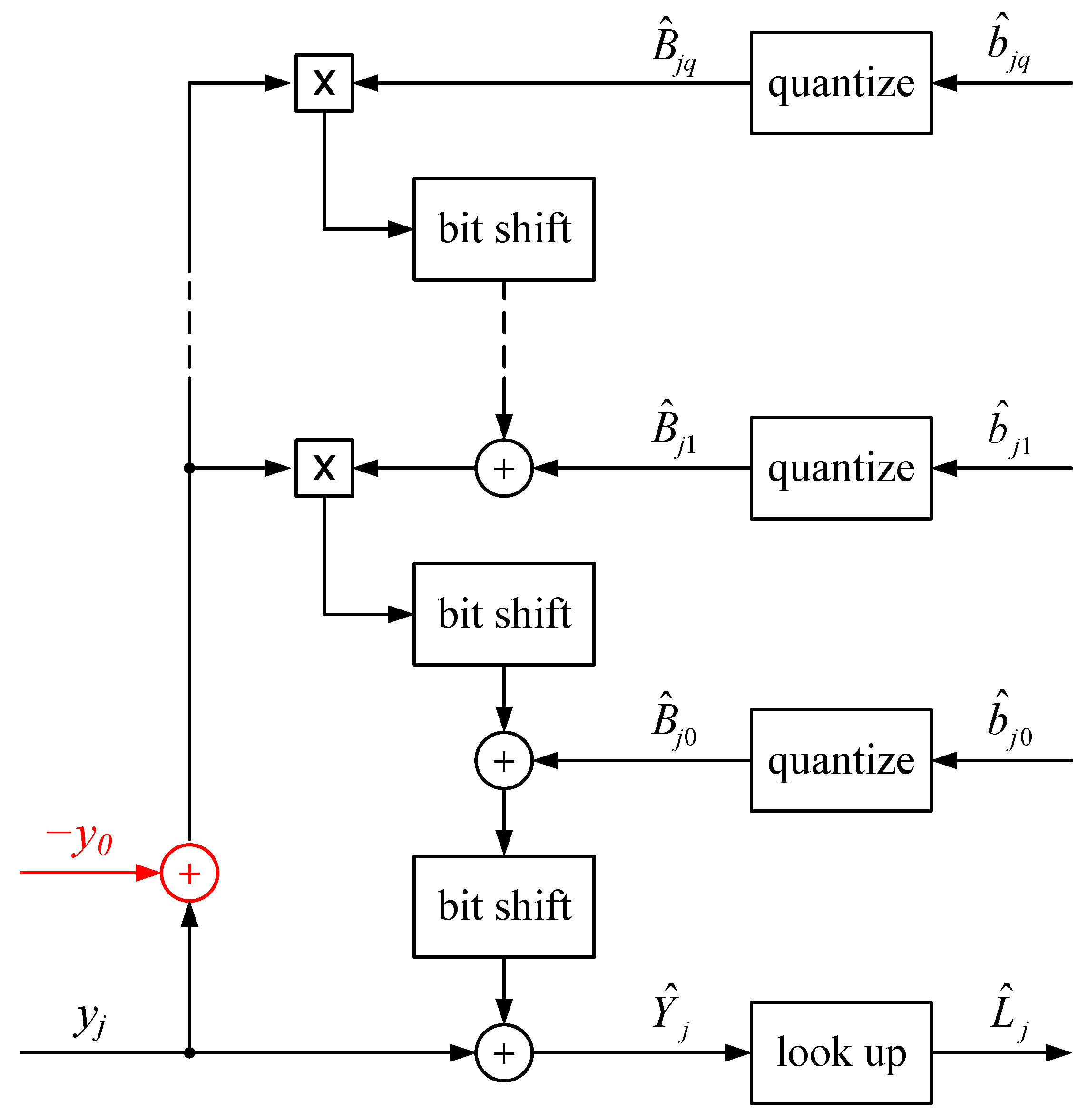
4.2. Fixed-Point Implementation
Whereas calibration is done once for an image sensor, FPN and photometric correction must be done repeatedly and in real time for a video-rate image sensor. Although a floating-point implementation is feasible for small pixel arrays operating at low frame rates, a fixed-point implementation is expected to be more scalable, especially for low-power applications. Another advantage of fixed point is reduced storage requirements, relative to floating point, for the parameters estimated during calibration.
A fixed-point implementation, however, may cause a loss of performance. For FPN calibration, this is quantifiable by comparing to the overall goodness of fit,
, introduced in the previous section. The fixed-point version,
, uses a revised overall RMS residual FPN,
, defined as follows:
where corrected images
are obtained from raw images
according to
Figure 2, with
and
replaced by
and
, respectively. As before, the complexity,
l, of this IPR(
q) calibration is
.
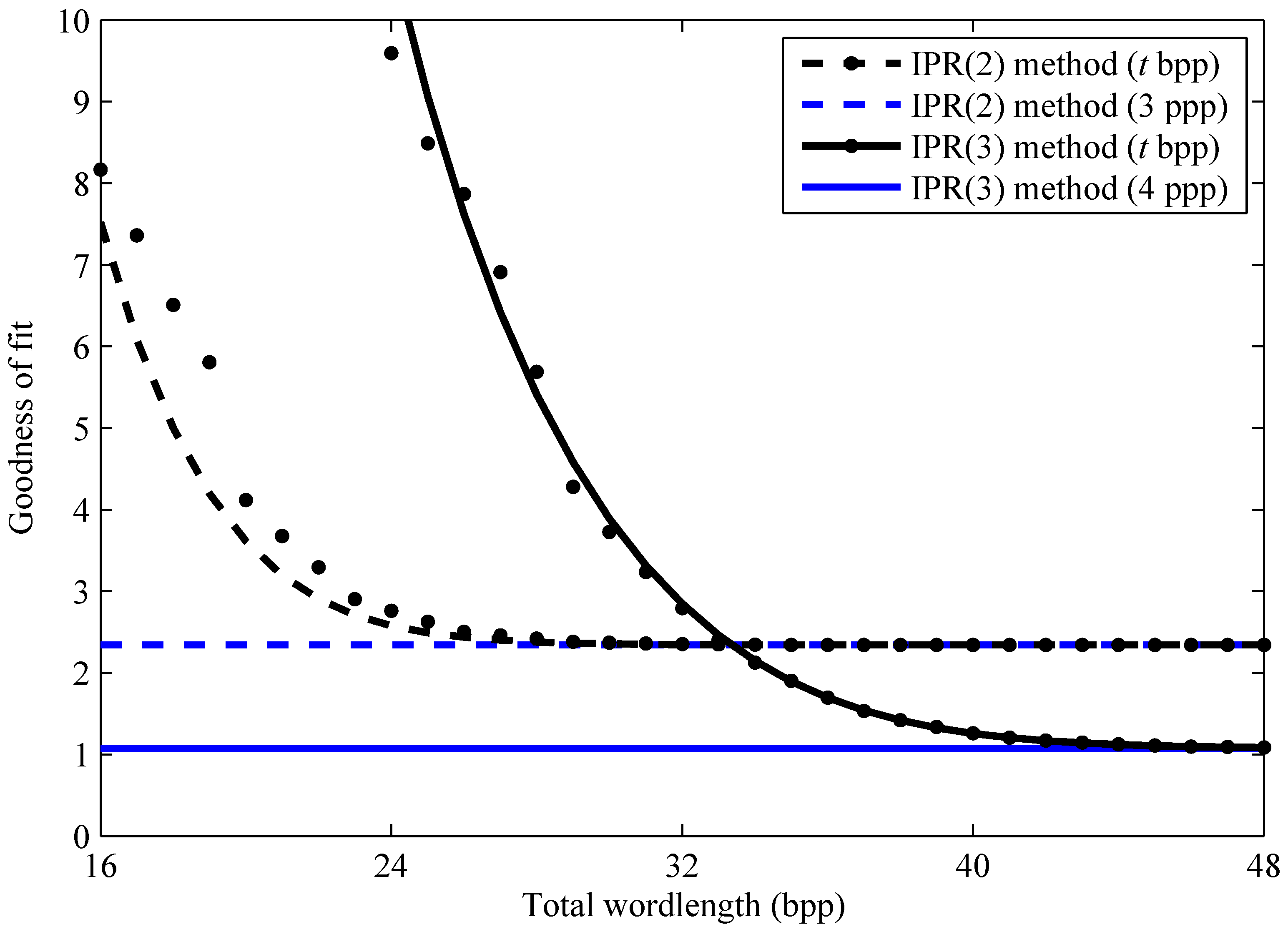
Figure 6 plots the overall goodnesses of fit, for fixed-point implementations of the IPR(2) and IPR(3) calibrations, versus the total wordlength,
t, used to quantize the estimated parameters,
. In addition to the actual goodnesses, as defined in the previous paragraph, modeled goodnesses are shown. The only difference is in the calculation of
in Equation (
55). As explained in
Section 3, an approximate but differentiable model is defined, which is optimized to minimize the impact of parameter quantization.
Figure 6.
Fixed and floating-point implementations. For the fixed-point FPN calibration, actual (dots) and modeled (curved lines) goodness results are shown. Both are computed, at each total wordlength t, after optimization of the model. The floating-point FPN calibration results (horizontal lines) are the limiting values. Here, bpp stands for bits per pixel.
Figure 6.
Fixed and floating-point implementations. For the fixed-point FPN calibration, actual (dots) and modeled (curved lines) goodness results are shown. Both are computed, at each total wordlength t, after optimization of the model. The floating-point FPN calibration results (horizontal lines) are the limiting values. Here, bpp stands for bits per pixel.
Figure 6 demonstrates that the fixed-point results converge on the floating-point ones—the horizontal lines—with a sufficient total wordlength,
t. Moreover,
Figure 6 validates the differentiable model as an approximation of the actual fixed-point results. This is important because the model is used to determine how many bits,
, to allocate to each parameter, as well as their binary-point positions,
. Examples are given in
Table 2. IPR parameters
are quantized to integers
, according to Equation (
45).
Table 2.
Details of fixed-point implementations. Total wordlengths
t, in
, are selected to be integer multiples of whole bytes. Here,
represents the wordlengths, also in
, of parameters
, shown in
Figure 2, and
represents their binary-point positions. For each pixel
j, floating-point parameters
are quantized to get integer parameters
.
Table 2.
Details of fixed-point implementations. Total wordlengths t, in , are selected to be integer multiples of whole bytes. Here, represents the wordlengths, also in , of parameters , shown in Figure 2, and represents their binary-point positions. For each pixel j, floating-point parameters are quantized to get integer parameters .
| | (a) IPR(2) method () | (b) IPR(3) method () |
|---|
| | | | | | | | | | | | | | |
|---|
| 16 | 7 | 6 | 3 | 8 | | | 4 | 4 | 5 | 3 | 10 | | | |
| 24 | 10 | 8 | 6 | 5 | | | 6 | 7 | 6 | 5 | 8 | | | |
| 32 | 12 | 11 | 9 | 3 | | | 8 | 9 | 8 | 7 | 6 | | | |
| 40 | 15 | 14 | 11 | 0 | | | 10 | 11 | 10 | 9 | 4 | | | |
| 48 | 18 | 16 | 14 | | | | 12 | 13 | 12 | 11 | 2 | | | |
Figure 6 also illustrates that fixed-point considerations may be the deciding factor when choosing between polynomial degrees. For example, if one decided to limit the FPN correction parameters to four or fewer bytes per pixel,
i.e.,
, then there is no advantage in using cubic over quadratic polynomials. Considering that an integer number of bytes or nibbles (half bytes) tends to be efficient from a hardware perspective, there is little advantage in using a fixed-point IPR method for
, at least with this particular image sensor. Accordingly, one could use a fixed-point IPR(2) method with three bytes per pixel (
) or a fixed-point IPR(3) method with five bytes per pixel (
).
Hoefflinger [
13] reports a fixed-point implementation for a log CMOS image sensor with an active pixel sensor (APS) architecture. His implementation uses
to represent parameters of the OGB model. While he achieves a residual FPN comparable to temporal noise, the temporal noise, relative to signal, was
times (
) higher than with our log CMOS image sensor, based on a DPS array. The PSNR of his image sensor was
[
13], whereas the PSNR of ours is
[
3]. Furthermore, Hoefflinger does not show that his
fixed-point implementation is optimal in any sense.
A fixed-point implementation is also required for our photometric correction. As shown in
Figure 2, this can be done simply using an LUT. The input and output of the FPN correction (
i.e.,
and
in
Figure 2, respectively) are both 16-bit integers. As such, an LUT with
words, at most, may be pre-computed to perform ISI correction in real time. This correction is essentially an inverse mapping of the average response function shown in
Figure 1. ISI correction may be effectively combined with “tone mapping,” explained in the next section. This specifies the size of each word in the LUT to be one byte. Thus, a 64 kilobyte LUT, at most, suffices to implement both photometric correction and tone mapping. Only one LUT is required to perform these operations for the whole pixel array.
4.3. FPN and Photometric Correction
Tone mapping refers to the processing used to properly display images from wide DR cameras [
13]. Standard displays, such as monitors and printers, can depict a relatively narrow DR of intensities. For the purposes of this paper, which is not about tone mapping, a simple approach is adopted based on the sRGB specification [
15], which is the default colour space of modern displays. Because our image sensor is monochromatic, the colour processing part of the sRGB specification is ignored.
For an image with
n pixels, let
be the estimated scene luminance of the
jth pixel, where
. The displayed image
, which is an integer from 0 to 255 at each pixel, is computed as follows:
where saturation is given by the white point,
, and “gamma correction” by the exponent,
.
According to the sRGB specification, modern displays simulate the gamma response of legacy cathode ray tubes (CRTs). This “CRT” gamma cancels out the exponent in Equation (
56) to achieve overall a linear mapping from estimated luminances
to displayed tones. Given
instead of
, as with ISI correction, the above tone mapping may be rewritten as follows, where
ℓ represents
:
Median filtering is employed to remove salt-and-pepper noise caused by “dead” pixels, i.e., outliers where responses are essentially useless. For interior pixels, the neighbourhood is a five-pixel cross made up of the pixel and its four nearest neighbours. For border and corner pixels, the pixel and its nearest two border pixels make up a three-pixel neighbourhood. These are the smallest symmetric neighbourhoods possible, where odd sizes ensure that means are never needed to compute medians.
The chosen median filter has low complexity, which is good for real-time processing. Furthermore, the avoidance of means implies that the median filter may be placed equally before or after any monotonic transform. ISI correction and simple tone mapping are each monotonic transforms. Although the median filter may be placed before either of these transforms, with no impact on final images, median filtering is most efficiently done after the simple tone mapping because of the format.
As described in
Section 2.1, additional images
were collected of the 22 calibration scenes, each of uniform luminance
, where
. These images were not used for calibration. Also, unlike the calibration images
, these images were not averaged over time and, thus, include unfiltered temporal noise. For brevity, every third additional image,
i.e., where
, was selected. Corresponding luminances, which cover a DR of
, are indicated by vertical lines in
Figure 1 and
Figure 5.
Figure 7 depicts the outcome of FPN correction, photometric correction, simple tone mapping, and median filtering for the eight selected additional images, using six different correction methods, including fixed-point implementations of two IPR methods. At each selected luminance
, which ranged from
to
, the white point chosen for the simple tone mapping was
. With this choice, perfect FPN and photometric correction would result in a uniform mid-level grey image,
i.e.,
would equal
for all pixels, after simple tone mapping.
Figure 7.
Corrected images versus correction method. Top to bottom: (a) the PR(1) method (); (b) the IPR(2) method (); (c) the IPR(2) method (); (d) the IPR(3) method (); (e) the IPR(3) method (); and (f) the OGB method (). With perfect FPN and photometric correction, all pixels would have a uniform grey value.
Figure 7.
Corrected images versus correction method. Top to bottom: (a) the PR(1) method (); (b) the IPR(2) method (); (c) the IPR(2) method (); (d) the IPR(3) method (); (e) the IPR(3) method (); and (f) the OGB method (). With perfect FPN and photometric correction, all pixels would have a uniform grey value.
To interpret
Figure 7, consider both
Figure 1 and
Figure 5. A better goodness per luminance,
i.e., a lower value, in
Figure 5 means that residual FPN is less significant relative to temporal noise. However, a more horizontal slope in
Figure 1, for the average response as a function of log luminance, means that residual FPN and temporal noise have a greater impact on estimated luminance and, hence, image quality.
Figure 7 depicts the results of floating-point PR(1), IPR(2), and IPR(3), plus ISI, corrections. In these cases, Equation (
57) specifies the tone mapping. Image quality improves with increasing polynomial degree, especially going from the linear to the quadratic model. Note the non-uniform greyness with the PR(1) results, even at higher luminances. The figure also depicts the results of fixed-point IPR(2) and IPR(3) corrections, using 24 and
, respectively. In these cases, Equation (
57) specifies the tone mapping with
instead of
, where
is the result of the fixed-point ISI correction, as shown in
Figure 2. Compared to the corresponding floating-point results, there is little to no difference.
Figure 7 also depicts the results of the floating-point OGB method, for which Equation (
56) specifies the tone mapping. Although not ideal, image quality is better at
, compared to all other methods. However, image quality is worse at
. What is happening is a problem with the photometric correction, not with the FPN correction, because the OGB method is sensitive to measurement errors in
, which determines the white point. Overall, compared to the OGB method, the quadratic and cubic IPR, plus ISI, methods offer satisfactory image quality, over a wide DR, and this performance is achievable using a fixed-point implementation based largely on simple arithmetic.
The IPR(2) and ISI methods were programmed to operate in real time on a desktop computer that controlled our image sensor. Videos were displayed and recorded of multiple non-uniform scenes. Each used a different white point chosen manually.
Figure 8 depicts several frames taken from these videos. Notwithstanding the low spatial resolution of the camera, which had only
pixels [
3], the image quality is good after tone mapping, further validation for the polynomial-based methods.
Figure 8.
Polynomial-based correction in real time. Because the visual quality of quadratic FPN correction was deemed sufficient, with simple tone mapping, and the fixed-point work was unfinished at the time, the IPR(2) method () was implemented at a frame rate. Top row (left to right): a building against the sky; a plant by a window; and a bookshelf in sunlight. Bottom row: three views of a face with highlights and shadows.
Figure 8.
Polynomial-based correction in real time. Because the visual quality of quadratic FPN correction was deemed sufficient, with simple tone mapping, and the fixed-point work was unfinished at the time, the IPR(2) method () was implemented at a frame rate. Top row (left to right): a building against the sky; a plant by a window; and a bookshelf in sunlight. Bottom row: three views of a face with highlights and shadows.