Collusion-Aware Privacy-Preserving Range Query in Tiered Wireless Sensor Networks †
Abstract
: Wireless sensor networks (WSNs) are indispensable building blocks for the Internet of Things (IoT). With the development of WSNs, privacy issues have drawn more attention. Existing work on the privacy-preserving range query mainly focuses on privacy preservation and integrity verification in two-tiered WSNs in the case of compromised master nodes, but neglects the damage of node collusion. In this paper, we propose a series of collusion-aware privacy-preserving range query protocols in two-tiered WSNs. To the best of our knowledge, this paper is the first to consider collusion attacks for a range query in tiered WSNs while fulfilling the preservation of privacy and integrity. To preserve the privacy of data and queries, we propose a novel encoding scheme to conceal sensitive information. To preserve the integrity of the results, we present a verification scheme using the correlation among data. In addition, two schemes are further presented to improve result accuracy and reduce communication cost. Finally, theoretical analysis and experimental results confirm the efficiency, accuracy and privacy of our proposals.1. Introduction
As indispensable building blocks for the Internet of Things (IoT), wireless sensor networks (WSNs) have been widely used in many applications, such as smart home, e-health and environment monitoring. In these applications, range query is an important type of query in WSNs, which aims at seeking all data falling into an attribute range specified by users. However, due to the openness and non-supervision of WSNs, privacy problems have been exposed when data are collected, transmitted or analyzed. For instance, in the field of e-health, wearable or fixed medical sensors are used to monitor patients' physical parameters (e.g., blood pressure) and respond to an emergency rapidly when needed. During the process of data collection, transmission or analysis, information of patients may be overheard by an adversary, such that patient privacy is compromised. Therefore, privacy-preserving range query processing is especially urgent.
Due to resource savings, rapid response and high scalability, a two-tiered architecture [1] is adopted in the existing work [2–9] on privacy-preserving range queries. Figure 1 shows a typical two-tiered WSN, which consists of resource-limited sensor nodes in the lower tier and resource-rich master nodes, also called storage nodes, in the upper tier. Data are gathered by sensor nodes and transmitted to associated master nodes, and then, master nodes calculate and return results to the sink. Since WSNs are often deployed in hostile and unpredictable environments, the two-tiered architecture brings in serious security challenges. On the one hand, master nodes are untrustworthy and curious about data stored in themselves, so original data should be concealed before being submitted to master nodes. What is worse, the compromised master node may reply with fake or incomplete results. On the other hand, master nodes are required to perform queries efficiently and correctly, which is hindered if data are encrypted. As a result, it is challenging to preserve privacy and at the same time achieve efficient performance and correct results.
Previous studies [2–9] only focused on privacy preservation and integrity verification when the master node is compromised, without the consideration of collusion attacks. Besides, these studies preserve privacy and integrity at the detriment of efficiency and accuracy. To address the problem, we investigate a secure range query in two-tiered WSNs with the following contributions:
We first propose a privacy-preserving range query protocol (PRQ) in two-tiered WSNs. In PRQ, we design a novel encoding scheme to preserve the privacy of data and queries and a verification scheme to check the result integrity. The encoding scheme represents data and queries by the special code, while the verification scheme discovers wrong results based on the ordinal relation of data.
We then present a series of collusion-aware privacy-preserving range query protocols (CPRQ) based on PRQ. To the best of our knowledge, this paper is the first to fulfill the need for resistance to collusion attacks for a range query in tiered WSNs.
We further present two schemes for improvements. The first scheme reduces communication cost by compressing the codes of the data. The second scheme improves result accuracy by denoting the query range as multiple codes.
Theoretical analysis and experimental results indicate that our proposals can reduce the communication cost and accomplish more accurate results while preserving privacy and integrity.
The rest of the paper is organized as follows. Section 2 summarizes related work. Models and the problem statement are described in Section 3. Section 4 introduces preliminary knowledge. Then, the PRQ protocol and a series of CPRQ protocols are elaborated in Sections 5 and 6, respectively. These protocols are further improved in Section 7 and analyzed theoretically in Section 8. Section 9 evaluates our proposals using thorough experiments. We conclude this paper in Section 10.
2. Related Work
In recent years, privacy issues of WSNs have drawn increasing concerns [10]. The work in [11–22] and the work in [23–27] study the privacy preservation in data aggregation and the top-k query, respectively. However, our paper focuses on the range query. Privacy-preserving range query in two-tiered WSNs has been explored in [2–9].
The work in [2] is a milestone in the privacy-preserving range query. It uses the bucketing technique to divide the data domain into multiple disjoint buckets and represents data and queries by bucket IDs. If there are no data falling into a certain bucket, an encoding number is created for this bucket. After receiving a range query, storage nodes return satisfactory encrypted data and all encoding numbers. The bucketing technique protects privacy, while the encoding number verifies the integrity of the results. Nevertheless, it enables adversaries to obtain a reasonable estimation of the data and queries according to the range of the bucket and generates false positives in the results.
The work in [3] investigates the spatial and temporal relation among data. The major idea is similar to [2]. The difference is that it verifies the integrity by the bitmap instead of the encoding number. It cannot avoid false positives, and produces more communication. To reduce communication cost, [4] presents a probabilistic spatial-temporal crosscheck scheme, which fails to detect the compromised storage node absolutely.
SafeQ [5,6] adopts the prefix membership verification scheme [28,29] to ensure privacy and constructs the neighborhood chain to protect integrity. In addition, [6] establishes Merkle hash trees to examine the results. The disadvantage is that SafeQ needs more computation and communication.
The work in [7] proposes a privacy-preserving range query protocol on the basis of the order-preserving function, the permutation function and the d-disjunct matrix. The order-preserving function is used to process the query. The permutation function and the d-disjunct matrix are used to encrypt data and get the exact frequency of any value. It requires extra space to store matrices and cannot verify integrity.
Our previous paper [9] also focuses on the problem of the privacy-preserving range query in tiered WSNs. This paper is an extended version of [9] and is the first to take destructive collusion attacks into account for range query in tiered WSNs. Although [30] proposes a privacy-preserving location proof updating the system towards collusion resistance, it only protects location privacy in location-sensitive applications and is not suitable for privacy preservation of data and queries for the range query in WSNs. More protocols, theorems, improvements, theoretical analysis and experimental results are added in this paper.
3. Models and Problem Statement
3.1. Network Model
As illustrated in Figure 1, a two-tiered WSN is composed of three types of nodes: many sensor nodes, a few master nodes and a single sink. Sensor nodes have limited storage, computation, bandwidth and energy, while master nodes have strong capabilities and abundant resources as the sink. At the beginning of the network, system parameters are preloaded into sensor nodes. During the network lifetime, sensor nodes collect data (e.g., temperature and humidity) from their surroundings with a fixed frequency and then periodically transmit data to their master nodes. Master nodes store the data of their affiliated sensor nodes. Once they receive a range query from the sink, master nodes immediately search for required data and transmit the results to the sink. The network is considered to be separated into some non-overlapping subnetworks, and each subnetwork comprises a master node and several sensor nodes. Suppose all sensor nodes are synchronized, so that they keep consistent in epochs.
Compared with the traditional sensor network without master nodes, three major advantages of this architecture benefit the development of WSNs. First, resources are saved for sensor nodes. Master nodes store a large number of data and process complicated calculations, which cuts down the cost of storage and computation for sensor nodes and prolongs the network lifetime. Second, it improves the speed of the query response. Master nodes handle queries locally and send answers to the sink directly. Finally, network scalability is enhanced. The network is divided into subnetworks based on master nodes, and these subnetworks may be heterogeneous and run independently. As described in Section 1, the two-tiered architecture brings security challenges. More details will be given in the next subsection.
3.2. Adversary Model
There are two assumptions in our adversary model: (1) the sink is reliable, as assumed in [2–9]; otherwise, the entire network is trustless, since the sink can fabricate results; and (2) the number of compromised sensor nodes and master nodes is limited; if not, the network is disabled.
An adversary generally tries to eavesdrop on the sensitive data of the network through the wireless link layer, which violates data privacy. Moreover, once a node is compromised by the adversary, it will submit the wrong data, which breaches result integrity. Three cases against result integrity are discussed in the following:
Compromising a sensor node: If a sensor node is compromised, the adversary can access its data and manipulate it to send incorrect data to its master node. For a certain range query, it has a slight and negligible effect on the final result. It is difficult to overcome this problem unless the hardware progresses.
Compromising a master node: Storing lots of data, master nodes easily become the target of attacks. If a master node is compromised, it has a great impact on the network security. On the one hand, the adversary is enabled to obtain sensitive data stored in this master node. On the other hand, the master node dominated by the adversary may deliberately inject fake data or delete partial data, so that the sink receives incorrect results.
Node collusion: If collusion occurs among sensor nodes, the influence on the network security is limited, as mentioned in the first case. However, if sensor nodes collude with their master nodes, all data stored in master nodes may be disclosed, and the damage to the whole network may be destructive.
It is clear that compromising the master node causes graver threats than the sensor node. Hence, our paper first pays attention to solving the problem of compromising master nodes in Section 5, and then enhances network security against collusion attacks in Section 6.
3.3. Problem Statement
A good privacy-preserving range query protocol should fulfill the following requirements.
Data privacy: Since data are private and sensitive, all data should not be obtained by master nodes. Furthermore, data should be only known by their owner and the sink.
Query privacy: The query range implicitly reveals the interest of users. Adversaries have the capability to infer the user's preference from the captured query range. Consequently, the query range should be only known by the sink.
Result integrity: (1) All data in the results should be authentic, i.e., forged data are not permitted; and (2) the result should include all data satisfying the query, i.e., an incomplete result is not acceptable. At the least, the protocol should entitle the sink to detect actions of injecting fake data and removing legitimate data. Network security is reinforced by result integrity.
Efficiency: Energy is the bottleneck of network lifetime. The work in [31] shows that communication consumes more energy than other processing in sensor nodes. Therefore, the less the communication cost, the higher the efficiency.
Accuracy: Only the satisfactory data should exist in the result, and incorrect data should be excluded.
4. Preliminaries
The Bloom filter [32] is a space-efficient probabilistic data structure, which uses hash functions to support the membership test of a set. Although the Bloom filter may generate false positives, the benefit of space savings outweighs this drawback. In addition, hash functions can encode data. We adopt the Bloom filter to preserve privacy while testing membership in Section 5. In this section, we first briefly review the standard Bloom filter.
Assume that a Bloom filter consists of two parts: an array of m bits initialized to 0 and k independent one-way hash functions hi, …,hk mapping elements in the universe to a random number uniformly over the range {1, 2, …,m}. Given a set S = {xi|1 ≤ i ≤ n}, add an element x into S, just by setting all hj(x)-th (1 ≤ j ≤ k) bits to 1. Thus, the Bloom filter of S is constructed by setting all hj(xi)-th (1 ≤ i ≤ n, 1 ≤ j ≤ k) bits to 1. To examine if an element y is in S, check whether all of the hj(y)-th (1 ≤ j ≤ k) bits are set to 1. If not, y is definitely not in S. Otherwise, y may be in S. Either y is really in S or the k bits have been set to 1 by chance during the insertion of other elements in S, which is called a false positive. Figure 2 is an example of the Bloom filter. 0110101101011100 is the Bloom filter of the set S = {11,12,13,14,15}. Examine if S contains 7, 12 and 16, which are hashed to bits (2, 4, 6), 〈3, 5, 8〉 and 〈7,10,14〉, respectively. It is found that 7 is definitely not in S; 12 and 16 are considered to be in S, although 16 is actually not in S.
The probability of false positives is already given in [33]. It should be noticed that the probability of a false positive in [33] is different from that in this paper, because of the different properties of hash functions. False positives are allowable, as long as their probability is sufficiently low. In spite of efficient insertion and testing, the deletion of an element is troublesome. Because setting the related bits to 0 may result in removing any other elements hashed to those bits, this is called a false negative. False negatives are not permitted.
5. Privacy-Preserving Range Query
In this section, we propose a privacy-preserving range query protocol (PRQ). The protocol is divided into four steps: system initialization, privacy preservation, membership test and integrity verification. At the beginning, system parameters are initialized. Both nodes' data and users' queries are encoded to hide private information before being sent to master nodes. Then, master nodes search for matching data upon codes. Finally, result integrity is verified by the sink. More details are elaborated in the following. Table 1 summarizes the notation used in this paper.
5.1. System Initialization
Without loss of generality, let the data domain be a set of positive integers and H = {h1, h2, …} be a set of independent and randomly distributed hash functions, satisfying: for each datum d, there is hi(d) ≠ hj(d) (i ≠ j). The sink selects k different hash functions h1,…, hk from H. At the beginning of the network, h1,…, hk and ki,0 are preloaded in each sensor node si, where ki,0 is a seed key and is only shared between the sensor node si and the sink. si encrypts its data by ki,t, which is the secret key of si at epoch t. Let ki,t = hash(ki,t–1), and erase ki,t–1 at epoch t.
5.2. Privacy Preservation
As discussed in Section 3, data collected by sensor nodes and queries issued by users are private. Moreover, master nodes are unreliable and curious about private information. It is necessary to protect data and queries. In this subsection, a special encoding scheme is devised to preserve privacy by virtue of the excellent property of the Bloom filter.
We first consider privacy preservation of data. Assume the sensor node si gathers data d1, d2, …, dθ at epoch t. For each datum, construct a special code of m bits initialized to 0 by rules: map the datum to k positions by hash functions h1,…, hk, and set these positions of the code to 1. The encoding scheme is similar to the construction of the Bloom filter of a set with an element, so we call the special code BFcode. The message that the sensor node si sends to its master node M is:
Next, we discuss how to protect query privacy. Let 〈T, [a, b]〉 be a range query, where T is the time slot and [a, b] is the range of data in which the user is interested. Construct the range's BFcode of m bits by rules: hash each positive integer in [a, b] to k positions by hash functions h1, …,hk, and set these positions of the code to 1. In other words, the BFcode of the range is the union of the BFcodes of all positive integers in [a, b]. The message that the sink issues to the master node M is:
5.3. Membership Test
BFcodes not only preserve the privacy of data and queries, but also enable master nodes to find required data without revealing any private information. Master nodes test the membership according to Theorem 1 (proven in Appendix A).
Theorem 1
Given a range [a, b] and data d, BFd and BF[a, b] are respectively referred to the BFcode of d and the BFcode of [a, b] using k hash functions h1,…, hk. If BFd ∩ BF[a, b] ≠ BFd, there must be d ∉ [a, b].
However, the negative of Theorem 1 is not always true. That is, if BFd ∩ BF[a, b] ≠ BFd, there may be d ∉ [a, b], i.e., false positive. For instance, in Figure 2, the range is [11,15]. There is BF16 ∩ BF[11,15] = BF16, but 16 ∉ [11,15]. As already mentioned in Section 4, a few false positives are allowable. The probability pp that data are considered to be in the query range after membership test is:
Receiving a query 〈T, BF[a,b]〉, master nodes begin to determine two bounds, denoted as α and β, for each sensor node si with reference to Equations (1) and (2). Obviously, dα denotes the lower bound of data satisfying Equation (1), and dβ denotes the upper bound of data satisfying Equation (2). It should be noticed that false positives may be generated during the membership test process, which is further improved in Section 7.
The message that the master node M sends to the sink depends on 〈α, β〉 as follows:
If α < β, that means the sensor node si has multiple data in [a, b]. The message that M sends to the sink is:
where {dα, …, dβ} is the result set, while {dα –1, dβ+1} is the verification set.If α = β, that means the sensor node si has only one datum in [a, b]. The message that M sends to the sink is:
where {dα} (dα = dβ) is the result set, while {dα –1, dα+1} is the verification set.If α > β (actually α = θ + 1), that means all data of the sensor node si are outside of [a, b]. The message that M sends to the sink is:
where {dα, dβ} is the verification set.
5.4. Integrity Verification
If each master node submits its local result honestly, the sink will obtain a correct final result. However, in a malicious environment, master nodes are attractive to adversaries. The compromised master node may submit the wrong local result to the sink. As a result, it is indispensable for the sink to verify the local results.
For the sensor node si, let {E(dα –1‖α − 1),…, E(dβ+1‖β+ 1)}{BFdα –1,…, BFdβ+1} be the message that the master node M sends to the sink. Thus, RS = {dα, …, dβ} is the local result calculated based on the membership test, and VS = {dα –1, dβ+1} is the verification set. Given a range query 〈T, BF[a,b]〉, result integrity is verified under various circumstances:
If the encrypted part in the message cannot be decrypted using the right key, or the BFcode in the message is not equal to the correct one, the sink can know that the corresponding data are unauthentic; because only the authentic data are able to be decrypted by the right key and the BFcode should be equal to the correct one.
If a datum d is in RS and its BFcodes, denoted as BFd, satisfy BFd ∩ BF[a,b] ≠ BFd, the sink can detect this error. Because for any data d in RS, there must be BFd ∩ BF[a,b] = BFd.
If all orders of dα –1,dα,…,dβ,dβ+1 cannot keep continuity, the sink can discover this error. Because these orders increase continuously.
If the master node returns nothing for the sensor node si, the sink can find that this master node is compromised. Because the master node is required to submit {E(dα‖α), E(dβ‖β)}, {BFdα,BFdβ}, even if there is no data in [a, b], besides, α = (θ + 1) and β = θ. If these two equalities do not hold simultaneously, the sink can know that the local result is incomplete.
Following the above rules, result integrity is verified and the compromised master node is detected.
5.5. Computational Complexity
We next present the computational complexity of PRQ. We report the time complexity of operations in each sensor node for data privacy preservation and the time complexity of operations in each master node for membership testing.
For any datum, the sensor node generates an encrypted part and a BFcode. It takes O(k) time to encode each datum to a BFcode, where k is the number of hash functions. Additionally, it generates an encrypted part with O(1) time by the encryption function. Assume the sensor node collects θ data. The overall time complexity of operations in each sensor node for data privacy preservation is O(θ · k).
For any encrypted data, the master node tests membership with O(m) time by comparing the BFcode of the data with the BFcode of the query, where m is the number of bits in a BFcode. Assume the master node receives N BFcodes. The overall time complexity of operations in each master node for membership testing is O(N · m).
6. Collusion-Aware Privacy-Preserving Range Query
Imagine a scenario where a sensor node colludes with its master node. The master node obtains hash functions stored in the sensor node and then uses these functions to infer the original data and queries from their corresponding BFcodes through enumeration methods. Therefore, collusion attacks between sensor nodes and master nodes will destroy network security and should be prevented effectively.
PRQ offers the preservation of privacy and integrity, but it is incapable of resisting collusion attacks. On the basis of PRQ, we propose a series of collusion-aware privacy-preserving range query protocols (CPRQ), which overcome the shortcoming of PRQ.
6.1. Confusion-Based Collusion-Aware Privacy-Preserving Range Query
In PRQ, the same hash functions h1,…,hk are shared with each sensor node and used to encode both data and queries. Once adversaries compromise any sensor node and the corresponding master node, private information will leak. Hence, different sensor nodes should use different hash functions to encode data, such that the impact of node collusion is limited.
Here, we design a confusion-based collusion-aware privacy-preserving range query protocol (c-CPRQ). c-CPRQ consists of the same steps as PRQ: system initialization, privacy preservation, membership testing and integrity verification. The differences between c-CPRQ and PRQ are in system initialization, privacy preservation and membership testing.
In system initialization, c-CPRQ defines the same data domain, hash function set H and key ki,t as PRQ. The query hash set (QH), a subset of H, is only secretly kept in the sink for encoding users' queries and |QH| = k. The node hash set (NHi) denotes the set of secret hash functions for encoding data of the sensor node si and |NHi| = k. NHi, also a subset of H, is specified by the sink as follows: The sink selects l (0 < l < k) hash functions from QH and k − l hash functions from . NHi is preloaded in si. For example, assume H = {h1, h2,…, h10}, k = 4 and l = 3. First, the sink determines QH = {h2,h5,h6,h9}, and then, . The sink may select NH1 = {h2,h5,h6,h1} for the sensor node s1 and NH2 = {h5,h6,h9,h3} for the sensor node s2.
In privacy preservation, instead of using the identical hash functions for encoding, we use NHi and QH to construct the BFcodes of data of the sensor node si and the BFcodes of queries, respectively. Different sensor nodes employ different hash functions, which results in two consequences: (1) the same data collected by different sensor nodes may be encoded to different BFcodes; (2) the same BFcode constructed by different sensor nodes may be derived from different data. Since the sensor node knows nothing except its own hash functions, its master node cannot infer the original data and the query range based on their BFcodes, even if it colludes with the sensor node. c-CPRQ protects privacy under node collusion conditions.
If c-CPRQ adopts the same membership test of PRQ, false negatives will be produced. That is because Theorem 1 used in the membership test of PRQ assumes that NHi = QH for each sensor node si. In fact, NHi ≠ QH in c-CPRQ. To eliminate false negatives, we present a relaxed membership test according to Theorem 2 (proven in Appendix C).
Theorem 2
Given a range [a, b] and data d, BFd is referred to the BFcode of d using the hash function set NH, and BF[a, b] is referred to the BFcode of [a, b] using the hash function set QH. Let η represent the number of 1-bits in BFd ∩ BF[a, b] and IH = NH ∩ QH. If η < |IH|, there must be d ∉ [a, b].
The probability pc that data are regarded as the members of the query range after membership testing is:
The master node processes the query 〈T, BF[a,b]〉 depending on Theorem 2. For each sensor node si, the master node tries to find two bounds α and β according to Equations (3) and (4), where ηi represents the number of 1-bits in BFdi ∩ BF[a,b] and IH = NHi ∩ QH. After determining α and β, the result that the master node sends to the sink is constructed following the same rules in PRQ.
The sink knows any NHi. After receiving the local results from master nodes, the sink starts to verify result integrity according to the integrity verification of PRQ.
False negatives are avoided in c-CPRQ based on Theorem 2. However, since \NHi ∩ QH| < |NHi|, more data not in [a, b] are transmitted by master nodes, thus causing the growth of false positives. This problem is settled in the next subsection.
6.2. l-Uncertainty Collusion-Aware Privacy-Preserving Range Query
To overcome the shortcoming of c-CPRQ, we put forward an l-uncertainty collusion-aware privacy-preserving range query protocol (u-CPRQ). The differences between u-CPRQ and c-CPRQ are in the system initialization and membership testing.
In system initialization, the sink chooses the query hash set (QH) from H and determines the node hash set (NHi) for each sensor node si by randomly selecting at least l (0 < l ≤ |QH|) hash functions from QH, where l is a system parameter. NHi is preloaded in si. |NHi| may be assigned to an arbitrary value in {l, l +1,.., |QH| − 1, |QH|}. Moreover, the hash functions in NHi may be an arbitrary combination of |NHi| hash functions in QH. Thus, |NHi| and NHi are both uncertain. For example, assume H = {h1, h2,…, h10}, k = 4 and l = 2. First, the sink determines |QH| = {h2,h5,h6,h9}. Then, the sink may select NH1 = {h2,h5} for the sensor node s1 and NH2 = {h5,h6,h9} for the sensor node s2.
In privacy preservation, NHi is used to encode data of the sensor node si, while QH is used to construct the BFcodes of queries.
Unlike c-CPRQ, u-CPRQ uses the same membership test of PRQ. Additionally, the probability that data belong to the query range after membership testing is:
After finding two bounds 〈α, β〉, master nodes return local results to the sink. Finally, the sink checks result integrity. It is noted that |NHi| ≤ |QH|, so there is pu < pc, i.e., false positives decrease.
6.3. Computational Complexity
We here discuss the computational complexity of c-CPRQ and u-CPRQ. We also report the time complexity of operations in each sensor node for data privacy preservation and the time complexity of operations in each master node for membership testing. Let θ denote the average number of data collected by the sensor node, N denote the average number of data received by the master node, k denote the number of hash functions and m denote the number of bits in a BFcode.
Similar to PRQ, in c-CPRQ, the sensor node needs to generate an encrypted parts and a BFcodes for each datum. The overall time complexity of operations in each sensor node for data privacy preservation is O (θ · k). The master node tests membership with O (m) time. The overall time complexity of operations in each master node for membership testing is O(N · m).
u-CPRQ is different from c-CPRQ in system initialization and membership testing. The sensor node encodes each datum with O(l) time instead of O(k) time, where l(0 < l ≤ k) is the system parameter and denotes the number of hash functions for data encoding. The overall time complexity of operations in each sensor node for data privacy preservation is O(θ ·l). The master node uses the membership test of PRQ. Therefore, the overall time complexity of operations in each master node for membership testing is O(N · m).
7. Schemes for Improvements
Given a certain query range, false positives decrease, but the cost of communication and storage grows as the size of a BFcode increases. In this section, two schemes are proposed to reduce communication cost and false positives. To simplify the description, we take PRQ as an example, but the series of CPRQ protocols can be improved by these schemes.
7.1. Data Compression for Lower Communication Cost
In PRQ, it is difficult to balance efficiency and accuracy. For one thing, fewer false positives require a larger size of a BFcode and higher communication cost for sensor nodes. For another, the size of messages sent by sensor nodes is expected to be as short as possible in order to lessen communication overhead and prolong the network lifetime.
It can be observed that the BFcode is filled with a few 1-bits and an enormous amount of 0-bits, so that data compression [34] is appropriate to find the tradeoff between efficiency and accuracy. Two efficient lossless compression schemes are provided as follows.
Absolute 1-position compression: The BFcode can be represented by a set of positions of 1-bits, rather than the 0-1 string. For example, the BFcode 00001000000000011000000000000010 with four hash functions is represented by 〈5,16,17, 31〉, where 5, 16, 17 and 31 are the positions of 1-bits in the BFcode. Thus, instead of 32 bits, (⌊log2 5⌋ + 1) + (⌊log2 16⌋ + 1) + (⌊log2 17⌋ + 1) + (〈log2 31〉 +1) = 18 bits are enough to represent the original BFcode, and the compression ratio is 32/18 ≈ 1.78. Equations (5) and (6) respectively show the maximum and minimum number of bits required by absolute 1-position compression, where k denotes the number of hash functions, Pj denotes the position of the j-th 1-bit in the BFcode and m denotes the length of an uncompressed BFcode. Bmax bits are needed when all k 1-bits fall into the last k positions of the BFcode, and Bmin bits are needed when all k positions are hashed to the first k positions of the BFcode.
Differential 1-position compression: The BFcode can be represented by differences between two adjacent positions of 1-bits. For instance, the same BFcode mentioned in absolute 1-position compression is encoded to 〈5,11,1,14〉, where 5 is the position of the first 1-bit, while 11, 1 and 14 are the position differences between the second 1-bit and the first 1-bit, the third 1-bit and the second 1-bit and the forth 1-bit and the third 1-bit, respectively. It needs (⌊log2 5⌋ + 1) + (⌊log2 11⌋ + 1) + (⌊log2 1⌋ + 1) + (⌊log2 14⌋ + 1) = 12 bits, and the compression ratio 32/12 ≈ 2.67, which is larger than that of absolute 1-position compression. The maximum number of bits required by differential 1-position compression is illustrated in Equation (7), where P0 = 0. bits are needed when all k 1-bits are distributed uniformly in the BFcode. The minimum number of bits is the same as that in absolute 1-position compression.
The two compression algorithms compress a BFcode with O(m) time by scanning an uncompressed BFcode of m bits. Each sensor node compresses θ data with O(θ · m) time. After data compression, the size of messages is shortened and communication cost is cut down dramatically for sensor nodes. Besides, these two compression schemes are lossless. Thus, master nodes can decompress accurate BFcodes.
7.2. Multiple BFcodes for Fewer False Positives
Assume the query is denoted by 〈T, [a, b]〉. In PRQ, [a, b] is converted to a single BFcode BF[a,b], which is the union of the BFcodes of data in [a, b]. If [a, b] contains more data, more positions of BF[a,b] will be set to 1. The positions, to which data not in [a, b] are hashed, are likely to be set to 1 by the BFcodes of data in [a, b]. As a result, this leads to undesirable false positives.
To reduce false positives, PRQ is improved by constructing multiple BFcodes for the query range [a, b]. The basic idea is: divide all data in [a, b] into w disjoint groups G1,…, Gw (Gi ∩ Gj = Ø, i ≠ j) and then construct a BFcode, denoted as , for each group Gi. Therefore, [a, b] is transformed to w BFcodes. If the original BFcode is of m bits, using w BFcodes to represent [a, b] is equivalent to assigning w × m bits for the original single BFcode. The message that the sink sends to the master node M is changed to:
The data of sensor nodes are still encoded to a BFcode in the way mentioned in Section 5. When a query arrives, master nodes begin to search for the bounds α and β according to Equations (8) and (9).
Assume m is the number of bits in a BFcode. Using the multiple BFcodes scheme, each master node needs O(m · w) time to test the membership of each datum, while false positives are reduced.
The partition of w groups affects the performance of eliminating false positive. Here, we give two schemes. The first scheme separates [a, b] uniformly into w consecutive sub-ranges, which is called consecutive multiple BFcodes (CMB). The second one inserts data into a certain group with a probability 1/w, which is called random multiple BFcodes (RMB). The two schemes are evaluated in Section 9.
8. Theoretical Analysis
Section 3 describes the requirements for a good privacy-preserving range query protocol. Result accuracy is affected by the probability of false positives, which is discussed in Sections 5 and 6. In this section, we analyze efficiency and privacy.
8.1. Efficiency Analysis
In WSNs, communication cost is the main factor to influence the efficiency of a protocol. As in [2–9], we analyze the proposed protocol in terms of communication cost, which is defined as the communication consumption in bits during query processing. It is generated during data submission from sensor nodes to master nodes and result submission from master nodes to the sink, i.e., communication cost of sensor nodes and communication cost of master nodes. The lower the communication cost, the higher the efficiency.
Assume N denotes the number of sensor nodes, le denotes the average length of an encrypted part, m denotes the size of a BFcode, θ denotes the average number of data collected by a sensor node and p denotes the probability that data are considered to be in the query range.
8.1.1. Communication Cost of Sensor Nodes
In any protocol, sensor nodes transmit encrypted data and associated BFcodes to the nearest master nodes, so the communication cost of sensor nodes is:
8.1.2. Communication Cost of Master Nodes
The rules of membership testing influence the accuracy of 〈α, β〉, and thus, the accuracy of 〈α, β〉 affects the communication cost of master nodes. Three cases should be considered: (1) if α > β, the expectation of communication cost is N × 2 × (le + m) × (1 − p)θ; (2) if α = β, the expectation of communication cost is N × 2 × (le + m) × (1 − p)θ−1 × p; and (3) if α < β, the expectation of communication cost is . Therefore, the total communication cost of master nodes is:
Since the accuracies of 〈α, β〉 are different in different protocols, p is protocol-specific.
8.2. Privacy Analysis
First, we analyze privacy under non-collusion conditions and then discuss privacy under node collusion conditions later.
8.2.1. Privacy under Non-Collusion Conditions
Data privacy: In any protocol, original data are stored in the encrypted format and will be disclosed if master nodes have the right key. If the master node knows the length lk of each key, the probability that it guesses the correct data is:
If lk is large enough, the probability is negligible. Furthermore, keys change constantly at different epochs, such that past keys are invalid at the current epoch.
There is another way to obtain original data. If the master node is aware of the hash functions NH for data d and the associated BFd, it can derive from BFd, where m′ is the number of 1-bits in BFd. Each BFcode may be mapped from |NH|! data. Therefore, the probability that the master node guesses the correct data is:
Query privacy: In any protocol, given a query 〈T, [a, b]〉, the sink transforms [a, b] to BF[a,b]. Because BF[a,b] is the union of many BFcodes and each BFcode cannot be distinguished from others, BF[a,b] is meaningless for the master node. Let QH be the hash functions for [a, b]. If the master node knows QH, it can derive from BF[a,b], where m′ is the number of 1-bits in BFa,b]. Each BFcode may be hashed from |QH|! data. Thus, the probability that the master node guesses the correct query range is:
If QH is unavailable, the probability can be neglected.
8.2.2. Privacy under Collusion Conditions
If master nodes collude with sensor nodes, they can obtain the hash functions and deduce original data and the query range by enumeration methods. The key point is to keep adversaries from the hash functions. As mentioned in Section 6, PRQ cannot resist node collusion. We analyze the series of CPRQ protocols.
Assume H is the hash function pool; NH and QH are the hash functions for data and queries, respectively. Since different sensor nodes have different NH, each sensor node cannot infer the real data of others according to the BFcodes. However, H can be deduced by compromising enough sensor nodes; thus, QH or NH may be further guessed by choosing |QH| or |NH| hash functions from H. On the premise of knowing H, the probability that QH is deduced and the probability that NH is deduced are and , respectively. Now, we discuss how many sensor nodes are needed to figure out H. This is an instance of the coupon collector's problem [35].
Let x be the number of collusive sensor nodes and be the number of different hash functions obtained by these x sensor nodes. Assume , i.e., , . Equation (15) indicates the probability that x nodes collude to gain |NH| + x − 1 different hash functions after x − 1 nodes get |NH| + x − 2 different ones.
To get H, the expected number of collusive sensor nodes, denoted as
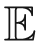
Since limited sensor nodes and master nodes could be compromised by adversaries, if
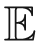
9. Evaluation
As mentioned in Section 2, node collusion is not taken into account in previous related work. Therefore, we first analyze the parameters of improvements and then evaluate PRQ by comparing with Encoding [2], ST-crosscheck [3] and SafeQ [6] under non-collusion conditions and, finally, contrast the series of CPRQ protocols with PRQ considering collusion attacks. Performance is thoroughly evaluated on the same two-tiered model in terms of efficiency, accuracy and privacy.
All protocols are implemented on OMNet++4.1, a widely-used simulator for WSNs. The network is set to 400 m × 400 m. Sensor nodes are uniformly deployed in the network, and the number of sensor nodes changes from 200 to 600. Assume that the network is separated into four identical cells and a master node is at the center of each cell. The transmission radius of each sensor node is 50 m. The real dataset, LUCE (Lausanne Urban Canopy Experiment) [36], is used in the experiments. LUCE is a measurement campaign, which took place on the EPFLcampus from July 2006, to May 2007, and aimed at better understanding micrometeorology and atmospheric transport in the urban environment. It contains 97 sensor nodes, but we need more sensor nodes. Therefore, we use data collected in LUCE. We adopt the revised Bernstein hash [37], which holds the property that for any hash function hi and hj (i ≠ j), there is hi(d) = hj(d). Unless there is a particular specification, our protocols encode data and queries to a BFcode of 128 bits by using four hash functions, while the data domain is partitioned into 10 buckets for Encoding and ST-crosscheck.
9.1. Parameters of Improvements
To simplify the description, we also take PRQ as an example, but these schemes are able to improve the series of CPRQ protocols.
9.1.1. Data Compression
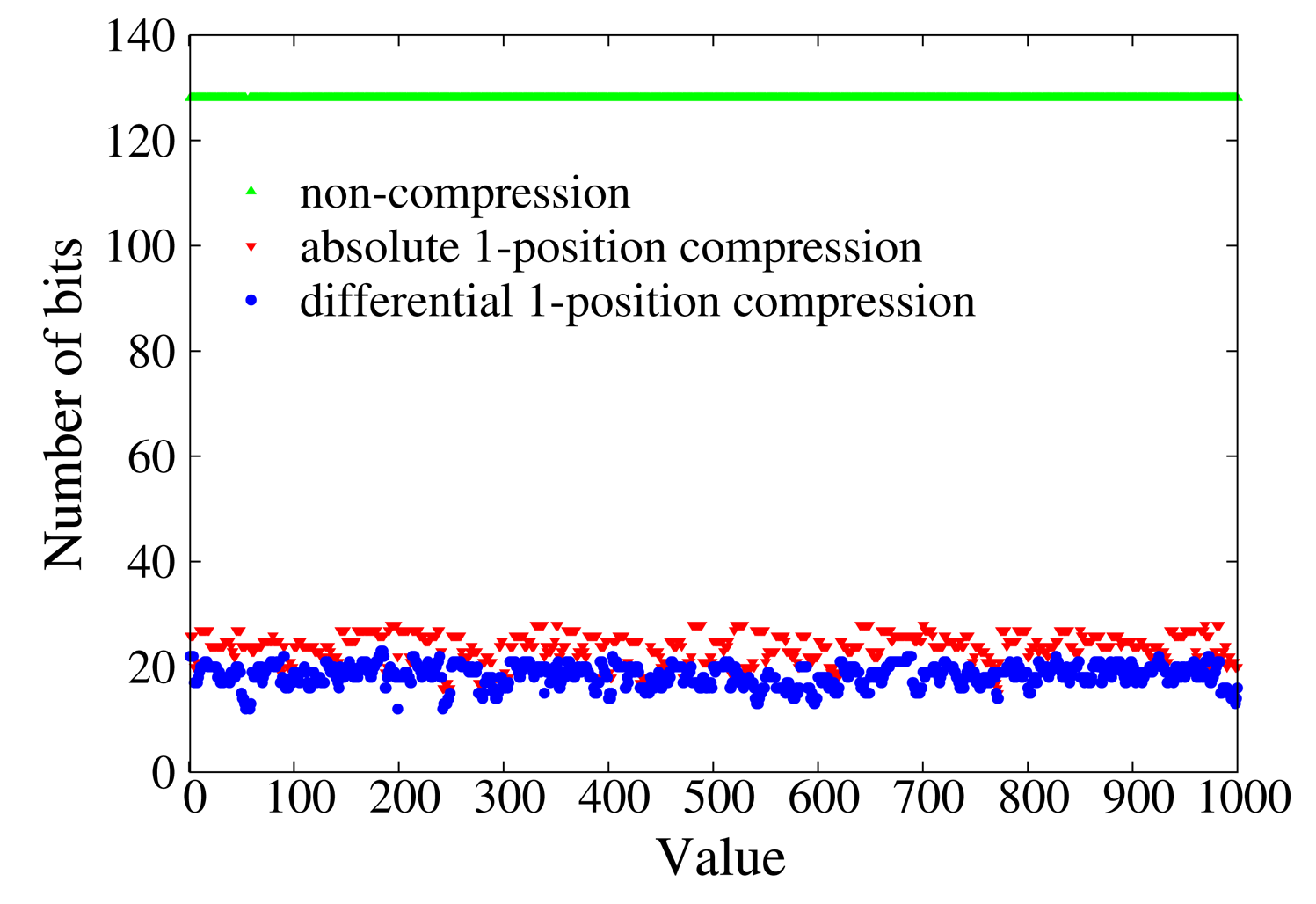
Data compression is theoretically confirmed to be efficient enough to shorten the size of messages sent by sensor nodes in Section 7. The two proposed data compression schemes and the non-compression scheme are compared in Figure 3 by compressing BFcodes of integers in [0, 1000]. The size of an uncompressed BFcode is 128 bits, and 4 revised Bernstein hash functions [37] are used to encode data. Absolute 1-position compression compresses a BFcode to about 18 bits, while differential 1-position compression compresses that to about 24 bits. We define the compression ratio as the ratio of the number of bits of an uncompressed BFcode to the number of bits of a compressed BFcode. The larger the compression ratio, the shorter the message and the less the communication cost. The compression ratio of absolute 1-position compression and differential 1-position compression are about 7 and 5, respectively. It is obvious that differential 1-position compression can make messages shorter and save more on the communication cost. Our protocols adopt differential 1-position compression.
9.1.2. Multiple BFcodes
Given a query range [a, b], result accuracy is affected by false positives. The probability of false positives is defined as the ratio of the number of unsatisfactory data in the result to the number of data in the result. The fewer the false positives, the better the accuracy.
Figure 4 demonstrates the impact of multiple BFcodes on false positives. In this experiment, the size of a BFcode is 128 bits. The data domain is [0, 1000]. We randomly choose 10 ranges in the data domain for each proportion of a query range and take the average probability of false positives. w (w = 1,2, 3) denotes the number of BFcodes for queries. Consecutive multiple BFcodes (CMB) and random multiple BFcodes (RMB) are the proposed partition schemes of a query range.
Given w, the probability of false positives first increases and then declines. Sensor nodes generate the same data for different proportions of the query range [a, b]. When the proportion is small, few data are included in [a, b], such that few bits of BF[a,b] are set to 1 and lots of unsatisfactory data are filtered out correctly. When the proportion increases to a certain extent, the probability of false positives peaks. The reason is that more bits of BF[a,b] are set to 1, failing to filter unsatisfactory data out. As the proportion continues growing, more bits of BF[a,b] are set to 1, but the probability of false positives decreases, because more and more data really belong to [a, b].
Given the partition scheme, the probability of false positives with w = 2, 3 is smaller than that with w = 1, because the scheme using w BFcodes potentially assigns w×m bits for the BFcode of [a, b]. For a certain w, RMB produces fewer false positives than CMB. This may be explained by the reason that adjacent data are likely to be hashed to similar positions, and RMB divides [a, b] randomly to eliminate the position correlation. It is found that the probability of false positives with w = 2 is similar to that with w = 3. In the meanwhile, the computational cost of master nodes increases as w grows. After comprehensive consideration, our protocols use the scheme with RMB and w = 2.
9.2. Performance Evaluation under Non-Collusion Conditions
9.2.1. Efficiency
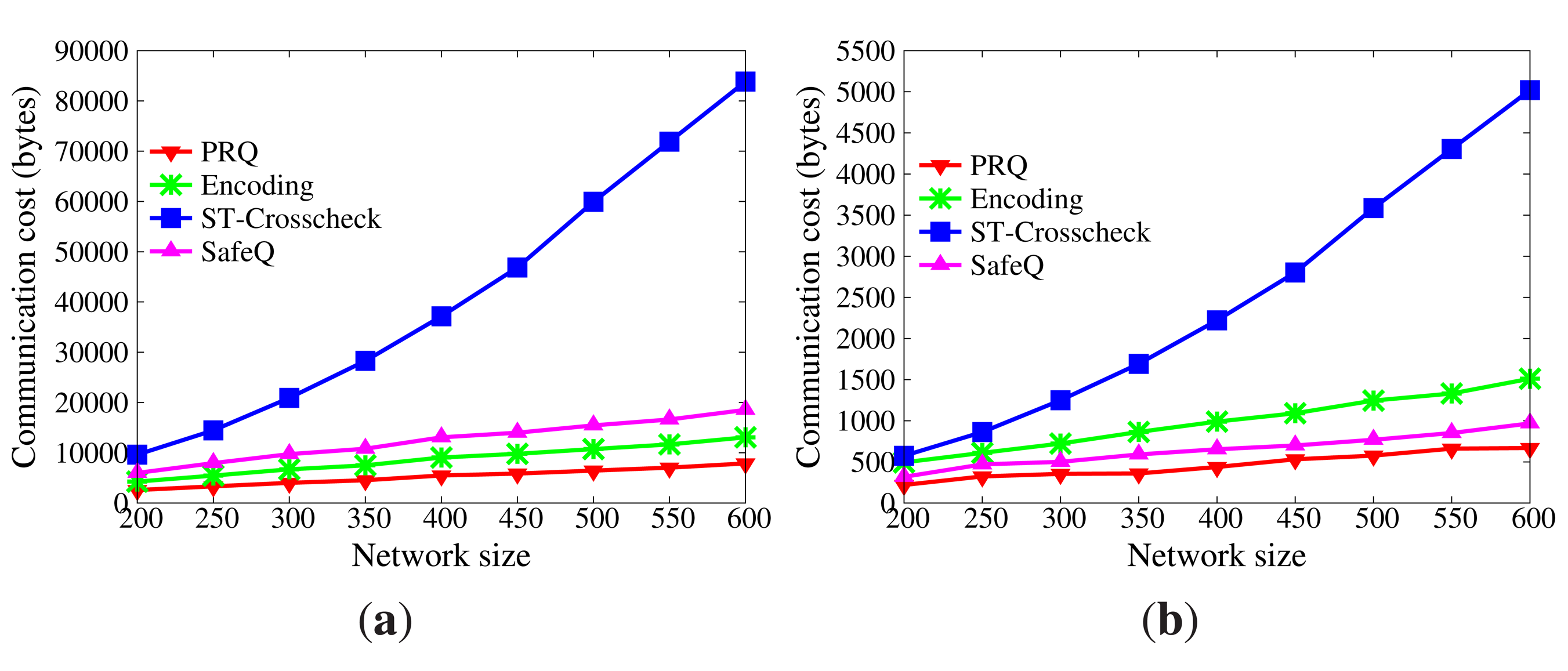
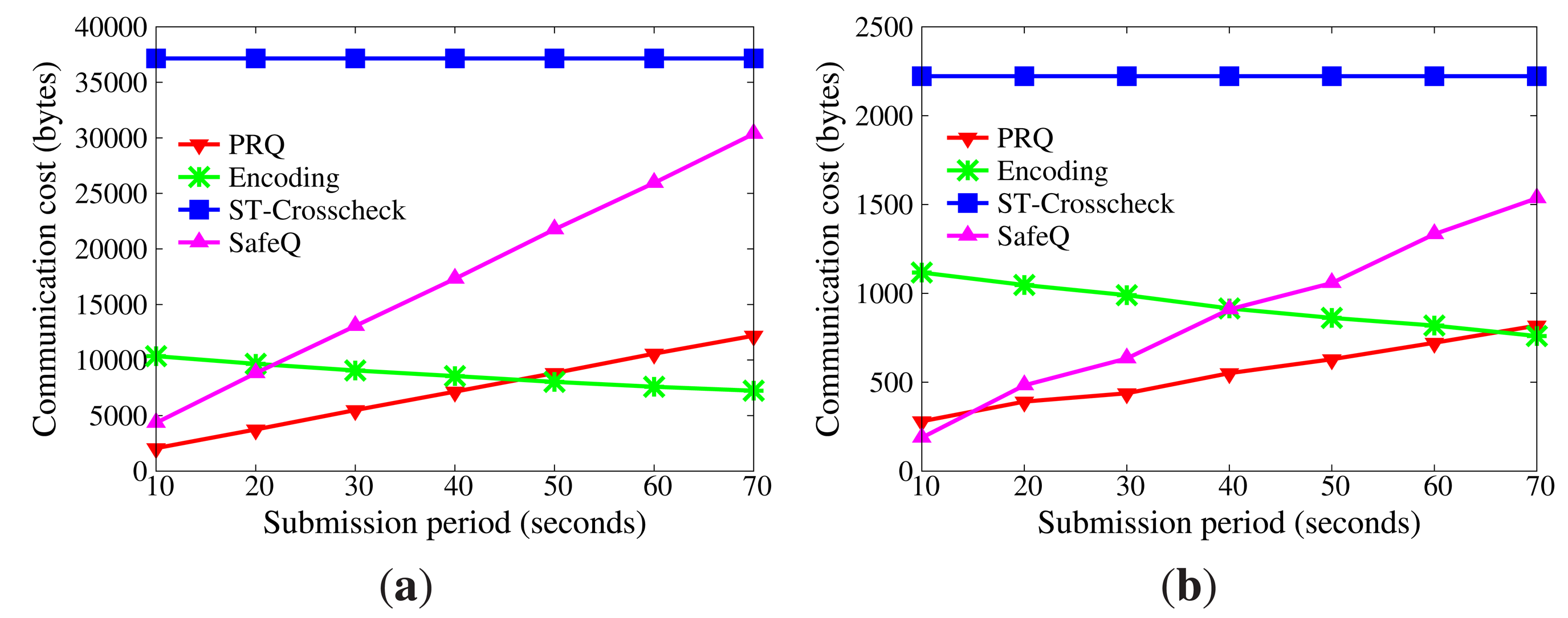
In WSNs, communication is the dominant factor of energy consumption. The lower the communication cost, the better the efficiency Figure 5 displays the impact of network size on communication cost without collusion attacks (the submission period is 30 s). As the size of the network grows, more data are transmitted from sensor nodes to master nodes, and more data stored in master nodes satisfy the query range. Therefore, communication cost increases. Besides, the communication cost of sensor nodes goes far beyond that of master nodes, because master nodes only submit satisfactory data. It is evident that the communication cost of sensor nodes in PRQ is much less than that of other protocols. In ST-crosscheck, each bucket of sensor nodes attaches the bucket information of all neighbors, and its communication cost of sensor nodes is related to the product of the number of their neighbors and the square of the bucket number. In Encoding, the more the empty buckets, the more the attached codes. SafeQ constructs a prefix family for data as the attached code. Given the data d, their prefix family needs (⌊log2 d⌋ + 1)2 bits. However, PRQ just appends a compressed BFcode to the data.
Figure 6 demonstrates the impact of submission period on communication cost without node collusion (the network size is 400). The submission period is defined as the interval time between two successive submissions. It is observed that the submission period has no effect on the communication cost of the sensor node in ST-crosscheck, because it is only related to the number of neighbors and the number of buckets. Due to the reduction of empty buckets, the communication cost of sensor nodes in Encoding decreases as the submission period increases, which is opposite to what occurs in PRQ and SafeQ. When the submission period is below 40 s, the communication cost of sensor nodes in PRQ is less than the others. When the submission period continues growing, the communication cost of sensor nodes in PRQ increases slowly. Each datum d in SafeQ needs to attach (⌊log2 d⌋ + 1) prefix-membership codes, whereas only one compressed BFcode is appended in our PRQ.
Under non-collusion conditions, PRQ saves more communication cost and energy consumption than others.
9.2.2. Accuracy
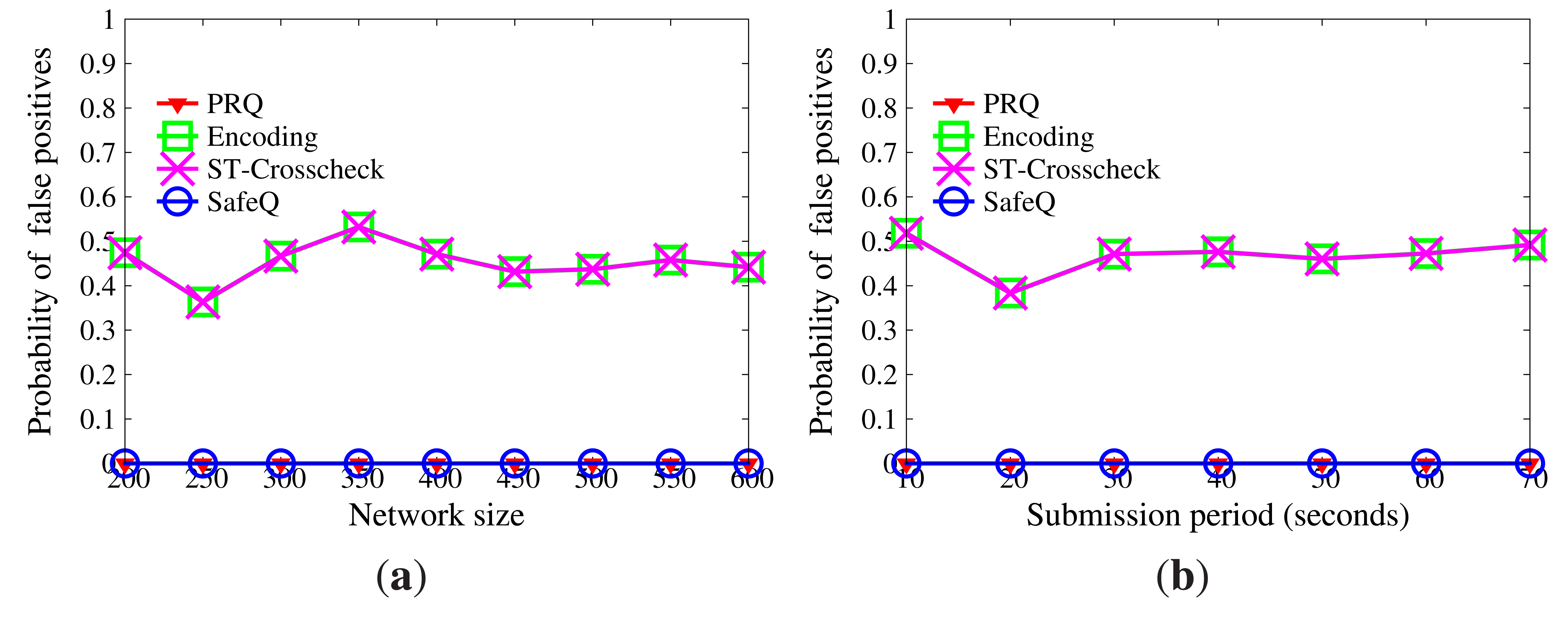
Incomplete results can be detected in PRQ, Encoding, ST-crosscheck and SafeQ, but false positives are difficult to eliminate. The probability of false positives is defined the same as in Section 9.1.2. The lower probability of false positives, the higher the accuracy.
Figure 7 reveals how the probability of false positives is influenced by network size and submission period. The result of SafeQ is accurate, and there are no false positives. Encoding and ST-crosscheck are built on the bucketing technique, which has a great effect on accuracy. The more the buckets, the fewer the false positives, but the weaker the privacy. On account of multiple BFcodes, PRQ achieves accurate results, as SafeQ does. Besides, the network size and submission period have no impact on the probability of false positives.
9.2.3. Privacy
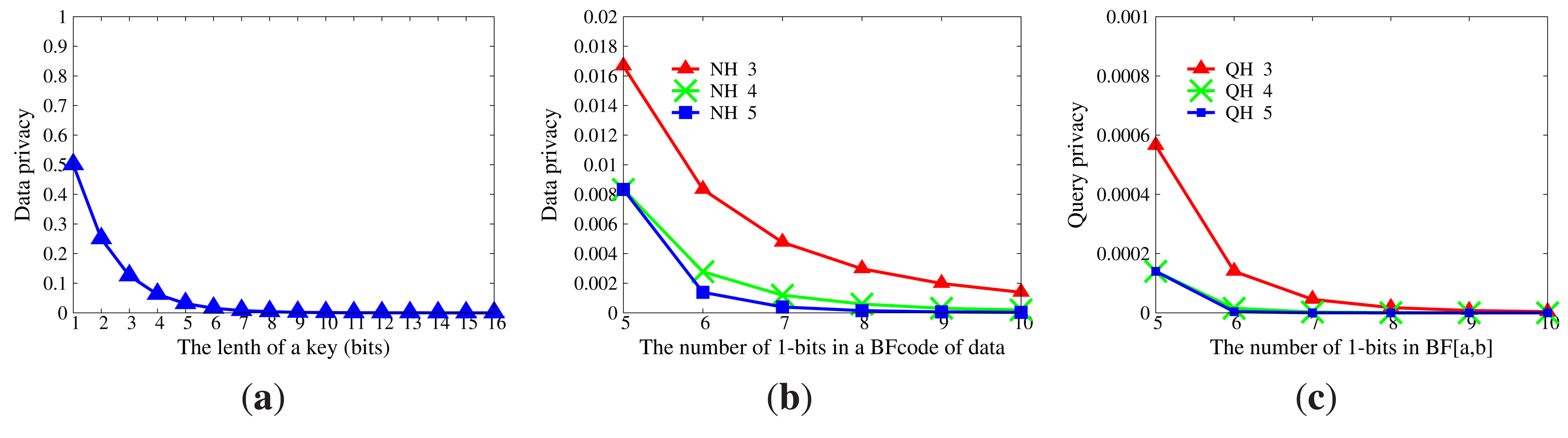
Data privacy will be disclosed if master nodes acquire either the correct key or the correct hash functions NH for data encoding, as mentioned in Section 8.2.1. The privacy of data is shown in Figure 8a,b. The probability that master nodes can decrypt data correctly is extremely tiny if the length of a key is large than 8 bits. The probability that master nodes can guess actual data upon their BFcodes and right hash functions NH is less than 0.01 when |NH| ≥ 4. Figure 8c displays the privacy intensity of queries. For a certain range [a, b], it is obvious that the probability that [a, b] is deduced from the BF[a,b] can be neglected, even though the set of hash functions QH for query encoding is reachable.
9.3. Performance Evaluation under Collusion Conditions
In the following experiments, in PRQ, c-CPRQ and u-CPRQ, the number k of hash functions for query encoding is set to 4. Since the parameter l in c-CPRQ satisfies 0 < l < k and l in u-CPRQ satisfies 0 < l ≤ k, we set l = 3.
9.3.1. Efficiency
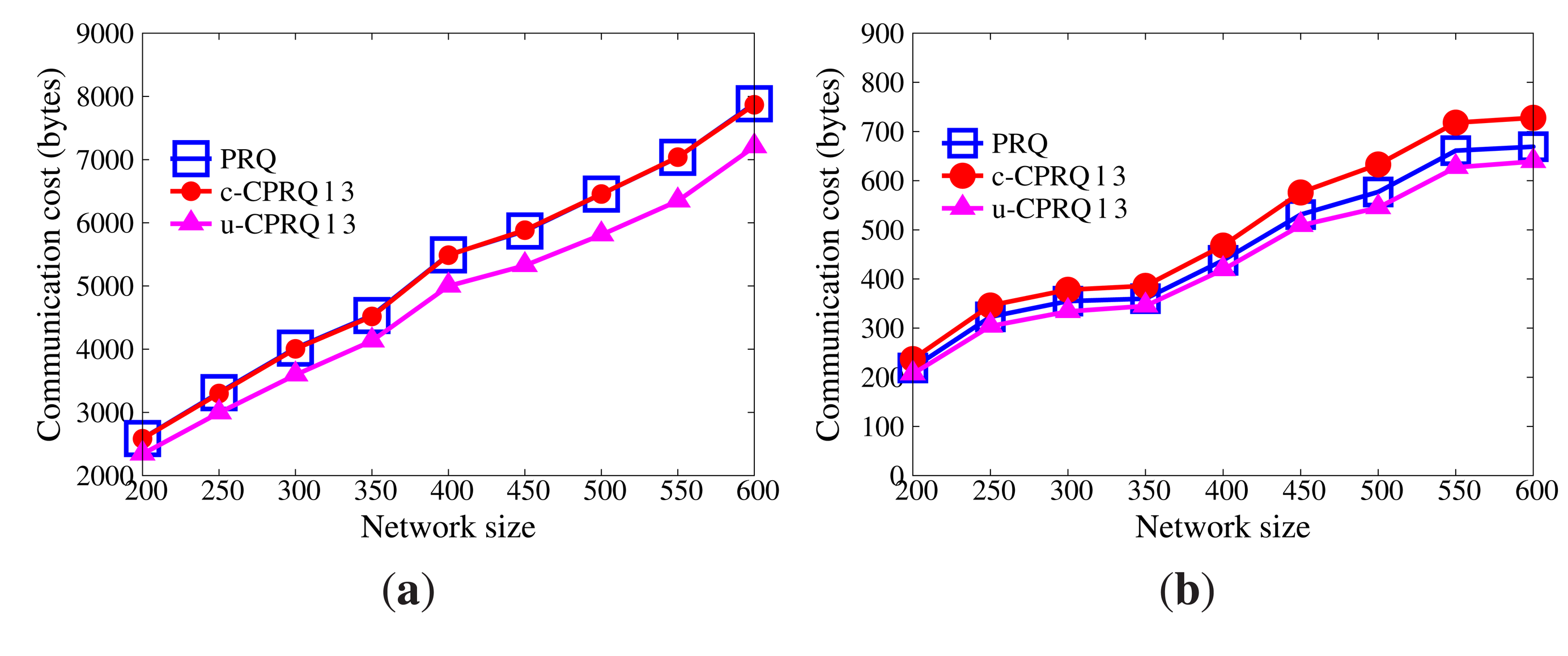
Node collusion may be destructive. The series of CPRQ protocols not only preserves privacy and integrity, but also resists collusion attacks, while PRQ is disabled under collusion conditions.
Figures 9 and 10 demonstrate the communication cost of the series of CPRQ protocols compared with PRQ. It is observed that the communication cost of sensor nodes in u-CPRQ is less than those in c-CPRQ and PRQ. Sensor nodes transmit all encrypted data and corresponding BFcodes to master nodes. Since the size of the encrypted part for each protocol is identical, the size of a compressed BFcode determines the communication cost of sensor nodes. Because the number of hash functions for data in u-CPRQ is less than those in c-CPRQ and PRQ, the size of a compressed BFcode in u-CPRQ is smaller than those of others. Besides, this shows that the communication cost of master nodes in PRQ is less than that in c-CPRQ, but is greater than that in u-CPRQ. Since c-CPRQ adopts a relaxed membership test, it produces more false positives than PRQ. The size of a compressed BFcode in u-CPRQ is smaller than that of PRQ, such that the communication cost of master nodes in u-CPRQ is less than that in PRQ.
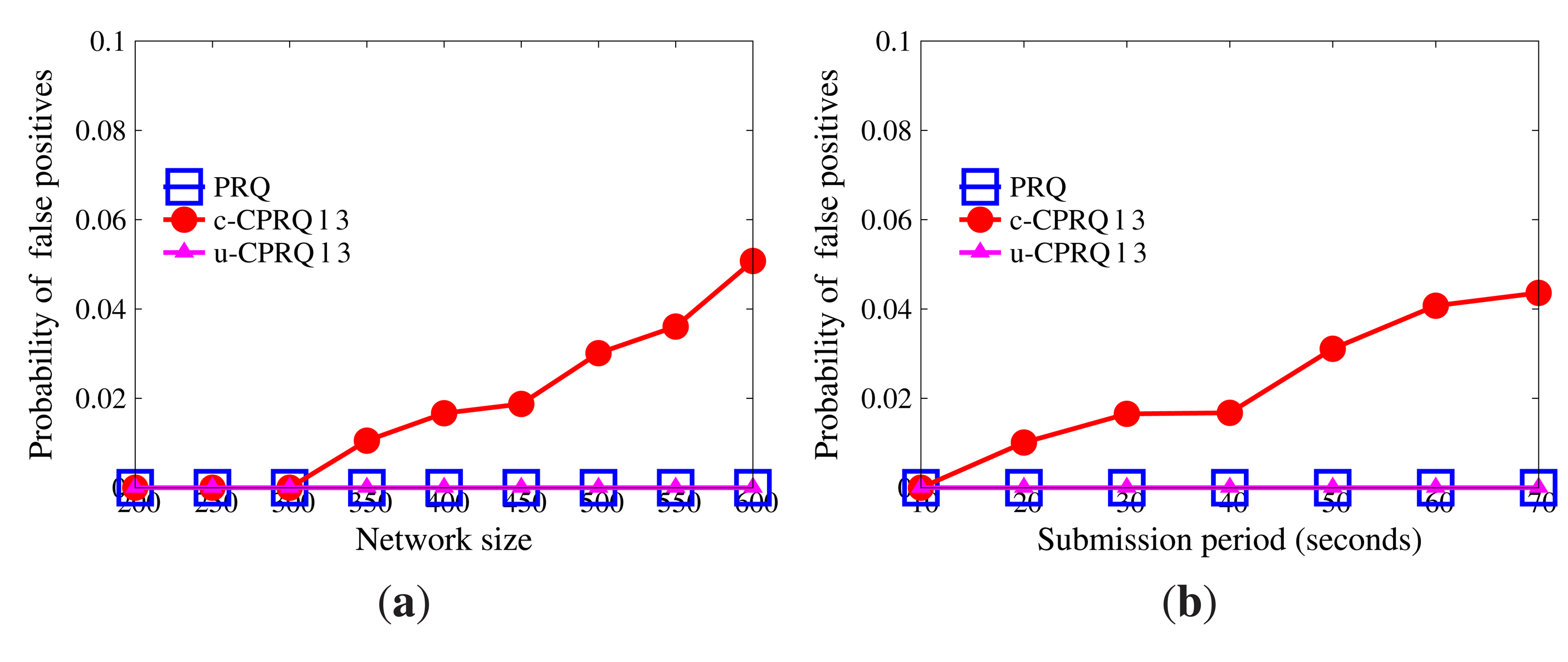
9.3.2. Accuracy
Given a range query, the definition of the probability of false positives is the same as that in Section 9.1.2. Figure 11 indicates the probability of false positives. It can be seen that the probability of false positives in both u-CPRQ and PRQ is 0%, while that in c-CPRQ increases with the growth of the network size and submission period. The reason is that the relaxed membership test in c-CPRQ brings in false positives, and there are no false positives generated in PRQ and u-CPRQ based on the precise bounds. However, u-CPRQ and c-CPRQ can resist collusion attacks, while PRQ cannot. c-CPRQ is also acceptable for users if the probability of false positives in c-CPRQ is small enough.
9.3.3. Privacy
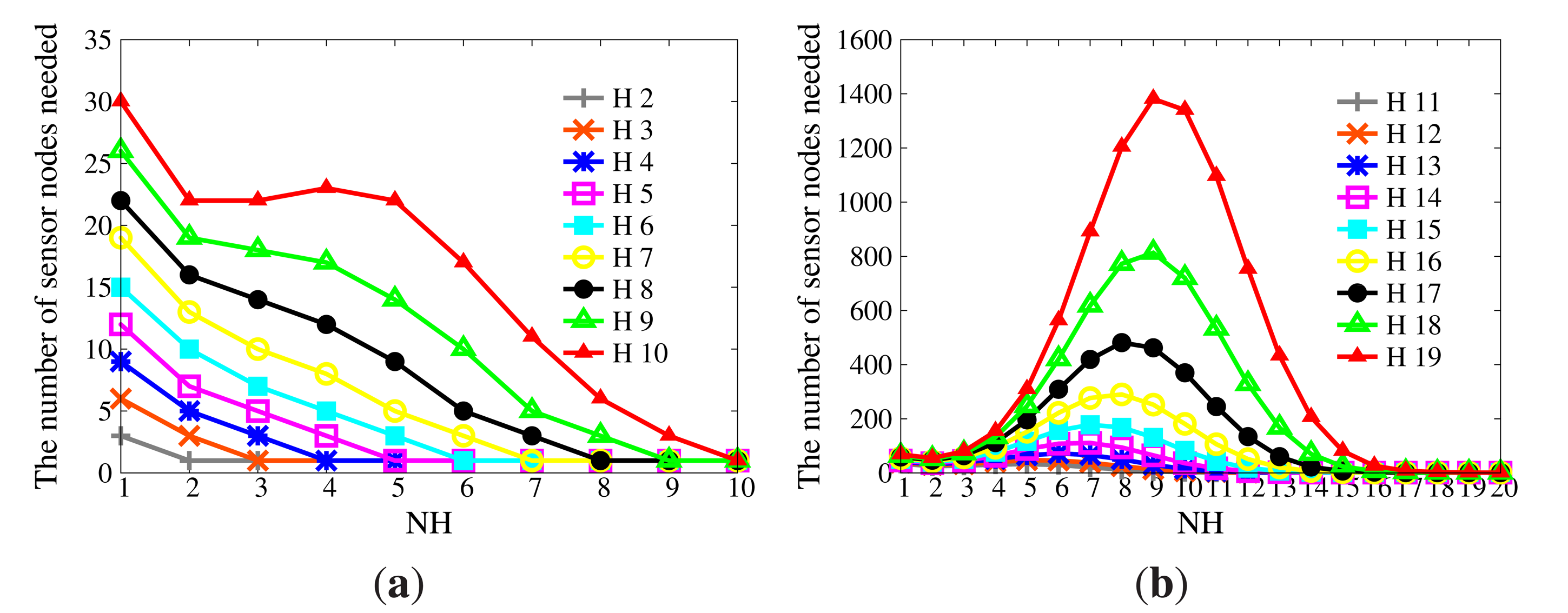
If there are sufficient collusive sensor nodes, H will be inferred based on NH. The expectation of the number of sensor nodes needed to infer H is provided in Figure 12. When |H| is large enough, it becomes a bell curve, whose axis of symmetry is the line |NH| = |H|/2. Thus, |NH| should be selected from the left side of the axis of symmetry in order to control the size of the compressed BFcode. To guarantee the availability of WSNs, the number of collusive sensor nodes should be limited. For example, the size of the network is 1000, and at most, 10% of sensor nodes will be compromised. Given |H| = 20, if |NH| = 4, at least 179 sensor nodes are needed, while if |NH| = 10, at least 2397 sensor nodes are needed. Due to the limited attack ability, it is impossible for adversaries to compromise so many sensor nodes. Therefore, the series of CPRQ can prevent collusion attacks.
From the above, c-CPRQ and u-CPRQ are robust to collusion attacks, while preserving privacy and integrity. Especially u-CPRQ outperforms PRQ in terms of efficiency, accuracy and privacy. If the probability of false positives is very small, c-CPRQ is also a good choice for users.
10. Conclusions
Privacy issues restrict the widespread adoption of WSNs and even threaten the security of the IoT. In this paper, we propose a privacy-preserving range query protocol, PRQ, and then present a series of collusion-aware privacy-preserving range query protocols: c-CPRQ and u-CPRQ. To the best of our knowledge, this paper is the first to take collusion attacks into account for a privacy-preserving range query in tiered WSNs. In our protocols, data and queries are represented by BFcodes to hide the original information, while result integrity is verified through ordinal relation among data. In the series of CPRQ protocols, sensor nodes use diverse hash functions to prevent node collusion. The performance of our proposals is evaluated by comparing with Encoding, ST-crosscheck and SafeQ. Theoretical analysis and simulation results demonstrate the high performance of our protocols in terms of efficiency, accuracy and privacy. In the future, we will focus on the privacy preservation of more complex queries, such as top-k and kNN, in two-tiered WSNs. For these two queries, the final result relies on global comparison information. It is challenging to compare data without information leakage and to achieve accurate results.
Appendix
A. Proof of Theorem 1
Proof
We prove the theorem using reduction to absurdity. Assume ∃d′ ϵ [a, b] satisfying BFd′ ∩ BF[a,b] ≠ BFd′. Because BF[a,b] = ∪dϵ|a,b|BFd, we have:
B. Derivation of pp
Given a large enough m, we can construct k hash functions h1, …, hk, holding the property that ∀d, hi(d) ≠ hj(d) (1 ≤ i ≠ j ≤ k), which is different from hash functions in [33].
The probability that the i-th 1-bit of BFd is 0 in BF[a,b] is . In other words, the probability that the i-th 1-bit of BFd is 1 in BF|a,b| is . The probability that all 1-bits of BFd are 1 in BF[a,b] is .
C. Proof of Theorem 2
Proof
We prove the theorem using reduction to absurdity.
Assume ∃d′ ∈ [a, b] satisfying η < |I H|. According to the construction of BF[a,b], BF[a,b] = ∪dϵ|a,b|BFd. That means the positions to which d′ is mapped are set to 1 in BF|a,b|. Let denote the BFcode of X using hash function set H♯. Then, we have:
Let n1, n2, n3 and n4 denote the number of 1-bits in , , and , respectively. For any hash functions hi and hj (i ≠ j), there is hi(d′) ≠ hj(d′). Hence, we have that: n1 = |IH|, 0 ≤ n2 ≤ min{|IH|, |NH\IH|}, 0 ≤ n3 ≤ min{|IH|, |QH\IH|} and 0 ≤ n4 ≤ min{|NH\IH|,|QH\IH|}. That is, ηd ≥ |IH|, which contradicts the assumption. Therefore, d′ ∉ [a, b], i.e., if η < |IH|, there must be d ∉ [a, b].
Acknowledgments
This work is supported by the National High Technology Research and Development Program of China (863 Program) (No. 2014AA015204), the National Basic Research Program of China (973 Program) (No. 2012CB316205), the National Natural Science Foundation of China (Grant Nos. 61070056, 61033010, 61272137, 61202114) and the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (10XNI018). This work was partially done when the authors visited SACenter for Big Data Research hosted at Renmin University of China. This Center is partially funded by the Chinese National “111” Project “Attracting International Talents in Data Engineering and Knowledge Engineering Research”.
Author Contributions
Xiaoying Zhang conceived of and designed the protocol. Lei Dong designed and performed the experiments. Xiaoying Zhang, Hui Peng and Suyun Zhao analyzed and proved the theorems. All of the authors discussed the results and co-wrote and commented on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Paek, J.; Greenstein, B.; Gnawali, O.; Jang, K.Y.; Joki, A.; Vieira, M.A.M.; Hicks, J.; Estrin, D.; Govindan, R.; Kohler, E. The Tenet architecture for tiered sensor networks. ACM Trans. Sens. Netw. 2010, 6, 34. [Google Scholar]
- Sheng, B.; Li, Q. Verifiable Privacy-Preserving Range Query in Two-Tiered Sensor Networks. Proceedings of the IEEE International Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 46–50.
- Shi, J.; Zhang, R.; Zhang, Y. Secure Range Queries in Tiered Sensor Networks. Proceedings of the IEEE International Conference on Computer Communications, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 945–953.
- Zhang, R.; Shi, J.; Zhang, Y. Secure multidimensional range queries in sensor networks. Proceedings of the ACM International Symposium on Mobile Ad Hoc Networking and Computing, Hong Kong, China, 18–21 May 2009; pp. 197–206.
- Chen, F.; Liu, A.X. SafeQ: Secure and Efficient Query Processing in Sensor Networks. Proceedings of the IEEE International Conference on Computer Communications, San Diego, CA, USA, 15–19 March 2010; pp. 2642–2650.
- Chen, F.; Liu, A.X. Privacy and integrity-preserving range queries in sensor networks. IEEE/ACM Trans. Netw. 2012, 20, 1774–1787. [Google Scholar]
- Nguyen, T.D.; Bui, TV.; Dang, V.H.; Choi, D. Efficiently Preserving Data Privacy Range Queries in Two-Tiered Wireless Sensor Networks. Proceedings of the International Conference on Ubiquitous Intelligence and Computing and International Conference on Autonomic and Trusted Computing, Fukuoka, Japan, 4–7 September 2012; pp. 973–978.
- Li, R.; Lin, Y.; Yi, Y.; Hu, Y. A Privacy and Integrity Preserving Range Query Protocol in Two-Tiered Sensor Networks. Chin. J. Comput. 2013, 36, 1194–1209. [Google Scholar]
- Zhang, X.; Dong, L.; Peng, H.; Chen, H.; Li, D.; Li, C. Achieving Efficient and Secure Range Query in Two-Tiered Wireless Sensor Networks. Proceedings of the IEEE/ACM International Symposium on Quality of Service, Hong Kong, China, 26–27 May 2014; pp. 380–388.
- Li, N.; Zhang, N.; Das, S.K.; Thuraisingham, B. Privacy preservation in wireless sensor networks: A state-of-the-art survey. Ad. Hoc. Netw. 2009, 7, 1501–1514. [Google Scholar]
- He, W.; Liu, X.; Nguyen, H.; Nahrstedt, K.; Abdelzaher, T.F. PDA: Privacy-Preserving Data Aggregation in Wireless Sensor Networks. Proceedings of the IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 2045–2053.
- He, W.; Nguyen, H.; Liu, X.; Nahrstedt, K.; Abdelzaher, T. iPDA: An Integrity-Protecting Private Data Aggregation Scheme for Wireless Sensor Networks. Proceedings of the IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008; pp. 1–7.
- Groat, M.M.; He, W.; Forrest, S. KIPDA: k-Indistinguishable Privacy-Preserving Data Aggregation in Wireless Sensor Networks. Proceedings of the IEEE International Conference on Computer Communications, Shanghai, China, 10–15 April 2011; pp. 2024–2032.
- Yao, Y.; Xiong, N.; Park, J.H.; Ma, L.; Liu, J. Privacy-preserving max/min query in two-tiered wireless sensor networks. Comput. Math. Appl. 2013, 65, 1318–1325. [Google Scholar]
- Zhang, W.; Wang, C.; Feng, T. GP2S: Generic Privacy-Preservation Solutions for Approximate Aggregation of Sensor Data. Proceedings of the IEEE Pervasive Computing and Communications, Hong Kong, China, 17–21 March 2008; pp. 179–184.
- Roy, S.; Conti, M.; Setia, S.; Jajodia, S. Secure Data Aggregation in Wireless Sensor Networks. IEEE Trans. Inf. Foren. Sec. 2012, 7, 1040–1052. [Google Scholar]
- Zhang, X.; Chen, H.; Wang, K.; Peng, H.; Fan, Y.; Li, D. Rotation-Based Privacy-Preserving Data Aggregation in Wireless Sensor Networks. Proceedings of the IEEE International Conference on Communications, Sydney, Australia, 10–14 June 2014; pp. 4184–4189.
- Castelluccia, C.; Mykletun, E.; Tsudik, G. Efficient aggregation of encrypted data in wireless sensor networks. Proceedings of the International Conference Mobile and Ubiquitous Systems: Networking and Services, San Diego, CA, USA, 17–21 July 2005; pp. 109–117.
- Girao, J.; Westhoff, D.; Schneider, M. CDA: Concealed data aggregation for reverse multicast traffic in wireless sensor networks. Proceedings of the IEEE International Conference on Communications, Seoul, Korea, 16–20 May 2005; pp. 3044–3049.
- Stavros, P.; Kiayias, A.; Papadias, D. Secure and efficient in-network processing of exact SUM queries. Proceedings of the IEEE International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 517–528.
- Chen, C.; Lin, Y.; Lin, Y.; Sun, H. RCDA: Recoverable Concealed Data Aggregation for Data Integrity in Wireless Sensor Networks. IEEE Trans. Parall. Distr. 2012, 23, 727–734. [Google Scholar]
- Dai, H.; Qin, X.L.; Liu, L.; Ji, Y.M.; Fu, X.; Sun, Y. Z-O Encoding Based Privacy-Preserving MAX/MIN Query Protocol in Two-Tiered Wireless Sensor Networks. J. Electron. Inf. Technol. 2013, 35, 970–976. [Google Scholar]
- Zhang, R.; Shi, J.; Liu, Y.; Zhang, Y. Verifiable Fine-Grained Top-k Queries in Tiered Sensor Networks. Proceedings of the IEEE International Conference on Computer Communications, San Diego, CA, USA, 15–19 March 2010; pp. 1199–1207.
- Yongjian, F.; Hong, C. Verifiable Privacy-Preserving Top-k Query Protocol in Two-Tiered Sensor Networks. Chin. J. Comput. 2012, 35, 423–433. [Google Scholar]
- Liao, X.; Li, J. Privacy-Preserving and Secure Top-k Query in Two-Tier Wireless Sensor Network. Proceedings of the IEEE Global Communications Conference, Anaheim, CA, USA, 3–7 December 2012; pp. 335–341.
- Zhou, T.; Lin, Y.; Zhang, W.; Xiao, S.; Li, J. Secure and Verifiable Top-k Query in Two-Tiered Sensor Networks. Proceedings of the Security and Privacy in Communication Networks, Sydney, Australia, 25–28 September 2013; pp. 19–34.
- Yu, C.; Ni, G.; Chen, I.; Gelenbe, E.; Kuo, S.Y. Top-k Query Result Completeness Verification in Tiered Sensor Networks. IEEE Trans. Inf. Foren. Sec. 2014, 9, 109–124. [Google Scholar]
- Cheng, J.; Yang, H.; Wong, S.H.Y.; Zerfos, P.; Lu, S. Design and Implementation of Cross-Domain Cooperative Firewall. Proceedings of the International Conference on Network Protocols, Beijing, China, 16–19 October 2007; pp. 284–293.
- Liu, A.X.; Chen, F. Collaborative enforcement of firewall policies in virtual private networks. Proceedings of the ACM Symposium on Principles of Distributed Computing, Toronto, ON, Canada, 18–21 August 2008; pp. 95–104.
- Zhu, Z.; Cao, G. Toward Privacy Preserving and Collusion Resistance in a Location Proof Updating System. IEEE Trans. Mob. Comput. 2013, 12, 51–64. [Google Scholar]
- Szewczyk, R.; Ferencz, A. In Energy Implications of Network Sensor Designs; Technical Report; Berkeley Wireless Research Center Report. Santa Clara, CA, USA, 2000. [Google Scholar]
- Bloom, B.H. Space/Time Trade-Offs in Hash Coding with Allowable Errors. Commun. ACM 1970, 13, 422–426. [Google Scholar]
- Li, F.; Cao, P.; Almeida, J.; Broder, A.Z. Summary cache: A scalable wide-area web cache sharing protocol. IEEE/ACM Trans. Netw. 2000, 8, 281–293. [Google Scholar]
- Sayood, K. Introduction to Data Compression, 3rd ed; Morgan Kaufmann: San Francisco, CA, USA; 15; December; 2005. [Google Scholar]
- Papanicolaou, V.G.; Kokolakis, G.E.; Boneh, S. Asymptotics for the random coupon collector problem. J. Comput. Appl. Math. 1998, 93, 95–105. [Google Scholar]
- LUCE Deployment. Available online: http://lcav.epfl.ch/cms/lang/en/pid/86035 (accessed on 15 September 2014).
- Bernstein, D.J. Bernstein Hash. Available online: http://www.cse.yorku.ca/oz/hash.html (accessed on 15 September 2014).




| Symbol | Meaning |
|---|---|
| H | hash function pool |
| hi | a hash function in H |
| t | an epoch |
| T | a time slot |
| M | a master node |
| si | a sensor node with the unique identifier i |
| ki,t | a secret key of si at epoch t |
| dj | the j-th data of si |
| BFd | BFcode of data d |
| [a, b] | a query range |
| BF[a,b] | BFcode of range [a, b] |
| E() | an encryption function |
| QH | hash function set for queries |
| NHi | hash function set for data of si |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Dong, L.; Peng, H.; Chen, H.; Zhao, S.; Li, C. Collusion-Aware Privacy-Preserving Range Query in Tiered Wireless Sensor Networks. Sensors 2014, 14, 23905-23932. https://doi.org/10.3390/s141223905
Zhang X, Dong L, Peng H, Chen H, Zhao S, Li C. Collusion-Aware Privacy-Preserving Range Query in Tiered Wireless Sensor Networks. Sensors. 2014; 14(12):23905-23932. https://doi.org/10.3390/s141223905
Chicago/Turabian StyleZhang, Xiaoying, Lei Dong, Hui Peng, Hong Chen, Suyun Zhao, and Cuiping Li. 2014. "Collusion-Aware Privacy-Preserving Range Query in Tiered Wireless Sensor Networks" Sensors 14, no. 12: 23905-23932. https://doi.org/10.3390/s141223905
APA StyleZhang, X., Dong, L., Peng, H., Chen, H., Zhao, S., & Li, C. (2014). Collusion-Aware Privacy-Preserving Range Query in Tiered Wireless Sensor Networks. Sensors, 14(12), 23905-23932. https://doi.org/10.3390/s141223905




