Ecological Systems as Complex Systems: Challenges for an Emerging Science
Abstract
:1. Introduction
2. Contribution of CSS to Ecology
2.1. Simple Measures and Models
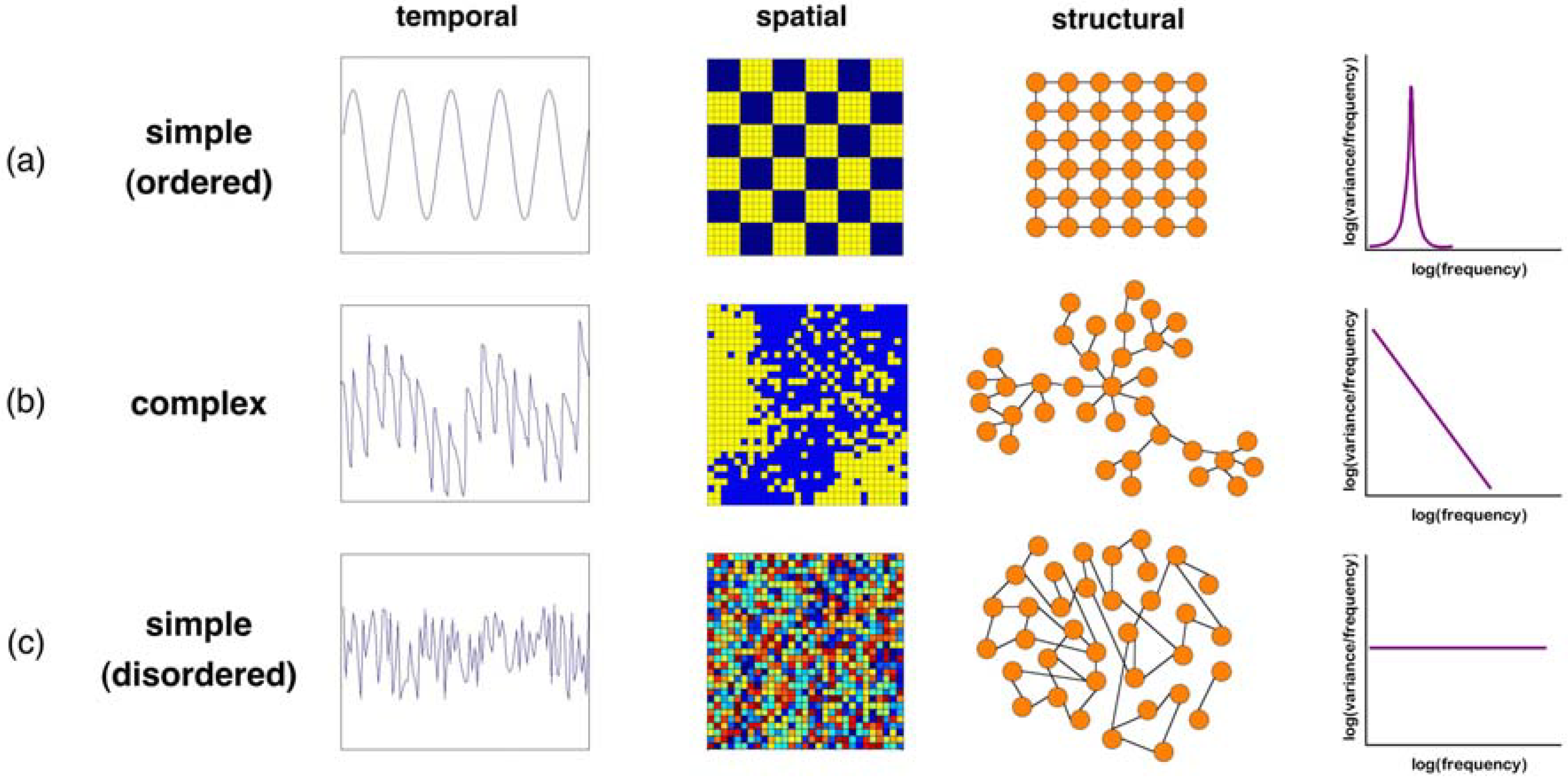
2.2. Food Webs
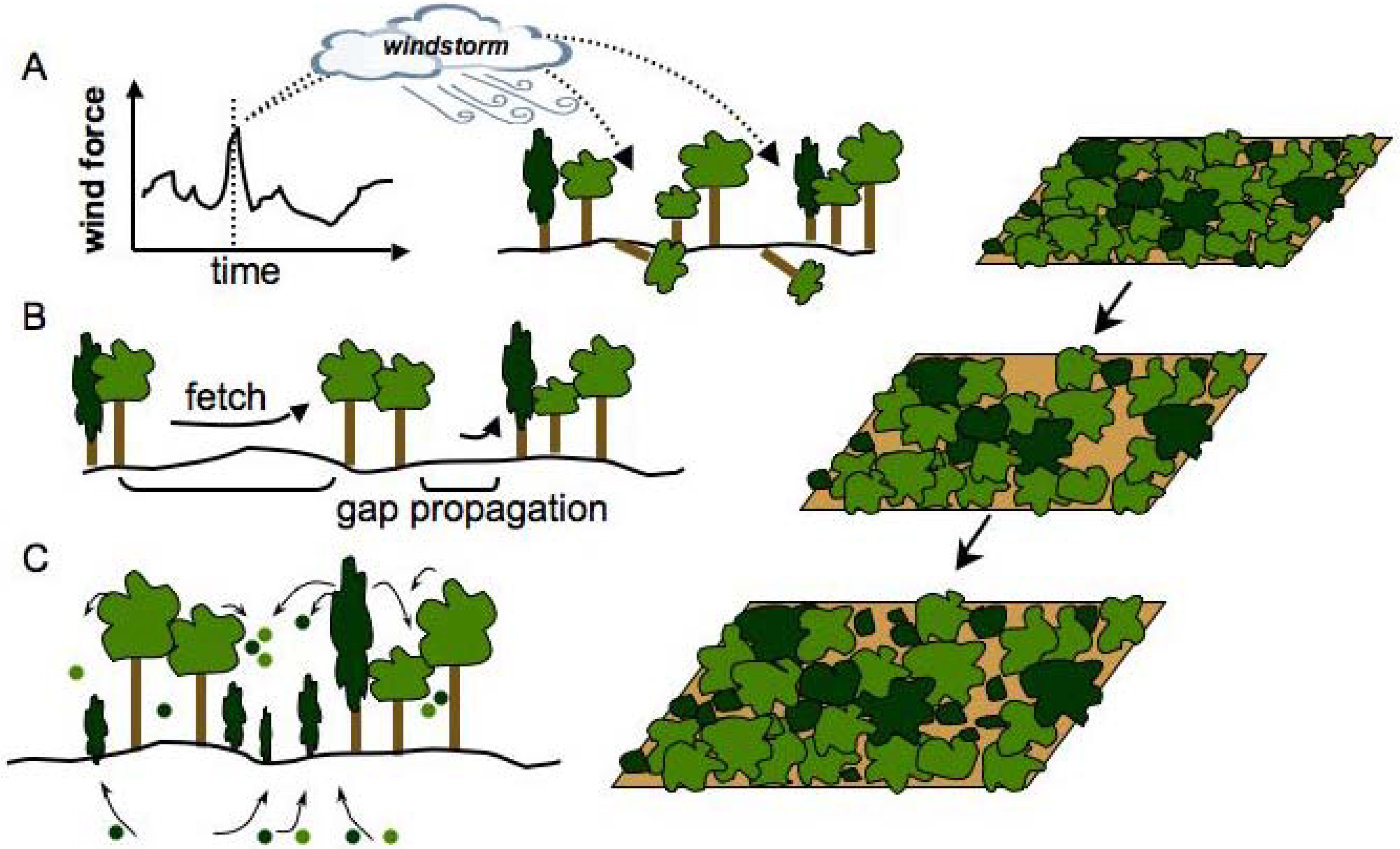
2.3. Patch Dynamics
2.4. Population Fluctuations
3. Contemporary Research in Ecological Complexity
3.1. Integrating Classical CSS with Ecological Complexity
3.2. New Measures: From Diversity to Complexity
3.3. The Role of Memory
3.4. Complex Effects of Environmental Variability
4. Conclusions
Acknowledgements
References
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 1973; p. 235. [Google Scholar]
- Allen, T.F.H.; Starr, T.B. Hierarchy: Perspectives for Ecological Complexity; University of Chicago Press: Chicago, IL, USA, 1982; p. 310. [Google Scholar]
- Maurer, B.A. Untangling Ecological Complexity: The Macroscopic Perspective; University of Chicago Press: Chicago, IL, USA, 1999; p. 251. [Google Scholar]
- Levin, S.A. Ecosystems and the biosphere as complex adaptive systems. Ecosystems 1998, 1, 431–436. [Google Scholar] [CrossRef]
- Michener, W.K.; Baerwald, T.J.; Firth, P.; Palmer, M.A.; Rosenberger, J.L.; Sandlin, E.A.; Zimmerman, H. Defining and unraveling biocomplexity. Bioscience 2001, 51, 1018–1023. [Google Scholar] [CrossRef]
- Rosen, R. Life Itself: A Comprehensive Inquiry into the Nature, Origin, and Fabrication Of Life; Columbia University Press: New York, NY, USA, 1991; p. 285. [Google Scholar]
- Collot, F. Correlations entre complexification et instabilite dans une formalisation du concept de complexite. Acta Biotheor. 1995, 43, 195–204. [Google Scholar] [CrossRef]
- Ahl, V.; Allen, T.F.H. Hierarchy Theory: A Vision, Vocabulary, And Epistemology; Columbia University Press: New York, NY, USA, 1996; p. 206. [Google Scholar]
- de Wailly, A. The ambiguity of the word “complexity” a proposal for clarification. Acta Biotheor. 1998, 46, 177–183. [Google Scholar] [CrossRef]
- Ricard, J. What do we mean by biological complexity? C. R. Biol. 2003, 326, 133–140. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Integration of Ecosystem Theories: A Pattern, 3rd ed.; Kluwer Academic Publishers: Boston, MA, USA, 2002; p. 420. [Google Scholar]
- Horgan, J. From complexity to perplexity. Sci. Amer. 1995, 272, 104–109. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Langton, C. Life at the edge of chaos. In Artificial Life II; Addison Wesley: New York, NY, USA, 1992; Volume 10, pp. 41–91. [Google Scholar]
- Schroeder, M.R. Fractals, Chaos, Power Laws: Minutes From an Infinite Paradise; W.H. Freeman: New York, NY, USA, 1991; p. 429. [Google Scholar]
- Brown, J.H.; Gupta, V.K.; Li, B.L.; Milne, B.T.; Restrepo, C.; West, G.B. The fractal nature of nature: power laws, ecological complexity and biodiversity. Phil. Trans. Roy. Soc. B-Biol. Sci. 2002, 357, 619–626. [Google Scholar] [CrossRef]
- Hubbell, S. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001; p. 448. [Google Scholar]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef]
- Boccara, N. Modeling Complex Systems; Springer: New York, NY, USA, 2004; p. 397. [Google Scholar]
- Bascompte, J.; Sole, R.V. Rethinking complexity—modeling spatiotemporal dynamics in ecology. Trend. Ecol. Evolut. 1995, 10, 361–366. [Google Scholar] [CrossRef]
- Storch, D.; Gaston, K.J. Untangling ecological complexity on different scales of space and time. Basic Appl. Ecol. 2004, 5, 389–400. [Google Scholar] [CrossRef]
- O’Dwyer, J.; Green, J. Field theory for biogeography: a spatially explicit model for predicting patterns of biodiversity. Ecol. Lett. 2010, 13, 87–95. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Pascual, M.; Dunne, J.A. Ecological Networks: Linking Structure to Dynamics in Food Webs; Oxford University Press: Oxford, NY, USA, 2006; p. 386. [Google Scholar]
- Banasek-Richter, C.; Bersier, L.F.; Cattin, M.F.; Baltensperger, R.; Gabriel, J.P.; Merz, Y.; Ulanowicz, R.E.; Tavares, A.F.; Williams, D.D.; De Ruiter, P.C.; Winemiller, K.O.; Naisbit, R.E. Complexity in quantitative food webs. Ecology 2009, 90, 1470–1477. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Nat. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Krause, A.E.; Frank, K.A.; Mason, D.M.; Ulanowicz, R.E.; Taylor, W.W. Compartments revealed in food-web structure. Nature 2003, 426, 282–285. [Google Scholar] [CrossRef]
- Allesina, S.; Pascual, M. Googling Food Webs: Can an eigenvector measure species’ importance for coextinctions? Plos Comp. Biol. 2009, 5, 1–6. [Google Scholar]
- Dunne, J.A.; Williams, R.J.; Martinez, N.D. Network structure and biodiversity loss in food webs: robustness increases with connectance. Ecol. Lett. 2002, 5, 558–567. [Google Scholar] [CrossRef]
- Melian, C.J.; Bascompte, J. Complex networks: two ways to be robust? Ecol. Lett. 2002, 5, 705–708. [Google Scholar] [CrossRef]
- Williams, R.J.; Martinez, N.D. Simple rules yield complex food webs. Nature 2000, 404, 180–183. [Google Scholar] [CrossRef]
- Rikvold, P.A.; Zia, R.K.P. Punctuated equilibria and 1/f noise in a biological coevolution model with individual-based dynamics. Phys. Rev. E 2003, 68, 31913. [Google Scholar] [CrossRef]
- McKane, A.; Drossel, B. Modelling evolving food webs. In Dynamical Food Webs; Elsevier: Amsterdam, The Netherlands, 2005; pp. 74–88. [Google Scholar]
- Christensen, K.; de Collobiano, S.A.; Hall, M.; Jensen, H.J. Tangled nature: A model of evolutionary ecology. J. Theor. Bio. 2002, 216, 73–84. [Google Scholar] [CrossRef]
- Filotas, E.; Grant, M.; Parrott, L.; Rikvold, P. The effect of positive interactions on community structure in a multi-species metacommunity model along an environmental gradient. Ecol. Model. 2010, 221, 885–894. [Google Scholar] [CrossRef]
- Bell, G. Experimental evolution. Heredity 2008, 100, 441–442. [Google Scholar] [CrossRef]
- Parrott, L.; Kok, R. A generic primary producer model for use in ecosystem simulation. Ecol. Model. 2001, 139, 75–99. [Google Scholar] [CrossRef]
- Wilson, W. Simulating ecological and evolutionary systems in C; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Huston, M. A general hypothesis of species diversity. Amer. Naturalist 1979, 113, 81. [Google Scholar]
- Levin, S.; Paine, R. Disturbance, patch formation, and community structure. Proc. Nat. Acad. Sci. 1974, 71, 2744. [Google Scholar] [CrossRef]
- Wiens, J. Population responses to patchy environments. Annu. Rev. Ecol. Syst. 1976, 7, 81–120. [Google Scholar]
- Pickett, S.; White, P. The Ecology of Natural Disturbance and Patch Dynamics; Academic Press: Orlando, Florida, USA, 1986. [Google Scholar]
- Schlicht, R.; Iwasa, Y. Forest gap dynamics and the Ising model. J. Theor. Biol. 2004, 230, 65–75. [Google Scholar] [CrossRef]
- Pagnutti, C.; Azzouz, M.; Anand, M. Propagation of local interactions create global gap structure and dynamics in a tropical rainforest. J. Theor. Biol. 2007, 247, 168–181. [Google Scholar] [CrossRef]
- Wootton, J.T. Local interactions predict large-scale pattern in empirically derived cellular automata. Nature 2001, 413, 841–844. [Google Scholar] [CrossRef]
- Guichard, F.; Halpin, P.M.; Allison, G.W.; Lubchenco, J.; Menge, B.A. Mussel disturbance dynamics: Signatures of oceanographic forcing from local interactions. Amer. Naturalist 2003, 161, 889–904. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Malamud, B.D.; Guzzetti, F.; Reichenbach, P. Self-organization, the cascade model, and natural hazards. Proc. Nat. Acad. Sci. U.S.A. 2002, 99, 2530–2537. [Google Scholar] [CrossRef]
- Pascual, M.; Guichard, F. Criticality and disturbance in spatial ecological systems. Trend. Ecol. Evol. 2005, 20, 88–95. [Google Scholar] [CrossRef]
- Lawton, J. H. Population Dynamics—More time means more variation. Nature 1988, 334, 563–563. [Google Scholar] [CrossRef]
- Pimm, S.; Redfearn, A. The variability of natural populations. Nature 1988, 334, 613–614. [Google Scholar] [CrossRef]
- Inchausti, P.; Halley, J. The long-term temporal variability and spectral colour of animal populations. Evol. Ecol. Res. 2002, 4, 1033–1048. [Google Scholar]
- Sole, R.V.; Manrubia, S.C.; Benton, M.J.; Kauffman, S.; Bak, P. Criticality and scaling in evolutionary ecology. Trend. Ecol. Evol. 1999, 14, 156–160. [Google Scholar] [CrossRef]
- Frigg, R. Self-organised criticality—what it is and what it isn’t. Stud. Hist. Philos. Sci. 2003, 34A, 613–632. [Google Scholar] [CrossRef]
- Kolasa, J. Complexity, system integration, and susceptibility to change: Biodiversity connection. Ecol. Complex. 2005, 2, 431–442. [Google Scholar] [CrossRef]
- Cohen, J.E. Unexpected dominance of high-frequencies in chaotic nonlinear population-models. Nature 1995, 378, 610–612. [Google Scholar] [CrossRef]
- Sugihara, G. Ecology—from out of the Blue. Nature 1995, 378, 559–560. [Google Scholar] [CrossRef]
- Blarer, A.; Doebeli, M. In the red zone. Nature 1996, 380, 589–590. [Google Scholar] [CrossRef]
- Miramontes, O.; Rohani, P. Intrinsically generated coloured noise in laboratory insect populations. Proc. Roy. Soc. London Ser. B. 1998, 265, 785–792. [Google Scholar] [CrossRef]
- Kaitala, V.; Ranta, E. Red/blue chaotic power spectra. Nature 1996, 381, 198–199. [Google Scholar] [CrossRef]
- White, A.; Begon, M.; Bowers, R.G. Explaining the colour of power spectra in chaotic ecological models. Proc. Roy. Soc. London Ser. B. 1996, 263, 1731–1737. [Google Scholar] [CrossRef]
- Taylor, P.J. Unruly Complexity: Ecology, Interpretation, Engagement; University of Chicago Press: Chicago, IL, USA, 2005; p. 289. [Google Scholar]
- Anand, M.; Orloci, L. Complexity in plant communities: The notion and quantification. J. Theor. Biol. 1996, 179, 179–186. [Google Scholar] [CrossRef]
- Dale, M.B.; Anand, M.; Desrochers, R.E. Measuring information-based complexity across scales using cluster analysis. Ecol. Inform. 2007, 2, 121–127. [Google Scholar]
- Li, S.C.; Chang, Q.; Peng, F.A.; Wang, Y.L. Indicating landscape fragmentation using L-Z complexity. Ecol. Indic. 2009, 9, 780–790. [Google Scholar] [CrossRef]
- Proulx, R.; Parrott, L. Measures of structural complexity in digital images for monitoring the ecological signature of an old-growth forest ecosystem. Ecol. Indic. 2008, 8, 270–284. [Google Scholar] [CrossRef]
- McCann, K.S. The diversity-stability debate. Nature 2000, 405, 228–233. [Google Scholar] [CrossRef]
- Borda-de-Agua, L.; Hubbell, S.P.; McAllister, M. Species-area curves, diversity indices, and species abundance distributions: A multifractal analysis. Amer. Naturalist 2002, 159, 138–155. [Google Scholar] [CrossRef]
- Ricotta, C.; Anand, M. Spatial complexity of ecological communities: Bridging the gap between probabilistic and non-probabilistic uncertainty measures. Ecol. Model. 2006, 197, 59–66. [Google Scholar]
- Luque, B.; Ballesteros, F.J.; Fernandez, M. Variances as order parameter and complexity measure for random Boolean networks. J. Phys.a-Math. Gen. 2005, 38, 1031–1038. [Google Scholar] [CrossRef]
- Murphy, H.T.; Lovett-Doust, J. Context and connectivity in plant metapopulations and landscape mosaics: does the matrix matter? Oikos 2004, 105, 3–14. [Google Scholar] [CrossRef]
- Demetrius, L.; Gundlach, V.M.; Ochs, G. Complexity and demographic stability in population models. Theor. Pop. Biol. 2004, 65, 211–225. [Google Scholar]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef]
- Rai, V.; Anand, M.; Upadhyay, R.K. Trophic structure and dynamical complexity in simple ecological models. Ecol. Complex. 2007, 4, 212–222. [Google Scholar] [CrossRef]
- Gouhier, T.C.; Guichard, F.; Gonzalez, A. Synchrony and stability of food webs in metacommunities. Amer. Naturalist 2010, 175, E16–E34. [Google Scholar] [CrossRef]
- Hendry, R.J.; Mcglade, J.M. The Role of Memory in Ecological-Systems. Proc. Roy. Soc. Lon. Ser. B 1995, 259, 153–159. [Google Scholar] [CrossRef]
- Padisak, J. Seasonal succession of phytoplankton in a large shallow lake (Balaton, Hungary)—a dynamic approach to ecological memory, its possible role and mechanisms. J. Ecol. 1992, 80, 217–230. [Google Scholar] [CrossRef]
- Hairston, N.G.; Lampert, W.; Caceres, C.E.; Holtmeier, C.L.; Weider, L.J.; Gaedke, U.; Fischer, J.M.; Fox, J.A.; Post, D.M. Lake ecosystems—Rapid evolution revealed by dormant eggs. Nature 1999, 401, 446–446. [Google Scholar]
- Peterson, G.D. Contagious disturbance, ecological memory, and the emergence of landscape pattern. Ecosystems 2002, 5, 329–338. [Google Scholar] [CrossRef]
- Schwinning, S.; Sala, O.E.; Loik, M.E.; Ehleringer, J.R. Thresholds, memory, and seasonality: understanding pulse dynamics in arid/semi-arid ecosystems. Oecologia 2004, 141, 191–193. [Google Scholar]
- Milinski, M. Long-term memory for food patches and implications for Ideal Free Distributions in sticklebacks. Ecology 1994, 75, 1150–1156. [Google Scholar] [CrossRef]
- Hirvonen, H.; Ranta, E.; Rita, H.; Peuhkuri, N. Significance of memory properties in prey choice decisions. Ecol. Model. 1999, 115, 177–189. [Google Scholar] [CrossRef]
- Ashby, W.R. An Introduction to Cybernetics; J. Wiley: New York, NY, USA, 1956; p. 295. [Google Scholar]
- Golinski, M.; Bauch, C.; Arland, M. The effects of endogenous ecological memory on population stability and resilience in a variable environment. Ecol. Model. 2008, 212, 334–341. [Google Scholar] [CrossRef]
- Grimm, V.; Railsback, S.F. Individual-Based Modeling and Ecology; Princeton University Press: Princeton, NJ, USA, 2005; p. 428. [Google Scholar]
- Hassell, M.; Godfray, H.; Comins, H. Effects of global change on the dynamics of insect host-parasitoid interactions. Biotic Interaction. Glob. Change 1993, 402–423. [Google Scholar]
- Halley, J. M. Ecology, evolution and 1/f-noise. Trend. Ecol. Evolut. 1996, 11, 33–37. [Google Scholar] [CrossRef]
- Ripa, J.; Ives, A.R. Food web dynamics in correlated and autocorrelated environments. Theor. Pop. Biol. 2003, 64, 369–384. [Google Scholar] [CrossRef]
- Ripa, J.; Lundberg, P.; Kaitala, V. A general theory of environmental noise in ecological food webs. Amer. Naturalist 1998, 151, 256–263. [Google Scholar]
- Gonzalez, A.; De Feo, O. Environmental variability modulates the insurance effects of diversity in nonequilibrium communities. In The Impact of Environmental Variability on Ecological Systems; Vasseur, D.A., McCann, K.S., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 133–158. [Google Scholar]
- Gonzalez, A.; Holt, R.D. The inflationary effects of environmental fluctuations in source-sink systems. Proc. Nat. Acad. Sci. USA 2002, 99, 14872–14877. [Google Scholar] [CrossRef]
- Turner, M.; Romme, W.; Tinker, D. Surprises and lessons from the 1988 Yellowstone fires. Fron. Ecol. Environ. 2003, 1, 351–358. [Google Scholar] [CrossRef]
- Vasseur, D.A.; Fox, J.W. Environmental fluctuations can stabilize food web dynamics by increasing synchrony. Ecol. Lett. 2007, 10, 1066–1074. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences: Chaos, Fractals, Self Organization, and Disorder: Concepts and Tools, 2nd ed.; Springer: Berlin, NY, USA, 2003; p. 528. [Google Scholar]
- Malamud, B.D.; Morein, G.; Turcotte, D.L. Log-periodic behavior in a forest-fire model. Nonlinear Process. Geophys. 2005, 12, 575–585. [Google Scholar] [CrossRef]
- Ferriere, R.; Cazelles, B. Universal power laws govern intermittent rarity in communities of interacting species. Ecology 1999, 80, 1505–1521. [Google Scholar] [CrossRef]
- Peters, D.P.C.; Pielke, R.A.; Bestelmeyer, B.T.; Allen, C.D.; Munson-McGee, S.; Havstad, K.M. Cross-scale interactions, nonlinearities, and forecasting catastrophic events. Proc. Nat. Acad. Sci. U.S.A. 2004, 101, 15130–15135. [Google Scholar]
- Whelan, R.J. The Ecology of Fire; Cambridge University Press: Cambridge, NY, USA, 1995; p. 346. [Google Scholar]
- Coreau, A.; Pinay, G.; Thompson, J.D.; Cheptou, P.O.; Mermet, L. The rise of research on futures in ecology: rebalancing scenarios and predictions. Ecol. Lett. 2009, 12, 1277–1286. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Anand, M.; Gonzalez, A.; Guichard, F.; Kolasa, J.; Parrott, L. Ecological Systems as Complex Systems: Challenges for an Emerging Science. Diversity 2010, 2, 395-410. https://doi.org/10.3390/d2030395
Anand M, Gonzalez A, Guichard F, Kolasa J, Parrott L. Ecological Systems as Complex Systems: Challenges for an Emerging Science. Diversity. 2010; 2(3):395-410. https://doi.org/10.3390/d2030395
Chicago/Turabian StyleAnand, Madhur, Andrew Gonzalez, Frédéric Guichard, Jurek Kolasa, and Lael Parrott. 2010. "Ecological Systems as Complex Systems: Challenges for an Emerging Science" Diversity 2, no. 3: 395-410. https://doi.org/10.3390/d2030395
APA StyleAnand, M., Gonzalez, A., Guichard, F., Kolasa, J., & Parrott, L. (2010). Ecological Systems as Complex Systems: Challenges for an Emerging Science. Diversity, 2(3), 395-410. https://doi.org/10.3390/d2030395



