Geographically Weighted Regression Enhances Spectral Diversity–Biodiversity Relationships in Inner Mongolian Grasslands
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Analysis Framework
2.3. In Situ Biodiversity Survey
2.4. Drone Multispectral Data Acquisition
2.5. Spectral Diversity (SD) Metrics
2.6. Statistical Analysis
2.6.1. Global Linear Statistical Analysis
2.6.2. Spatial Statistical Analysis
3. Results
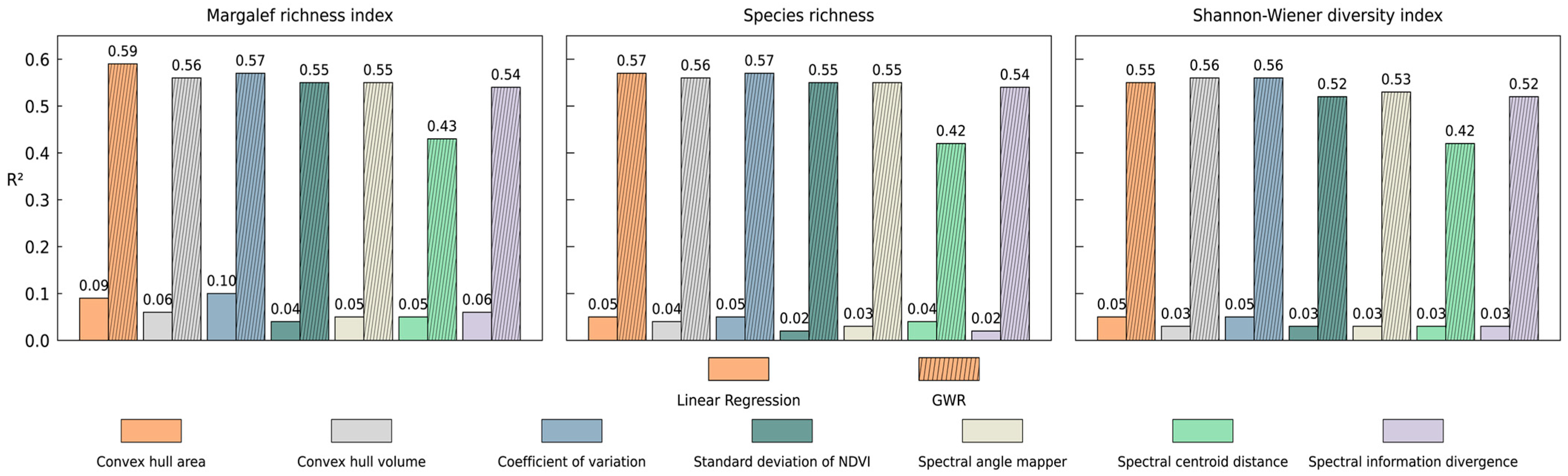
3.1. Global Linear Regression Modeling Results
3.2. Geographically Weighted Regression (GWR) Modeling Results
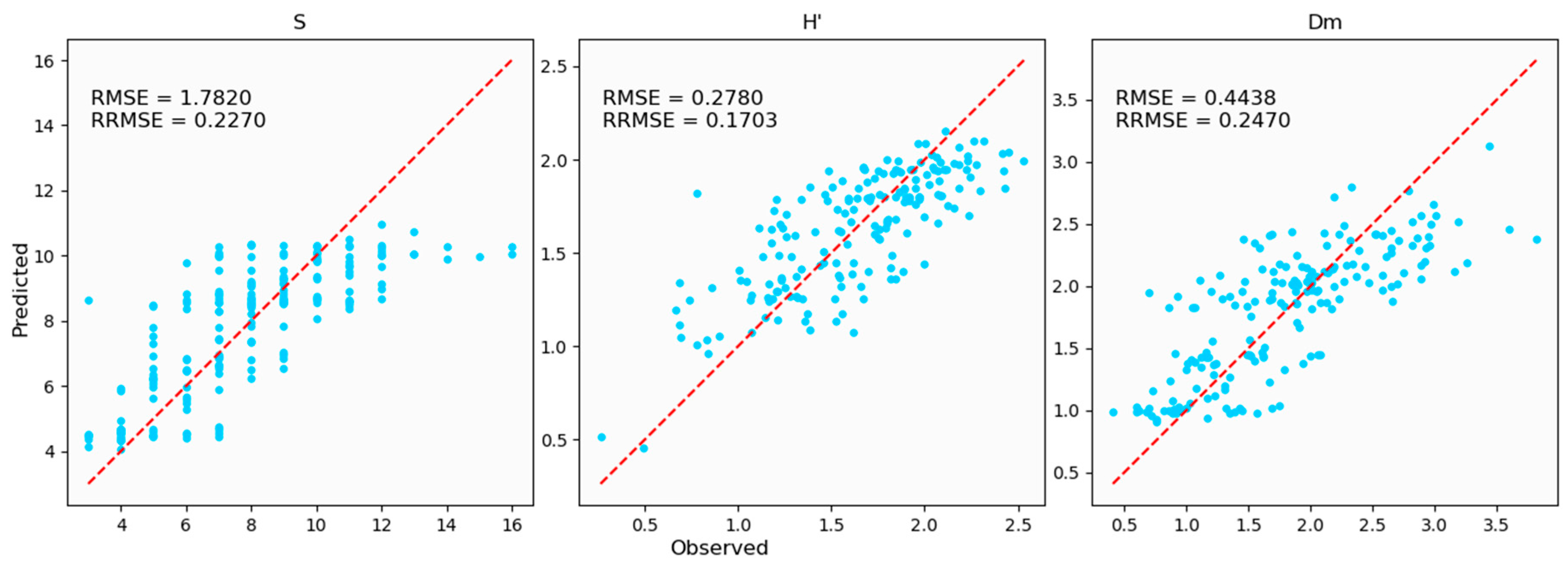
3.3. Predicted Biodiversity Indices Derived from Geographically Weighted Regression
4. Discussion
4.1. GWR Model Improved the Performance of Predicting Biodiversity Using SD Metrics
4.2. Complexity of Spectral Diversity
4.3. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balmford, A.; Gaston, K.J. Why biodiversity surveys are good value. Nature 1999, 398, 204–205. [Google Scholar] [CrossRef]
- Wagg, C.; Roscher, C.; Weigelt, A.; Vogel, A.; Ebeling, A.; De Luca, E.; Roeder, A.; Kleinspehn, C.; Temperton, V.M.; Meyer, S.T.; et al. Biodiversity–stability relationships strengthen over time in a long-term grassland experiment. Nat. Commun. 2022, 13, 7752. [Google Scholar] [CrossRef]
- Pereira, H.M.; Martins, I.S.; Rosa, I.M.D.; Kim, H.; Leadley, P.; Popp, A.; Van Vuuren, D.P.; Hurtt, G.; Quoss, L.; Arneth, A.; et al. Global trends and scenarios for terrestrial biodiversity and ecosystem services from 1900 to 2050. Science 2024, 384, 458–465. [Google Scholar] [CrossRef]
- Bawa, K.S.; Sengupta, A.; Chavan, V.; Chellam, R.; Ganesan, R.; Krishnaswamy, J.; Mathur, V.B.; Nawn, N.; Olsson, S.B.; Pandit, N.; et al. Securing biodiversity, securing our future: A national mission on biodiversity and human well-being for India. Biol. Conserv. 2021, 253, 108867. [Google Scholar] [CrossRef]
- Xu, W.; Xiao, Y.; Zhang, J.; Yang, W.; Zhang, L.; Hull, V.; Wang, Z.; Zheng, H.; Liu, J.; Polasky, S.; et al. Strengthening protected areas for biodiversity and ecosystem services in China. Proc. Natl. Acad. Sci. USA 2017, 114, 1601–1606. [Google Scholar] [CrossRef]
- Bardgett, R.D.; Bullock, J.M.; Lavorel, S.; Manning, P.; Schaffner, U.; Ostle, N.; Chomel, M.; Durigan, G.; Fry, E.L.; Johnson, D.; et al. Combatting global grassland degradation. Nat. Rev. Earth Environ. 2021, 2, 720–735. [Google Scholar] [CrossRef]
- Gang, C.; Zhou, W.; Chen, Y.; Wang, Z.; Sun, Z.; Li, J.; Qi, J.; Odeh, I. Quantitative assessment of the contributions of climate change and human activities on global grassland degradation. Environ. Earth Sci. 2014, 72, 4273–4282. [Google Scholar] [CrossRef]
- Petermann, J.S.; Buzhdygan, O.Y. Grassland biodiversity. Curr. Biol. 2021, 31, R1195–R1201. [Google Scholar] [CrossRef]
- Joly, C.A. The kunming-montréal global biodiversity framework. Biota Neotropica 2022, 22, e2022e001. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A. Remote sensing of terrestrial plant biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
- Nagendra, H. Using remote sensing to assess biodiversity. Int. J. Remote Sens. 2001, 22, 2377–2400. [Google Scholar] [CrossRef]
- Lyu, X.; Li, X.; Dang, D.; Dou, H.; Wang, K.; Lou, A. Unmanned aerial vehicle (UAV) remote sensing in grassland ecosystem monitoring: A systematic review. Remote Sens. 2022, 14, 1096. [Google Scholar] [CrossRef]
- Boykin, K.G.; Kepner, W.G.; Bradford, D.F.; Guy, R.K.; Kopp, D.A.; Leimer, A.K.; Samson, E.A.; East, N.F.; Neale, A.C.; Gergely, K.J. A national approach for mapping and quantifying habitat-based biodiversity metrics across multiple spatial scales. Ecol. Indic. 2013, 33, 139–147. [Google Scholar] [CrossRef]
- Brun, P.; Zimmermann, N.E.; Graham, C.H.; Lavergne, S.; Pellissier, L.; Münkemüller, T.; Thuiller, W. The productivity-biodiversity relationship varies across diversity dimensions. Nat. Commun. 2019, 10, 5691. [Google Scholar] [CrossRef]
- Huang, Z.; Bai, Y.; Alatalo, J.M.; Yang, Z. Mapping biodiversity conservation priorities for protected areas: A case study in xishuangbanna tropical area, China. Biol. Conserv. 2020, 249, 108741. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Puletti, N.; Chen, Q.; Corona, P.; Papale, D.; Valentini, R. Above ground biomass and tree species richness estimation with airborne lidar in tropical ghana forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 371–379. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Müllerová, J.; Conti, L.; Malavasi, M.; Schmidtlein, S. About the link between biodiversity and spectral variation. Appl. Veg. Sci. 2022, 25, e12643. [Google Scholar] [CrossRef]
- Fu, Y.; Yao, Y.; Wang, L.; Yi, H.; Shan, Y. How Spatial Resolution Mediates Canopy Spectral Diversity as a Proxy for Marsh Plant Diversity. Ecol. Inf. 2025, 90, 103253. [Google Scholar] [CrossRef]
- Rocchini, D.; Chiarucci, A.; Loiselle, S.A. Testing the spectral variation hypothesis by using satellite multispectral images. Acta Oecologica 2004, 26, 117–120. [Google Scholar] [CrossRef]
- Schmidtlein, S.; Fassnacht, F.E. The spectral variability hypothesis does not hold across landscapes. Remote Sens. Environ. 2017, 192, 114–125. [Google Scholar] [CrossRef]
- Imran, H.A.; Gianelle, D.; Scotton, M.; Rocchini, D.; Dalponte, M.; Macolino, S.; Sakowska, K.; Pornaro, C.; Vescovo, L. Potential and limitations of grasslands α-diversity prediction using fine-scale hyperspectral imagery. Remote Sens. 2021, 13, 2649. [Google Scholar] [CrossRef]
- Rossi, C.; Kneubühler, M.; Schütz, M.; Schaepman, M.E.; Haller, R.M.; Risch, A.C. Spatial resolution, spectral metrics and biomass are key aspects in estimating plant species richness from spectral diversity in species-rich grasslands. Remote Sens. Ecol. Conserv. 2022, 8, 297–314. [Google Scholar] [CrossRef]
- Lopes, M.; Fauvel, M.; Ouin, A.; Girard, S. Spectro-temporal heterogeneity measures from dense high spatial resolution satellite image time series: Application to grassland species diversity estimation. Remote Sens. 2017, 9, 993. [Google Scholar] [CrossRef]
- Van Cleemput, E.; Adler, P.; Suding, K.N. Making remote sense of biodiversity: What grassland characteristics make spectral diversity a good proxy for taxonomic diversity? Glob. Ecol. Biogeogr. 2023, 32, 2177–2188. [Google Scholar] [CrossRef]
- Ludwig, A.; Doktor, D.; Feilhauer, H. Is spectral pixel-to-pixel variation a reliable indicator of grassland biodiversity? A systematic assessment of the spectral variation hypothesis using spatial simulation experiments. Remote Sens. Environ. 2024, 302, 113988. [Google Scholar] [CrossRef]
- Klippel, A.; Hardisty, F.; Li, R. Interpreting spatial patterns: An inquiry into formal and cognitive aspects of tobler’s first law of geography. Ann. Assoc. Am. Geogr. 2011, 101, 1011–1031. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, P.; Wang, Z.; Lv, S.; Han, G.; Hou, D.; Wang, J.; Wang, H.; Zhu, A. Spatial distribution of shrubs and perennial plants under grazing disturbance in the desert steppe of inner mongolia. Glob. Ecol. Conserv. 2024, 54, e03193. [Google Scholar] [CrossRef]
- Adler, P.; Raff, D.; Lauenroth, W. The effect of grazing on the spatial heterogeneity of vegetation. Oecologia 2001, 128, 465–479. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Geographically weighted summary statistics—A framework for localised exploratory data analysis. Comput. Environ. Urban Syst. 2002, 26, 501–524. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, X.; Zhou, M.; He, S.; Gan, M.; Yang, L.; Wang, K. Impacts of urbanization and landscape pattern on habitat quality using OLS and GWR models in hangzhou, China. Ecol. Indic. 2020, 117, 106654. [Google Scholar] [CrossRef]
- Gao, C.; Feng, Y.; Tong, X.; Lei, Z.; Chen, S.; Zhai, S. Modeling urban growth using spatially heterogeneous cellular automata models: Comparison of spatial lag, spatial error and GWR. Comput. Environ. Urban Syst. 2020, 81, 101459. [Google Scholar] [CrossRef]
- Loke, L.H.L.; Chisholm, R.A. Measuring habitat complexity and spatial heterogeneity in ecology. Ecol. Lett. 2022, 25, 2269–2288. [Google Scholar] [CrossRef]
- Weng, C.; Bai, Y.; Chen, B.; Hu, Y.; Shu, J.; Chen, Q.; Wang, P. Assessing the vulnerability to climate change of a semi-arid pastoral social–ecological system: A case study in hulunbuir, China. Ecol. Inform. 2023, 76, 102139. [Google Scholar] [CrossRef]
- Na, R.; Du, H.; Na, L.; Shan, Y.; He, H.S.; Wu, Z.; Zong, S.; Yang, Y.; Huang, L. Spatiotemporal changes in the aeolian desertification of hulunbuir grassland and its driving factors in China during 1980–2015. Catena 2019, 182, 104123. [Google Scholar] [CrossRef]
- Sun, B.; Li, Z.; Gao, Z.; Guo, Z.; Wang, B.; Hu, X.; Bai, L. Grassland degradation and restoration monitoring and driving forces analysis based on long time-series remote sensing data in xilin gol league. Acta Ecol. Sin. 2017, 37, 219–228. [Google Scholar] [CrossRef]
- Li, X.; Lyu, X.; Dou, H.; Dang, D.; Li, S.; Li, X.; Li, M.; Xuan, X. Strengthening grazing pressure management to improve grassland ecosystem services. Glob. Ecol. Conserv. 2021, 31, e01782. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Zhang, Y.; Wang, B. Quantitative contribution of climate change and vegetation restoration to ecosystem services in the Inner Mongolia under ecological restoration projects. Ecol. Indic. 2025, 171, 113240. [Google Scholar] [CrossRef]
- Li, Z.; Ma, W.; Liang, C.; Liu, Z.; Wang, W.; Wang, L. Long-term vegetation dynamics driven by climatic variations in the inner mongolia grassland: Findings from 30-year monitoring. Landsc. Ecol. 2015, 30, 1701–1711. [Google Scholar] [CrossRef]
- Jing-yun, F.; Xiang-ping, W.; Ze-hao, S.; Zhi-yao, T.; Jin-sheng, H.; Dan, Y.; Yuan, J.; Zhi-heng, W.; Cheng-yang, Z.; Jiang-ling, Z.; et al. Methods and protocols for plant community inventory. Biodivers. Sci. 2009, 17, 533. [Google Scholar] [CrossRef]
- Izsák, J.; Papp, L. A link between ecological diversity indices and measures of biodiversity. Ecol. Model. 2000, 130, 151–156. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Gamon, J.A.; Zygielbaum, A.I.; Wang, R.; Schweiger, A.K.; Cavender-Bares, J. Remote sensing of biodiversity: Soil correction and data dimension reduction methods improve assessment of α-diversity (species richness) in prairie ecosystems. Remote Sens. Environ. 2018, 206, 240–253. [Google Scholar] [CrossRef]
- Mulya, H.; Santosa, Y.; Hilwan, I. Comparison of four species diversity indices in mangrove community. Biodiversitas J. Biol. Divers. 2021, 22, 9. [Google Scholar] [CrossRef]
- Das, G.K. Estimation of biodiversity indices and species richness. In Forests and Forestry of West Bengal; Springer International Publishing: Cham, Germany, 2021; pp. 183–217. ISBN 978-3-030-80705-4. [Google Scholar]
- Pommerening, A. Approaches to quantifying forest structures. Forestry 2002, 75, 305–324. [Google Scholar] [CrossRef]
- Gamito, S. Caution is needed when applying margalef diversity index. Ecol. Indic. 2010, 10, 550–551. [Google Scholar] [CrossRef]
- Czyża, S.; Szuniewicz, K.; Kowalczyk, K.; Dumalski, A.; Ogrodniczak, M.; Zieleniewicz, Ł. Assessment of accuracy in unmanned aerial vehicle (UAV) pose estimation with the REAL-time kinematic (RTK) method on the example of DJI matrice 300 RTK. Sensors 2023, 23, 2092. [Google Scholar] [CrossRef]
- Zeng, N.; Ma, L.; Zheng, H.; Zhao, Y.; He, Z.; Deng, S.; Wang, Y. Machine learning based inversion of water quality parameters in typical reach of rural wetland by unmanned aerial vehicle images. Water 2024, 16, 3163. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, Q.; Gao, S. Enhancing multi-flight unmanned-aerial-vehicle-based detection of wheat canopy chlorophyll content using relative radiometric correction. Remote Sens. 2025, 17, 1557. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A.; Schweiger, A.K.; Cavender-Bares, J.; Townsend, P.A.; Zygielbaum, A.I.; Kothari, S. Influence of species richness, evenness, and composition on optical diversity: A simulation study. Remote Sens. Environ. 2018, 211, 218–228. [Google Scholar] [CrossRef]
- Madonsela, S.; Cho, M.; Ramoelo, A.; Mutanga, O. Investigating the relationship between tree species diversity and landsat-8 spectral heterogeneity across multiple phenological stages. Remote Sens. 2021, 13, 2467. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Perrone, M.; Di Febbraro, M.; Conti, L.; Divíšek, J.; Chytrý, M.; Keil, P.; Carranza, M.L.; Rocchini, D.; Torresani, M.; Moudrý, V.; et al. The relationship between spectral and plant diversity: Disentangling the influence of metrics and habitat types at the landscape scale. Remote Sens. Environ. 2023, 293, 113591. [Google Scholar] [CrossRef]
- Rocchini, D. Effects of spatial and spectral resolution in estimating ecosystem α-diversity by satellite imagery. Remote Sens. Environ. 2007, 111, 423–434. [Google Scholar] [CrossRef]
- Chang, C.-I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Dahlin, K.M. Spectral diversity area relationships for assessing biodiversity in a wildland–agriculture matrix. Ecol. Appl. 2016, 26, 2758–2768. [Google Scholar] [CrossRef]
- Griffiths, P.; Needleman, J. Statistical significance testing and p-values: Defending the indefensible? A discussion paper and position statement. Int. J. Nurs. Stud. 2019, 99, 103384. [Google Scholar] [CrossRef]
- Das, P. Linear regression model: Relaxing the classical assumptions. In Econometrics in Theory and Practice; Springer: Singapore, 2019; pp. 109–135. ISBN 978-981-329-018-1. [Google Scholar]
- Renaud, O.; Victoria-Feser, M.-P. A robust coefficient of determination for regression. J. Stat. Plan. Inference 2010, 140, 1852–1862. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Dieste, Á.G.; Argüello, F.; Heras, D.B.; Magdon, P.; Linstädter, A.; Dubovyk, O.; Muro, J. ResNeTS: A ResNet for time series analysis of sentinel-2 data applied to grassland plant-biodiversity prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 17349–17370. [Google Scholar] [CrossRef]
- Conti, L.; Malavasi, M.; Galland, T.; Komárek, J.; Lagner, O.; Carmona, C.P.; De Bello, F.; Rocchini, D.; Šímová, P. The relationship between species and spectral diversity in grassland communities is mediated by their vertical complexity. Appl. Veg. Sci. 2021, 24, avsc.12600. [Google Scholar] [CrossRef]
- Li, L.; Mu, X.; Jiang, H.; Chianucci, F.; Hu, R.; Song, W.; Qi, J.; Liu, S.; Zhou, J.; Chen, L.; et al. Review of ground and aerial methods for vegetation cover fraction (fCover) and related quantities estimation: Definitions, advances, challenges, and future perspectives. ISPRS J. Photogramm. Remote Sens. 2023, 199, 133–156. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Jin, X.; Bian, L.; Ge, Y. High-throughput phenotyping of plant leaf morphological, physiological, and biochemical traits on multiple scales using optical sensing. Crop J. 2023, 11, 1303–1318. [Google Scholar] [CrossRef]
- Passalacqua, N.G.; Aiello, S.; Bernardo, L.; Gargano, D. Monitoring biomass in two heterogeneous mountain pasture communities by image based 3D point cloud derived predictors. Ecol. Indic. 2021, 121, 107126. [Google Scholar] [CrossRef]
- Heumann, B.W.; Hackett, R.A.; Monfils, A.K. Testing the spectral diversity hypothesis using spectroscopy data in a simulated wetland community. Ecol. Inform. 2015, 25, 29–34. [Google Scholar] [CrossRef]
- Angel, Y.; Raiho, A.; Kathuria, D.; Chadwick, K.D.; Brodrick, P.G.; Lang, E.; Ochoa, F.; Shiklomanov, A.N. Deciphering the spectra of flowers to map landscape-scale blooming dynamics. Ecosphere 2025, 16, e70127. [Google Scholar] [CrossRef]
- Perrone, M.; Conti, L.; Galland, T.; Komárek, J.; Lagner, O.; Torresani, M.; Rossi, C.; Carmona, C.P.; De Bello, F.; Rocchini, D.; et al. “flower power”: How flowering affects spectral diversity metrics and their relationship with plant diversity. Ecol. Inform. 2024, 81, 102589. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A.; Cavender-Bares, J. Seasonal patterns of spectral diversity at leaf and canopy scales in the cedar creek prairie biodiversity experiment. Remote Sens. Environ. 2022, 280, 113169. [Google Scholar] [CrossRef]
- Din, M.; Zheng, W.; Rashid, M.; Wang, S.; Shi, Z. Evaluating hyperspectral vegetation indices for leaf area index estimation of Oryza sativa L. at diverse phenological stages. Front. Plant Sci. 2017, 8, 820. [Google Scholar] [CrossRef]
- Crofts, A.L.; Wallis, C.I.B.; St-Jean, S.; Demers-Thibeault, S.; Inamdar, D.; Arroyo-Mora, J.P.; Kalacska, M.; Laliberté, E.; Vellend, M. Linking aerial hyperspectral data to canopy tree biodiversity: An examination of the spectral variation hypothesis. Ecol. Monogr. 2024, 94, e1605. [Google Scholar] [CrossRef]
- Wallis, C.I.B.; Kothari, S.; Jantzen, J.R.; Crofts, A.L.; St-Jean, S.; Inamdar, D.; Pablo Arroyo-Mora, J.; Kalacska, M.; Bruneau, A.; Coops, N.C.; et al. Exploring the spectral variation hypothesis for α- and β-diversity: A comparison of open vegetation and forests. Environ. Res. Lett. 2024, 19, 064005. [Google Scholar] [CrossRef]
- Chlus, A.; Townsend, P.A. Characterizing seasonal variation in foliar biochemistry with airborne imaging spectroscopy. Remote Sens. Environ. 2022, 275, 113023. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Sun, C.; Huang, C.; Zhang, H.; Chen, B.; An, F.; Wang, L.; Yun, T. Individual tree crown segmentation and crown width extraction from a heightmap derived from aerial laser scanning data using a deep learning framework. Front. Plant Sci. 2022, 13, 914974. [Google Scholar] [CrossRef] [PubMed]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and temporal weighted regression (GTWR): Geographical and temporal weighted regression. Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]


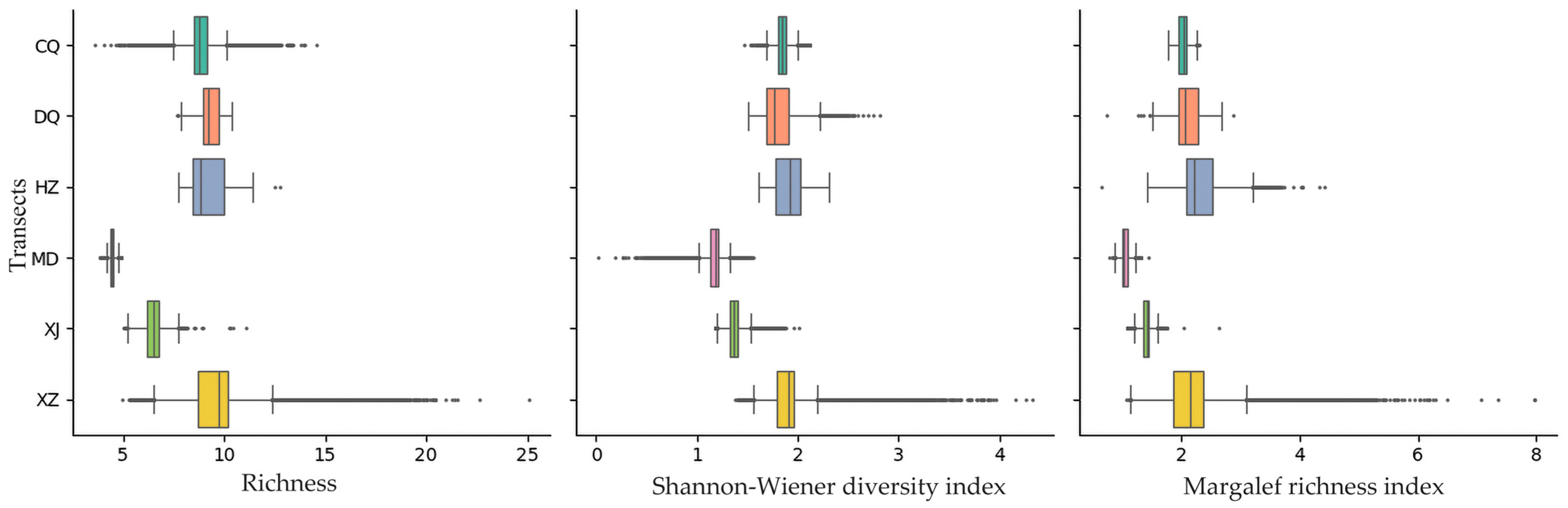
| Experimental Areas | Administrative Region | Grassland Type | Coordinates | Orientation | Size (L × W, m) | Area (m2) |
|---|---|---|---|---|---|---|
| CQ | Hulunbuir | meadow steppe | 49.57966° N, 118.93102° E | 27° NE | 290 × 80 | 23,200 |
| DQ | Hulunbuir | meadow steppe | 49.88535° N, 119.31487° E | 0° NE | 300 × 98 | 29,400 |
| HZ | Hulunbuir | meadow steppe | 49.30057° N, 119.99951° E | 86° NW | 490 × 67 | 32,830 |
| MD | Xilingol | typical steppe | 44.26940° N, 116.33487° E | 15° NW | 302 × 88 | 26,576 |
| XZ | Xilingol | meadow steppe | 43.38046° N, 116.20906° E | 87° NW | 317 × 96 | 30,432 |
| XJ | Xilingol | typical steppe | 44.06262° N, 116.86243° E | 77° NW | 224 × 82 | 18,368 |
| Biodiversity Indices | Definition | Equation |
|---|---|---|
| Species richness (Richness) | The number of species in the community [42]. | The number of species in the community. |
| Shannon–Wiener diversity index (Shannon) | An index considering species richness and relative abundance [45]. | , where is the relative abundance of the i-th species. |
| Margalef richness index (Margalef) | A normalized measure of species richness that incorporates abundance [46]. | , where N is the total species abundance in the community. |
| SD Metrics | Definition |
|---|---|
| Coefficient of variation | The average coefficient of variation in the band values in the quadrat [50,51]. |
| Spectral angle mapper | The angle between the multidimensional vector of the pixel reflectance and the average spectral vector [52]. |
| Standard deviation of NDVI | The standard deviation of the normalized difference vegetation index (NDVI) [53]. |
| Spectral centroid distance | The average of the Euclidean distance from all spectral vectors to the mean spectral reflectance in the quadrat [54]. |
| Spectral information divergence | The spectral information divergence compares the similarity between two pixels by measuring the probability difference between two corresponding spectral features [55]. |
| Convex hull volume | The volume of the convex hull of the first three principal components of the pixels in the quadrat in a three-dimensional space [56,57]. |
| Convex hull area | The area enclosed by the smallest convex polygon of the mean band reflectance and the corresponding pixel reflectance values in the quadrat [42]. |
| Response Variables | Explanatory Variables | Pearson’s r | Linear Regression | GWR | ||
|---|---|---|---|---|---|---|
| R2 | R2 | R2 Adjusted | AICc | |||
| Margalef | Convex hull area | 0.29 *** | 0.09 | 0.59 | 0.50 | 285.31 |
| Convex hull volume | 0.25 *** | 0.06 | 0.56 | 0.50 | 282.01 | |
| Coefficient of variation | 0.31 *** | 0.10 | 0.57 | 0.50 | 282.14 | |
| Standard deviation of NDVI | 0.21 *** | 0.04 | 0.55 | 0.48 | 288.48 | |
| Spectral angle mapper | 0.22 *** | 0.05 | 0.55 | 0.48 | 287.41 | |
| Spectral centroid distance | 0.23 *** | 0.05 | 0.43 | 0.40 | 300.91 | |
| Spectral information divergence | 0.24 *** | 0.06 | 0.54 | 0.47 | 290.34 | |
| Richness | Convex hull area | 0.21 *** | 0.05 | 0.57 | 0.49 | 777.89 |
| Convex hull volume | 0.20 *** | 0.04 | 0.56 | 0.50 | 774.32 | |
| Coefficient of variation | 0.23 *** | 0.05 | 0.57 | 0.50 | 774.41 | |
| Standard deviation of NDVI | 0.16 ** | 0.02 | 0.55 | 0.48 | 780.94 | |
| Spectral angle mapper | 0.16 ** | 0.03 | 0.55 | 0.48 | 779.66 | |
| Spectral centroid distance | 0.20 *** | 0.04 | 0.42 | 0.38 | 797.82 | |
| Spectral information divergence | 0.16 ** | 0.02 | 0.54 | 0.47 | 783.34 | |
| Shannon | Convex hull area | 0.21 *** | 0.05 | 0.55 | 0.48 | 118.50 |
| Convex hull volume | 0.17 ** | 0.03 | 0.56 | 0.50 | 109.55 | |
| Coefficient of variation | 0.23 *** | 0.05 | 0.56 | 0.49 | 114.74 | |
| Standard deviation of NDVI | 0.17 ** | 0.03 | 0.52 | 0.45 | 124.68 | |
| Spectral angle mapper | 0.17 ** | 0.03 | 0.53 | 0.46 | 123.34 | |
| Spectral centroid distance | 0.18 ** | 0.03 | 0.42 | 0.39 | 132.16 | |
| Spectral information divergence | 0.18 ** | 0.03 | 0.52 | 0.45 | 125.05 | |
| Variable | Moran I | Z-Score | p-Value |
|---|---|---|---|
| Species richness | 0.47 | 14.90 | 0.00 |
| Shannon–Wiener diversity index | 0.47 | 15.00 | 0.00 |
| Margalef richness index | 0.47 | 14.98 | 0.00 |
| Coefficient of variation | 0.74 | 23.23 | 0.00 |
| Spectral angle mapper | 0.70 | 22.09 | 0.00 |
| Standard deviation of NDVI | 0.66 | 21.01 | 0.00 |
| Spectral centroid distance | 0.79 | 25.03 | 0.00 |
| Spectral information divergence | 0.59 | 18.61 | 0.00 |
| Convex hull area | 0.71 | 22.51 | 0.00 |
| Convex hull volume | 0.64 | 20.24 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Wan, H.; Lu, L.; Wan, F.; Duan, H.; Xiao, C.; Zhang, Y.; Zhang, Z.; Wang, Y.; Shi, P.; et al. Geographically Weighted Regression Enhances Spectral Diversity–Biodiversity Relationships in Inner Mongolian Grasslands. Diversity 2025, 17, 541. https://doi.org/10.3390/d17080541
Dai Y, Wan H, Lu L, Wan F, Duan H, Xiao C, Zhang Y, Zhang Z, Wang Y, Shi P, et al. Geographically Weighted Regression Enhances Spectral Diversity–Biodiversity Relationships in Inner Mongolian Grasslands. Diversity. 2025; 17(8):541. https://doi.org/10.3390/d17080541
Chicago/Turabian StyleDai, Yu, Huawei Wan, Longhui Lu, Fengming Wan, Haowei Duan, Cui Xiao, Yusha Zhang, Zhiru Zhang, Yongcai Wang, Peirong Shi, and et al. 2025. "Geographically Weighted Regression Enhances Spectral Diversity–Biodiversity Relationships in Inner Mongolian Grasslands" Diversity 17, no. 8: 541. https://doi.org/10.3390/d17080541
APA StyleDai, Y., Wan, H., Lu, L., Wan, F., Duan, H., Xiao, C., Zhang, Y., Zhang, Z., Wang, Y., Shi, P., & Sun, X. (2025). Geographically Weighted Regression Enhances Spectral Diversity–Biodiversity Relationships in Inner Mongolian Grasslands. Diversity, 17(8), 541. https://doi.org/10.3390/d17080541






