BetaBayes—A Bayesian Approach for Comparing Ecological Communities
Abstract
1. Introduction
2. Methods for Modelling Changes in Community Similarity and Dissimilarity
2.1. Mantel Test
2.2. Generalised Dissimilarity Modelling
3. BetaBayes
3.1. General Overview
μ = α + βC
3.2. Prior Predictive Checking
3.3. Model Validation and Interpretation
4. Comparing BetaBayes with Mantel Tests and Generalised Dissimilarity Modelling
4.1. Mantel Test
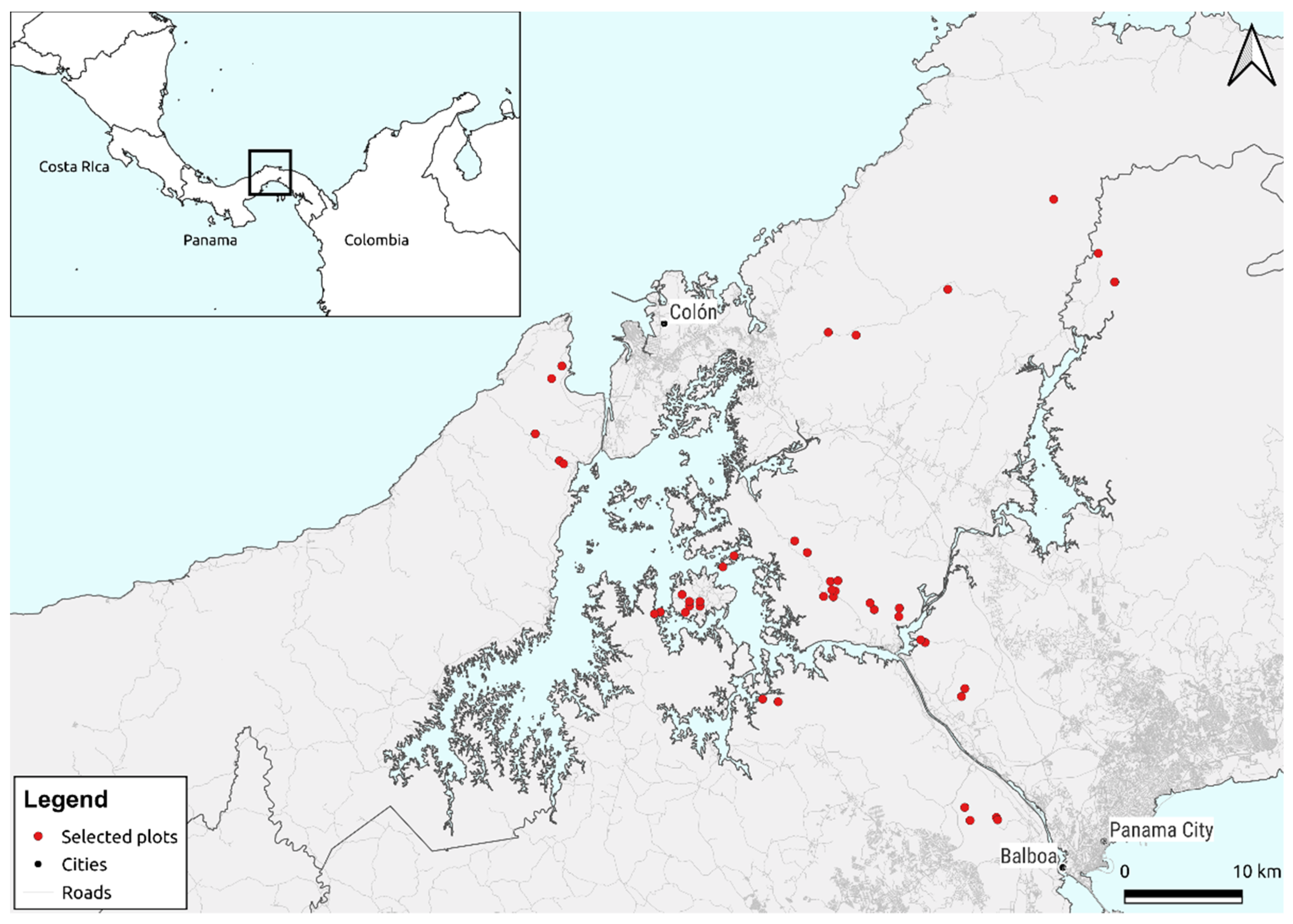
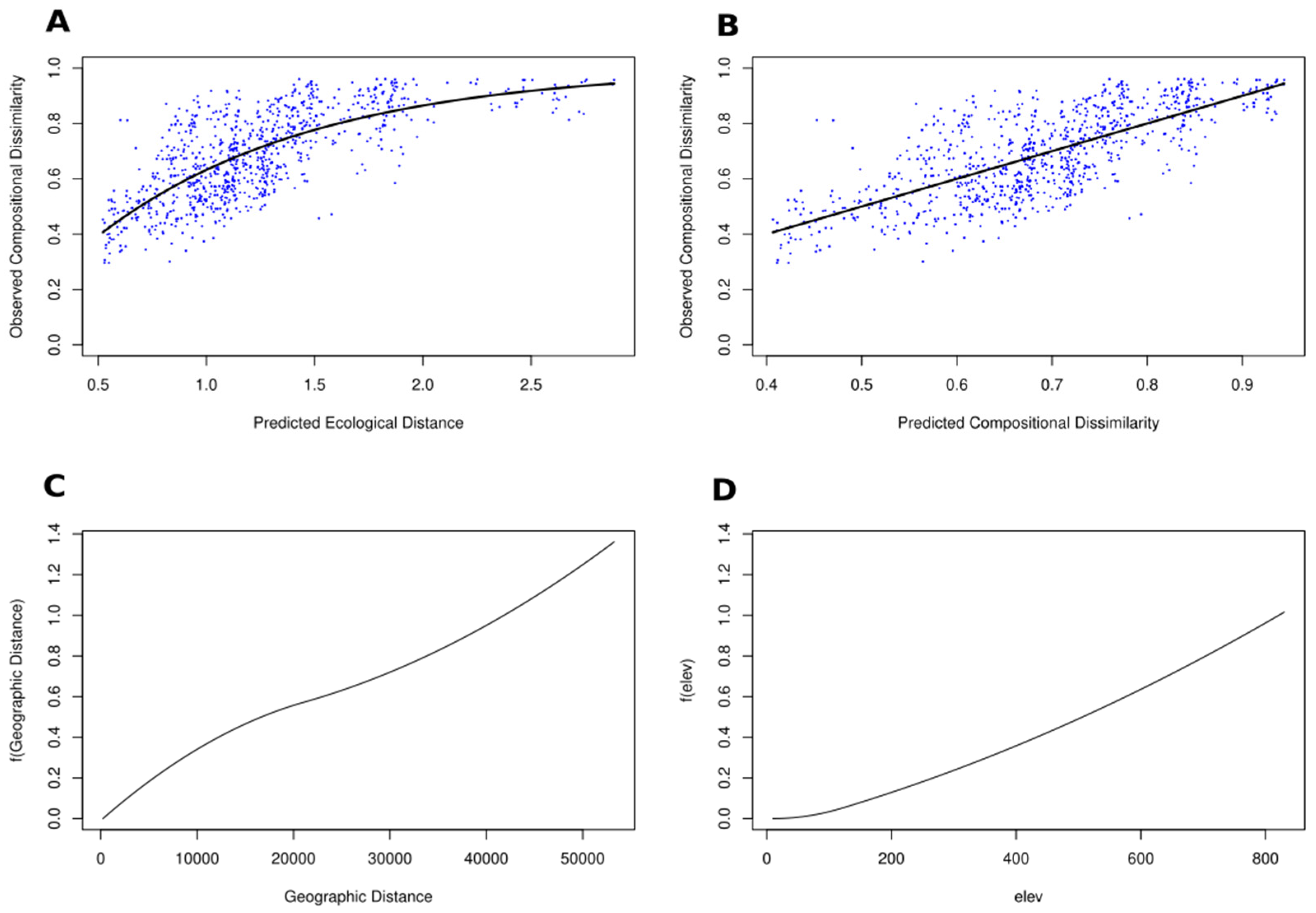
4.2. Generalised Dissimilarity Modelling
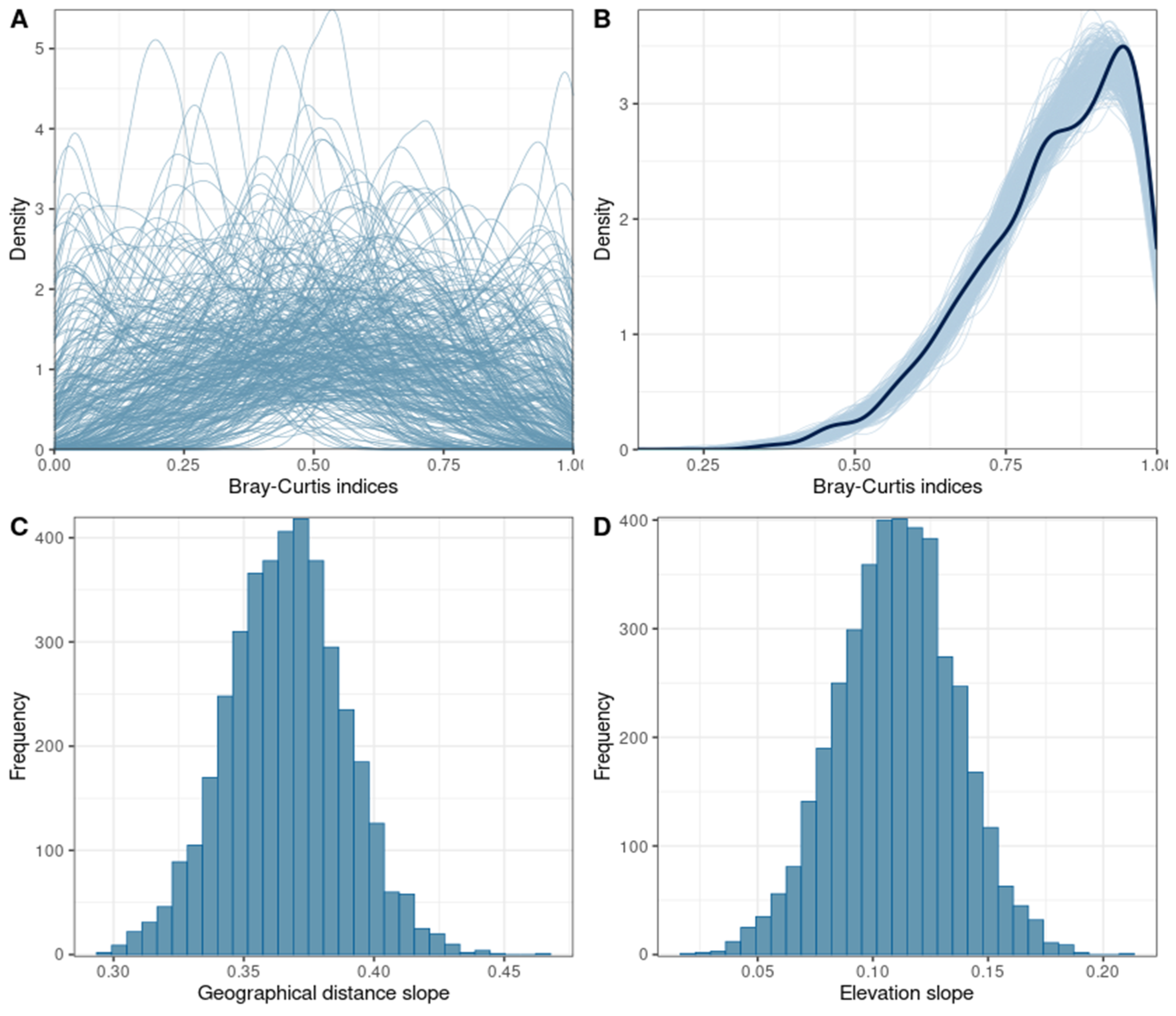
4.3. BetaBayes
5. BetaBayes Extensions
5.1. Varying Effects
5.2. Spatial Autocorrelation
5.3. Complex Nonlinear Relationships
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, C.C.; Turner, B.L. Ecological Succession in a Changing World. J. Ecol. 2019, 107, 503–509. [Google Scholar] [CrossRef]
- Hubbell, S. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001; ISBN 978-0-691-02128-7. [Google Scholar]
- Magurran, A.E.; Deacon, A.E.; Moyes, F.; Shimadzu, H.; Dornelas, M.; Phillip, D.A.T.; Ramnarine, I.W. Divergent Biodiversity Change within Ecosystems. Proc. Natl. Acad. Sci. USA 2018, 115, 1843–1847. [Google Scholar] [CrossRef] [PubMed]
- Pereira, H.M.; Navarro, L.M.; Martins, I.S. Global Biodiversity Change: The Bad, the Good, and the Unknown. Annu. Rev. Environ. Resour. 2012, 37, 25–50. [Google Scholar] [CrossRef]
- Ferrier, S.; Guisan, A. Spatial Modelling of Biodiversity at the Community Level. J. Appl. Ecol. 2006, 43, 393–404. [Google Scholar] [CrossRef]
- D’Amen, M.; Rahbek, C.; Zimmermann, N.E. Spatial Predictions at the Community Level: From Current Approaches to Future Frameworks. Biol. Rev. 2017, 92, 169–187. [Google Scholar] [CrossRef]
- Graco-Roza, C.; Aarnio, S.; Abrego, N.; Acosta, A.T.R.; Alahuhta, J.; Altman, J.; Angiolini, C.; Aroviita, J.; Attorre, F.; Baastrup-Spohr, L.; et al. Distance Decay 2.0—A Global Synthesis of Taxonomic and Functional Turnover in Ecological Communities. Glob. Ecol. Biogeogr. 2022, 31, 1399–1421. [Google Scholar] [CrossRef]
- MacKenzie, D.I.; Nichols, J.D.; Royle, J.A.; Pollock, K.H.; Bailey, L.; Hines, J.E. Occupancy Estimation and Modeling: Inferring Patterns and Dynamics of Species Occurrence, 2nd ed.; Academic Press: London, UK, 2017; ISBN 978-0-12-814691-0. [Google Scholar]
- Ferrier, S.; Manion, G.; Elith, J.; Richardson, K. Using Generalized Dissimilarity Modelling to Analyse and Predict Patterns of Beta Diversity in Regional Biodiversity Assessment. Divers. Distrib. 2007, 13, 252–264. [Google Scholar] [CrossRef]
- Pollock, L.J.; O’Connor, L.M.J.; Mokany, K.; Rosauer, D.F.; Talluto, M.V.; Thuiller, W. Protecting Biodiversity (in All Its Complexity): New Models and Methods. Trends Ecol. Evol. 2020, 35, 1119–1128. [Google Scholar] [CrossRef]
- Viana, D.S.; Keil, P.; Jeliazkov, A. Disentangling Spatial and Environmental Effects: Flexible Methods for Community Ecology and Macroecology. Ecosphere 2022, 13, e4028. [Google Scholar] [CrossRef]
- Mokany, K.; Ware, C.; Woolley, S.N.C.; Ferrier, S.; Fitzpatrick, M.C. A Working Guide to Harnessing Generalized Dissimilarity Modelling for Biodiversity Analysis and Conservation Assessment. Glob. Ecol. Biogeogr. 2022, 31, 802–821. [Google Scholar] [CrossRef]
- Legendre, P.; Borcard, D.; Peres-Neto, P.R. Analyzing Beta Diversity: Partitioning the Spatial Variation of Community Composition Data. Ecol. Monogr. 2005, 75, 435–450. [Google Scholar] [CrossRef]
- Mantel, N. The Detection of Disease Clustering and a Generalized Regression Approach. Cancer Res. 1967, 27, 209–220. [Google Scholar] [PubMed]
- Smouse, P.E.; Long, J.C.; Sokal, R.R. Multiple Regression and Correlation Extensions of the Mantel Test of Matrix Correspondence. Syst. Zool. 1986, 35, 627–632. [Google Scholar] [CrossRef]
- Legendre, P. Comparison of Permutation Methods for the Partial Correlation and Partial Mantel Tests. J. Stat. Comput. Simul. 2000, 67, 37–73. [Google Scholar] [CrossRef]
- Guillot, G.; Rousset, F. Dismantling the Mantel Tests. Methods Ecol. Evol. 2013, 4, 336–344. [Google Scholar] [CrossRef]
- Legendre, P.; Fortin, M.-J.; Borcard, D. Should the Mantel Test Be Used in Spatial Analysis? Methods Ecol. Evol. 2015, 6, 1239–1247. [Google Scholar] [CrossRef]
- Crabot, J.; Clappe, S.; Dray, S.; Datry, T. Testing the Mantel Statistic with a Spatially-Constrained Permutation Procedure. Methods Ecol. Evol. 2019, 10, 532–540. [Google Scholar] [CrossRef]
- McElreath, R. Statistical Rethinking: A Bayesian Course with Examples in R and Stan, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Ferrier, S.; Drielsma, M.; Manion, G.; Watson, G. Extended Statistical Approaches to Modelling Spatial Pattern in Biodiversity in Northeast New South Wales. II. Community-Level Modelling. Biodivers. Conserv. 2002, 11, 2309–2338. [Google Scholar] [CrossRef]
- Woolley, S.N.C.; Foster, S.D.; O’Hara, T.D.; Wintle, B.A.; Dunstan, P.K. Characterising Uncertainty in Generalised Dissimilarity Models. Methods Ecol. Evol. 2017, 8, 985–995. [Google Scholar] [CrossRef]
- Koleff, P.; Gaston, K.J.; Lennon, J.J. Measuring Beta Diversity for Presence–Absence Data. J. Anim. Ecol. 2003, 72, 367–382. [Google Scholar] [CrossRef]
- Bradley, R.A.; Terry, M.E. Rank Analysis of Incomplete Block Designs: I. The Method of Paired Comparisons. Biometrika 1952, 39, 324–345. [Google Scholar] [CrossRef]
- Zermelo, E. Die Berechnung der Turnier-Ergebnisse als ein Maximumproblem der Wahrscheinlichkeitsrechnung. Math. Z. 1929, 29, 436–460. [Google Scholar] [CrossRef]
- Agresti, A. Categorical Data Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-46363-5. [Google Scholar]
- McHale, I.; Morton, A. A Bradley-Terry Type Model for Forecasting Tennis Match Results. Int. J. Forecast. 2011, 27, 619–630. [Google Scholar] [CrossRef]
- Koehler, K.J.; Ridpath, H. An Application of a Biased Version of the Bradley-Terry-Luce Model to Professional Basketball Results. J. Math. Psychol. 1982, 25, 187–205. [Google Scholar] [CrossRef]
- Hunter, D.R. MM Algorithms for Generalized Bradley-Terry Models. Ann. Stat. 2004, 32. [Google Scholar] [CrossRef]
- Jeon, J.-J.; Kim, Y. Revisiting the Bradley-Terry Model and Its Application to Information Retrieval. J. Korean Data Inf. Sci. Soc. 2013, 24, 1089–1099. [Google Scholar] [CrossRef]
- Rodríguez Montequín, V.; Villanueva Balsera, J.M.; Díaz Piloñeta, M.; Álvarez Pérez, C. A Bradley-Terry Model-Based Approach to Prioritize the Balance Scorecard Driving Factors: The Case Study of a Financial Software Factory. Mathematics 2020, 8, 276. [Google Scholar] [CrossRef]
- Ehrlich, J.; Potter, J.; Sanders, S. The Effect of Attendance on Home Field Advantage in the National Football League: A Natural Experiment; Syracuse University: Syracuse, NY, USA, 2021. [Google Scholar]
- Gabry, J.; Simpson, D.; Vehtari, A.; Betancourt, M.; Gelman, A. Visualization in Bayesian Workflow. J. R. Stat. Soc. Ser. A Stat. Soc. 2019, 182, 389–402. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013; ISBN 978-1-4398-4095-5. [Google Scholar]
- Stan Development Team. Stan Modeling Language Users Guide and Reference Manual, Version 2.2.4; 2020. Available online: http://mc-stan.org (accessed on 10 December 2021).
- Condit, R.; Pitman, N.; Leigh, E.G.; Chave, J.; Terborgh, J.; Foster, R.B.; Núñez, P.; Aguilar, S.; Valencia, R.; Villa, G.; et al. Beta-Diversity in Tropical Forest Trees. Science 2002, 295, 666–669. [Google Scholar] [CrossRef]
- Chust, G.; Chave, J.; Condit, R.; Aguilar, S.; Lao, S.; Pérez, R. Determinants and Spatial Modeling of Tree Β-diversity in a Tropical Forest Landscape in Panama. J. Veg. Sci. 2006, 17, 83–92. [Google Scholar] [CrossRef]
- Bray, J.R.; Curtis, J.T. An Ordination of the Upland Forest Communities of Southern Wisconsin. Ecol. Monogr. 1957, 27, 325–349. [Google Scholar] [CrossRef]
- Oksanen, J.; Blanchet, F.G.; Friendly, M.; Kindt, R.; Legendre, P.; McGlinn, D.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; et al. Vegan: Community Ecology Package—Version 2.7-7. 2021. Available online: http://CRAN.R-project.org/package=vegan (accessed on 12 December 2021).
- Fitzpatrick, M.; Mokany, K.; Manion, G.; Nieto-Lugilde, D.; Ferrier, S. gdm: Generalized Dissimilarity Modeling 2022. Available online: https://cran.r-project.org/web/packages/gdm/index.html (accessed on 12 May 2022).
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2009; ISBN 1-4419-0317-8. [Google Scholar]
- Morlon, H.; Chuyong, G.; Condit, R.; Hubbell, S.; Kenfack, D.; Thomas, D.; Valencia, R.; Green, J.L. A General Framework for the Distance-Decay of Similarity in Ecological Communities. Ecol. Lett. 2008, 11, 904–917. [Google Scholar] [CrossRef]
- Soininen, J.; McDonald, R.; Hillebrand, H. The Distance Decay of Similarity in Ecological Communities. Ecography 2007, 30, 3–12. [Google Scholar] [CrossRef]
- Cattelan, M.; Varin, C.; Firth, D. Dynamic Bradley–Terry Modelling of Sports Tournaments. J. R. Stat. Soc. Ser. C Appl. Stat. 2013, 62, 135–150. [Google Scholar] [CrossRef]
- Menke, J.E.; Martinez, T.R. A Bradley–Terry Artificial Neural Network Model for Individual Ratings in Group Competitions. Neural Comput. Appl. 2008, 17, 175–186. [Google Scholar] [CrossRef]
- Yan, T. Ranking in the Generalized Bradley–Terry Models When the Strong Connection Condition Fails. Commun. Stat. Theory Methods 2016, 45, 340–353. [Google Scholar] [CrossRef][Green Version]
- Shev, A.; Fujii, K.; Hsieh, F.; McCowan, B. Systemic Testing on Bradley-Terry Model against Nonlinear Ranking Hierarchy. PLoS ONE 2014, 9, e115367. [Google Scholar] [CrossRef]
- Stern, S.E. Moderated Paired Comparisons: A Generalized Bradley-Terry Model for Continuous Data Using a Discontinuous Penalized Likelihood Function. J. R. Stat. Soc. Ser. C Appl. Stat. 2011, 60, 397–415. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias, F.S.; Betancourt, M.; Rodríguez-González, P.M.; Borda-de-Água, L. BetaBayes—A Bayesian Approach for Comparing Ecological Communities. Diversity 2022, 14, 858. https://doi.org/10.3390/d14100858
Dias FS, Betancourt M, Rodríguez-González PM, Borda-de-Água L. BetaBayes—A Bayesian Approach for Comparing Ecological Communities. Diversity. 2022; 14(10):858. https://doi.org/10.3390/d14100858
Chicago/Turabian StyleDias, Filipe S., Michael Betancourt, Patricia María Rodríguez-González, and Luís Borda-de-Água. 2022. "BetaBayes—A Bayesian Approach for Comparing Ecological Communities" Diversity 14, no. 10: 858. https://doi.org/10.3390/d14100858
APA StyleDias, F. S., Betancourt, M., Rodríguez-González, P. M., & Borda-de-Água, L. (2022). BetaBayes—A Bayesian Approach for Comparing Ecological Communities. Diversity, 14(10), 858. https://doi.org/10.3390/d14100858






