Abstract
Spatial ecological information is necessary to guide the conservation efforts of river turtles, but it is lacking for many species including the smooth softshell turtle (Apalone mutica). We investigated the spatial ecology of A. mutica in two reaches of the Kaskaskia River in Illinois, USA to determine variables influencing movement rates, the best estimate of home range, and variables influencing home range size. We radio-tracked 28 A. mutica from 2013 to 2014 and used an information theoretic approach to select the best models describing movement and home range estimates. Mean movement rate was 142.3 m/day and was highly variable with some movements >2 km/day. Movement peaked at moderate water temperatures early in the active season, increased at higher water levels for females, and was greater in the higher stream order. The sexes responded differently to environmental variation, with female movement higher in most but not all conditions. The most informative home range estimate was a 95% kernel density estimate using likelihood cross-validation (CVh) smoothing clipped to the river channel. The mean home range size was 18.1 hectares and increased with movement rate, number of radio-locations, and stream order. Most turtles had well-defined home ranges, though a few were possibly nomadic. Our methods also provide a framework for spatial ecological studies of other riverine species.
1. Introduction
Animal movements reflect the influence of biotic and abiotic factors on space and habitat use [1,2]. Thus, understanding movement patterns is an important consideration for determining spatial requirements and habitat management [3]. Movement may be non-oriented and based on nearby perceptual cues, oriented toward distant perceptual cues, or oriented based on memory [4]. Animal movements fit into two temporal categories: Daily movements and long-term seasonal or annual movements [5]. The distance and frequency of daily movements are useful to describe activity, whereas movements over longer distances and periods indicate annual patterns or dispersal.
Most daily animal movements occur inside a defined area that an animal uses to survive, reproduce, and acquire resources; this area is termed a home range [2,6,7]. Home range size often varies with sex, body size, or environmental factors [6]. In the context of measuring a home range from movement data, defining it as “an area repeatedly traversed by an animal” is necessary [5]. For animals constrained to linear habitats such as rivers, a simple linear range is sometimes used [8]. However, examining the size, shape, and structure of an animal’s home range can help answer biological questions [5]. Estimates of home range size are often made using the minimum convex polygon (MCP) or kernel density estimators (KDE) [9,10].
An important realization is no one home range estimate is appropriate for all species or ecological situations [5]. The choice of a method should be based on addressing the biological questions being asked. For instance, determining concentrated areas of activity or sexual differences in space use requires an estimator that does not include large amounts of unused space. Spaces traversed moving between core use areas may function as important movement corridors, but they may not represent preferred habitat or home range of an animal. Once movement rate and appropriate home range estimates are calculated, it is useful to compare different models to determine what factors affect space use estimates [11]. Quantitative determination using a combined modeling and information theoretic approach (Akaike’s information criterion) [12] to select the best models from an a priori candidate set is a robust way to determine factors affecting space use. Ultimately, movement and home range describe an organism’s spatial ecology and form a base of information essential to conservation [13,14].
Spatial ecology is important for riverine turtles because it relates to adaptations for acquiring resources, reproducing, and surviving in a dynamic environment [15]. Studies documenting the spatial ecology of river turtles often examine the linear range [16,17] or the MCP home range [18,19,20] which provide only a broad view of space use. Detailed spatial ecological information is lacking for many North American river turtle species [15,21]. There is a need for studies providing a refined explanation of movement rates and home range size, particularly for the genus Apalone, which is one of the lesser studied groups of turtles in North America despite being abundant in aquatic ecosystems [22]. The highly aquatic smooth softshell turtle (Apalone mutica) is a prime example of a little-studied river turtle at risk of population declines [23,24].
Apalone mutica inhabits predominately medium to large rivers in the Midwest and southern United States [25]. It is characterized by an orangish-brown, round, flat, leathery carapace and a hingeless white plastron [25]. Sexual size dimorphism is evident, with males maturing at 80 mm plastron length and females at 140 mm plastron length [26]. The diet of A. mutica is primarily insects [27,28], and nesting occurs in late spring and early summer [29]. Water level or discharge appear to influence the space use of A. mutica to some degree [30]. Past field studies of A. mutica are sparse, with most knowledge derived from one spatial ecology study in the Kansas River [17].
While some spatial ecological work has been conducted for A. mutica, the overall picture is far from clear, particularly over multi-year time scales. A previous study described the movement and linear range of A. mutica but followed individuals for only a short duration per turtle (average 34 days) [17,30], which may have resulted in relationships that cannot be broadly applied to other situations [31]. A Mississippi River study tracked movement of A. mutica but only located individuals in summer and fall months within a five kilometer reach [32]. Studies that calculate home range areas over multiple seasons, compare spatial ecology between stream orders, and determine variables influencing movement rate and home range size are needed. Morphological, sexual, temporal, and environmental variables could conceivably predict estimates of space use for A. mutica. Overall, the knowledge gap makes it difficult to assess threats, possibly hindering the management of the species.
Given the importance of spatial data for understanding an organisms’ ecology and the knowledge gaps for softshell turtles, the overall objective of our study was to thoroughly describe the movement and home range of A. mutica. Our first objective was to determine what variables affect movement rates. Variables affecting movement rate are important to key life history processes because movement is a reflection of foraging and reproduction. Our second objective was to determine the most biologically meaningful home range estimate for A. mutica. Home ranges indicate the amount of space a turtle requires and represent areas of high use. Our third objective was to determine if home range size asymptotes with enough radio-locations. Home ranges that asymptote indicate well-defined space use, whereas home ranges that do not indicate either inadequate sampling or nomadic behavior. Our final objective was to determine what variables affect home range size. This analysis indicates if observed variations in space use results from traits specific to individual turtles, site characteristics, or sampling bias.
2. Materials and Methods
Our study site was the Kaskaskia River in south-central Illinois, which flows approximately 523 km from its headwaters in Champaign County to its terminus at the Mississippi River. We chose two study sites, a 6th order reach (upstream) and a 7th order reach (downstream) [33,34]. The reaches are separated by a dam, large reservoir, and a considerable distance, so turtle movement between the sites is unlikely. Both reaches have a single thread, mainly a meandering channel with some straighter sections, and the river bed is mostly silt, sand, and some gravel [35]. Bank erosion, channel widening, and the accumulation of large woody debris are a result of land use changes upstream and headcutting downstream [35,36]. The main difference between the sites was stream order; during our study, water levels were relatively low, and within-bank flows predominated.
We captured A. mutica (Figure 1) using single throat hoop nets (throat downstream) held in place by wooden stakes and baited with chopped fish. Traps were checked and re-baited daily. Traps were initially placed along point bars to target A. mutica and later placed every 200 m along the river at each site on the most accessible shoreline. Upstream, we trapped a reach spanning 7.4 river km, and downstream we trapped a reach spanning 7.1 river km.

Figure 1.
Female Apalone mutica with radio-transmitter from the Kaskaskia River, Illinois, USA in 2013.
We used a hole punch to create a unique mark on the outside carapacial edge of each A. mutica captured for identification [37], and assigned each turtle an ID number. We measured plastron length (PL; mm) using tree calipers. Male A. mutica were identified by cloacal vent extension beyond the posterior carapace margin and a general lack of blotchy carapace patterning. Female A. mutica were identified by a cloacal vent not extending beyond the posterior carapace margin, blotchy carapace patterning, and attaining a larger size than males. We classified A. mutica males as adults at 80 mm PL (unless secondary sexual characteristics were not pronounced) and females at 140 mm PL [26].
We attached radio-transmitters to A. mutica by putting four holes in the posterior side of the carapace with a sterilized awl and securing the transmitter with 2.54 mm width cable ties (Figure 2). Radio-transmitter size did not exceed 10% of turtle mass. We initially used two zip ties to attach a radio-transmitter, but the ties began to pull out of the shell (especially with males because of a thinner shell). Thus, we switched to using six zip ties with a cross configuration (Figure 2). The six zip tie method worked better for transmitter retention. We radio-tracked turtles by motorized boat, canoe, kayak, and wading from June 2013 to December 2014 (turtles were tracked beyond the trapping areas).

Figure 2.
Radio-transmitter attachment for A. mutica seen from: (a) Dorsal view; (b) ventral view.
We intensively tracked turtles from June 2013 through late October 2013 and April 2014 through late October 2014. The distance between sites made tracking at both concurrently unfeasible, so we attempted to track turtles at each site for five consecutive days every other week. Tracking at one site for multiple days was done to gather accurate movement rate (m/day) data. The frequency of tracking was ultimately somewhat sporadic due to occasional equipment issues. We tracked turtles occasionally during winter months as weather and ice cover permitted.
We collected GPS coordinates (Universal Transverse Mercator, North American Datum of 1983) and estimated coordinate error (m) using a Garmin handheld GPS receiver at every radio-location. If the exact location could not be accessed, we estimated location based on signal strength and direction. We measured water temperature (°C) using a substrate thermometer.
We obtained water level data from the United States Geological Survey’s streamflow gauging station on the Kaskaskia River near Cowden (upstream) and the United States Army Corps of Engineers’ gauging station at Fayetteville (downstream). When conducting analyses using gage height as a variable, we set the minimum gage height observed during tracking at each site to 0 and adjusted all other gage heights appropriately. The resulting gage ranges were 0–3.21 m upstream and 0–3.35 m downstream. Flooding was minimal during the study.
2.1. Movement Analysis
Given the highly aquatic nature of A. mutica, we assumed movements were restricted to the river channel. We determined movement distance (m) through the river using the Fishtracker Toolbox [38] in ArcGIS 10.1 [39], which calculates the shortest path between consecutive points along a polygon representing the river. The polygon was calibrated to a gage height of 21.9 m downstream and 1.9 m upstream (mean gage heights during 2013–2014). Thus, movement distances were the shortest curved lines between consecutive points within the river channel and represented the minimum movement required to travel between locations. Turtles could have taken longer routes, but we have no way of quantifying this, so we used the minimum distance traveled between locations to compare movement rates.
We estimated movement rate in m/day by dividing the distance by the time between consecutive locations taken within two days of each other. We exported movement data to Microsoft Excel to calculate movement parameters of minimum, maximum, and mean movement rate for each turtle by sex, by site, and for all turtles. The minimum movement rate was the shortest movement rate observed, and the maximum movement rate was the highest movement rate observed.
In areas with no emergent structure and constantly changing water levels, it was sometimes difficult to determine if a turtle moved or not. Thus, to estimate the frequency of movement (% time turtles moved between consecutive radio-locations), we first calculated the average GPS error of all radio-locations and assumed any consecutive radio-locations within the error range indicated a turtle had not moved. We then divided the number of radio-locations with movement by the total number of radio-locations. We defined the active season as beginning when turtles start moving after winter inactivity and ending when turtles stop moving in late fall or early winter.
For the mixed model analysis, all continuous predictor variables were z-transformed and thus are represented as standard deviation units (variables were back-transformed after analysis for figures). We created 20 candidate mixed-effects models to explain the movement rate (m/day) of adult turtles. To test for the multicollinearity of predictor variables, we calculated the variance inflation factor (VIF) using the vif function from the R package usdm [40]. A VIF >10 indicated that multicollinearity was problematic [41] and required a re-assessment of variables. Predictor variables were chosen based on previous studies and included gage height [30], day of the year [42], water temperature [25], sex [43], and site [44]. The null model included only the intercept, and the global model included all covariates and two-way interactions. We examined the residual plot and histogram of the global model to check for patterns and normality. If normality and variance assumptions were an issue, we used a natural log transformation on the movement rate variable. Gage height, day of the year, and water temperature were set as quadratic terms to account for potential peaks and troughs in movement patterns. Individual turtles were included as a random effect. When conducting analyses, we included turtles with at least 10 known movement rates.
Mixed-effects models were created in R version 3.5.3 [45] using the lme4 package [46]. We ranked all models using AICC with the R package AICcmodavg [47]. Models within 2 AICC units of the top model had substantial support and were included in the confidence set of models [12]. We used maximum likelihood estimation (ML) when ranking mixed models and then used restricted maximum likelihood (REML) for the top model to obtain parameter estimates. Parameters with 95% confidence intervals (CI) not broadly overlapping zero were considered strong predictors. We calculated the marginal and conditional R2 values using the r.squaredGLMM function from the R package MuMIn [48,49]. We did not use model averaging because there are issues with the interpretability of model averaged parameters, particularly when averaging models with varying interaction and polynomial terms [50,51].
We ran a principal component analysis (PCA) in R version 3.5.3 [45] with variables of minimum, maximum, and mean movement rate and frequency of movement. We used the Kaiser–Meyer–Olkin measure of sampling adequacy (KMO test) [52] and Bartlett’s test of sphericity [53] to determine if the data benefited from variable reduction. We kept principal components with eigenvalues >1 and used a varimax rotation on the PCA loadings to aid the interpretation of principal components [54]. We then created and ranked linear models using AICC to explain each principal component in terms of sex, site, and the number of radio-locations.
2.2. Home Range Analysis
To determine the space use for each radio-tracked A. mutica, we calculated linear range, 100% minimum convex polygon (MCP), and fixed kernel density estimates (KDE; 50% and 95%). It is often worthwhile to calculate the kernel smoothing parameter (h) using multiple methods to evaluate parameter effects on home range size [55]. We calculated the smoothing parameter using both least squares cross-validation (LSCV) and likelihood cross-validation (CVh) for comparison [56]. We used the median CVh and LSCV parameter of all turtles so the home range area estimates would be comparable [5]. We considered the 50% KDE a core use area [5] and counted the number of core use areas for each turtle.
To calculate linear range, we used ArcGIS version 10.1 [39] to measure the distance along the middle of the river between the furthest upstream and downstream locations. For two dimensional home range estimates, we used R version 3.1.3 [45]. We calculated MCP using the mcp function in the package AdehabitatHR [57]. We calculated kernel density estimates using the kernelUD and getverticesHR functions in the AdehabitatHR package, and we calculated the smoothing parameters using the Animal Space Use Program [58]. For animals constrained to linear habitats, area estimates typically include large amounts of unused space [59]. There is strong evidence A. mutica do not inhabit terrestrial areas much beyond the shoreline [17], so we clipped the kernel density contours to the river [60]. When calculating summary home range statistics for MCP and KDE, we included turtles with at least 25 radio-locations. We included some turtles with fewer radio-locations in linear range calculations because they were lost for multiple weeks and then found long distances (>10 km) from initial locations. Disregarding these long movements would risk underestimating mean linear range sizes.
We used bootstrapped KDE to determine if home range size asymptotes for turtles with over 25 radio-locations [61,62]. For each turtle, we bootstrapped estimated the home range area by increments of five radio-locations for 100 iterations per increment using R version 3.1.3 [45]. To determine if home range size reached an asymptote, we created a line of best fit through the bootstrapped locations and used nonlinear regression with a monomolecular growth function [63] to estimate asymptotic home range size. If home range size was at least 95% of the asymptote, it indicated we had enough radio-locations to determine the home range of that individual accurately. Turtles with non-asymptotic home ranges were not included in mean home range or core area estimates.
We created 13 candidate linear models to explain home range size (95% KDE in hectares, CVh smoothing) in R version 3.5.3 [45]. All continuous predictor variables were z-transformed. Predictor variables were chosen based on previous studies and included mean movement rate [44], the number of radio-locations [64], plastral length (as measure of body size) [65], sex [19], and site [66]. We examined the residual plot and histogram of the global model to check for patterns and normality. If normality and variance assumptions were an issue, we used a natural log transformation on the home range size variable. The null model included only the intercept, whereas the global model included all variables and two-way interactions. We included turtles with non-asymptotic home ranges because we controlled for the sampling effect by using the number of radio-locations as a covariate.
3. Results
We attached radio-transmitters to 15 female and 3 male A. mutica upstream and to 10 female and 12 male A. mutica downstream. Unequal sample sizes were due to the difficulty of capturing large males upstream. The mean PL was 163 mm (SE = 2) for females and 116 mm (SE = 2) for males (Table A1). We documented one male mortality and three female mortalities, although two of the females died in a trap. Four other instances of lost turtles were most likely mortalities as well. We obtained 1989 locations between 19 July 2013 and 16 December 2014 for turtles with sufficient data for analyses. By site, we obtained 434 locations upstream and 1555 downstream. By sex, we obtained 901 locations for females and 1088 for males. By site and sex, we obtained 318 locations for upstream females, 116 for upstream males, 583 for downstream females, and 972 for downstream males. The average GPS error for radio-locations was 3 m.
3.1. Movement Analysis
The frequency of movement was 97.44% from April through October; thus, turtles rarely stayed in the same location for multiple days. We radio-tracked 28 adult A. mutica (7 upstream females, 2 upstream males, 8 downstream females, 11 downstream males) with at least 10 known movement rates (Table 1). The number of movements used for each turtle varied from 10 to 68, and the period of tracking varied from 70 to 498 days.

Table 1.
Sample size and the overall mean of minimum, maximum, and mean movement rates (m/day) with standard errors for A. mutica radio-tracked in the Kaskaskia River, Illinois, USA.
Minimum movement rates were <10 m/day for all turtles, and the overall minimum movement rate was 0 m/day for both males and females (Table A1). Maximum movement rates varied greatly, with the overall maximum movement rate observed at 2873 m/day for a female and 2455 m/day for a male (Table A1). In contrast, some turtles had maximum movement rates at an order of magnitude lower at <500 m/day (Table A1). Maximum movement rates tended to be higher downstream (Table 1). Mean movement rates also varied greatly for both males and females. The mean movement rate for females was slightly greater than for males, and it was greater downstream than upstream (Table 1). The mean movement rate for all turtles was 142.3 m/day (Table 1).
The VIF values were <1.8 for all predictor variables in our movement rate models, indicating that multicollinearity was not problematic. An inspection of the global model residual plot indicated overdispersion. We applied a natural log transformation to movement rate to correct the issue (back-transformed after analysis for figures).
The top mixed effects model for movement rate was the “Main Effects with Sex and Temp Interactions” model (Table 2 and Table A2). A number of effects had confidence intervals not overlapping zero (Table 3). Movement rate peaked at moderate water temperatures (Figure 3a) and decreased with the day of year (Figure 3b). The interaction of the water temperature and the day of the year showed that the effect of the water temperature was stronger earlier in the active season (Figure 3c). Though sex (Figure 3d) and gage height (Figure 3e) had moderate effects considered separately, the interaction of sex and gage height (Figure 3f) was strong. Movement rate increased for females and decreased for males with increasing gage height. Movement also decreased at a faster rate with the day of the year for males (Figure 3g). The interaction of sex with water temperature was moderate, with female movement peaking slightly higher than male movement (Figure 3h). The site effect indicated larger movement rates at the higher order downstream site (Figure 3i). The remaining interaction terms had weaker effects, with the confidence intervals broadly overlapping zero (Table 3).

Table 2.
Model rank, model name, number of parameters (K), −2 Log likelihood (−2LL), Akaike information criterion adjusted for small samples (AICC), difference of AICC value from top model value (ΔAICC), Akaike weight (wi), marginal R2 (R2(m)), and conditional R2 (R2(c)) for the top five and intercept-only mixed effects models describing movement rate of A. mutica in the Kaskaskia River, IL, USA (Full model structures in Appendix Table A2).

Table 3.
Real parameter estimates, standard error (SE), lower confidence interval (LCI), and upper confidence interval (UCI) for top mixed effects model describing movement rate of A. mutica in the Kaskaskia River, IL, USA.
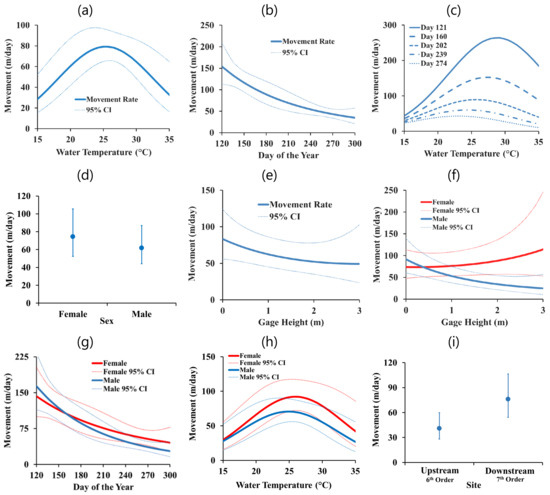
Figure 3.
Movement rate (m/day) and 95% confidence intervals for A. mutica for covariate effects of: (a) Water temperature (°C); (b) day of the year; (c) water temperature and day of the year interaction; (d) sex; (e) gage height (m); (f) sex and gage height interaction; (g) sex and day of the year interaction; (h) sex and water temperature interaction; and (i) site.
Bartlett’s test of sphericity (p < 0.001) indicated the summary movement data were appropriate for PCA. However, the KMO test (0.495) showed it was only marginally acceptable; thus, we ran the PCA with a cautious interpretation of results. The first two principal components (PC1 and PC2) had eigenvalues >1, which explained 84% of the variance. The varimax rotation showed that PC1 was a measure of vagility because it grouped mean and maximum movement rate, and PC2 was a measure of sedentary behavior because it grouped minimum movement rate and movement frequency. Model selection (AICC) showed the top model for PC1 (Weight = 0.37) and for PC2 (Weight = 0.37) included only site. The parameter confidence intervals showed the site effect was strong for PC1 but not PC2.
3.2. Home Range Analysis
The home range size estimated by MCP was much larger than any of the KDE (Table 4). The mean MCP area for all radio-tracked A. mutica was 260.5 ha and was generally larger for males and at the downstream site (Table 4). The mean linear range was higher for females (8.0 km, SD = 9.2) than for males (5.8 km, SD = 4.3), though this is likely due to a few females with very long ranges. The largest linear range documented was a female that was found dead 36.2 km upstream of the initial capture location (cause of death could not be determined). Linear range varied from 1.0 to 36.2 km for females and from 0.6 to 15.2 km for males. Linear range also varied greatly at both sites, ranging from 0.6 to 36.2 km upstream and from 1.1 to 15.2 km downstream.

Table 4.
Sample size and mean of minimum convex polygon (MCP; ha) and 50% and 95% kernel density estimates (KDE; clipped to river channel; ha) using likelihood cross-validation (CVh) and least squares cross-validation (LSCV) smoothing with standard errors for A. mutica radio-tracked in the Kaskaskia River, Illinois, USA.
Clipped KDE home ranges (Figure 4 and Figure S1) were larger using the median CVh smoothing (h = 58.5) than LSCV smoothing (h = 11.2; Table 4). The mean clipped 50% KDE (CVh) for all radioed turtles was 5.1 ha, and the 95% was 18.1 ha (Table 4). The clipped 50% KDE was similar for both sexes, whereas the clipped 95% KDE was larger for males (Table 4 and Figure 5). Both clipped 50% and 95% KDE (CVh) were larger downstream (Table 4). The number of core areas (clipped 50% KDE CVh) varied from 1 to 10 with some male and female turtles having only one core use area. Though the mean home range sizes stated here sometimes suggest sexual differences, our modelling generally indicated otherwise. Differences in mean by sex are likely complicated by unequal sample sizes between sites, and other variables actually explained the variation better than sex.
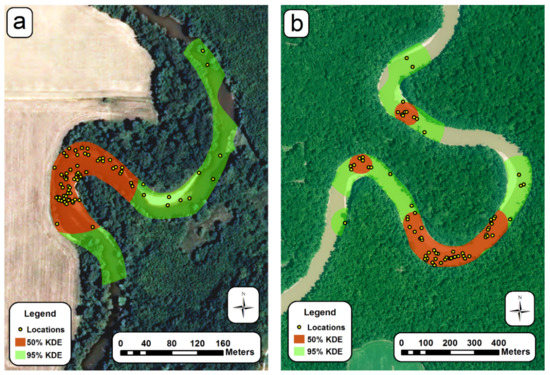
Figure 4.
Clipped 50% and 95% kernel density estimates (CVh smoothing) for A. mutica: (a) Male #29 at upstream site; (b) female #16 at downstream site.
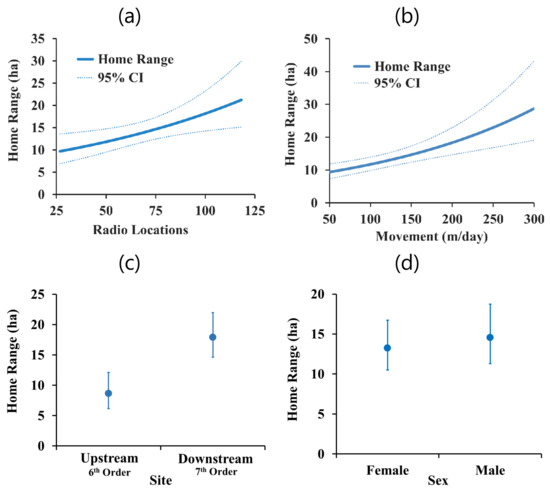
Figure 5.
Home range size (ha) and 95% confidence intervals for A. mutica for covariate effects of: (a) Number of radio-locations (top model); (b) movement rate (m/day; top model); (c) site (top model); and (d) sex (second best model).
Home range size reached an asymptote for 23 of 28 turtles, representing 7 of 9 turtles upstream and 16 of 19 downstream, and it reached an asymptote for 11 of 15 females and 12 of 13 males when grouped by sex (Table A1 and Figure S2). Often, if a home range does not asymptote, it is discarded from further analysis because it may invalidate comparisons of home range size; however, we accounted for bias in the linear models by including the number of radio-locations as a covariate. The number of radio-locations needed for a home range to reach 95% of the asymptote based on fitted curves ranged from 20 to 126 (Table A1). The mean number of locations to asymptote was 56 overall, 49 for only females, 65 for only males, 64 downstream, and 41 upstream (Table A1).
The VIF values (>10) for sex and plastron length indicated the variables were strongly correlated. This is likely because our study focused on adults which show strong sexual size dimorphism (females much larger than males). Plastron lengths within each sex were very similar and formed two clusters, which was ultimately a redundant measure of sex, so we did not use plastron length in our models. Plastron length would be more relevant in a study comparing turtles in varying stage classes than in our study which focused on adults. After removing plastron length, all VIF values were <1.5.
An inspection of the global model residual plot indicated overdispersion. We applied a natural log transformation to home range size to correct the issue (back-transformed after analysis for figures).
We had two linear models for home range size (clipped 95% KDE CVh) within 2 AICC units (Table 5 and Table A3). Both models included the number of radio-locations, movement rate, and site (Table 6). Home range size increased with both the number of radio-locations (Figure 5a) and movement rate (Figure 5b). Home range size was larger downstream (Figure 5c). The interaction between site and movement rate in the top model was not strong (Table 6). The second best model also included sex (Table 5), but the effect was weak (Figure 5d).

Table 5.
Model rank, model name, number of parameters (K), −2 Log likelihood (−2LL), Akaike information criterion adjusted for small samples (AICC), difference of AICC value from top model value (ΔAICC), Akaike weight (wi), and adjusted R2 (Adj. R2) for the top five, global, and intercept-only linear models describing home range size (clipped 95% KDE CVh) of A. mutica in the Kaskaskia River, IL, USA (Full model structures in Appendix Table A3).

Table 6.
Real parameter estimates, standard error (SE), lower confidence interval (LCI), and upper confidence interval (UCI) for top linear models describing home range size (clipped 95% KDE CVh) of A. mutica in the Kaskaskia River, IL, USA.
4. Discussion
4.1. Movement
The magnitude of river turtle movements varies depending on life history requirements related to foraging, reproduction, and survival [15]. Turtles in temperate regions typically have temporal patterns in movement rates [25]. Turtles were rarely inactive during intensive tracking from April through October, and our regular tracking did not extend late enough in the year to adequately document a cease in activity. Thus, the active season for A. mutica in south-central Illinois is at least April through October and possibly longer. In Kansas, A. mutica was most active from May through September, with some activity occurring in April and October [30]. Thus, our population had an active season at least as long as populations from Kansas. The closely related spiny softshell turtle (Apalone spinifera) also has an active season of April through October in most of its range [25] and potentially as long as March through mid-November [67].
Long distance movements spanning many river kilometers are noteworthy because of their potential relevance to nesting and migration. Such large-scale movements were often reflected in large linear ranges in our study. Some upstream females made long-term, possibly permanent movements after being captured (36.23 km upriver, 22.97 km upriver, 13.17 km upriver, and 11.31 km downriver). It is possible extensive movements were related to nesting, as many turtles are known to make migrations to nesting areas [68]. Some long-distance movements by A. mutica in Kansas coincided with the nesting season, and females did not return to previously inhabited areas [17]. An alternative explanation for the long movements of some females is an escape response brought on by the stress of being captured [17], although other turtles captured in the same areas did not leave. Some downstream males had long linear ranges because they moved large distances south, then moved back north to previously used areas. The timing of some large movements suggested overwintering migrations, whereas others were quick downstream and back movements in spring/early summer that were probably exploratory or for foraging. Both A. mutica and A. spinifera made exploratory movements in other studies [17,67].
The mixed-effects model showed movement rate decreased with day of the year for both sexes during the active season of A. mutica. Increased feeding to restore depleted energy reserves after overwintering, seeking mates, and nesting are possible causes of higher movements earlier in the active season [42]. Thus, this is consistent with the reproductive strategies hypothesis, which predicts higher movements early in the year for males associated with mate searching and females associated with nesting forays [69]. There was a larger change in male movement rate (started higher and ended lower) with day of the year, so perhaps males are particularly active in the early spring seeking mates. The interaction of water temperature and the day of the year showed higher water temperatures resulting in increased movement earlier in the season. Thus, A. mutica responds quickly to warming temperatures in the spring, likely related to reproduction and foraging, and it responds progressively less to warmer temperatures as the season progresses.
Movement rate increased steadily with increasing water temperature until it peaked in the mid-20 s (°C) and then declined at higher temperatures. Movement rate was similar for both sexes at low water temperatures. Female movement rate was slightly higher than males as water temperatures increased. As temperatures rise, the metabolic rate of turtles increases, and, thus, they increase in activity [70]. The pattern of increased movement at intermediate temperatures is found in many turtles [25,42]. An eventual decrease in movement as temperatures became hotter was also noted for A. mutica in Kansas [30]. Overall, the effect of water temperature on movement rate in our study is consistent with expected patterns for turtles.
Male movement rate was slightly higher at very low gage heights. However, female movement rate increased steadily with increasing gage height, whereas male movement rate decreased. Similar results were found in a Kansas study, whereby females were more likely to move away from the shoreline during floods than males [17]. There is evidence larger northern map turtles (Graptemys geographica) have higher swimming speeds and can handle strong currents better [71]. It may be the larger body size of adult female A. mutica affords them the strength to move more effectively in stronger currents associated with high flows.
Our analysis showed summary movement rates of A. mutica can be divided into two principal components. The relationship between the mean and maximum movement rate was positive; thus, turtles with high mean movement rates tended to exhibit higher maximum movement rates (vagility). The positive relationship indicates some turtles tended to make long movements and others generally moved shorter distances. The relationship between the frequency of movement and minimum movement rate indicated turtles with smaller minimum movement rates moved less frequently (sedentary behavior). Interestingly, the separation of principal components suggests that highly vagile turtles do not necessarily move more frequently. For instance, a turtle may show sedentary behavior more often than normal, but when active, still move large distances. One caveat is that minimum movement rates and movement frequency did not vary much between turtles, which is possibly why they loaded together. Thus, mean and maximum movement represent more relevant biological variation between turtles.
The top models for vagility and sedentary behavior both contained only site; however, the sedentary behavior confidence intervals indicated the effect of site was not strong. Thus, there was no discernable explanation for variation in minimum movement and frequency of movement, possibly because the variables were similar for most turtles. For vagility, it indicated higher movement downstream than upstream. The mixed model for movement rate also indicated site was a predictor. The narrower 6th order upstream channel may have an effect of restricting lateral movement compared to the 7th order downstream channel. The larger downstream channel may also necessitate greater movements between core areas. The movement of fish is also known to be higher in larger rivers [44]. Thus, water body size can play an important role in determining the overall magnitude of movement for riverine organisms. Heterogeneity in resource availability can also result in different movement patterns [4]. Perhaps resources were more densely concentrated upstream. Overall, variation in movement between sites is likely due to a combination of stream size and resource availability.
The mean movement rate was slightly higher for females than males, though not to the degree seen in a Kansas study, where females (165 m/day) had significantly higher rates than males (61 m/day) [17]. Males in Kansas had similar maximum movement rates (2–3 km/day) in our study, whereas females in Kansas sometimes moved 3–4 km/day [17]. Other river turtle species have also shown sexual differences in movement. Male false map turtles (Graptemys pseudogeographica) and sliders (Trachemys scripta) in the Missouri River and its backwaters had significantly lower mean and maximum movement than females [43]. However, the mean movement rate of A. spinifera males (141 m/day) and females (122 m/day) in Arkansas was not significantly different [67]. A possible explanation when movement differs is sexual size dimorphism because of size-specific influences in turtles [15,72].
Our study indicates that the magnitude of sexual differences in movement rate vary with environmental conditions and time of year. Thus, simple comparisons of mean movement rate between sexes may result in an incomplete understanding of behavior. The interaction terms in our model indicate female movement is higher in most but not all conditions. For instance, at low water temperatures or gage heights, the movement of A. mutica males and females is similar. Female movement becomes greater at higher temperatures and flows. Ultimately, we need to consider interactions to understand such nuances. For instance, a study in the Mississippi River found that females moved larger average distances than males, but this study did not track turtles during spring months [32], a time where males in our study had higher movement rates. Thus, the Mississippi River study may have missed some of the larger male movements. Understanding turtle movements is largely about weighing the potential risks and benefits of moving [67,72]. Movement decisions may depend on environmental factors, the spatial context of resources used by each sex, the availability of nesting habitat for females, and mate searching in males. Overall, sexual differences in movement rates appear to vary among different river turtle species and possibly within a species based on environmental factors and geographic location.
While the overall trend was for higher movement downstream, there were noteworthy exceptions contributing to the high variability in mean and maximum movement rates. For instance, one downstream female had a very high mean movement rate of 537.4 m/day, whereas some moved <100 m/day. Upstream, one male moved only 56.6 m/day whereas another moved 126.5 m/day. Meandering rivers provide habitat heterogeneity [73], and heterogeneous landscapes may result in an increased variability in movement [74]. Furthermore, the shifting success of resource acquisition strategies may result in individual variation in movements [67,72]. It is possible some turtles in our study employed a strategy of reduced movement while exploiting modest but spatially consistent resources, whereas others had equal success moving longer distances between seasonally abundant resources or searching out less predictable resources (nomadism) [4].
4.2. Home Range
We found linear ranges of A. mutica varied greatly by individual. A few stayed in short reaches only 1–2 km even when tracked for well over a year, whereas other ranges spanned over 10 km. In the Kansas River, the average length of ranges using point clusters was 474 m and 1228 m for male and female A. mutica, respectively, and variation between individuals was high [17]. The Kansas study considered long movements to be the establishment of new home ranges, and, thus, the linear range for all radio-locations regularly spanned several km [17]. Our results are in agreement that linear range varies and can be large. The linear range of closely related A. spinifera in Vermont and Quebec was 13.7 km for females and 3.9 km for males [19]. Thus, most males in our study had larger linear ranges and females smaller linear ranges than A. spinifera. Large linear ranges may highlight important movement corridors between different core areas of highly aquatic river species or may simply result from exploratory movements to find new resources or mates. However, linear range does not describe frequency or size of space use.
Our study estimated two-dimensional space use for A. mutica by calculating home range area. Estimates of home range area given by MCP typically included large areas of terrestrial habitat not used or even accessible to A. mutica under normal conditions, particularly for turtles with long linear ranges. The inclusion of unavailable space using MCPs has been noted in other studies, and sometimes the estimates are clipped to the river boundary [8,59]. For our study, the meandering of the river coupled with large distances between locations would include seemingly random areas of the river and exclude others. Thus, MCP is not a meaningful indicator of home range size for organisms constrained to meandering rivers, and clipping does not completely address the issue.
Kernel density estimates (KDE) also include some areas of terrestrial habitat not used—but to a much lesser degree than MCP. Furthermore, the density estimates are only in areas of point locations. Clipping the KDE to the river boundary provides a more reasonable estimate of space use within the confines of the river [60]. KDE using the CVh smoothing were larger than estimates using LSCV smoothing. LSCV has a tendency to under-smooth [56], potentially resulting in unrealistically fragmented home ranges [55]. The undersmoothing may result in numerous disjunct areas of home range around individual points [75], as was the case in our study. CVh also resulted in disjunct areas, but these were mostly clusters of points in different river reaches. Given there is no consensus on which smoothing parameter is best, it is helpful to keep in mind the biological relevance of any KDE in regards to the study animal. The extreme undersmoothing of LSCV did not provide reasonable areas of activity for a highly vagile species. Thus, we conclude that clipped 95% KDE using CVh smoothing give a meaningful home range estimate for A. mutica, with clipped 50% KDE (CVh) considered core areas [5].
Serial autocorrelation occurs when radio-locations are not independent of one another (location is partly dependent on the previous location) and can potentially render home range estimates invalid [76]. The effect is strongest when locations are taken at very small time intervals that do not afford animals the opportunity to move to a different area. In our study, autocorrelation was minimal because radio-locations were never taken on the same day (intervals were often multiple days) and A. mutica are capable of quickly moving large distances. Furthermore, simulation studies show that even if a moderate level of autocorrelation existed, it is not problematic when calculating home ranges using KDE [77,78,79]. Our sampling frequency could have introduced some bias, because we typically tracked for five days every other week at each site. Clustered samples could potentially overestimate space use in certain areas [77]. This would manifest as areas of high use defined by four-to-five radio-locations, which was not apparent for most turtles. It was occasionally noticeable for turtles found to be more nomadic or having smaller samples with home range sizes not asymptoting in the bootstrap analysis.
With enough samples, home range size attains an asymptote for animals that do not wander excessively or behave nomadically [11,61]. Most home ranges in our study asymptoted. Small sample size is a possible explanation for why four turtle home ranges with <40 locations did not asymptote. One female turtle home range that did not asymptote with 66 radio-locations over one year was possibly nomadic, and some of the upstream turtles with long linear ranges which could not be tracked sufficiently to calculate a home range may have been nomadic as well. Some turtles made occasional sizeable exploratory movements but returned to their home ranges afterward. Overall, the majority of A. mutica in the Kaskaskia River have well-defined home ranges, and a small minority behave nomadically. The Kansas study concluded that A. mutica continually redefined its home range [17], suggesting that home range size for A. mutica does not typically asymptote. However, their definition of home ranges as shifting is possibly analogous to movement between core areas in our study, so actual differences may not be that great. Another complicating factor for comparison is the short period of tracking in the Kansas study (technological limitations). If turtles in Kansas could have been tracked over a longer time, they might have moved back to previously inhabited areas.
Some A. mutica home ranges contained few core areas whereas others had several. Roughly a third of all turtles had only one core area, the majority had between two and five, and a few had greater than eight. The variation is not surprising considering the large differences observed in movement rates, and it is not uncommon for animals to have multimodal home ranges [2]. Space use often varies along a continuum from sedentary to nomadic [4], and our study indicates there is variation among individual A. mutica. In Kansas, A. mutica did not restrict space use to single areas [17], which was true for some turtles in our study but not all. The number of radio-locations needed to determine home range size averaged 56 overall, though it was higher downstream. Thus, as a general guide, we recommend that future studies use a minimum of 56 radio-locations to determine A. mutica home range size, preferably obtained over multiple seasons. Obtaining the locations over multiple seasons will ensure areas of home range are not overlooked; for instance, if different core areas are used throughout the year.
For our top models of home range area, mean movement rate was a predictor in both. The effect of site is reasonable given it was also in the mixed model for movement rate. The top two models had an effect for the number of radio-locations, which is known to influence home range size [64]. Sex was in the second model, indicating a small effect. Body size is often considered a strong predictor of home range size [65], but it was removed from our analysis because it was strongly correlated with sex. Our home range estimates only include adults so body size may still be an important factor when considering a larger ontogenetic series of individuals.
Movement rate was a predictor in both top models and had an effect of increasing home range size. The relationship is not surprising, as home ranges reflect the distances traveled by an animal [44]. Optimal foraging theory suggests home range size should be positively related to movement rate, with animals exploiting scarcer resources requiring increased movement throughout larger areas [80]. Perhaps some individuals maintained smaller home ranges because they were better at exploiting a concentrated resource. If all animals were using resources similarly, one would expect less variation in home range size. The specialization of individual animals can occur if there are trade-offs between using different resources [81]. Overall, turtles with higher movement rates will have larger home ranges, possibly because they have specialized foraging strategies.
The effect of site was strong, with home range size larger downstream. The difference may be due to the kernels being clipped to the smaller channel width upstream. However, the physical boundary typically limits lateral movement, thus A. mutica living in smaller streams should have more confined space use. The only instance where turtles may move inland is when females move to the higher areas of sand bars to nest [29]. We did not observe nesting during our study, so our home range estimates do not encompass nesting grounds. Our results are in agreement with previous findings where aquatic turtle home range sizes increase with water body size [66]. Water body size is also a good predictor of home range size for riverine fish [44]. Lower movement rates could be driving the smaller home ranges upstream. It also suggests A. mutica does not increase home range size longitudinally simply because lateral movement is restricted.
The top two models showed that, as the number of radio-locations increased, so did home range size. The positive relationship is because home range size did not reach an asymptote for some turtles, particularly ones with fewer radio-locations. It has been shown when using KDE with a sample size <50, the number of radio-locations can influence home range estimates [64]. It also provides further evidence that a minority of A. mutica display nomadic behavior and continually expand their home range (or change home range depending on definition). However, some individuals with many radio-locations had only one or two core areas and most home ranges asymptoted, so nomadism appears to be uncommon. In Mississippi, the number of radio-locations was not correlated with home range area for yellow-blotched map turtles (Graptemys flavimaculata) [18]. Perhaps softshell turtles are more likely to display nomadic behavior than hard shelled river turtles. Overall, the number of radio-locations had an effect resulting from small sample size for some turtles and the possible nomadism of a few others.
Sex was in the second best model, with males having slightly larger home range size than females. The effect was not strong, and confidence intervals overlapped. In contrast, females had significantly longer linear ranges and more lateral movement in Kansas, so they were considered to have larger home ranges than males [17,67]. Female A. spinifera in Vermont and Quebec have much larger home ranges than males [19]. The smaller sexual differences in our study are likely due to site-specific variability and differing home range calculations. Male and female A. mutica are known to have different dietary preferences also [28]. Thus, sexual differences in home range size at different sites may be due to the relative distribution and availability of preferred resources.
5. Conclusions
Our study has important implications for the study of river turtles. Movement rates should be calculated along the course of the river rather than straight line distances. Our findings indicate a number of environmental factors influence the movement of A. mutica including water temperature, the day of the year, and gage height. While these findings are supported by other studies, our study highlights the importance of including variable interactions, particularly related to sex. The effect of sex alone did not sufficiently explain variation in the movement data, but interactions of sex with environmental variables indicated interesting relationships. Stream order may also have a considerable effect and should be taken into account if making comparisons between sites or studies. Vagility varied greatly between individuals but was overall greater in the higher stream order, whereas sedentary behavior was similar at both sites. The patterns are attributable to physical boundaries of the stream and possibly resource acquisition and, as such, may vary for species with different mobility or dietary preferences. The river morphology and substrate at our sites was similar, but comparisons between different river systems should also consider these factors.
Linear ranges are useful to highlight the entire movement corridor needed for highly aquatic river species, but clipped kernel density estimates should be used to calculate home range size because they provide a more meaningful description of frequently used areas within the linear range. The median CVh smoothing value provided reasonable KDE home range estimates (clipped to river channel) for A. mutica in our meandering river system, but the best smoothing parameter may vary depending on the life history of an organism and site characteristics. Minimum convex polygon (MCP) methods should not be used for animals constrained to meandering river channels.
Home range size was influenced by site in our study and likely will be in any system where animals are confined by physical stream boundaries. Turtles that had higher movement rates also tended to have larger home ranges. Though there were sexual differences in movement, sex was not a strong factor determining home range size. The magnitude of sexual differences may depend on the relative distribution and availability of preferred resources, so it should not be assumed that sexual size dimorphism will result in large differences in home range size. The number of radio-locations should be included in home range size analysis to account for any inadequate sampling (too few radio-locations) of individuals. Furthermore, predictive power for number of locations at large sample sizes may indicate nomadic behavior. Bootstrap estimates are also helpful in determining if home range size stabilizes and indicated that most A. mutica have well-defined home ranges. Overall, the methods used to calculate and explain movement and home range can provide a framework for future spatial ecological studies of highly aquatic river turtles and riverine organisms.
One final note is that there was not major flooding during our study, so results indicate the spatial ecology of A. mutica during within bank flows. It is unknown how movement and home range could be affected during extended overbank flows. Some turtles generally inhabiting main channels move into the floodplain to exploit different resources during floods [82], and some fish use the floodplain as a refuge [83]. Further studies should examine the spatial ecology of A. mutica during major flood events to determine how movement rates and home range sizes are affected. Future studies could also examine spatial ecology of A. mutica in even larger channels such as the Mississippi River and those with differing morphology.
Supplementary Materials
The following are available online at https://www.mdpi.com/1424-2818/11/8/124/s1, Figure S1: Apalone mutica home range maps, Figure S2: Bootstrapped KDE home range curves.
Author Contributions
Conceptualization, J.P.R., R.D.B. and M.J.D.; data curation, J.P.R. and M.J.D.; formal analysis, J.P.R.; funding acquisition, J.P.R., R.D.B. and M.J.D.; investigation, J.P.R., R.D.B. and M.J.D.; methodology, J.P.R., R.D.B. and M.J.D.; project administration, J.P.R. and M.J.D.; resources, R.D.B. and M.J.D.; software, J.P.R. and M.J.D.; supervision, J.P.R. and M.J.D.; validation, J.P.R., R.D.B. and M.J.D.; visualization, J.P.R., R.D.B. and M.J.D.; writing – original draft, J.P.R.; writing – review & editing, R.D.B. and M.J.D.
Funding
This research was funded by a State Wildlife Grant (SWG; T-87-D-1) from the Illinois Department of Natural Resources (IDNR), a graduate student research grant from the Chicago Herpetological Society, the University of Illinois at Urbana–Champaign, and the Illinois State Toll Highway Authority. All work was covered under appropriate permits with the Illinois Department of Natural Resources T&E permit and in accordance with approved IACUC protocol #14000 with the University of Illinois.
Acknowledgments
We thank Christopher Phillips and Michael Ward for helpful comments on early drafts. We thank field assistants Travis Russell, Ethan Kessler, Christina Yen Feng, Cassandra Henry, Lisa LaBudde, and Sean Hegland for their work on the study. We also thank four anonymous reviewers whose comments and suggestions have improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A

Table A1.
ID number, site, sex, plastron length (mm, PL), number of radio-locations (n), duration of tracking (days), linear range (km), movement analysis sample size (Move n), minimum movement rate (m/day, Min Move), maximum movement rate (m/day, Max Move), mean movement rate (m/day, Mean Move), mean movement standard error (Move SE), minimum convex polygon size (ha, MCP), clipped 50% KDE (CVh smoothing, ha), clipped 95% KDE (CVh smoothing, ha), clipped 50% KDE (LSCV smoothing, ha), clipped 95% KDE (LSCV smoothing, ha), minimum number of radio-locations for home range to asymptote (HR Min. Loc.), home range proportion of asymptotic size (Prop. Asy.), and asymptotic home range size (ha, Asy. HR) for A. mutica radio-tracked in the Kaskaskia River, Illinois, USA from 2013 to 2014.
Table A1.
ID number, site, sex, plastron length (mm, PL), number of radio-locations (n), duration of tracking (days), linear range (km), movement analysis sample size (Move n), minimum movement rate (m/day, Min Move), maximum movement rate (m/day, Max Move), mean movement rate (m/day, Mean Move), mean movement standard error (Move SE), minimum convex polygon size (ha, MCP), clipped 50% KDE (CVh smoothing, ha), clipped 95% KDE (CVh smoothing, ha), clipped 50% KDE (LSCV smoothing, ha), clipped 95% KDE (LSCV smoothing, ha), minimum number of radio-locations for home range to asymptote (HR Min. Loc.), home range proportion of asymptotic size (Prop. Asy.), and asymptotic home range size (ha, Asy. HR) for A. mutica radio-tracked in the Kaskaskia River, Illinois, USA from 2013 to 2014.
| ID | Site | Sex | PL | n | Duration | Linear Range | Move n | Min Move | Max Move | Mean Move | Move SE | MCP | 50% KDE CVh | 95% KDE CVh | 50% KDE LSCV | 95% KDE LSCV | HR Min. Loc. | Prop. Asy. | Asy. HR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Downstream | Female | 168 | 74 | 345 | 1.4 | 41 | 6.48 | 686.1 | 89.8 | 17.9 | 26 | 3 | 9.6 | 0.89 | 3.88 | 36 | 1.01 | 9.54 |
| 2 | Downstream | Male | 131 | 119 | 498 | 11.05 | 65 | 1.69 | 1328.7 | 133.0 | 29.5 | 750 | 3.27 | 27.26 | 1.34 | 7.33 | 94 | 1.00 | 27.17 |
| 4 | Downstream | Male | 123 | 96 | 496 | 9.83 | 57 | 0 | 873.4 | 132.5 | 21.4 | 662 | 7.78 | 36.76 | 2.22 | 8.77 | 106 | 0.95 | 38.65 |
| 5 | Downstream | Female | 182 | 71 | 352 | 3.5 | 46 | 1.96 | 1862.0 | 202.0 | 49.9 | 68 | 7.38 | 17.66 | 1.76 | 6.73 | 35 | 1.00 | 17.62 |
| 6 | Downstream | Female | 166 | 66 | 371 | 14.5 | 38 | 3.86 | 2872.5 | 537.4 | 123.5 | 1762 | 19.71 | 72.35 | 2.48 | 10.7 | 126 | 0.81 | 89.78 |
| 8 | Downstream | Male | 118 | 110 | 469 | 10.17 | 65 | 2.73 | 2454.6 | 198.0 | 53.7 | 754 | 7.95 | 28.29 | 1.71 | 7.75 | 78 | 1.01 | 28.11 |
| 9 | Downstream | Male | 121 | 112 | 435 | 6.76 | 68 | 2.64 | 2329.6 | 193.1 | 46.5 | 199 | 7.25 | 29.21 | 1.8 | 8.49 | 91 | 1.00 | 29.33 |
| 10 | Downstream | Male | 113 | 51 | 260 | 5.11 | 33 | 1.86 | 358.5 | 70.9 | 15.1 | 46 | 2.97 | 12.74 | 0.82 | 3.44 | 38 | 0.99 | 12.85 |
| 11 | Downstream | Male | 113 | 111 | 435 | 3.75 | 68 | 2.07 | 451.0 | 87.8 | 12.0 | 99 | 4.47 | 17.72 | 1.53 | 6.36 | 64 | 1.01 | 17.60 |
| 12 | Downstream | Male | 117 | 99 | 435 | 15.24 | 59 | 0 | 1165.7 | 144.8 | 28.0 | 2322 | 14.95 | 57.56 | 2.26 | 10.71 | 97 | 0.97 | 59.30 |
| 13 | Downstream | Female | 167 | 105 | 435 | 2.17 | 62 | 0 | 1030.3 | 142.1 | 29.8 | 48 | 6.15 | 15.52 | 1.97 | 6.94 | 37 | 1.02 | 15.22 |
| 14 | Downstream | Female | 156 | 66 | 321 | 2.32 | 42 | 0 | 472.5 | 83.3 | 16.1 | 41 | 4.38 | 16.96 | 1.07 | 5.06 | 66 | 0.95 | 17.77 |
| 15 | Downstream | Female | 161 | 104 | 435 | 4.88 | 64 | 1.94 | 774.1 | 143.0 | 20.9 | 154 | 13.1 | 29.87 | 2.84 | 10.48 | 53 | 1.01 | 29.60 |
| 16 | Downstream | Female | 151 | 71 | 335 | 2.22 | 45 | 5.31 | 677.0 | 143.2 | 27.0 | 37 | 5.74 | 15.45 | 1.46 | 5.54 | 37 | 1.01 | 15.37 |
| 17 | Downstream | Male | 115 | 46 | 248 | 1.14 | 29 | 4.63 | 261.5 | 72.3 | 13.7 | 18 | 1.94 | 8.44 | 0.63 | 2.97 | 28 | 1.00 | 8.48 |
| 18 | Downstream | Male | 115 | 96 | 416 | 7.62 | 57 | 1.92 | 1642.2 | 124.7 | 35.5 | 363 | 6.91 | 29.2 | 1.62 | 7.19 | 83 | 0.98 | 29.70 |
| 19 | Downstream | Male | 114 | 95 | 403 | 3.98 | 56 | 0 | 1247.3 | 125.5 | 28.3 | 79 | 5.9 | 19.48 | 1.45 | 6.28 | 55 | 1.01 | 19.26 |
| 20 | Downstream | Male | 109 | 37 | 98 | 2.1 | 20 | 2.85 | 795.2 | 164.1 | 46.7 | 46 | 2.88 | 13.64 | 0.54 | 3.1 | 52 | 0.89 | 15.35 |
| 21 | Upstream | Female | 157 | 67 | 470 | 1.88 | 38 | 0 | 710.1 | 153.4 | 27.6 | 31 | 2.4 | 6.53 | 0.72 | 2.98 | 42 | 1.00 | 6.54 |
| 25 | Upstream | Female | 157 | 53 | 366 | 1.41 | 29 | 0 | 717.0 | 153.3 | 34.5 | 15 | 1.24 | 4.88 | 0.72 | 2.59 | 31 | 1.00 | 4.88 |
| 26 | Upstream | Female | 157 | 63 | 469 | 6.64 | 33 | 5.28 | 991.0 | 212.5 | 47.5 | 184 | 4.73 | 14.85 | 1.23 | 4.56 | 63 | 0.98 | 15.11 |
| 27 | Upstream | Female | 176 | 26 | 468 | 11.31 | 10 | 2.03 | 275.7 | 85.3 | 28.1 | 213 | 0.88 | 6.02 | 0.34 | 1.69 | 80 | 0.66 | 9.09 |
| 29 | Upstream | Male | 120 | 75 | 458 | 0.61 | 44 | 0 | 245.3 | 56.6 | 7.8 | 4 | 1.06 | 2.7 | 0.36 | 1.66 | 20 | 1.03 | 2.62 |
| 30 | Upstream | Female | 167 | 50 | 443 | 1.89 | 24 | 1.95 | 663.5 | 109.8 | 33.8 | 32 | 2.32 | 5.48 | 0.86 | 2.59 | 30 | 1.00 | 5.49 |
| 32 | Upstream | Female | 147 | 26 | 397 | 13.84 | 11 | 1.94 | 346.0 | 110.3 | 38.2 | 480 | 3.83 | 10.37 | 0.73 | 2.66 | 31 | 0.93 | 11.12 |
| 33 | Upstream | Male | 102 | 41 | 180 | 2.31 | 24 | 9.27 | 738.8 | 126.5 | 33.2 | 49 | 2.23 | 6.17 | 0.83 | 2.9 | 37 | 0.97 | 6.39 |
| 35 | Upstream | Female | 160 | 33 | 127 | 1.03 | 20 | 4.96 | 162.2 | 34.4 | 8.3 | 8 | 0.9 | 3.61 | 0.27 | 1.19 | 34 | 0.97 | 3.74 |
| 41 | Downstream | Female | 171 | 26 | 70 | 1.55 | 15 | 8.19 | 1111.7 | 154.8 | 76.4 | 23 | 2.89 | 8.88 | 0.64 | 2.36 | 36 | 0.91 | 9.74 |
Appendix B

Table A2.
Model name and general structure for the 20 mixed-effects models describing movement rate (m/day) of A. mutica radio-tracked in the Kaskaskia River, Illinois, USA from 2013 to 2014 (G = Gage height; W = Water temperature; D = Day of the year; Sx = Sex; S = Site; id = Turtle ID).
Table A2.
Model name and general structure for the 20 mixed-effects models describing movement rate (m/day) of A. mutica radio-tracked in the Kaskaskia River, Illinois, USA from 2013 to 2014 (G = Gage height; W = Water temperature; D = Day of the year; Sx = Sex; S = Site; id = Turtle ID).
| Model Name | Structure |
|---|---|
| Main Effects with Sex and Temp Interactions | 1 + G + G2 + W + W2 + D + D2 + S + Sx + W * D + W * G + D * G + D * Sx + W * Sx + G * Sx + 1|id |
| Global | 1 + G + G2 + W + W2 + D + D2 + Sx + S + G * W + G * D + Sx * G + S * G + D * W + Sx * W + S * W + Sx * D + S * D + Sx * S + 1|id |
| Temp and Day Interaction and Site | 1 + W + W2 + D + D2 + S + D * W + 1|id |
| Main Effects with Sex Interactions | 1 + G + G2 + W + W2 + D + D2 + S + Sx + D * Sx + W * Sx + G * Sx + 1|id |
| Temp, Day, and Gage Interactions | 1 + W + W2 + D + D2 + G + G2 + S + D * W + G * D + W * G + 1|id |
| Main Effects with Site and Temp Interaction | 1 + G + G2 + W + W2 + D + D2 + S + Sx + W * D + W * G + D * G + D * S + W * S + G * S + 1|id |
| Temp and Day Interaction | 1 + W + W2 + D + D2 + D * W + 1|id |
| Temp, Day, and Gage Interactions and Sex | 1 + W + W2 + D + D2 + G + G2 + Sx + D * W + G * D + W * G + 1|id |
| Temp and Day Interaction and Sex | 1 + W + W2 + D + D2 + Sx + D * W + 1|id |
| Main Effects | 1 + G + G2 + W + W2 + D + D2 + S + Sx + 1|id |
| Gage and Day Interaction with Sex | 1 + Sx + D + D2 + G + G2 + G*D + Sx * D + Sx * G + 1|id |
| Temp and Day | 1 + W + W2 + D + D2 + 1|id |
| Main Linear Effects | 1 + G + Sx + W + D + S + 1|id |
| Gage and Temp Interactions with Sex | 1 + Sx + W + W2 + G + G2 + G * W + Sx * W + Sx * G + 1|id |
| Sex and Site Interactions with Temp | 1 + Sx + S + W + W2 + W * Sx + S * W + 1|id |
| Gage and Temp Interaction | 1 + G + G2 + W + W2 + G * W + 1|id |
| Temp | 1 + W + W2 + 1|id |
| Temp and Sex | 1 + Sx + W + W2 + W * Sx + 1|id |
| Day and Sex | 1 + Sx + D + D2 + D * Sx + 1|id |
| Null | 1 + 1|id |

Table A3.
Model name and general structure for the 13 linear models describing home range size (ha) of A. mutica radio-tracked in the Kaskaskia River, Illinois, USA from 2013 to 2014 (R = Number of Radio-locations; M = Movement Rate; Sx = Sex; S = Site).
Table A3.
Model name and general structure for the 13 linear models describing home range size (ha) of A. mutica radio-tracked in the Kaskaskia River, Illinois, USA from 2013 to 2014 (R = Number of Radio-locations; M = Movement Rate; Sx = Sex; S = Site).
| Model Name | Structure |
|---|---|
| Movement and Site Interaction and Locations | 1 + R + M + S + M * S |
| Main Effects | 1 + R + M + Sx + S |
| Main Effects with Sex and Movement Interaction | 1 + R + M + Sx + S + M * Sx |
| Movement, Sex, and Site | 1 + M + Sx + S |
| Movement and Site | 1 + M + S + M * S |
| Site and Locations | 1 + R + S |
| Global | 1 + R + M + Sx + S + R * M + S * R + S * M + Sx * R + Sx * M + S * Sx |
| Site | 1 + S |
| Site and Sex | 1 + Sx + S + Sx * S |
| Locations | 1 + R |
| Movement | 1 + M |
| Null | 1 |
| Sex | 1 + Sx |
References
- Forester, J.D.; Ives, A.R.; Turner, M.G.; Anderson, D.P.; Fortin, D.; Beyer, H.L.; Smith, D.W.; Boyce, M.S. State-space models link elk movement patterns to landscape characteristics in Yellowstone National Park. Ecol. Monogr. 2007, 77, 285–299. [Google Scholar] [CrossRef]
- Börger, L.; Dalziel, B.D.; Fryxell, J.M. Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecol. Lett. 2008, 11, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Nathan, R.; Getz, W.M.; Revilla, E.; Holyoak, M.; Kadmon, R.; Saltz, D.; Smouse, P.E. A movement ecology paradigm for unifying organismal movement research. Proc. Natl. Acad. Sci. USA 2008, 105, 19052–19059. [Google Scholar] [CrossRef] [PubMed]
- Mueller, T.; Fagan, W.F. Search and navigation in dynamic environments—From individual behaviors to population distributions. Oikos 2008, 117, 654–664. [Google Scholar] [CrossRef]
- Kenward, R. A Manual for Wildlife Radio Tagging; Academic Press: London, UK, 2001; pp. 1–311. [Google Scholar]
- Burt, W.H. Territoriality and home range concepts as applied to mammals. J. Mammal. 1943, 24, 346–352. [Google Scholar] [CrossRef]
- Burt, W.H. Territorial behavior and populations of some small mammals in southern Michigan. Misc. Publ. Mus. Zool. Univ. Mich. 1940, 45, 1–58. [Google Scholar]
- Ouellette, M.; Cardille, J.A. The complex linear home range estimator: Representing the home range of river turtles moving in multiple channels. Chelonian Conserv. Biol. 2011, 10, 259–265. [Google Scholar] [CrossRef]
- Worton, B.J. A review of models of home range for animal movement. Ecol. Model. 1987, 38, 277–298. [Google Scholar] [CrossRef]
- Worton, B.J. Kernel methods for estimating the utilization distribution in home-range studies. Ecology 1989, 70, 164–168. [Google Scholar] [CrossRef]
- Kernohan, B.J.; Gitzen, R.A.; Millspaugh, J.J. Analysis of animal space use and movements. In Radio Tracking and Animal Populations; Millspaugh, J.J., Marzluff, J.M., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 125–166. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information—Theoretic Approach, 2nd ed.; Springer-Verlag: New York, NY, USA, 2002; pp. 1–488. [Google Scholar] [CrossRef]
- Millar, C.S.; Blouin-Demers, G. Spatial ecology and seasonal activity of Blanding’s Turtles (Emydoidea blandingii) in Ontario, Canada. J. Herpetol. 2011, 45, 370–378. [Google Scholar] [CrossRef]
- Aarts, G.; MacKenzie, M.; McConnell, B.; Fedak, M.; Matthiopoulos, J. Estimating space-use and habitat preference from wildlife telemetry data. Ecography 2008, 31, 140–160. [Google Scholar] [CrossRef]
- Moll, D.; Moll, E.O. The Ecology, Exploitation and Conservation of River Turtles; Oxford University Press: New York, NY, USA, 2004; pp. 1–393. [Google Scholar]
- Pluto, T.G.; Bellis, E.D. Seasonal and annual movements of riverine map turtles, Graptemys geographica. J. Herpetol. 1988, 22, 152–158. [Google Scholar] [CrossRef]
- Plummer, M.V.; Shirer, H.W. Movement Patterns in A River Population of the Softshell Turtle, Trionyx Muticus; Occasional Papers of the Museum of Natural History; The University of Kansas: Lawrence, KS, USA, 1975; Volume 43, pp. 1–26. [Google Scholar]
- Jones, R.L. Home range and seasonal movements of the turtle Graptemys flavimaculata. J. Herpetol. 1996, 30, 376–385. [Google Scholar] [CrossRef]
- Galois, P.; Léveillé, M.; Bouthillier, L.; Daigle, C.; Parren, S. Movement patterns, activity, and home range of the Eastern Spiny Softshell Turtle (Apalone spinifera) in northern Lake Champlain, Québec, Vermont. J. Herpetol. 2002, 36, 402–411. [Google Scholar] [CrossRef]
- Slavenko, A.; Itescu, Y.; Ihlow, F.; Meiri, S. Home is where the shell is: Predicting turtle home range sizes. J. Anim. Ecol. 2016, 85, 106–114. [Google Scholar] [CrossRef] [PubMed]
- Sterrett, S.C.; Kaeser, A.J.; Katz, R.A.; Smith, L.L.; Brock, J.C.; Maerz, J.C. Spatial ecology of female Barbour’s Map Turtles (Graptemys barbouri) in Ichawaynochaway Creek, Georgia. Copeia 2015, 103, 263–271. [Google Scholar] [CrossRef]
- Lovich, J.E.; Ennen, J.R. A quantitative analysis of the state of knowledge of turtles of the United States and Canada. Amphib. Reptil. 2013, 34, 11–23. [Google Scholar] [CrossRef]
- van Dijk, P.P. Apalone Mutica. IUCN Red List of Threatened Species. Available online: http://www.iucnredlist.org/details/full/165596/0 (accessed on 10 January 2014).
- Moll, D. Dirty river turtles. Nat. Hist. 1980, 89, 42–49. [Google Scholar]
- Ernst, C.H.; Lovich, J.E. Turtles of the United States and Canada, 2nd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 2009; pp. 1–827. [Google Scholar]
- Plummer, M.V. Reproduction and growth in the turtle Trionyx muticus. Copeia 1977, 1977, 440–447. [Google Scholar] [CrossRef]
- Pierce, L. Diet content and overlap of six species of turtle among the Wabash River. Master’s Thesis, Eastern Illinois University, Charleston, IL, USA, 28 January 1992. [Google Scholar]
- Plummer, M.V.; Farrar, D.B. Sexual dietary differences in a population of Trionyx muticus. J. Herpetol. 1981, 15, 175–179. [Google Scholar] [CrossRef]
- Plummer, M.V. Some aspects of nesting success in the turtle, Trionyx muticus. Herpetologica 1976, 32, 353–359. [Google Scholar]
- Plummer, M.V. Activity, habitat and population structure in the turtle, Trionyx muticus. Copeia 1977, 1977, 431–440. [Google Scholar] [CrossRef]
- Morrison, M.L.; Marcot, B.; Mannan, W. Wildlife-Habitat Relationships: Concepts and Applications; Island Press: Washington, DC, USA, 2006; pp. 1–520. [Google Scholar]
- Reinertsen, C.J.; Mitchell, S.M.; Bao, K.H.; Halvorson, K.M.; Pappas, M.J.; Freedberg, S. Genetic Variation and Gene Flow at the Range Edge of Two Softshell Turtles. J. Herpetol. 2016, 50, 357–365. [Google Scholar] [CrossRef]
- Pierson, S.M.; Rosenbaum, B.J.; McKay, L.D.; Dewald, T.G. Strahler stream order and Strahler calculator values in NHDPlus. USGS USA 2008, 30, 1–10. [Google Scholar]
- USEPA; USGS. National Hydrography Dataset Plus—NHDPlus, 1.0 ed.; United States Environmental Protection Agency and United States Geological Survey: Washington, DC, USA, 2005.
- Gordon, D.C.; Davinroy, R.D. Headcutting Investigation Upstream of the Kaskaskia River Navigation Project, Illinois; M27; United States Army Corps of Engineers: St. Louis, MO, USA, 2003; pp. 1–26. [Google Scholar]
- Davinroy, R.D.; Rogers, M.T.; Brauer, E.J.; Lamm, D.M. Bank Erosion and Historical River Morphology Study of the Kaskaskia River, Lake Shelbyville Spillway to Upper End of Carlyle Lake; United States Army Corps of Engineers: St. Louis, MO, USA, 2003; pp. 1–60. [Google Scholar]
- Plummer, M.V. A notching system for marking softshell turtles. Herpetol. Rev. 2008, 39, 64–65. [Google Scholar]
- Laffan, S.W.; Taylor, M.D. FishTracker: A GIS toolbox for kernel density estimation of animal home ranges that accounts for transit times and hard boundaries. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; pp. 1617–1623. [Google Scholar]
- ESRI. ArcGIS Desktop: Release 10; Environmental Systems Research Institute: Redlands, CA, USA, 2011. [Google Scholar]
- Naimi, B.; Hamm, N.A.; Groen, T.A.; Skidmore, A.K.; Toxopeus, A.G. Where is positional uncertainty a problem for species distribution modelling? Ecography 2014, 37, 191–203. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Lovich, J.E. Geographic variation in the seasonal activity cycle of spotted turtles, Clemmys guttata. J. Herpetol. 1988, 22, 482–485. [Google Scholar] [CrossRef]
- Bodie, J.R.; Semlitsch, R.D. Spatial and temporal use of floodplain habitats by lentic and lotic species of aquatic turtles. Oecologia 2000, 122, 138–146. [Google Scholar] [CrossRef]
- Woolnough, D.A.; Downing, J.A.; Newton, T.J. Fish movement and habitat use depends on water body size and shape. Ecol. Freshwat. Fish 2009, 18, 83–91. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Mazerolle, M.J. AICcmodavg: Model Selection and Multimodel Inference Based on (Q)AIC(c). R Package Version 2.2-1. Available online: http://CRAN.R-project.org/package=AICcmodavg (accessed on 19 March 2019).
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- B Barton, K. MuMIn: Multi-Model Inference. R Package Version 1.42.1. 2018. Available online: https://CRAN.R-project.org/package=MuMIn (accessed on 6 April 2019).
- Cade, B.S. Model averaging and muddled multimodel inferences. Ecology 2015, 96, 2370–2382. [Google Scholar] [CrossRef]
- Dochtermann, N.A.; Jenkins, S.H. Developing multiple hypotheses in behavioral ecology. Behav. Ecol. Sociobiol. 2011, 65, 37–45. [Google Scholar] [CrossRef]
- Kaiser, H.F. A second generation little jiffy. Psychometrika 1970, 35, 401–415. [Google Scholar] [CrossRef]
- Bartlett, M.S. Properties of sufficiency and statistical tests. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 160, 268–282. [Google Scholar] [CrossRef]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Steury, T.D.; McCarthy, J.E.; Roth, T.C.; Lima, S.L.; Murray, D.L. Evaluation of root-n bandwidth selectors for kernel density estimation. J. Wildl. Manag. 2010, 74, 539–548. [Google Scholar] [CrossRef]
- Horne, J.S.; Garton, E.O. Likelihood cross-validation versus least squares cross-validation for choosing the smoothing parameter in kernel home-range analysis. J. Wildl. Manag. 2006, 70, 641–648. [Google Scholar] [CrossRef]
- Calenge, C. The package “adehabitat” for the R software: A tool for the analysis of space and habitat use by animals. Ecol. Model. 2006, 197, 516–519. [Google Scholar] [CrossRef]
- Horne, J.S.; Garton, E.O. Animal Space Use 1.3. Available online: http://www.webpages.uidaho.edu/population_ecology/animal_space_use.htm (accessed on 13 February 2015).
- Blundell, G.M.; Maier, J.A.; Debevec, E.M. Linear home ranges: Effects of smoothing, sample size, and autocorrelation on kernel estimates. Ecol. Monogr. 2001, 71, 469–489. [Google Scholar] [CrossRef]
- Hodder, K.H.; Masters, J.E.G.; Beaumont, W.R.C.; Gozlan, R.E.; Pinder, A.C.; Knight, C.M.; Kenward, R.E. Techniques for evaluating the spatial behaviour of river fish. Hydrobiologia 2007, 582, 257–269. [Google Scholar] [CrossRef]
- Harris, S.; Cresswell, W.J.; Forde, P.G.; Trewhella, W.J.; Woollard, T.; Wray, S. Home-range analysis using radio-tracking data—A review of problems and techniques particularly as applied to the study of mammals. Mamm. Rev. 1990, 20, 97–123. [Google Scholar] [CrossRef]
- Laver, P.N.; Kelly, M.J. A critical review of home range studies. J. Wildl. Manag. 2008, 72, 290–298. [Google Scholar] [CrossRef]
- Koya, P.R.; Goshu, A.T. Solutions of rate-state equation describing biological growths. Am. J. Math. Stat. 2013, 3, 305–311. [Google Scholar] [CrossRef]
- Seaman, D.E.; Millspaugh, J.J.; Kernohan, B.J.; Brundige, G.C.; Raedeke, K.J.; Gitzen, R.A. Effects of sample size on kernel home range estimates. J. Wildl. Manag. 1999, 63, 739–747. [Google Scholar] [CrossRef]
- Harestad, A.S.; Bunnell, F.L. Home range and body weight—A reevaluation. Ecology 1979, 60, 389–402. [Google Scholar] [CrossRef]
- Schubauer, J.P.; Gibbons, J.W.; Spotila, J.R. Home range and movement patterns of slider turtles inhabiting Par Pond. In Life History and Ecology of the Slider Turtle; Gibbons, J.W., Ed.; Smithsonian Institution Press: Washington, DC, USA, 1990; pp. 223–232. [Google Scholar]
- Plummer, M.V.; Mills, N.E.; Allen, S.L. Activity, habitat, and movement patterns of softshell turtles (Trionyx spiniferus) in a small stream. Chelonian Conserv. Biol. 1997, 2, 514–520. [Google Scholar]
- Obbard, M.E.; Brooks, R.J. Nesting migrations of the snapping turtle (Chelydra serpentina). Herpetologica 1980, 36, 158–162. [Google Scholar]
- Morreale, S.J.; Gibbons, J.W.; Congdon, J.D. Significance of activity and movement in the yellow-bellied slider turtle (Pseudemys scripta). Can. J. Zool. 1984, 62, 1038–1042. [Google Scholar] [CrossRef]
- Ultsch, G.R. Ecology and physiology of hibernation and overwintering among freshwater fishes, turtles, and snakes. Biol. Rev. 1989, 64, 435–516. [Google Scholar] [CrossRef]
- Pluto, T.G.; Bellis, E.D. Habitat utilization by the turtle, Graptemys geographica, along a river. J. Herpetol. 1986, 20, 22–31. [Google Scholar] [CrossRef]
- Gibbons, J.W. The slider turtle. In Life History and Ecology of the Slider Turtle; Gibbons, J.W., Ed.; Smithsonian Institution Press: Washington, DC, USA, 1990; pp. 3–18. [Google Scholar]
- Brierly, G.J.; Fryirs, K.A. Geomorphology and River Management: Applications of the River Styles Framework; Blackwell Publishing: Malden, MA, USA, 2005; pp. 1–398. [Google Scholar]
- Morales, J.M.; Fortin, D.; Frair, J.L.; Merrill, E.H. Adaptive models for large herbivore movements in heterogeneous landscapes. Landsc. Ecol. 2005, 20, 301–316. [Google Scholar] [CrossRef]
- Huck, M.; Davison, J.; Roper, T.J. Comparison of two sampling protocols and four home-range estimators using radio-tracking data from urban badgers Meles meles. Wildl. Biol. 2008, 14, 467–477. [Google Scholar] [CrossRef]
- Swihart, R.K.; Slade, N.A. Influence of sampling interval on estimates of home-range size. J. Wildl. Manag. 1985, 49, 1019–1025. [Google Scholar] [CrossRef]
- Swihart, R.K.; Slade, N.A. On testing for independence of animal movements. J. Agric. Biol. Environ. Stat. 1997, 2, 48–63. [Google Scholar] [CrossRef]
- De Solla, S.R.; Bonduriansky, R.; Brooks, R.J. Eliminating autocorrelation reduces biological relevance of home range estimates. J. Anim. Ecol. 1999, 68, 221–234. [Google Scholar] [CrossRef]
- Fieberg, J. Kernel density estimators of home range: Smoothing and the autocorrelation red herring. Ecology 2007, 88, 1059–1066. [Google Scholar] [CrossRef]
- Ford, R.G. Home range in a patchy environment: Optimal foraging predictions. Am. Zool. 1983, 23, 315–326. [Google Scholar] [CrossRef]
- Svanbäck, R.; Bolnick, D.I. Intraspecific competition affects the strength of individual specialization: An optimal diet theory method. Evol. Ecol. Res. 2005, 7, 993–1012. [Google Scholar]
- Moll, D. Food and feeding strategies of the Ouachita map turtle (Graptemys pseudogeographica ouachitensis). Am. Midl. Nat. 1976, 96, 478–482. [Google Scholar] [CrossRef]
- Schwartz, J.S.; Herricks, E.E. Fish use of stage-specific fluvial habitats as refuge patches during a flood in a low-gradient Illinois stream. Can. J. Fish. Aquat. Sci. 2005, 62, 1540–1552. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).