4. Discussion
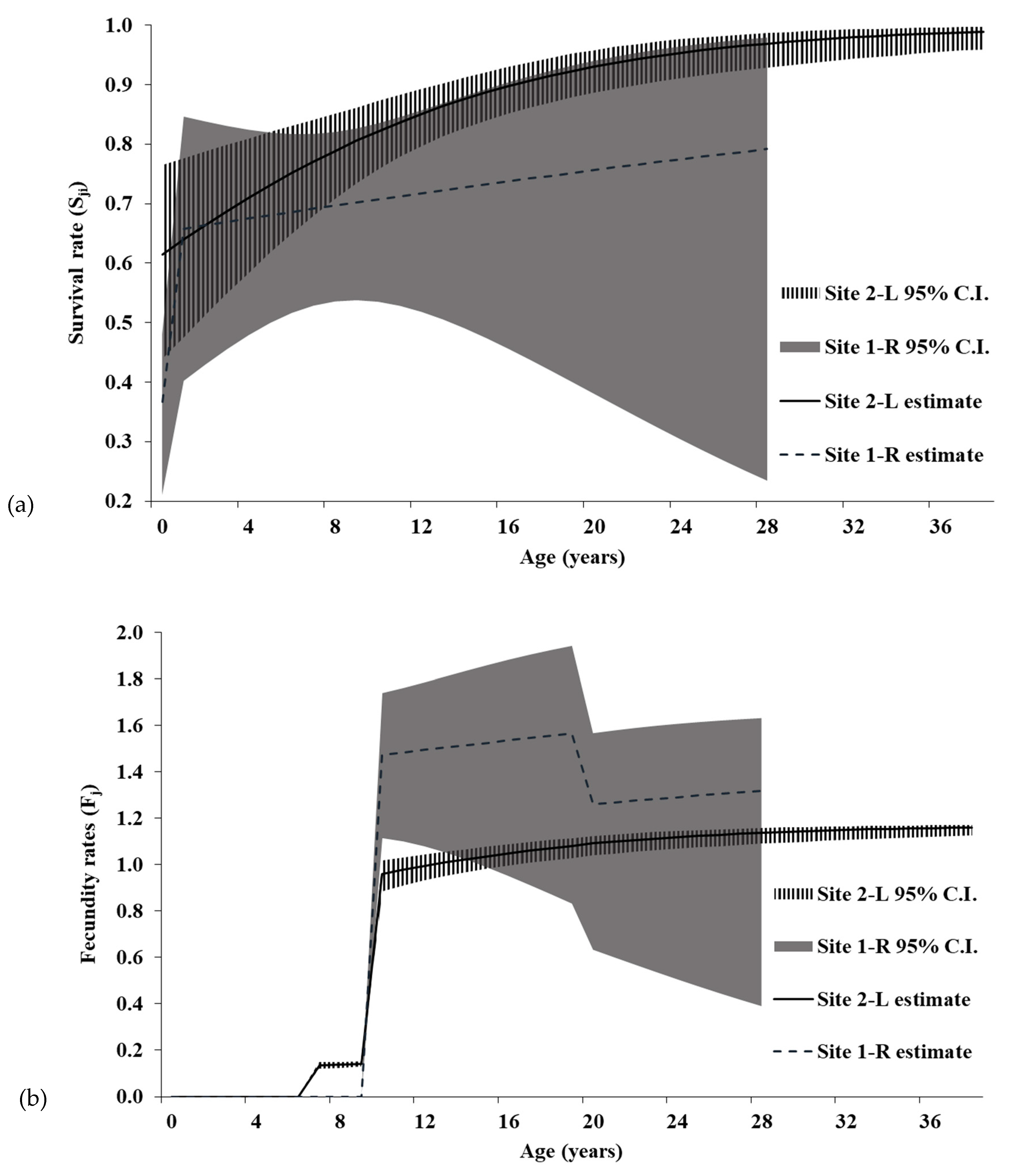
Our results indicate that age-specific survival rates for Illinois Spotted Turtles (
Clemmys guttata) follow a similar ontogenetic trend and value as those documented for other freshwater turtle species [
24], with survival sometimes reaching over 90% in adults [
27,
47]. Old adults have higher survival rates than young adults, similar to what is found in the Blanding’s Turtle (
Emydoidea blandingii) [
48]. Illinois populations show elastic prioritization of vital rates often seen in long-lived turtle species [
24], using a bet-hedging life history strategy with adult survival having the largest proportional impact on population growth rate. Our study also indicates a demographic divergence between Illinois populations and suggests clinal variation in demographic rates when viewed in a larger geographic context. Though estimated population sizes have increased since 1988 [
45], current projections from the Leslie matrices suggests both populations will likely begin to decline. Management to ensure high adult survival and conserve or expand existing habitat will likely be necessary.
A review of survivorship in 25 turtle species showed an average survival rate of 86.6%, with all but four species having >80% annual survival [
49]. Illinois populations of
C. guttata have comparable survival rates to turtles documented in the review [
49]. Site 2-L bounds the estimate from an Ontario
C. guttata population of 96.5% [
15], suggesting adults in demographically healthy
C. guttata populations should be above 90% annual survival. The juvenile
C. guttata survival rate from the northern edge of the range was 81.6% [
15], one of the highest reported for freshwater turtle species and comparable to the upper 95% C.I. estimates for Illinois populations. Furthermore, these estimated survival rates were within the range reported for other species. For instance, juvenile
Emydoidea blandingii [
32], Yellow Mud Turtles (
Kinosternon flavescens) [
50], Eastern Mud Turtles (
K. subrubrum) [
34], and Painted Turtles (
Chrysemys picta) [
9] all had survival estimates ranging from 64.0% to 80.6%.
Female age-specific fecundity results support findings from an Ontario study [
30], which concluded
C. guttata exemplifies the ‘terminal investment hypothesis’ of reproduction in which individuals with a low probability of surviving to future reproductive events increase their present reproductive investment [
51]. Higher ASRO could represent a trade-off in resource allocation [
52] whereby greater present maternal investment correlates with reduced future body condition, growth, and survival [
53]. For instance, studies on
C. guttata from South Carolina and Canada found larger clutch sizes correlated with both poor and good maternal body condition [
30,
54]. The Chicken Turtle (
Deirochelys reticularia) exhibits an extreme version of the terminal investment life history strategy where females have high fertility (annual reproduction of large clutches), mature early (age 2–5 years), and have >30% mortality rates in response to extreme environmental stochasticity [
55]. Although individuals at Site 1-R have greater ASRO than at Site 2-L, all fecundity elements of the Leslie matrices have low sensitivities and elasticities, suggesting the increased clutch size has minimal ability to alter the population trajectory at Site 1-R (
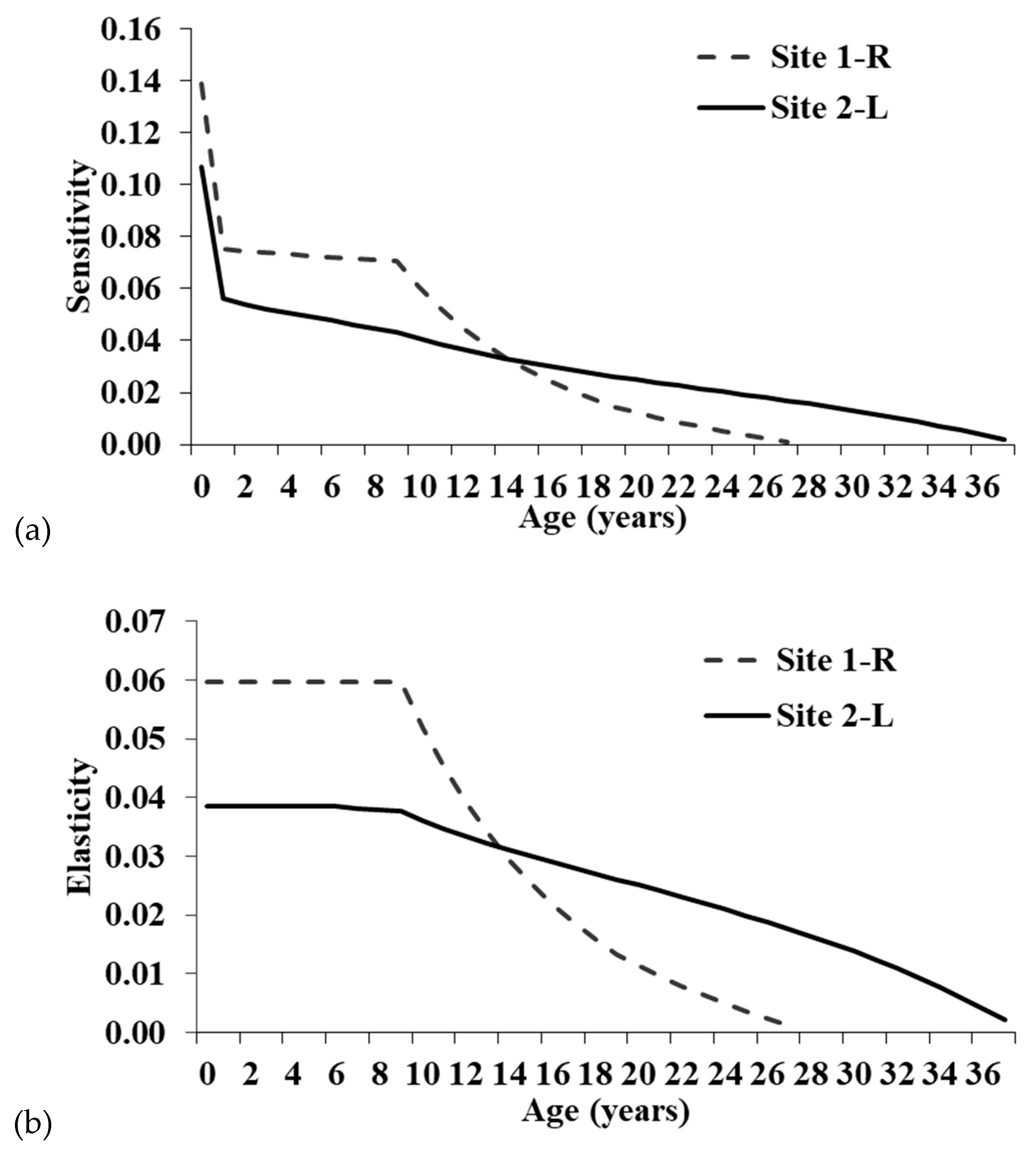
Figure 6).
While the single-year age classes with the greatest proportional influence on population growth were pre-reproductive survival, adult survival has the highest summed elasticity of the three main stage groups (hatchling, juvenile, and adult). Thus, conservation actions targeting adults will have the greatest proportional impact on the population growth rate. Focusing on the summed elasticities is preferable because management will typically impact a life history stage, not specific age classes [
24]. Though adult elasticity is highest, juvenile survival also has moderate elasticity, particularly at Site 1-R.
The summed elasticities are comparable to those derived from a stage-based matrix for an Ontario population [
15]. Elasticities for Site 2-L were very similar to the Ontario population, whereas elasticities were relatively higher for juveniles and lower for adults at Site 1-R. The increased elasticity for younger turtles at Site 1-R is likely related to the maximum age in the models and lower annual survival. The maximum age for Site 1-R was only 28 years, whereas Site 2-L was 38 years, and the Ontario study did not include a maximum age [
15]. Having fewer individuals surviving to old age will increase the importance of younger turtles in maintaining the population and result in higher elasticity values. This is also noticeable when comparing the three adult stage categories for the Illinois populations. Mature adult elasticity is similar between sites, but the relatively high elasticity seen for old adults at Site 2-L is shifted to juveniles and young adults at Site 1-R.
Clemmys guttata are estimated to live at least 60 and maybe even >100 years [
37], so in areas where individuals attain higher maximum ages, mature adult survival elasticity should be higher. Elasticities for fecundity were also similar between the Illinois and Ontario populations.
Our results support previous studies that concluded
C. guttata uses a bet-hedging life history strategy where higher adult survival and longevity compensate for lower juvenile survival and recruitment [
15,
37]. However, the bet hedging is not as extreme as seen in some other chelonian species. For instance, total adult elasticity typically increases with the amount of bet hedging [
29], and a Snapping Turtle (
Chelydra serpentina) population in Ontario had a total adult elasticity of ~87% [
29]. At Site 1-R, longevity and adult survival elasticity were somewhat lower than Site 2-L. However, if mortality rates at Site 1-R are high due to anthropogenic disturbances, the juvenile elasticities may be elevated simply because the maximum age of adults is not as high as it would be in an undisturbed natural landscape. Thus, in an undisturbed population, adults would attain higher maximum ages and have higher summed elasticity.
Further examination of life-history traits can highlight interesting differences between
C. guttata and other sympatric wetland turtle species.
Clemmys guttata attains sexual maturity at a moderate age [
49], has comparably high adult survivorship [
27,
56,
57], low reproductive output [
58,
59], and moderate longevity [
60]. Among animals with high adult survival rates, some species have multiple clutches per year and/or large clutch sizes, whereas others invest more heavily in one or a few offspring [
61]. Some studies have found
C. guttata have multiple clutches per year [
62], though clutch size is relatively small compared to species such as
C. serpentina or
E. blandingii [
63,
64]. Thus,
C. guttata may be investing slightly more in fewer offspring than sympatric wetland turtle species. This could account for pre-reproductive age-classes having the highest single elasticity values in our study.
Though many turtles rely on longevity and high adult survival as a life-history strategy, there are exceptions. For example, recent demographic studies on the genus
Chelodina counter the assumed chelonian life-history strategies. The population growth rates of the Snake-necked Turtle (
Chelodina rugosa) are fairly resistant to adult removal [
65], whereas
λ of the congeneric Eastern Long-necked Turtle (
Chelodina longicollis) is most sensitive to adult survival but cannot exceed 1.0 without increased hatchling survival [
66]. Moreover, while lengthy studies are resource-intensive, short-term evaluation may simply not consistently represent a population’s fundamental demographic behavior and lead to spurious conclusions [
67]. As more long-term demographic analyses are produced for more species, we will improve our understanding of the variation in turtle life-history strategies.
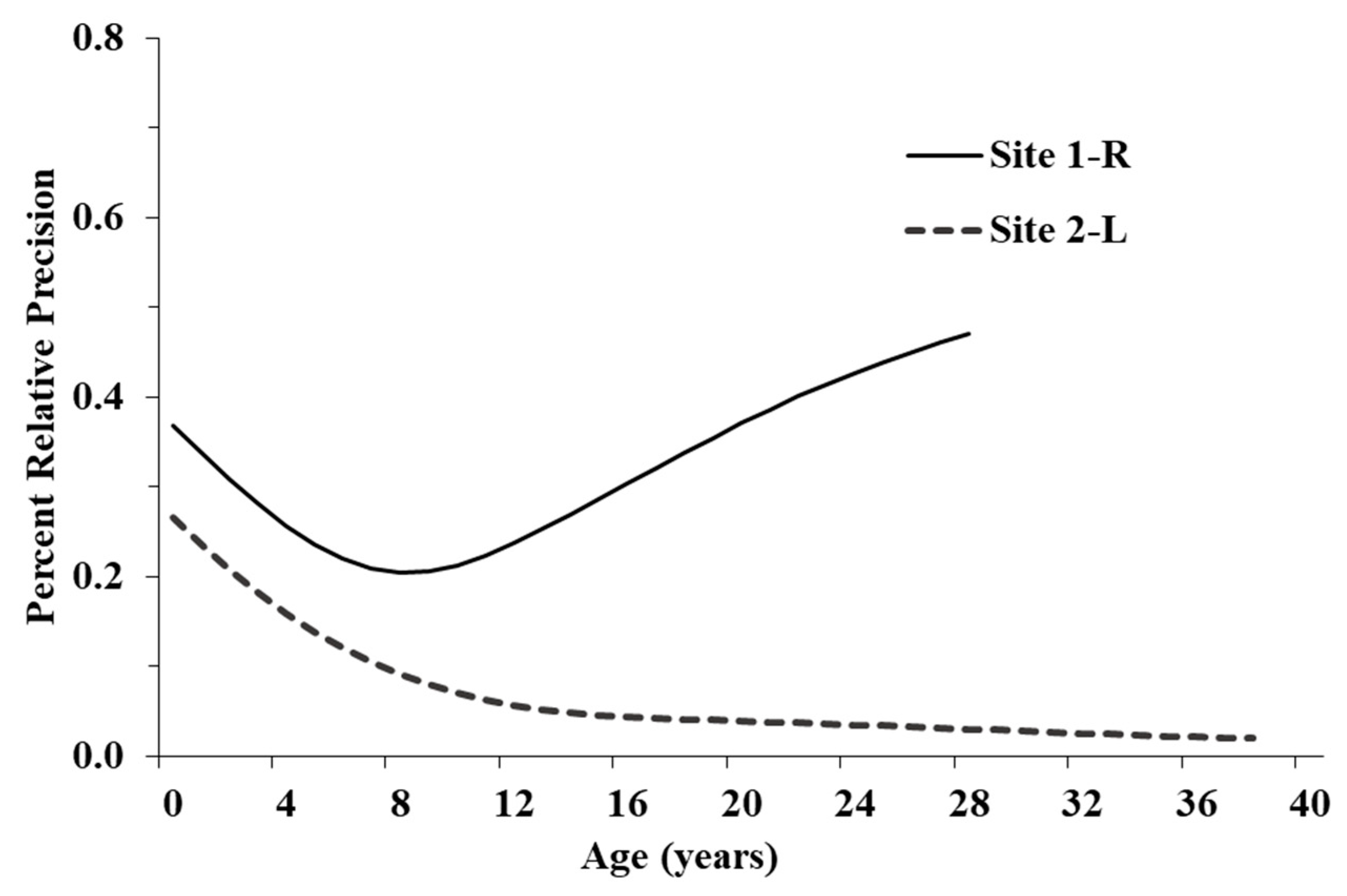
Our results additionally show evidence of demographic divergence between the Illinois populations. First, the Illinois populations were not consistent with each other concerning the shape of the survival curves and their estimated magnitudes. More specifically, at Site 1-R, determining if and where an asymptote exists may only be resolved through continued monitoring to track older marked individuals. The 10-yr dataset of >100 individuals for Site 1-R may be insufficient to characterize the population despite its 21-yr span. More frequent surveys as were conducted at Site 2-L may be required to produce reliable estimates and mitigate the low certainty in Site 1-R survival rates. Alternatively, if the modeled variability in survival for adults is not exaggerated, the given estimates reveal a population vulnerable to the effects of demographic and environmental stochasticity, which can quickly lead to extirpation [
68]. Selection may temper this risk for larger clutch sizes leading to higher ASRO at Site 1-R to compensate for lower or more variable adult survival than at Site 2-L. We speculate the demographic divergence between populations to be an adaptive response to human-induced rapid environmental change, which can lead to sudden increases in trait plasticity [
69]. Previous research has demonstrated fast evolutionary responses with large populations or short generation times [
70,
71], but our results show a demographic response to recent habitat loss and fragmentation (~200 years or ~10 generations). Research at the northern range limit of
C. guttata demonstrated substantial demographic variability could occur at more local scales between disparate habitat types [
72], but we further demonstrate detectable demographic plasticity between conspecific populations located in similar and nearby sites. This variation is evidence of the demographic expression of genetic divergence between Illinois populations [
39].
Our study also provides further support for clinal variation in demographic properties. In general, chelonian size and egg mass positively correlate with latitude [
73,
74], whereas clutch size decreases with latitude [
75]. In the Wood Turtle (
Glyptemys insculpta), life-history traits of body size and clutch size vary by latitude due to a combination of demographic and environmental factors [
76]. Likewise, in
C. picta, northern populations produce an average of 10.7 eggs per clutch as compared with 4.1 eggs per clutch in southern populations [
77]. Life-history traits are thus known to vary, sometimes starkly, within species [
78,
79]. Similarly,
C. guttata exhibits clinal variation in average clutch size across its broad range [
80]. We documented average clutch size (eggs per reproductive female) in Illinois populations (41°N; Site 1-R = 4.35 ± 0.95, Site 2-L = 3.34 ± 0.91) as intermediate between Ontario (45°N; 5.3 ± 0.04) and Pennsylvania (40°N; 3.9 ± 0.01) but with greater variability [
62]. Survival estimates for
C. picta from Michigan show two-fold higher survival rates compared with estimates from South Carolina [
9,
81], and
C. guttata appears to follow a similar trend with increasing juvenile survival with latitude.
The variation from our calculation of age-specific traits revealed trends between Illinois populations and between Illinois and Canadian
C. guttata. First,
G1-R (14.9 years) was roughly 65% of
G2-L (22.8 years), indicating the mean age of reproduction is significantly younger for Site 1-R than Site 2-L individuals, likely due to lower adult survival rates [
82]. Both Illinois populations had shorter generation times than the Ontario population (
Table 2;
Gont = 27.8 years), reinforcing the known positive correlation between
G and latitude in ectotherms [
83,
84]. The most accurate estimate of maximum longevity (
a) using the Litzgus [
37] formulation for either site is obscured by the sensitivity of the equation to small changes in survival and the large C.I. for adult survival. At Site 2-L, for example, a difference in estimated survival of ~2.5% resulted in a 35-yr alteration between the
PE and
UCE estimates. However,
a for female
C. guttata was much lower in Illinois than in Canada even when using the larger
UCE from Illinois for comparison. In
C. guttata, the clinal trend may be further explained by the short active season of northern turtle species, which experience lower annual metabolic activity [
31] due to an overwintering period of six months per year [
85]. The restrictive environmental conditions in Canada are consequently reflected in
C. guttata life history and include higher survival by stage [
15], later attainment of sexual maturity [
37], and greater estimated longevity [
37]. It follows that
G, as a measure of the average age of mothers at childbirth [
3], would be larger at higher latitudes. However, larger estimates of
G correspond to slower recovery from overexploitation or other high mortality events [
27,
65], which may pose a threat to Canadian
C. guttata.
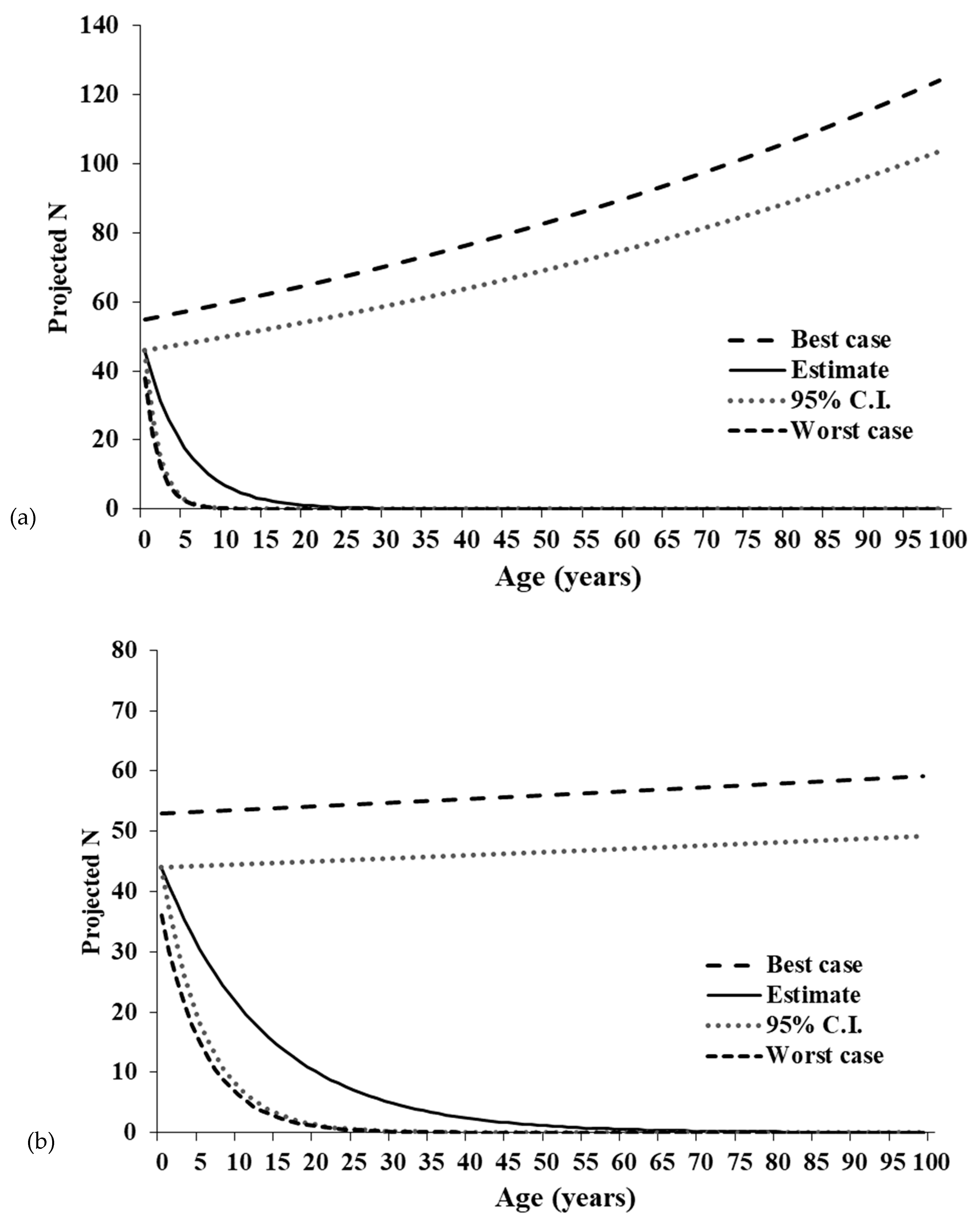
Moreover, the related terms of R0 and λ suggest a greater divergence in deterministic trends between Illinois and Canada. Our results show a demographically driven decline in the Site 1-R population, made obvious by population projections. Given deterministic conditions, the estimated 95% LCE, and worst-case scenarios closely track one another to show an estimated reduction to one female individual within 17 years in the Site 1-R population. The projections showing rapid population growth for the Site 1-R UCE and best-case scenarios are thus likely exaggerated and unreliable. The Site 2-L population exhibits only minor growth even in the deterministic best case and UCE scenarios, so it is likely that neither population is demographically viable under stochastic conditions. In contrast, the Ontario population exhibits a positive λ and R0 an order of magnitude above Illinois estimates.
The negative population growth rates derived from the Leslie matrices were surprising because population size estimates from a POPAN model previously indicated the populations were experiencing stable to increasing abundance since 1988 [
45]. We posit three related causes for the discrepancy in our findings. First, our initial abundance estimates included males, while our matrix models were female-only. We assumed the single-sex model was representative of the entire population, but it is possible male dynamics differ from and obscure trends in female dynamics [
86]. We do not consider this problematic as
C. guttata reproduces sexually, and female abundance is a limiting factor for population growth. Second, our previous estimates of
λ were based on a small sample size of capture data (
n1-R = 6,
n2-L = 11) and may be elevated as a result of population momentum [
82]. In other words, the populations were sampled while experiencing short-term, transient dynamics, not representative of the general trend [
87]. This explanation only reemphasizes the necessity of long-term datasets for long-lived species [
88]. Finally, our calculation of
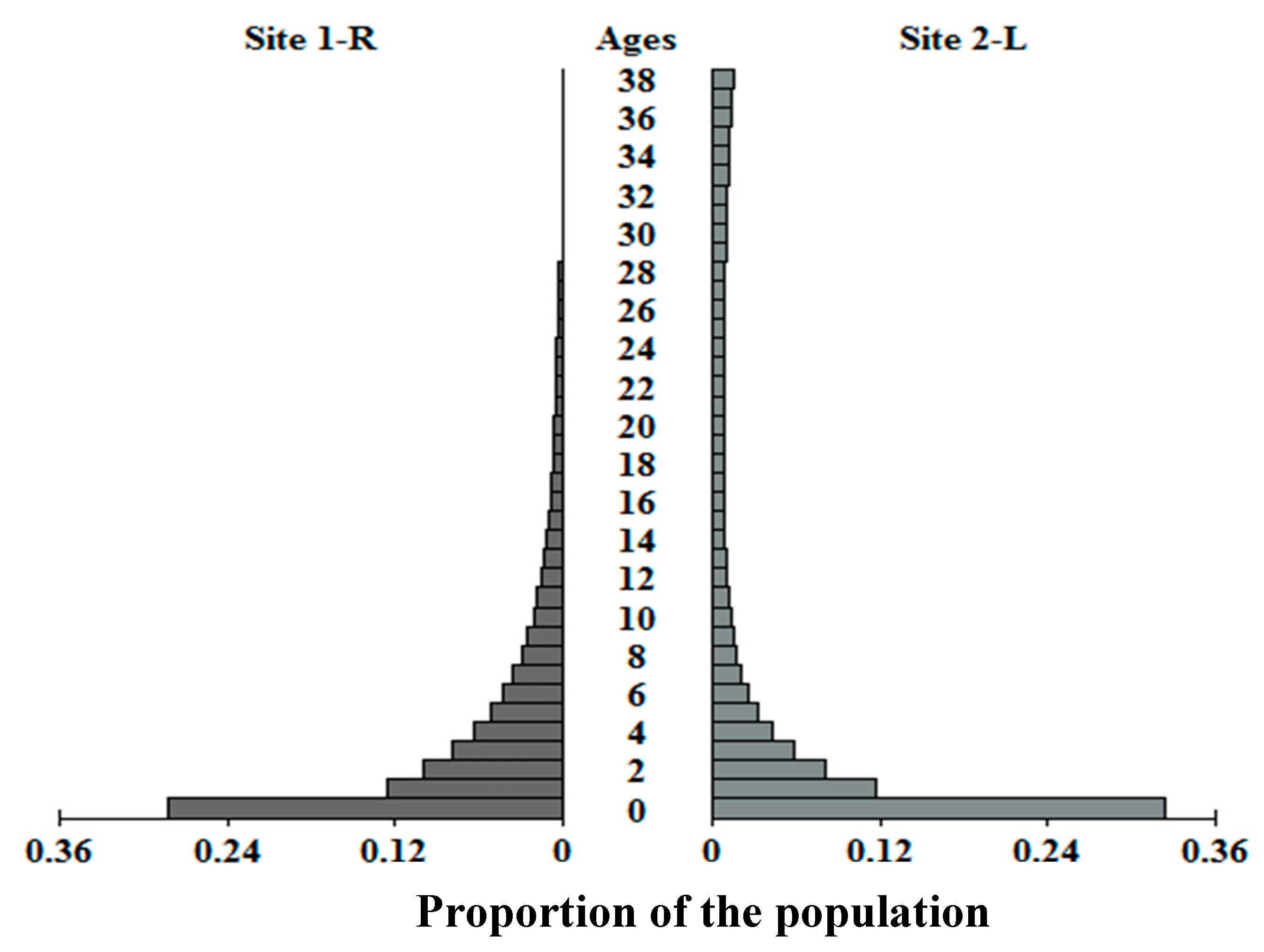
λ assumes the populations have achieved a stable age distribution. However, the damping ratio (
ρ), a measure of the rapidity of convergence on the stable age distribution (
n;
Figure 4), is low for each population (
ρ < 1.1). While low
ρ is expected for a long-lived species [
89], it also suggests
C. guttata recovers slowly from alterations to the age distribution. Illinois populations may be experiencing short-term growth over the length of the study (equal to 1–2 generation times) while equilibrating toward
n, but this growth is unlikely to be sustained.
The intraspecific variation between our highly proximate populations of
C. guttata suggests demographic plasticity is an adaptive response to site-specific challenges. However, we add the caveat that elasticity matrices derived from inaccurate estimates of vital rates over the short term [
11] or from changes in vital rates over time [
90] could lead to misprioritization of age classes to target for conservation. In our analysis, the incorrect ranking could be due to two main factors. First, ASRO based on size is likely more appropriate than age-based ASRO as size correlates more strongly with the onset of sexual maturity and clutch size in turtles [
91]. We recommend restructuring fecundity based on size classes and using regression analysis to relate size classes with age classes. Second, the large confidence intervals and high PRP (
Figure 4) for younger age classes, most noticeably at Site 1-R, suggest future research should focus on eggs, hatchlings, and juveniles [
37]. Major changes between current and future vital rates will likely be attributable to habitat improvements and can be recalculated to determine the efficacy of our recommendations to promote population growth. Moreover, it would be interesting to see if both populations respond to the same management actions to the same degree.
Our study indicates management actions targeting adult survival will have the greatest proportional impact on population growth rate. The other long-term study on
C. guttata in Ontario also found adult survival to be important [
15], so this is likely the case throughout the species range. In Illinois, adult survival likely needs to be increased at Site 1-R and at least maintained at Site 2-L. Preventing adult removal or mortality from collecting and roads will be beneficial. The variation in vital rates and relatively higher elasticity of juveniles at Site 1-R indicates a demographic divergence between populations. Thus, prioritization of vital rates can vary even over a small geographic area, so juvenile and age 0-1 survival cannot be totally ignored. In some cases, mesopredators can eliminate entire cohorts of turtles in isolated populations [
92]. If adult survival is known to be high and a population is still declining, management targeting juvenile or egg and hatchling survival could still be necessary. Caging nests and trapping mesopredators are effective methods to reduce predation of nests and juveniles [
93,
94]. Captive rearing and head-starting are more manipulative methods for recovering small, highly impacted populations [
24]. Though adults are more resilient to predation attempts than juveniles [
95] and often only lose limbs or accrue shell scours (pers. obs.), they may also benefit from fewer interactions with predators [
96,
97] or from allocating fewer resources to recovering from predator-induced injury [
98]. Thus, the removal of mesopredators would likely benefit all stages simultaneously. Increasing high-quality nesting habitat would also increase the number of surviving eggs and reduce predation risks to adult females [
99,
100].
Clemmys guttata inhabits a variety of shallow aquatic habitats in variable climates throughout the eastern United States, including swamps, bogs, fens, ephemeral pools, cattail marshes, sedge meadows, and drainage ditches [
60,
101]. Thus, habitat management aimed at increasing survival rate or population size should consider habitat characteristics and vegetation at a site-specific or regional scale. Our trapping indicates Illinois populations are limited to core habitat areas featuring necessary components, such as permanent shallow-water wetlands with overwintering burrows. These areas need to be carefully maintained at a minimum, and additional habitat restoration may be beneficial. For instance, at Site 2-L, we captured new individuals in a habitat that was restored in the late 1990s. However, at Site 1-R, changes in plant community composition have occurred in core habitats, with a pronounced expansion of
Typha spp. at the expense of more open
Carex wetlands. Expanding the amount of suitable habitat through restoration and management is particularly needed at Site 1-R to increase adult survival rates. The change in vegetation has also caused a drawdown of available standing water, perhaps contributing to lower survival rates and longevity. Given that wetlands inhabited by
C. guttata are already shallow, any additional lowering of water levels would greatly hinder conservation efforts. Controlled burns during the non-active season of
C. guttata can be used to help reverse unwanted successional trends in vegetation [
102].